Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures
Abstract
:1. Introduction
2. Formulation of Problem
3. Numerical Procedure
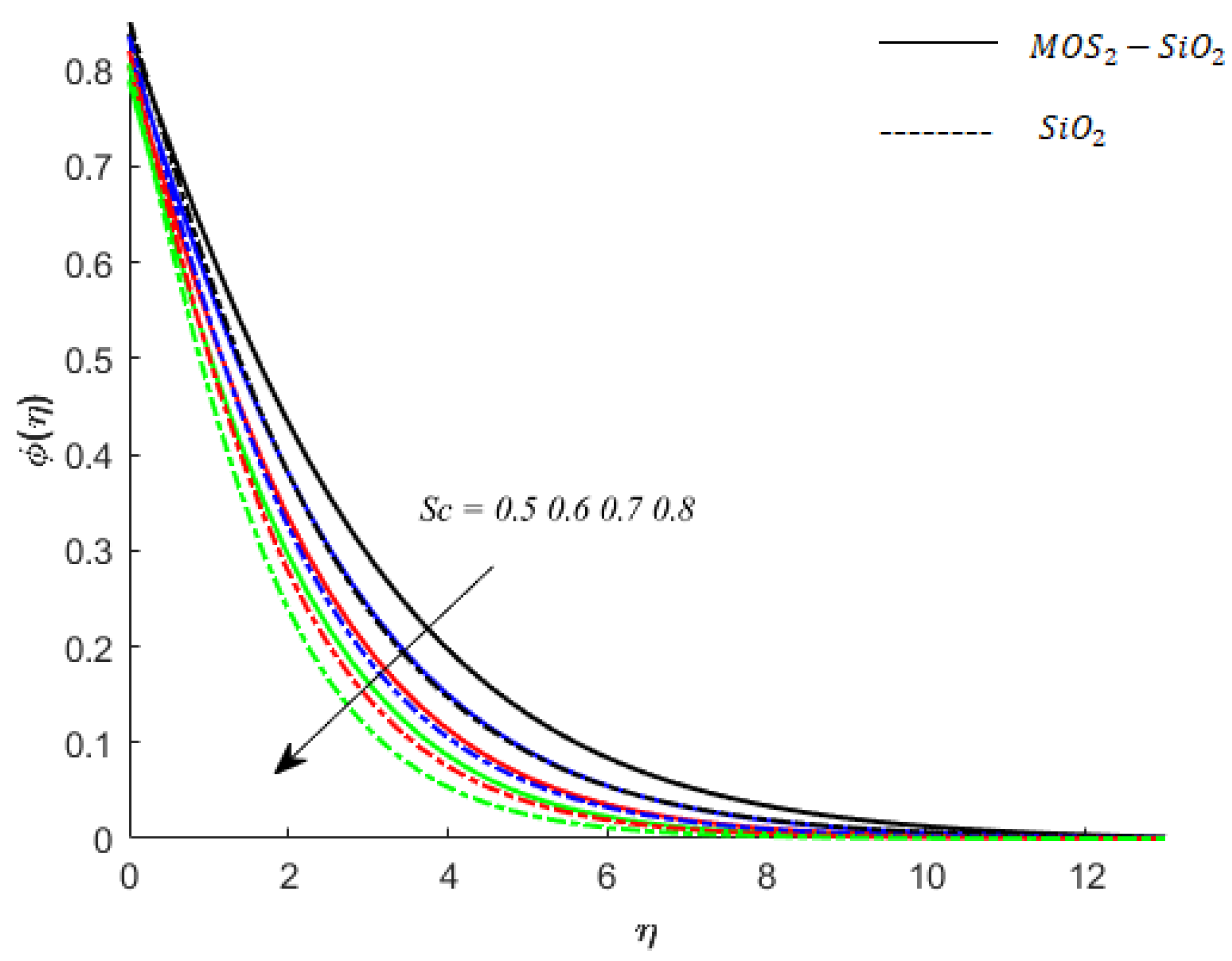
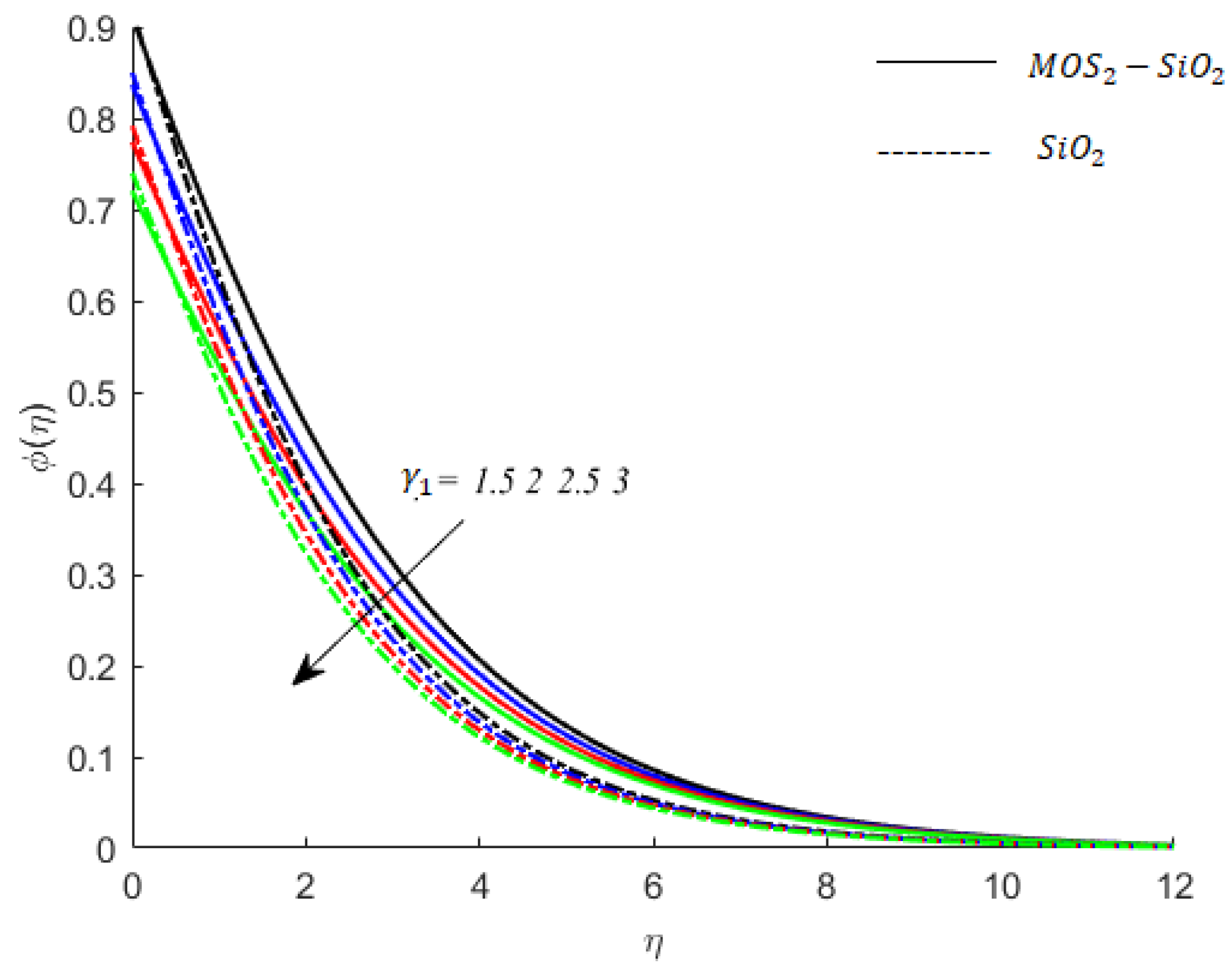
4. Results and Discussion
5. Conclusions
- FEM provides convergent solutions.
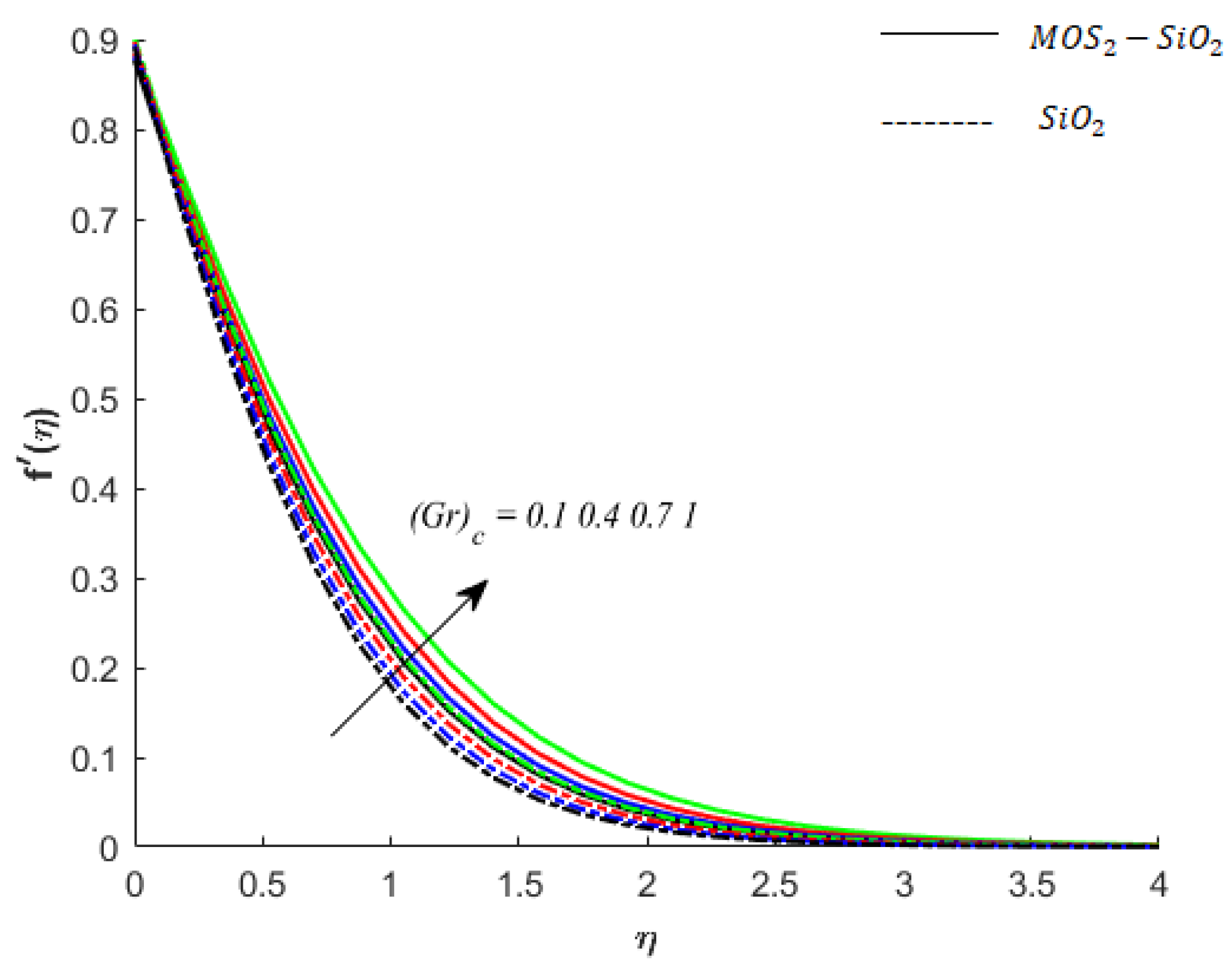
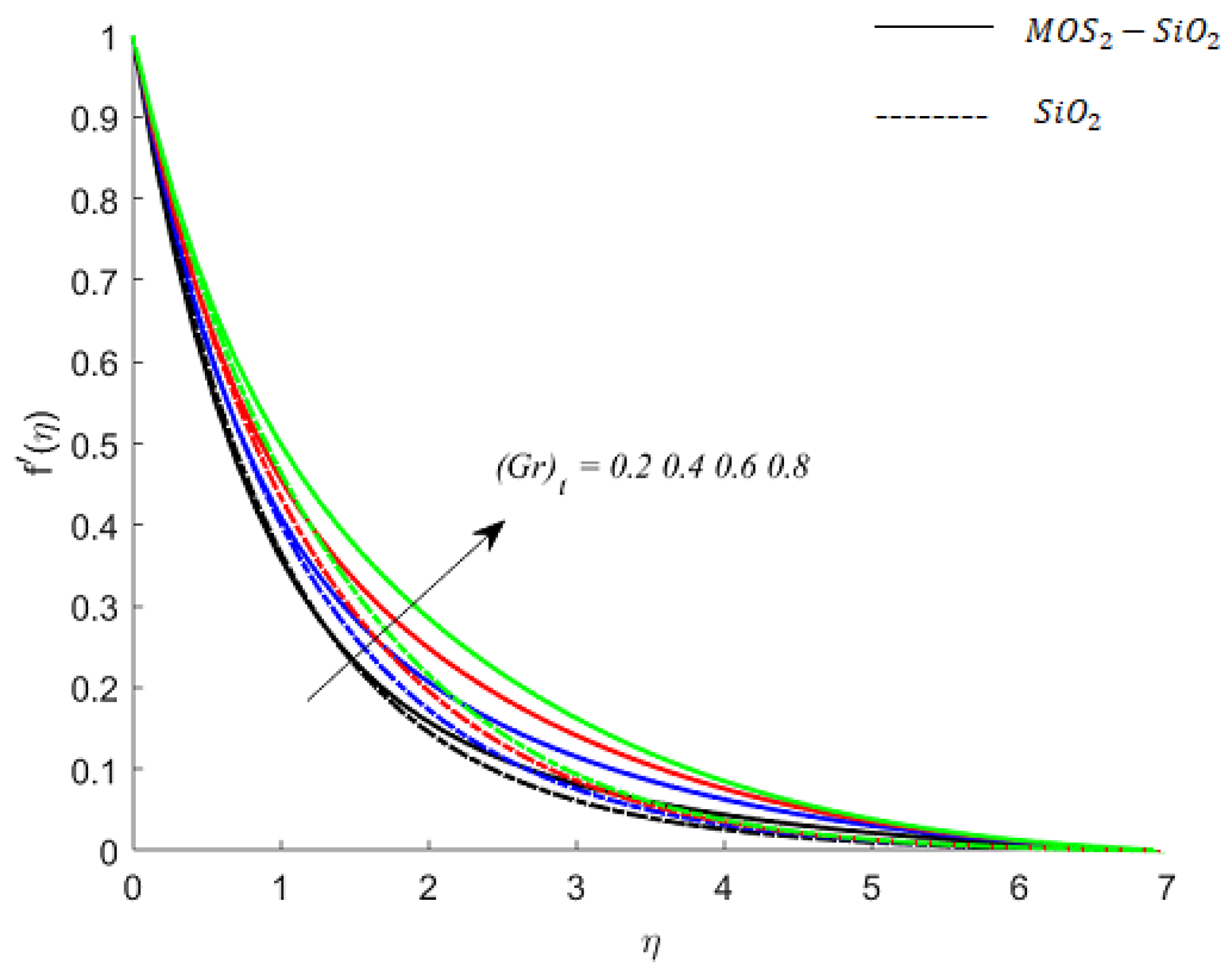
- The relaxation time phenomenon is responsible for the restoration of thermal and solutal changes, due to which, the thermal and solutal equilibrium states can be restored.
- The phenomenon of yield stress is responsible for controlling momentum boundary layer thickness.
- Porous medium exerts retarding force on the flow, and therefore, the deceleration inflow is observed.
- The thermal efficiency of Casson fluid is greater than the thermal efficiency of Casson fluid.
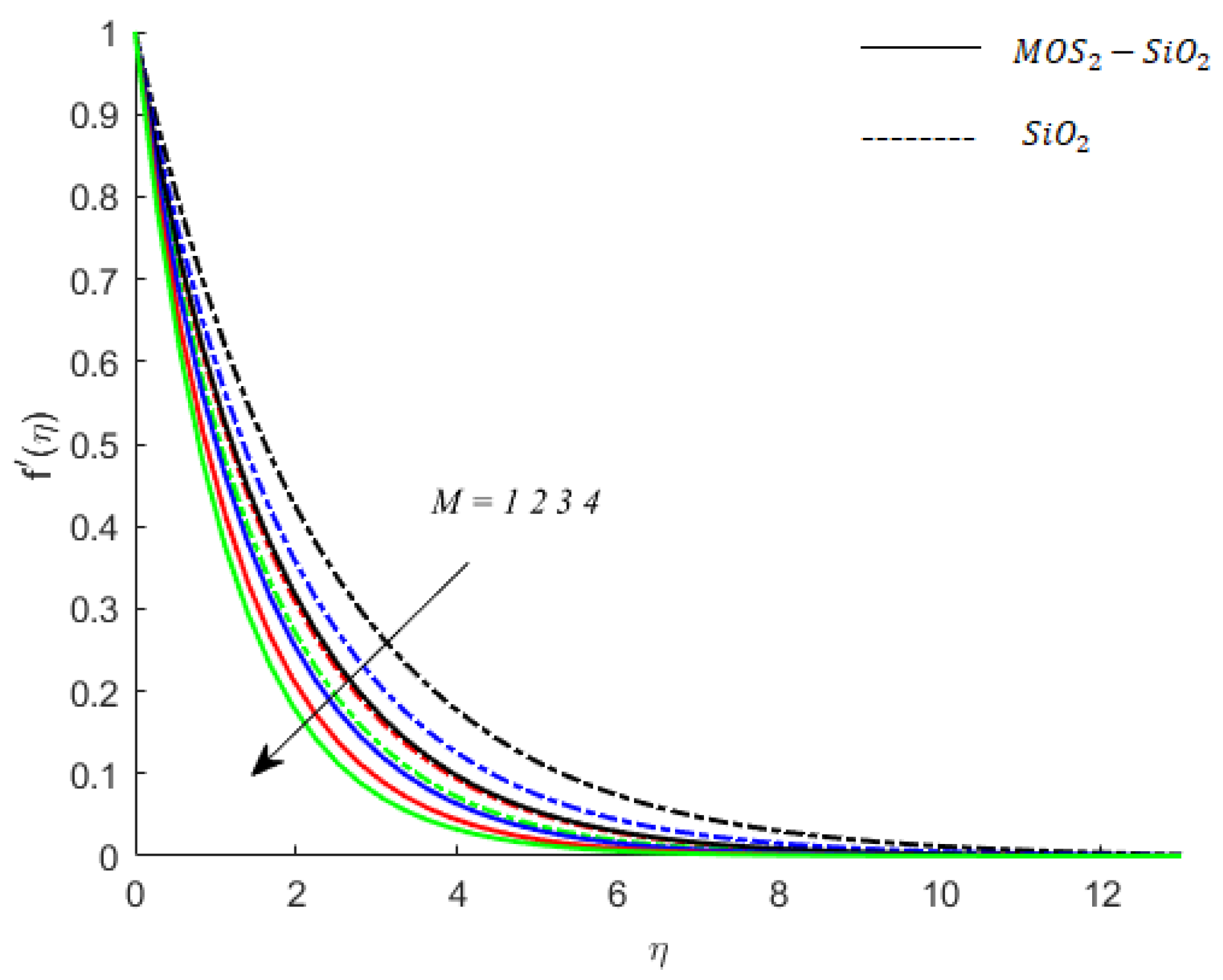
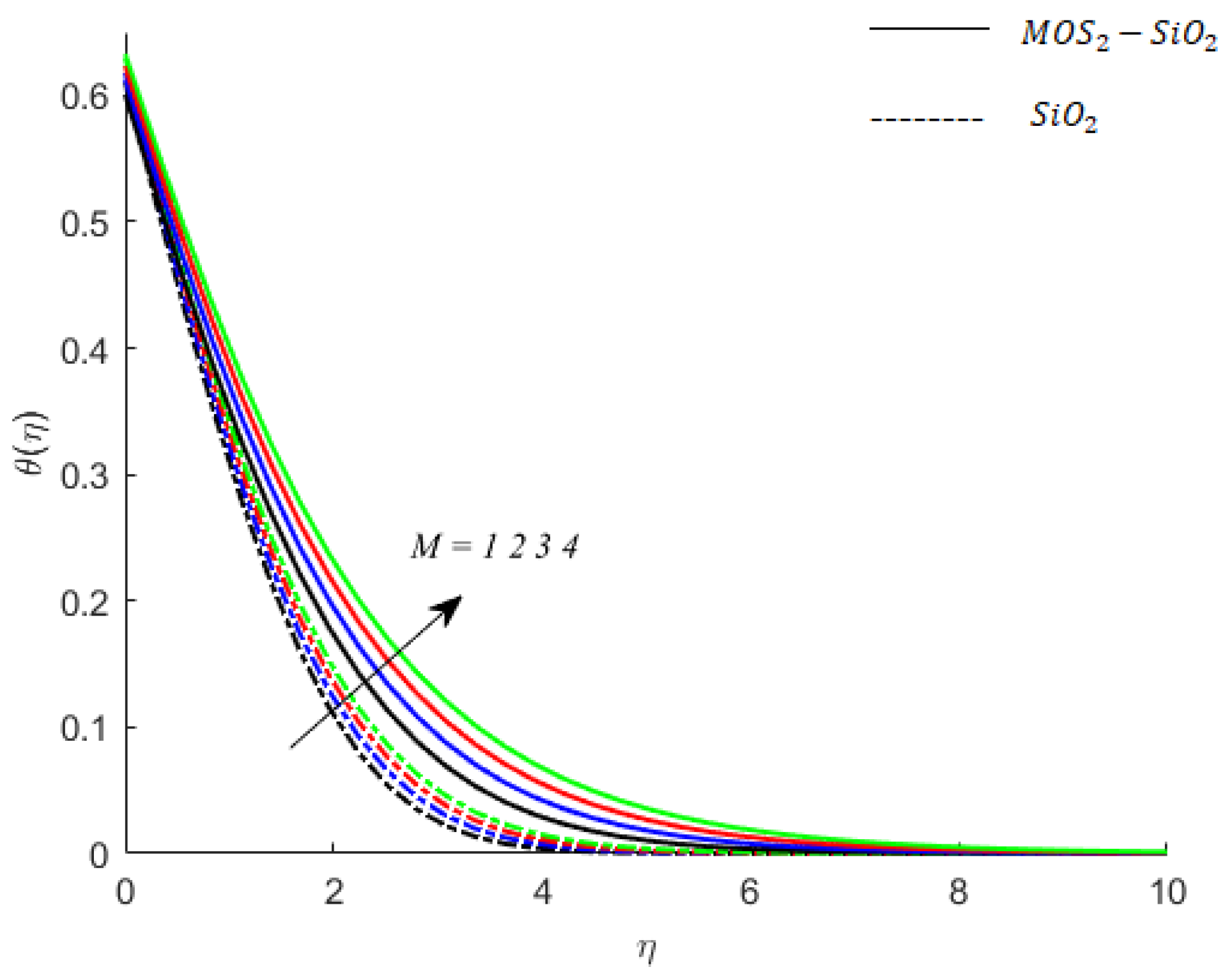
- The change in magnetic flux by the motion of the fluid particles results in a Lorentz force that opposes the flow, and the boundary layer thickness becomes shorter. It can be noticed also noticed that the Lorentz force associated with the motion of —nanofluid has a smaller magnitude relative to the Lorentz force induced by the motion of hybrid nanofluid (—nanofluid). Thus, the viscous region for momentum boundary layer flow nanofluid is wider than that for the flow of hybrid nanofluid.
- The vortex viscosity is responsible for decreasing the macromotion of fluid particles. Thus, velocity of Newtonian fluid is greater than the velocity of micropolar fluid. Further, the impact of vortex motion of solid structures in the fluid on velocity of nanofluid is negligible in comparison with the case of hybrid nanofluid.
- Joule heating associated with hybrid nanofluid flow has greater value in comparison with Joule heating in nanofluid. Thus, the temperature of hybrid nanofluid increases more rapidly than the temperature of nanofluid. Moreover, the Ohmic heating process in hybrid nanofluid is stronger than that in nanofluid.
- Viscous dissipation results an increase in temperature of the fluids (both mono- and hybrid nanofluids).
- The thermal relaxation time is responsible for decreasing the temperature of fluid. This is because of the ability of the fluid to restore thermal changes in order to attain thermal equilibrium.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | Abbreviation |
| The stretching rate of sheet | |
| Cauchy stress tensor | |
| Pressure | |
| Identity tensor | |
| Casson fluid | |
| Dynamic viscosity | |
| First Rivlin–Eriksen tensor | |
| Velocity component | |
| Temperature | |
| Concentration | |
| Gravitational acceleration | |
| Density | |
| Specific heat | |
| Thermal conductivity | |
| Hybrid nanofluid | |
| Mass diffusion coefficient | |
| Thermal relaxation time | |
| Concentration relaxation time | |
| Electrical conductivity | |
| Temperature at ambient position | |
| Concentration at ambient position | |
| Magnetic parameter | |
| Grashof number for temperature | |
| Grashof number for concentration | |
| Heat generation parameter | |
| Porous medium parameter | |
| Prandtl number | |
| Schmidt number | |
| Eckert number | |
| Dimensionless thermal relaxation time parameter | |
| Dimensionless concentration relaxation time parameter | |
| Biot number for heat and mass, respectively | |
| Skin friction | |
| Nusselt number | |
| Sherwood number | |
| Local Reynolds number | |
| Weight function | |
| Volume fraction | |
| Finite element method |
References
- Hamid, M.; Usman, M.; Khan, Z.; Ahmad, R.; Wang, W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys. Lett. A 2019, 383, 2400–2408. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Hayat, T.; Shehzad, S.A.; Alsaedi, A. Soret and Dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid. Appl. Math. Mech. 2012, 33, 1301–1312. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017, 498, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4-water nanofluid. Comput. Methods Appl. Mech. Eng. 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Seyednezhad, M. Nanofluid heat transfer in a permeable enclosure in presence of variable magnetic field by means of CVFEM. Int. J. Heat Mass Transf. 2017, 114, 1169–1180. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ganji, D.D. Thermal radiation effect on the nano-fluid buoyancy flow and heat transfer over a stretching sheet considering Brownian motion. J. Mol. Liq. 2016, 223, 521–527. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Chamkha, A.J.; Hashemi-Tilehnoee, M.; Seyyedi, S.M.; Haq, R.-U.; Ganji, D.D. Effects of homogeneous-heterogeneous reactions and thermal radiation on magneto-hydrodynamic Cu-water nanofluid flow over an expanding flat plate with non-uniform heat source. J. Cent. South Univ. 2019, 26, 1161–1171. [Google Scholar] [CrossRef]
- Ayub, M.; Malik, M.Y.; Ijaz, M.; AlQarni, M.S.; Alqahtani, A.S. Cattaneo–Christov double-diffusion model for viscoelastic nanofluid with activation energy and nonlinear thermal radiation. Multidiscip. Model. Mater. Struct. 2019, 16, 93–120. [Google Scholar] [CrossRef]
- Rana, S.; Nawaz, M. Investigation of enhancement of heat transfer in Sutterby nanofluid using Koo–Kleinstreuer and Li (KKL) correlations and Cattaneo–Christov heat flux model. Phys. Scr. 2019, 94, 115213. [Google Scholar] [CrossRef]
- Ahmed, S.; Xu, H. Forced convection with unsteady pulsating flow of a hybrid nanofluid in a microchannel in the presence of EDL, magnetic and thermal radiation effects. Int. Commun. Heat Mass Transf. 2021, 120, 105042. [Google Scholar] [CrossRef]
- Iftikhar, N.; Rehman, A.; Sadaf, H. Theoretical investigation for convective heat transfer on Cu/water nanofluid and (SiO2-copper)/water hybrid nanofluid with MHD and nanoparticle shape effects comprising relaxation and contraction phenomenon. Int. Commun. Heat Mass Transf. 2021, 120, 105012. [Google Scholar] [CrossRef]
- Benkhedda, M.; Boufendi, T.; Tayebi, T.; Chamkha, A.J. Convective heat transfer performance of hybrid nanofluid in a horizontal pipe considering nanoparticles shapes effect. J. Therm. Anal. Calorim. 2019, 140, 411–425. [Google Scholar] [CrossRef]
- Aziz, A.; Jamshed, W.; Aziz, T.; Bahaidarah, H.M.S.; Rehman, K.U. Entropy analysis of Powell–Eyring hybrid nanofluid including effect of linear thermal radiation and viscous dissipation. J. Therm. Anal. Calorim. 2021, 143, 1331–1343. [Google Scholar] [CrossRef]
- Subhani, M.; Nadeem, S. Numerical investigation into unsteady magnetohydrodynamics flow of micropolar hybrid nanofluid in porous medium. Phys. Scr. 2019, 94, 105220. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer along a permeable stretching/shrinking curved surface in a hybrid nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]
- Kaneez, H.; Nawaz, M.; Alaoui, M.K.; Abdelmalek, Z. An enhancement in transportation of heat energy in yield stress dusty fluid via mono and hybrid nanoparticles. Phys. Scr. 2020, 95, 085216. [Google Scholar] [CrossRef]
- Nawaz, M.; Rana, S.; Qureshi, I.H.; Hayat, T. Three-dimensional heat transfer in the mixture of nanoparticles and micropolar MHD plasma with Hall and ion slip effects. AIP Adv. 2018, 8, 105109. [Google Scholar] [CrossRef] [Green Version]
- Nawaz, M.; Hayat, T.; Alsaedi, A. Dufour and Soret effects on MHD flow of viscous fluid between radially stretching sheets in porous medium. Appl. Math. Mech. 2012, 33, 1403–1418. [Google Scholar] [CrossRef]
- Arif, U.; Nawaz, M.; Alharbi, S.O.; Saleem, S. Investigation on the impact of thermal performance of fluid due to hybrid nano-structures. J. Therm. Anal. Calorim. 2021, 144, 729–737. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Influence of Lorentz forces on nanofluid flow in a porous cylinder considering Darcy model. J. Mol. Liq. 2017, 225, 903–912. [Google Scholar] [CrossRef]
- Rehman, K.U.; Saba, N.U.; Zehra, I.; Malik, M.Y.; Bilal, S.M. Numerical study of thermal radiations and thermal stratification mechanisms in magnetohydrodynamic casson fluid-flow. Therm. Sci. 2020, 24, 1093–1104. [Google Scholar] [CrossRef]
- Awais, M.; Awan, S.E.; Raja, M.A.Z.; Parveen, N.; Khan, W.U.; Malik, M.Y.; He, Y. Effects of variable transport properties on heat and mass transfer in MHD bioconvective nanofluid rheology with gyrotactic microorganisms: Numerical approach. Coatings 2021, 11, 231. [Google Scholar] [CrossRef]
- Pal, D. Heat and mass transfer in stagnation-point flow towards a stretching surface in the presence of buoyancy force and thermal radiation. Meccanica 2008, 44, 145–158. [Google Scholar] [CrossRef]
- Liu, X.; Xu, X.; Liu, C.; Ye, J.; Li, H.; Bai, W.; Dang, C. Numerical study of the effect of buoyancy force and centrifugal force on heat transfer characteristics of supercritical CO2 in helically coiled tube at various inclination angles. Appl. Therm. Eng. 2017, 116, 500–515. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D.G.-D.; Rana, P.; Soleimani, S. Magnetohydrodynamic free convection of Al2O3–water nanofluid considering Thermophoresis and Brownian motion effects. Comput. Fluids 2014, 94, 147–160. [Google Scholar] [CrossRef]
- Kandasamy, R.; Muhaimin, I.; Mohamad, R. Thermophoresis and Brownian motion effects on MHD boundary-layer flow of a nanofluid in the presence of thermal stratification due to solar radiation. Int. J. Mech. Sci. 2013, 70, 146–154. [Google Scholar] [CrossRef] [Green Version]
- Makinde, O.; Animasaun, I. Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. J. Mol. Liq. 2016, 221, 733–743. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, Y. Effects of Brownian motion and thermophoresis on nanofluids in a rotating circular groove: A numerical simulation. Int. J. Heat Mass Transf. 2018, 123, 569–582. [Google Scholar] [CrossRef]
- Animasaun, I.; Adebile, E.; Fagbade, A. Casson fluid flow with variable thermo-physical property along exponentially stretching sheet with suction and exponentially decaying internal heat generation using the homotopy analysis method. J. Niger. Math. Soc. 2016, 35, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Alruwashid, F.S.; Dar, M.A.; Alharthi, N.H.; Abdo, H.S. Effect of graphene concentration on the electrochemical properties of cobalt ferrite nanocomposite materials. Nanomaterials 2021, 11, 2523. [Google Scholar] [CrossRef]
- Pal, N.; Sunwoo, Y.; Park, J.-S.; Kim, T.; Cho, E.-B. Newly designed mesoporous silica and organosilica nanostructures based on pentablock copolymer templates in weakly acidic media. Nanomaterials 2021, 11, 2522. [Google Scholar] [CrossRef]
- Nasr, O.; Jiang, J.-R.; Chuang, W.-S.; Lee, S.-W.; Chen, C.-Y. Ag nanoparticle-decorated Cu2S nanosheets for surface enhanced raman spectroscopy detection and photocatalytic applications. Nanomaterials 2021, 11, 2508. [Google Scholar] [CrossRef]
- Zemtsova, E.G.; Yurchuk, D.V.; Morozov, P.E.; Korusenko, P.M.; Kudymov, V.K.; Smirnov, V.M. Features of the synthesis of the dispersed TiC phase with nickel nanostructures on the surface to create an aluminum-based metal composite. Nanomaterilas 2021, 11, 2499. [Google Scholar] [CrossRef]


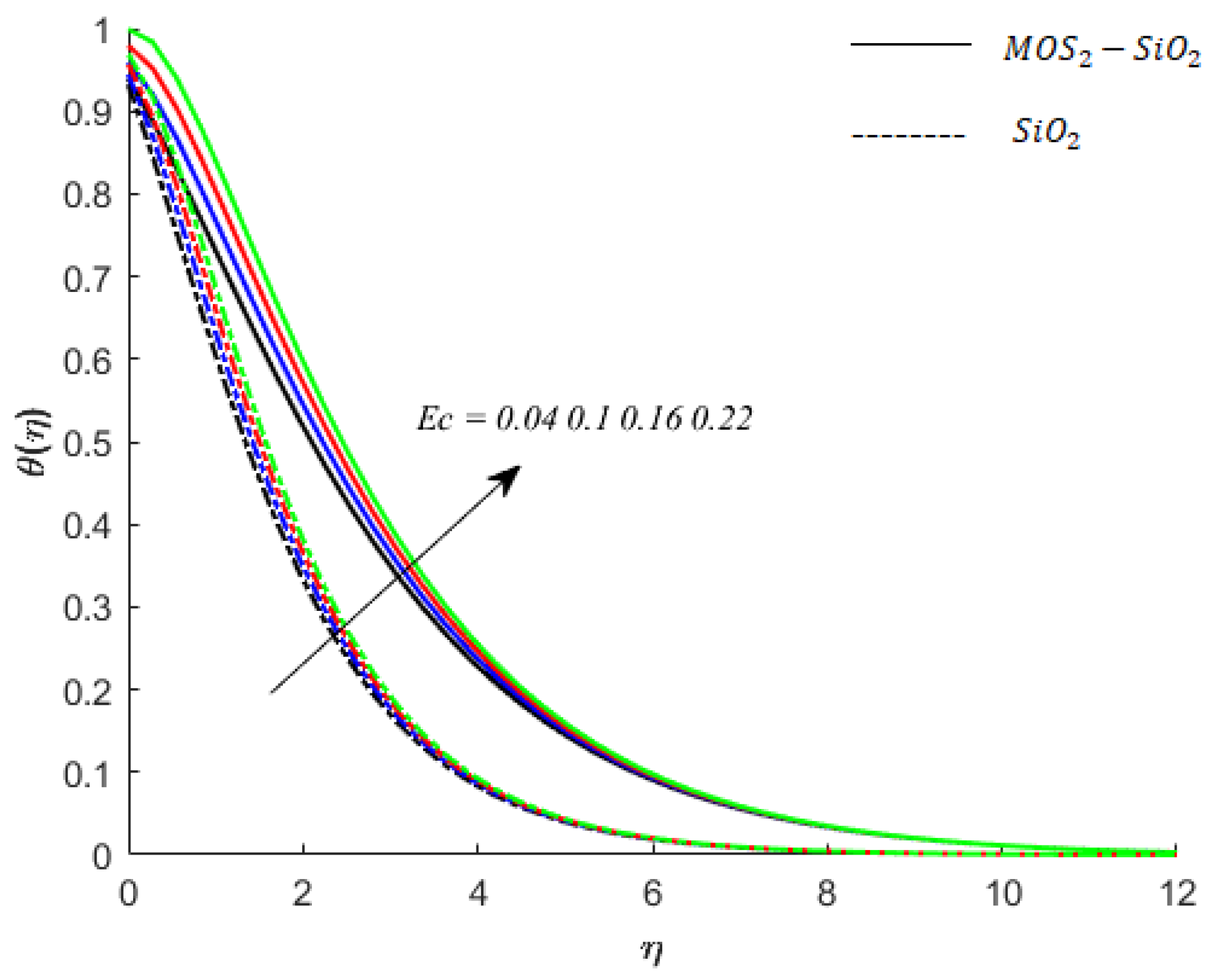
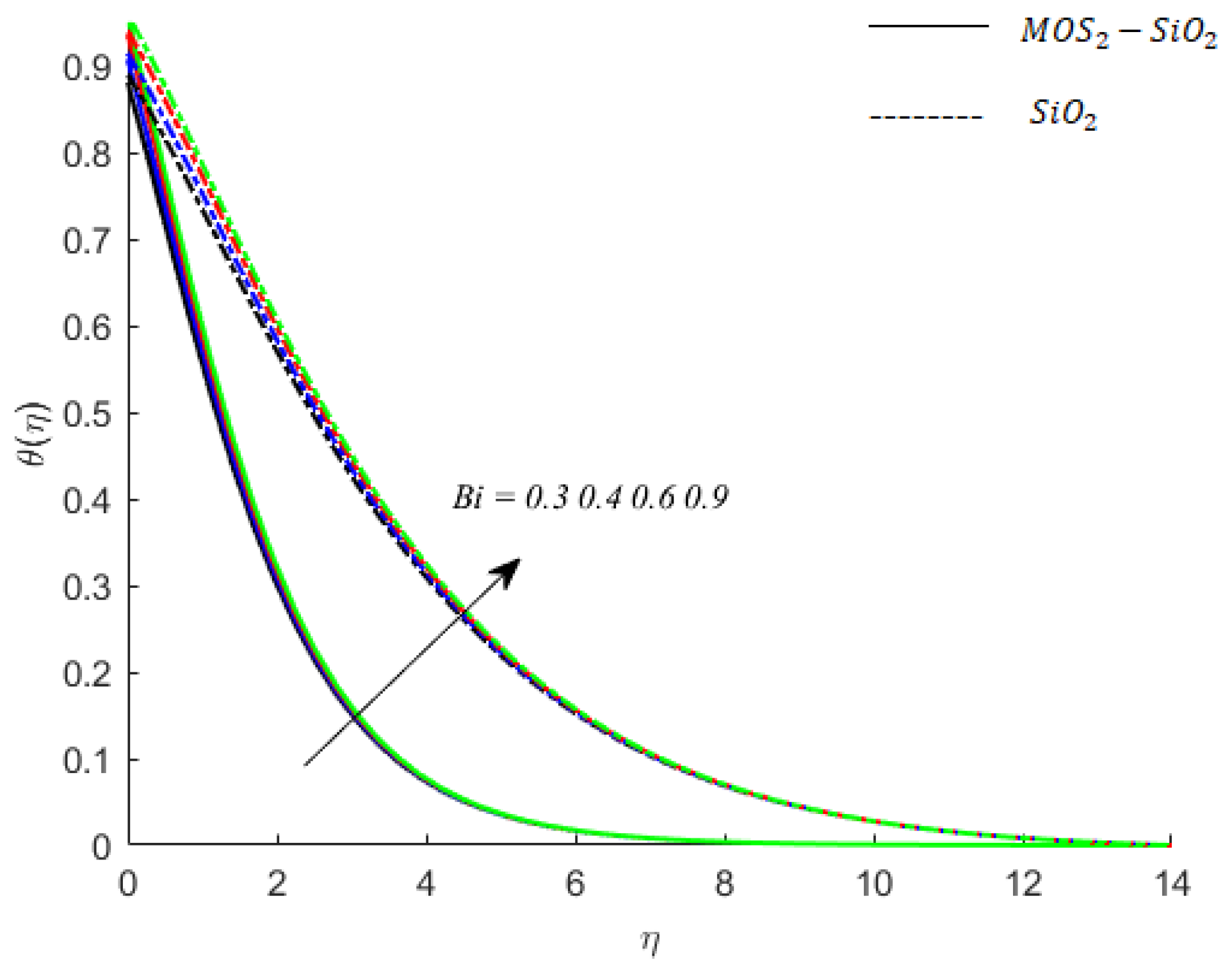
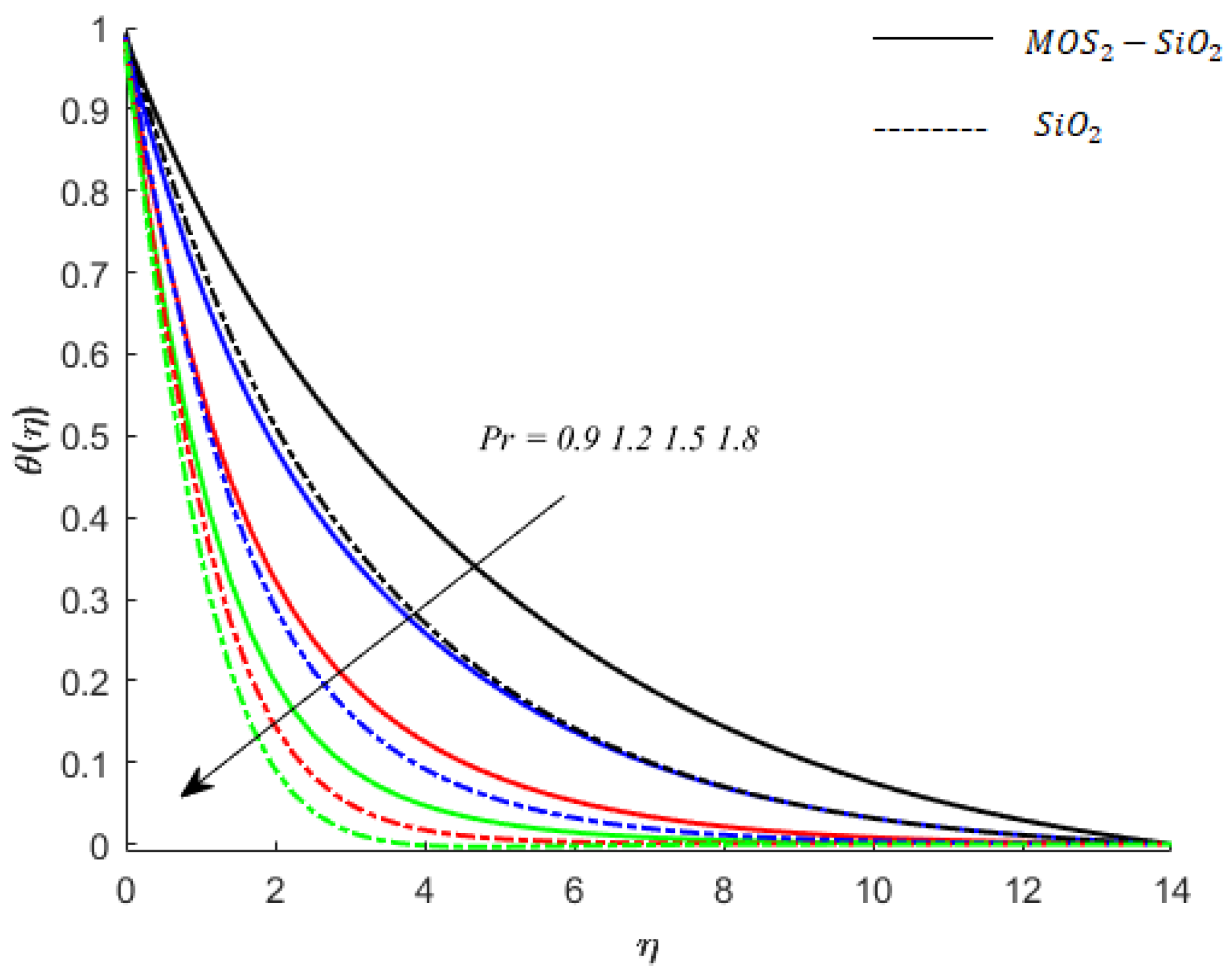
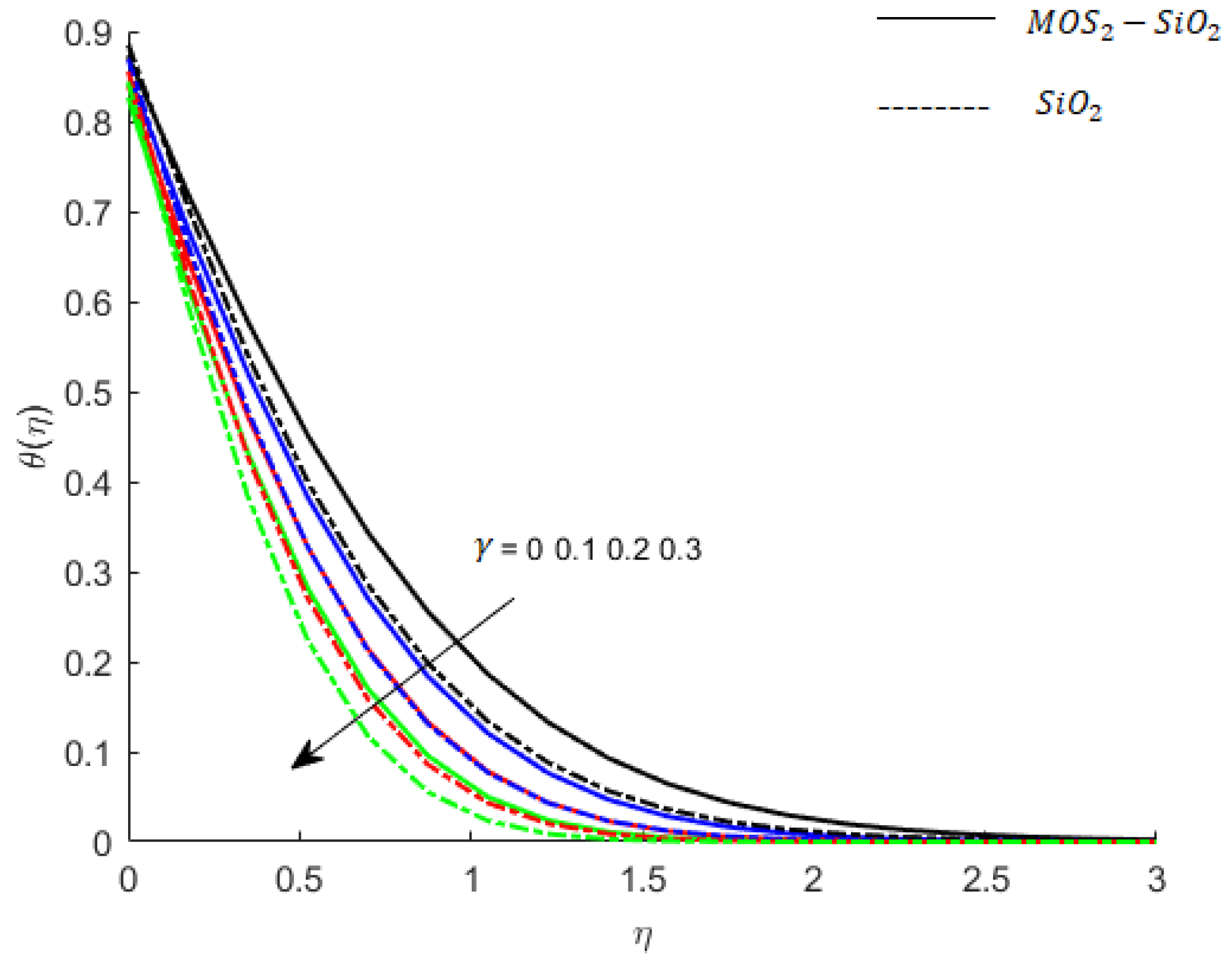
| Physical Property | Blood/Base Fluid | ||
|---|---|---|---|
| 0.0 | 0.05 | 0.25 | |
| 1060 | 5060 | 2200 | |
| 0.429 | 34.5 | 1.2 | |
| 3770 | 397.746 | 703 | |
| e | |||
|---|---|---|---|
| 10 | 2.6528312 | 0.3647946 | 0.3346214 |
| 50 | 2.9699726 | 0.3553285 | 0.3265893 |
| 100 | 2.9864624 | 0.3547900 | 0.3261574 |
| 150 | 2.9897546 | 0.3546829 | 0.3260747 |
| 200 | 2.9909392 | 0.3546445 | 0.3260456 |
| 250 | 2.9914955 | 0.3546265 | 0.3260320 |
| 300 | 2.9918005 | 0.3546166 | 0.3260247 |
| 350 | 2.9919856 | 0.3546106 | 0.3260202 |
| 400 | 2.9921062 | 0.3546067 | 0.3260173 |
| 450 | 2.9921892 | 0.3546040 | 0.3260153 |
| 500 | 2.9922388 | 0.3546021 | 0.3260139 |
| 550 | 2.9922630 | 0.3546007 | 0.3260129 |
| 600 | 2.9922866 | 0.3545001 | 0.3260121 |
| Pr | Aninasaun et al. [35] | Present Work |
|---|---|---|
| 1 | 0.67650698 | 0.6751263 |
| 2 | 1.07352135 | 1.0755124 |
| 3 | 1.38075427 | 1.3808321 |
| 0.3 | 2.983196 | 0.332254 | 0.327839 | 1.550508 | 0.331809 | 0.274995 | |
| 0.4 | 2.975124 | 0.346307 | 0.327080 | 1.547106 | 0.343833 | 0.273122 | |
| 0.6 | 2.966398 | 0.361610 | 0.326245 | 1.543475 | 0.356726 | 0.271111 | |
| 0.9 | 2.960175 | 0.372594 | 0.325640 | 1.540915 | 0.365853 | 0.269686 | |
| 0.9 | 2.969972 | 0.355328 | 0.326589 | 1.544956 | 0.351459 | 0.271933 | |
| 1.2 | 2.982838 | 0.407449 | 0.318419 | 1.556270 | 0.426194 | 0.254630 | |
| 1.5 | 2.995592 | 0.462848 | 0.310154 | 1.565150 | 0.492608 | 0.239609 | |
| 1.8 | 3.007677 | 0.518502 | 0.302151 | 1.572221 | 0.551755 | 0.226381 | |
| 0.2 | 2.931015 | 0.008746 | 0.371463 | 1.532676 | 0.171288 | 0.313080 | |
| 0.4 | 2.659066 | 0.058366 | 0.376682 | 1.409872 | 0.199231 | 0.315051 | |
| 0.6 | 2.401254 | 0.094303 | 0.381388 | 1.292906 | 0.220905 | 0.317027 | |
| 0.8 | 2.152702 | 0.121027 | 0.385802 | 1.180107 | 0.238387 | 0.318995 | |
| 0.8 | 3.091709 | 0.228875 | 0.401115 | 1.597960 | 0.235893 | 0.352285 | |
| 0.7 | 3.082004 | 0.215412 | 0.404166 | 1.594813 | 0.226250 | 0.355104 | |
| 0.6 | 3.071976 | 0.201547 | 0.407300 | 1.591568 | 0.216313 | 0.357992 | |
| 0.5 | 3.061600 | 0.187249 | 0.410520 | 1.588223 | 0.206071 | 0.360951 | |
| 3.0 | 2.994940 | 0.086758 | 0.511548 | 1.568195 | 0.132043 | 0.467676 | |
| 2.5 | 2.992579 | 0.088335 | 0.486832 | 1.566804 | 0.134235 | 0.442385 | |
| 2.0 | 2.990092 | 0.089963 | 0.461265 | 1.565340 | 0.136479 | 0.416249 | |
| 1.5 | 2.987473 | 0.091642 | 0.434826 | 1.563799 | 0.138768 | 0.389274 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiq, M.A.; Bahaidarah, H.M.S. Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures. Nanomaterials 2021, 11, 2675. https://doi.org/10.3390/nano11102675
Sadiq MA, Bahaidarah HMS. Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures. Nanomaterials. 2021; 11(10):2675. https://doi.org/10.3390/nano11102675
Chicago/Turabian StyleSadiq, Muhammad A., and Haitham M. S. Bahaidarah. 2021. "Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures" Nanomaterials 11, no. 10: 2675. https://doi.org/10.3390/nano11102675
APA StyleSadiq, M. A., & Bahaidarah, H. M. S. (2021). Numerical Study on Generalized Heat and Mass in Casson Fluid with Hybrid Nanostructures. Nanomaterials, 11(10), 2675. https://doi.org/10.3390/nano11102675





