Dimension-Dependent Bandgap Narrowing and Metallization in Lead-Free Halide Perovskite Cs3Bi2X9 (X = I, Br, and Cl) under High Pressure
Abstract
:1. Introduction
2. Computational Model and Method
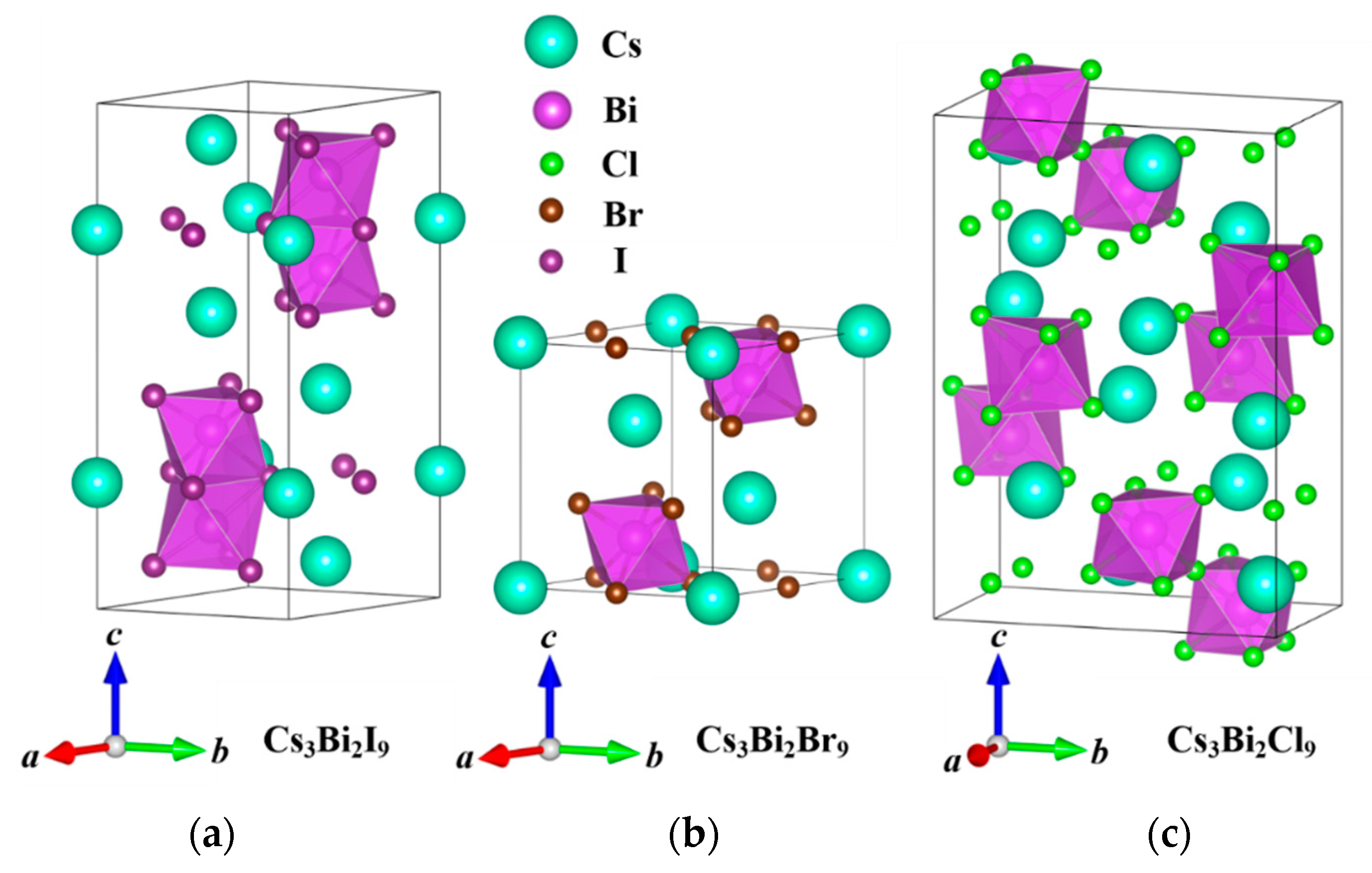
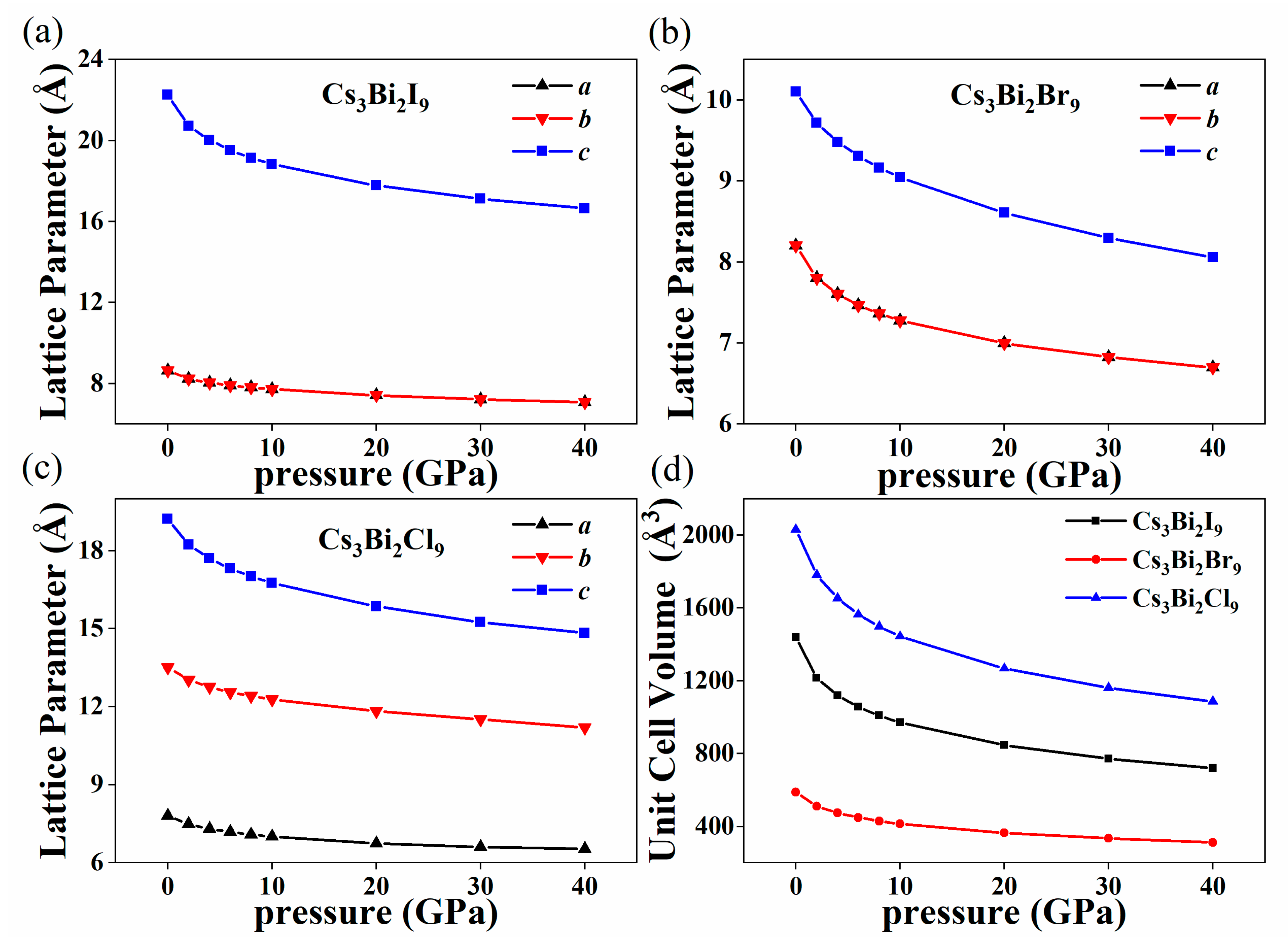
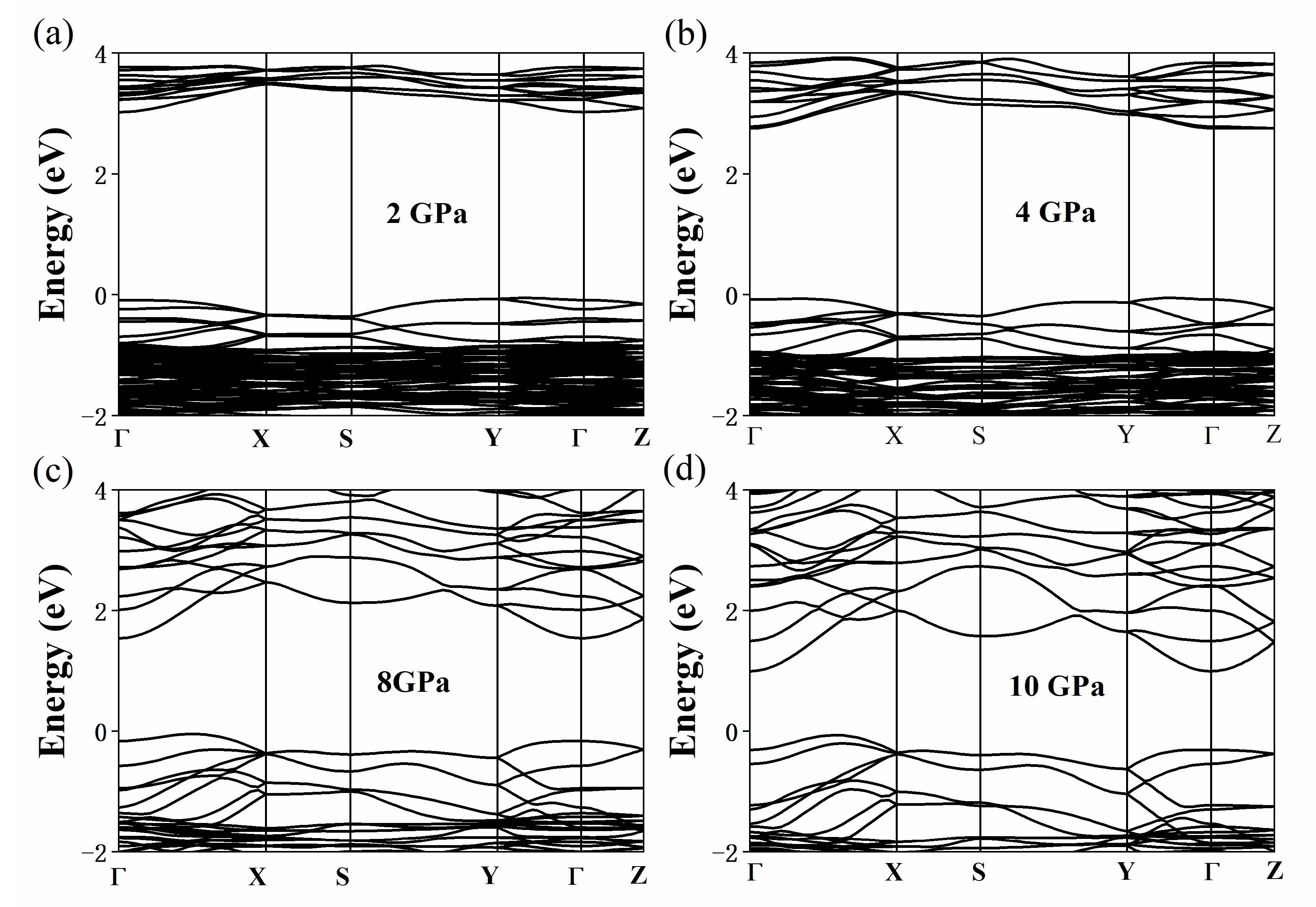
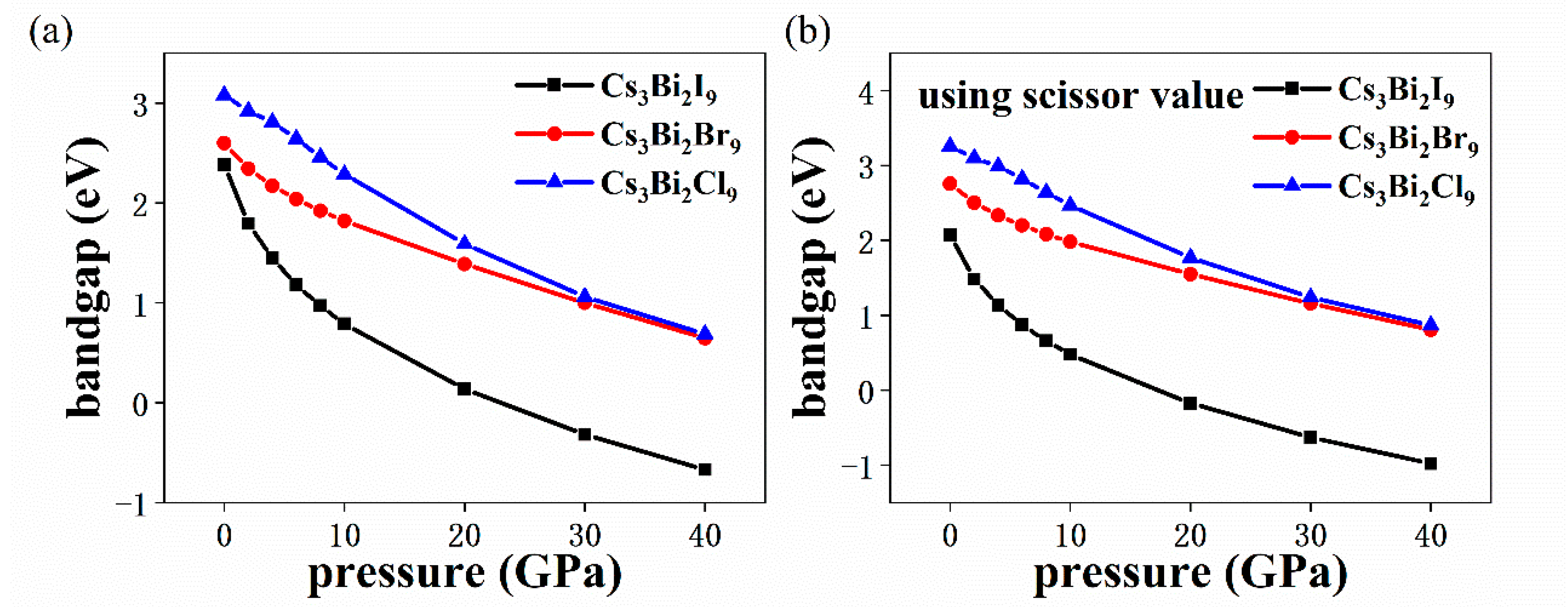
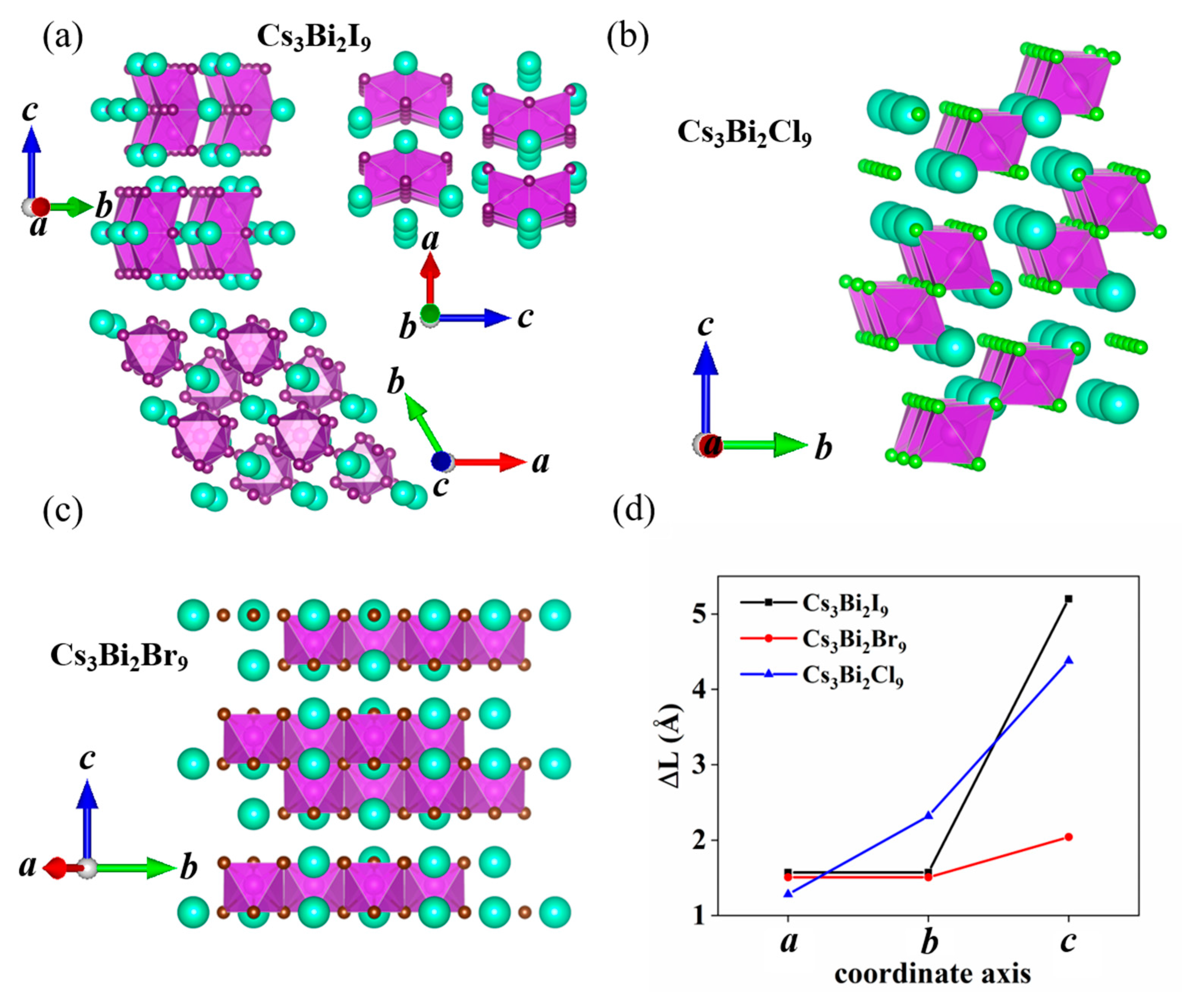
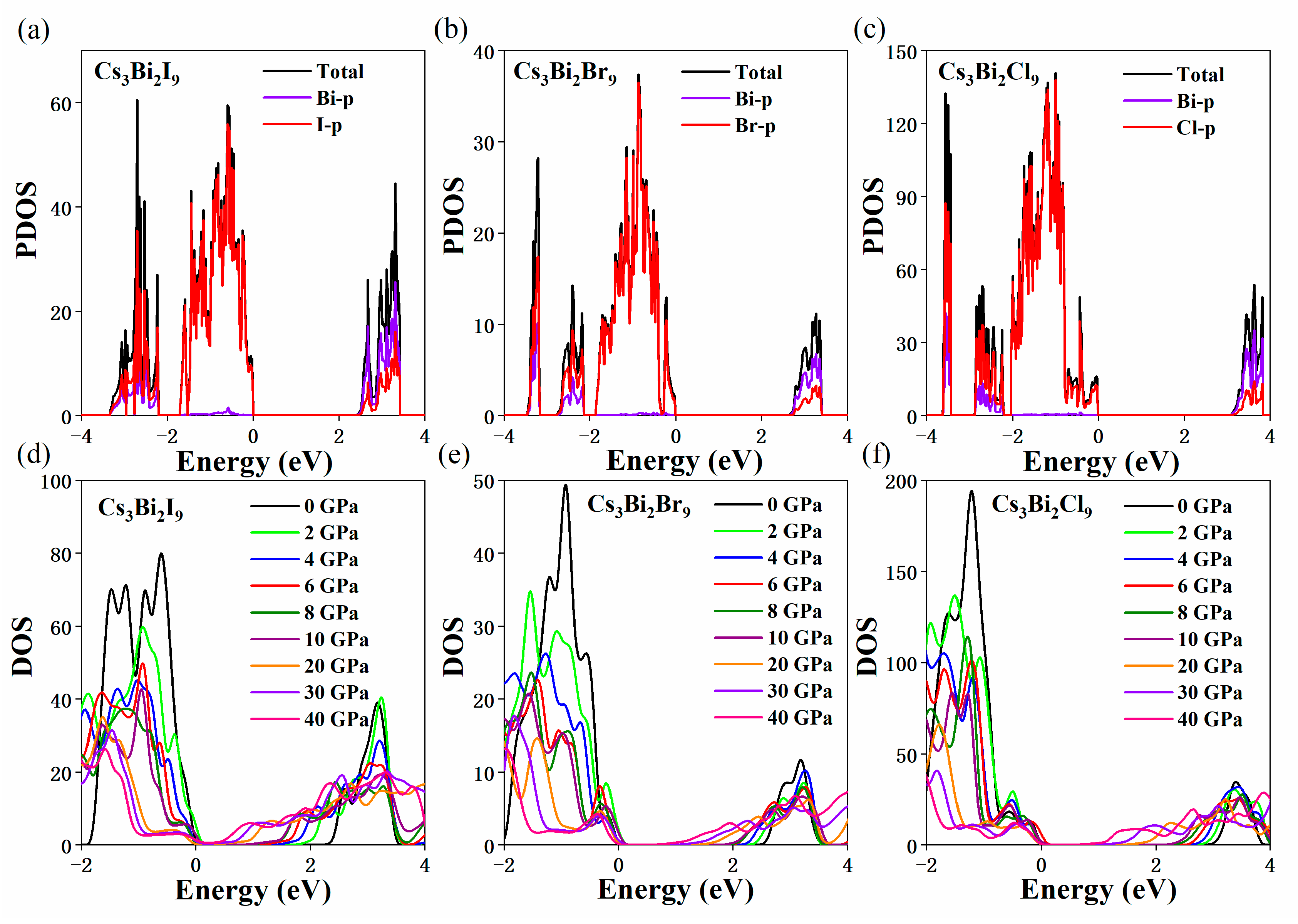
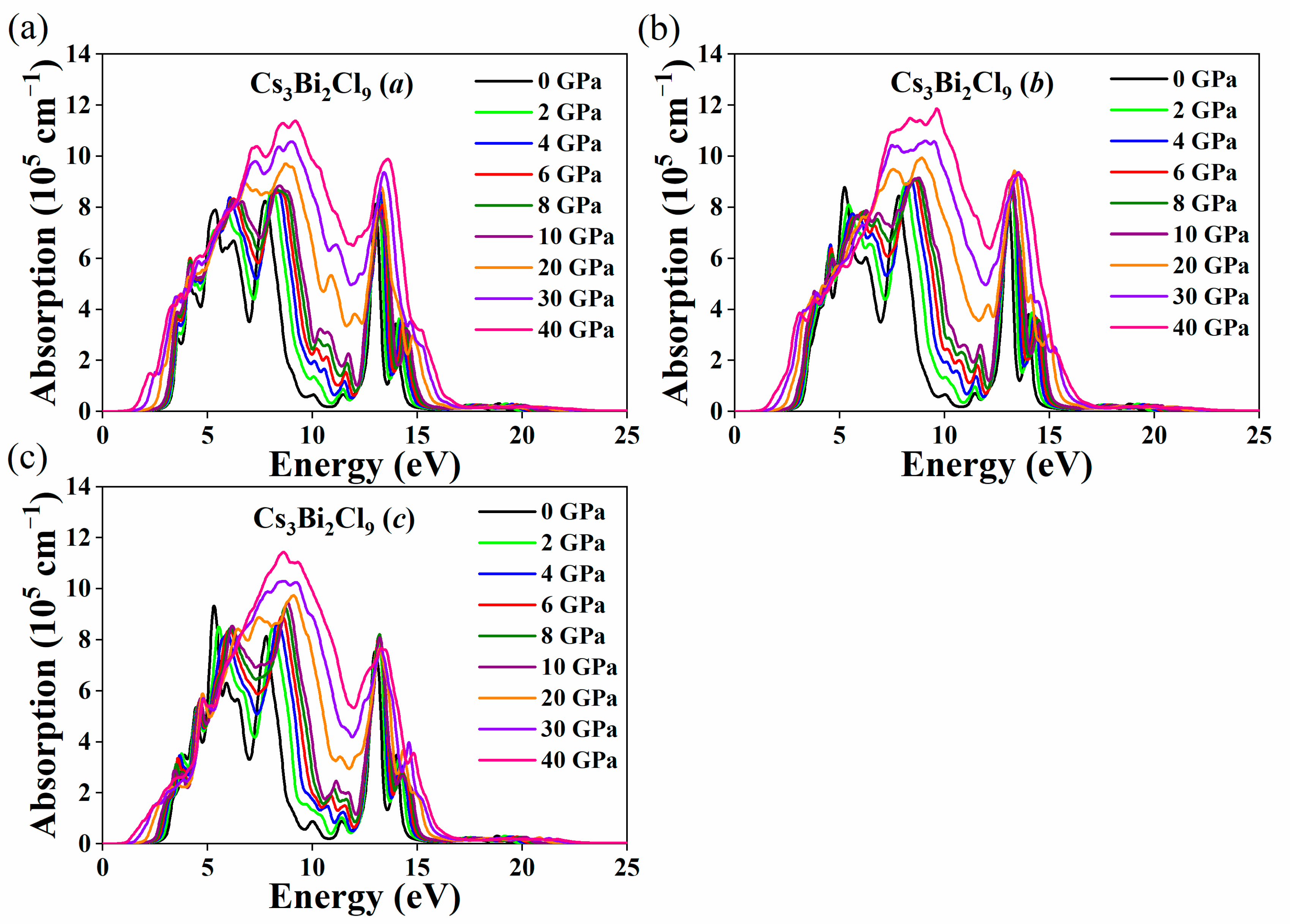
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Xu, W.; Bai, S.; Jin, Y.; Wang, J.; Friend, R.H.; Gao, F. Metal halide perovskites for light-emitting diodes. Nat. Mater. 2021, 20, 10–21. [Google Scholar] [CrossRef]
- Jia, Y.; Kerner, R.A.; Grede, A.J.; Rand, B.P.; Giebink, N.C. Continuous-wave lasing in an organic-inorganic lead halide semiconductor. Nat. Photonics 2017, 11, 784–788. [Google Scholar] [CrossRef]
- Lin, K.; Xing, J.; Quan, L.; Arquer, F.P.G.; Gong, X.; Lu, J.; Xie, L.; Zhao, W.; Zhang, D.; Yan, C.; et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature 2018, 562, 245–248. [Google Scholar] [CrossRef]
- Chen, B.; Baek, S.W.; Hou, Y.; Aydin, E.; Bastiani, M.D.; Scheffel, B.; Proppe, A.; Huang, Z.; Wei, M.; Wang, Y.; et al. Enhanced optical path and electron diffusion length enable high-efficiency perovskite tandems. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Leng, K.; Abdelwahab, I.; Verzhbitskiy, I.; Telychko, M.; Chu, L.; Fu, W.; Chi, X.; Guo, N.; Chen, Z.; Chen, Z.; et al. Molecularly thin two-dimensional hybrid perovskites with tunable optoelectronic properties due to reversible surface relaxation. Nat. Mater. 2018, 17, 908–914. [Google Scholar] [CrossRef]
- Shao, H.; Bai, X.; Cui, H.; Pan, G.; Jing, P.; Qu, S.; Zhu, J.; Zhai, Y.; Dong, B.; Song, H. White light emission in Bi3+/Mn2+ ion co-doped CsPbCl3 perovskite nanocrystals. Nanoscale 2018, 10, 1023–1029. [Google Scholar] [CrossRef]
- Yang, S.; Chen, S.; Mosconi, E.; Fang, Y.; Xiao, X.; Wang, C.; Zhou, Y.; Yu, Z.; Zhao, J.; Gao, Y.; et al. Stabilizing halide perovskite surfaces for solar cell operation with wide-bandgap lead oxysalts. Science 2019, 365, 473–478. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Guo, X.; Lin, Z.; Ma, J.; Su, J.; Hu, Z.; Zhang, C.; Liu, S.; Chang, J.; Hao, Y. Interface engineering of low temperature processed all-inorganic CsPbI2Br perovskite solar cells toward PCE exceeding 14%. Nano Energy 2019, 60, 583–590. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Tang, S.; Bing, J.; Zheng, J.; Tang, J.; Li, Y.; Mayyas, M.; Cho, Y.; Jones, T.W.; Yang, T.C.J.; Yuan, L.; et al. Complementary bulk and surface passivations for highly efficient perovskite solar cells by gas quenching. Cell Rep. Phys. Sci. 2021, 2, 100511. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Hong, F.; Mao, X.; Zheng, K.; Yang, S.; Li, Y.; Pullerits, T.; Deng, W.; Han, K. Lead-Free, Air-Stable All-Inorganic Cesium Bismuth Halide Perovskite Nanocrystals. Angew. Chem. Int. Ed. 2017, 56, 12471–12475. [Google Scholar] [CrossRef]
- Leng, M.; Yang, Y.; Zeng, K.; Chen, Z.; Tan, Z.; Li, S.; Li, J.; Xu, B.; Li, D.; Hautzinger, M.P.; et al. All-Inorganic Bismuth-Based Perovskite Quantum Dots with Bright Blue Photoluminescence and Excellent Stability. Adv. Funct. Mater. 2017, 28, 1704446. [Google Scholar] [CrossRef]
- Lou, Y.; Fang, M.; Chen, J.; Zhao, Y. Formation of highly luminescent cesium bismuth halide perovskite quantum dots tuned by anion exchange. Chem. Commun. 2018, 54, 3779–3782. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Z.; Li, L.; Zhang, J.; Zhu, J. An Improved Strategy for High-Quality Cesium Bismuth Bromine Perovskite Quantum Dots with Remarkable Electrochemiluminescence Activities. Anal. Chem. 2019, 91, 8607–8614. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Shi, Z.; Wang, L.; Zhang, F.; Wu, D.; Yang, D.; Chen, X.; Zhang, Y.; Shan, C.; Li, X. Water-induced fluorescence enhancement of lead-free cesium bismuth halide quantum dots by 130% for stable white light-emitting devices. Nanoscale 2020, 12, 3637–3645. [Google Scholar] [CrossRef]
- Ji, Z.; Liu, Y.; Li, W.; Zhao, C.; Mai, W. Reducing current fluctuation of Cs3Bi2Br9 perovskite photodetectors for diffuse reflection imaging with wide dynamic range. Sci. Bull. 2020, 65, 1371–1379. [Google Scholar] [CrossRef]
- Gu, J.; Yan, G.; Lian, Y.; Mu, Q.; Jin, H.; Zhang, Z.; Deng, Z.; Peng, Y. Bandgap engineering of a lead-free defect perovskite Cs3Bi2I9 through trivalent doping of Ru3+. RSC Adv. 2018, 8, 25802–25807. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Le, Q.V.; Kim, H.; Lee, Y.J.; Lee, D.E.; Im, I.H.; Lee, M.K.; Kim, S.J.; Kim, J.; Kwak, K.J.; et al. Lead-Free Dual-Phase Halide Perovskites for Preconditioned Conducting-Bridge Memory. Small 2020, 16, 2003225. [Google Scholar] [CrossRef]
- Liu, D.; Yu, B.; Liao, M.; Jin, Z.; Zhou, L.; Zhang, X.; Wang, F.; He, H.; Gatti, T.; He, Z. Self-powered and broadband lead-free inorganic perovskite photodetector with high stability. ACS Appl. Mater. Interfaces 2020, 12, 30530–30537. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Liao, J.; Jiang, Y.; Kuang, D. Enhanced On–Off Ratio Photodetectors Based on Lead-Free Cs3Bi2I9 Single Crystal Thin Films. Adv. Funct. Mater. 2020, 30, 1909701. [Google Scholar] [CrossRef]
- Khadka, D.B.; Shirai, Y.; Yanagida, M.; Miyano, K. Tailoring the film morphology and interface band offset of caesium bismuth iodide-based Pb-free perovskite solar cells. J. Mater. Chem. C 2019, 7, 8335–8343. [Google Scholar] [CrossRef]
- Johansson, M.B.; Philippe, B.; Banerjee, A.; Phuyal, D.; Mukherjee, S.; Chakraborty, S.; Cameau, M.; Zhu, H.; Ahuja, R.; Boschloo, G.; et al. Cesium Bismuth Iodide Solar Cells from Systematic Molar Ratio Variation of CsI and BiI3. Inorg. Chem. 2019, 58, 12040–12052. [Google Scholar] [CrossRef]
- Ge, S.; Guan, X.; Wang, Y.; Lin, C.; Cui, Y.; Huang, Y.; Zhang, X.; Zhang, R.; Yang, X.; Wu, T. Low-Dimensional Lead-Free Inorganic Perovskites for Resistive Switching with Ultralow Bias. Adv. Funct. Mater. 2020, 30, 2002110. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Xu, Z.; Ye, H.; Yang, Z.; You, J.; Liu, M.; He, Y.; Kanatzidis, M.G.; Liu, S. Nucleation-controlled growth of superior lead-free perovskite Cs3Bi2I9 single-crystals for high-performance X-ray detection. Nat. Commun. 2020, 11, 1–11. [Google Scholar]
- Hu, Y.; Zhang, S.; Miao, X.; Su, L.; Bai, F.; Qiu, T.; Liu, J.; Yuan, G. Ultrathin Cs3Bi2I9 Nanosheets as an Electronic Memory Material for Flexible Memristors. Adv. Mater. Interfaces 2017, 4, 1700131. [Google Scholar] [CrossRef]
- Liang, J.; Fang, Q.; Wang, H.; Xu, R.; Jia, S.; Guan, Y.; Ai, Q.; Gao, G.; Guo, H.; Shen, K.; et al. Perovskite-Derivative Valleytronics. Adv. Mater. 2020, 32, 2004111. [Google Scholar] [CrossRef]
- Samanta, D.; Saha, P.; Ghosh, B.; Chaudhary, S.P.; Bhattacharyya, S.; Chatterjee, S.; Mukherjee, G.D. Pressure-Induced Emergence of Visible Luminescence in Lead Free Halide Perovskite Cs3Bi2Br9: Effect of Structural Distortion. J. Phys. Chem. C 2021, 125, 3432–3440. [Google Scholar] [CrossRef]
- Nagaoka, Y.; Hills-Kimball, K.; Tan, R.; Li, R.; Wang, Z.; Chen, O. Nanocube Superlattices of Cesium Lead Bromide Perovskites and Pressure-Induced Phase Transformations at Atomic and Mesoscale Levels. Adv. Mater. 2017, 29, 1606666. [Google Scholar] [CrossRef]
- Lü, X.; Wang, Y.; Stoumpos, C.C.; Hu, Q.; Guo, X.; Chen, H.; Yang, L.; Smith, J.S.; Yang, W.; Zhao, Y.; et al. Enhanced Structural Stability and Photo Responsiveness of CH3NH3SnI3 Perovskite via Pressure-Induced Amorphization and Recrystallization. Adv. Mater. 2016, 28, 8663–8668. [Google Scholar] [CrossRef] [Green Version]
- Postorino, P.; Malavasi, L. Pressure-Induced Effects in Organic−Inorganic Hybrid Perovskites. J. Phys. Chem. Lett. 2017, 8, 2613–2622. [Google Scholar] [CrossRef]
- Szafranski, M.; Katrusiak, A. Mechanism of Pressure-Induced Phase Transitions, Amorphization, and Absorption-Edge Shift in Photovoltaic Methylammonium Lead Iodide. J. Phys. Chem. Lett. 2016, 7, 3458–3466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Zeng, Q.; Wang, K. Pressure-Induced Structural and Optical Properties of Inorganic Halide Perovskite CsPbBr3. J. Phys. Chem. Lett. 2017, 8, 3752–3758. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lü, X.; Yang, W.; Wen, T.; Yang, L.; Ren, X.; Wang, L.; Lin, Z.; Zhao, Y. Pressure-Induced Phase Transformation, Reversible Amorphization, and Anomalous Visible Light Response in Organolead Bromide Perovskite. J. Am. Chem. Soc. 2015, 137, 11144–11149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, C.; Wang, L.; Liu, C.; Wang, K.; Zou, B. Pressure-Induced Emission Enhancement, Band Gap Narrowing and Metallization of Halide Perovskite Cs3Bi2I9. Angew. Chem. Int. Ed. 2018, 57, 11213–11217. [Google Scholar] [CrossRef]
- Geng, T.; Wei, S.; Zhao, W.; Ma, Z.; Fu, R.; Xiao, G.; Zou, B. Insight into the structure–property relationship of two-dimensional lead-free halide perovskite Cs3Bi2Br9 nanocrystals under pressure. Inorg. Chem. Front. 2021, 8, 1410–1415. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Islam, J.; Hossain, A. Semiconducting to metallic transition with outstanding optoelectronic properties of CsSnCl3 perovskite under pressure. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Morgan, E.E.; Mao, L.; Teicher, S.M.L.; Wu, G.; Seshadri, R. Tunable Perovskite-Derived Bismuth Halides: Cs3Bi2(Cl1−xIx)9. Inorg. Chem. 2020, 59, 3387–3393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khoram, P.; Brittman, S.; Dzik, W.I.; Reek, J.N.H.; Garnett, E.C. Growth and Characterization of PDMS-Stamped Halide Perovskite Single Microcrystals. J. Phys. Chem. C 2016, 120, 6475–6481. [Google Scholar] [CrossRef]
- Creutz, S.E.; Liu, H.; Kaiser, M.E.; Li, X.; Gamelin, D.R. Structural Diversity in Cesium Bismuth Halide Nanocrystals. Chem. Mater. 2019, 31, 4685–4697. [Google Scholar] [CrossRef]
- Ghosh, B.; Chakraborty, S.; Wei, H.; Guet, C.; Li, S.; Mhaisalkar, S.; Mathews, N. Poor Photovoltaic Performance of Cs3Bi2I9: An Insight through First Principles Calculations. J. Phys. Chem. C 2017, 121, 17062–17067. [Google Scholar] [CrossRef]
- Bass, K.K.; Estergreen, L.; Savory, C.N.; Buckeridge, J.; Scanlon, D.O.; Djurovich, P.I.; Bradforth, S.E.; Thompson, M.E.; Melot, B.C. Vibronic Structure in Room Temperature Photoluminescence of the Halide Perovskite Cs3Bi2Br9. Inorg. Chem. 2017, 56, 42–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiang, G.; Wu, Y.; Li, Y.; Cheng, C.; Leng, J.; Ma, H. Structural and Optoelectronic Properties of Two-Dimensional Ruddlesden–Popper Hybrid Perovskite CsSnBr3. Nanomaterials 2021, 11, 2119. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, G.; Wu, Y.; Zhang, M.; Cheng, C.; Leng, J.; Ma, H. Dimension-Dependent Bandgap Narrowing and Metallization in Lead-Free Halide Perovskite Cs3Bi2X9 (X = I, Br, and Cl) under High Pressure. Nanomaterials 2021, 11, 2712. https://doi.org/10.3390/nano11102712
Xiang G, Wu Y, Zhang M, Cheng C, Leng J, Ma H. Dimension-Dependent Bandgap Narrowing and Metallization in Lead-Free Halide Perovskite Cs3Bi2X9 (X = I, Br, and Cl) under High Pressure. Nanomaterials. 2021; 11(10):2712. https://doi.org/10.3390/nano11102712
Chicago/Turabian StyleXiang, Guangbiao, Yanwen Wu, Man Zhang, Chen Cheng, Jiancai Leng, and Hong Ma. 2021. "Dimension-Dependent Bandgap Narrowing and Metallization in Lead-Free Halide Perovskite Cs3Bi2X9 (X = I, Br, and Cl) under High Pressure" Nanomaterials 11, no. 10: 2712. https://doi.org/10.3390/nano11102712
APA StyleXiang, G., Wu, Y., Zhang, M., Cheng, C., Leng, J., & Ma, H. (2021). Dimension-Dependent Bandgap Narrowing and Metallization in Lead-Free Halide Perovskite Cs3Bi2X9 (X = I, Br, and Cl) under High Pressure. Nanomaterials, 11(10), 2712. https://doi.org/10.3390/nano11102712





