Thermal Transfer Characteristics of Flat Plate Micro Heat Pipe with Copper Spiral Woven Mesh and a Copper Foam Composite Wick
Abstract
:1. Introduction
2. CW-FMHP Structural Design and Preparation
2.1. CW-FMHP Structure
2.2. Two-Phase Flow Characteristics
2.2.1. Pressure Balance
2.2.2. Composite Wick Wettability
- 1.
- The composite wick was ultrasonically cleaned in methanol and ethanol solution in turn for 10 min to remove the oil from the surface. Any subsequent operations were carried out with clean tweezers to prevent oil contamination;
- 2.
- The composite wick was ultrasonically cleaned with 1 mol/L HCl solution in a constant temperature chamber at 50 C for 5 min and rinsed clean with deionized water;
- 3.
- The composite wick was then sealed in 125 mL of 30 %wt HO and ultrasonicated for 15 min, placed in a constant temperature chamber at 100 C for 3 h;
- 4.
- It was finally rinsed with deionized water and dried in a drying chamber at 70 C.
2.3. Heat Transfer Power Analysis
2.4. CW-FMHP Preparation
3. CW-FMHP Performance Test
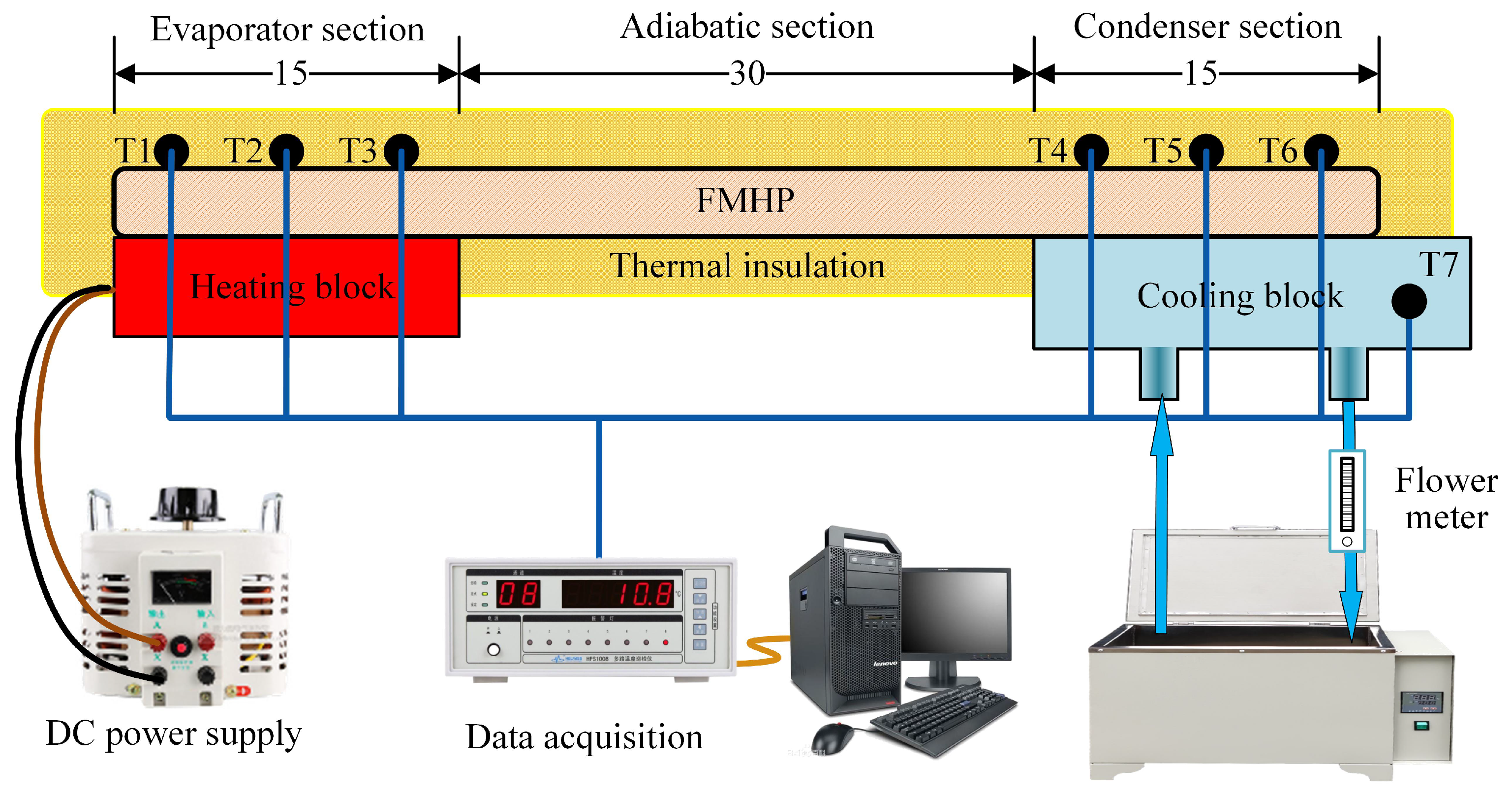
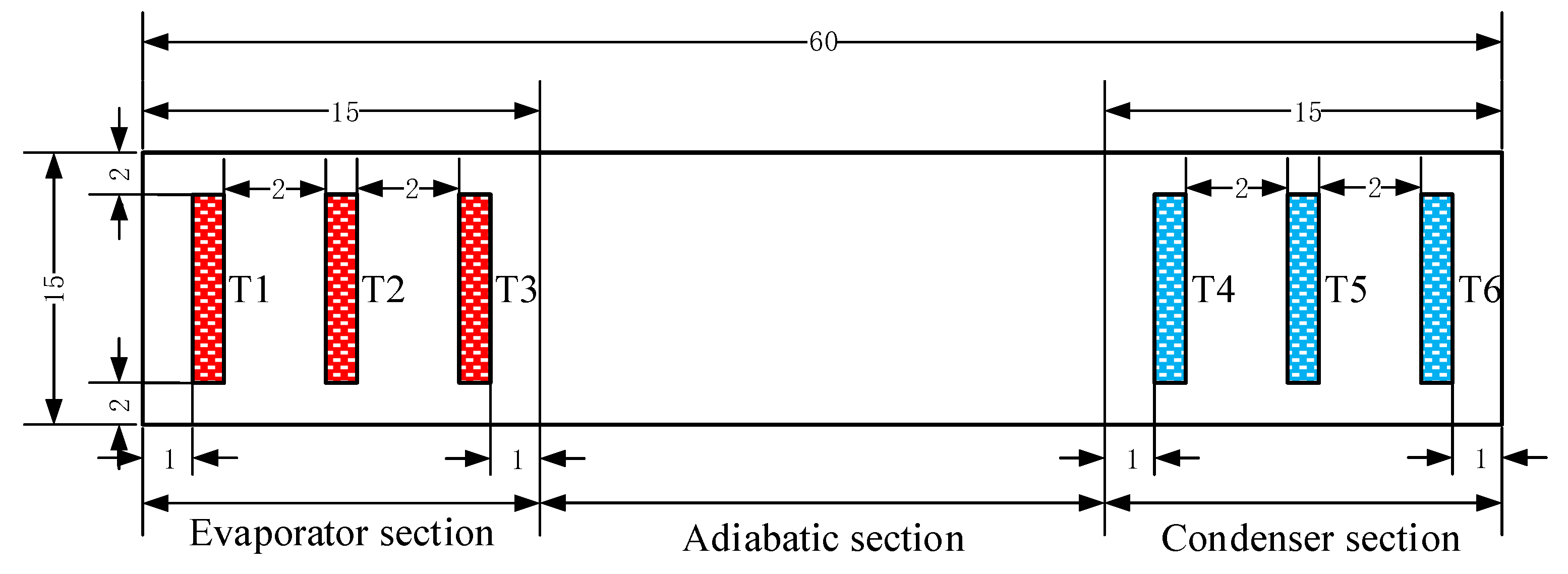
3.1. Experiment Settings
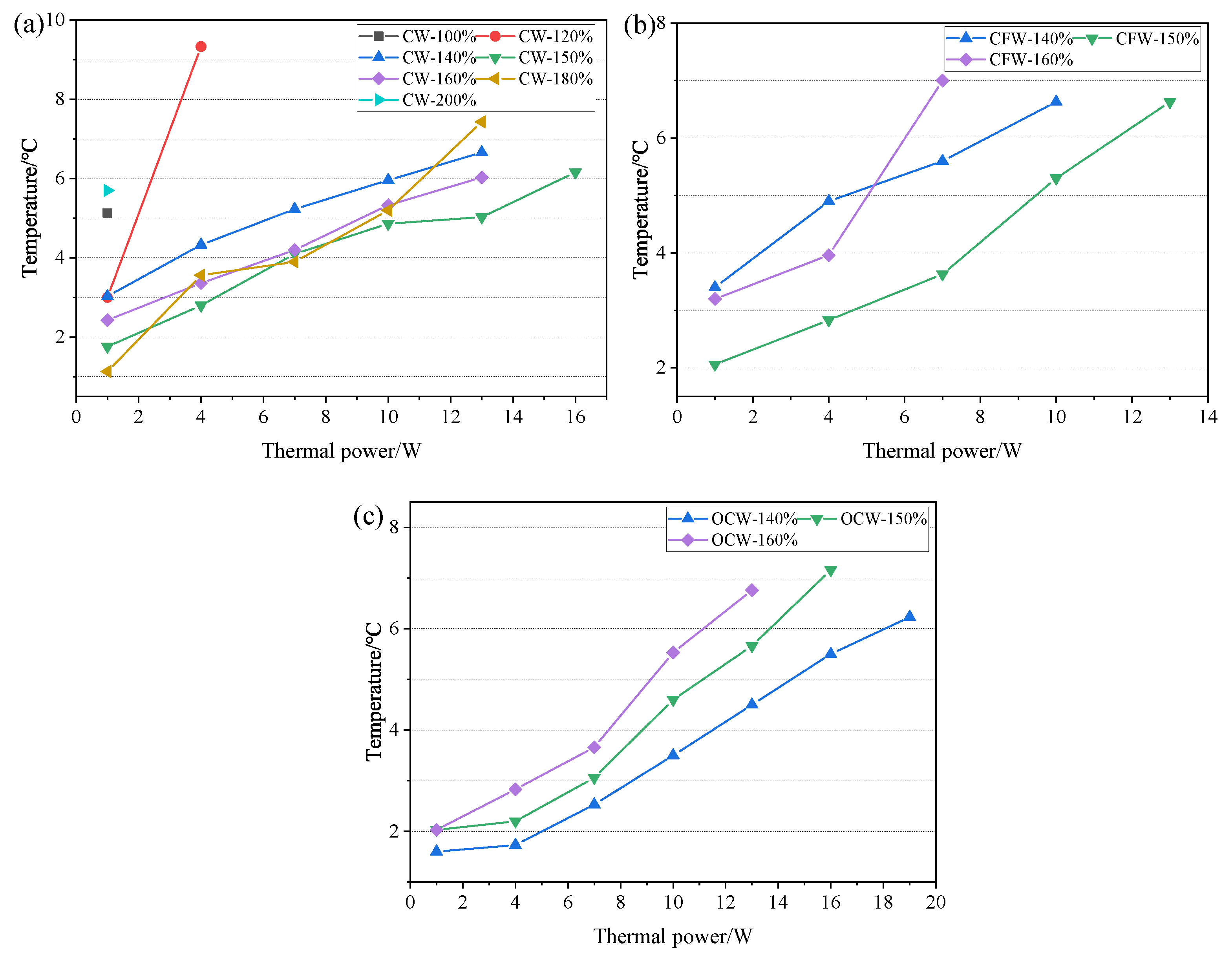
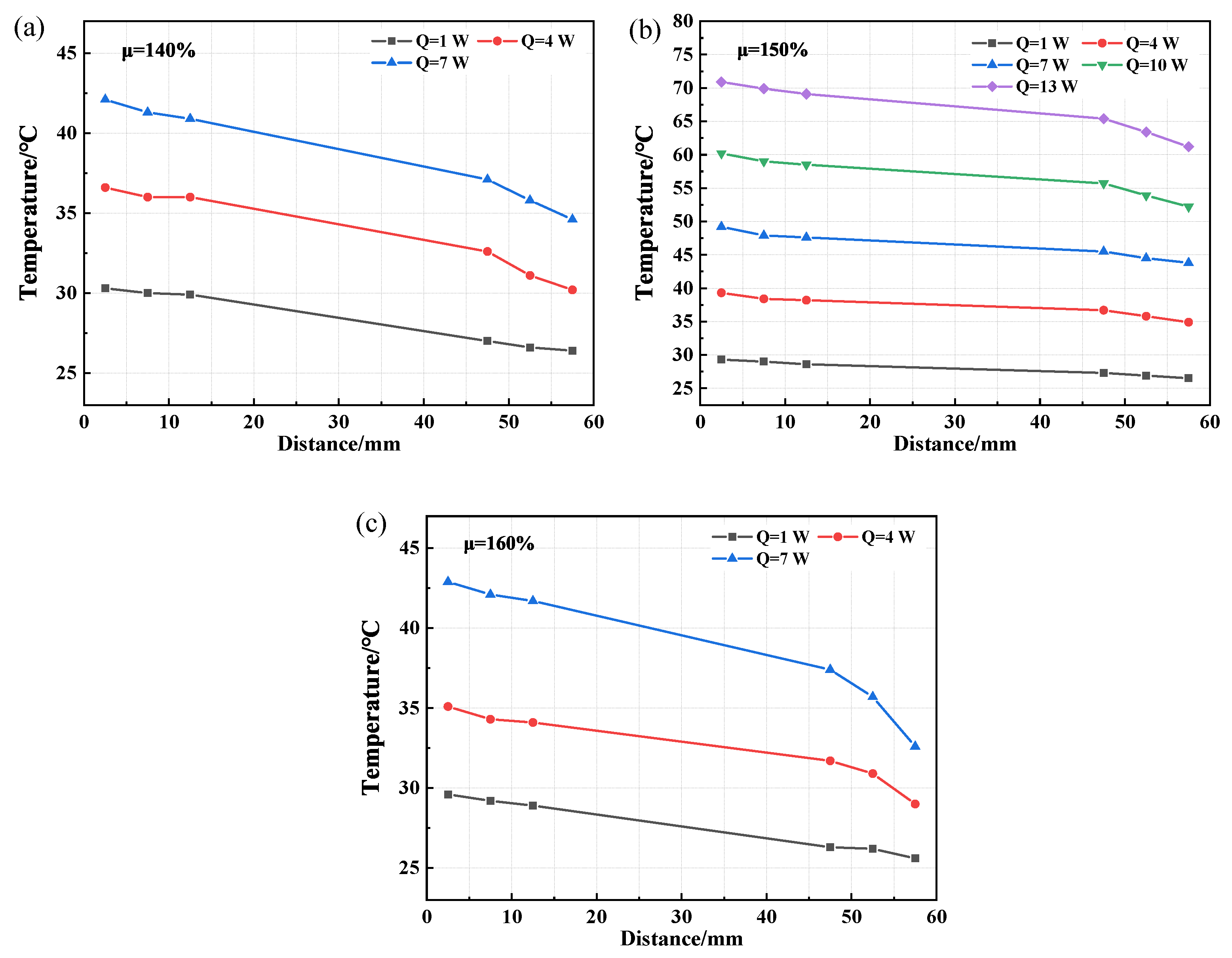
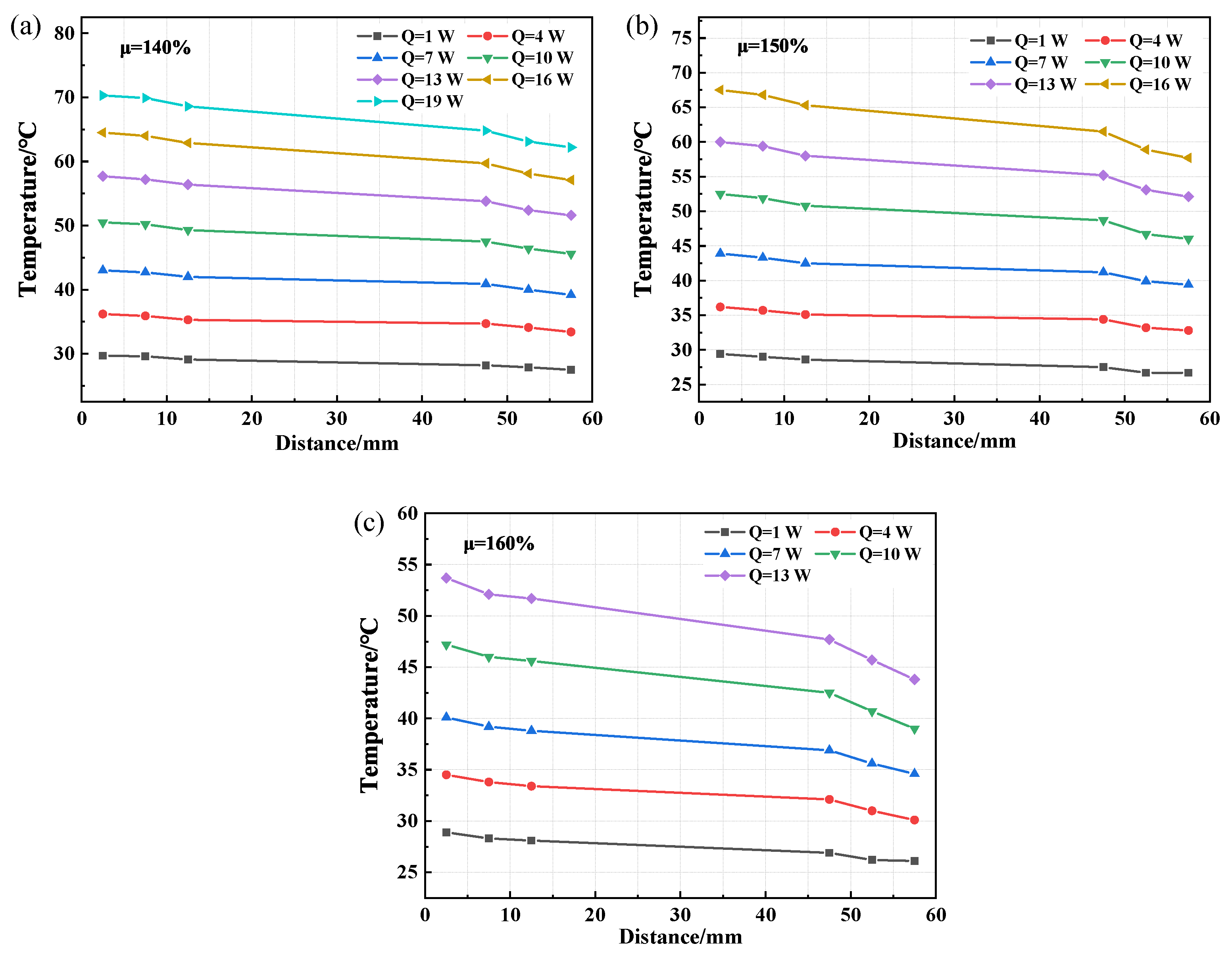
3.2. CW-FMHP Axial Temperature Distribution and Maximum Thermal Power
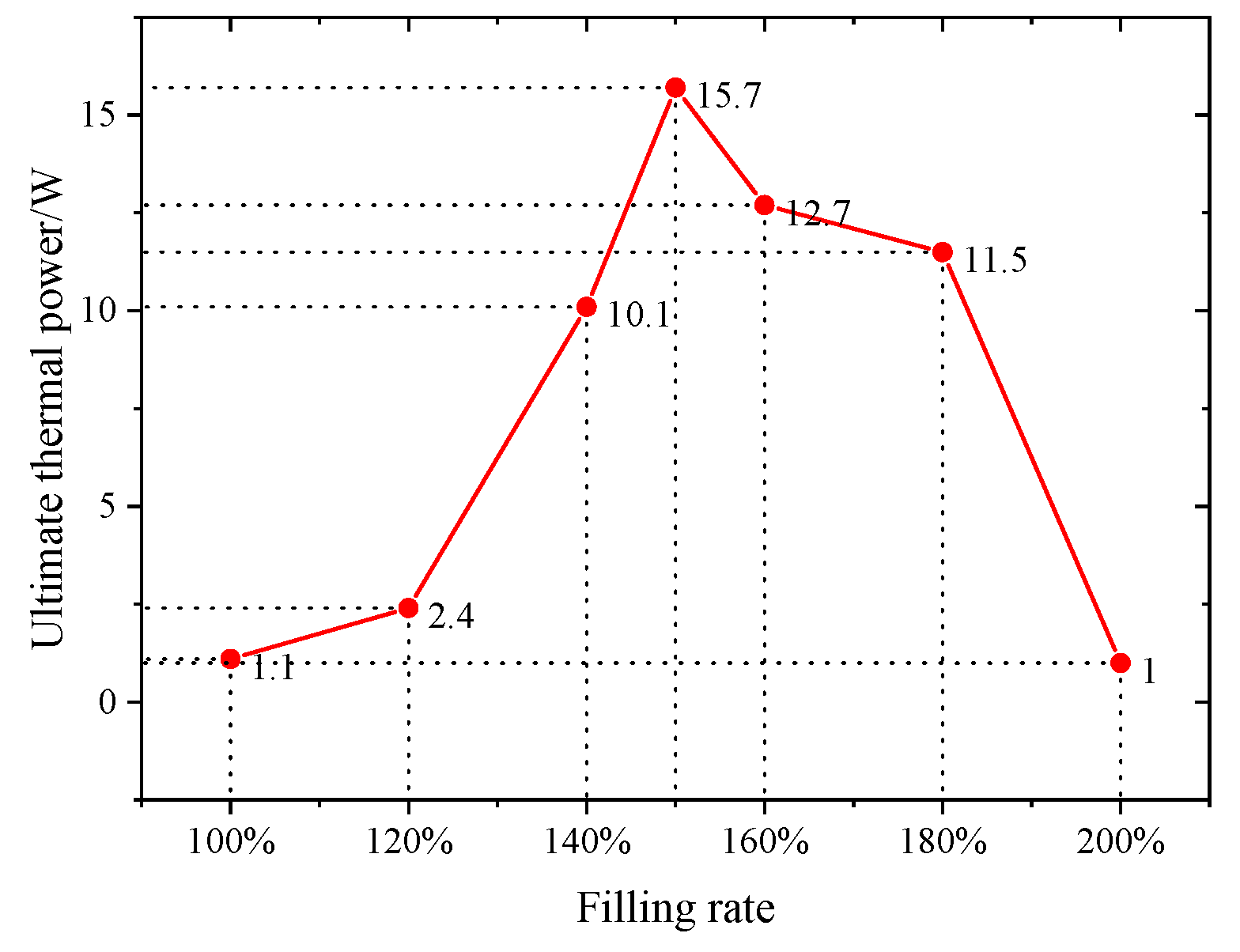
3.2.1. CW-FMHP Maximum Thermal Power under Different Filling Rate
3.2.2. Comparation of CW-FMHP, CFW-FMHP and OCW-FMHP
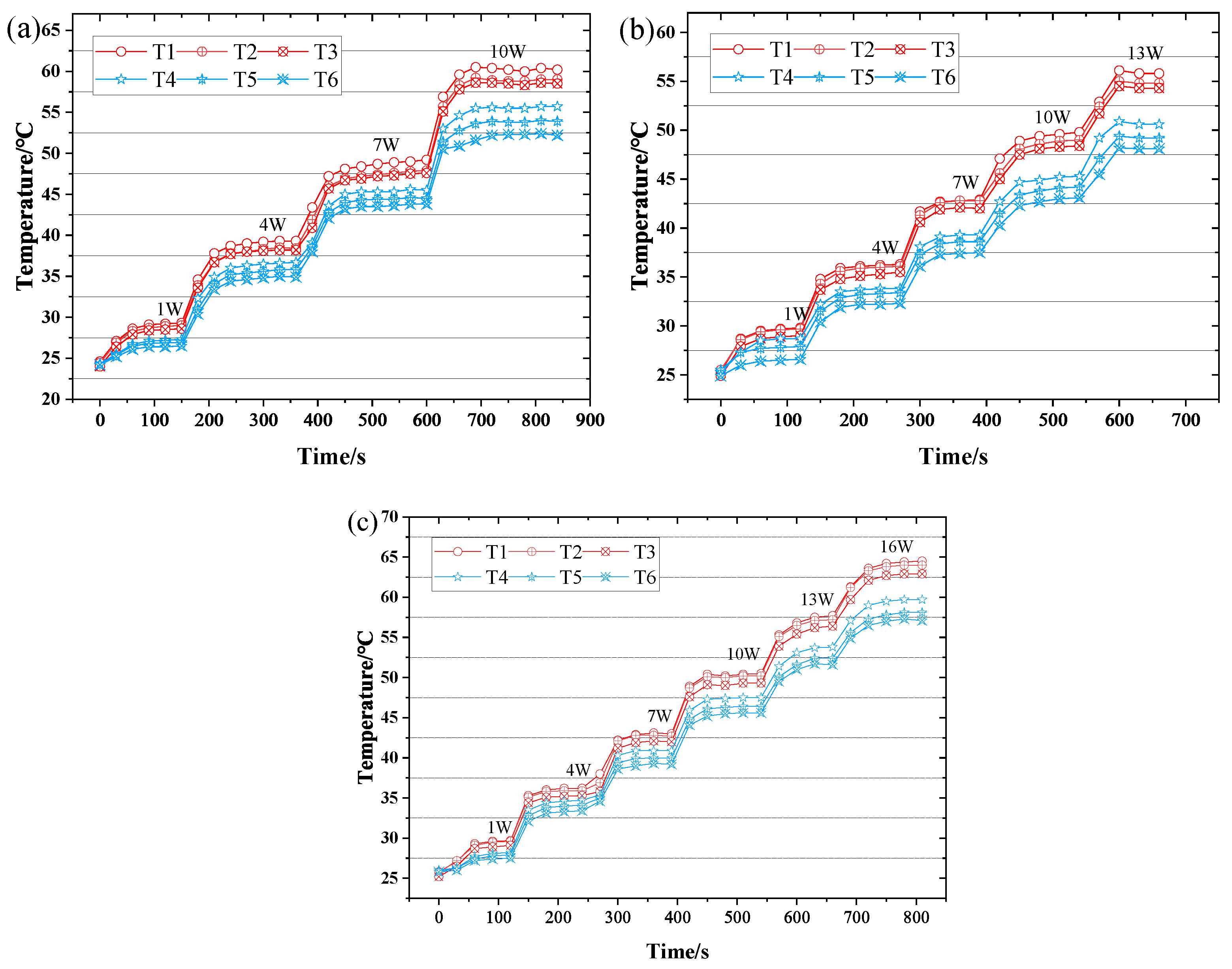
3.3. Dynamic Response Characteristics
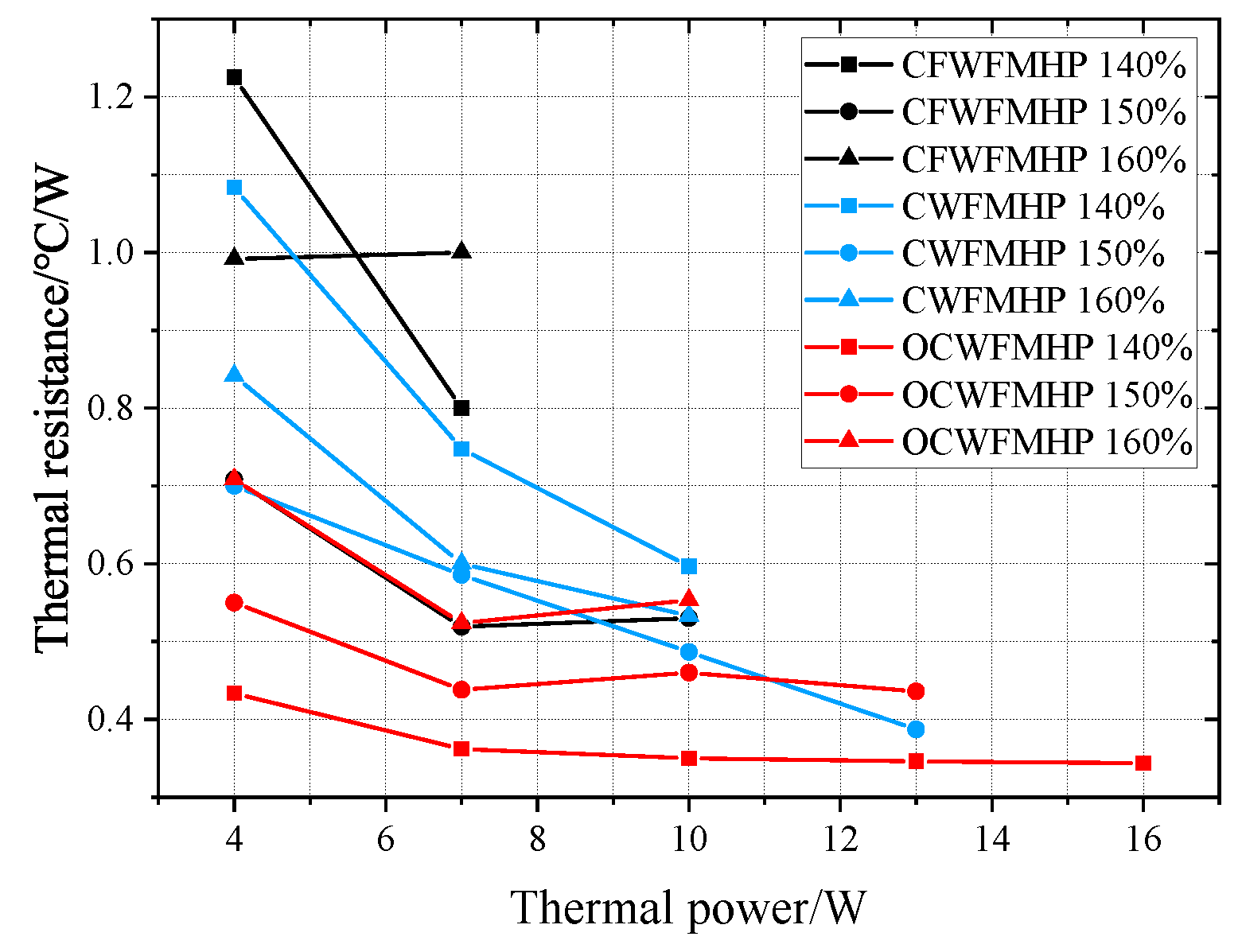
3.4. Thermal Resistance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FMHP | Flat-plate Micro Heat Pipe |
| CW | Composite Wick |
| CFW | Copper Foam Wick |
| OCW | Oxidized Composite Wick |
| P | Pressure |
| L | Length |
| Q | Thermal power |
| A | Cross-sectional area |
| h | Latent heat of evaporation |
| Viscosity;Liquid filling rate | |
| Density | |
| K | Permeability |
| Liquid reflux mass | |
| Surface tension | |
| Contact angle | |
| r | Capillary radius |
| Roughness | |
| Relative proportion of liquid–solid contact | |
| Maximum reflux mass | |
| %wt | %Weight |
| V | Volume |
| Porosity | |
| M | Mass |
| T | Temperature |
| Temperature difference | |
| Thermal resistance |
References
- Sohel Murshed, S.M.; Nieto de Castro, C.A. A critical review of traditional and emerging techniques and fluids for electronics cooling. Renew. Sustain. Energy Rev. 2017, 78, 821–833. [Google Scholar] [CrossRef]
- Thang, B.H.; Van Trinh, P.; Quang, L.D.; Huong, N.T.; Khoi, P.H.; Minh, P.N. Heat dissipation for the Intel Core i5 processor using multiwalled carbon-nanotube-based ethylene glycol. J. Korean Phys. Soc. 2014, 65, 312–316. [Google Scholar] [CrossRef]
- Patankar, G.; Weibel, J.A.; Garimella, S.V. Working-fluid selection for minimized thermal resistance in ultra-thin vapor chambers. Int. J. Heat Mass Transf. 2017, 106, 648–654. [Google Scholar] [CrossRef] [Green Version]
- Jo, J.; Kim, J.; Kim, S.J. Experimental investigations of heat transfer mechanisms of a pulsating heat pipe. Energy Convers. Manag. 2019, 181, 331–341. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Zhou, J.; Ma, X.; Akhlaghi, Y.G. Experimental study and exergy analysis of photovoltaic-thermoelectric with flat plate micro-channel heat pipe. Energy Convers. Manag. 2020, 207, 112515. [Google Scholar] [CrossRef]
- Song, Z.; Ji, J.; Cai, J.; Li, Z.; Han, K. Performance analyses on a novel heat pump with a hybrid condenser combined with flat plate micro-channel heat pipe plus TEG and FPV evaporator. Energy Convers. Manag. 2021, 228, 113606. [Google Scholar] [CrossRef]
- Qu, Z.G.; Chen, G.; Zhou, L.; Miao, J.Y. Numerical study on the operating characteristics of cryogenic loop heat pipes based on a one-dimensional heat leak model. Energy Convers. Manag. 2018, 172, 485–496. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Qu, Z.G. Lithium–ion battery thermal management using heat pipe and phase change material during discharge–charge cycle: A comprehensive numerical study. Appl. Energy 2019, 242, 378–392. [Google Scholar] [CrossRef]
- Tang, H.; Tang, Y.; Wan, Z.; Li, J.; Yuan, W.; Lu, L.; Li, Y.; Tang, K. Review of applications and developments of ultra-thin micro heat pipes for electronic cooling. Appl. Energy 2018, 223, 383–400. [Google Scholar] [CrossRef]
- Aoki, H.; Ikeda, M.; Kimura, Y. Ultra Thin Heat Pipe and its Application. Front. Heat Pipes 2012, 2, 043003. [Google Scholar] [CrossRef]
- Singh, M. Capillarity enhancement of micro heat pipes using grooves with variable apex angle. Int. J. Therm. Sci. 2020, 150, 106239. [Google Scholar] [CrossRef]
- Zu, S.; Liao, X.; Huang, Z.; Li, D.; Jian, Q. Visualization study on boiling heat transfer of ultra-thin flat heat pipe with single layer wire mesh wick. Int. J. Heat Mass Transf. 2021, 173, 121239. [Google Scholar] [CrossRef]
- Mishra, D.K.; Saravanan, T.T.; Khanra, G.P.; Girikumar, S.; Sharma, S.C.; Sreekumar, K.; Sinha, P.P. Studies on the processing of nickel base porous wicks for capillary pumped loop for thermal management of spacecrafts. Adv. Powder Technol. 2010, 21, 658–662. [Google Scholar] [CrossRef]
- Deng, D.; Tang, Y.; Huang, G.; Lu, L.; Yuan, D. Characterization of capillary performance of composite wicks for two-phase heat transfer devices. Int. J. Heat Mass Transf. 2013, 56, 283–293. [Google Scholar] [CrossRef]
- Shouguang, Y.; Jiangwei, D.; Dong, S.; Sheng, L.; Jian, L. Experimental investigation on the heat transfer performance of heat pipes with porous copper foam wicks. Mater. Res. Innov. 2015, 19, S5-617–S5-622. [Google Scholar] [CrossRef]
- Mahdavi, M.; Tiari, S.; De Schampheleire, S.; Qiu, S. Experimental study of the thermal characteristics of a heat pipe. Exp. Therm. Fluid Sci. 2018, 93, 292–304. [Google Scholar] [CrossRef]
- Mizuta, K.; Fukunaga, R.; Fukuda, K.; Nii, S.; Asano, T. Development and characterization of a flat laminate vapor chamber. Appl. Therm. Eng. 2016, 104, 461–471. [Google Scholar] [CrossRef]
- Zhou, G.; Li, J.; Lv, L. An ultra-thin miniature loop heat pipe cooler for mobile electronics. Appl. Therm. Eng. 2016, 109, 514–523. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, W.; Li, Z.; Chen, Z.; Gan, Y. Experimental analysis of thin vapor chamber with composite wick structure under different cooling conditions. Appl. Therm. Eng. 2019, 156, 471–484. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Feng, C.; Liu, L.; Luan, T. Study of copper chemical-plating modified polyacrylonitrile-based carbon fiber wick applied to compact loop heat pipe. Exp. Therm. Fluid Sci. 2019, 100, 104–113. [Google Scholar] [CrossRef]
- Li, J.; Lv, L.; Zhou, G.; Li, X. Mechanism of a microscale flat plate heat pipe with extremely high nominal thermal conductivity for cooling high-end smartphone chips. Energy Convers. Manag. 2019, 201, 112202. [Google Scholar] [CrossRef]
- Zhou, W.; Xie, P.; Li, Y.; Yan, Y.; Li, B. Thermal performance of ultra-thin flattened heat pipes. Appl. Therm. Eng. 2017, 117, 773–781. [Google Scholar] [CrossRef]
- Zhou, W.; Ling, W.; Duan, L.; Hui, K.S.; Hui, K.N. Development and tests of loop heat pipe with multi-layer metal foams as wick structure. Appl. Therm. Eng. 2016, 94, 324–330. [Google Scholar] [CrossRef]
- Ling, W.; Zhou, W.; Liu, R.; Qiu, Q.; Liu, J. Thermal performance of loop heat pipe with porous copper fiber sintered sheet as wick structure. Appl. Therm. Eng. 2016, 108, 251–260. [Google Scholar] [CrossRef]
- Xu, S.; Lewis, R.J.; Liew, L.A.; Lee, Y.C.; Yang, R. Development of Ultra-Thin Thermal Ground Planes by Using Stainless-Steel Mesh as Wicking Structure. J. Microelectromechanical Syst. 2016, 25, 842–844. [Google Scholar] [CrossRef]
- Huang, S.; Wan, Z.; Zhang, X.; Yang, X.; Tang, Y. Evaluation of capillary performance of a stainless steel fiber–powder composite wick for stainless steel heat pipe. Appl. Therm. Eng. 2019, 148, 1224–1232. [Google Scholar] [CrossRef]
- Zhou, W.; Li, Y.; Chen, Z.; Deng, L.; Gan, Y. A novel ultra-thin flattened heat pipe with biporous spiral woven mesh wick for cooling electronic devices. Energy Convers. Manag. 2019, 180, 769–783. [Google Scholar] [CrossRef]
- Jafari, D.; Wits, W.W.; Geurts, B.J. Phase change heat transfer characteristics of an additively manufactured wick for heat pipe applications. Appl. Therm. Eng. 2020, 168, 114890. [Google Scholar] [CrossRef]
- Wang, G.; Quan, Z.; Zhao, Y.; Wang, H. Effect of geometries on the heat transfer characteristics of flat-plate micro heat pipes. Appl. Therm. Eng. 2020, 180, 115796. [Google Scholar] [CrossRef]
- Takata, Y.; Hidaka, S.; Cao, J.M.; Nakamura, T.; Yamamoto, H.; Masuda, M.; Ito, T. Effect of surface wettability on boiling and evaporation. Energy 2005, 30, 209–220. [Google Scholar] [CrossRef]
- Nam, Y.; Ju, Y.S. A comparative study of the morphology and wetting characteristics of micro/nanostructured Cu surfaces for phase change heat transfer applications. J. Adhes. Sci. Technol. 2013, 27, 2163–2176. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, D.; Wang, H.; Qu, J.; Li, J.; Qiu, H. Development of ultrathin thermal ground plane with multiscale micro/nanostructured wicks. Case Stud. Therm. Eng. 2020, 22, 100738. [Google Scholar] [CrossRef]
- Chen, G.; Tang, Y.; Duan, L.; Tang, H.; Zhong, G.; Wan, Z.; Zhang, S.; Fu, T. Thermal performance enhancement of micro-grooved aluminum flat plate heat pipes applied in solar collectors. Renew. Energy 2020, 146, 2234–2242. [Google Scholar] [CrossRef]
- Tang, H.; Weng, C.; Tang, Y.; Li, H.; Xu, T.; Fu, T. Thermal performance enhancement of an ultra-thin flattened heat pipe with multiple wick structure. Appl. Therm. Eng. 2021, 183, 116203. [Google Scholar] [CrossRef]
- Shi, J.; Jia, X.; Feng, D.; Chen, Z.; Dang, C. Wettability effect on pool boiling heat transfer using a multiscale copper foam surface. Int. J. Heat Mass Transf. 2020, 146, 118726. [Google Scholar] [CrossRef]
- Shirazy, M.R.S.; Blais, S.; Fréchette, L.G. Mechanism of wettability transition in copper metal foams: From superhydrophilic to hydrophobic. Appl. Surf. Sci. 2012, 258, 6416–6424. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, K.; Li, H.; Tang, B.; Zhou, G. Experimental study on capillary and mechanical properties of a porous nickel–copper composite. Mater. Sci. Technol. 2019, 35, 1572–1582. [Google Scholar] [CrossRef]






| Wick Type | Filling Rate | Maximum Thermal Power |
|---|---|---|
| Copper Foam (CFW-FMHP) | W | |
| Composite (CW-FMHP) | W | |
| Oxidized Composite (OCW-FMHP) | W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhao, Z.; Luo, C.; Zhang, D. Thermal Transfer Characteristics of Flat Plate Micro Heat Pipe with Copper Spiral Woven Mesh and a Copper Foam Composite Wick. Nanomaterials 2021, 11, 2821. https://doi.org/10.3390/nano11112821
Zhang Y, Zhao Z, Luo C, Zhang D. Thermal Transfer Characteristics of Flat Plate Micro Heat Pipe with Copper Spiral Woven Mesh and a Copper Foam Composite Wick. Nanomaterials. 2021; 11(11):2821. https://doi.org/10.3390/nano11112821
Chicago/Turabian StyleZhang, Yanhui, Zhengang Zhao, Chuan Luo, and Dacheng Zhang. 2021. "Thermal Transfer Characteristics of Flat Plate Micro Heat Pipe with Copper Spiral Woven Mesh and a Copper Foam Composite Wick" Nanomaterials 11, no. 11: 2821. https://doi.org/10.3390/nano11112821
APA StyleZhang, Y., Zhao, Z., Luo, C., & Zhang, D. (2021). Thermal Transfer Characteristics of Flat Plate Micro Heat Pipe with Copper Spiral Woven Mesh and a Copper Foam Composite Wick. Nanomaterials, 11(11), 2821. https://doi.org/10.3390/nano11112821







