The Surface Photogalvanic and Photon Drag Effects in Ag/Pd Metal-Semiconductor Nanocomposite
Abstract
:1. Introduction
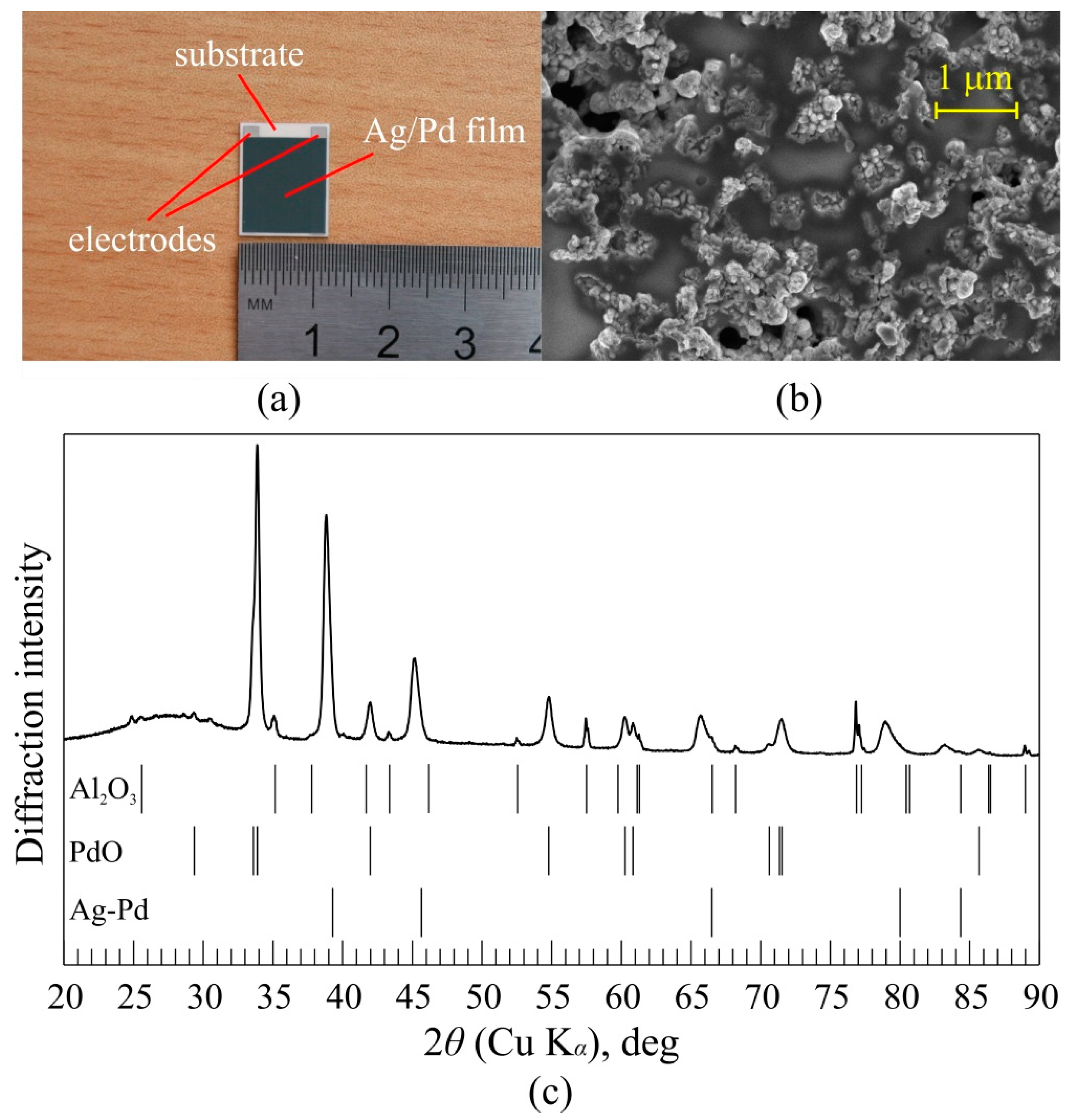
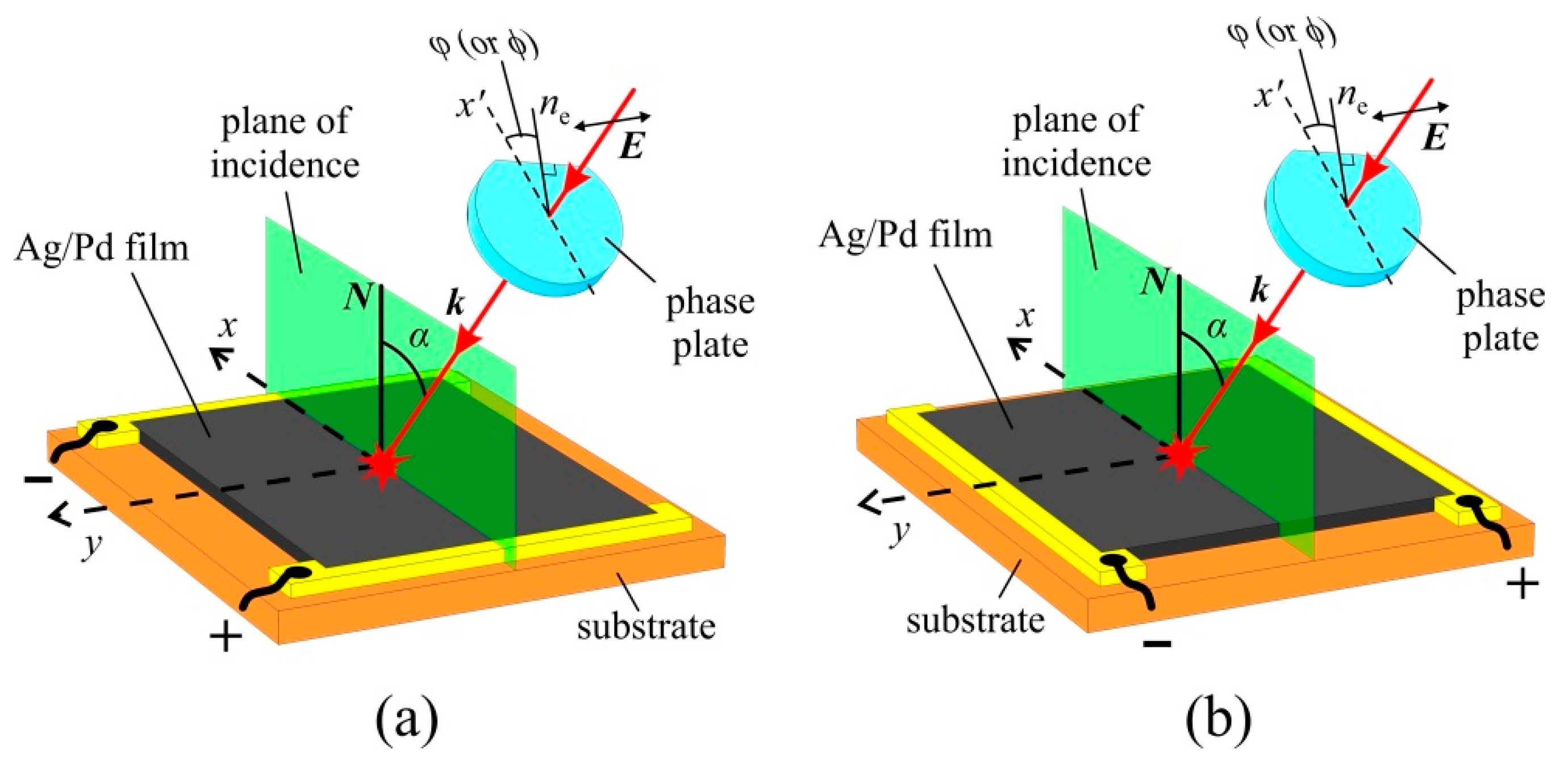
2. Materials and Methods
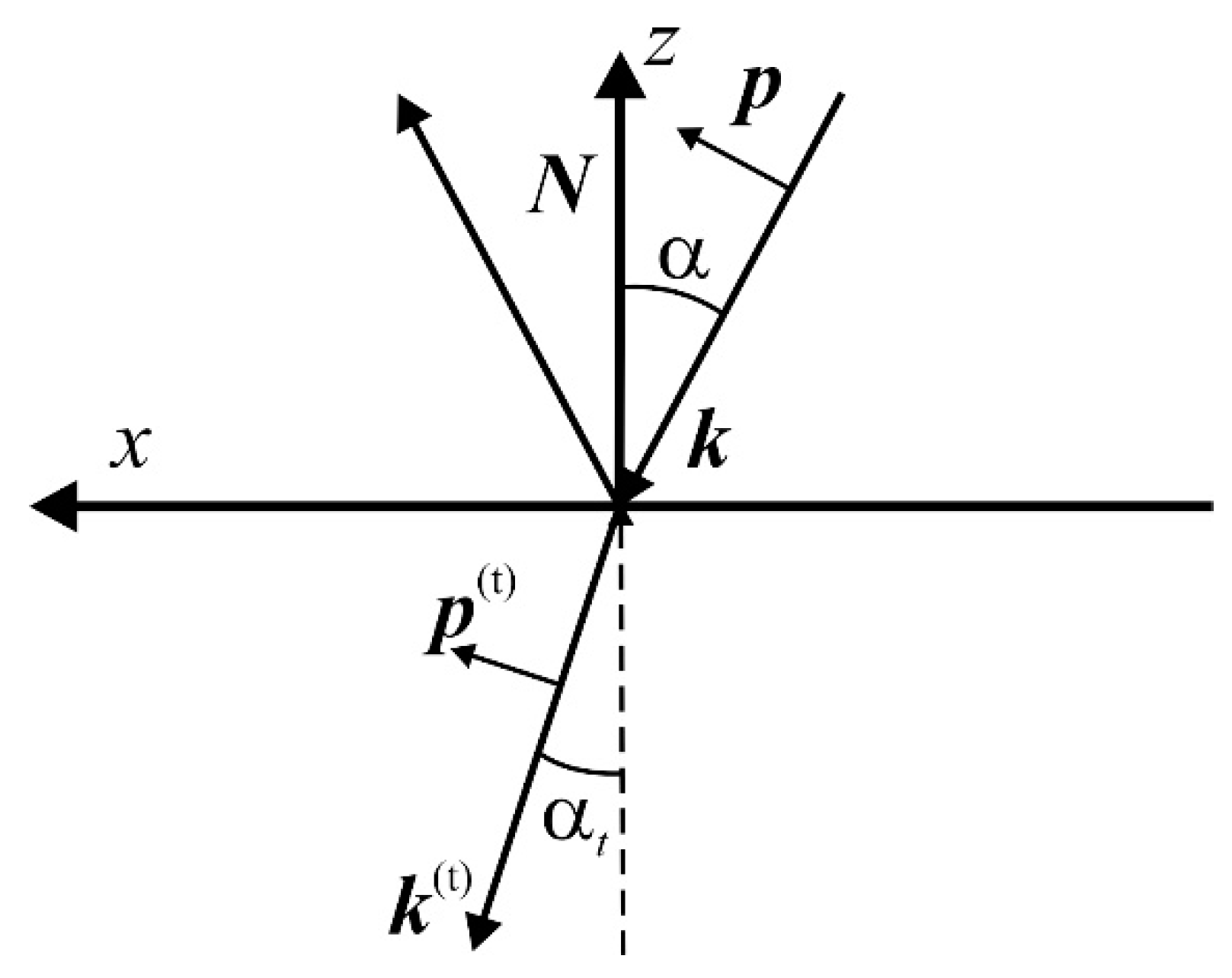
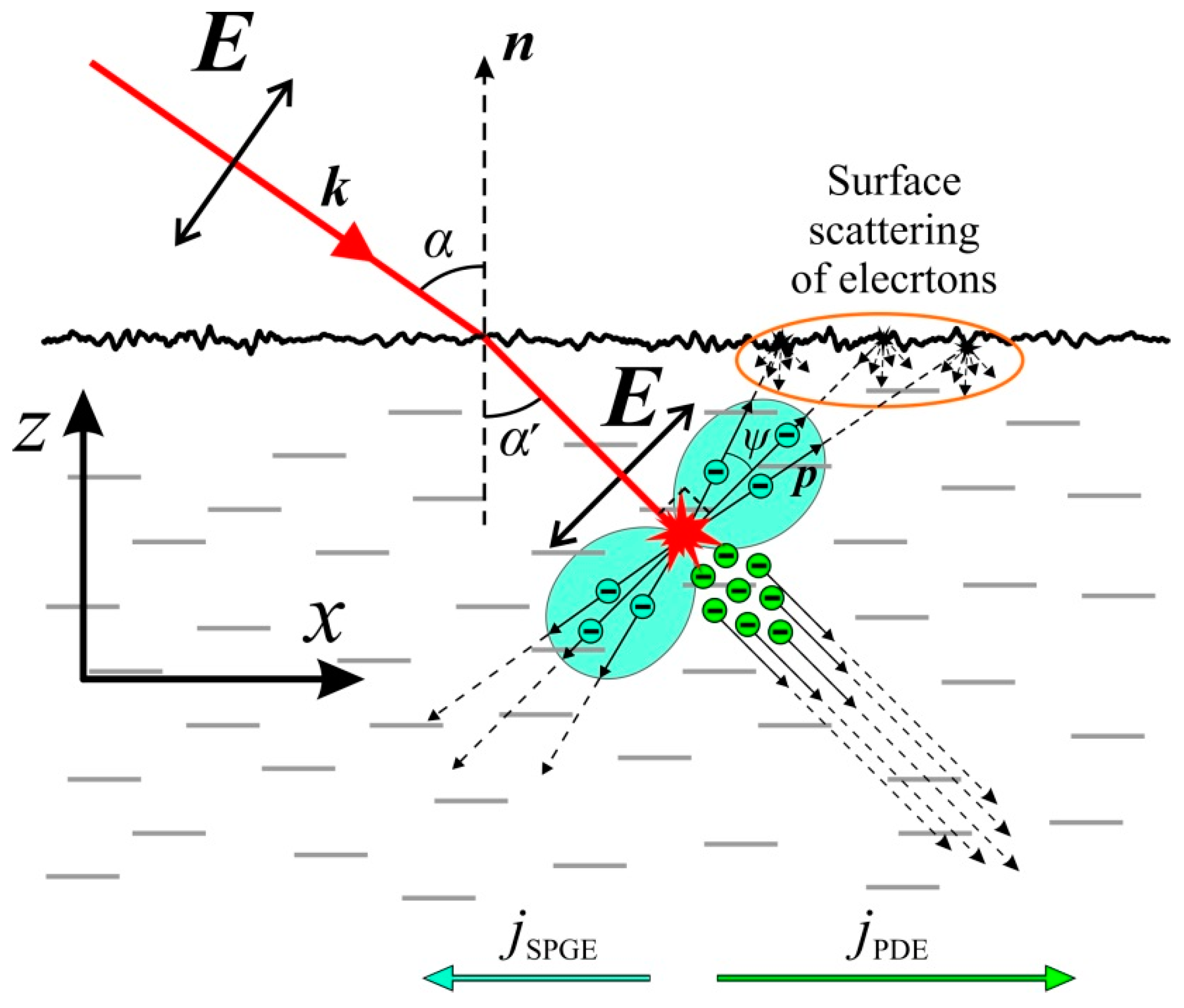
3. Phenomenological Theory of the Light-Induced Current in the Ag/Pd Nanocomposite
3.1. SPGE
3.2. PDE
3.3. Polarization-Sensitive Photoresponse
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ivchenko, E.L. Optical Spectroscopy of Semiconductor Nanostructures; Springer: Berlin, Germany, 2004; p. 423. [Google Scholar]
- Alperovich, V.L.; Belinicher, V.I.; Novikov, V.N.; Terekhov, A.S. Surface photovoltaic effect in solids. Theory and experiment for interband transitions in gallium arsenide. JETP 1981, 53, 1201–1208. [Google Scholar]
- Danishevskii, A.M.; Kastal’skii, A.A.; Ryvkin, S.M.; Yaroshetskii, I.D. Dragging of free carriers by photons in direct interband transitions. JETP 1970, 58, 544–550. [Google Scholar]
- Shalygin, V.A.; Moldavskaya, M.D.; Danilov, S.N.; Farbshtein, I.I.; Golub, L.E. Circular photon drag effect in bulk tellurium. Phys. Rev. B 2016, 93, 045207. [Google Scholar] [CrossRef] [Green Version]
- Glazov, M.M.; Ganichev, S.D. High frequency electric field induced nonlinear effects in graphene. Phys. Rep. 2014, 535, 101–138. [Google Scholar] [CrossRef] [Green Version]
- Gurevich, V.L.; Laiho, R. Photomagnetism of metals. First observation of dependence on polarization of light. Phys. Solid State 2000, 42, 1762–1767. [Google Scholar] [CrossRef]
- Magarill, L.I.; Entin, V.M. Surface photogalvanic effect in metals. JETP 1982, 54, 531–535. [Google Scholar]
- Gurevich, V.L.; Laiho, R. Photomagnetism of metals: Microscopic theory of the photoinduced surface current. Phys. Rev. B 1993, 48, 8307–8315. [Google Scholar] [CrossRef] [PubMed]
- Alperovich, V.L.; Belinicher, V.I.; Novikov, V.N.; Terekhov, A.S. Surface photovoltaic effect in gallium arsenide. JETP Lett. 1980, 31, 546–549. [Google Scholar]
- Mikheev, G.M.; Kogai, V.Y.; Mikheev, K.G.; Mogileva, T.N.; Saushin, A.S.; Svirko, Y.P. Polarization-sensitive photoresponse of the CuSe/Se nanocomposite prepared by vacuum thermal deposition. Mater. Today Commun. 2019, 21, 100656. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Kogai, V.Y.; Mogileva, T.N.; Mikheev, K.G.; Saushin, A.S.; Svirko, Y.P. Photon helicity driven surface photocurrent in CuSe films. Appl. Phys. Lett. 2019, 115, 061101. [Google Scholar] [CrossRef] [Green Version]
- Karch, J.; Olbrich, P.; Schmalzbauer, M.; Zoth, C.; Brinsteiner, C.; Fehrenbacher, M.; Wurstbauer, U.; Glazov, M.M.; Tarasenko, S.A.; Ivchenko, E.L.; et al. Dynamic hall effect driven by circularly polarized light in a graphene layer. Phys. Rev. Lett. 2010, 105, 227402–227406. [Google Scholar] [CrossRef] [PubMed]
- Belinicher, V.I.; Sturman, B.I. The photogalvanic effect in media lacking a center of symmetry. Sov. Phys. Uspekhi 1980, 23, 199–223. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Saushin, A.S.; Styapshin, V.M.; Svirko, Y.P. Interplay of the photon drag and the surface photogalvanic effects in the metal-semiconductor nanocomposite. Sci. Rep. 2018, 8, 8644. [Google Scholar] [CrossRef]
- Gibson, A.F.; Kimmitt, M.F.; Walker, A.C. Photon drag in germanium. Appl. Phys. Lett. 1970, 17, 75–77. [Google Scholar] [CrossRef]
- Luryi, S. Photon-drag effect in intersubband absorption by a two-dimensional electron gas. Phys. Rev. Lett. 1987, 58, 2263–2266. [Google Scholar] [CrossRef] [PubMed]
- Grinberg, A.A.; Luryi, S. Comment on “Light-induced drift of quantum-confined electrons in semiconductor heterostructures”. Phys. Rev. Lett. 1991, 67, 156. [Google Scholar] [CrossRef] [PubMed]
- Shalaev, V.M.; Douketis, C.; Moskovits, M. Light-induced drift of electrons in metals. Phys. Lett. A 1992, 169, 205–210. [Google Scholar] [CrossRef]
- Grinberg, A.A. Theory of the photoelectric and photomagnetic effects produced by light pressure. JETP 1970, 31, 531–534. [Google Scholar]
- Valov, P.M.; Ryvkin, B.S.; Ryvkin, S.M.; Yaroshetskii, I.D. An anisotropic photon drag effect in nonspherical—Band cubic semiconductors. Phys. Status Solidi 1972, 53, 65–70. [Google Scholar] [CrossRef]
- Alperovich, V.L.; Belinicher, V.I.; Novikov, V.N.; Terekhov, A.S. Photon drag of electrons and holes in interband transitions in semiconductors and the resonant-recoil effect. JETP Lett. 1981, 33, 557–560. [Google Scholar]
- Ribakovs, G.; Gundjian, A.A. TEA CO2 laser radiation induced EMF’s in tellurium. J. Appl. Phys. 1977, 48, 4601–4608. [Google Scholar] [CrossRef]
- Yee, J.H. Quantum theory of photon-drag transport phenomena in solids and its application to tellurium crystall. Phys. Rev. B 1974, 9, 5209–5216. [Google Scholar] [CrossRef]
- Marchetti, S.; Simili, R. Photon drag detection of 10 μm radiation in Bi thin-films evaporated on amorphous substrates. Nuovo Cim. D 1987, 9, 311–318. [Google Scholar] [CrossRef]
- Sigg, H.; Kwakernaak, M.H.; Margotte, B.; Emi, D.; Van Son, P.; Kohler, K. Ultrafast far-infrared GaAs/AlGaAs photon drag detector in microwave transmittion line topology. Appl. Phys. Lett. 1995, 67, 2827–2829. [Google Scholar] [CrossRef]
- Goff, J.; Schaich, W. Theory of the photon-drag effect in simple metals. Phys. Rev. B 2000, 61, 10471–10477. [Google Scholar] [CrossRef] [Green Version]
- Pashinin, P.P.; Prokhorov, A.M. Effect of electron dragging by photons in a laser plasma. JETP Lett. 1977, 26, 526–528. [Google Scholar]
- Keller, O. Photon drag in a single-level metallic quantum well. Phys. Rev. B 1993, 48, 4786–4798. [Google Scholar] [CrossRef]
- Hatano, T.; Nishikawa, B.; Iwanaga, M.; Ishihara, T. Optical rectification effect in 1D metallic photonic crystal slabs with asymmetric unit cell. Opt. Express 2008, 16, 8236–8241. [Google Scholar] [CrossRef]
- Wieck, A.D.; Sigg, H.; Ploog, K. Observation of resonant photon drag in a two-dimensional electron gas. Phys. Rev. Lett. 1990, 64, 463–466. [Google Scholar] [CrossRef]
- Rodrigues, C.; Fonseca, A.L.A.; Agrello, D.A.; Nunes, O.A.C. The phonon-assisted photon-drag effect in a two-dimensional semiconductor quantum-well structure. Superlattices Microstruct. 2001, 29, 33–42. [Google Scholar] [CrossRef]
- Beregulin, E.V.; Valov, P.M.; Ryvkin, S.M.; Yaroshetskii, I.D.; Lisker, I.S.; Pukshanskii, A.L. Dragging of electrons by light in semimetals. JETP Lett. 1977, 25, 113–116. [Google Scholar]
- Vengurlekar, A.S.; Ishihara, T. Surface plasmon enhanced photon drag in metal films. Appl. Phys. Lett. 2005, 87, 091118. [Google Scholar] [CrossRef]
- Durach, M.; Rusina, A.; Stockman, M.I. Giant surface-plasmon-induced drag effect in metal nanowires. Phys. Rev. Lett. 2009, 103, 186801. [Google Scholar] [CrossRef] [Green Version]
- Obraztsov, P.A.; Mikheev, G.M.; Garnov, S.V.; Obraztsov, A.N.; Svirko, Y.P. Polarization-sensitive photoresponse of nanographite. Appl. Phys. Lett. 2011, 98, 091903–091905. [Google Scholar] [CrossRef]
- Larry, J.; Rosenberg, R.; Uhler, R. Thick-film Technology: An Introduction to the Materials. IEEE Trans. Compon. Hybrids Manuf. Technol. 1980, 3, 211–225. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Saushin, A.S.; Goncharov, O.Y.; Dorofeev, G.A.; Gil’mutdinov, F.Z.; Zonov, R.G. Effect of the burning temperature on the phase composition, photovoltaic response, and electrical properties of Ag/Pd resistive films. Phys. Solid State 2014, 56, 2286–2293. [Google Scholar] [CrossRef]
- Wang, S.F.; Huebner, W. Thermodynamic modeling of equilibrium subsolidy phase relations in the Ag-Pd-O2 system. J. Am. Ceram. Soc. 1991, 74, 1349–1353. [Google Scholar] [CrossRef]
- Wang, S.F.; Dougherty, J.P. Silver-palladium thick-film conductors. J. Am. Ceram. Soc. 1994, 77, 3051–3072. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Saushin, A.S.; Zonov, R.G.; Styapshin, V.M. Spectral dependence of circular photocurrent in silver—Palladium resistive films. Tech. Phys. Lett. 2014, 40, 424–428. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Saushin, A.S.; Vanyukov, V.V. Helicity-dependent photocurrent in the resistive Ag/Pd films excited by IR laser radiation. Quantum Electron. 2015, 45, 635–639. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Saushin, A.S.; Vanyukov, V.V.; Mikheev, K.G.; Svirko, Y.P. Femtosecond circular photon drag effect in the Ag/Pd nanocomposite. Nanoscale Res. Lett. 2017, 12, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Saushin, A.S.; Mikheev, K.G.; Styapshin, V.M.; Mikheev, G.M. Direct measurement of the circular photocurrent in the Ag/Pd nanocomposites. J. Nanophotonics 2017, 11, 032508. [Google Scholar] [CrossRef]
- Popov, S.V.; Svirko, Y.P.; Zheludev, N.I. Susceptibility Tensors for Nonlinear Optics; Institute of Physics Publishing: Philadelphia, PA, USA, 1995; p. 194. [Google Scholar]
- Normantas, E.; Pikus, G.E. EMF induced by entrainment current in a magnetic field. Sov. J. Exp. Theor. Phys. 1989, 67, 1169–1172. [Google Scholar]
- Crowell, C.R.; Spitzer, W.G.; Howarth, L.E.; LaBate, E.E. Attenuation length measurements of hot electrons and hot holes in metal films. Phys. Rev. 1962, 127, 2006–2015. [Google Scholar] [CrossRef]
- Winsemius, P.; Van Kampen, F.F.; Lengkeek, H.P.; Van Went, C.G. Temperature dependence of the optical properties of Au, Ag and Cu. J. Phys. F Met. Phys. 1976, 6, 1583–1606. [Google Scholar] [CrossRef]
- Kesselring, R.; Kälin, A.W.; Sigg, H.; Kneubühl, F.K. Picosecond response of photon-drag detectors for the 10-μm wavelength range. Rev. Sci. Instrum. 1992, 63, 3317–3320. [Google Scholar] [CrossRef]
- Mikheev, G.M.; Zonov, R.G.; Aleksandrov, V.A. Light-induced EMF in silver-palladium film resistors. Tech. Phys. Lett. 2010, 36, 675–678. [Google Scholar] [CrossRef]
- Heras, J.M.; Estiu, G.; Viscido, L. Annealing behaviour of clean and oxygen covered polycrystalline palladium films: A work function and electrical resistance study. Thin Solid Film. 1990, 188, 165–172. [Google Scholar] [CrossRef]
- Rogal, J.; Reuter, K.; Scheffler, M. The thermodynamic stability of PdO surfaces. Phys. Rev. B 2004, 69, 075421. [Google Scholar] [CrossRef] [Green Version]
- Chelvayohan, M.; Mee, C.H.B. Work function measurements on (100) and (110) surfaces of silver. Phys. Status Solidi 1982, 15, 2305–2312. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Pal’ti, A.M.; Ashcheulov, A.A. Anisotropic thermocouples. Semiconductors 1997, 31, 1281–1298. [Google Scholar] [CrossRef]
- Stubbe, L.; Gossick, B. Measurements of the Dember potential in bulk germanium. J. Appl. Phys. 1959, 30, 507–508. [Google Scholar] [CrossRef]
- Rappaport, P. The Photovotaic Effect and its Utilization. Sol. Energy 1959, 3, 8–18. [Google Scholar] [CrossRef]
- Obraztsov, P.A.; Kanda, N.; Konishi, K.; Kuwata-Gonokami, M.; Garnov, S.V.; Obraztsov, A.N.; Svirko, Y.P. Photon-drag-induced terahertz emission from graphene. Phys. Rev. B 2014, 90, 241416. [Google Scholar] [CrossRef]
- Wang, M.; Yang, E.-H. THz applications of 2D materials: Graphene and beyond. Nano-Struct. Nano-Objects 2018, 15, 107–113. [Google Scholar] [CrossRef]
- Huang, S.; Li, W.; Zhu, L.; He, M.; Yao, Z.; Zhou, Y.; Xu, X.; Ren, Z.; Bai, J. Terahertz emission from vertically aligned multi-wall carbon nanotubes and their composites by optical excitation. Carbon 2018, 132, 335–342. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, Y.; Yao, Z.; Quan, B.; Zhang, L.; Li, J.; Gu, C.; Xu, X.; Ren, Z. Enhanced polarization-sensitive terahertz emission from vertically grown graphene by a dynamical photon drag effect. Nanoscale 2017, 9, 10301–10311. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.; Lifshitz, E.; Berestetskii, V.; Pitaevskii, L. Course of Theoretical Physics; Addison-Wesley: Boston, MA, USA, 2005; Volume 8, p. 649. [Google Scholar]

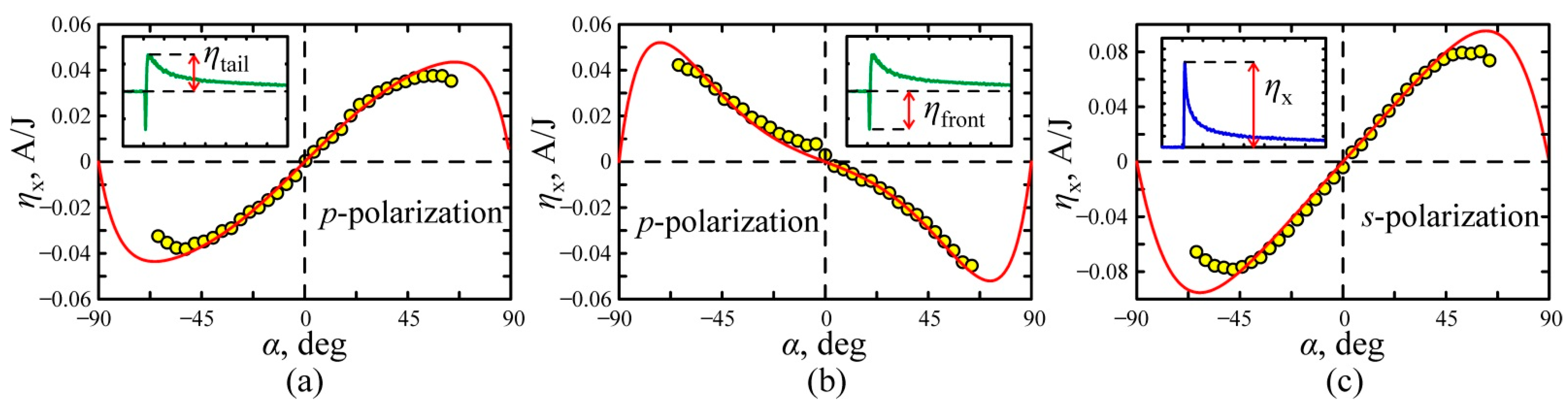


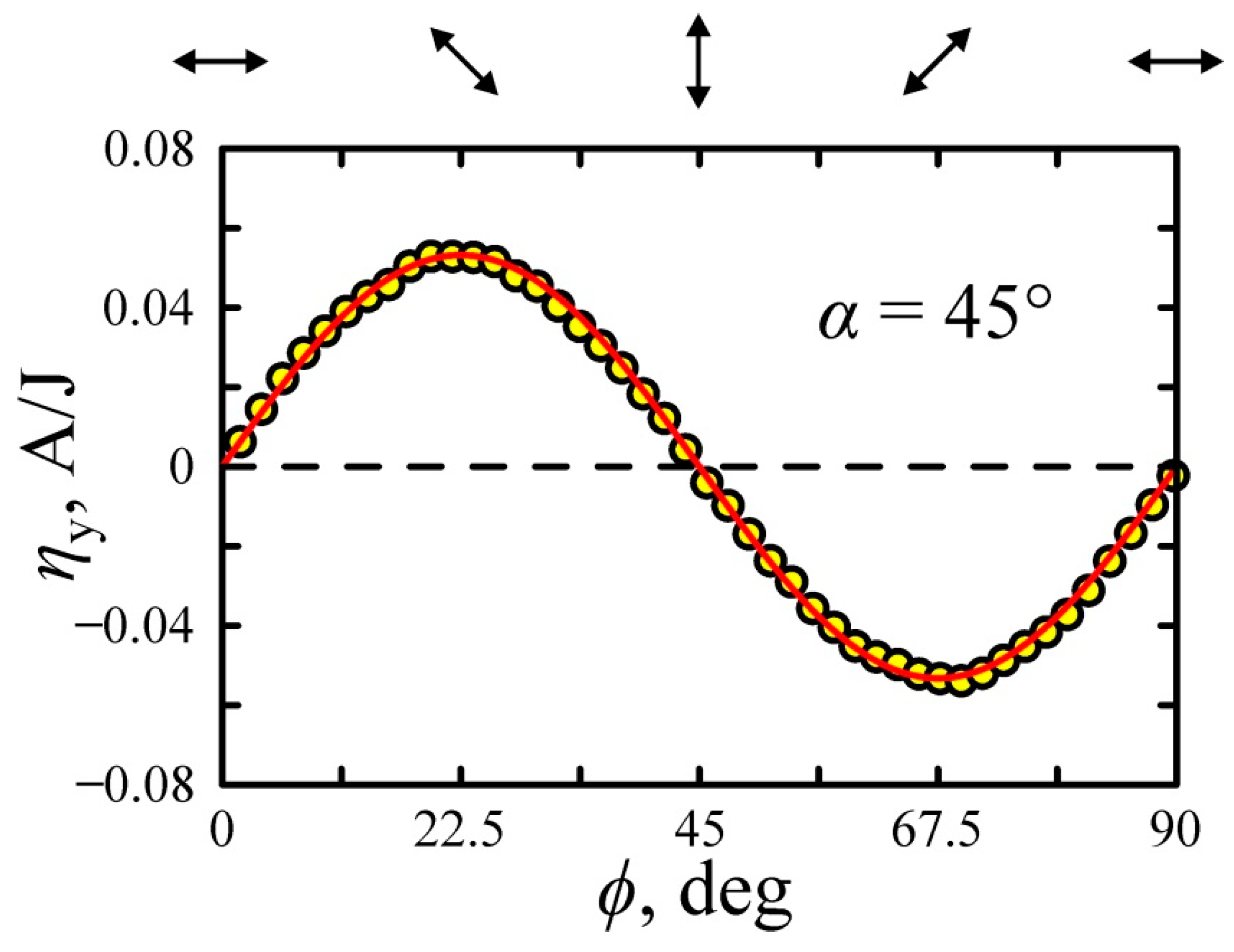
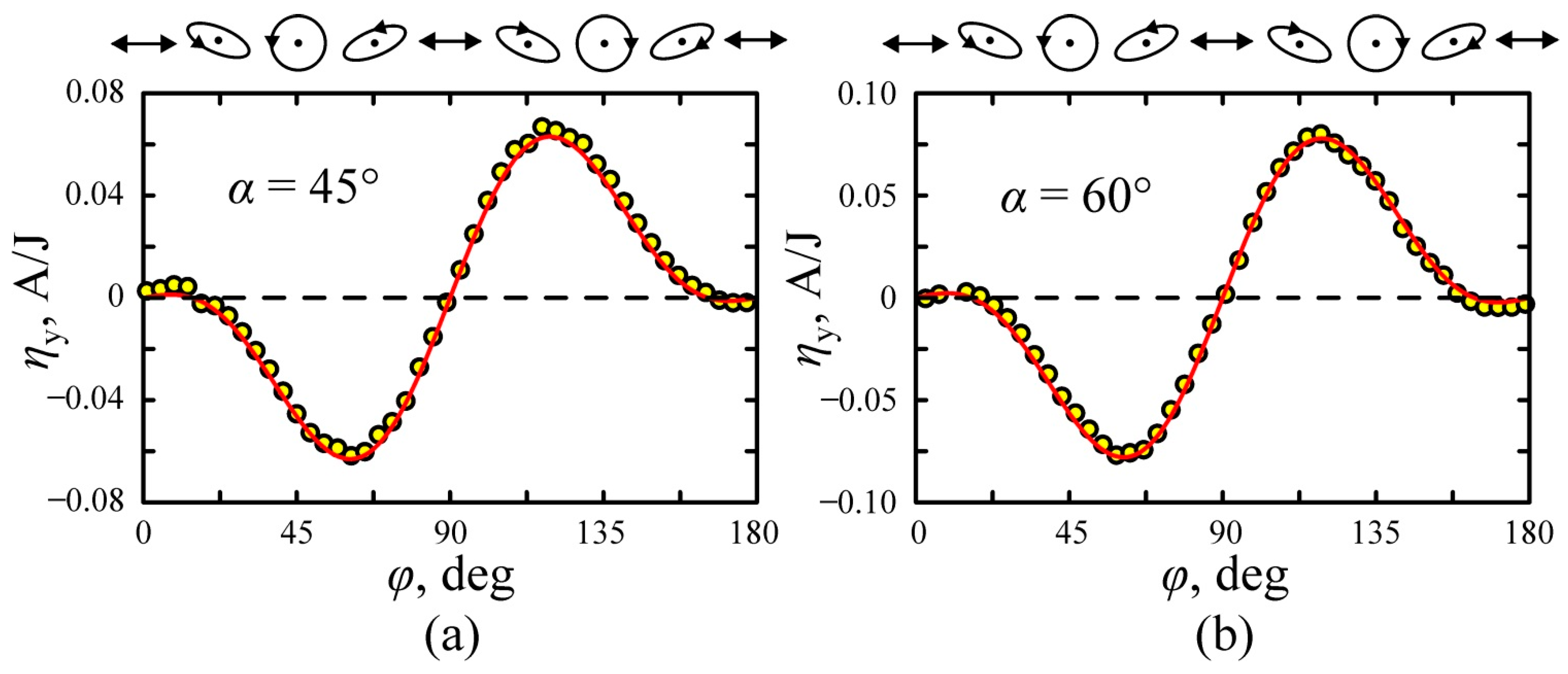
| Gxxzz, 10−14, m/(ΩV) | Γxxyy, 10−14, m/(ΩV) | Γxyxy, 10−14, m/(ΩV) | Γxyyx, 10−14, m/(ΩV) | n | |
| 4.2 + 3.3i | 11.65 − 7.7i | 11.65 + 6.4i | 164.1 + 76.9i | 1.44 − 0.29i | |
| TSPGE, ns | TPDE, ns | TPd, ns | TAg, ns | ||
| 1 | 1.5 | 65 | 800 | 0.269 | 0.146 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saushin, A.S.; Mikheev, G.M.; Vanyukov, V.V.; Svirko, Y.P. The Surface Photogalvanic and Photon Drag Effects in Ag/Pd Metal-Semiconductor Nanocomposite. Nanomaterials 2021, 11, 2827. https://doi.org/10.3390/nano11112827
Saushin AS, Mikheev GM, Vanyukov VV, Svirko YP. The Surface Photogalvanic and Photon Drag Effects in Ag/Pd Metal-Semiconductor Nanocomposite. Nanomaterials. 2021; 11(11):2827. https://doi.org/10.3390/nano11112827
Chicago/Turabian StyleSaushin, Aleksandr S., Gennady M. Mikheev, Viatcheslav V. Vanyukov, and Yuri P. Svirko. 2021. "The Surface Photogalvanic and Photon Drag Effects in Ag/Pd Metal-Semiconductor Nanocomposite" Nanomaterials 11, no. 11: 2827. https://doi.org/10.3390/nano11112827
APA StyleSaushin, A. S., Mikheev, G. M., Vanyukov, V. V., & Svirko, Y. P. (2021). The Surface Photogalvanic and Photon Drag Effects in Ag/Pd Metal-Semiconductor Nanocomposite. Nanomaterials, 11(11), 2827. https://doi.org/10.3390/nano11112827






