Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency
Abstract
:1. Introduction
2. Materials and Methods
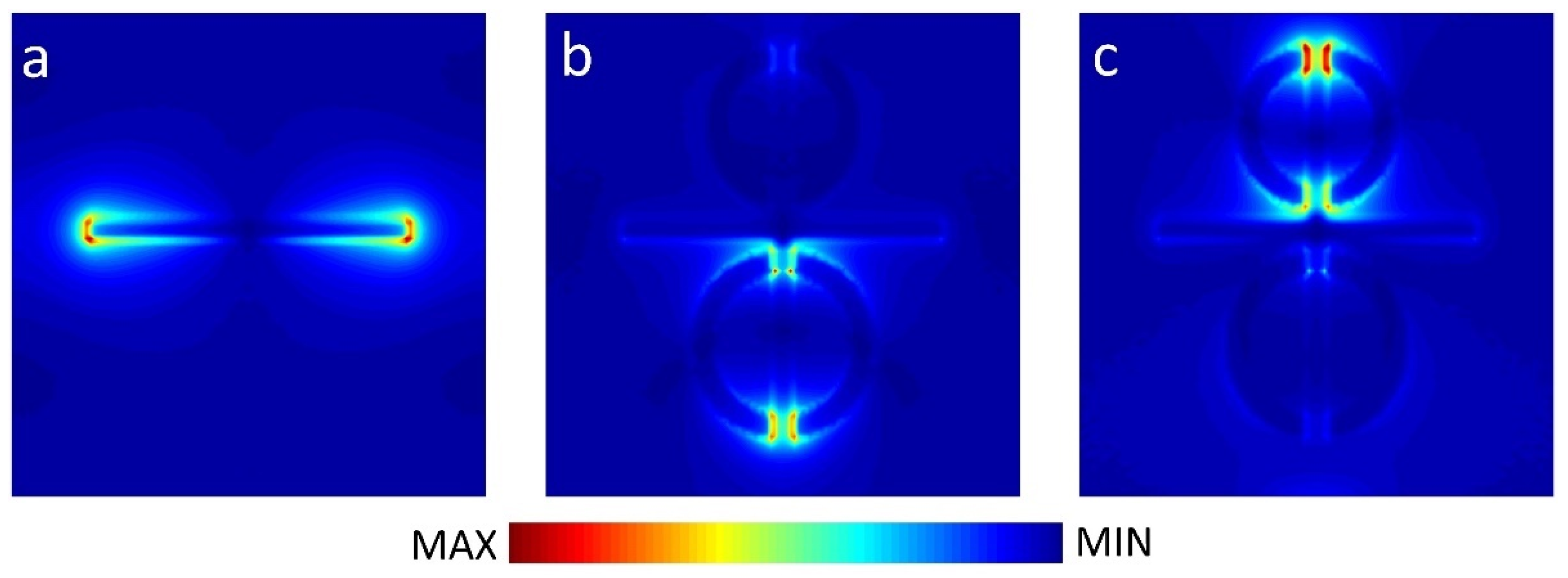
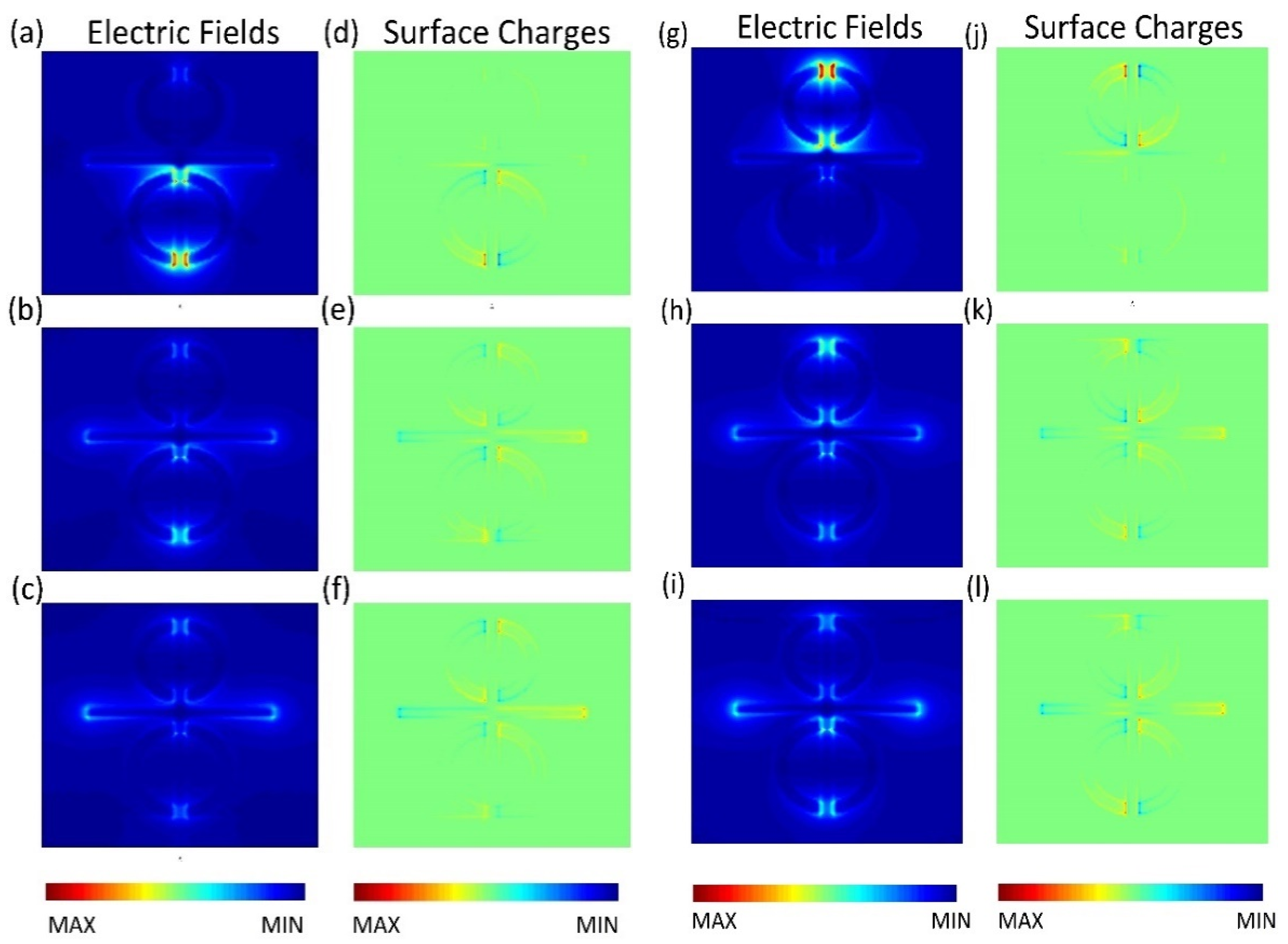
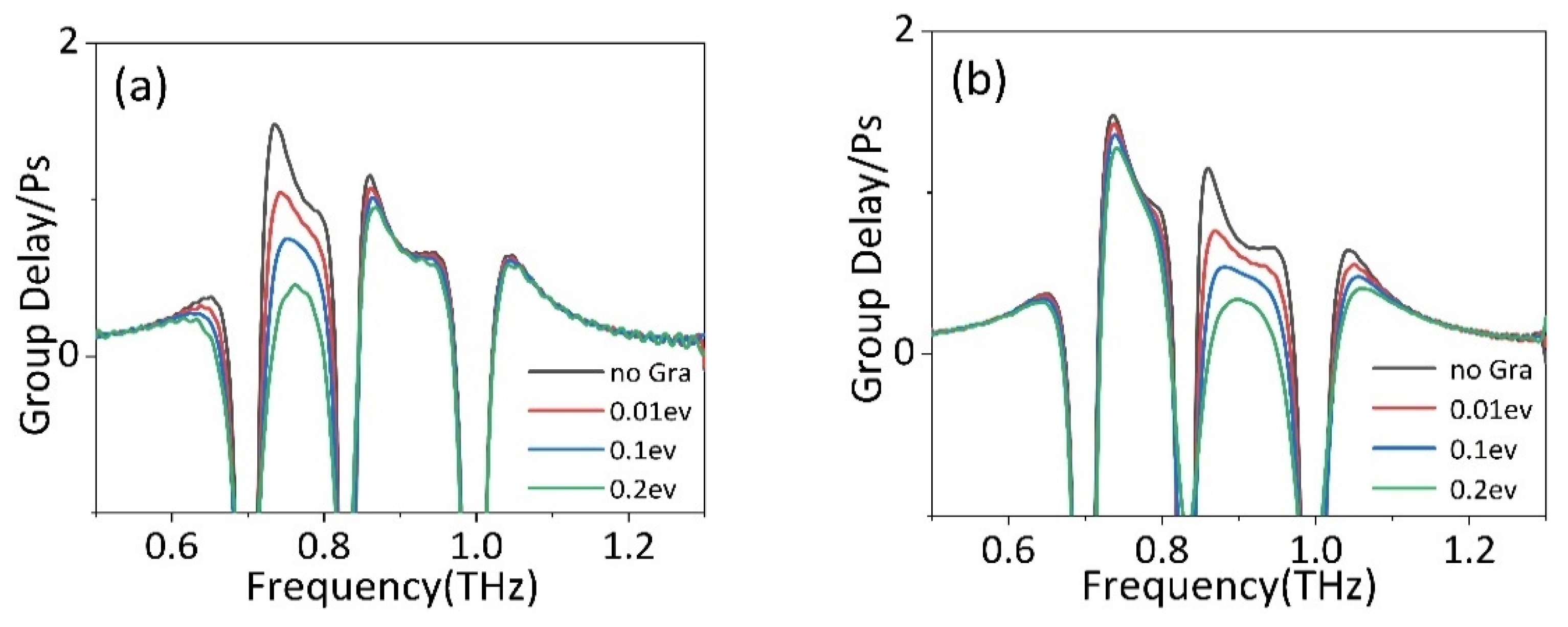
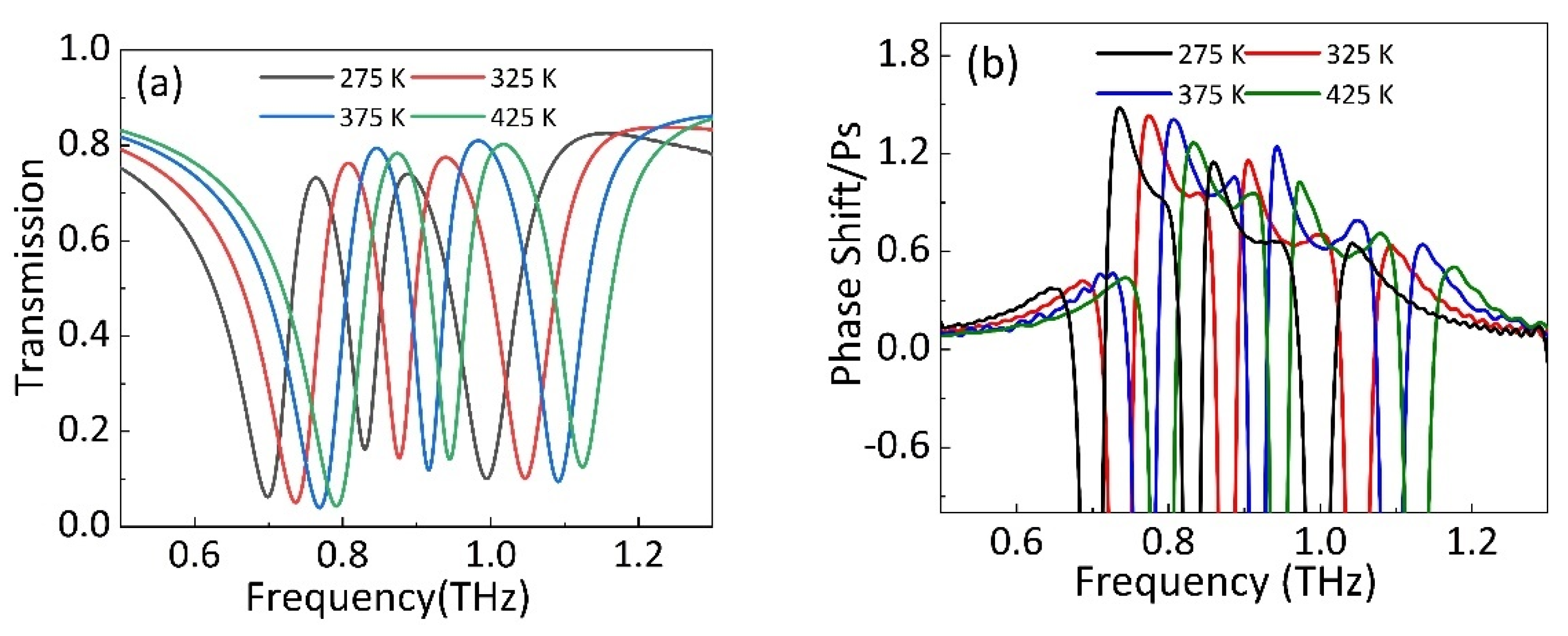
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harris, S.E. Electromagnetically Induced Transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Miller, F.P.; Vandome, A.F.; Mcbrewster, J. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar]
- Lu, X.Q.; Shi, J.H.; Liu, R.; Guan, C. Highly-dispersive electromagnetic induced transparency in planar symmetric metamaterials. Opt. Express 2012, 20, 17581–17590. [Google Scholar] [CrossRef]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Sonnichsen, C.; Giessen, H. Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. 2010, 10, 1103–1107. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fedotov, V.A.; Zheludev, N.I.; Prosvirnin, S.L. Metamaterial Analog of Electromagnetically Induced Transparency. Phys. Rev. Lett. 2008, 101, 53903. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.H.; Yang, X.; Gu, J.Q.; Jiang, J.; Yue, W. Broadband plasmon induced transparency in terahertz metamaterials. Nanotechnology 2013, 24, 214003. [Google Scholar] [CrossRef]
- Yang, Y.M.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Liu, D.; Yang, H.L. Electromagnetically induced transparency in an integrated metasurface based on bright–dark–bright mode coupling. J. Phys. D Appl. Phys. 2019, 52, 175305. [Google Scholar] [CrossRef]
- Tassin, P.; Zhang, L.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Planar designs for electromagnetically induced transparency in metamaterials. Opt. Express 2009, 17, 5595–5605. [Google Scholar] [CrossRef]
- Singh, R.; Rockstuhl, C.; Lederer, F.; Zhang, W. Coupling between a dark and a bright eigenmode in a terahertz metamaterial. Phys. Rev. B 2009, 79, 144–147. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhang, H.Y.; Zhao, Y.K.; Liu, S.D.; Cao, M.Y.; Zhang, Y.P. Broadband tunable terahertz plasmon-induced transparency in Dirac semimetals. Opt. Laser Technol. 2018, 104, 210–215. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Li, J.; Li, H.Y.; Yao, C.B.; Yuan, P. Plasmon-induced-transparency in subwavelength structures. Opt. Laser Technol. 2013, 49, 202–208. [Google Scholar] [CrossRef]
- Phillips, D.F.; Fleischhauer, A.; Mair, R.A.; Walsworth, L.; Lukin, M.D. Storage of light in atomic vapor. Phys. Rev. Lett. 2001, 86, 783–786. [Google Scholar] [CrossRef] [Green Version]
- Liu, X. Electromagnetically induced transparency in terahertz plasmonic metamaterials via dual excitation pathways of the dark mode. Appl. Phys. Lett. 2012, 100, 36. [Google Scholar]
- Niu, X.X.; Hu, X.Y.; Yan, Q.C.; Zhu, J.K.; Cheng, H.D.; Huang, Y.F.; Lu, C.C.; Fu, Y.L.; Gong, Q.H. Plasmon-induced transparency effect for ultracompact on-chip devices. Nanophotonics 2019, 8, 1125–1149. [Google Scholar] [CrossRef]
- Zhao, Z.; Zheng, X.; Wei, P.; Zhang, J.; Shi, W. Localized terahertz electromagnetically-induced transparency-like phenomenon in a conductively coupled trimer metamolecule. Opt. Express 2017, 25, 24410. [Google Scholar] [CrossRef] [PubMed]
- He, X.J.; Wang, Y.; Tao, M.N.; Yu, Y.Z.; Pei, Z.; Wang, B.H.; Yang, Y.Q.; Jiang, J.X.; Geng, Z.G. Dynamical switching of electromagnetically induced reflectance in complementary terahertz metamaterials. Opt. Commun. 2019, 448, 98–103. [Google Scholar] [CrossRef]
- Chen, M.M.; Xiao, Z.Y.; Lu, X.J.; Lv, F.; Zhou, Y.J. Simulation of dynamically tunable and switchable electromagnetically induced transparency analogue based on metal-graphene hybrid metamaterial. Carbon 2020, 159, 273–282. [Google Scholar] [CrossRef]
- He, X.; Liu, F.; Lin, F.T.; Shi, W. Graphene patterns supported terahertz tunable plasmon induced transparency. Opt. Express 2018, 26, 9931–9944. [Google Scholar] [CrossRef] [PubMed]
- Shu, C.; Mei, J.S. Analogue of tunable electromagnetically induced transparency based on graphene-nanostrip in two perpendicular polarization directions. Opt. Commun. 2019, 439, 16–20. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, M.Z.; Zheng, M.F.; Xiong, C.; Zhang, B.; Peng, Y.; Li, H. Dual plasmon-induced transparency and slow light effect in monolayer graphene structure with rectangular defects. J. Phys. D Appl. Phys. 2018, 52, 025104. [Google Scholar] [CrossRef]
- Liu, T.; Wang, H.; Yong, L.; Xiao, L.; Zhou, C.; Liu, Y.; Xu, C.; Xiao, S. Independently tunable dual-spectral electromagnetically induced transparency in a terahertz metal-graphene metamaterial. J. Phys. D Appl. Phys. 2018, 51, 415105. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.X.; Jin, K.L.; He, X.Y.; Zhang, W.J.; Lin, X.; Jin, Z.M.; Ma, G.H. Independently tunable dual-band plasmon induced transparency enabled by graphene-based terahertz metamaterial. Appl. Phys. Express 2019, 12, 075010. [Google Scholar] [CrossRef]
- Liu, Z.M.; Zhang, X.; Zhang, Z.B.; Gao, E.D.; Zhou, F.Q.; Li, H.J.; Luo, X. Simultaneous switching at multiple frequencies and triple plasmon-induced transparency in multilayer patterned graphene-based terahertz metamaterial. New J. Phys. 2020, 22, 083006. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, B.; Lan, C.; Ke, B.; Qu, Z. Tunable silicon-based all-dielectric metamaterials with strontium titanate thin film in terahertz range. Opt. Express 2017, 25, 22158. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M. Design and modulation of the plasmon-induced transparency based on terahertz metamaterials. Infrared Phys. Technol. 2020, 108, 103377. [Google Scholar] [CrossRef]
- Song, Z.Y.; Chen, A.; Zhang, J.H. Terahertz switching between broadband absorption and narrowband absorption. Opt. Express 2020, 28, 2037–2044. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Meng, H.; Deng, S.; Lao, C.; Wei, Z.; Wang, F.; Tan, C.; Huang, X. Hybrid Metal Graphene-Based Tunable Plasmon-Induced Transparency in Terahertz Metasurface. Nanomaterials 2019, 9, 385. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Choi, M.; Kim, T.T.; Lee, S.; Liu, M.; Yin, X.; Choi, H.K.; Lee, S.S.; Choi, C.G.; Choi, S.Y. Switching teraherz waves with gate-controlled active graphene metamaterials. Nat. Mater. 2012, 11, 936–941. [Google Scholar] [CrossRef] [Green Version]
- Němec, H.; Kuzel, P.; Duvillaret, L.; Pashkin, A.; Dressel, M.; Sebastian, M.T. Highly tunable photonic crystal filter for the terahertz range. Opt. Lett. 2005, 30, 549–551. [Google Scholar] [CrossRef]
- Kužel, P.; Kadlec, F. Tunable structures and modulators for THz light. C. R. Phys. 2008, 9, 197–214. [Google Scholar] [CrossRef]
- Liu, T.T.; Zhou, C.B.; Cheng, L.; Jiang, X.Y.; Wang, G.Z.; Xu, C.; Xiao, S.Y. Actively tunable slow light in a terahertz hybrid metal-graphene metamaterial. J. Opt. 2019, 21, 035101. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.L.; Zhang, S.; Wang, Y.; Park, Y.S.; Zentgraf, T.; Bartal, G.; Yin, X.B.; Zhang, X. Mapping the near-field dynamics in plasmon-induced transparency. Phys. Rev. B 2012, 86, 155148. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.M.; Gao, E.D.; Zhang, Z.B.; Li, H.J.; Xu, H.; Zhang, X.; Luo, X.; Zhou, F.Q. Dual-mode on-to-off modulation of plasmon-induced transparency and coupling effect in patterned graphene-based terahertz metasurface. Nanoscale Res. Lett. 2020, 159, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Miyata, M.; Hirohata, J.; Nagasaki, Y.; Takahara, J. Multi-spectral plasmon induced transparency via in-plane dipole and dual-quadrupole coupling. Opt. Express 2014, 22, 11399–11406. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Hua, L.; Liu, X.; Dong, M. Plasmonic analog of electromagnetically induced transparency in multi-nanoresonator-coupled. Phys. Rev. A 2012, 85, 1–7. [Google Scholar]
- Anonymous. Frequency selective surfaces: Theory and design [Book Review]. IEEE Signal. Proc. Mag. 2001, 18, 94. [Google Scholar] [CrossRef]
- Qi, L.M.; Liu, C. Broadband multilayer graphene metamaterial absorbers. Opt. Mater. Express 2019, 9, 1298–1309. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Wang, G.; Jia, Y.; Shao, Y.; Chen, C.; Han, J.; Gao, Y.; Gao, Y. Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency. Nanomaterials 2021, 11, 2876. https://doi.org/10.3390/nano11112876
Wu T, Wang G, Jia Y, Shao Y, Chen C, Han J, Gao Y, Gao Y. Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency. Nanomaterials. 2021; 11(11):2876. https://doi.org/10.3390/nano11112876
Chicago/Turabian StyleWu, Tong, Guan Wang, Yang Jia, Yabin Shao, Chen Chen, Jing Han, Yang Gao, and Yachen Gao. 2021. "Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency" Nanomaterials 11, no. 11: 2876. https://doi.org/10.3390/nano11112876
APA StyleWu, T., Wang, G., Jia, Y., Shao, Y., Chen, C., Han, J., Gao, Y., & Gao, Y. (2021). Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency. Nanomaterials, 11(11), 2876. https://doi.org/10.3390/nano11112876





