The Size and Shape Effects on the Melting Point of Nanoparticles Based on the Lennard-Jones Potential Function
Abstract
:1. Introduction
2. Theory and Model
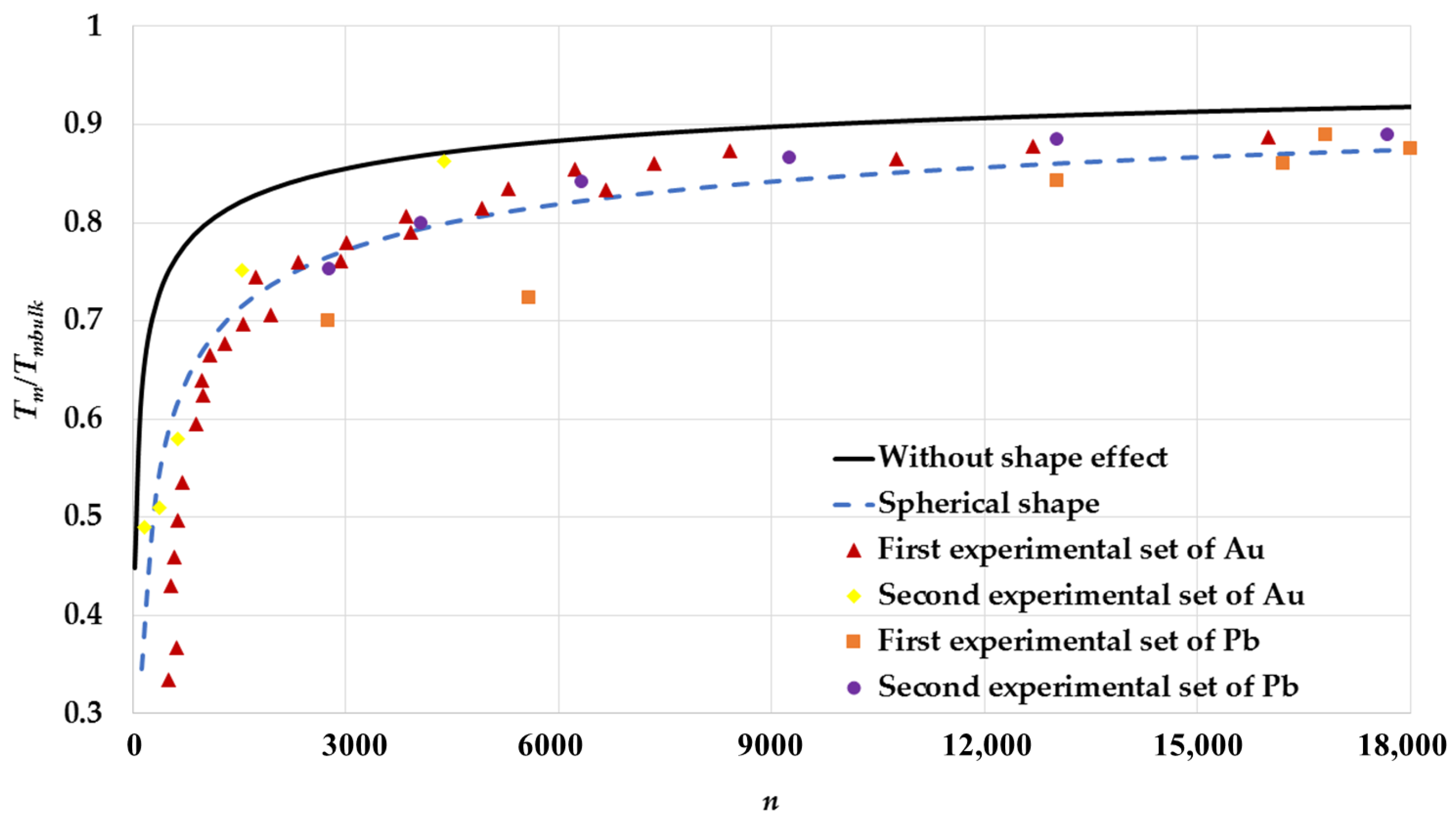
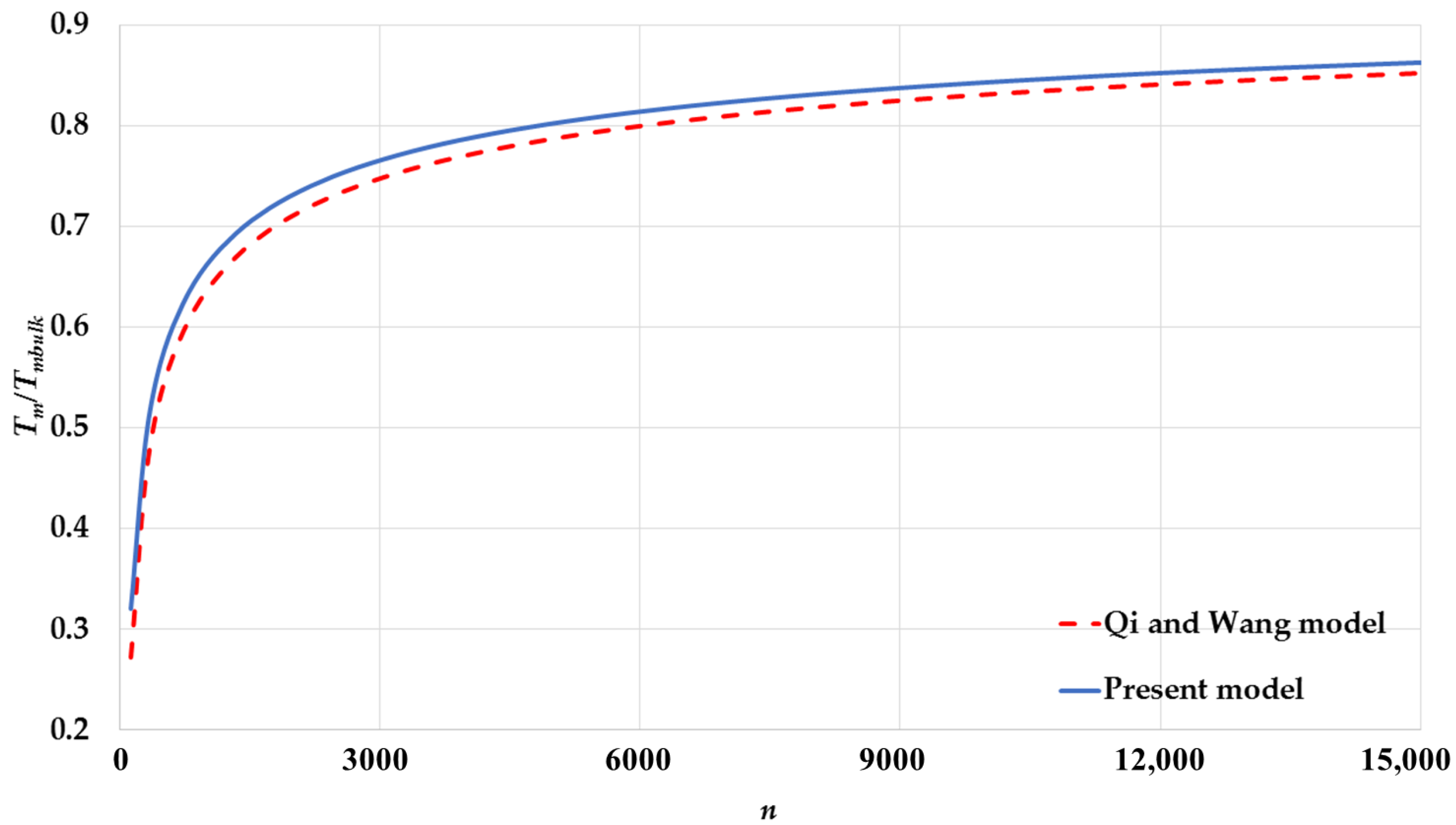
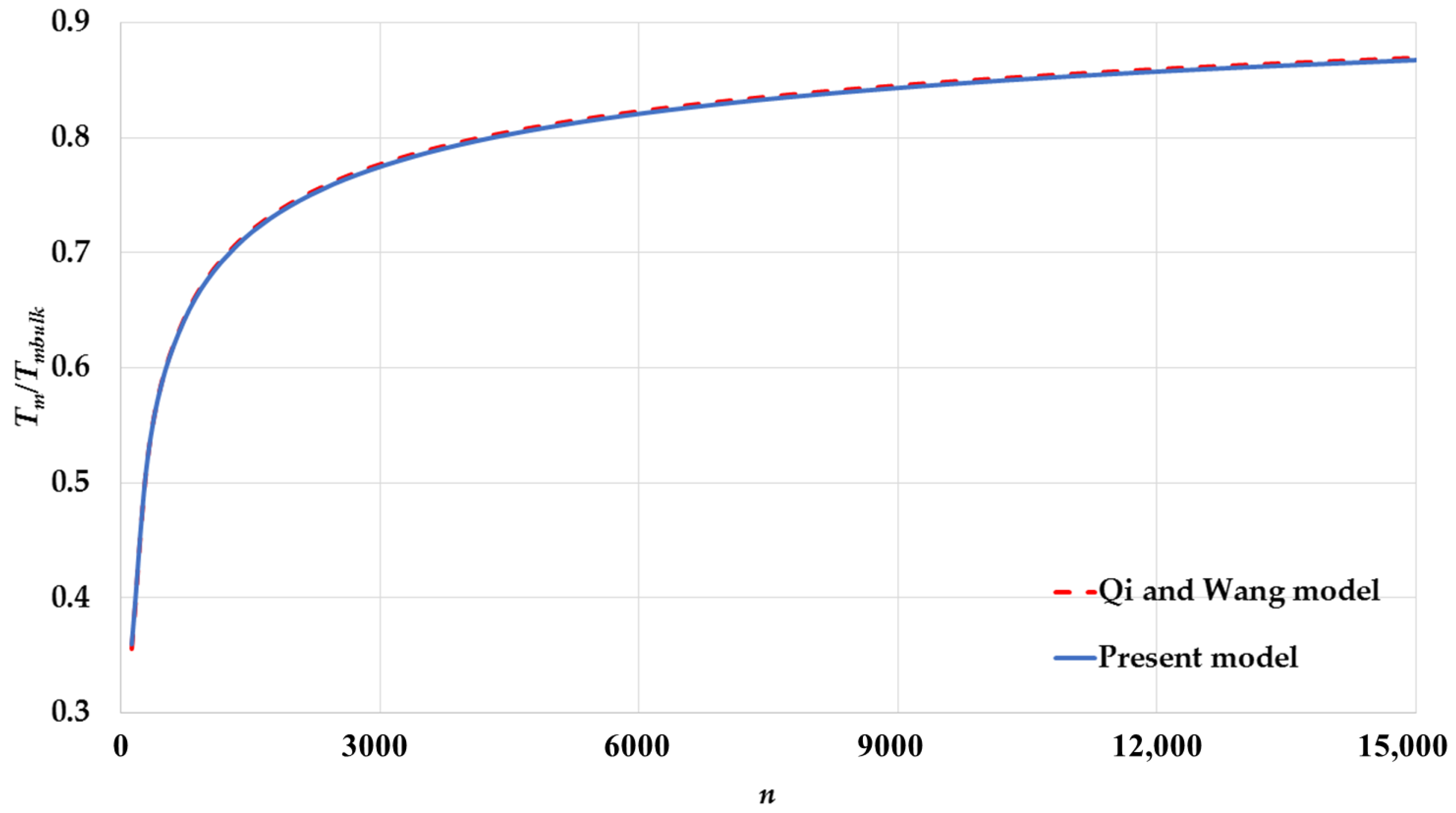
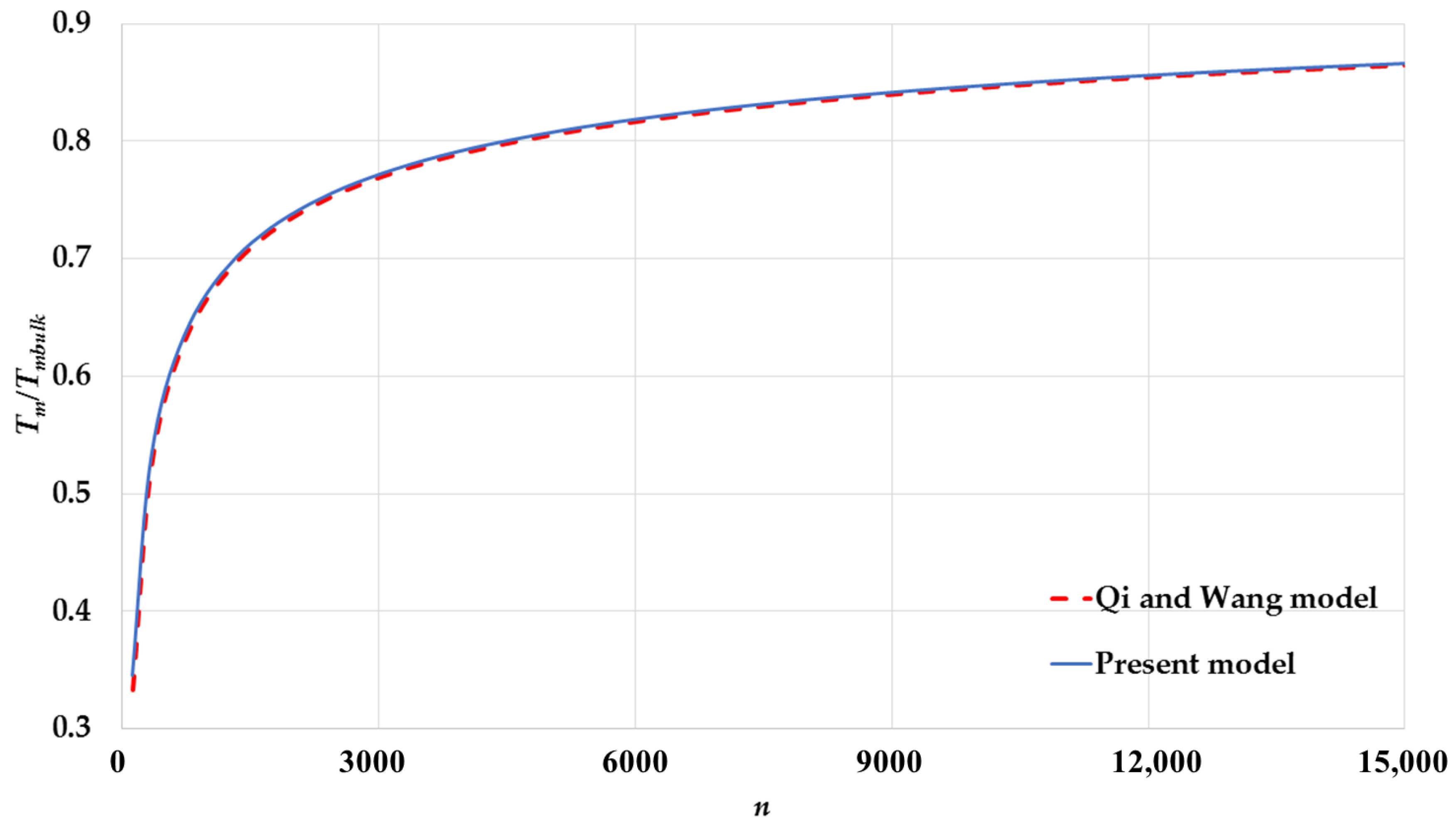
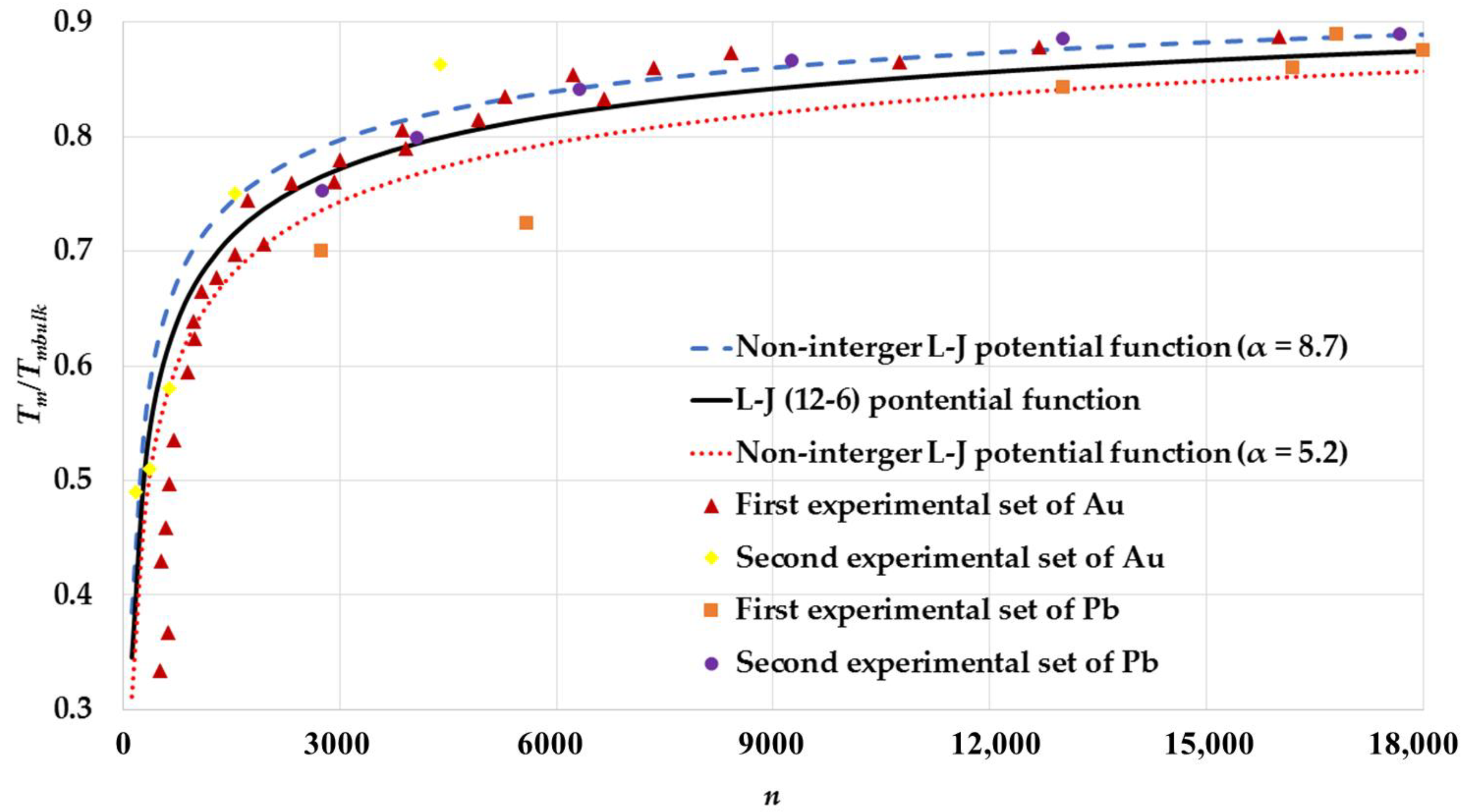
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Takagi, M. Electron-Diffraction Study of Liquid-Solid Transition of Thin Metal Films. J. Phys. Soc. Jpn. 1954, 9, 359–363. [Google Scholar] [CrossRef]
- Buffat, P.; Borel, J.-P. Size effect on the melting temperature of gold particles. Phys. Rev. A 1976, 13, 2287–2298. [Google Scholar] [CrossRef] [Green Version]
- Levitas, V.I.; Pantoya, M.L.; Chauhan, G.; Rivero, I. Effect of the Alumina Shell on the Melting Temperature Depression for Aluminum Nanoparticles. J. Phys. Chem. C 2009, 113, 14088–14096. [Google Scholar] [CrossRef] [Green Version]
- Lai, S.L.; Ramanath, G.; Allen, L.H.; Infante, P.; Ma, Z. High-speed (104 °C/s) scanning microcalorimetry with monolayer sensitivity (J/m2). Appl. Phys. Lett. 1995, 67, 1229–1231. [Google Scholar] [CrossRef]
- Dick, K.; Dhanasekaran, T.; Zhang, Z.; Meisel, D. Size-Dependent Melting of Silica-Encapsulated Gold Nanoparticles. J. Am. Chem. Soc. 2002, 124, 2312–2317. [Google Scholar] [CrossRef] [PubMed]
- Coombes, C.J. The melting of small particles of lead and indium. J. Phys. F Met. Phys. 1972, 2, 441–449. [Google Scholar] [CrossRef]
- Skripov, V.P.; Koverda, V.P.; Skokov, V.N. Size effect on melting of small particles. Phys. Status Solidi 1981, 66, 109–118. [Google Scholar] [CrossRef]
- Jiang, H.; Moon, K.-S.; Dong, H.; Hua, F.; Wong, C. Size-dependent melting properties of tin nanoparticles. Chem. Phys. Lett. 2006, 429, 492–496. [Google Scholar] [CrossRef]
- Cui, Q.; Rajathurai, K.; Jia, W.; Li, X.; Gao, F.; Lei, Y.; Gu, Z. Synthesis of Single Crystalline Tin Nanorods and Their Application as Nanosoldering Materials. J. Phys. Chem. C 2010, 114, 21938–21942. [Google Scholar] [CrossRef]
- Zou, G.; Yan, J.; Mu, F.; Wu, A.; Ren, J.; Hu, A. Low Temperature Bonding of Cu Metal through Sintering of Ag Nanoparticles for High Temperature Electronic Application. Open Surf. Sci. J. 2010, 3, 70–75. [Google Scholar] [CrossRef]
- Goldstein, A.N.; Echer, C.M.; Alivisatos, A.P. Melting in Semiconductor Nanocrystals. Science 1992, 256, 1425–1427. [Google Scholar] [CrossRef]
- Pawlow, P. Über die abhängigkeit des schmelzpunktes von der oberflächenenergie eines festen körpers. Z. Phys. Chem. 1909, 65, 1–35. [Google Scholar] [CrossRef]
- Shi, F.G. Size dependent thermal vibrations and melting in nanocrystals. J. Mater. Res. 1994, 9, 1307–1314. [Google Scholar] [CrossRef]
- Letellier, P.; Mayaffre, A.; Turmine, M. Melting point depression of nanosolids: Nonextensive thermodynamics approach. Phys. Rev. B 2007, 76, 045428. [Google Scholar] [CrossRef]
- Nanda, K.K. Size-dependent melting of nanoparticles: Hundred years of thermodynamic model. Pramana 2009, 72, 617–628. [Google Scholar] [CrossRef]
- Petters, M.; Kasparoglu, S. Predicting the influence of particle size on the glass transition temperature and viscosity of secondary organic material. Sci. Rep. 2020, 10, 15170. [Google Scholar] [CrossRef]
- Zhang, M.; Efremov, M.Y.; Schiettekatte, F.; Olson, E.A.; Kwan, A.T.; Lai, S.L.; Wisleder, T.; Greene, J.E.; Allen, L.H. Size-dependent melting point depression of nanostructures: Nanocalorimetric measurements. Phys. Rev. B 2000, 62, 10548–10557. [Google Scholar] [CrossRef] [Green Version]
- Reiss, H.; Wilson, I.B. The effect of surface on melting point. J. Colloid Sci. 1948, 3, 551–561. [Google Scholar] [CrossRef]
- Lai, S.L.; Carlsson, J.R.A.; Allen, L.H. Melting point depression of Al clusters generated during the early stages of film growth: Nanocalorimetry measurements. Appl. Phys. Lett. 1998, 72, 1098–1100. [Google Scholar] [CrossRef]
- Couchman, P.R.; Jesser, W.A. Thermodynamic theory of size dependence of melting temperature in metals. Nature 1977, 269, 481–483. [Google Scholar] [CrossRef]
- Vanfleet, R.R.; Mochel, J. Thermodynamics of melting and freezing in small particles. Surf. Sci. 1995, 341, 40–50. [Google Scholar] [CrossRef]
- Xie, D.; Wang, M.P.; Qi, W.H. A simplified model to calculate the surface-to-volume atomic ratio dependent cohesive energy of nanocrystals. J. Physics Condens. Matter 2004, 16, L401–L405. [Google Scholar] [CrossRef]
- Qi, W.H.; Wang, M.P.; Liu, Q.H. Shape factor of nonspherical nanoparticles. J. Mater. Sci. 2005, 40, 2737–2739. [Google Scholar] [CrossRef]
- Qi, W.; Wang, M. Size and shape dependent melting temperature of metallic nanoparticles. Mater. Chem. Phys. 2004, 88, 280–284. [Google Scholar] [CrossRef]
- Qi, W. Nanoscopic Thermodynamics. Accounts Chem. Res. 2016, 49, 1587–1595. [Google Scholar] [CrossRef] [PubMed]
- Qi, W.H.; Wang, M.P.; Zhou, M.; Hu, W.Y. Surface-area-difference model for thermodynamic properties of metallic nanocrystals. J. Phys. D Appl. Phys. 2005, 38, 1429–1436. [Google Scholar] [CrossRef]
- Safaei, A.; Shandiz, M.A.; Sanjabi, S.; Barber, Z.H. Modelling the size effect on the melting temperature of nanoparticles, nanowires and nanofilms. J. Phys. Condens. Matter 2007, 19, 216216. [Google Scholar] [CrossRef]
- Safaei, A. Shape, Structural, and Energetic Effects on the Cohesive Energy and Melting Point of Nanocrystals. J. Phys. Chem. C 2010, 114, 13482–13496. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Wu, D.; Deng, Y.; Shao, J.; Chen, L.; Fang, D. Size and shape dependent melting temperature of metallic nanomaterials. J. Phys. Condens. Matter 2018, 31, 075701. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Ma, Y.; Fu, X.; Li, M. A Comprehensive Understanding of the Melting Temperature of Nanocrystals: Implications for Catalysis. ACS Appl. Nano Mater. 2020, 3, 1583–1591. [Google Scholar] [CrossRef]
- Dash, J.G. History of the search for continuous melting. Rev. Mod. Phys. 1999, 71, 1737–1743. [Google Scholar] [CrossRef]
- Aldossary, O.M. Generalized non-integer Lennard-Jones potential function vs. generalized Morse potential function for calculating cohesive energy and melting point of nanoparticles. J. King Saud Univ. Sci. 2020, 33, 101316. [Google Scholar] [CrossRef]
- Aldossary, O.M.; Al Rsheed, A. A New Generalized Morse Potential Function for Calculating Cohesive Energy of Nanoparticles. Energies 2020, 13, 3323. [Google Scholar] [CrossRef]
- Qi, W.; Wang, M.; Hu, W. Calculation of the cohesive energy of metallic nanoparticles by the Lennard–Jones potential. Mater. Lett. 2004, 58, 1745–1749. [Google Scholar] [CrossRef]
- Nayak, P.; Naik, S.R.; Sar, D.K. Improved Cohesive Energy of Metallic Nanoparticles by Using L–J Potential with Structural Effect. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 2705–2711. [Google Scholar] [CrossRef]
- Barakat, T.; Al-Dossary, O.; Alharbi, A.A. The Effect of mie-type potential range on the cohesive energy of metallic nanoparticles. Int. J. Nanosci. 2007, 6, 461–466. [Google Scholar] [CrossRef]
- Aldossary, O.M.; Al Rsheed, A. The effect of the parameter α of Morse potential on cohesive energy. J. King Saud Univ. Sci. 2019, 32, 1147–1151. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Morse, P.M. Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Carlsson, A. Beyond Pair Potentials in Elemental Transition Metals and Semiconductors. Solid State Phys. 1990, 43, 1–91. [Google Scholar] [CrossRef]
- Baskes, M.I. Many-Body Effects in fcc Metals: A Lennard-Jones Embedded-Atom Potential. Phys. Rev. Lett. 1999, 83, 2592–2595. [Google Scholar] [CrossRef]
- Eberhard, B. Computer Simulations for Thorium Doped Tungsten Crystals. Ph.D. Thesis, Augsburg University, Minneapolis, MN, USA, December 2008. [Google Scholar]
- Mardiyah, R.U.; Arkundato, A.; Misto; Purwandari, E. Energy Cohesive Calculation for Some Pure Metals Using the Lennard-Jones Potential in Lammps Molecular Dynamics. J. Physics Conf. Ser. 2020, 1491, 012020. [Google Scholar] [CrossRef]
- Mardiyah, R.U.; Arkundato, A.; Misto, M.; Purwandari, E. Parameters (σ, ε) of Lennard-Jones for Fe, Ni, Pb for Potential and Cr based on Melting Point Values Using the Molecular Dynamics Method of the LAMMPS Program. J. Phys. Conf. Ser. 2020, 1491, 012022. [Google Scholar]
- Qi, W. Size effect on melting temperature of nanosolids. Phys. B Condens. Matter 2005, 368, 46–50. [Google Scholar] [CrossRef]
- Solliard, C.; Flueli, M. Surface stress and size effect on the lattice parameter in small particles of gold and platinum. Surf. Sci. 1985, 156, 487–494. [Google Scholar] [CrossRef]
- Qi, W.; Wang, M.; Zhou, M.; Shen, X.; Zhang, X. Modeling cohesive energy and melting temperature of nanocrystals. J. Phys. Chem. Solids 2006, 67, 851–855. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1924, 106, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Guinea, F.; Rose, J.H.; Smith, J.R.; Ferrante, J. Scaling relations in the equation of state, thermal expansion, and melting of metals. Appl. Phys. Lett. 1984, 44, 53–55. [Google Scholar] [CrossRef]
- Periodic Table of Elements. Available online: https://www.webelements.com (accessed on 15 January 2021).
- Lee, J.; Nakamoto, M.; Tanaka, T. Thermodynamic study on the melting of nanometer-sized gold particles on graphite substrate. J. Mater. Sci. 2005, 40, 2167–2171. [Google Scholar] [CrossRef]
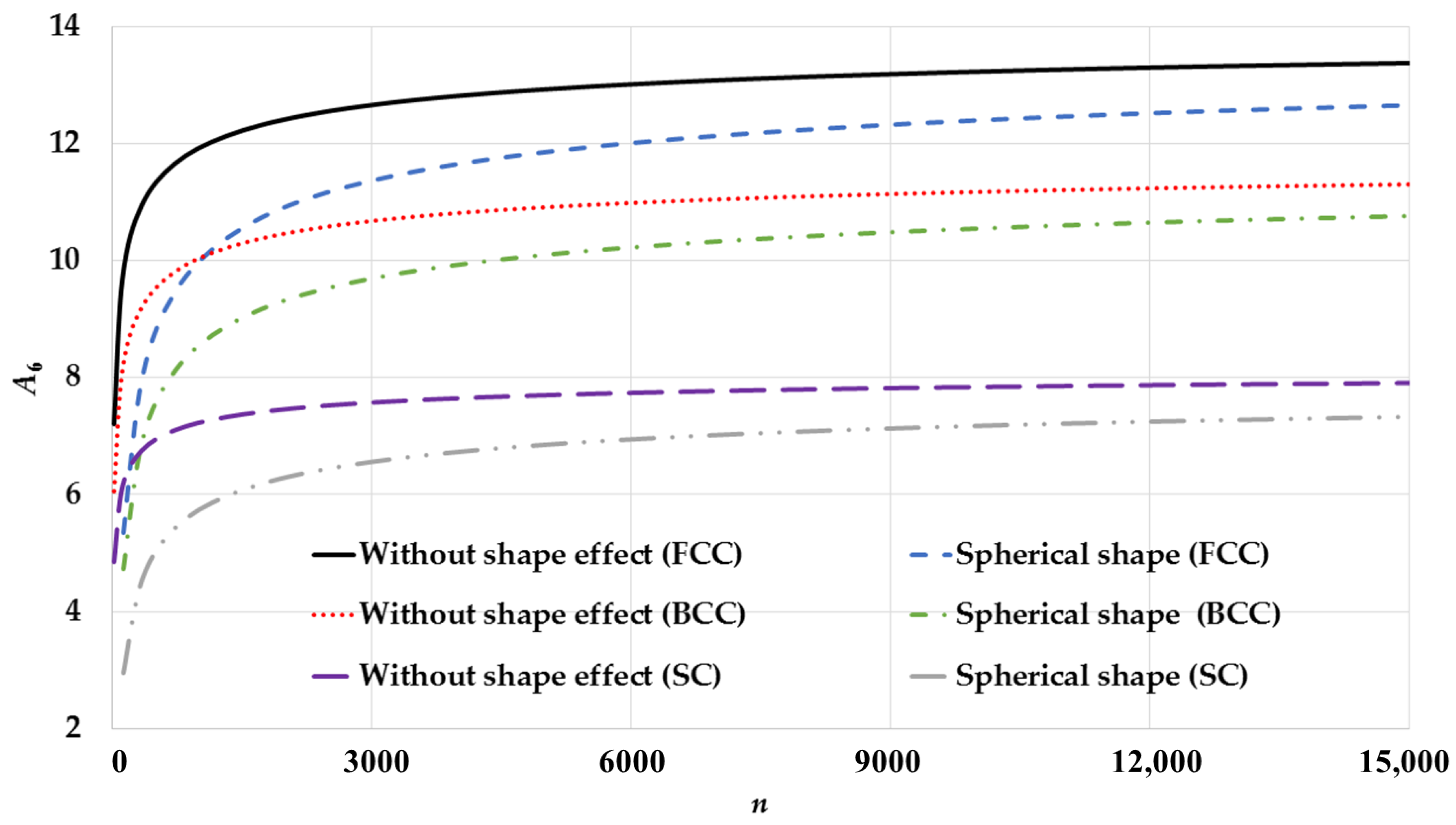
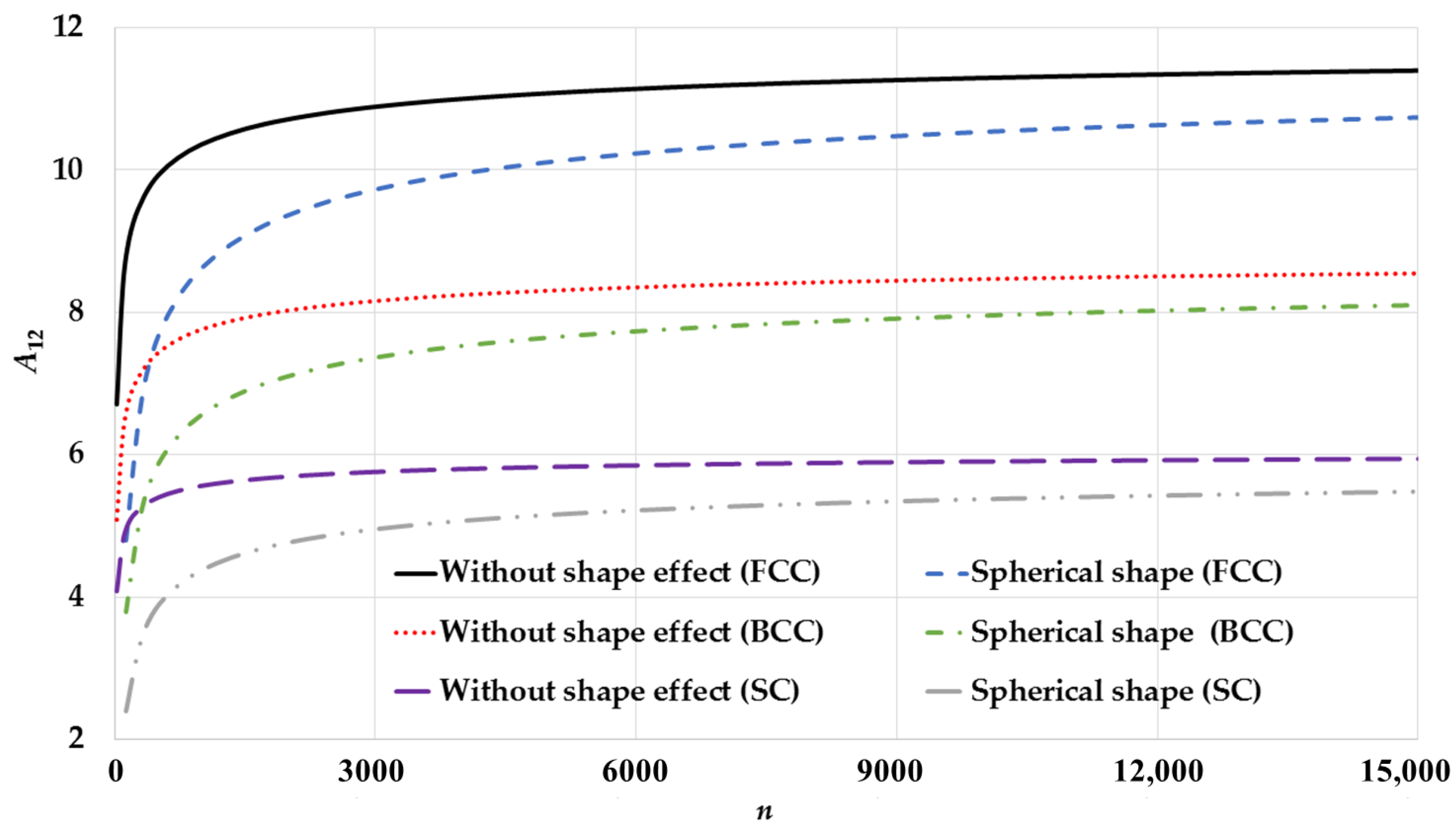

| Cubic Structure | ||
|---|---|---|
| FCC | ||
| BCC | ||
| SC |
| Cubic Structure | ||
|---|---|---|
| FCC | 14.45 | 12.13 |
| BCC | 12.25 | 9.11 |
| SC | 8.40 | 6.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Rsheed, A.; Aldawood, S.; Aldossary, O.M. The Size and Shape Effects on the Melting Point of Nanoparticles Based on the Lennard-Jones Potential Function. Nanomaterials 2021, 11, 2916. https://doi.org/10.3390/nano11112916
Al Rsheed A, Aldawood S, Aldossary OM. The Size and Shape Effects on the Melting Point of Nanoparticles Based on the Lennard-Jones Potential Function. Nanomaterials. 2021; 11(11):2916. https://doi.org/10.3390/nano11112916
Chicago/Turabian StyleAl Rsheed, Anwar, Saad Aldawood, and Omar M. Aldossary. 2021. "The Size and Shape Effects on the Melting Point of Nanoparticles Based on the Lennard-Jones Potential Function" Nanomaterials 11, no. 11: 2916. https://doi.org/10.3390/nano11112916
APA StyleAl Rsheed, A., Aldawood, S., & Aldossary, O. M. (2021). The Size and Shape Effects on the Melting Point of Nanoparticles Based on the Lennard-Jones Potential Function. Nanomaterials, 11(11), 2916. https://doi.org/10.3390/nano11112916






