Multifunctional Plasmonic Grating Based on the Phase Modulation of Excitation Light
Abstract
:1. Introduction
2. Results and Discussion
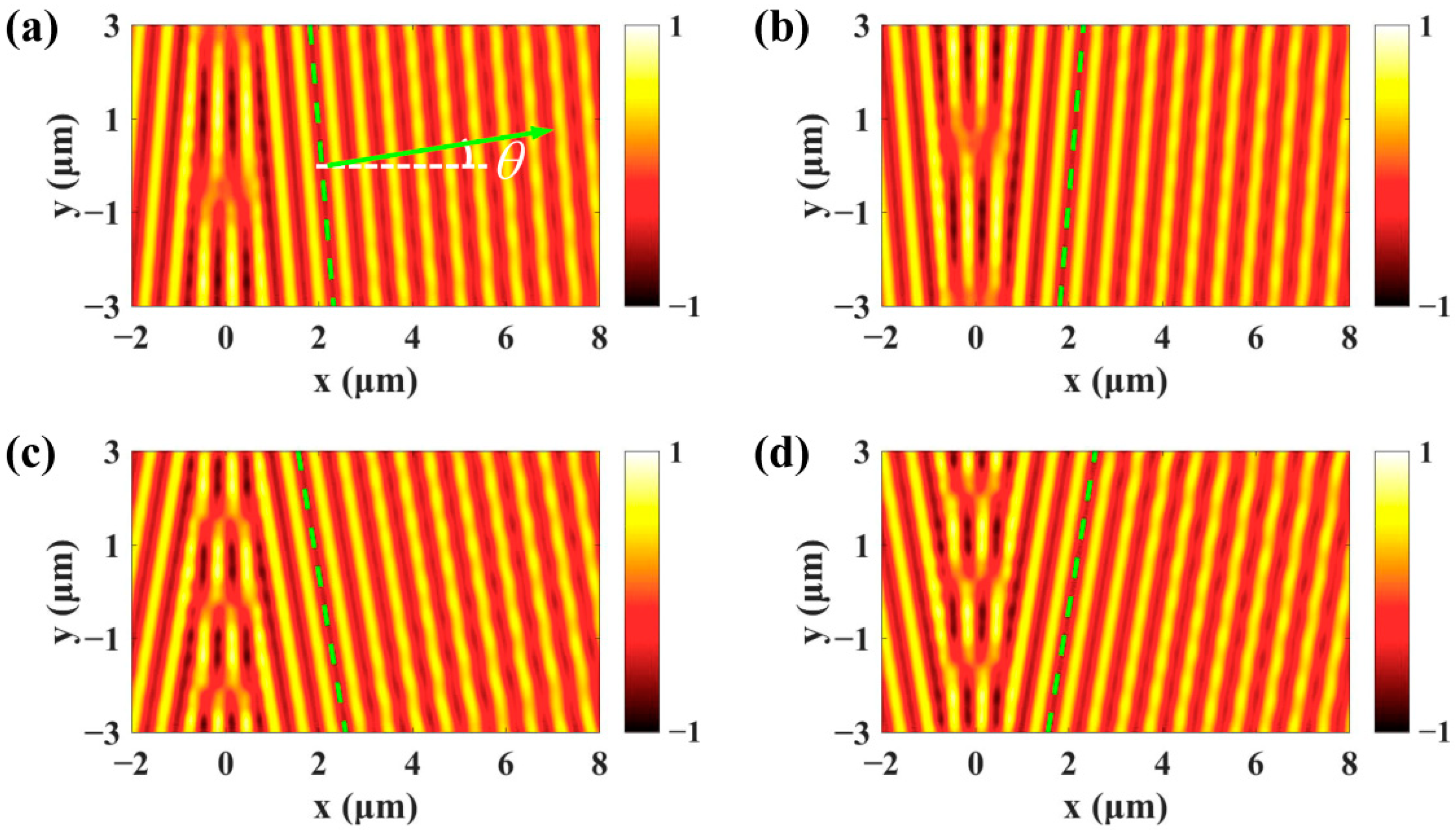
2.1. Cherenkov SPPs Wake
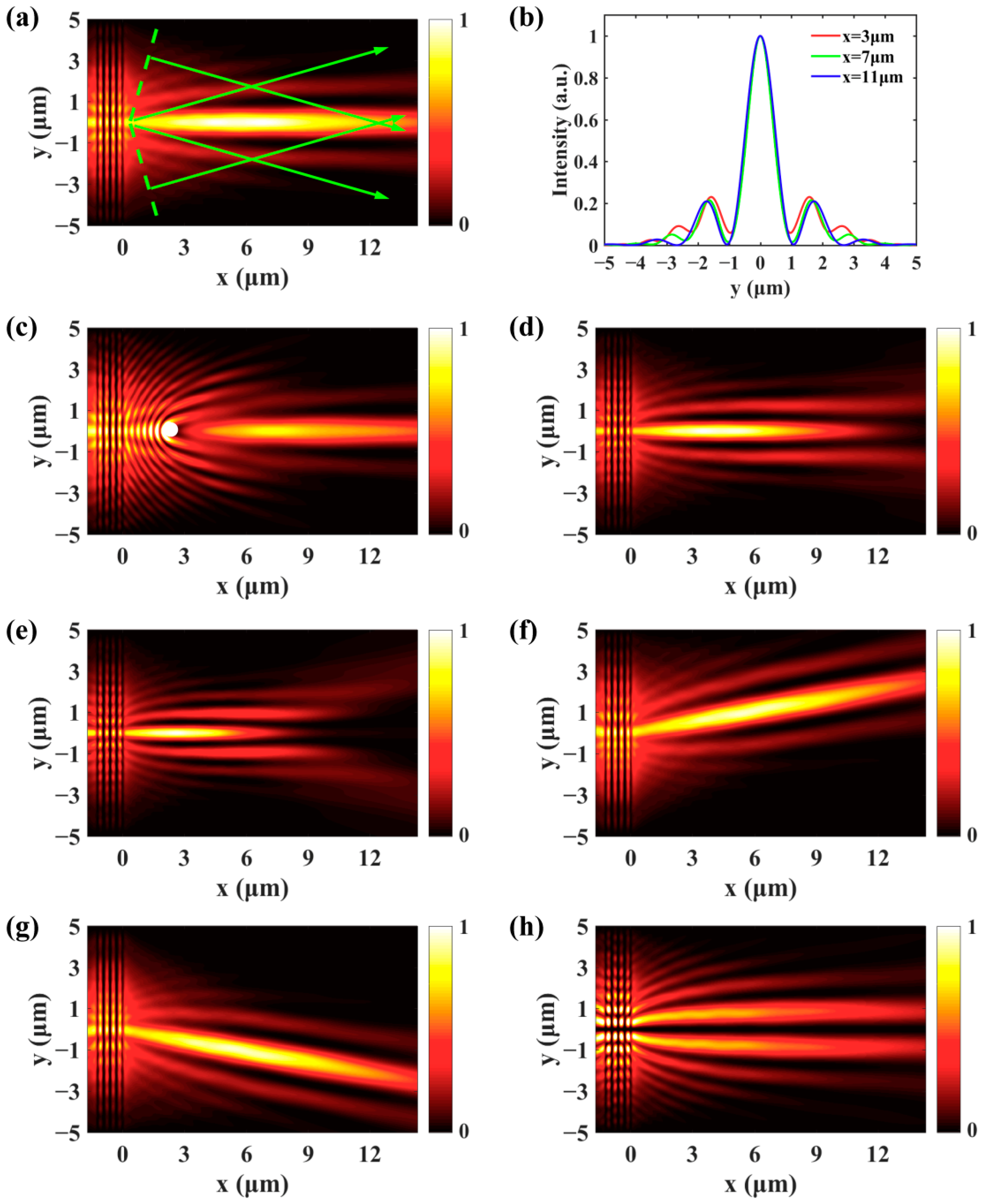
2.2. Nondiffracting SPPs Bessel Beam
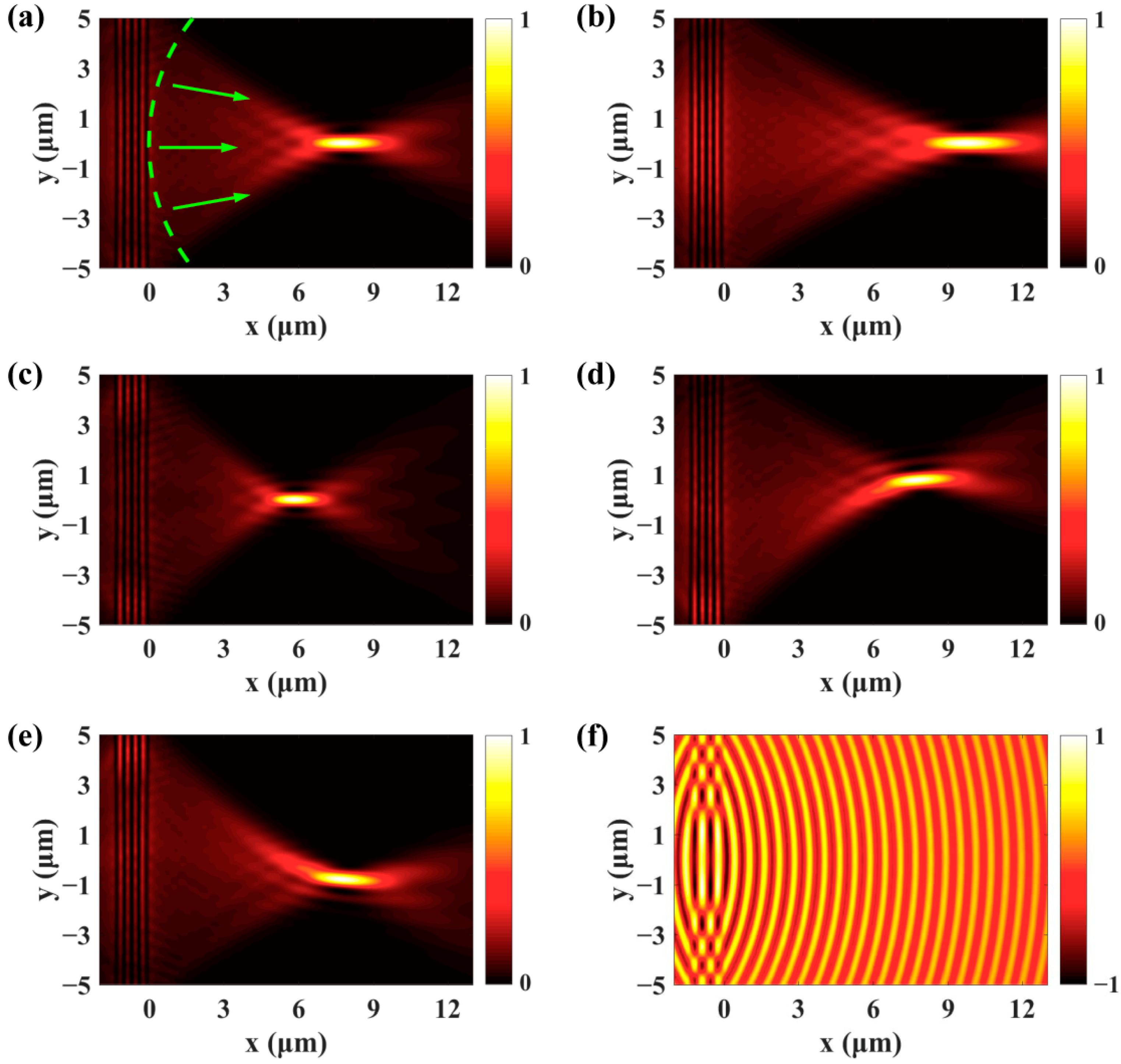
2.3. Focusing of SPPs
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Fukuda, M.; Tonooka, Y.; Inoue, T.; Ota, M. Feasibility of plasmonic circuits for on-chip interconnects. Solid-State Electron. 2019, 156, 33–40. [Google Scholar] [CrossRef]
- Willets, K.A.; Wilson, A.; Sundaresan, V.; Joshi, P. Super-Resolution Imaging and Plasmonics. Chem. Rev. 2017, 117, 7538–7582. [Google Scholar] [CrossRef] [PubMed]
- Anker, J.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Zhang, Y.; Min, C.; Dou, X.; Wang, X.; Urbach, H.P.; Somekh, M.G.; Yuan, X. Plasmonic tweezers: For nanoscale optical trapping and beyond. Light Sci. Appl. 2021, 10, 59. [Google Scholar] [CrossRef] [PubMed]
- Boriskina, S.V.; Ghasemi, H.; Chen, G. Plasmonic materials for energy: From physics to applications. Mater. Today 2013, 16, 375–386. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, L.; Gao, F.; Luo, Y.; Zhang, B. Spoof Plasmonics: From Metamaterial Concept to Topological Description. Adv. Mater. 2018, 30, e1706683. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Peng, Q.; Song, W.; Hao, F.; Wang, J.; Nordlander, P.; Zhu, X. Plasmonic Focusing in Symmetry Broken Nanocorrals. Nano Lett. 2011, 11, 893–897. [Google Scholar] [CrossRef]
- Li, G.; Sun, Y.; Wang, S. Spin-Independent Plasmonic Lens. Nanoscale Res. Lett. 2019, 14, 156. [Google Scholar] [CrossRef] [Green Version]
- Randhawa, S.; González, M.U.; Renger, J.; Enoch, S.; Quidant, R. Design and properties of dielectric surface plasmon Bragg mirrors. Opt. Express 2010, 18, 14496–14510. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, M.; Kato, J.-I.; Kawata, S. Surface-Plasmon Holography with White-Light Illumination. Science 2011, 332, 218–220. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, X.; Lu, C.; Yue, S.; Yang, H.; Gong, Q. All-Optical Logic Gates Based on Nanoscale Plasmonic Slot Waveguides. Nano Lett. 2012, 12, 5784–5790. [Google Scholar] [CrossRef]
- Zang, X.; Zhu, Y.; Mao, C.; Xu, W.; Ding, H.; Xie, J.; Cheng, Q.; Chen, L.; Peng, Y.; Hu, Q.; et al. Manipulating Terahertz Plasmonic Vortex Based on Geometric and Dynamic Phase. Adv. Opt. Mater. 2018, 7, 1801328. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Cho, S.-W.; Lee, S.-Y.; Kang, M.; Lee, B. Synthesis and Dynamic Switching of Surface Plasmon Vortices with Plasmonic Vortex Lens. Nano Lett. 2010, 10, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Wang, S.; Liu, Y.; Yin, X.; Lu, C.; Chen, Z.; Zhang, X. Plasmonic Airy beams with dynamically controlled trajectories. Opt. Lett. 2011, 36, 3191–3193. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, Y. Simultaneous Airy beam generation for both surface plasmon polaritons and transmitted wave based on metasurface. Opt. Express 2017, 25, 23589–23596. [Google Scholar] [CrossRef]
- Lin, J.; Dellinger, J.; Genevet, P.; Cluzel, B.; De Fornel, F.; Capasso, F. Cosine-Gauss Plasmon Beam: A Localized Long-Range Nondiffracting Surface Wave. Phys. Rev. Lett. 2012, 109, 093904. [Google Scholar] [CrossRef]
- Tanemura, T.; Balram, K.C.; Ly-Gagnon, D.-S.; Wahl, P.; White, J.S.; Brongersma, M.L.; Miller, D.A.B. Multiple-Wavelength Focusing of Surface Plasmons with a Nonperiodic Nanoslit Coupler. Nano Lett. 2011, 11, 2693–2698. [Google Scholar] [CrossRef] [PubMed]
- Gjonaj, B.; Aulbach, J.; Johnson, P.M.; Mosk, A.P.; Kuipers, L.; Lagendijk, A. Active spatial control of plasmonic fields. Nat. Photonics 2011, 5, 360–363. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, J. Flexible wavefront manipulation of surface plasmon polaritons without mechanical motion components. Appl. Phys. Lett. 2011, 98, 211108. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Coriolis Effect in Optics: Unified Geometric Phase and Spin-Hall Effect. Phys. Rev. Lett. 2008, 101, 030404. [Google Scholar] [CrossRef] [Green Version]
- Gorodetski, Y.; Niv, A.; Kleiner, V.; Hasman, E. Observation of the Spin-Based Plasmonic Effect in Nanoscale Structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Zhao, C.; Li, G.; Li, X.; Wang, S. Enlarging spin-dependent transverse displacement of surface plasmon polaritons focus. Opt. Express 2019, 27, 11112–11121. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Xie, Z.; Si, G.; Yang, A.; Li, C.; Lin, J.; Li, G.; Wang, H.; Yuan, X. On-Chip Photonic Spin Hall Lens. ACS Photonics 2019, 6, 1840–1847. [Google Scholar] [CrossRef]
- Wintz, D.; Genevet, P.; Ambrosio, A.; Woolf, A.; Capasso, F. Holographic Metalens for Switchable Focusing of Surface Plasmons. Nano Lett. 2015, 15, 3585–3589. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Zhang, X.; Xu, Y.; Ouyang, C.; Tian, Z.; Gu, J.; Li, J.; Zhang, S.; Han, J.; Zhang, W. Polarization-controlled surface plasmon holography. Laser Photonics Rev. 2017, 11, 1600212. [Google Scholar] [CrossRef]
- Xiao, S.; Zhong, F.; Liu, H.; Zhu, S.; Li, J. Flexible coherent control of plasmonic spin-Hall effect. Nat. Commun. 2015, 6, 8360. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Zhang, Y. Polarization-based dynamic manipulation of Bessel-like surface plasmon polaritons beam. Opt. Express 2018, 26, 5461–5468. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, Z.; Zhang, X.; Xiao, J.; Gong, Q. Submicron bidirectional all-optical plasmonic switches. Sci. Rep. 2013, 3, srep01451. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Liu, Y.; Zhao, Y.; Fang, N.; Huang, T.J. A reconfigurable plasmofluidic lens. Nat. Commun. 2013, 4, 2305. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Shi, G.; Jin, Z.; Shu, J.; Zhang, Q.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Xu, Q. Excitation and Active Control of Propagating Surface Plasmon Polaritons in Graphene. Nano Lett. 2013, 13, 3698–3702. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Capasso, F. Broadband Multifunctional Efficient Meta-Gratings Based on Dielectric Waveguide Phase Shifters. Nano Lett. 2015, 15, 6709–6715. [Google Scholar] [CrossRef]
- Ji, R.; Jin, C.; Song, K.; Wang, S.-W.; Zhao, X. Design of Multifunctional Janus Metasurface Based on Subwavelength Grating. Nanomaterials 2021, 11, 1034. [Google Scholar] [CrossRef] [PubMed]
- Genevet, P.; Wintz, D.; Ambrosio, A.; She, A.; Blanchard, R.; Capasso, F. Controlled steering of Cherenkov surface plasmon wakes with a one-dimensional metamaterial. Nat. Nanotechnol. 2015, 10, 804–809. [Google Scholar] [CrossRef]
- Iqbal, T.; Afsheen, S. Coupling Efficiency of Surface Plasmon Polaritons for 1D Plasmonic Gratings: Role of Under- and Over-Milling. Plasmonics 2016, 11, 1247–1256. [Google Scholar] [CrossRef]
- Li, D.; Pacifici, D. Strong amplitude and phase modulation of optical spatial coherence with surface plasmon polaritons. Sci. Adv. 2017, 3, e1700133. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-Controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef]
- Iqbal, T. Propagation length of surface plasmon polaritons excited by a 1D plasmonic grating. Curr. Appl. Phys. 2015, 15, 1445–1452. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Zhang, Y.; Ma, L.; He, C.; Ren, X.; Liu, C.; Cheng, C. Slit width oriented polarized wavefields transition involving plasmonic and photonic modes. New J. Phys. 2018, 20, 063037. [Google Scholar] [CrossRef]
- Garcia-Ortiz, C.E.; Coello, V.; Han, Z.; Bozhevolnyi, S.I. Generation of diffraction-free plasmonic beams with one-dimensional Bessel profiles. Opt. Lett. 2013, 38, 905–907. [Google Scholar] [CrossRef] [Green Version]
- Yuan, G.H.; Wang, Q.; Tan, P.S.; Lin, J.; Yuan, X.-C. A dynamic plasmonic manipulation technique assisted by phase modulation of an incident optical vortex beam. Nanotechnology 2012, 23, 385204. [Google Scholar] [CrossRef] [PubMed]
- Yuan, G.H.; Yuan, X.-C.; Bu, J.; Tan, P.S.; Wang, Q. Manipulation of surface plasmon polaritons by phase modulation of incident light. Opt. Express 2011, 19, 224–229. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Si, G.; Malek, M.; Earl, S.K.; Du, L.; Kou, S.S.; Yuan, X.; Lin, J. Toward broadband, dynamic structuring of a complex plasmonic field. Sci. Adv. 2018, 4, eaao0533. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhang, J.; Fu, M.; He, J.; Li, X. Multifunctional Plasmonic Grating Based on the Phase Modulation of Excitation Light. Nanomaterials 2021, 11, 2941. https://doi.org/10.3390/nano11112941
Wang S, Zhang J, Fu M, He J, Li X. Multifunctional Plasmonic Grating Based on the Phase Modulation of Excitation Light. Nanomaterials. 2021; 11(11):2941. https://doi.org/10.3390/nano11112941
Chicago/Turabian StyleWang, Sen, Jing Zhang, Maixia Fu, Jingwen He, and Xing Li. 2021. "Multifunctional Plasmonic Grating Based on the Phase Modulation of Excitation Light" Nanomaterials 11, no. 11: 2941. https://doi.org/10.3390/nano11112941
APA StyleWang, S., Zhang, J., Fu, M., He, J., & Li, X. (2021). Multifunctional Plasmonic Grating Based on the Phase Modulation of Excitation Light. Nanomaterials, 11(11), 2941. https://doi.org/10.3390/nano11112941




