Robust Simulations of Nanoscale Phase Change Memory: Dynamics and Retention
Abstract
:1. Introduction
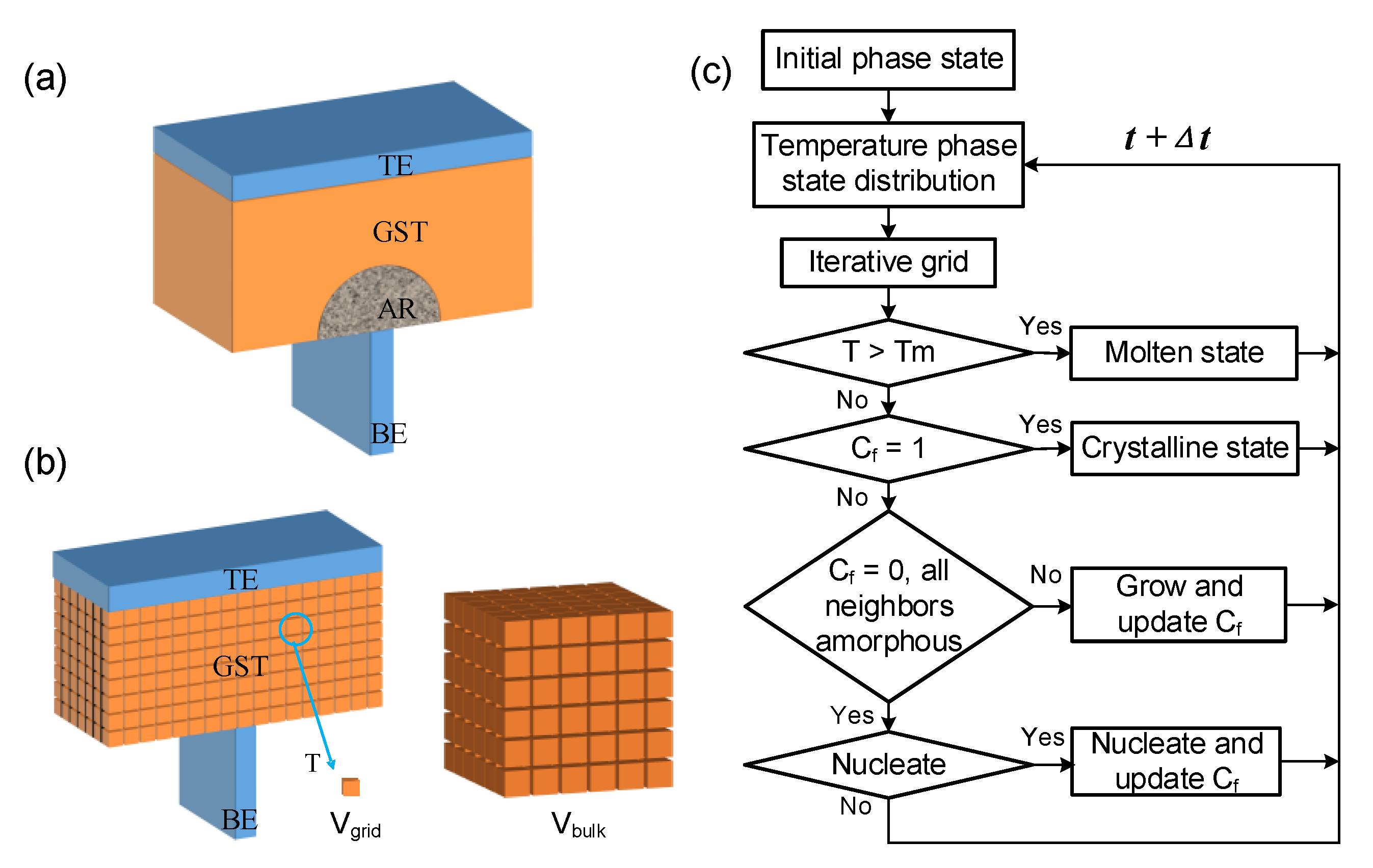
2. The Theory and Simulation Algorithm
2.1. Electrothermal Module
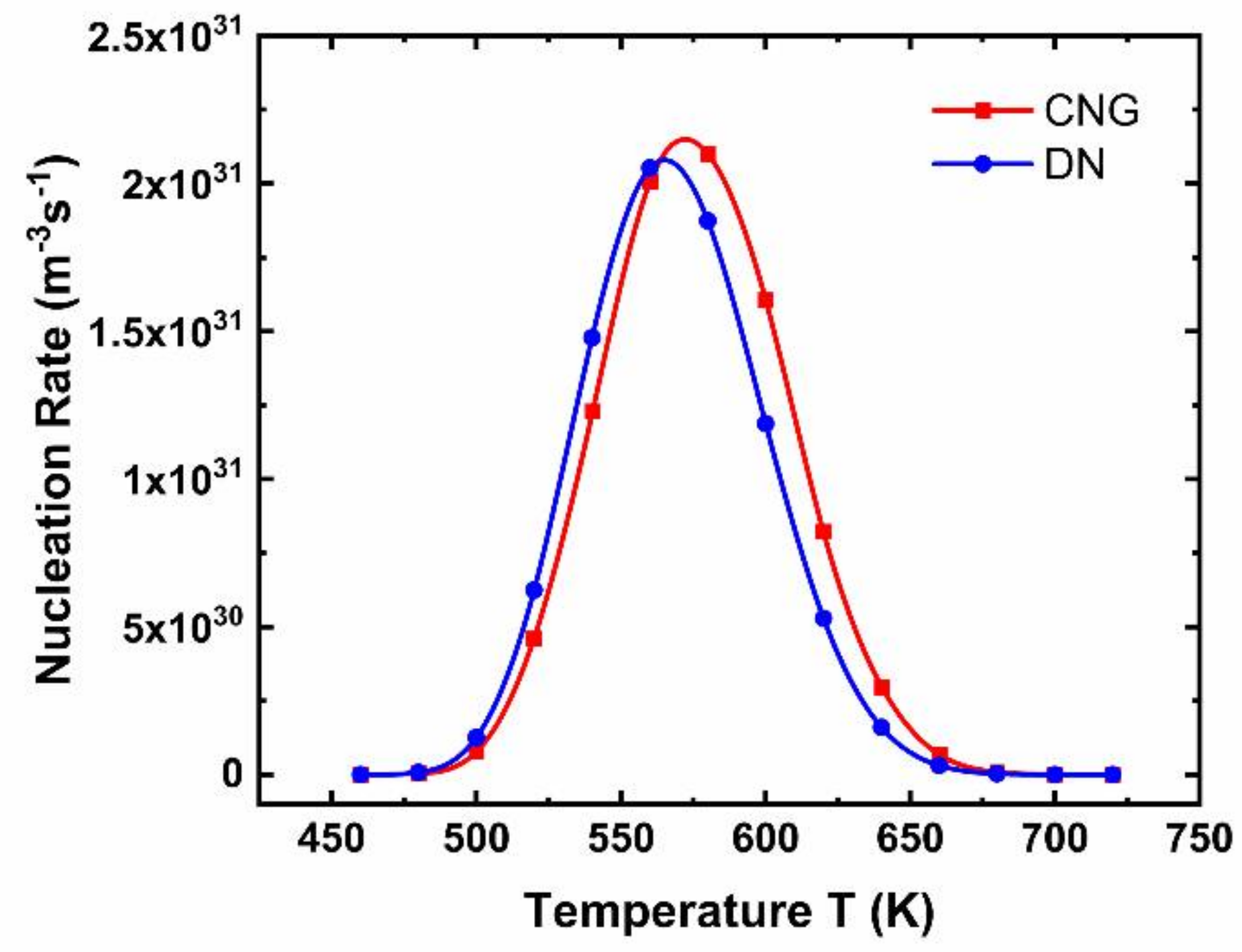
2.2. Dynamic Nucleation
2.3. The Algorithm and Improved Crystallization Model
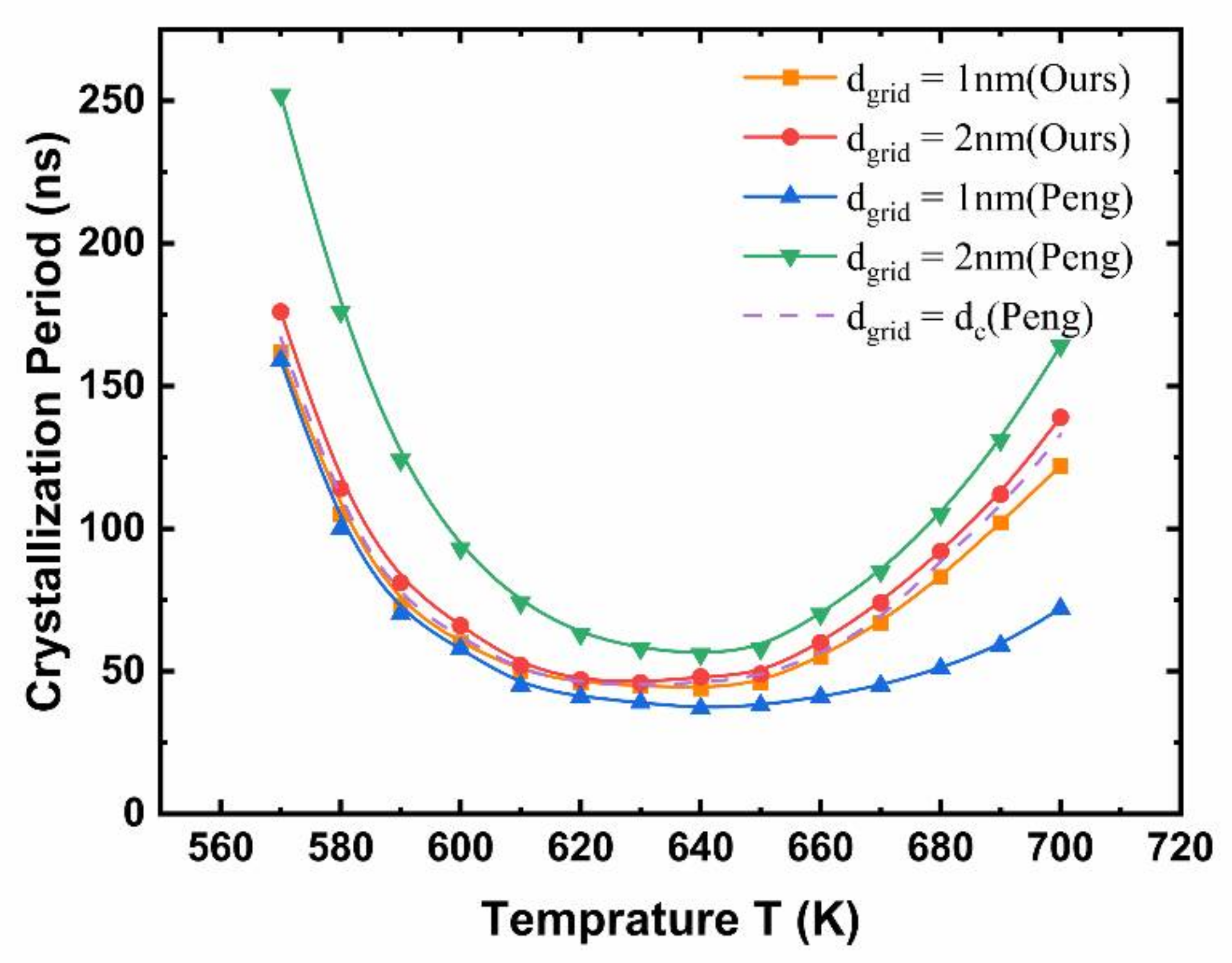
2.4. Simulation Robustness
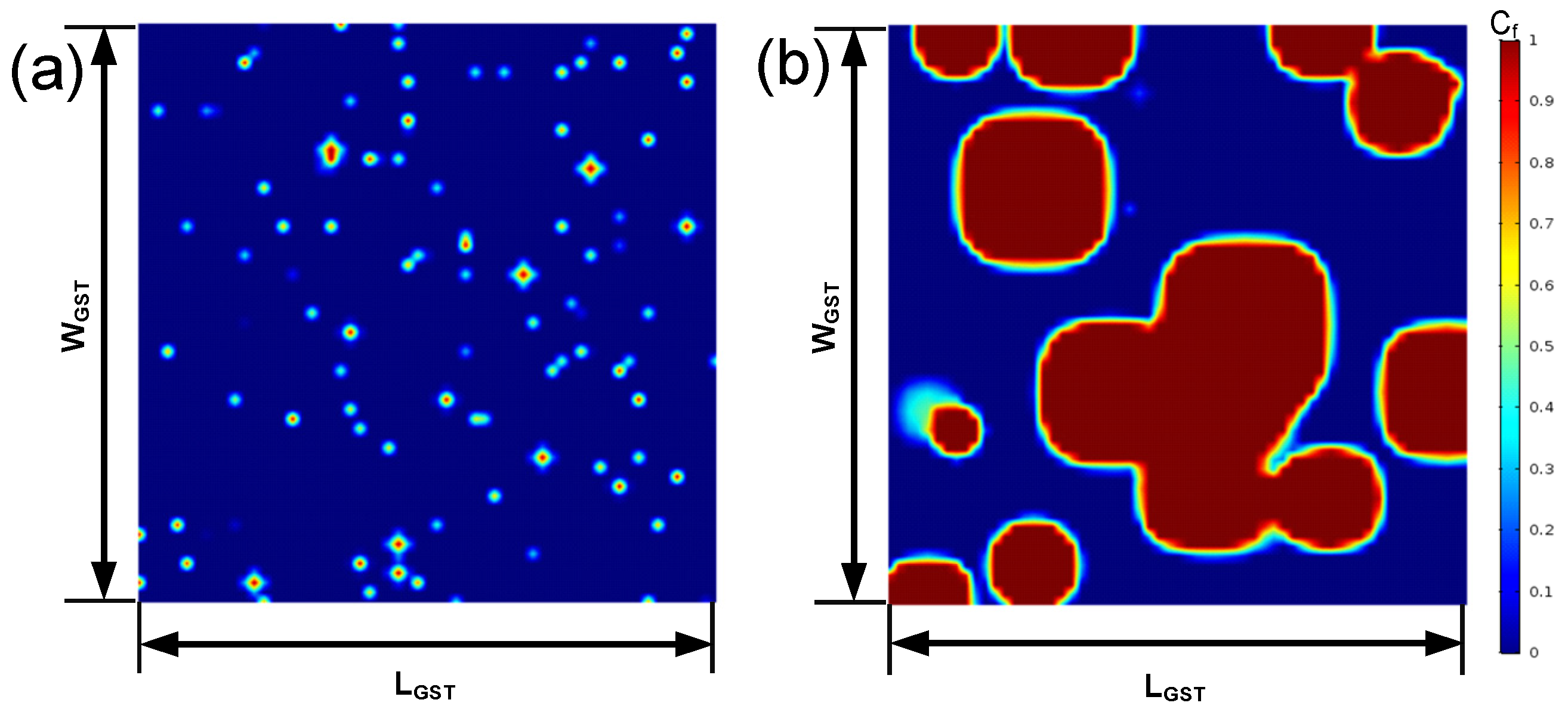
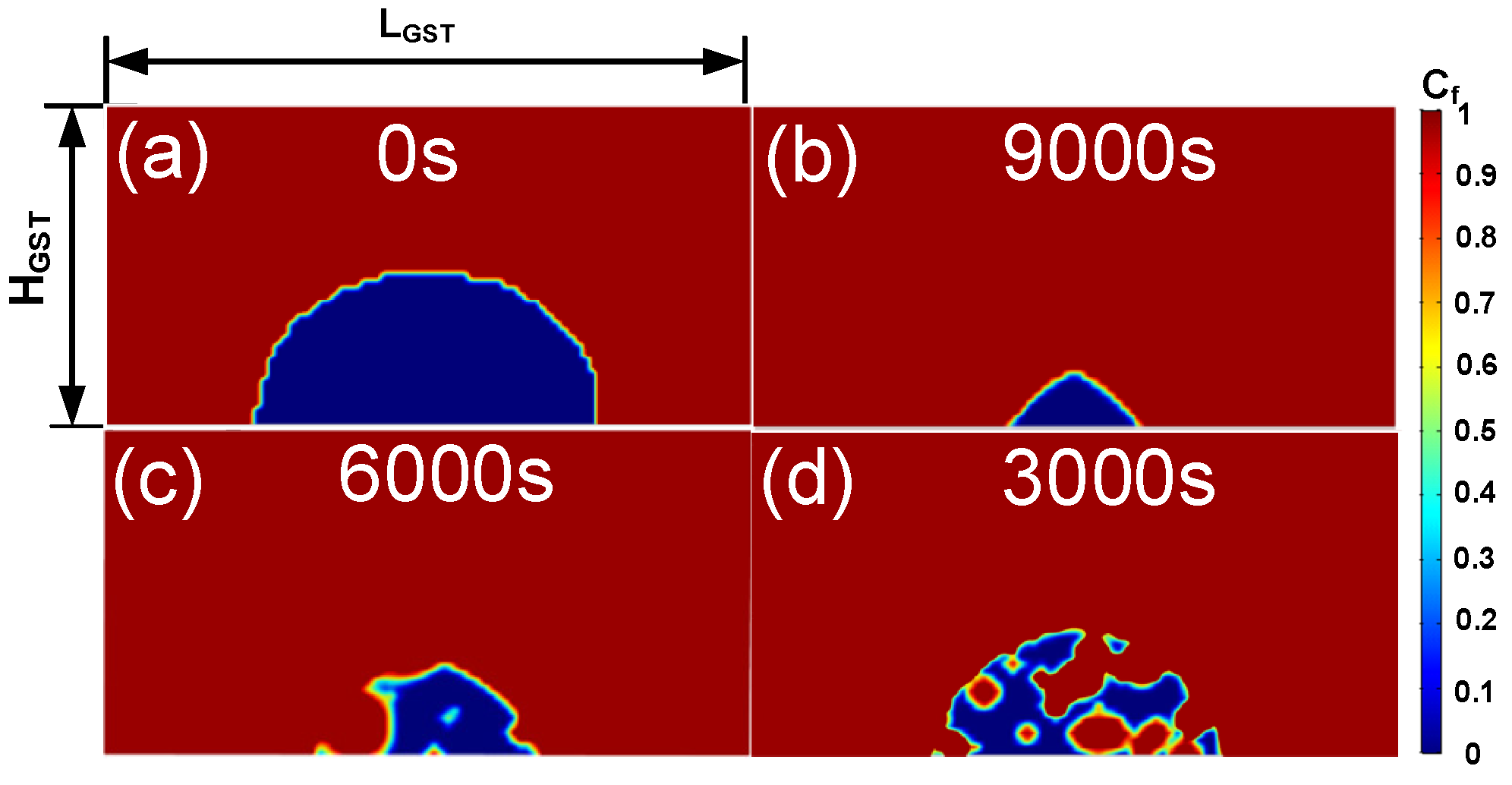
2.5. The Incubation Period
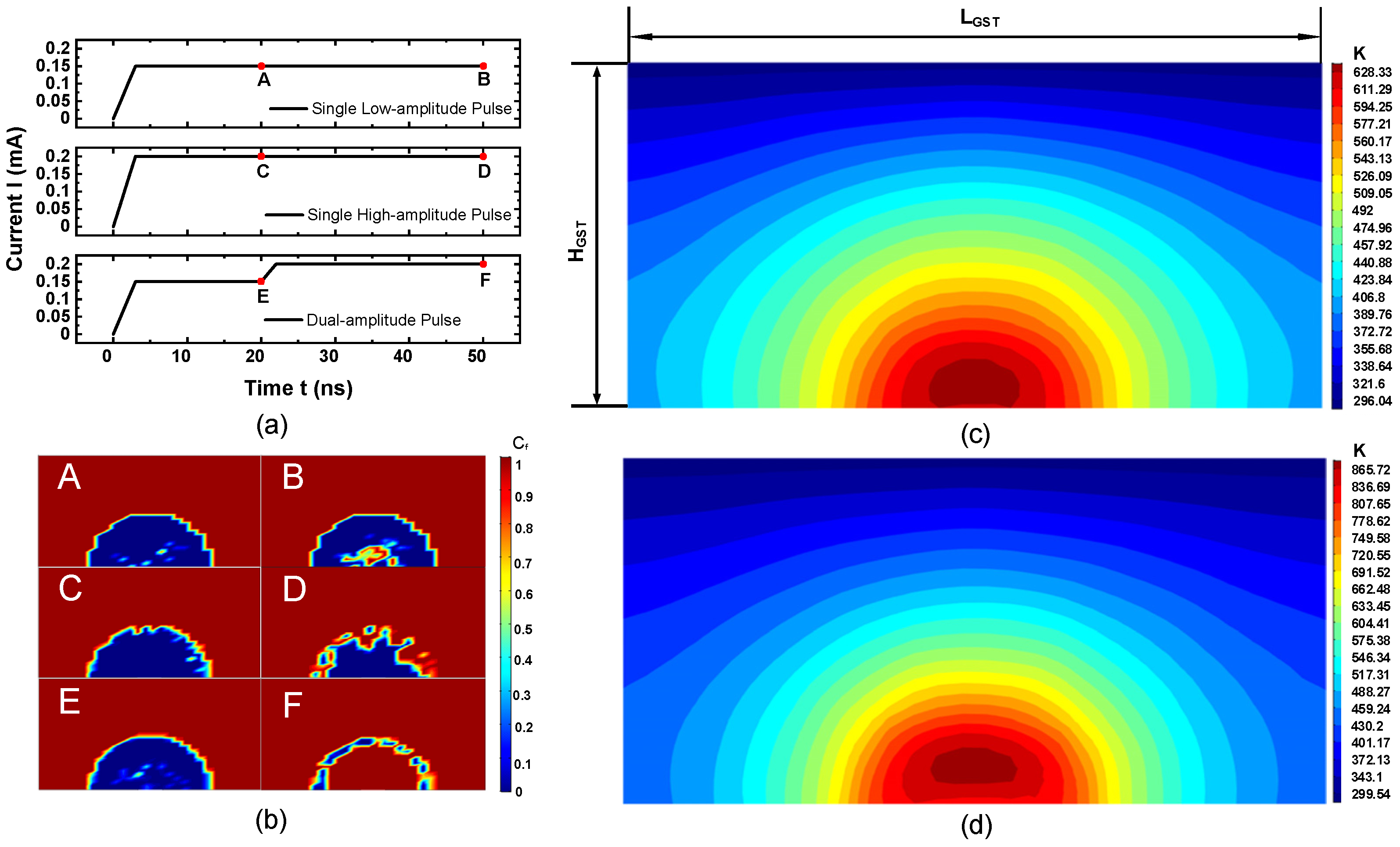
3. Implication on PCM Cell Operations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, T.; Lee, S. Evolution of Phase-Change Memory for the Storage-Class Memory and Beyond. IEEE Trans. Electron Devices 2020, 67, 1394–1406. [Google Scholar] [CrossRef]
- Noé, P.; Vallée, C.; Hippert, F.; Fillot, F.; Raty, J.Y. Phase Change Materials for Non-Volatile Memory devices: From Technological Challenges to Materials Science Issues. Semicond. Sci. Technol. 2017, 33, 013002. [Google Scholar] [CrossRef]
- Zhao, Z.; Hua, S.; Wu, W.; Shen, B.; Zhai, J.; Lai, T.; Song, S.; Song, Z. Improvement of phase change speed and thermal stability in Ge5Sb95/ZnSb multilayer thin films for phase change memory application. Semicond. Sci. Technol. 2019, 34, 105022. [Google Scholar] [CrossRef]
- Loke, D.; Lee, T.H.; Wang, W.J.; Shi, L.P.; Zhao, R.; Yeo, Y.C.; Chong, T.C.; Elliott, S.R.J.S. Breaking the Speed Limits of Phase-Change Memory. Science 2012, 336, 1566–1569. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lacaita, A.L.; Ielmini, D. IEEE Reliability issues and scaling projections for phase change non volatile memories. In Proceedings of the 2007 IEEE International Electron Devices Meeting, Washington, DC, USA, 10–12 December 2007; pp. 157–160. [Google Scholar]
- Russo, U.; Ielmini, D.; Lacaita, A.L. Analytical Modeling of Chalcogenide Crystallization for PCM Data-Retention Extrapolation. IEEE Trans. Electron Devices 2007, 54, 2769–2777. [Google Scholar] [CrossRef]
- Shih, Y.H.; Wu, J.Y.; Rajendran, B.; Lee, M.H.; Cheek, R.; Lamorey, M.; Breitwisch, M.; Zhu, Y.; Lai, E.K.; Chen, C.F.; et al. Mechanisms of retention loss in Ge2Sb2Te5-based phase-change memory. In Proceedings of the 2008 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; pp. 1–4. [Google Scholar]
- Jung, C.M.; Lee, E.S.; Min, K.S.; Kang, S.M. Compact Verilog-A model of phase-change RAM transient behaviors for multi-level applications. Semicond. Sci. Technol. 2011, 26, 105018. [Google Scholar] [CrossRef]
- Chen, X.H.; Ding, F.L.; Huang, X.Q.; Lin, X.N.; Wang, R.S.; Chan, M.S.; Zhang, L.N.; Huang, R. A Robust and Efficient Compact Model for Phase-Change Memory Circuit Simulations. IEEE Trans. Electron Devices 2021, 68, 4404–4410. [Google Scholar] [CrossRef]
- Chen, X.H.; Hu, H.F.; Huang, X.Q.; Cai, W.R.; Liu, M.; Lam, C.; Lin, X.N.; Zhang, L.N.; Chan, M.S. A SPICE Model of Phase Change Memory for Neuromorphic Circuits. IEEE Access 2020, 8, 95278–95287. [Google Scholar] [CrossRef]
- Hu, H.F.; Liu, D.Y.; Chen, X.H.; Dong, D.Q.; Cui, X.L.; Liu, M.; Lin, X.N.; Zhang, L.N.; Chan, M.S. A Compact Phase Change Memory Model With Dynamic State Variables. IEEE Trans. Electron Devices 2020, 67, 133–139. [Google Scholar] [CrossRef]
- Peng, C.; Cheng, L.; Mansuripur, M. Experimental and theoretical investigations of laser-induced crystallization and amorphization in phase-change optical recording media. J. Appl. Phys. 1997, 82, 4183–4191. [Google Scholar] [CrossRef]
- Song, D.; Liu, X.; Du, G.; Han, R.; Kang, J. Self-consistent simulation of PRAM with comprehensive physical models. In Proceedings of the 2010 10th IEEE International Conference on Solid-State and Integrated Circuit Technology, Shanghai, China, 1–4 November 2010; pp. 1154–1156. [Google Scholar]
- Li, Z.; Jeyasingh, R.G.D.; Lee, J.; Asheghi, M.; Wong, H.S.P.; Goodson, K.E. Electrothermal Modeling and Design Strategies for Multibit Phase-Change Memory. IEEE Trans. Electron Devices 2012, 59, 3561–3567. [Google Scholar] [CrossRef]
- Ciocchini, N.; Laudato, M.; Leone, A.; Fantini, P.; Ielmini, D. Universal Thermoelectric Characteristic in Phase Change Memories. In Proceedings of the 2015 IEEE International Memory Workshop, Monterey, CA, USA, 17–20 May 2015; pp. 185–188. [Google Scholar]
- Russo, U.; Ielmini, D.; Redaelli, A.; Lacaita, A.L. Intrinsic Data Retention in Nanoscaled Phase-Change Memories—Part I: Monte Carlo Model for Crystallization and Percolation. IEEE Trans. Electron Devices 2006, 53, 3032–3039. [Google Scholar] [CrossRef]
- Rizzi, M.; Ciocchini, N.; Montefiori, A.; Ferro, M.; Fantini, P.; Lacaita, A.L.; Ielmini, D. Intrinsic retention statistics in phase change memory (PCM) arrays. In Proceedings of the 2013 IEEE International Electron Devices Meeting, 9–11 December 2013; pp. 21.27.21–21.27.23. [Google Scholar]
- Kwon, Y.; Kang, D.; Lee, K.; Park, Y.; Chung, C. Analysis of Intrinsic Variation of Data Retention in Phase-Change Memory Using Phase-Field Method. IEEE Electron Device Lett. 2013, 34, 411–413. [Google Scholar] [CrossRef]
- Cueto, O.; Sousa, V.; Navarro, G.; Blonkowski, S. Coupling the Phase-Field Method with an electrothermal solver to simulate phase change mechanisms in PCRAM cells. In Proceedings of the 2015 International Conference on Simulation of Semiconductor Processes and Devices, 9–11 September 2015; pp. 301–304. [Google Scholar]
- Dong, D.; Hu, H.; Liu, D.; Lin, X. A3-D Simulation Model and Study of Priming Effect for Phase Change Memory. In Proceedings of the 2019 Electron Devices Technology and Manufacturing Conference, Singapore, 12–15 March 2019; pp. 458–460. [Google Scholar]
- Liang, J.; Jeyasingh, R.G.D.; Chen, H.; Wong, H.P. An Ultra-Low Reset Current Cross-Point Phase Change Memory With Carbon Nanotube Electrodes. IEEE Trans. Electron Devices 2012, 59, 1155–1163. [Google Scholar] [CrossRef]
- Proft, A.D.; Garbin, D.; Donadio, G.L.; Hody, H.; Witters, T.; Lodewijks, K.; Rottenberg, X.; Goux, L.; Delhougne, R.; Kar, G.S. Carbon-Based Liner for RESET Current Reduction in Self-Heating Phase-Change Memory Cells. IEEE Trans. Electron Devices 2020, 67, 4228–4233. [Google Scholar] [CrossRef]
- Kim, D.H.; Merget, F.; Laurenzis, M.; Bolivar, P.H.; Kurz, H. Electrical percolation characteristics of Ge2Sb2Te5 and Sn doped Ge2Sb2Te5 thin films during the amorphous to crystalline phase transition. J. Appl. Phys. 2005, 97, 6157. [Google Scholar] [CrossRef]
- Thompson, C.V.; Spaepen, F. Approximation of the free-energy change on crystallization. Acta Metall. 1979, 27, 1855–1859. [Google Scholar] [CrossRef]
- Kelton, K.F.; Greer, A.L.; Thompson, C.V. Transient nucleation in condensed systems. J. Chem. Phys. 1983, 79, 6261–6276. [Google Scholar] [CrossRef]
- Kelton, K.F.; Weinberg, M.C. Calculation of macroscopic growth rates from nucleation data. J. Non-Cryst. Solids 1994, 180, 17–24. [Google Scholar] [CrossRef]


| Symbol | Description | Value | Unit |
|---|---|---|---|
| WGST | width of GST region | 190 | nm |
| LGST | length of GST region | 190 | nm |
| HGST | height of GST region | 90 | nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, F.; Dong, D.; Chen, Y.; Lin, X.; Zhang, L. Robust Simulations of Nanoscale Phase Change Memory: Dynamics and Retention. Nanomaterials 2021, 11, 2945. https://doi.org/10.3390/nano11112945
Ding F, Dong D, Chen Y, Lin X, Zhang L. Robust Simulations of Nanoscale Phase Change Memory: Dynamics and Retention. Nanomaterials. 2021; 11(11):2945. https://doi.org/10.3390/nano11112945
Chicago/Turabian StyleDing, Feilong, Deqi Dong, Yihan Chen, Xinnan Lin, and Lining Zhang. 2021. "Robust Simulations of Nanoscale Phase Change Memory: Dynamics and Retention" Nanomaterials 11, no. 11: 2945. https://doi.org/10.3390/nano11112945
APA StyleDing, F., Dong, D., Chen, Y., Lin, X., & Zhang, L. (2021). Robust Simulations of Nanoscale Phase Change Memory: Dynamics and Retention. Nanomaterials, 11(11), 2945. https://doi.org/10.3390/nano11112945






