Abstract
For the first time, a specific time-delayed peak was registered in the femtosecond transient absorption (TA) spectra of ZnxCd1−xS/ZnS (x~0.5) alloy quantum dots (QDs) doped with Mn2+, which was interpreted as the electrochromic Stark shift of the band-edge exciton. The time-delayed rise and decay kinetics of the Stark peak in the manganese-doped QDs significantly distinguish it from the kinetics of the Stark peak caused by exciton–exciton interaction in the undoped QDs. The Stark shift in the Mn2+-doped QDs developed at a 1 ps time delay in contrast to the instantaneous appearance of the Stark shift in the undoped QDs. Simultaneously with the development of the Stark peak in the Mn2+-doped QDs, stimulated emission corresponding to 4T1-6A1 Mn2+ transition was detected in the subpicosecond time domain. The time-delayed Stark peak in the Mn2+-doped QDs, associated with the development of an electric field in QDs, indicates the appearance of charge transfer intermediates in the process of exciton quenching by manganese ions, leading to the ultrafast Mn2+ excitation. The usually considered mechanism of the nonradiative energy transfer from an exciton to Mn2+ does not imply the development of an electric field in a QD. Femtosecond TA data were analyzed using a combination of empirical and computational methods. A kinetic scheme of charge transfer processes is proposed to explain the excitation of Mn2+. The kinetic scheme includes the reduction of Mn2+ by a 1Se electron and the subsequent oxidation of Mn1+ with a hole, leading to the formation of an excited state of manganese.
1. Introduction
Doped quantum dots (QDs) are promising materials for different applications in photovoltaics, spintronics, bioimaging, photonics, and other modern technological applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Doping II-VI semiconductor QDs with Mn2+ ions makes it possible to obtain brightly luminescent nanomaterials, which are used in bioimaging, photocatalysis, and other applications [5,11,20,21,22]. The orange-red luminescence of Mn2+ in the 580–600 nm region associated with the 4T1-6A1 transition is induced in the QDs through an exciton absorption. The 4T1-6A1 transition is forbidden by the selection rule since a spin flip-flop is required, and it therefore has low oscillator strength [2,6,10,11,23]. At the same time, the Mn2+ ion effectively quenches the exciton, and the Mn2+ 4T1-6A1 luminescence quantum yield can reach ~45–65%, which means a high probability of energy transfer from the exciton to Mn2+ [24,25,26]. The mechanism of energy transfer from the exciton to the d5 levels of the Mn2+ ion remains controversial [10,11,12,15,19,21,23,27,28]. The excitation of Mn2+ can either be due to the energy transfer or charge transfer by the host or the surface ligand. The prevailing opinion in the literature is that the Mn2+ excitation is realized by nonradiative energy transfer processes Förster-, Dexter-, or Auger-like rather than charge transfer [10,12,16,23,27,29].
The magnetic ion Mn2+ has five electrons that half-fill the d5 levels. In II-VI semiconductors, the ground state Mn2+(d5) is characterized by a spin S = 5/2, an angular momentum L = 0, and a negligible spin-orbit splitting. The Mn2+(d5) as a magnetic impurity in a semiconductor is characterized by a strong exchange interaction of the d electrons of Mn2+(d5) with electrons in the conduction bands (s-band) and holes from the valence band (p-band). The exchange coupling between the sp-electrons of exciton and the d-electrons of Mn2+(d5) ions (sp-d mixing) determines the formation of the exciton magnetic polaron [4,9,12,18]. It was suggested that the sp–d mixing and direct exchange interactions could be responsible for the energy transfer between exciton and Mn2+ [23,30]. This mechanism implies that non-radiative recombination remains efficient even when the bandgap Eg substantially exceeds the energy of the 6A1-4T1 transition, i.e., the energy transfer is directed into the upper Mn2+ excited states in that case. The Förster dipole–dipole mechanism, despite the forbidden transition for Mn2+, was also considered [27,29]. Y. Yang et al. suggested a two-step mechanism for energy transfer [31]. In core/shell CdS/ZnS QDs, the energy transfer from an exciton inside the CdS core occurs to a bound exciton around a Mn center. This is the rate-determining step, which is then proceeded by the Förster mechanism [31]. The second step is the energy transfer from the bound exciton to the d5 levels of Mn2+. It might be a dark exciton (triplet exciton) or an Auger transfer mechanism [31]. Two sequential charge transfer reactions between exciton and manganese dopant were suggested for the explanation of manganese excitation in CdxZn1−xSe (x = 0–0.2) [28]. In this system, a band near 2.5 eV was reported in the luminescence and TA spectra, and it has been attributed to the spin-allowed 5T2-5E transition of Mn3+. Based on this assignment of 2.5eV band, a scheme of Mn2+(4T1) excitation was proposed with Mn3+ as an intermediate appearing due to Mn2+ oxidation by the hole. The hole scavenging by Mn2+ and the excitation of the Mn3+(5T2) state occur with a characteristic time of ~200 fs. It was declared that the luminescent Mn2+(4T1) state arises from the Mn3+(5T2) state with a characteristic time of 300–800 ps [28].
Recently, we reported the stimulated emission of Mn2+ (4T1-6A1) registration in femtosecond TA spectra at subpicosecond time delays in Mn2+-doped QDs Zn0.5Cd0.5S in a short letter, but the mechanism of manganese excitation remained unclear [26]. It is noteworthy that the characteristic band near the 2.5 eV of Mn3+ (5T2-5E) transition was not observed in the Mn2+: Zn0.5Cd0.5S QDs [26]. Therefore, the purpose of this work is to carry out additional studies of the femtosecond kinetics of TA spectra of Mn2+ alloy-doped and undoped QDs Zn0.5 Cd0.5S in a spectral range of 390–700 nm. In the current work, we report for the first time that the TA spectra of the manganese-doped QDs revealed a time-delayed absorption peak appearing at the red side of the edge exciton. This specific peak can be attributed to an electrochromic Stark shift of the band-edge exciton. The kinetics of this absorption peak, related to the delayed Stark shift of the exciton band, can expose the dynamics of charge transfer intermediates in the process of Mn2+(d5) excitation. A global analysis of TA spectra dynamics, taking into account the dynamics of Stark shift, suggests the mechanism of manganese excitation through the charge transfer intermediates formation.
2. Materials and Methods
Chemicals. Zinc acetate dihydrate (Zn(OAc)2•2H2O, 98%), cyclohexane (99+%, for spectroscopy), 1-octadecene (ODE, 90%, tech.), manganese (II) chloride (MnCl2, anhydrous, 99%), tetramethylammonium hydroxide (TMAH, 25 wt% in methanol), CdO (99.5%), cadmium acetate dihydrate (Cd(OAc)2•2H2O, ≥98%), oleic acid (90%, tech.), stearic acid (HSt, 95%), oleylamine (OlAm, C18 content 80–90%), and stearic acid (HSt, 95%) were acquired from Merck (Merck KGaA, Darmstadt, Germany). Magnesium turnings (Mg, 99%) and sulfur (reagent grade, 100 mesh) were bought from Sigma-Aldrich (Sigma-Aldrich Chemie GmbH, Steinheim, Germany). Anhydrous methyl alcohol (MeOH) was prepared from chemically pure grade MeOH by boiling it with magnesium methylate. Manganese stearate (MnSt2) was synthesized from MnCl2.
Transmission electron microscopy (TEM) images were registered using a LEO 912 AB OMEGA (Karl Zeiss, (Jena, Germany)) microscope. The accelerating voltage was 100 kV. The particle diameters distribution in a group of 300 QDs was measured with ImageJ software.
Elemental microanalysis. An atomic absorption spectrometer with flame atomization KVANT-2AT (CORTEC, Moscow, Russia) was used to characterize the elemental composition of QDs. QDs were digested by acid mineralization (micro-Kjeldahl digestion) before injection in the atomic absorption spectrometer.
EPR spectra. X-band EPR spectra were recorded on a Bruker EMX (Karlsruhe, Germany) spectrometer operating at 9.7 GHz and 100 kHz magnetic field modulation. The samples were placed into a resonator of the spectrometer using 4 mm i.d. quartz tubes. The spectral acquisition was carried out with following parameters: QDs colloids in cyclohexane; temperature, 293 K; conversion time, 327.7 ms; time constant, 40.96 ms; modulation amplitude, 0.9 G; the number of points, 2048; microwave power, 6.5 mW; and sweep width 1200 G. WINEPR and SIMPHONIA (Bruker) programs were used for the mathematical treatment of EPR spectra.
Optical spectra. Absorption spectra were recorded with a Shimadzu 3600 spectrophotometer (Kyoto, Japan). Photoluminescence excitation (PLE) and photoluminescence (PL) experiments were performed on a Shimadzu RF-5301PC spectrofluorimeter at room temperature. Coumarin 6 in ethanol, rhodamine 6G, and rhodamine B in methanol in ethanol as a PL reference were used to measure the quantum yield (QY) [32]. Coumarin 6 was used for the estimation of QY of exciton luminescence in the range of ~430–460 nm, whereas Rhodamine B and Rhodamine 6G were used to estimate the QY of Mn2+ luminescence. Rhodamine B and rhodamine 6G were used to estimate the QY luminescence of Mn2+. Coumarin 6 was used to estimate the QY of exciton luminescence in the range of ~430–460 nm.
Femtosecond transient absorption (TA). TA spectra were measured by the broadband femtosecond pump-to-probe technique (Federal Research Center of Chemical Physics RAS, Moscow, Russia). The pump pulse was 30 fs centered, 360 nm, 40 nJ. The diameter of the pump spot was 300 µm, and the probe pulse was 120 µm. The pump–pulse operation frequency was 100 Hz. The sample was refreshed between incident laser pulses by a pump in a 500 μm cell. The polarization of the pump–probe was oriented at a magic angle of 54.7°. The solvent was cyclohexane. The temperature of the cell was 293 K. The measured spectra were corrected to account for the group delay dispersion of the supercontinuum by the procedure described in Supplementary Information (Section S1). Details of the setup are presented elsewhere [26,33,34].
3. Results and Discussion
3.1. QDs Characterization
Femtosecond transient spectroscopy experiments were carried out with two types of QDs. The quantum dots of the first type (QD-1) had the composition ZnxCd1−xS, x = 0.5 with a diameter of 5.7 ± 0.9 nm and were not doped with Mn2+. The synthesis protocols, TEM images, and nanoparticle size distribution are shown in Figure S1. The second type of quantum dots (QD-2) had a composition core/shell Mn:ZnxCd1−xS/ZnS, x = 0.46 with a diameter of 7.6 ± 0.9 nm and were doped with Mn2+. The Mn/Cd molar ratio was 0.06 mol%, which corresponds to the average number of Mn ions per quantum dot <μMn> = 7.8. The shell prevented Mn2+ ions from washing out from the QDs and provided a sufficiently high quantum yield (QY~0.6) of Mn2+ luminescence upon excitation at a wavelength of 360 nm.
Figure 1 shows the absorption spectra of QD-1 and QD-2 quantum dots. A presentation of QDs spectra in the form of the second derivative made it possible to determine the positions of exciton peaks [35]. The absorption spectra were decomposed into four Gaussian peaks of the exciton bands (see Table 1).
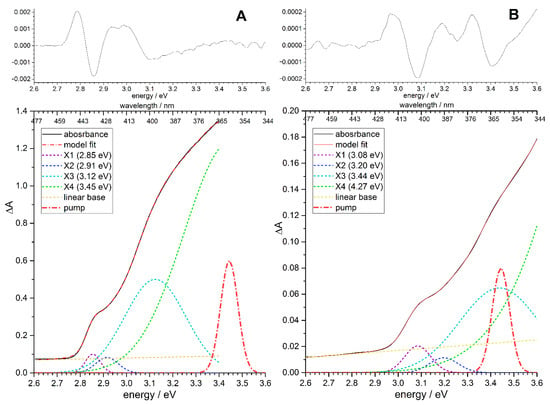
Figure 1.
Absorption spectra of QD-1 (A) and QD-2 (B) quantum dots. Upper subplots show absorption spectra in the form of the second derivative. Lower subplots show absorption spectra and their decomposition into Gaussian peaks.

Table 1.
Gaussian decomposition of the absorption and TA spectra of QD-1 and QD-2 samples.
Figure 2 demonstrates the PL spectra of the QD-1 and QD-2 samples. The undoped QD-1 sample reveals an intense PL peak at 2.831 eV (438 nm) associated with the band-edge exciton luminescence, and a very weak broad band at 2.127 eV (583 nm) fwhm = 360 meV (~130 nm) attributed to traps (Figure 2A). The PL amplitude of the traps band was 80 times less than the amplitude of the exciton peak. Figure 2B demonstrates that in the doped QD-2 Mn2+:Zn0.46Cd0.54S/ZnS sample, exciton emission was suppressed and the band close to ~2.1 eV, associated with the PL of Mn2+ ions, dominated. This band was inhomogeneous, and several peaks can be distinguished corresponding to the minima of the second derivative [35]. The PLE spectrum of Mn2+ is similar to the absorption spectrum of QD-2 Mn2+:Zn0.46Cd0.54S/ZnS sample in the region close to the band-edge exciton (Figure S2). This indicates that the Mn2+ luminescence appears to be due to exciton absorption in the Zn0.46Cd0.54S/ZnS QD, and the quantum yield of ~60% indicates high efficiency of the energy transfer from exciton to d5 levels of manganese ion.
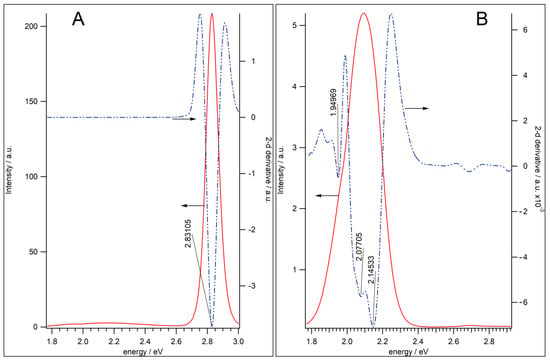
Figure 2.
PL spectra of undoped QD-1 (A) and Mn2+-doped QD-2 (B) samples. The PL spectra (red solid lines, left y-axis) are compared with the second derivatives of spectra (blue dash-dotted line, right y-axis).
Electron paramagnetic resonance (EPR) spectroscopy can provide insight into crystal field features and the distribution of dopant ions inside QD-2 nanocrystals.
Figure 3 shows the EPR spectrum of Mn2+:Zn0.46Cd0.54S/ZnS QD-2 measured at 293 K. The experimental spectrum can be considered as a superposition of two signals. Spectral simulation of experimentally recorded ESR spectrum (spectrum 1a on Figure 3) made using Bruker SIMFONIA and WINEPR software package has allowed us to identify the Mn-related features in the EPR spectrum.
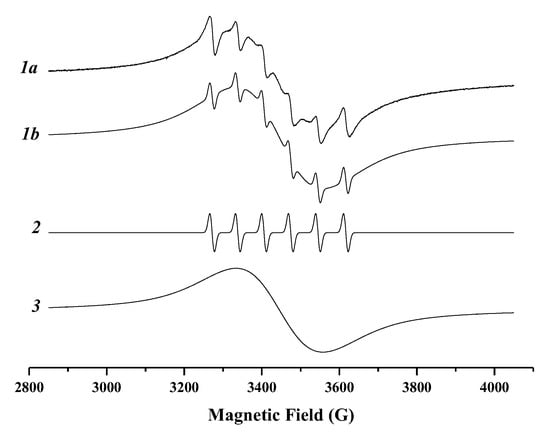
Figure 3.
The EPR spectrum of Mn2+:ZnS:CdS/Zns nanoparticles measured at 293 K: 1a—the experimental spectrum, 1b—the sum of the 2 and 3 simulated spectra.
Signal I (spectrum 2 on Figure 3) consists of six well-resolved lines originated from the interaction between the unpaired electronic spin of Mn and the nuclear spin (I = 5/2). The hyperfine coupling constant Aiso = 68.8 ± 0.5 Gauss and giso = 2.0027 ± 0.0005 obtained from the simulation correspond to isolated Mn2+ ions located in the tetrahedral crystal field environment inside the core of the nanoparticle [36,37,38,39,40,41,42]. Thus, the signal I can be assigned to isolated Mn2+ ions presented inside the Zn0.46Cd0.54S core of QD-2. It should be noted that the values of magnetic resonance parameters of Mn2+ ions located in ZnS and CdS nanoparticles are very close [36,37,38,39,40,41,42]. So, it is very complicated to separate Mn2+ ions present in Zn-rich domains from ZnxCd1−x-rich domains. The slight broadening of lines (linewidth ~ 13.0 Gauss) could be caused by Mn2+–Mn2+ dipolar interaction inside the Zn0.46Cd0.54S core.
Signal II (spectrum 3 on Figure 3) is a single broad background line. Such a broad spectral feature was observed in many Mn-doped nanoparticles and, usually, was assigned to Mn2+–Mn2+ strong dipolar interaction and/or exchange interaction [36,37,38,43,44]. It is reasonable to assume that the formation of ZnS shell leads to a displacement of some part of Mn2+ ions at the ZnS:CdS/ZnS core/shell interface, bringing them closer together. The proximity of Mn2+ ions at the interface causes Mn2+–Mn2+ strong dipolar and exchange interactions and, as a result, the single broad line is detected in EPR spectrum.
It is necessary to notice that another reason for the broadening of the ESR signal of Mn2+ ions could be crystal field distribution [37,45,46]. This suggests a distribution of hyperfine interaction, which could originate from isolated Mn2+ ions localized inside the nanocrystals, but near the surface in a strongly distorted crystal field.
Thus, according to the EPR results, the Mn2+ ions that could contribute to the PL band are the following: isolated Mn2+ ions inside the core of nanoparticle, dipolar interacting Mn2+ ions inside the core, Mn2+–Mn2+ strong dipolar interacting ions at the ZnS:CdS/ZnS core/shell interface, Mn2+–Mn2+ exchange interacting ions at the core/shell interface, dipolar interacting Mn2+ ions inside the core and core/shell interface, and Mn2+ ions in strongly distorted crystal field. Qualitatively, this is in accord with the observation of an inhomogeneous Mn2+ PL band due to the different ion localization in the host.
3.2. Femtosecond Transient Absorption (TA) Spectra
The femtosecond pump-probe TA spectra of QD-1 and QD-2 samples for several representative time-delays are shown in Figure S3. The whole TA spectral matrices of the QD-1 and QD-2 samples are presented in Figure 4 in the form of color maps. The TA color maps show significant differences between the QD-1 and QD-2 samples. Firstly, a time-delayed absorption peak, marked in Figure 4B as “Stark” was detected in manganese-doped QD-2 sample at the red side of the exciton bleaching (BL) band, whereas no similar time-delayed peaks were seen in the undoped QD-1 sample (Figure 4A). In the undoped QD-1 sample, the peak of the Stark shift was recorded at the initial but not delayed time due to the biexciton interaction of the upper excitons with the band-edge exciton [47,48]. The decay of the Stark peak in QD-1 occured in parallel with the relaxation of the upper excitons (Figure 4A). Secondly, in the QD-2 sample with Mn2+ ions, the BL band associated with the band-edge exciton decayed much faster than the analogous band in the undoped QD-1 sample. This is qualitatively consistent with previously published femtosecond spectroscopy data for other quantum dots doped with Mn2+ [22,23,24,49] and suggests the exciton quenching by manganese. In the Mn2+-doped QD-2 sample, the development of the Stark peak took place concomitantly with the decay of the BL band of the band-edge exciton when the upper exciton states had already relaxed (Figure 4B). Since the Stark peak is associated with an electric field, its delayed appearance suggests a delayed growth of the electric field in the QD-2 sample, which may indicate oxidation of the Mn2+ ions by holes or reduction of Mn2+ by 1Se exciton electron. The intensity of the BL band is substantially controlled by the filling of the 1Se electronic level [50]; therefore, the correlated decay of the BL band and the development of the Stark peak suggest that the 1Se electron was captured by Mn2+. This observation means that a reduction of Mn2+ by 1Se electron could be preferable to the Mn2+ oxidation by the hole to Mn3+ at the stage of Stark peak development.
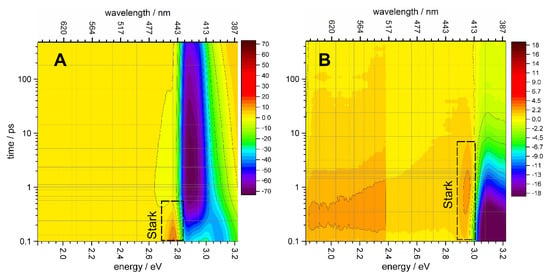
Figure 4.
TA spectra of QD-1 (A) and QD-2 (B) samples in the form of the color map. TA signal in the range of ~1.95–2.35 eV (vertical black solid line is the border) is shown on the expanded scale with factor 3. ESA peaks corresponding to the Stark shift are indicated by dashed-line boxes.
Figure 5 shows the TA spectra of the QD-2 sample at different delays in the spectral domain around to Mn2+(4T1-6A1) transition. The negative peaks close to 590 nm can be tentatively attributed to the stimulated emission (SE) bands of Mn2+(4T1-6A1) (Figure 5B). The positions of the SE(592) band and the Mn2+(4T1-6A1) photoluminescence band coincided, as shown in Figure 5A. This coincidence suggests that the SE(592) band is associated with the luminescence of manganese. The wide positive background for the SE band can be attributed to the excited state absorption of charge carries in traps [51]. The SE(592) band in Figure 5B was detected at the sensitivity limit. The weak intensity of the SE(592) band is due to the small value of the transient dipole moment of the 4T1-6A1 transition. Weak SE(592) signal makes it difficult to quantitatively analyze the kinetics of manganese luminescence development. For this reason, in this work, we carried out a detailed analysis of the TA spectra in a wide spectral range for QDs doped and not doped with manganese.
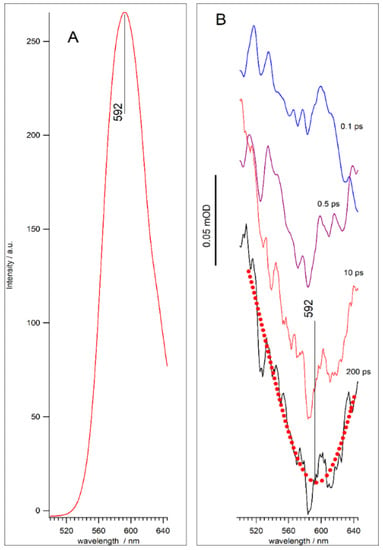
Figure 5.
Mn2+ PL band (A) and transient spectra of QD-2 sample at different delay times (B). Red dotted line is Gaussian fitting curve.
3.3. Distribution of Relaxation Processes in the Photoinduced Transient Absorption
The characteristic times of the observed relaxation processes in the TA dynamics were calculated using the program CONTIN [52]. This program implements the inverse Laplace transform to deconvolute non-monotonous relaxation into a distribution of exponential components
resulting in a quasi-continuous spectrum with the local smoothness determined by the Tikhonov–Phillips regularization. In contrast to a global fitting analysis, the CONTIN program determines the characteristic times of the observed relaxation processes independently at each probing frequency ν and can in principle determine how many processes are observed at different probing frequencies [53]. This is important for the analysis of coherent hot multi-exciton relaxation, which may proceed by several parallel channels. The results of CONTIN analysis are presented in Figure 6 in the form of spectrograms displaying the aν,k distribution in the energy range between 2.5 and 3.3 eV. The absorption increase or decrease (negative or positive aν,k in Equation (1)) is shown in red or blue in Figure 6, respectively.
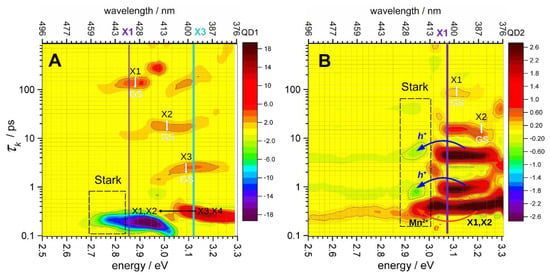
Figure 6.
Distribution of the kinetic exponential components calculated by inverse Laplace transform of the TA dynamics of QD-1 (A) and QD-2 (B) in the range of 2.5–3.3 eV using the CONTIN program [52]. The amplitudes of the kinetic components are shown as colored bars. The Stark shift regions are indicated by dashed-line boxes, and the X1 and X3 peaks are marked by vertical lines. The red arrow in Figure 6B refers to the presumable process of Mn2+ → Mn1+ reduction, whereas the blue arrows mark the processes of Mn1+ oxidation and formation of the excited [Mn2+]* in the 2 inhomogeneous Mn2+ locations.
3.4. Decomposition of Transient Absorption into Gaussian Components
According to Norris and Bawendi, among four Gaussian components distinguishable in the linear absorption spectra (Figure 1, Table 1), the lowest X1 can be attributed to the 1Se-1S3/2 transition, whereas other three represent combinations of several transitions: the second X2 includes 1Se-2S3/2 and 1Se-1S1/2, the third X3 includes 1Pe-1P3/2 and 1Se-2S1/2, and the broad fourth X4 may include a combination of 1Pe-1P1/2, 1Pe-1P5/2, and 1Se-3S1/2 transitions [54]. Interpretation of the TA spectra in terms of the spherical electron and hole envelope wave functions is complicated by the overlap of bleach and induced absorption features. Several other effects have to be taken into consideration: the fine-structure splitting of the band-edge transitions, the multi-particle inter-exciton interactions, the statistical distribution of multi-exciton states, and the complicated Stokes shift structure [55,56,57]. The simplest quantitative interpretation is the Stark redshift of the lowest X1 peak (1Se-1S3/2 transition), the biexciton interactions of which were previously thoroughly analyzed [58]. The observed biexciton red shift ΔXX of the X1 peak in the TA spectra of CdSe nanoparticles of various sizes upon pumping into the 1P exciton (the X3 peak) was in the range of 9–18 meV, whereas the redshift was almost zero upon pumping into the 1S band-edge exciton (the X1 peak) [56,57]. Zhang et al. [50] analyzed the absorption changes in pump–probe measurements by using double-sided Feynman diagrams techniques and suggested an approximation where the TA spectra are modeled in the visible range by a sum of three Gaussian functions
where G(ω − ωk) is the Gaussian function
The peak positions ωk and the widths wk of the unshifted Gaussian functions are usually taken from the decomposition of the X1, X2, and X3 bands in the linear absorption spectrum. Because the X2 and X3 bands comprise combinations of several transitions and their bleach and induced absorption features essentially overlap in the TA spectra, we simplified Equation (2), confining ourselves to the linear term of the expansion of G2(ω − ω2 + Δ2) and G3(ω − ω3 + Δ3) in the Taylor series:
Here G′k(ω − ωk) are the first derivatives of Gk(ω − ωk), which correspond to the spectral features of the Stark shifts of X2 and X3; the positions of the peaks ωk and the widths wk of the Gaussian functions Gk were determined from the decomposition of the linear absorption spectra into Gaussians (see Figure 1 and Table 1, Figure S4); the amplitudes Bk(t) and Ck(t), corresponding to bleaching and Stark shift features, respectively, were found using linear least-squares regression of the TA spectra in the entire time range shown on the TA colormaps in Figure 5. The magnitude of the electrochromic shift δ1 of the band-edge exciton was found as a single parameter for the entire matrix of TA spectral changes by nonlinear minimization, as described previously [31,53]. Figure 7 shows the fitting of the TA spectra by Equation (3) for several selected delay times. The amplitudes of bleach peaks B1(t), B2(t), and B3(t) can be assigned to the populations of the three predominant exciton states 1Se − 1S3/2, 1Se − 2S3/2, and 1Pe − 1P3/2, respectively [54]. The dynamics of the B1,2,3(t) bleach peaks amplitude and the C1(t) amplitude associated with the electrochromic Stark shift of the band-edge exciton obtained as a result of the simulation are shown in Figure 8.
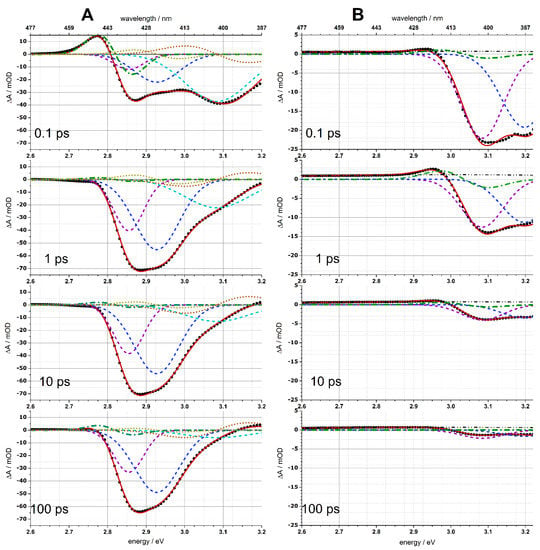
Figure 7.
TA spectra at different delay times after 30 fs, 360 nm pump. (A) QD-1, without Mn2+ ions. (B) Mn2+-doped QD-2. TA experimental data are shown as black circle marks. Solid red lines represent the fitting model (Equation (3)) with parameters in Table 1. BL bands are X1 (violet, dashed), X2 (blue, dashed), X3 (cyan, dashed). Stark spectral feature of the band-edge exciton (X1) is indicated by S-like dash-dotted green lines. The Stark features of X2 and X3 excitons are indicated by yellow and brown dots, respectively.
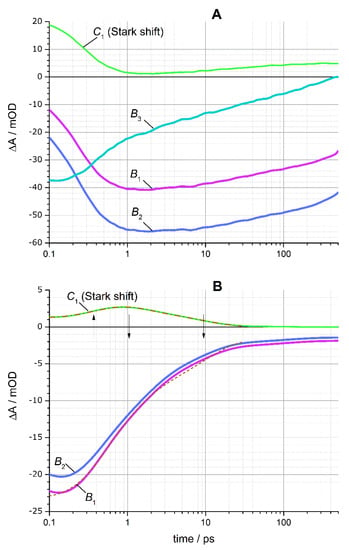
Figure 8.
Kinetics of the B1,2,3(t) bleach peaks amplitude and the C1(t) amplitude associated with the electrochromic Stark shift of the band-edge exciton X1. (A) QD-1 sample without Mn2+ ions. Green solid line is the experimental Stark shift. (B) QD-2 sample doped with Mn2+. Green solid line is the experimental Stark shift, red dash-dotted line is the model (5). The fitting of TA spectra from Figure 5A,B by 3 and 2 Gaussian components, respectively, was done using Equation (3) as illustrated in Figure 7. The kinetic model (4) of sequential electron-hole transfer in the Mn2+-doped QD-2 sample is shown by dashed lines according to Equation (5). Up and down arrows indicate the characteristic times of electron and hole transfer processes, respectively.
Figure 8A shows that in the QD-1 sample, the growth of the X1 and X2 bleach amplitudes B1(t) and B2(t) in the time range of ≤0.5 ps occurred in parallel with a decay of the Stark shift C1(t) of the band-edge exciton X1. Since the X3 bleach amplitude B3(t) did not change significantly in the time range up to 0.5 ps, the Stark shift C1(t) is attributed mainly to the X4-X1 biexciton interaction; such attribution is consistent with a large magnitude of the Stark shift (δ1 = 70 meV, see Table 1), which substantially exceeds the estimates of 10–20 meV obtained for the X3-X1 biexciton interaction [56,57,58,59]. In the QD-1, the decrease of the Stark shift to almost zero in parallel with the relaxation of the upper excitons indicates that the terminal stage of electronic transitions X4 → X3 → X2, X1 proceeds at a timescale of ~300 fs in agreement with previous studies of hot exciton relaxation in different QDs [60,61,62]. The slow decrease of the B3(t) amplitude in the time range of 1–100 ps proceeded in parallel with a small increase of the Stark shift C1(t); both effects can be explained by the trapping of free charges on the surface of the nanoparticle [31,56].
Figure 8B shows that in the QD-2 sample with Mn2+ ions, a fast decay of the X1, X2 bleach peaks took place in the time window of ≤1 ps, and in the same time scale a substantial Stark shift of the X1 band was developing. In this sample, the X3 bleaching was not resolved; however, based on the increase in the X1/X2 bleaching at the shortest delays of ≤200 fs, the presence of a small contribution of the X3 → X2/X1 transition, ξ3, is suggested for this sample.
The transient dynamics of the QD-2 sample differed significantly from that of the QD-1 in two aspects. First, the X1 bleaching disappeared in the QD-2 sample at the timescale of 1 ps, whereas the X1 exciton in the QD-1 sample decayed three orders of magnitude slower in the nanosecond time scale. Second, the electrochromic shift of the X1 band C1(t) in QD-2 was small at the shortest delays (because of the small yield of the X4 exciton in this sample), but C1(t) increased at delays of ~1 ps. The decay of the X1/X2 BL amplitude is somewhat ahead of the kinetics of the Stark shift disappearance. The concomitant decay of the X1/X2 bleach and the transient rising of the Stark shift suggests that the energy transfer from the X1 and X2 excitons to the Mn2+ ions proceeds a two-step charge transfer mechanism, as was suggested previously by Gahlot et al. [28]. We attributed the kinetics of the transient Stark shift upturn to transiently recharging Mn2+ ions, the localized charges of which induced a large electrochromic band shift of the X1 band (ħδ1 = 0.1 eV, see Table 1) due to strong charge-exciton interaction.
The sequential transfer of two charges may occur in two different ways: (A) the Mn2+ ion is oxidized to Mn3+ by a hole transfer from the valence band, after which an electron is transferred to the Mn3+ from the conduction band; (B) alternatively, the Mn2+ ion is reduced in the first step to Mn1+ by an electron transfer from the conduction band, after which a hole is transferred from the valence band (see boxes A and B in Scheme 1). The first mechanism prevails if the redox potential of the Mn3+/Mn2+ transition lies below the redox potential of the valence band, and the second case may take place if the redox potential of the Mn2+/Mn1+ transition lies above the redox potential of the conduction band.
The redox potentials of the conduction band were determined for the CdS and ZnS nanoparticles by direct electrochemical measurements in the range between −2.15 and −2.3 V vs NHE and were found to be weakly dependent on the size of nanoparticles, whereas the redox potentials of the valence band were in the range from +0.55 to +0.75 V vs NHE [19]. The reduction potentials for the Mn2+/Mn+ transition in several organic complexes varied between−0.7 and−1.3 V vs. NHE [63,64,65,66], and the reduction potentials for the Mn3+/Mn2+ couple in an aqueous solutions of various ionic ligands were between +0.8 and +1.5 V vs. NHE [67]. This means that the energy level of the Mn2+/Mn+ transition is most likely within the bandgap of the QD-2 particle, while the Mn3+/Mn2+ level is submerged in the valence band. Beaulac and Gamelin calculated energy levels of the Mn2+ orbitals for different Mn2+-doped semiconductors and found out that the energy level of 3d5 orbital (Mn2+/3+ transition) is located deep in the valence band, whereas the unoccupied Mn2+ orbitals participate in exchange interactions with electrons of the conduction band, allowing Mn2+ to be a 3d-based electron acceptor (Mn2+/+ transition) [68].
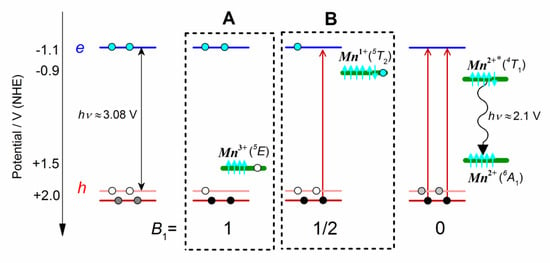
Scheme 1.
Electronic configurations of the 2 alternative charge-transfer intermediates (A,B) that can be responsible for a 2-step energy transfer from the X1 exciton to Mn2+ ions + and the overall 6A1 → 4T1 transition. The electronic states of Mn3+ and Mn+ ions correspond to the 2E (3d4) and 5T2 (3d6) configurations, in accordance with the DFT calculations [69].
Kinetic modeling of the absorption dynamics gives allows us to distinguish which of the two probable mechanisms the reaction follows. The B1 amplitude of the X1 band is determined by the filling of the 1Se electron and 1S3/2 hole states. The scavenge of holes (mechanism A) has little effect on the BL amplitude [47], the relative extent of which is indicated in Scheme 1 by the dimensionless coefficient θ = 1. Assuming that all 1Se states are initially filled, the loss of one electron from the X1 band in the result of the Mn2+ reduction (mechanism B) leads to a two-fold decrease in the BL amplitude due to a decrease in the population of the 1Se electronic state (θ = 1/2). To simplify the kinetic model, we assume that the X1 and X2 excitons are in thermal equilibrium and the transfer of the second electron to Mn2+ is compensated by the electron exchange between the 1Se and 2Se states. The kinetic scheme (4) includes therefore three transitions
where X3 and X1 are the generalized populations of the X3 and X2/X1 excitons, XCT is the population of the charge transfer intermediate A or B in Scheme 1, and XE is the population of the final 4T1 excited state of Mn2+. The transitions between these states are described by the kinetic constants k3, m1, and m2 for the first order reactions. The kinetics of the B1(t) bleach amplitude and the C1(t) amplitude of the X1 shift are
Here a1 is the absorbance of the X1 bleach peak, c3 and c0 are the electrochromic shifts of the X1 band due to the X3-X1 biexciton and the charge–exciton interactions, and θ is the dimensionless coefficient, the value of which is determined by the reaction mechanism. Numerical analysis showed that the kinetic model should take into account the heterogeneity of the sample, the presence of which also follows from the EPR data (Figure 3) and the CONTIN kinetic analysis (Figure 6). For this purpose, the model considered three fractions of the Mn2+ locations. The first two fractions, fA, and fB (Table 2), differed in the magnitude of the m2 charge transfer constant (two down arrows in Figure 8B), and in the third fraction fC there was no manganese in the nanoparticle (m2 = 0).

Table 2.
Kinetic model of the B1 bleach peak and the Stark shift C1 changes of the QD-2 sample.
The found value of coefficient θ = 0.49 (Table 2) agrees with the electron-to-hole mechanism of energy with the intermediate Mn2+ reduction (variant B in Scheme 1). The model includes the fast X3 → X1 transition (k3 = 9.5 ps−1) in 19% of the particles, the slower Mn2+ reduction (m1 = 2.7 ps−1), and the formation of excited [Mn2+]* state due to the slowest electron transfer reaction (m2A = 0.96 ps−1 in the fraction fA = 0.39 and m2B = 0.1 ps−1 in the fraction fB = 0.55). The model kinetic curves are shown in Figure 8B by dashed curves.
Different time-resolved measurements of the Mn2+ excitation time ranging from a few hundred fs to a few ns were reported in the literature. Chen et al. [23] estimated the time constant τET of ~60 ps for the exciton to Mn2+ energy transfer in CdS/ZnS QDs employing the pump–probe transient absorption technique to measure the exciton relaxation dynamics in doped and undoped QDs. A near-IR probe wavelength primarily monitoring the intraband transition of excitons was used [23]. S. Taguchi et al. [70] registered the τET value of ~2 ns in Mn2+-doped core/shell CdS/ZnS QDs. TA bleaching of the band-edge exciton was measured in doped and undoped QDs, and a model including the bimolecular recombination of e–h pairs and three-particle Auger recombination was used to extract τET value [70]. Chung et al. [71] measured a picosecond TA and subnanosecond fluorescence dynamics in Mn-doped ZnS nanoparticles. They reported the energy-transfer process to Mn2+ impurities occurring on the time scale of 700 ps [71]. Olano et al. studied energy-transfer dynamics in Mn2+-doped ZnSe QDs by registering the photoluminescence using time-integrated, time-resolved spectroscopic techniques and femtosecond TA spectroscopy. Mn2+ doping substantially shortens the average lifetimes of the band-edge excitonic state as well as shallow trap states, which suggests the energy transfer from ZnSe to Mn2+ follows two mechanisms, one through trap states and another without, on the time scale of tens of ps [72]. Shibata et al. analyzed the radiative and non-radiative recombination processes in the Mn-doped CdSe QDs monitoring luminescence by streak camera technique. They found out that the exciton energy transfer to Mn2+ 3d5 electrons occurs on a time scale of 20 ps [73]. Hsiang-Yun Chen et al. [74] studied dynamics of energy transfer in Mn-doped CdS/ZnS core/shell QDs via transient absorption measurement of exciton relaxation dynamics. They found the strong dependence of the Mn2+ excitation rate on doping location. It was found that the band-edge exciton decay of Mn2+(3d5) occurs as a multiexponential process. The average quenching time of the Mn2+ exciton is in the range 3.8–80 ps, depending on the concentration of Mn2+ ions and their location in the QD matrix. The faster time constant can be ~0.56 ps with the relative amplitude of ~62% [74]. The cited works [23,70,71,72,73,74] suggest that Mn2+ excitation can occur due to the non-radiative Auger-like exciton recombination, Dexter, and Förster energy-transfer mechanism [10,11,12,15,19,21,23,24,25,26,65,66,67,68,69] from an exciton to the d-d levels of manganese. An alternative way to excite Mn2+ may be a charge transfer mechanism [49]. K. Gahlot et al. [28] suggested that oxidation of Mn2+ occurs with a characteristic time of τp~100–200 fs for Mn2+:CdxZn1−xSe QDs. Our observation of redox reaction with a characteristic time of 1/m1 ~ 380 fs is in accord with τp ~ 200 fs. In contrast to the assumption about the oxidation of Mn2+ by the hole at the first step of the redox process made in [28], the results of this work suggest the reduction of Mn2+ is the first event in the manganese excitation process. According to K. Gahlot et al. [28], excited Mn2+* is formed from the intermediate charge transfer state of Mn3+ with a characteristic time of 300–800 ps [28]. This time value of 300–800 ps significantly exceeds the characteristic time of excitation of Mn2+ obtained in this work, which is approximately 1ps. The observation of stimulated emission of manganese ions SE(592) for Mn2+:Cd0.5Zn0.5S in the time window of 1 ps in the present work, and recently, [26] suggested that the excitation of manganese occurs much faster than it is assumed in [28] for Mn2+:CdxZn1−xSe QDs. Kinetics of the Stark peak at the time scale of ~1 ps and the observation of SE(592) at short times suggest the process of manganese excitation is completed by oxidation of Mn1+ by a hole (Scheme 1). The assumption about the reduction of Mn2+ to Mn+1 is consistent with the observation that manganese-doped QDs in QD solar cells has shown an enhancement in energy conversion efficiency by 20% compared to unalloyed analog [49,75].
4. Conclusions
The femtosecond transient absorption (TA) spectra of quantum dots (QDs) of the manganese-doped Mn2+:Zn~0.5Cd~0.5S/ZnS alloy reveals a specific feature that manifests itself as an absorption peak that appears with a time delay. The delayed absorption peak has spectral features of the electrochromic Stark shift of the band-edge exciton. The delayed development and decay kinetics of this Stark peak in manganese-doped QDs significantly distinguish it from the known Stark peak associated with electrochromic shift caused by exciton–exciton interactions in undoped QDs at the initial time delays. The delayed Stark shift in QDs doped with Mn2+ suggests the development of the electric field in QDs due to charge transfer. Charge transfer processes can be attributed to the reduction of Mn2+ by electrons from the 1Se state, followed by the oxidation of Mn1+ by holes with the formation of excited Mn2+(d5)* ions. The charge transfer mechanism solves the problem of a significant mismatch between the energy gaps of the band-edge exciton and the excited manganese and may not contradict the Wigner rule. This mechanism can provide a high rate of manganese excitation, which manifests itself in the TA spectra at short delay times. The revealed Stark peak suggests a charge-transfer mechanism of Mn2+ excitation by the QDs band-edge exciton in contrast to the non-radiative energy-transfer mechanism, which does not imply the development of an electric field in the QDs.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/nano11113007/s1, Figure S1: TEM images of QD-1 and QD-2 samples; Figure S2: Absorption, PLE and PL spectra of QD-2; Figure S3: Femtosecond Pump-Probe TA spectra of QD-1 and QD-2 samples; Figure S4: Decomposition of TA spectra into Gaussian peaks in the approximation of the model of exciton and biexciton transitions.
Author Contributions
Data analysis and preparation of the article, V.N. and D.C.; optical and femtosecond measurements, F.G., I.S. and A.K.; synthesis of samples, S.K. and Y.K.; measurement of EPR spectra, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Russian Science Foundation (grant number 17-13-01506).
Institutional Review Board Statement
Not applicable.
Acknowledgments
Femtosecond TA measurements were performed in the Federal Research Center of Chemical Physics RAS shared research facilities (No. 506694). The authors are deeply grateful to Alexandre Golub for measuring and interpreting the XRD spectra and Olga Antonova for elemental analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shan, S.P.; Chen, S.H.; Zhuang, R.Z.; Hu, C. Influence of magnetic field on the properties of polaron in an asymmetric quantum dot. Int. J. Mod. Phys. B 2019, 33, 1950263. [Google Scholar] [CrossRef]
- Rastrello, L.R.; Guimarães, E.V.; da Silva, M.A.T.; Dantas, N.O.; Cano, N.F.; Lourenço, S.A.; da Silva, R.S. Effect of thermal annealing and sp − d exchange interaction in the optical properties of Mn2+-doped PbS nanocrystals embedded in a glass matrix. J. Lumin. 2020, 222, 117144. [Google Scholar] [CrossRef]
- Mehata, M.S.; Ratnesh, R.K. Luminescence properties and exciton dynamics of core-multi-shell semiconductor quantum dots leading to QLEDs. Dalt. Trans. 2019, 48, 7619–7631. [Google Scholar] [CrossRef]
- Rice, W.D.; Liu, W.; Pinchetti, V.; Yakovlev, D.R.; Klimov, V.I.; Crooker, S.A. Direct Measurements of Magnetic Polarons in Cd1-xMnxSe Nanocrystals from Resonant Photoluminescence. Nano Lett. 2017, 17, 3068–3075. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLaurin, E.J.; Vlaskin, V.A.; Gamelin, D.R. Water-soluble dual-emitting nanocrystals for ratiometric optical thermometry. J. Am. Chem. Soc. 2011, 133, 14978–14980. [Google Scholar] [CrossRef]
- Li, C.; Wu, P. Cu-doped quantum dots: A new class of near-infrared emitting fluorophores for bioanalysis and bioimaging. Luminescence 2019, 34, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Archer, P.I.; Santangelo, S.A.; Gamelin, D.R. Direct observation of sp − d exchange interactions in colloidal Mn2+- and Co2+-doped CdSe quantum dots. Nano Lett. 2007, 7, 1037–1043. [Google Scholar] [CrossRef]
- Delikanli, S.; Akgul, M.Z.; Murphy, J.R.; Barman, B.; Tsai, Y.; Scrace, T.; Zhang, P.; Bozok, B.; Hernández-Martínez, P.L.; Christodoulides, J.; et al. Mn2+-Doped CdSe/CdS Core/Multishell Colloidal Quantum Wells Enabling Tunable Carrier-Dopant Exchange Interactions. ACS Nano 2015, 9, 12473–12479. [Google Scholar] [CrossRef] [PubMed]
- Nelson, H.D.; Bradshaw, L.R.; Barrows, C.J.; Vlaskin, V.A.; Gamelin, D.R. Picosecond Dynamics of Excitonic Magnetic Polarons in Colloidal Diffusion-Doped Cd1−xMnxSe Quantum Dots. ACS Nano 2015, 9, 11177–11191. [Google Scholar] [CrossRef]
- Pradhan, N.; Sarma, D.D. Advances in light-emitting doped semiconductor nanocrystals. J. Phys. Chem. Lett. 2011, 2, 2818–2826. [Google Scholar] [CrossRef]
- Chen, H.Y.; Son, D.H. Energy and charge transfer dynamics in doped semiconductor nanocrystals. Isr. J. Chem. 2012, 52, 1016–1026. [Google Scholar] [CrossRef]
- Barman, B.; Pientka, J.M.; Murphy, J.R.; Cartwright, A.N.; Chou, W.C.; Fan, W.C.; Oszwałdowski, R.; Petrou, A. Circular Polarization Dynamics during Magnetic Polaron Formation in Type-II Magnetic Quantum Dots. J. Phys. Chem. C 2020, 124, 12766–12773. [Google Scholar] [CrossRef]
- Qiao, T.; Parobek, D.; Son, D.H.; Son, D.H. Photons and charges from colloidal doped semiconductor quantum dots. J. Mater. Chem. C 2019, 7, 14788–14797. [Google Scholar] [CrossRef]
- Batista, E.A.; Silva, A.C.A.; de Lima, T.K.; Guimarães, E.V.; da Silva, R.S.; Dantas, N.O. Effect of the location of Mn2+ ions in the optical and magnetic properties of ZnO nanocrystals. J. Alloys Compd. 2021, 850, 156611. [Google Scholar] [CrossRef]
- Viswanatha, R.; Pietryga, J.M.; Klimov, V.I.; Crooker, S.A. Spin-polarized Mn2+ emission from mn-doped colloidal nanocrystals. Phys. Rev. Lett. 2011, 107, 067402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shornikova, E.V.; Yakovlev, D.R.; Tolmachev, D.O.; Ivanov, V.Y.; Kalitukha, I.V.; Sapega, V.F.; Kudlacik, D.; Kusrayev, Y.G.; Golovatenko, A.A.; Shendre, S.; et al. Magneto-Optics of Excitons Interacting with Magnetic Ions in CdSe/CdMnS Colloidal Nanoplatelets. ACS Nano 2020, 14, 9032–9041. [Google Scholar] [CrossRef] [PubMed]
- Beaulac, R.; Schneider, L.; Archer, P.I.; Bacher, G.; Gamelin, D.R. Light-induced spontaneous magnetization in doped colloidal quantum dots. Science 2009, 325, 973–976. [Google Scholar] [CrossRef]
- Lorenz, S.; Erickson, C.S.; Riesner, M.; Gamelin, D.R.; Fainblat, R.; Bacher, G. Directed Exciton Magnetic Polaron Formation in a Single Colloidal Mn2+:CdSe/CdS Quantum Dot. Nano Lett. 2020, 20, 1896–1906. [Google Scholar] [CrossRef]
- Harris, R.D.; Bettis Homan, S.; Kodaimati, M.; He, C.; Nepomnyashchii, A.B.; Swenson, N.K.; Lian, S.; Calzada, R.; Weiss, E.A. Electronic Processes within Quantum Dot-Molecule Complexes. Chem. Rev. 2016, 116, 12865–12919. [Google Scholar] [CrossRef]
- Xu, G.; Zeng, S.; Zhang, B.; Swihart, M.T.; Yong, K.T.; Prasad, P.N. New Generation Cadmium-Free Quantum Dots for Biophotonics and Nanomedicine. Chem. Rev. 2016, 116, 12234–12327. [Google Scholar] [CrossRef]
- Jing, L.; Kershaw, S.V.; Li, Y.Y.; Huang, X.; Li, Y.Y.; Rogach, A.L.; Gao, M. Aqueous Based Semiconductor Nanocrystals. Chem. Rev. 2016, 116, 10623–10730. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.Y.; Yu, Q.; Wei, H.; Liu, S.; Zhao, Q.; Huang, W. Long-Lived Emissive Probes for Time-Resolved Photoluminescence Bioimaging and Biosensing. Chem. Rev. 2018, 118, 1770–1839. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.Y.; Chen, T.Y.; Son, D.H. Measurement of energy transfer time in colloidal Mn-doped semiconductor nanocrystals. J. Phys. Chem. C 2010, 114, 4418–4423. [Google Scholar] [CrossRef]
- Deng, Z.; Tong, L.; Flores, M.; Lin, S.; Cheng, J.X.; Yan, H.; Liu, Y. High-quality manganese-doped zinc sulfide quantum rods with tunable dual-color and multiphoton emissions. J. Am. Chem. Soc. 2011, 133, 5389–5396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, J.; Cao, S.; Wang, L.; Gao, F.; Wei, G.; Yang, W. Temperature-dependent photoluminescence properties of Mn:ZnCdS quantum dots. RSC Adv. 2014, 4, 30948–30952. [Google Scholar] [CrossRef]
- Nadtochenko, V.; Kostrov, A.; Titov, A.; Aybush, A.; Gostev, F.; Shelaev, I.; Shepel, D.; Antonova, O.; Kochev, S.; Kabachii, Y. Multiexponential dynamics of Mn2+(3d5) excitation in manganese doped ZnCdS quantum dots: Stimulated emission band in femtosecond transient spectra reveals ultrafast nonradiative energy transfer to Mn2+(3d5). Chem. Phys. Lett. 2020, 743, 137160. [Google Scholar] [CrossRef]
- Chernenko, A.V. On the Dominant Mechanism of the Nonradiative Excitation of Manganese Ions in II–VI Diluted Magnetic Semiconductors. Semiconductors 2020, 54, 433–436. [Google Scholar] [CrossRef]
- Gahlot, K.; Pradeep, K.; Camellini, A.; Sirigu, G.; Cerullo, G.; Zavelani-Rossi, M.; Singh, A.; Waghmare, U.V.; Viswanatha, R. Transient Species Mediating Energy Transfer to Spin-Forbidden Mn d States in II-VI Semiconductor Quantum Dots. ACS Energy Lett. 2019, 4, 729–735. [Google Scholar] [CrossRef]
- Chernenko, A.V.; Brichkin, A.S.; Sobolev, N.A.; Carmo, M.C. Mechanisms of Manganese-Assisted Nonradiative Recombination in Cd(Mn)Se/Zn(Mn)Se Quantum Dots. J. Phys. Condens. Matter 2009, 22, 355306. [Google Scholar] [CrossRef]
- Chernenko, A.V.; Brichkin, A.S.; Kulakovskii, V.D.; Sobolev, N.A.; Ivanov, S.V. Effect of Mn ions on spin relaxation and life-time of e–h complexes in CdSe/ZnSe/ZnMnSe quantum dots. Int. J. Mod. Phys. B 2009, 23, 2984–2988. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, O.; Angerhofer, A.; Cao, Y.C. Radial-position-controlled doping of CdS/ZnS core/shell nanocrystals: Surface effects and position-dependent properties. Chem. Eur. J. 2009, 15, 3186–3197. [Google Scholar] [CrossRef] [PubMed]
- Fery-Forgues, S.; Lavabre, D. Are Fluorescence Quantum Yields So Tricky to Measure? A Demonstration Using Familiar Stationery Products. J. Chem. Educ. 1999, 76, 1260–1264. [Google Scholar] [CrossRef]
- Nadtochenko, V.; Denisov, N.; Aybush, A.; Gostev, F.; Shelaev, I.; Titov, A.; Umanskiy, S.; Cherepanov, D. Ultrafast spectroscopy of fano-like resonance between optical phonon and excitons in CdSe quantum dots: Dependence of coherent vibrational wave-packet dynamics on pump fluence. Nanomaterials 2017, 7, 371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cherepanov, D.A.; Gostev, F.E.; Shelaev, I.V.; Denisov, N.N.; Nadtochenko, V.A. Monitoring the electric field in CdSe quantum dots under ultrafast interfacial electron transfer: Via coherent phonon dynamics. Nanoscale 2018, 10, 22409–22419. [Google Scholar] [CrossRef]
- Butler, W.L.; Hopkins, D.W. Higher Derivative Analysis of Complex Absorption Spectra. Photochem. Photobiol. 1970, 12, 439–450. [Google Scholar] [CrossRef]
- Sambandam, B.; Manoharan, P.T. Davydov split PL emission and EPR correlation in β-mns layered cds nanorods. J. Phys. Chem. C 2009, 113, 9486–9496. [Google Scholar] [CrossRef]
- Counio, G.; Esnouf, S.; Gacoin, T.; Boilot, J.P. CdS:Mn nanocrystals in transparent xerogel matrices: Synthesis and luminescence properties. J. Phys. Chem. 1996, 100, 20021–20026. [Google Scholar] [CrossRef]
- Levy, L.; Feltin, N.; Ingert, D.; Pileni, M.P. Isolated Mn2+ in CdS quantum dots. Langmuir 1999, 15, 3386–3389. [Google Scholar] [CrossRef]
- Igarashi, T.; Isobe, T.; Senna, M. EPR study of electronic states for the nanosized ZnS:Mn powder modified by acrylic acid. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 56, 6444–6445. [Google Scholar] [CrossRef]
- Nistor, S.V.; Stefan, M.; Ghica, D.; Nistor, L.C. Nanosize induced effects in luminescent ZnS:Mn2+ quantum dots. Radiat. Meas. 2013, 56, 40–43. [Google Scholar] [CrossRef]
- Nistor, S.V.; Stefan, M.; Nistor, L.C.; Ghica, D.; Vlaicu, I.D. Distribution and interaction of Mn2+ ions incorporated in cubic ZnS quantum dots over a broad concentration range. J. Alloys Compd. 2016, 662, 193–199. [Google Scholar] [CrossRef]
- Gonzalez Beermann, P.A.; McGarvey, B.R.; Muralidharan, S.; Sung, R.C.W. EPR Spectra of Mn2+-Doped ZnS Quantum Dots. Chem. Mater. 2004, 16, 915–918. [Google Scholar] [CrossRef]
- Biswas, S.; Kar, S.; Chaudhuri, S. Optical and magnetic properties of manganese-incorporated zinc sulfide nanorods synthesized by a solvothermal process. J. Phys. Chem. B 2005, 109, 17526–17530. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, S.K.; Shinde, R.F.; Date, S.K. Effect of (formula presented) concentration in ZnS nanoparticles on photoluminescence and electron-spin-resonance spectra. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 60, 8659–8664. [Google Scholar] [CrossRef]
- Counio, G.; Gacoin, T.; Boilot, J.P.; Polytechnique, Ä.; Cedex, P. Synthesis and Photoluminescence of Cd1−xMnxS (x ≤ 5%). Nanocrystals 1998, 5647, 5257–5260. [Google Scholar]
- Kennedy, T.A.; Glaser, E.R.; Klein, P.B.; Bhargava, R.N. Symmetry and electronic structure of the Mn impurity in ZnS nanocrystals. Phys. Rev. B 1995, 52, R14356. [Google Scholar] [CrossRef]
- Klimov, V.I. Optical nonlinearities and ultrafast carrier dynamics in semiconductor nanocrystals. J. Phys. Chem. B 2000, 104, 6112–6123. [Google Scholar] [CrossRef]
- Klimov, V.; Hunsche, S.; Kurz, H. Biexciton effects in femtosecond nonlinear transmission of semiconductor quantum dots. Phys. Rev. B 1994, 50, 8110. [Google Scholar] [CrossRef]
- Pradeep, K.R.; Viswanatha, R. Mechanism of Mn emission: Energy transfer vs charge transfer dynamics in Mn-doped quantum dots. APL Mater. 2020, 8, 020901. [Google Scholar] [CrossRef]
- Zhang, C.; Do, T.N.; Ong, X.; Chan, Y.; Tan, H.S. Understanding the features in the ultrafast transient absorption spectra of CdSe quantum dots. Chem. Phys. 2016, 481, 157–164. [Google Scholar] [CrossRef]
- Rawalekar, S.; Kaniyankandy, S.; Verma, S.; Ghosh, H.N. Effect of surface states on charge-transfer dynamics in type II CdTe/ZnTe core-shell quantum dots: A femtosecond transient absorption study. J. Phys. Chem. C 2011, 115, 12335–12342. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Smitienko, O.A.; Feldman, T.B.; Petrovskaya, L.E.; Nekrasova, O.V.; Yakovleva, M.A.; Shelaev, I.V.; Gostev, F.E.; Cherepanov, D.A.; Kolchugina, I.B.; Dolgikh, D.A.; et al. Comparative Femtosecond Spectroscopy of Primary Photoreactions of Exiguobacterium sibiricum Rhodopsin and Halobacterium salinarum Bacteriorhodopsin. J. Phys. Chem. B 2021, 125, 995–1008. [Google Scholar] [CrossRef] [PubMed]
- Norris, D.; Bawendi, M. Measurement and assignment of the size-dependent optical spectrum in CdSe quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 53, 16338–16346. [Google Scholar] [CrossRef] [Green Version]
- Kambhampati, P. Multiexcitons in semiconductor nanocrystals: A platform for optoelectronics at high carrier concentration. J. Phys. Chem. Lett. 2012, 3, 1182–1190. [Google Scholar] [CrossRef]
- Sewall, S.L.; Franceschetti, A.; Cooney, R.R.; Zunger, A.; Kambhampati, P. Direct observation of the structure of band-edge biexcitons in colloidal semiconductor CdSe quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 081310. [Google Scholar] [CrossRef] [Green Version]
- Klimov, V.I. Spectral and Dynamical Properties of Multiexcitons in Semiconductor Nanocrystals. Annu. Rev. Phys. Chem. 2007, 58, 635–673. [Google Scholar] [CrossRef]
- Sewall, S.L.; Cooney, R.R.; Dias, E.A.; Tyagi, P.; Kambhampati, P. State-resolved observation in real time of the structural dynamics of multiexcitons in semiconductor nanocrystals. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 235304. [Google Scholar] [CrossRef]
- Nadtochenko, V.; Kostrov, A.; Titov, A.; Aybush, A.; Gostev, F.; Shelaev, I.; Shepel, D.; Antonova, O.; Kochev, S.; Kabachii, Y.; et al. The binding energy of biexcitons in alloy ZnxCd1−xS quantum dots detected by femtosecond laser spectroscopy. Appl. Phys. A Mater. Sci. Process. 2020, 126, 1–9. [Google Scholar] [CrossRef]
- Kambhampati, P. Hot exciton relaxation dynamics in semiconductor quantum dots: Radiationless transitions on the nanoscale. J. Phys. Chem. C 2011, 115, 22089–22109. [Google Scholar] [CrossRef]
- Sewall, S.L.; Cooney, R.R.; Anderson, K.E.H.; Dias, E.A.; Kambhampati, P. State-to-state exciton dynamics in semiconductor quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 74, 235328. [Google Scholar] [CrossRef]
- Sewall, S.L.; Cooney, R.R.; Anderson, K.E.H.; Dias, E.A.; Sagar, D.M.; Kambhampati, P. State-resolved studies of biexcitons and surface trapping dynamics in semiconductor quantum dots. J. Chem. Phys. 2008, 129, 084701. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.L.; Lee, C.C.; Ho, K.C. Spectroelectrochemical studies of manganese phthalocyanine thin films for applications in electrochromic devices. J. Electroanal. Chem. 2002, 524–525, 81–89. [Google Scholar] [CrossRef]
- Lever, A.B.P.; Pickens, S.R.; Minor, P.C.; Licoccia, S.; Ramaswamy, B.S.; Magnell, K. Charge-Transfer Spectra of Metallophthalocyanines: Correlation with Electrode Potentials. J. Am. Chem. Soc. 1981, 103, 6800–6806. [Google Scholar] [CrossRef]
- Sjödin, M.; Gätjens, J.; Tabares, L.C.; Thuéry, P.; Pecoraro, V.L.; Un, S. Tuning the redox properties of manganese(II) and its implications to the electrochemistry of manganese and iron superoxide dismutases. Inorg. Chem. 2008, 47, 2897–2908. [Google Scholar] [CrossRef] [PubMed]
- Takeda, H.; Kamiyama, H.; Okamoto, K.; Irimajiri, M.; Mizutani, T.; Koike, K.; Sekine, A.; Ishitani, O. Highly Efficient and Robust Photocatalytic Systems for CO2 Reduction Consisting of a Cu(I) Photosensitizer and Mn(I) Catalysts. J. Am. Chem. Soc. 2018, 140, 17241–17254. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, K.S.; Sawyer, D.T. The Redox Chemistry of Manganese(III) and -(IV) Complexes. Isr. J. Chem. 1985, 25, 164–176. [Google Scholar] [CrossRef]
- Beaulac, R.; Gamelin, D.R. Two-center formulation of Mn2+-electron sp − d exchange coupling in bulk and quantum-confined diluted magnetic semiconductors. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 224401. [Google Scholar] [CrossRef]
- Beaulac, R.; Feng, Y.; May, J.W.; Badaeva, E.; Gamelin, D.R.; Li, X. Orbital pathways for Mn2+-carrier sp − d exchange in diluted magnetic semiconductor quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 195324. [Google Scholar] [CrossRef] [Green Version]
- Taguchi, S.; Ishizumi, A.; Kanemitsu, Y. Multicarrier Recombination and Energy Transfer in Mn-Doped CdS Nanocrystals Studied by Femtosecond Pump–Probe Spectroscopy. J. Phys. Soc. Jpn. 2010, 79, 063710. [Google Scholar] [CrossRef]
- Chung, J.H.; Ah, C.S.; Jang, D.J. Formation and distinctive decay times of surface- and lattice-bound Mn2+ impurity luminescence in ZnS nanoparticles. J. Phys. Chem. B 2001, 105, 4128–4132. [Google Scholar] [CrossRef]
- Olano, E.M.; Grant, C.D.; Norman, T.J.; Castner, E.W.; Zhang, J.Z. Photoluminescence decay dynamics and mechanism of energy transfer in undoped and Mn2+ doped ZnSe nanoparticles. J. Nanosci. Nanotechnol. 2005, 5, 1492–1497. [Google Scholar] [CrossRef] [PubMed]
- Shibata, K.; Nakayama, E.; Souma, I.; Murayama, A.; Oka, Y. Exciton recombination processes in Cd1−xMnxSe/ZnSe quantum dots under magnetic fields. Phys. Status Solidi Basic Res. 2002, 229, 473–476. [Google Scholar] [CrossRef]
- Chen, H.Y.; Maiti, S.; Son, D.H. Doping location-dependent energy transfer dynamics in Mn-doped CdS/ZnS nanocrystals. ACS Nano 2012, 6, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Santra, P.K.; Kamat, P.V. Mn-doped quantum dot sensitized solar cells: A strategy to boost efficiency over 5%. J. Am. Chem. Soc. 2012, 134, 2508–2511. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).