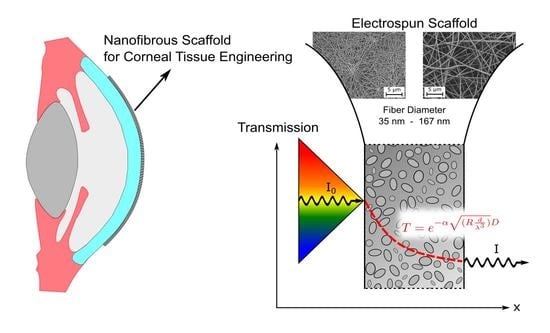
Examining the Transmission of Visible Light through Electrospun Nanofibrous PCL Scaffolds for Corneal Tissue Engineering
Abstract
:1. Introduction
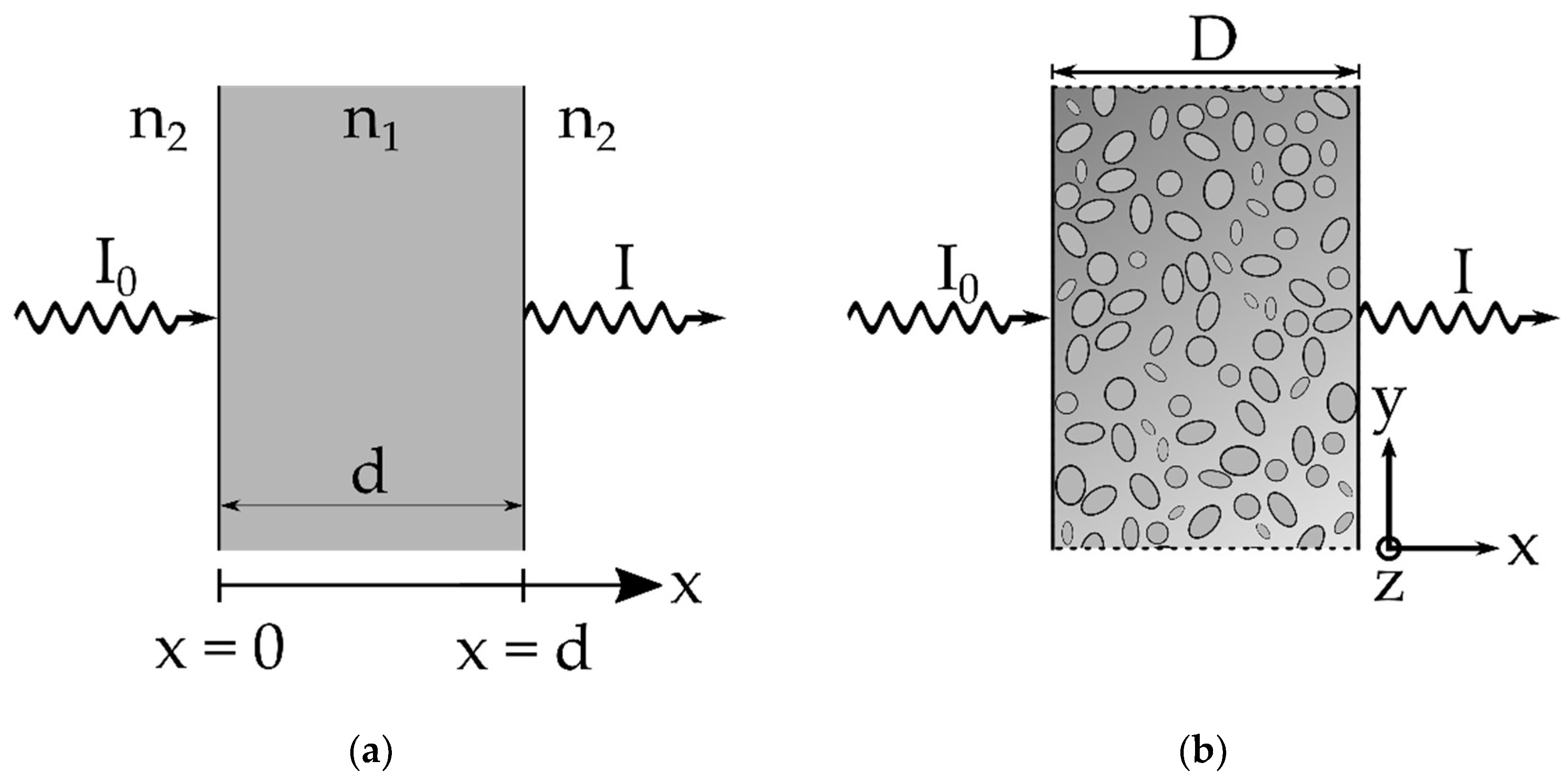
2. Materials and Methods
3. Results and Discussion
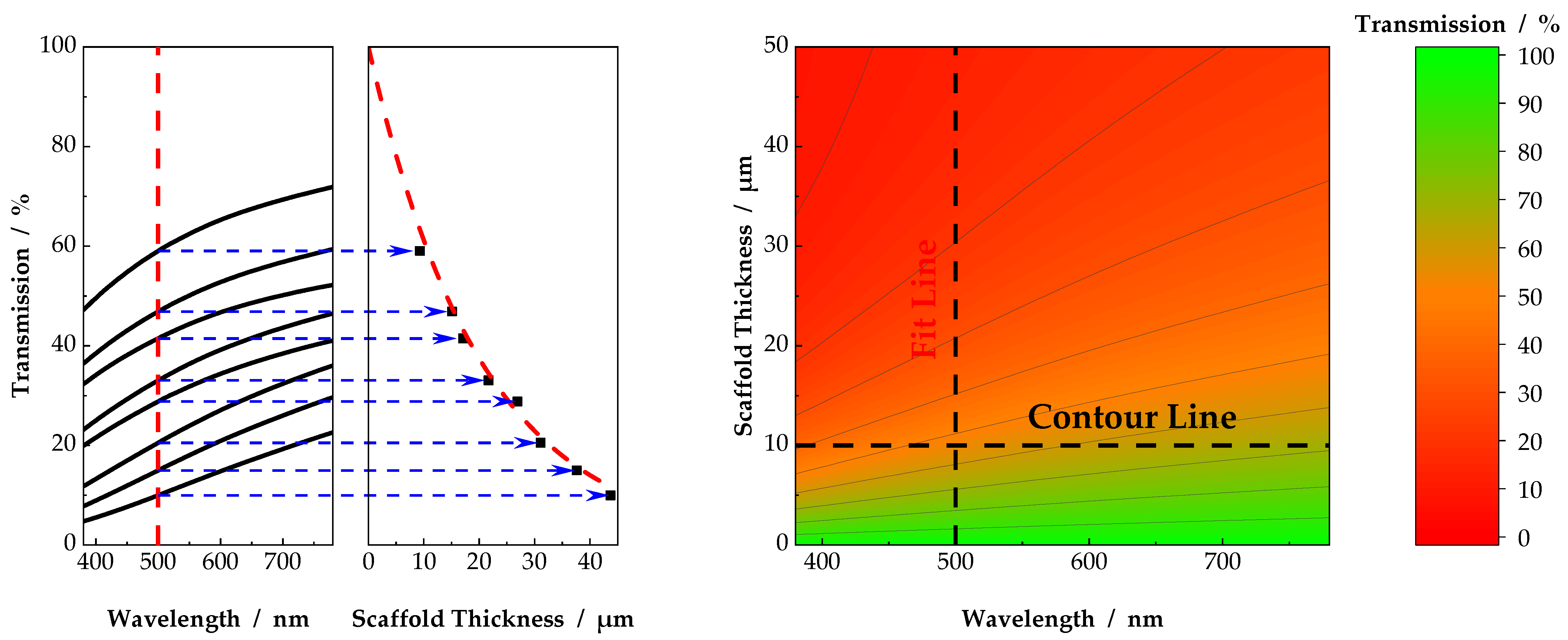
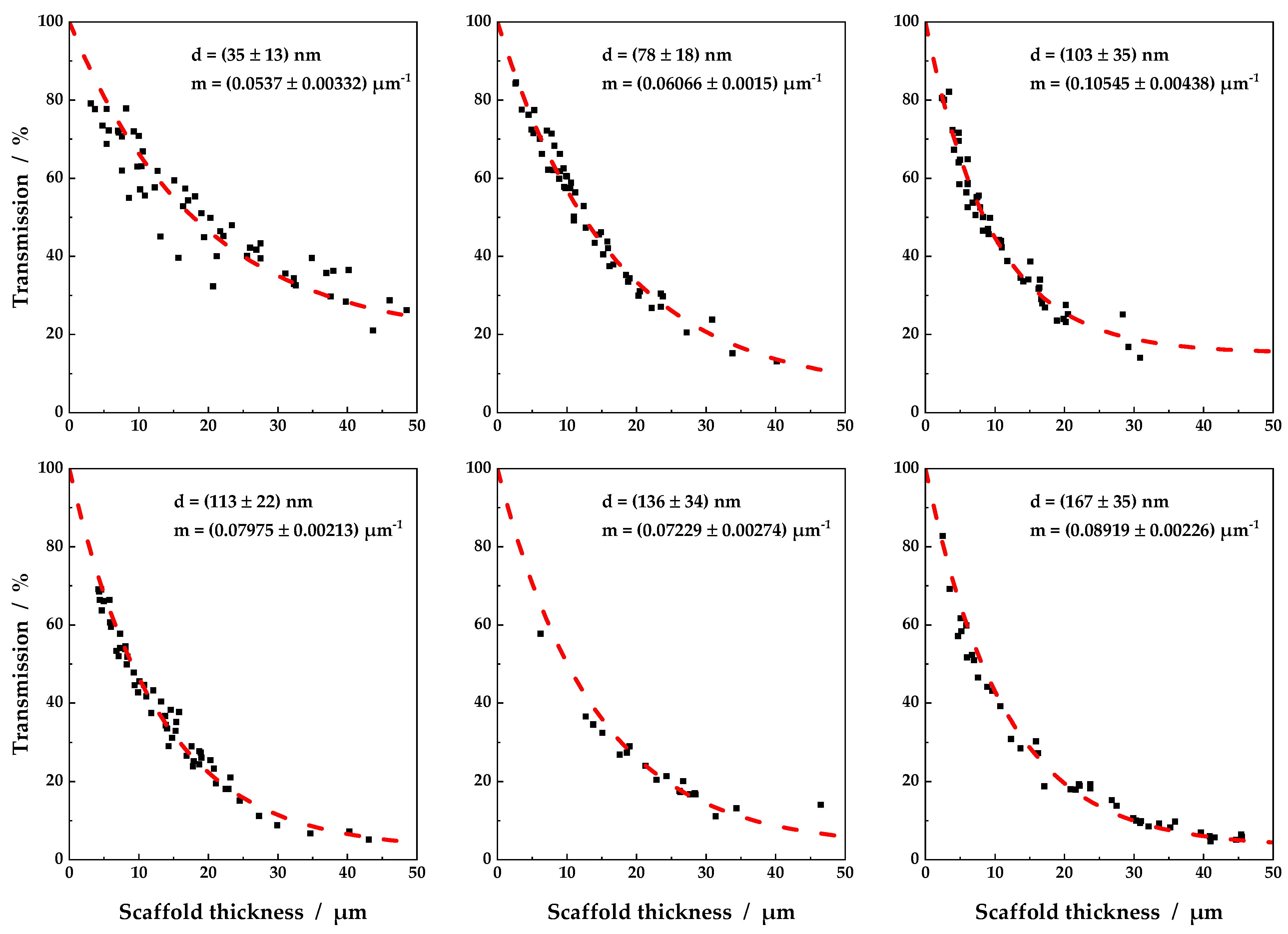
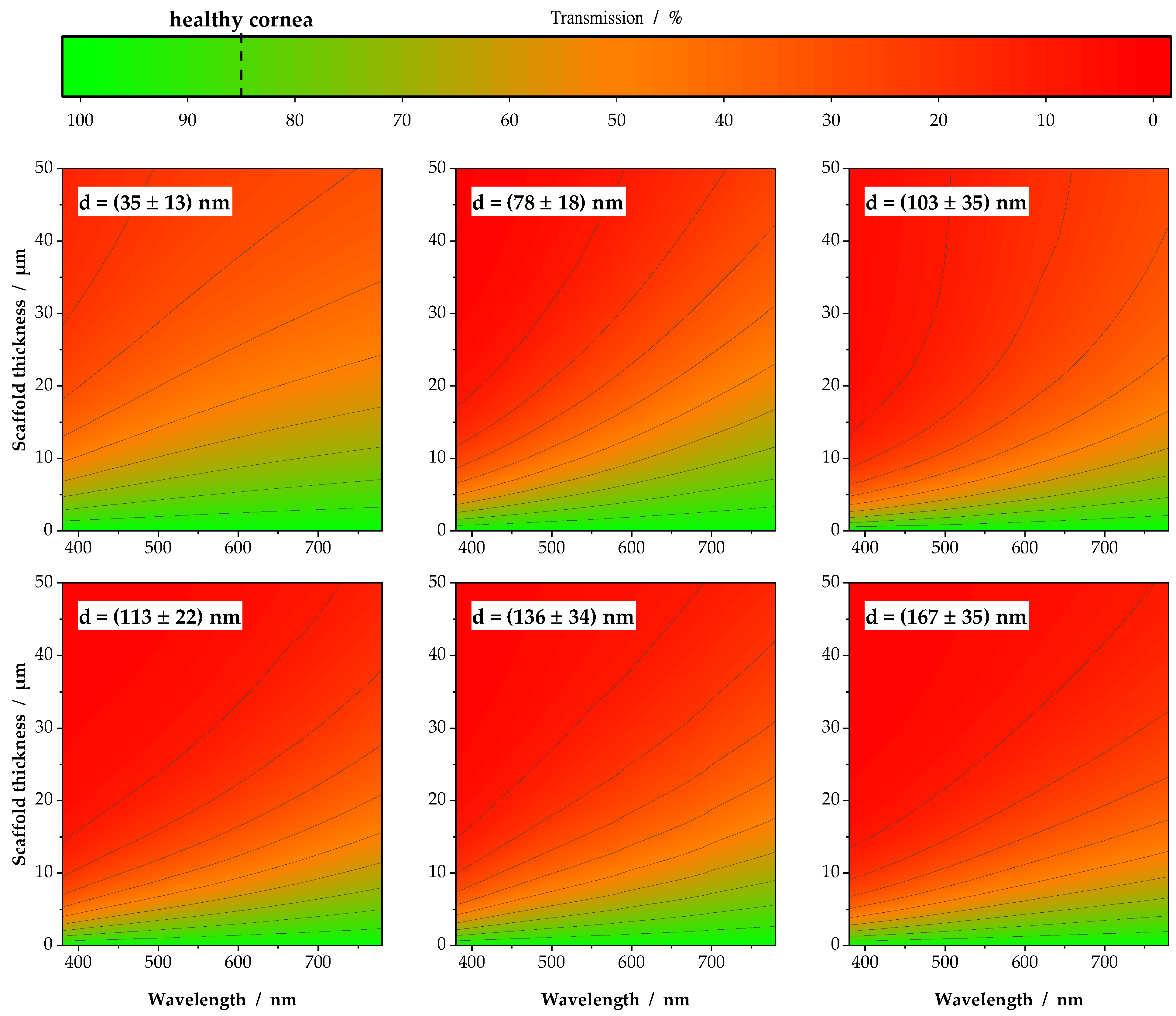
3.1. Individual Transmission Measurements and Resulting Contour Plots
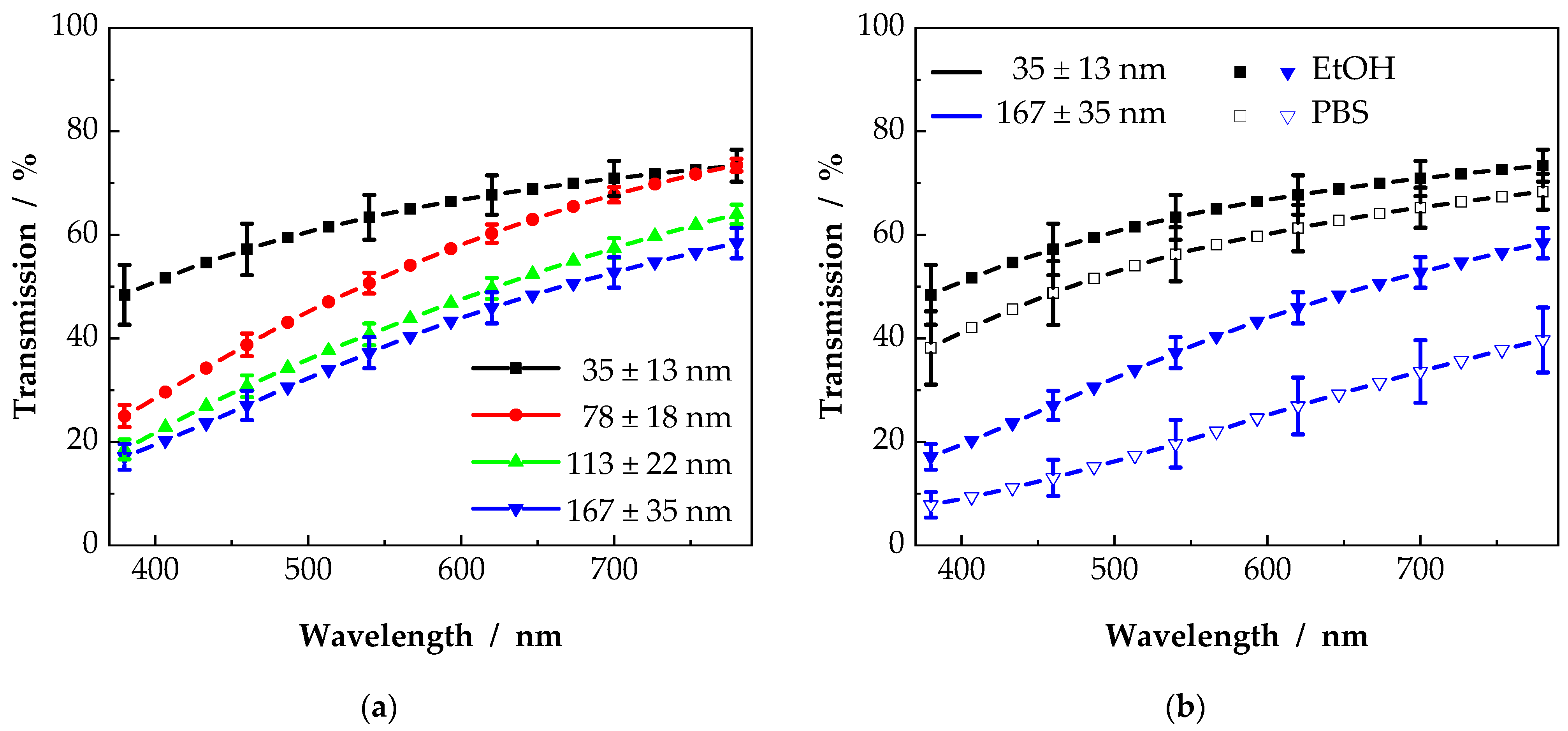
3.2. Influence of Fiber Diameter and Surrounding Medium
3.3. Semi-Empirical Description of Light Tranmission
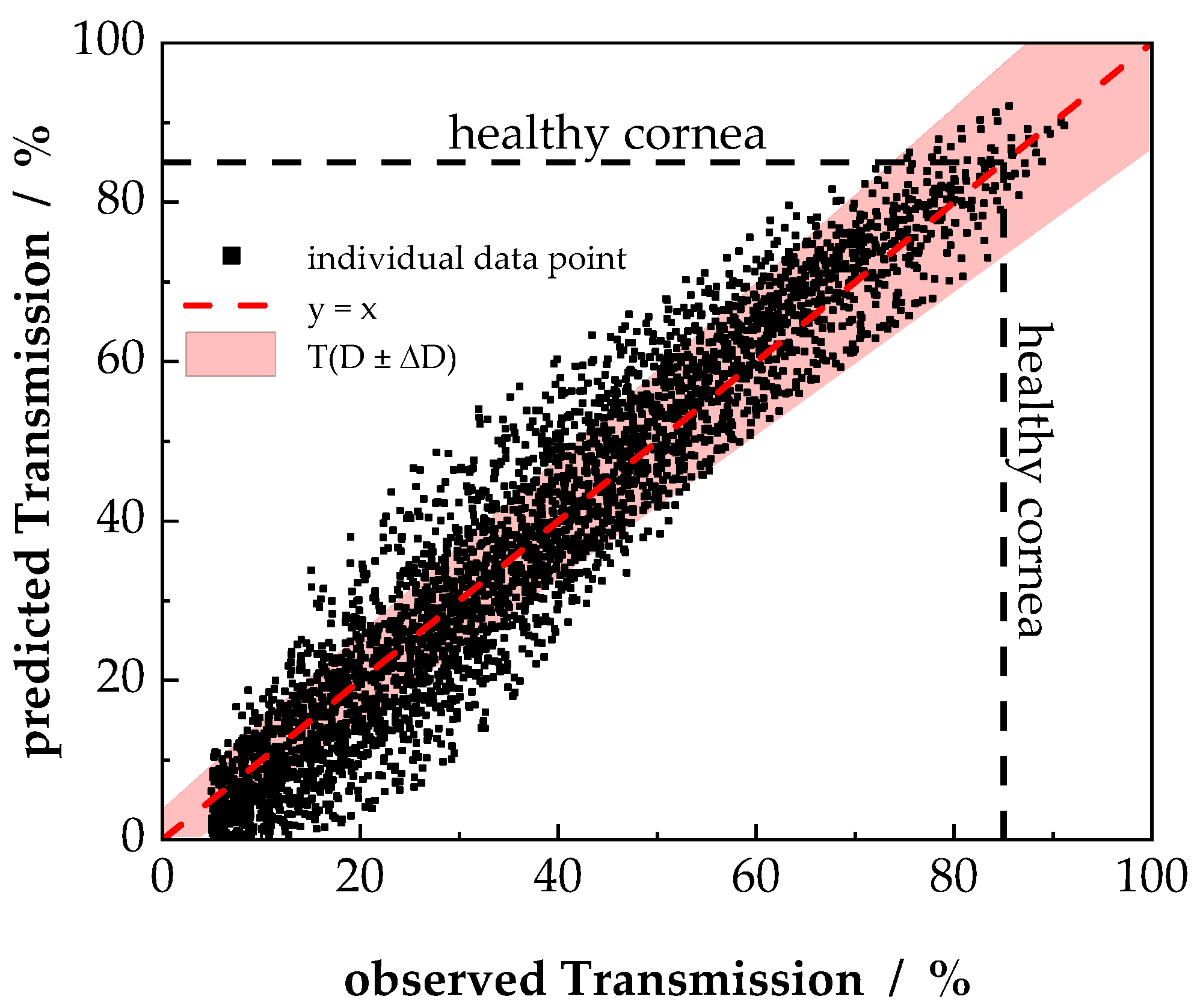
3.4. Formulation of the Design Principles
- Reducing the fiber diameter d;
- Reducing the scaffold thickness D;
- Selecting a material with a refractive index similar to that of the human cornea
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bosworth, L.A.; Downes, S. Electrospinning for Tissue Regeneration; Woodhead Pub.: Philadelphia, PA, USA, 2011; ISBN 1845697413. [Google Scholar]
- Küng, F.; Schubert, D.W.; Stafiej, P.; Kruse, F.E.; Fuchsluger, T.A. A novel suture retention test for scaffold strength characterization in ophthalmology. Mater. Sci. Eng. C Mater. Biol. Appl. 2016, 69, 941–946. [Google Scholar] [CrossRef] [PubMed]
- Küng, F.; Schubert, D.W.; Stafiej, P.; Kruse, F.E.; Fuchsluger, T.A. Influence of operating parameters on the suture retention test for scaffolds in ophthalmology. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 77, 212–218. [Google Scholar] [CrossRef]
- Stafiej, P.; Küng, F.; Kruse, F.E.; Schubert, D.W.; Fuchsluger, T. Mechanical and Optical Properties of PCL Nanofiber Reinforced Alginate Hydrogels for Application in Corneal Wound Healing. Biomater. Med Appl. 2018, 2. [Google Scholar] [CrossRef]
- Stafiej, P.; Küng, F.; Thieme, D.; Czugala, M.; Kruse, F.E.; Schubert, D.W.; Fuchsluger, T.A. Adhesion and metabolic activity of human corneal cells on PCL based nanofiber matrices. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 71, 764–770. [Google Scholar] [CrossRef]
- Kim, J.I.; Kim, J.Y.; Park, C.H. Fabrication of transparent hemispherical 3D nanofibrous scaffolds with radially aligned patterns via a novel electrospinning method. Sci. Rep. 2018, 8, 3424. [Google Scholar] [CrossRef] [PubMed]
- Kruse, M.; Walter, P.; Bauer, B.; Rütten, S.; Schaefer, K.; Plange, N.; Gries, T.; Jockenhoevel, S.; Fuest, M. Electro-spun Membranes as Scaffolds for Human Corneal Endothelial Cells. Curr. Eye Res. 2018, 43, 1–11. [Google Scholar] [CrossRef]
- Himmler, M.; Garreis, F.; Paulsen, F.; Schubert, D.W.; Fuchsluger, T.A. Optimization of polycaprolactone—Based nanofiber matrices for the cultivation of corneal endothelial cells. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Levin, L.A.; Kaufman, P.L. Adler’s Physiology of the Eye: Clinical Application, 11th ed.; Saunders/Elsevier: Edinburgh, UK; New York, NY, USA, 2011; ISBN 9780323057141. [Google Scholar]
- Yoeruek, E.; Bayyoud, T.; Maurus, C.; Hofmann, J.; Spitzer, M.S.; Bartz-Schmidt, K.-U.; Szurman, P. Decellularization of porcine corneas and repopulation with human corneal cells for tissue-engineered xenografts. Acta Ophthalmol. 2012, 90, e125–e131. [Google Scholar] [CrossRef] [PubMed]
- Lynch, A.P.; Ahearne, M. Strategies for developing decellularized corneal scaffolds. Exp. Eye Res. 2013, 108, 42–47. [Google Scholar] [CrossRef]
- Ponce Márquez, S.; Martínez, V.S.; McIntosh Ambrose, W.; Wang, J.; Gantxegui, N.G.; Schein, O.; Elisseeff, J. Decellularization of bovine corneas for tissue engineering applications. Acta Biomater. 2009, 5, 1839–1847. [Google Scholar] [CrossRef]
- Salehi, S.; Czugala, M.; Stafiej, P.; Fathi, M.; Bahners, T.; Gutmann, J.S.; Singer, B.B.; Fuchsluger, T.A. Poly (glycerol sebacate)-poly (ε-caprolactone) blend nanofibrous scaffold as intrinsic bio-and immunocompatible system for corneal repair. Acta Biomater. 2017, 50, 370–380. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, B.; Brown, K.D.; Blencowe, A.; Daniell, M.; Stevens, G.W.; Qiao, G.G. Ultrathin chitosan-poly (ethylene glycol) hydrogel films for corneal tissue engineering. Acta Biomater. 2013, 9, 6594–6605. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, B.; Brown, K.D.; Blencowe, A.; Ladewig, K.; Stevens, G.W.; Scheerlinck, J.-P.Y.; Abberton, K.; Daniell, M.; Qiao, G.G. Biodegradable and biocompatible poly (ethylene glycol)-based hydrogel films for the regeneration of corneal endothelium. Adv. Healthc. Mater. 2014, 3, 1496–1507. [Google Scholar] [CrossRef] [PubMed]
- Tummala, G.K.; Lopes, V.R.; Mihranyan, A.; Ferraz, N. Biocompatibility of Nanocellulose-Reinforced PVA Hydrogel with Human Corneal Epithelial Cells for Ophthalmic Applications. J. Funct. Biomater. 2019, 10, 35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kong, B.; Chen, Y.; Liu, R.; Liu, X.; Liu, C.; Shao, Z.; Xiong, L.; Liu, X.; Sun, W.; Mi, S. Fiber reinforced GelMA hydrogel to induce the regeneration of corneal stroma. Nat. Commun. 2020, 11, 1435. [Google Scholar] [CrossRef] [Green Version]
- Tonsomboon, K.; Oyen, M.L. Composite electrospun gelatin fiber-alginate gel scaffolds for mechanically robust tissue engineered cornea. J. Mech. Behav. Biomed. Mater. 2013, 21, 185–194. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Chang, Y.-H.; Huang, J.-L.; Chen, I.; Kuo, C. Light Scattering and Enhanced Photoactivities of Electrospun Titania Nanofibers. J. Phys. Chem. C 2012, 116, 3857–3865. [Google Scholar] [CrossRef]
- Wu, H.; Hu, L.; Rowell, M.W.; Kong, D.; Cha, J.J.; McDonough, J.R.; Zhu, J.; Yang, Y.; McGehee, M.D.; Cui, Y. Electrospun metal nanofiber webs as high-performance transparent electrode. Nano Lett. 2010, 10, 4242–4248. [Google Scholar] [CrossRef]
- Khudiyev, T.; Huseyinoglu, E.; Bayindir, M. Non-resonant Mie scattering: Emergent optical properties of core-shell polymer nanowires. Sci. Rep. 2014, 4, 4607. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud Salehi, A.O.; Heidari Keshel, S.; Sefat, F.; Tayebi, L. Use of polycaprolactone in corneal tissue engineering: A review. Mater. Today Commun. 2021, 27, 102402. [Google Scholar] [CrossRef]
- Park, C.; Woon Choi, H.; Lee, C.H.; Lannutti, J.J.; Farson, D.F. Optical scattering in electrospun poly (ε-caprolactone) tissue scaffolds. J. Laser Appl. 2014, 26, 32004. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Bhatia, A.B. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; 11th Reprinting; Cambridge Univ. Press: Cambridge, UK, 2016; ISBN 9780521642224. [Google Scholar]
- Bennett, J.M. Handbook of Optics: Volume I—Geometrical and Physical Optics, Polarized Light, Components and Instruments, 3rd ed.; Bass, M., Mahajan, V.N., Eds.; McGraw-Hill: New York, NY, USA, 2010; ISBN 9780071629256. [Google Scholar]
- Rayleigh, X. On the electromagnetic theory of light. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1881, 12, 81–101. [Google Scholar] [CrossRef] [Green Version]
- Light Scattering by Small Particles; van de Hulst, H.C. (Ed.) Dover Publications: Newburyport, MA, USA, 2012; ISBN 0486642283. [Google Scholar]
- Hart, R.W.; Farrell, R.A. Light scattering in the cornea. J. Opt. Soc. Am. 1969, 59, 766–774. [Google Scholar] [CrossRef]
- Cox, J.L.; Farrell, R.A.; Hart, R.W.; Langham, M.E. The transparency of the mammalian cornea. J. Physiol. 1970, 210, 601–616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freund, D.E.; McCally, R.L.; Farrell, R.A. Direct summation of fields for light scattering by fibrils with applications to normal corneas. Appl. Opt. 1986, 25, 2739. [Google Scholar] [CrossRef]
- Farrell, R.A.; McCally, R.L. Corneal Transparency. In Principles and Practice of Ophthalmology, 2nd ed.; Albert, D.M., Jakobiec, F.A., Eds.; Saunders: Philadelphia, PA, USA, 2000; pp. 629–643. ISBN 9780721675008. [Google Scholar]
- Freund, D.E.; McCally, R.L.; Farrell, R.A.; Cristol, S.M.; L’Hernault, N.L.; Edelhauser, H.F. Ultrastructure in anterior and posterior stroma of perfused human and rabbit corneas. Relation to transparency. Invest. Ophthalmol. Vis. Sci. 1995, 36, 1508–1523. [Google Scholar]
- Wendorff, J.H.; Agarwal, S.; Greiner, A. Electrospinning: Materials, Processing and Applications; Wiley-VCH Verlag: Weinheim, Germany, 2012; ISBN 9783527647705. [Google Scholar]
- Schubert, D.W. Revealing Novel Power Laws and Quantization in Electrospinning Considering Jet Splitting—Toward Predicting Fiber Diameter and Its Distribution. Macromol. Theory Simul. 2019, 28, 1900006. [Google Scholar] [CrossRef]
- Rheims, J.; Köser, J.; Wriedt, T. Refractive-index measurements in the near-IR using an Abbe refractometer. Meas. Sci. Technol. 1997, 8, 601–605. [Google Scholar] [CrossRef]
- Van Hoang, T.; Stępniewski, G.; Czarnecka, K.H.; Kasztelanic, R.; van Long, C.; Xuan, K.D.; Shao, L.; Śmietana, M.; Buczyński, R. Optical Properties of Buffers and Cell Culture Media for Optofluidic and Sensing Applications. Appl. Sci. 2019, 9, 1145. [Google Scholar] [CrossRef] [Green Version]
- Gladstone, J.H.; Dale, P.T. XIV. Researches on the refraction, dispersion, and sensitiveness of liquids. Phil. Trans. R. Soc. 1863, 153, 317–343. [Google Scholar] [CrossRef]
- Bigi, A.; Cojazzi, G.; Panzavolta, S.; Roveri, N.; Rubini, K. Stabilization of gelatin films by crosslinking with genipin. Biomaterials 2002, 23, 4827–4832. [Google Scholar] [CrossRef]
- Zhuang, C.; Tao, F.; Cui, Y. Anti-degradation gelatin films crosslinked by active ester based on cellulose. RSC Adv. 2015, 5, 52183–52193. [Google Scholar] [CrossRef]
- Han, Y.-L.; Xu, Q.; Lu, Z.-Q.; Wang, J.-Y. Preparation of transparent zein films for cell culture applications. Colloids Surf. B Biointerfaces 2014, 120, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Budi Santosa, F.X.; Padua, G.W. Tensile properties and water absorption of zein sheets plasticized with oleic and linoleic acids. J. Agric. Food Chem. 1999, 47, 2070–2074. [Google Scholar] [CrossRef] [PubMed]
- Remuñán-López, C.; Bodmeier, R. Mechanical, water uptake and permeability properties of crosslinked chitosan glutamate and alginate films. J. Control. Release 1997, 44, 215–225. [Google Scholar] [CrossRef]
- Jejurikar, A.; Seow, X.T.; Lawrie, G.; Martin, D.; Jayakrishnan, A.; Grøndahl, L. Degradable alginate hydrogels crosslinked by the macromolecular crosslinker alginate dialdehyde. J. Mater. Chem. 2012, 22, 9751. [Google Scholar] [CrossRef]
- Khalid, M.N.; Agnely, F.; Yagoubi, N.; Grossiord, J.L.; Couarraze, G. Water state characterization, swelling behavior, thermal and mechanical properties of chitosan based networks. Eur. J. Pharm. Sci. 2002, 15, 425–432. [Google Scholar] [CrossRef]
- Correlo, V.M.; Pinho, E.D.; Pashkuleva, I.; Bhattacharya, M.; Neves, N.M.; Reis, R.L. Water absorption and degradation characteristics of chitosan-based polyesters and hydroxyapatite composites. Macromol. Biosci. 2007, 7, 354–363. [Google Scholar] [CrossRef] [Green Version]


| Concentration (g/100 mL) | Distance (cm) | High Voltage (kV) | Flow Rate (mL/h) | Fiber Diameter (nm) |
|---|---|---|---|---|
| 5 | 15 | 15 | 0.2 | 35 ± 13 |
| 8 | 10 | 10 | 0.15 | 78 ± 18 |
| 10 | 15 | 15 | 0.1 | 103 ± 35 |
| 12 | 17 | 15 | 0.2 | 113 ± 22 |
| 14 | 15 | 15 | 0.25 | 136 ± 34 |
| 16 | 15 | 15 | 0.2 | 167 ± 35 |
| Polymer | Swelling 1/% | Reference |
|---|---|---|
| gelatin | 150–300 | [38,39] |
| zein | 5–35 | [40,41] |
| alginate | 50–150 | [42,43] |
| chitosan | 100–900% | [42,44,45] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Himmler, M.; Schubert, D.W.; Fuchsluger, T.A. Examining the Transmission of Visible Light through Electrospun Nanofibrous PCL Scaffolds for Corneal Tissue Engineering. Nanomaterials 2021, 11, 3191. https://doi.org/10.3390/nano11123191
Himmler M, Schubert DW, Fuchsluger TA. Examining the Transmission of Visible Light through Electrospun Nanofibrous PCL Scaffolds for Corneal Tissue Engineering. Nanomaterials. 2021; 11(12):3191. https://doi.org/10.3390/nano11123191
Chicago/Turabian StyleHimmler, Marcus, Dirk W. Schubert, and Thomas A. Fuchsluger. 2021. "Examining the Transmission of Visible Light through Electrospun Nanofibrous PCL Scaffolds for Corneal Tissue Engineering" Nanomaterials 11, no. 12: 3191. https://doi.org/10.3390/nano11123191
APA StyleHimmler, M., Schubert, D. W., & Fuchsluger, T. A. (2021). Examining the Transmission of Visible Light through Electrospun Nanofibrous PCL Scaffolds for Corneal Tissue Engineering. Nanomaterials, 11(12), 3191. https://doi.org/10.3390/nano11123191