Single-Port Coherent Perfect Loss in a Photonic Crystal Nanobeam Resonator
Abstract
:1. Introduction
2. Simulation
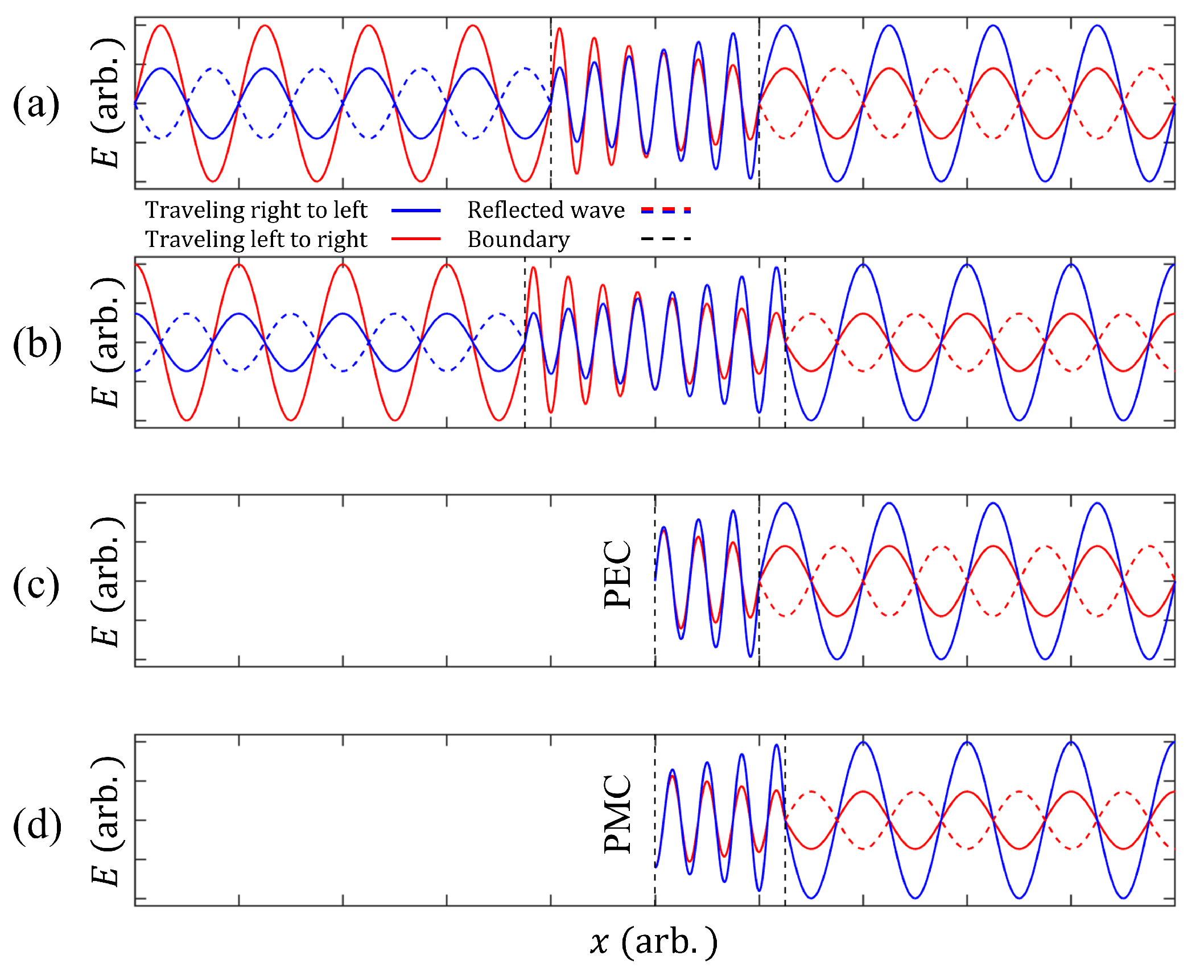
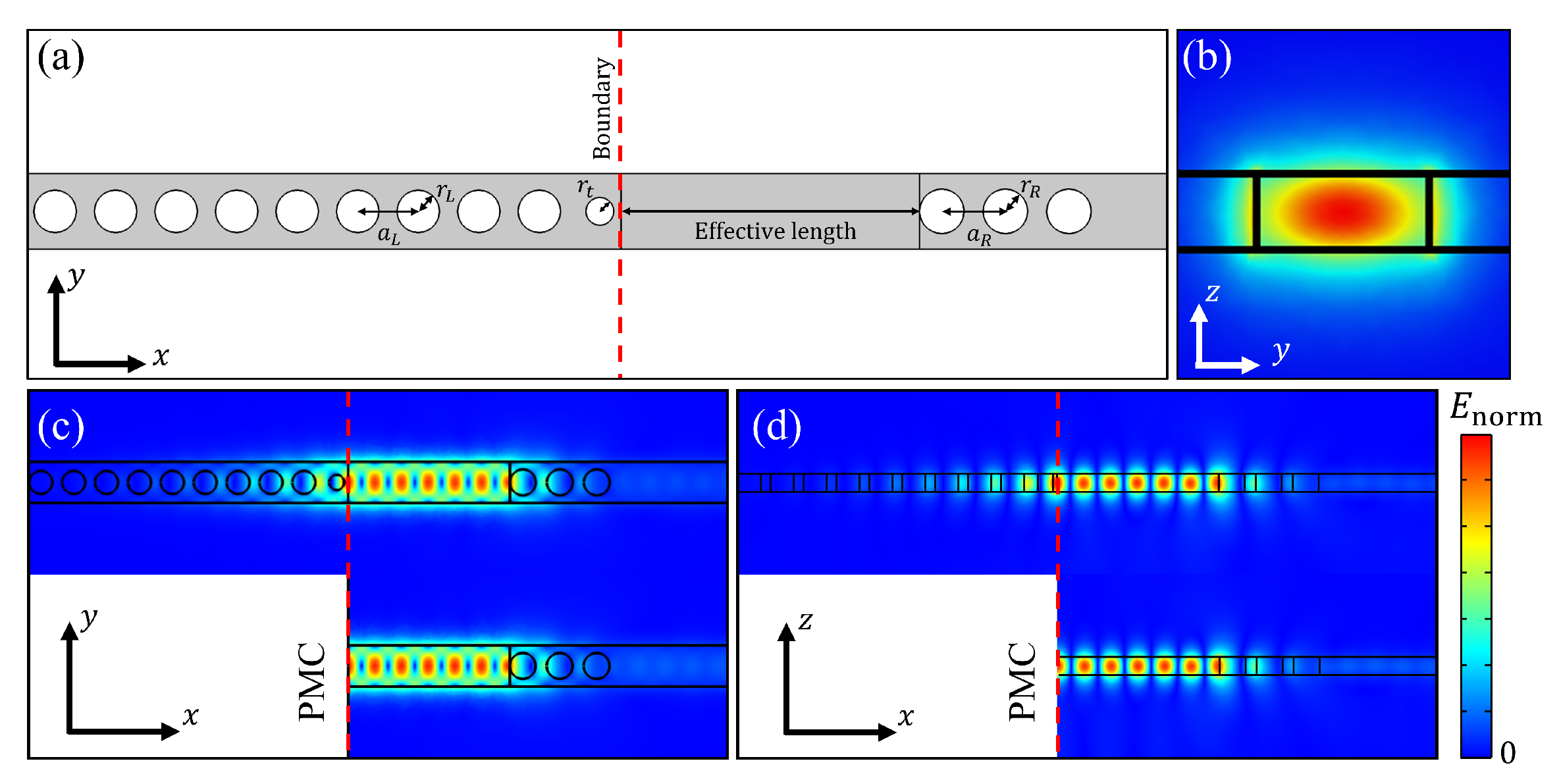
2.1. PMC-like Boundary
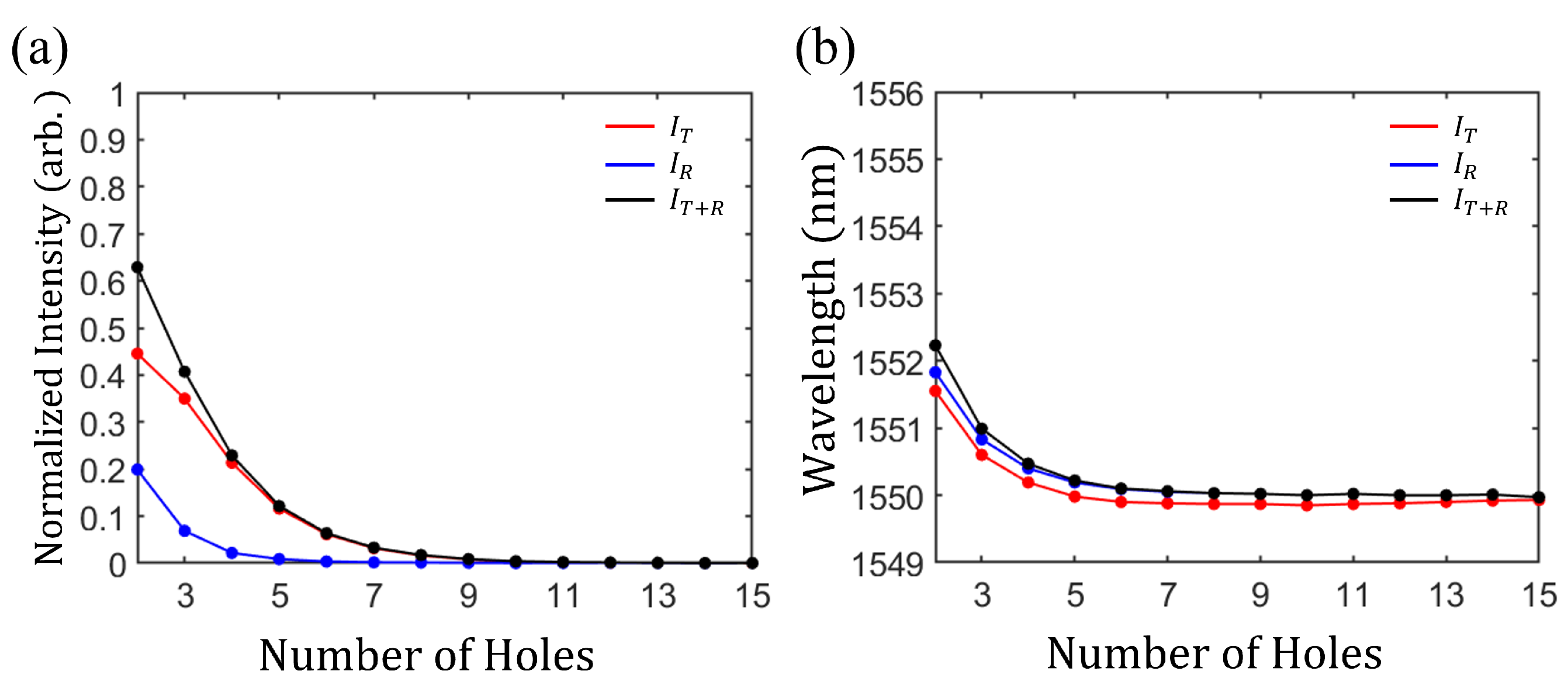
2.2. Single-Port Coherent Perfect Loss
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teperik, T.V.; García de Abajo, F.J.; Borisov, A.G.; Abdelsalam, M.; Bartlett, P.N.; Sugawara, Y.; Baumberg, J.J. Omnidirectional absorption in nanostructured metal surfaces. Nat. Photonics 2008, 2, 299–301. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Fan, Y.; Guo, C.; Zhu, Z.; Xu, W.; Wu, F.; Yuan, X.; Qin, S. Monolayer-graphene-based broadband and wide-angle perfect absorption structures in the near infrared. Sci. Rep. 2018, 8, 13709. [Google Scholar] [CrossRef] [PubMed]
- Li Voti, R. Optimization of a perfect absorber multilayer structure by genetic algorithms. J. Eur. Opt. Soc. Publ. 2018, 14, 11. [Google Scholar] [CrossRef] [Green Version]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Li, E.; Wang, A.X. Ultra-compact and broadband electro-absorption modulator using an epsilon-near-zero conductive oxide. Nat. Photonics Res. 2018, 6, 277. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Cao, H.; Stone, A.D. Coherent Perfect Absorbers: Time-Reversed Lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.; Chong, Y.; Ge, L.; Noh, H.; Stone, A.D.; Cao, H. Time-Reversed Lasing and Interferometric Control of Absorption. Science 2011, 331, 889–892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baranov, D.G.; Krasnok, A.; Shegai, T.; Alù, A.; Chong, Y. Coherent perfect absorbers: Linear control of light with light. Nat. Rev. Mater. 2017, 2, 17064. [Google Scholar] [CrossRef] [Green Version]
- Noh, H.; Chong, Y.; Stone, A.D.; Cao, H. Perfect coupling of light to surface plasmons by coherent absorption. Phys. Rev. Lett. 2012, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Noh, H. Enhanced absorption by coherent control in a photonic crystal resonator coupled with a microfiber. Opt. Lett. 2018, 43, 5532. [Google Scholar] [CrossRef] [PubMed]
- Pichler, K.; Kühmayer, M.; Böhm, J.; Brandstötter, A.; Ambichl, P.; Kuhl, U.; Rotter, S. Random anti-lasing through coherent perfect absorption in a disordered medium. Nature 2019, 567, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Alaee, R.; Vaddi, Y.; Boyd, R.W. Dynamic coherent perfect absorption in nonlinear metasurfaces. Opt. Lett. 2020, 45, 6414. [Google Scholar] [CrossRef]
- Longhi, S. PT-symmetric laser-absorber. Phys. Rev. A 2010, 82, 031801. [Google Scholar] [CrossRef] [Green Version]
- Farhat, M.; Yang, M.; Ye, Z.; Chen, P.Y. PT-Symmetric Absorber-Laser Enables Electromagnetic Sensors with Unprecedented Sensitivity. ACS Photonics 2020, 7, 2080–2088. [Google Scholar] [CrossRef]
- Ebrahimi Meymand, R.; Soleymani, A.; Granpayeh, N. All-optical AND, OR, and XOR logic gates based on coherent perfect absorption in graphene-based metasurface at terahertz region. Opt. Commun. 2020, 458, 124772. [Google Scholar] [CrossRef]
- Li, C.; Qiu, J.; Ou, J.-Y.; Liu, Q.H.; Zhu, J. High-Sensitivity Refractive Index Sensors Using Coherent Perfect Absorption on Graphene in the Vis-NIR Region. ACS Appl. Nano Mater. 2019, 2, 3231–3237. [Google Scholar] [CrossRef]
- Li, S.; Luo, J.; Anwar, S.; Li, S.; Lu, W.; Hang, Z.H.; Lai, Y.; Hou, B.; Shen, M.; Wang, C. An equivalent realization of coherent perfect absorption under single beam illumination. Sci. Rep. 2015, 4, 7369. [Google Scholar] [CrossRef] [Green Version]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A dielectric omnidirectional reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Lyu, K.; Hu, S.; Yao, M.; Xiao, S. Ultra-large omnidirectional photonic band gaps in one-dimensional ternary photonic crystals composed of plasma, dielectric and hyperbolic metamaterial. Opt. Mater. 2021, 111, 110680. [Google Scholar] [CrossRef]
- Li Voti, R. Optimization of transparent metal structures by genetic algorithms. Rom. Rep. Phys. 2012, 64, 446–466. [Google Scholar]
- Lončar, M.; Yoshie, T.; Scherer, A.; Gogna, P.; Qiu, Y. Low-threshold photonic crystal laser. Appl. Phys. Lett. 2002, 81, 2680–2682. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.-K.; Noh, H.; Rooks, M.J.; Solomon, G.S.; Vollmer, F.; Cao, H. Lasing in localized modes of a slow light photonic crystal waveguide. Appl. Phys. Lett. 2011, 98, 241107. [Google Scholar] [CrossRef] [Green Version]
- Naghizade, S.; Sattari-Esfahlan, S.M. Tunable High Performance 16-Channel Demultiplexer on 2D Photonic Crystal Ring Resonator Operating at Telecom Wavelengths. J. Opt. Commun. 2018, 41, 249–256. [Google Scholar] [CrossRef]
- Wu, F.; Wu, J.; Fan, C.; Guo, Z.; Xue, C.; Jiang, H.; Sun, Y.; Li, Y.; Chen, H. Omnidirectional optical filtering based on two kinds of photonic band gaps with different angle-dependent properties. Europhys. Lett. 2020, 129, 34004. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.; Chen, W.; Zhou, C.; Liu, T.; Xiao, S. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance. Phys. Rev. B 2020, 102, 1–7. [Google Scholar] [CrossRef]
- Wu, F.; Lu, G.; Guo, Z.; Jiang, H.; Xue, C.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Redshift gaps in one-dimensional photonic crystals containing hyperbolic metamaterials. Phys. Rev. Appl. 2018, 10, 064022. [Google Scholar] [CrossRef]
- Zhang, Y.; Khan, M.; Huang, Y.; Ryou, J.; Deotare, P.; Dupuis, R.; Lončar, M. Photonic crystal nanobeam lasers. Appl. Phys. Lett. 2010, 97, 95–98. [Google Scholar]
- Frank, I.W.; Deotare, P.B.; McCutcheon, M.W.; Lončar, M. Programmable photonic crystal nanobeam cavities. Opt. Express 2010, 18, 8705. [Google Scholar] [CrossRef] [PubMed]
- Deotare, P.B.; McCutcheon, M.W.; Frank, I.W.; Khan, M.; Lončar, M. Coupled photonic crystal nanobeam cavities. Appl. Phys. Lett. 2009, 95, 031102. [Google Scholar] [CrossRef] [Green Version]
- Quan, Q.; Lončar, M. Deterministic design of wavelength scale, ultra-high Q photonic crystal nanobeam cavities. Opt. Express 2011, 19, 18529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Istrate, E.; Sargent, E.H. Measurement of the phase shift upon reflection from photonic crystals. Appl. Phys. Lett. 2005, 86, 151112. [Google Scholar] [CrossRef] [Green Version]
- Tatian, B. Fitting refractive-index data with the Sellmeier dispersion formula. Appl. Opt. 1984, 23, 4477. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205. [Google Scholar] [CrossRef]
- Ma, F.; Liu, X. Phase shift and penetration depth of metal mirrors in a microcavity structure. Appl. Opt. 2007, 46, 6247. [Google Scholar] [CrossRef]
- Chen, Z.; Han, P.; Leung, C.W.; Wang, Y.; Hu, M.; Chen, Y. Study of optical Tamm states based on the phase properties of one-dimensional photonic crystals. Opt. Express 2012, 20, 21618. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Noh, H. Unidirectional incident wave for an electromagnetic wave simulation using the finite element method. J. Korean Phys. Soc. 2021, 78, 587–593. [Google Scholar] [CrossRef]
- Larciprete, M.C.; Sibilia, C.; Paoloni, S.; Leahu, G.; Li Voti, R.; Bertolotti, M.; Scalora, M.; Panajotov, K. Thermally induced transmission variations in ZnSe/MgF2 photonic band gap structures. J. Appl. Phys. 2002, 92, 2251–2255. [Google Scholar] [CrossRef]
- Li, H.H. Refractive index of silicon and germanium and its wavelength and temperature derivatives. J. Phys. Chem. Ref. 1980, 9, 561–658. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.; Noh, H. Single-Port Coherent Perfect Loss in a Photonic Crystal Nanobeam Resonator. Nanomaterials 2021, 11, 3457. https://doi.org/10.3390/nano11123457
Choi J, Noh H. Single-Port Coherent Perfect Loss in a Photonic Crystal Nanobeam Resonator. Nanomaterials. 2021; 11(12):3457. https://doi.org/10.3390/nano11123457
Chicago/Turabian StyleChoi, Jihoon, and Heeso Noh. 2021. "Single-Port Coherent Perfect Loss in a Photonic Crystal Nanobeam Resonator" Nanomaterials 11, no. 12: 3457. https://doi.org/10.3390/nano11123457
APA StyleChoi, J., & Noh, H. (2021). Single-Port Coherent Perfect Loss in a Photonic Crystal Nanobeam Resonator. Nanomaterials, 11(12), 3457. https://doi.org/10.3390/nano11123457





