Evaluation of Warpage and Residual Stress of Precision Glass Micro-Optics Heated by Carbide-Bonded Graphene Coating in Hot Embossing Process
Abstract
:1. Introduction
2. Materials and Methods
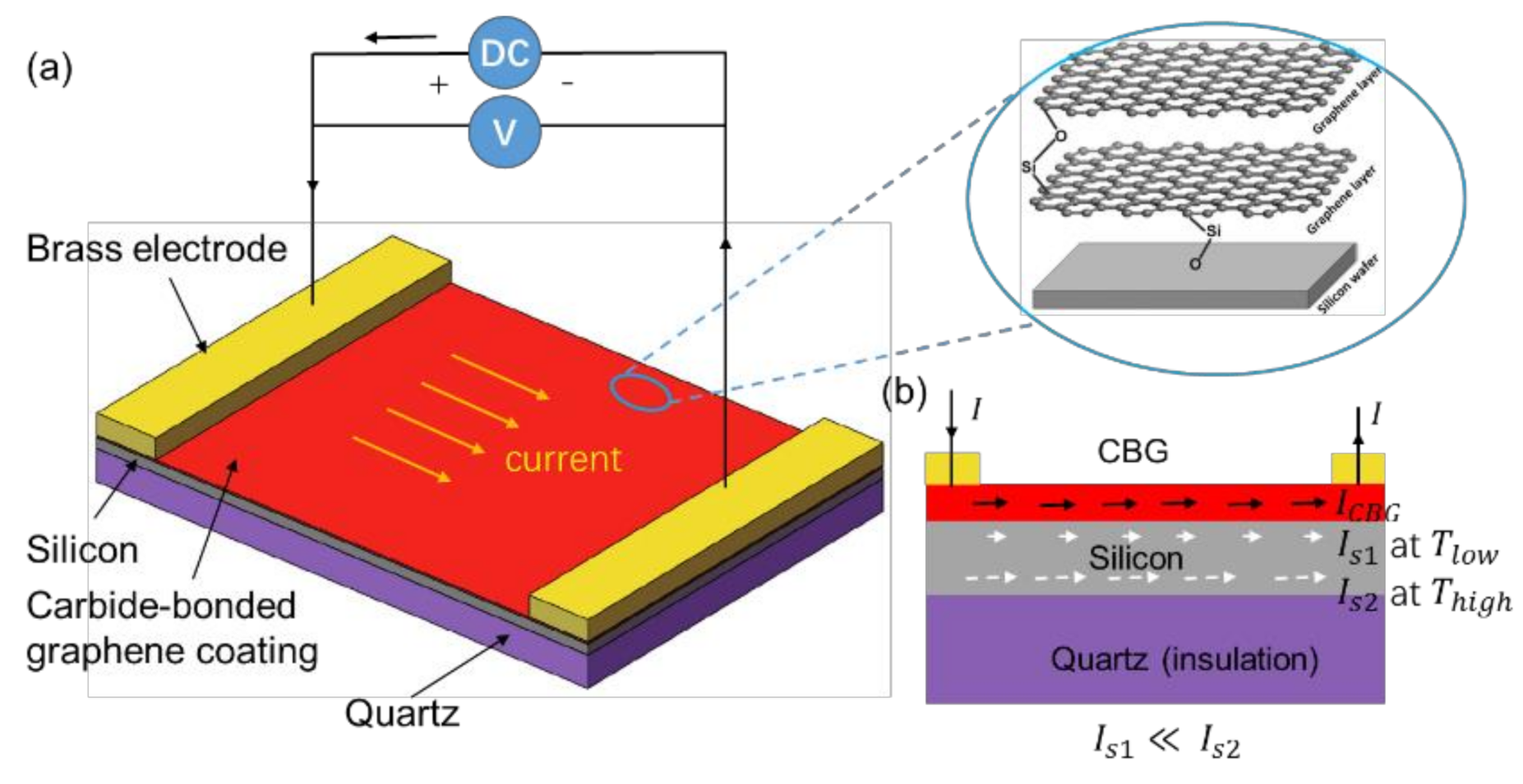
2.1. Carbide-Bonded Graphene Coating Based Hot Embossing Process
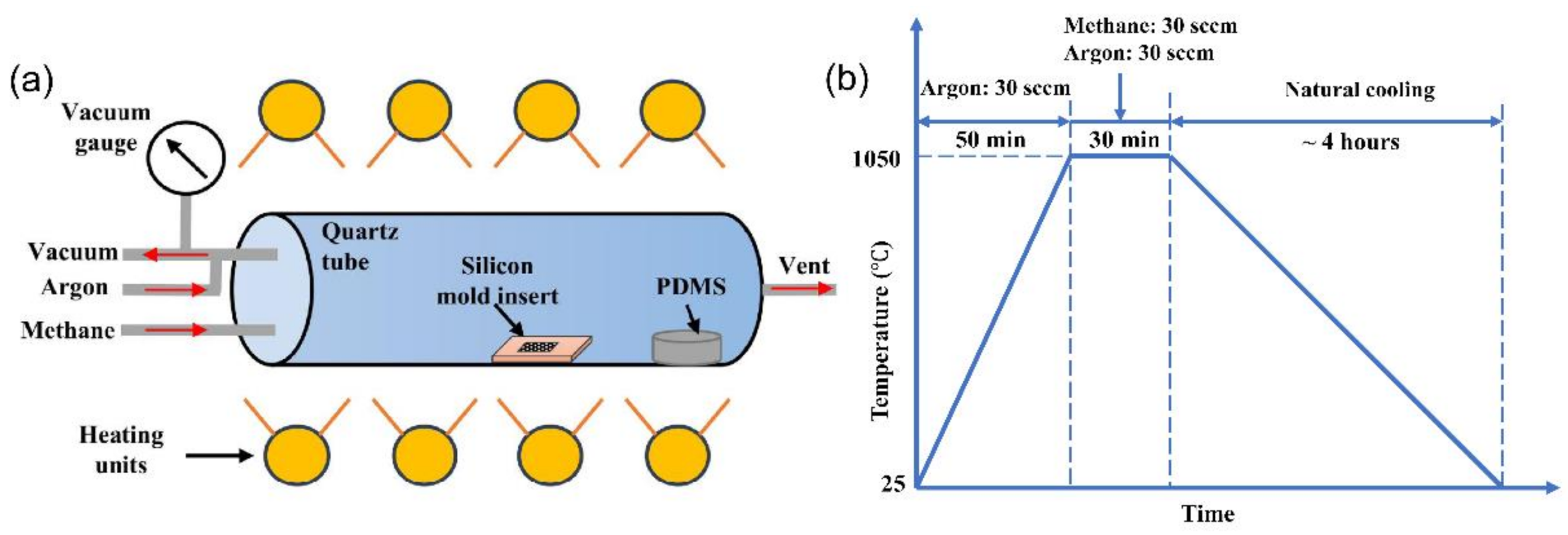
2.2. Deposition Method of Carbide-Bonding Graphene Coating
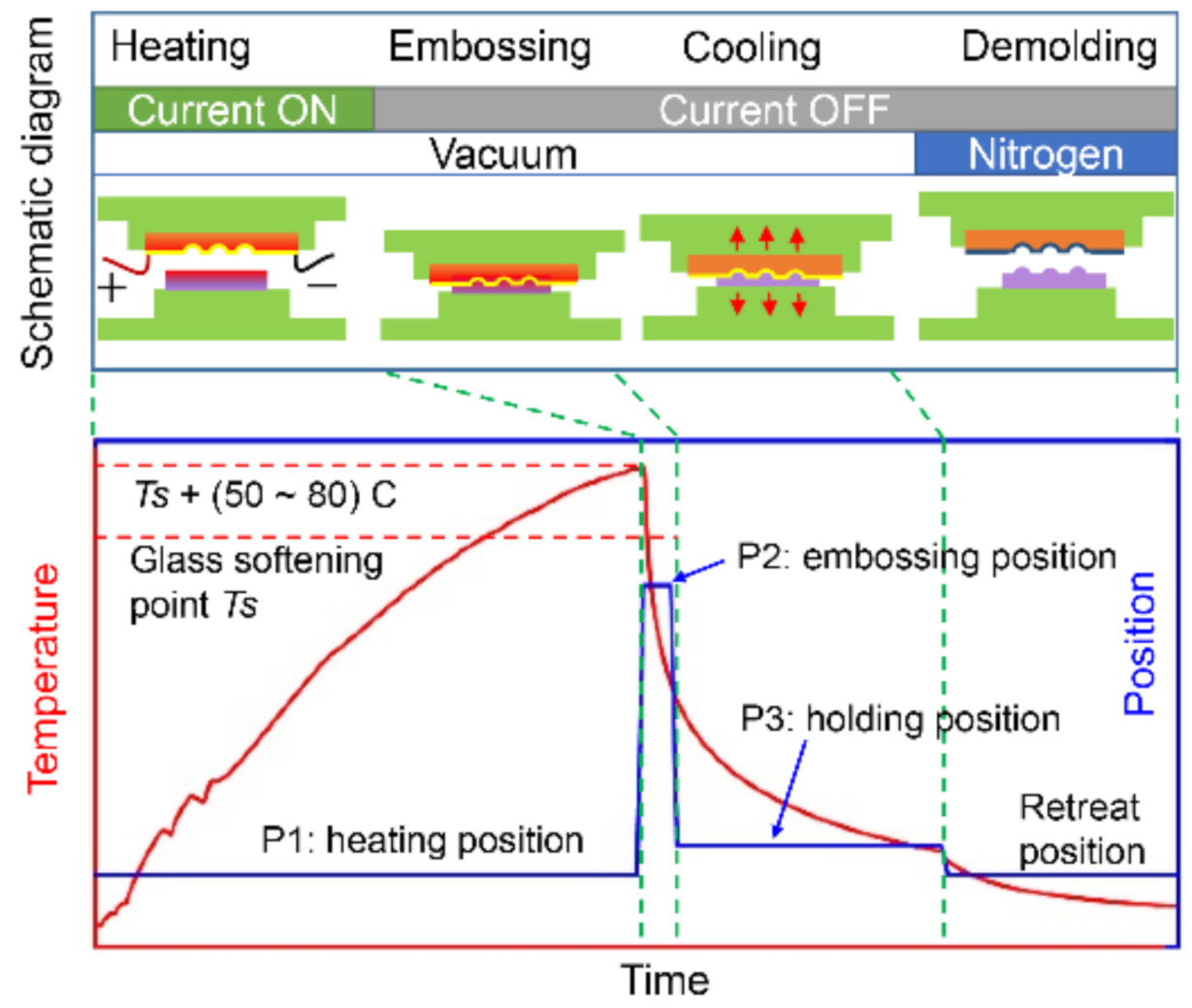
2.3. Schematic of CBG-Based Hot Embossing Process
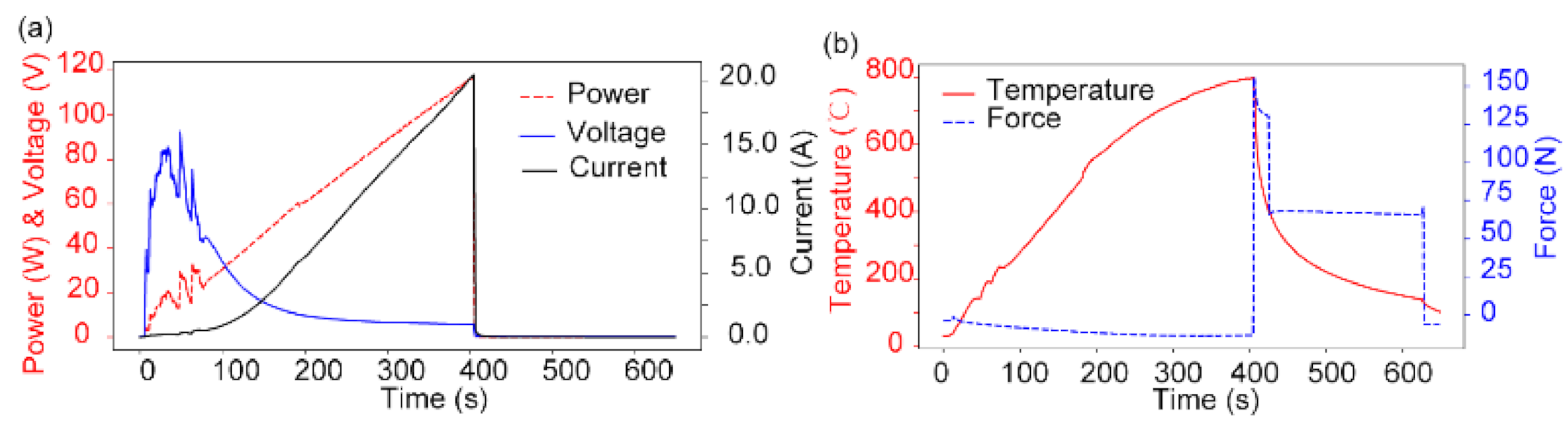
2.4. Embossing Process and Experiment Setup
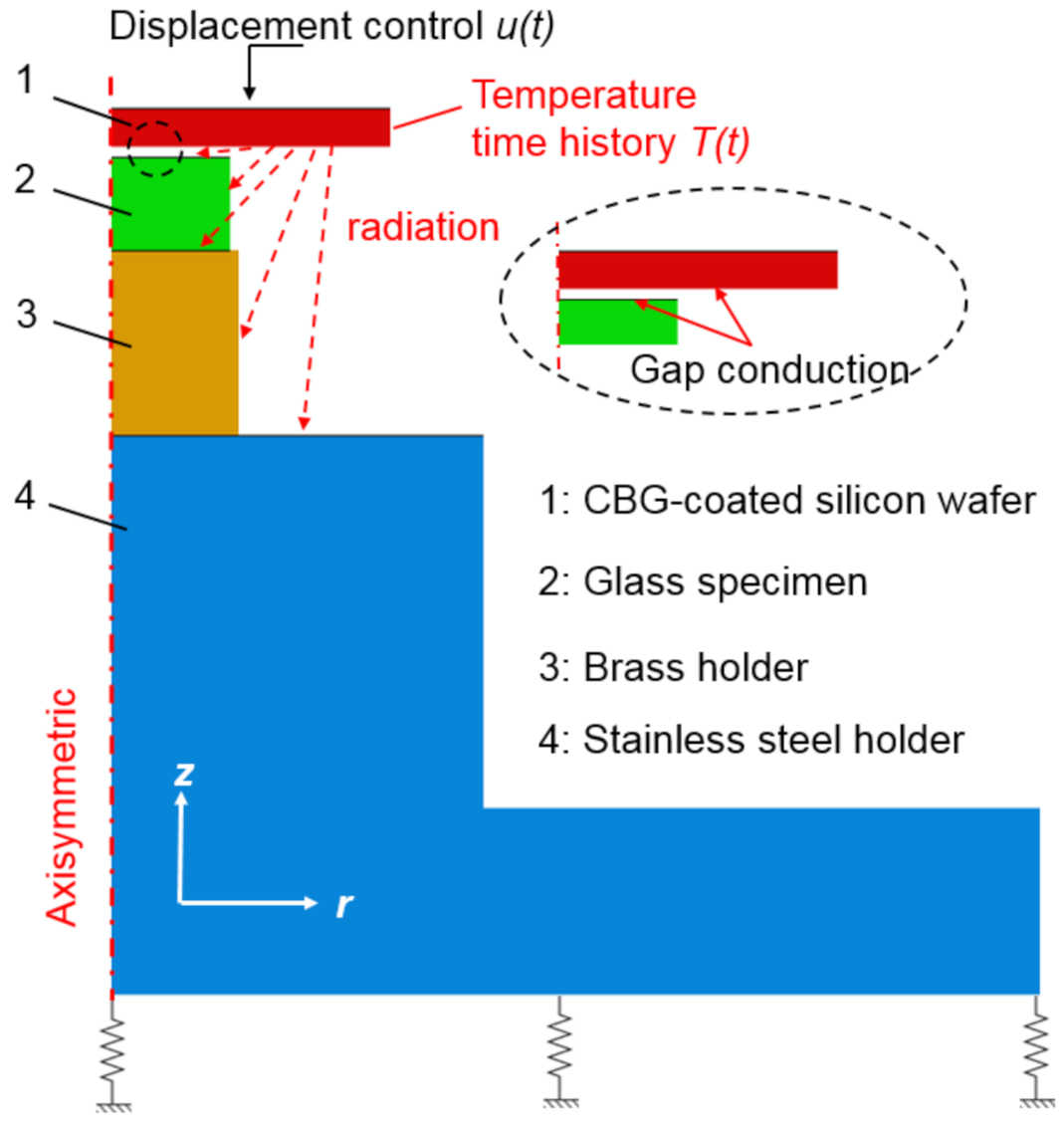
2.5. Finite Element Simulation of Embossing Process
3. Results
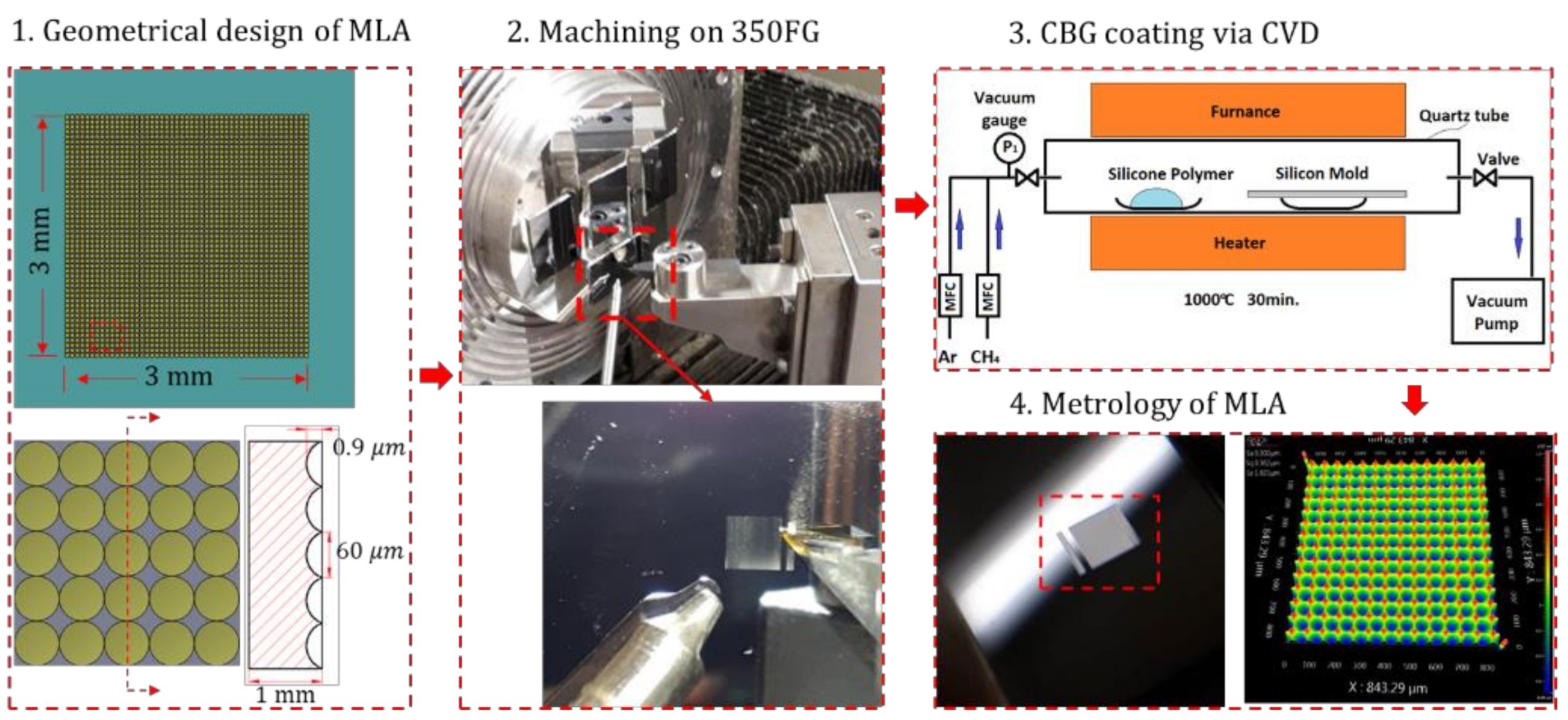
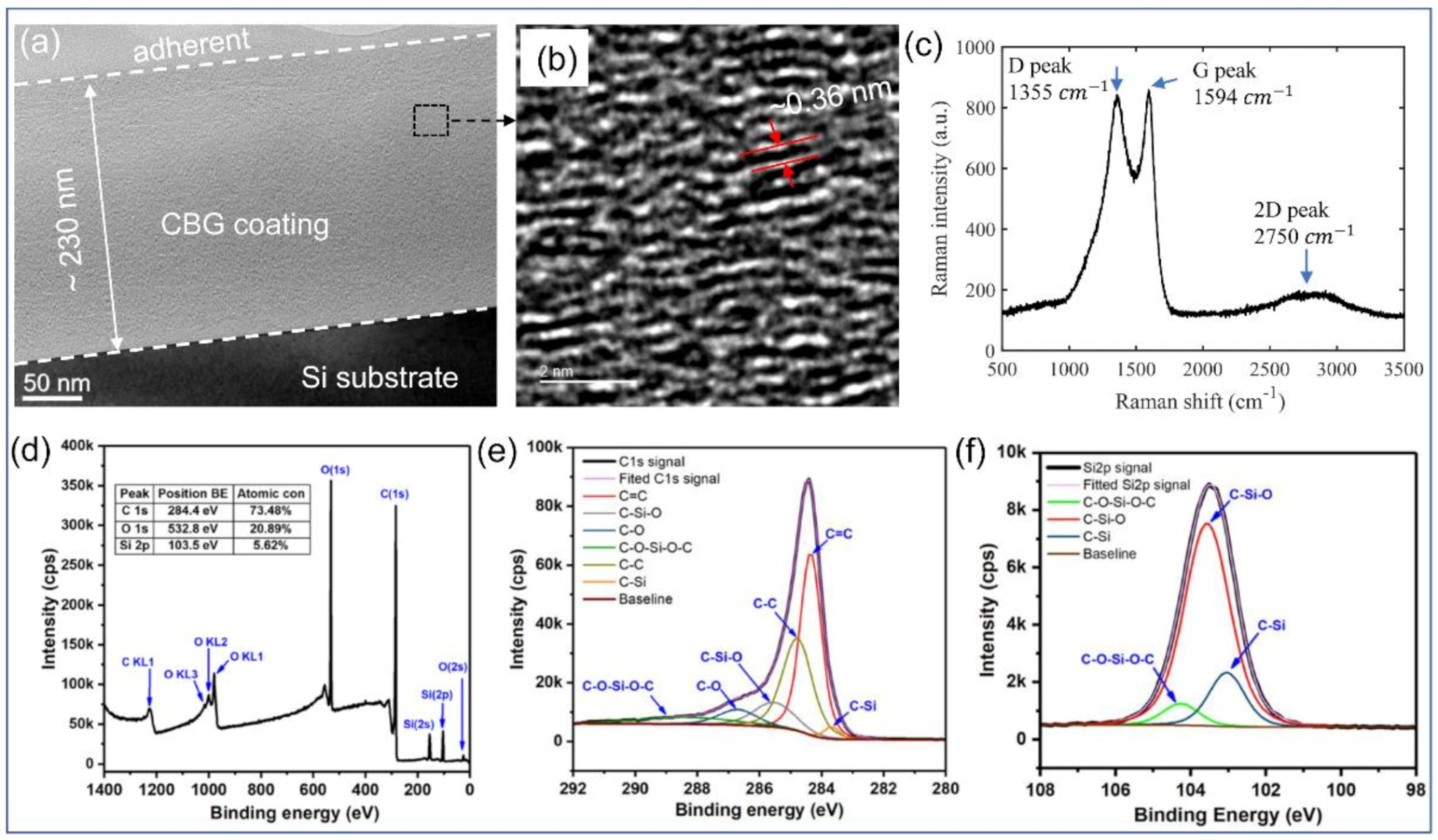
3.1. Characterization Results of the CBG Coating
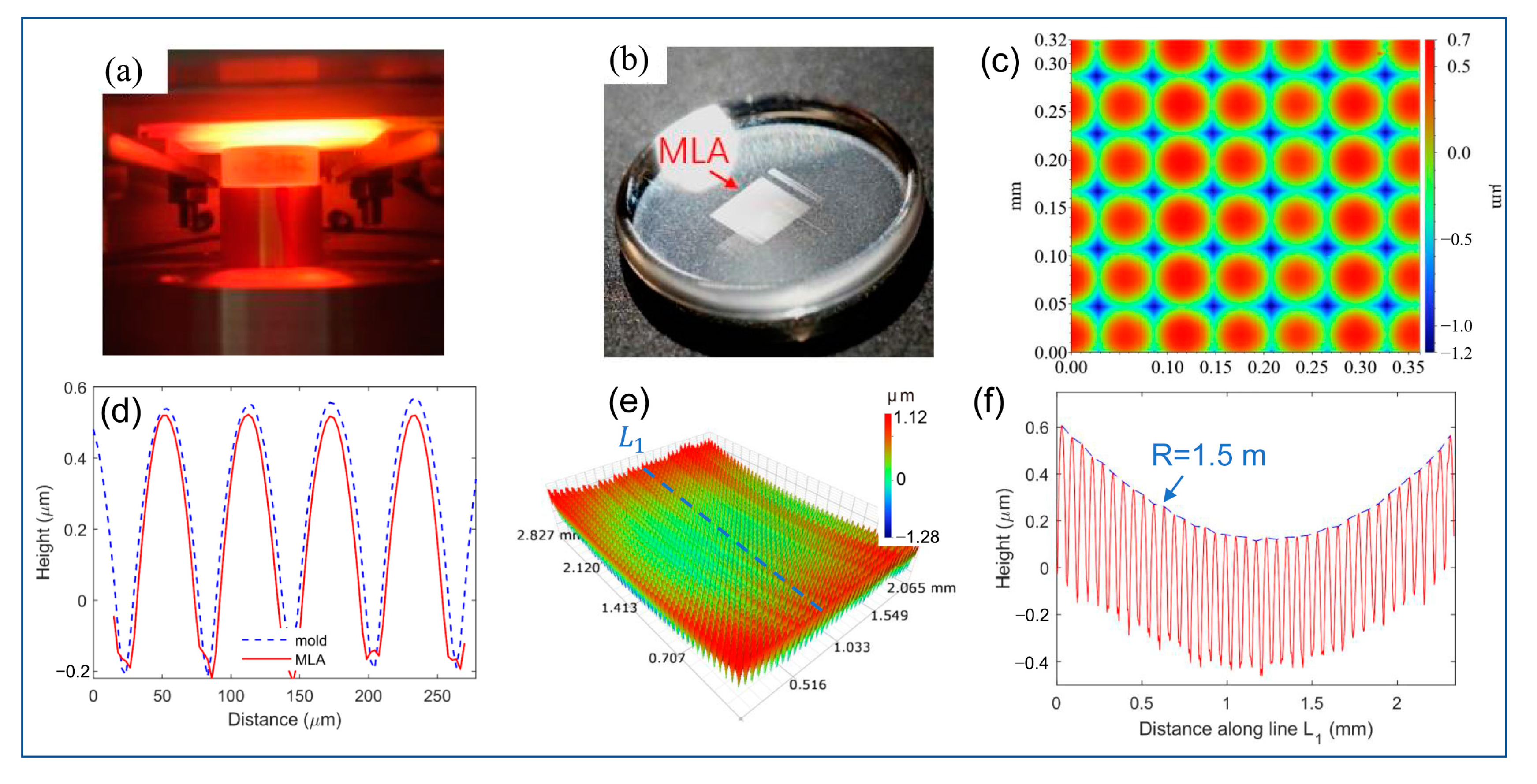
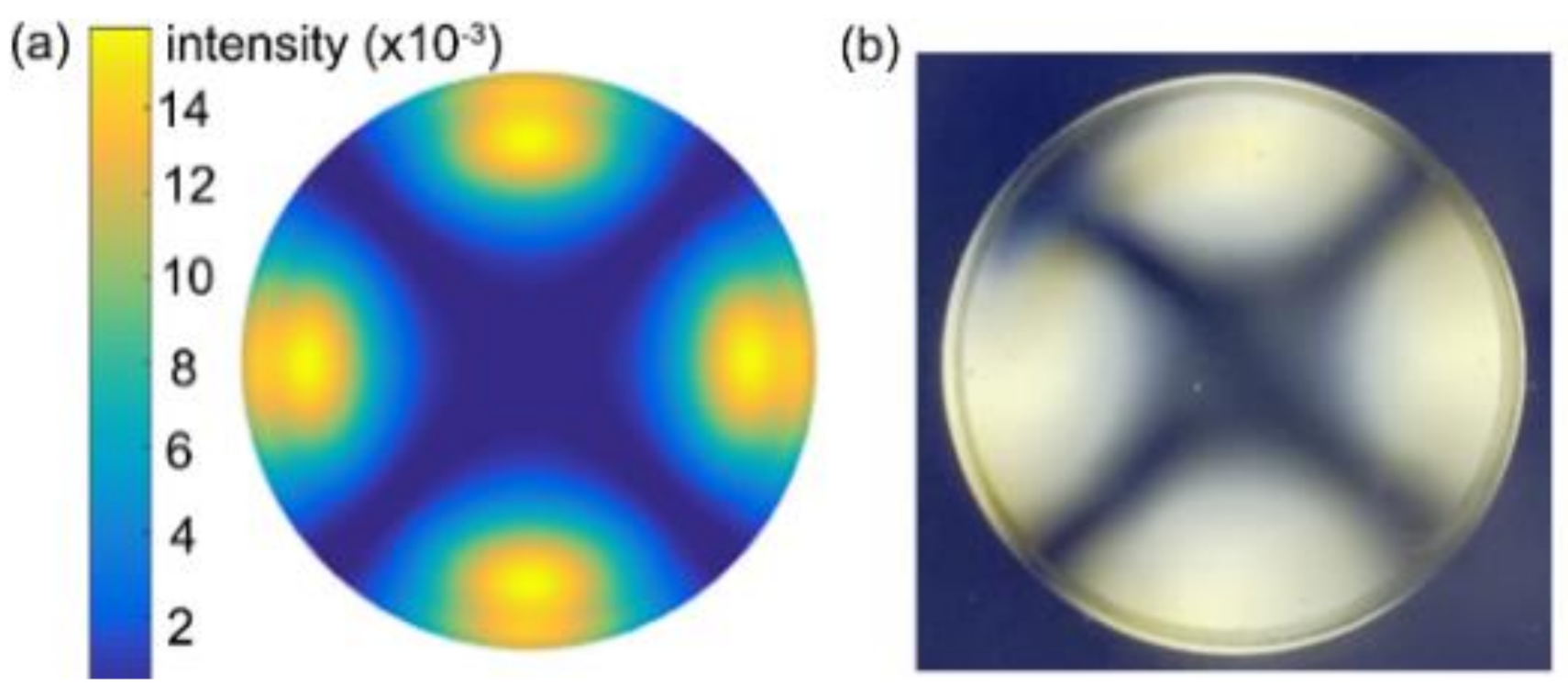
3.2. Embossed Microlens Array with Curvature
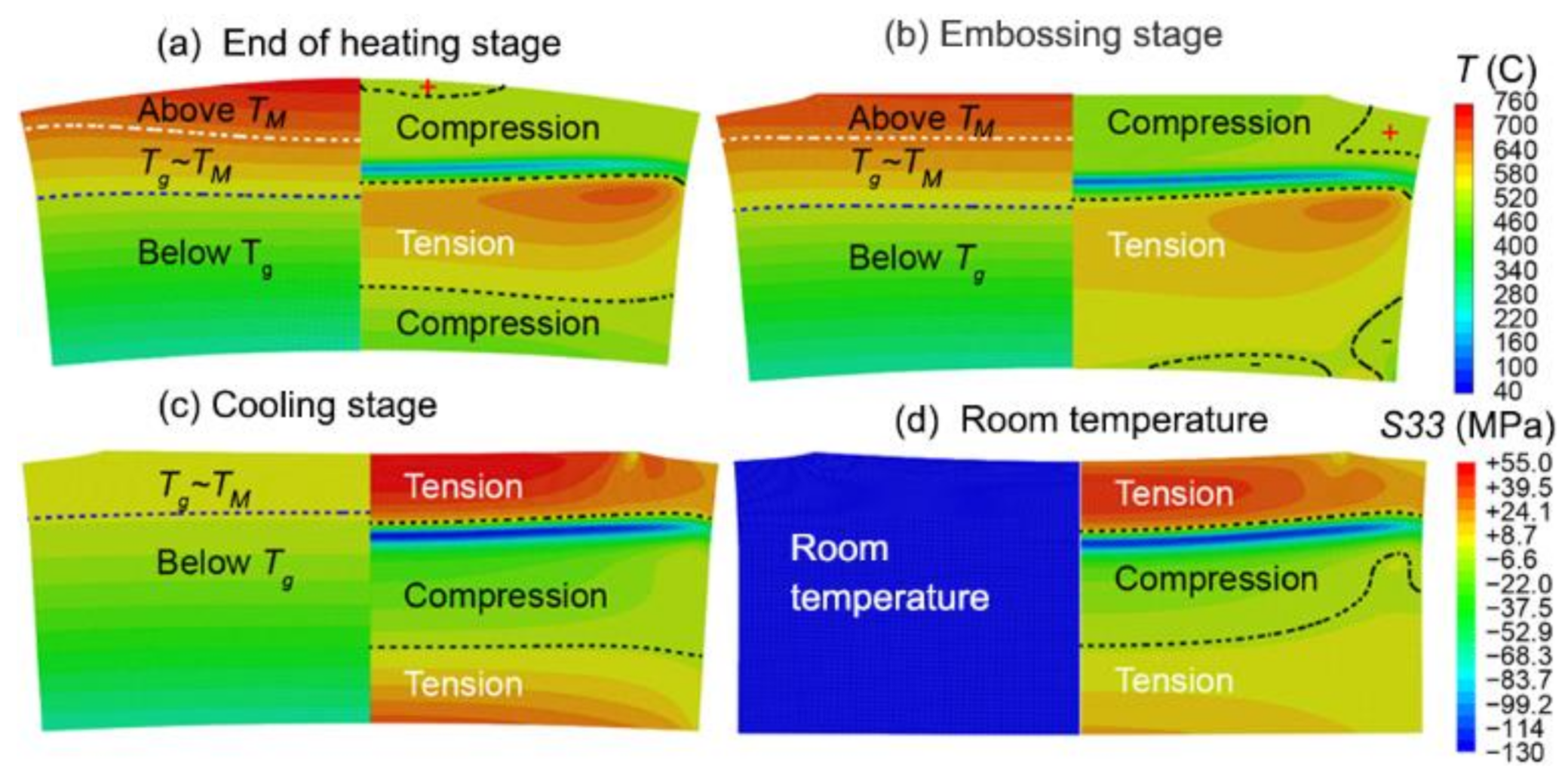
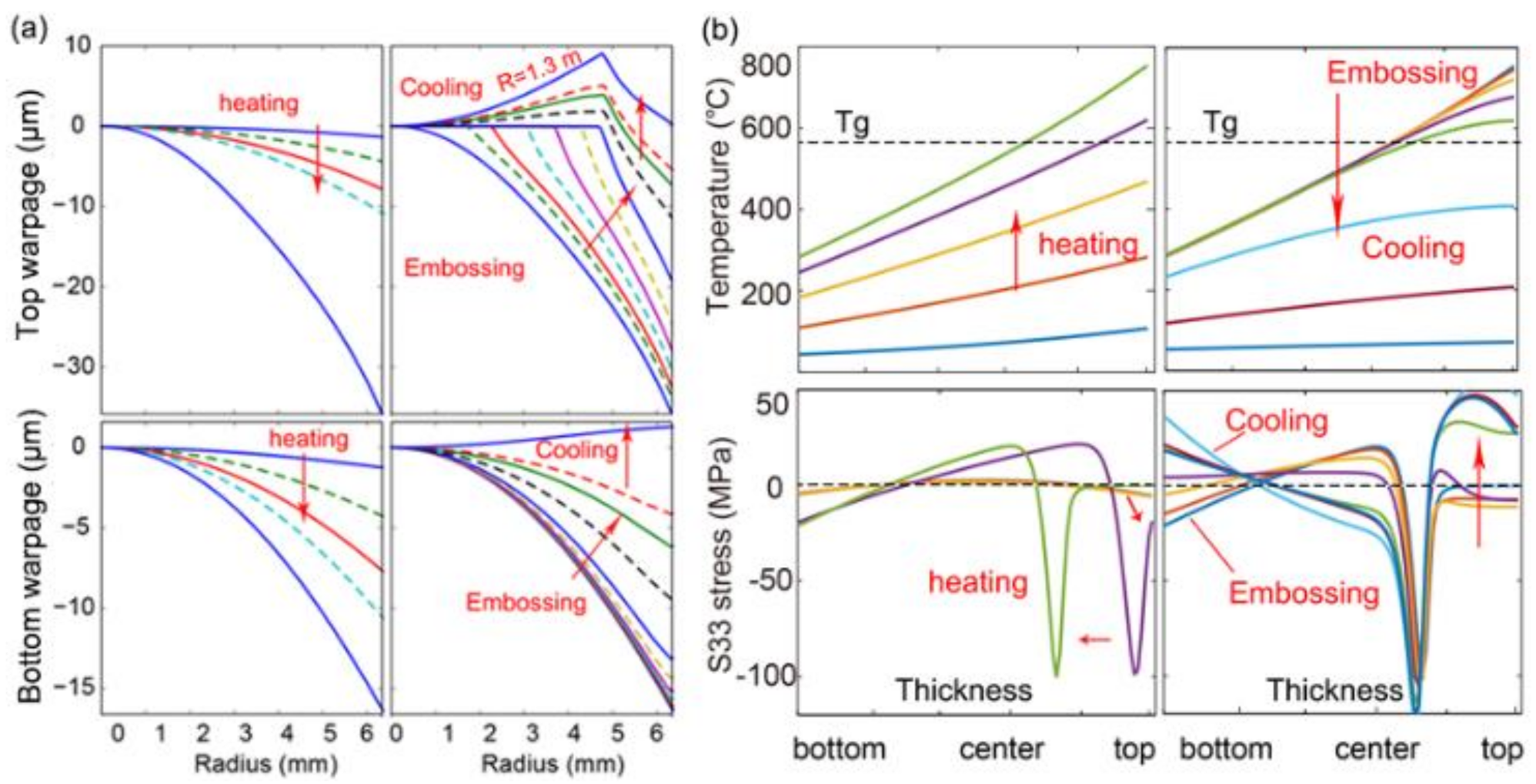
3.3. Evolution of Geometrical Warpage and Residual Stress
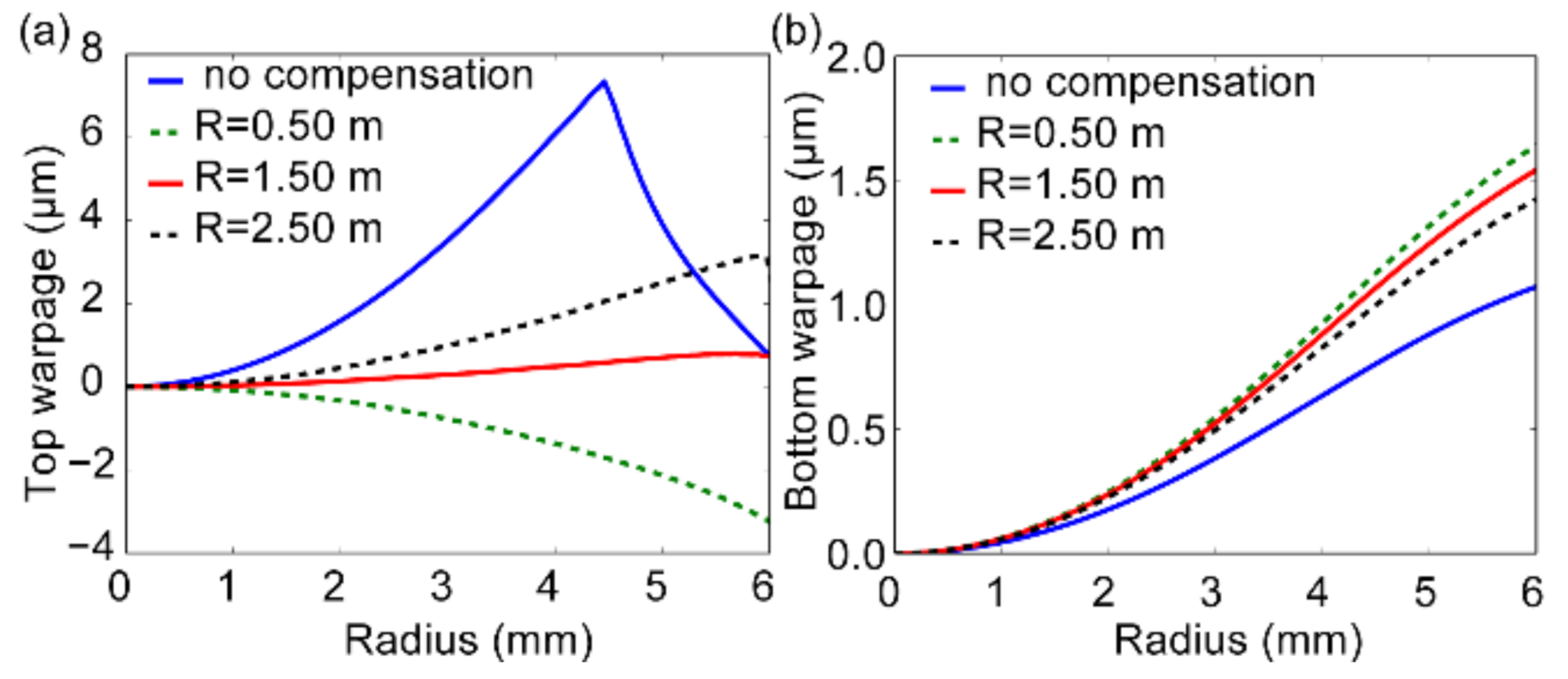
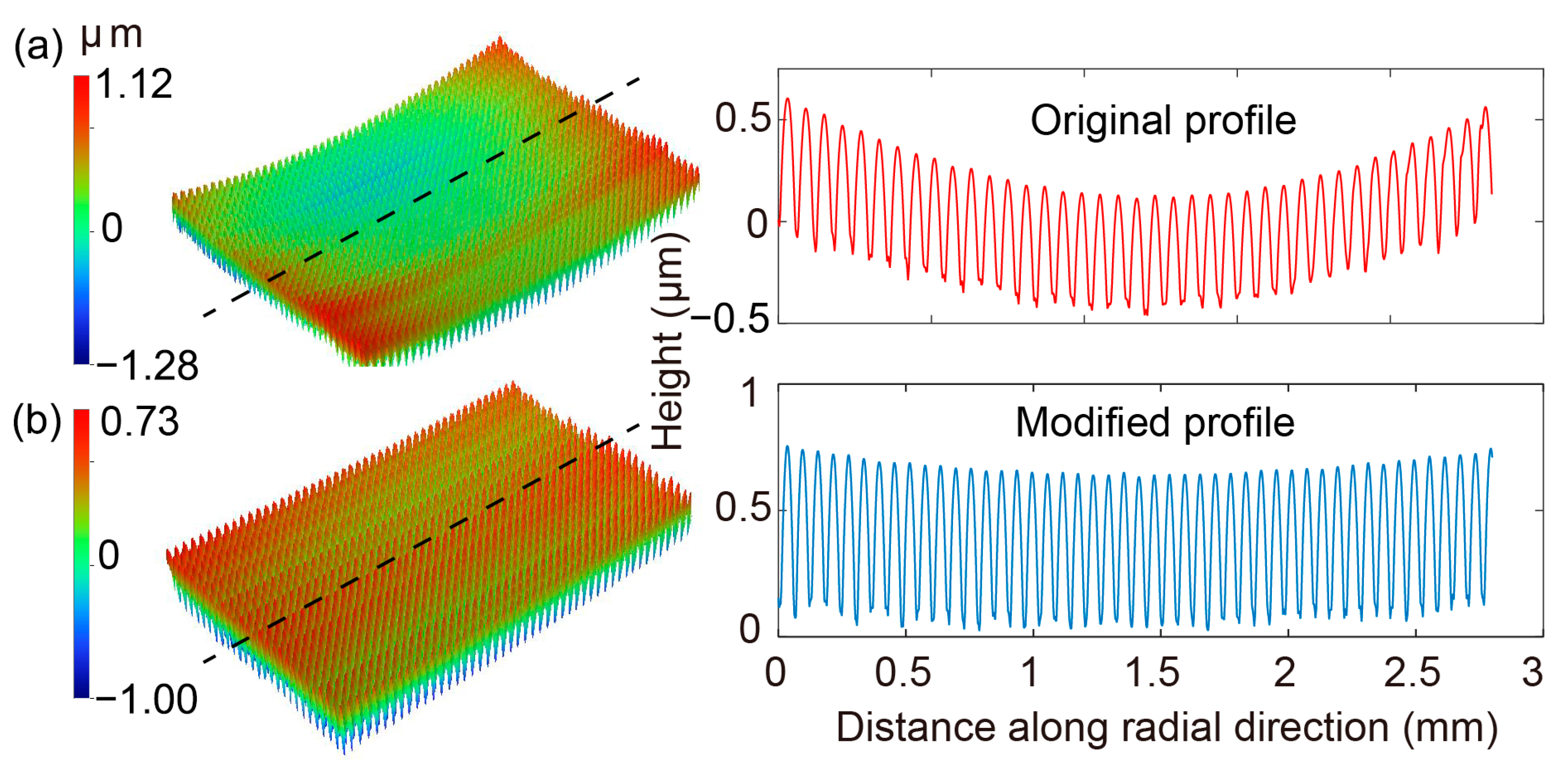
3.4. Decreasing Top Warpage through Curvature Compensation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Becker, H.; Heim, U. Hot embossing as a method for the fabrication of polymer high aspect ratio structures. Sens. Actuators A Phys. 2000, 83, 130–135. [Google Scholar] [CrossRef]
- Peng, L.F.; Deng, Y.J.; Yi, P.Y.; Lai, X.M. Micro hot embossing of thermoplastic polymers: A review. J. Micromechan. Microeng. 2014, 24, 013001. [Google Scholar] [CrossRef]
- Yi, A.; Chen, Y.; Klocke, F.; Pongs, G.; Demmer, A.; Grewell, D.; Benatar, A. A high volume precision compression molding process of glass diffractive optics by use of a micromachined fused silica wafer mold and low Tg optical glass. J. Micromechan. Microeng. 2006, 16, 2000–2009. [Google Scholar] [CrossRef]
- Heckele, M.; Schomburg, W.K. Review on micro molding of thermoplastic polymers. J. Micromechan. Microeng. 2004, 14, R1–R14. [Google Scholar] [CrossRef]
- Huang, W.; Yu, J.; Kwak, K.J.; Gallego-Perez, D.; Liao, W.C.; Yang, H.; Ouyang, X.; Li, L.; Lu, W.; Lafyatis, G.P.; et al. Atomic carbide bonding leading to superior graphene networks. Adv. Mater. 2013, 25, 4668–4672. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Li, L.; Yu, J.; Huang, W.; Yen, Y.C.; Lee, L.J.; Yi, A.Y. Graphene-coated Si mold for precision glass optics molding. Opt. Lett. 2013, 38, 2625–2628. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Xu, G.; Wen, X.; Zhou, J.; Gong, F. High-temperature friction behavior of amorphous carbon coating in glass molding process. Friction 2020. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Yi, A.Y. Rapid localized heating of graphene coating on a silicon mold by induction for precision molding of polymer optics. Opt. Lett. 2017, 42, 1369–1372. [Google Scholar] [CrossRef]
- Zhou, J.; He, P.; Yu, J.; Lee, L.J.; Shen, L.; Yi, A.Y. Investigation on the friction coefficient between graphene-coated silicon and glass using barrel compression test. J. Vac. Sci. Technol. B 2015, 33, 031213. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Zhou, W.; Zhou, T.; Yu, J.; Lee, L.J.; Allen, Y.Y. Fabrication of Plano-Concave Plastic Lens by Novel Injection Molding Using Carbide-Bonded Graphene-Coated Silica Molds. J. Micromechan. Microeng. 2018, 28, 075008. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, L.; Cabrera, E.D.; Pan, J.-J.; Yang, H.; Zhang, D.; Yang, Z.-G.; Yu, J.-F.; Castro, J.; Huang, H.-X. Carbide-bonded graphene coated zirconia for achieving rapid thermal cycling under low input voltage and power. Ceram. Int. 2019, 45, 24318–24323. [Google Scholar] [CrossRef]
- Li, H.; He, P.; Yu, J.F.; Lee, L.J.; Yi, A.Y. Localized rapid heating process for precision chalcogenide glass molding. Opt. Laser Eng. 2015, 73, 62–68. [Google Scholar] [CrossRef]
- Xie, P.C.; He, P.; Yen, Y.C.; Kwak, K.J.; Gallego-Perez, D.; Chang, L.Q.; Liao, W.C.; Yi, A.; Lee, L.J. Rapid hot embossing of polymer microstructures using carbide-bonded graphene coating on silicon stampers. Surf. Coat. Technol. 2014, 258, 174–180. [Google Scholar] [CrossRef]
- Xie, P.C.; Yang, H.G.; Zhao, Y.G.; Yu, W.X.; Cheng, L.S.; Yang, W.M.; Yan, H.; Tan, J. Carbide-bonded graphene coating of mold insert for rapid thermal cycling in injection molding. Appl. Therm. Eng. 2017, 122, 19–26. [Google Scholar] [CrossRef]
- Yang, G.; Li, L.; Lee, W.B.; Ng, M.C.; Chan, C.Y. Investigation of the heating behavior of carbide-bonded graphene coated silicon wafer used for hot embossing. Appl. Surf. Sci. 2018, 435, 130–140. [Google Scholar] [CrossRef]
- Li, L.; Chan, M.-K.; Lee, W.-B.; Ng, M.-C.; Chan, K.-L. Modeling and experimental performance analysis of a novel heating system and its application to glass hot embossing technology. Opt. Lett. 2019, 44, 3454–3457. [Google Scholar] [CrossRef]
- Li, L.; Yang, G.; Lee, W.B.; Ng, M.C.; Chan, K.L. Carbide-bonded graphene-based Joule heating for embossing fine microstructures on optical glass. Appl. Surf. Sci. 2020, 500, 144004. [Google Scholar] [CrossRef]
- Zhou, J.; Li, L.H.; Gong, F.; Liu, K. Quality dependence study on dimensions for plano-concave molded glass lenses. Int. J. Appl. Glass Sci. 2017, 8, 266–275. [Google Scholar] [CrossRef]
- Fischer, R.E.; Tadic-Galeb, B.; Yoder, P.R.; Galeb, R. Optical System Design; McGraw Hill: NewYork, NY, USA, 2000. [Google Scholar]
- Liu, X.; Zhou, T.; Zhang, L.; Zhou, W.; Yu, J.; James Lee, L.; Yi, A.Y. Simulation and Measurement of Refractive Index Variation in Localized Rapid Heating Molding for Polymer Optics. J. Manuf. Sci. Eng. 2017, 140, 011004. [Google Scholar] [CrossRef]
- Fulkerson, W.; Moore, J.P.; Williams, R.K.; Graves, R.S.; McElroy, D.L. Thermal Conductivity, Electrical Resistivity, and Seebeck Coefficient of Silicon from 100 to 1300 K. Phys. Rev. 1968, 167, 765–782. [Google Scholar] [CrossRef]
- Maji, B.K.; Jena, H.; Asuvathraman, R. Electrical conductivity and glass transition temperature (Tg) measurements on some selected glasses used for nuclear waste immobilization. J. Non-Cryst. Solids 2016, 434, 102–107. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Narayanaswamy, O.S. A model of structural relaxation in glass. J. Am. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Su, L.; Chen, Y.; Allen, Y.Y.; Klocke, F.; Pongs, G. Refractive index variation in compression molding of precision glass optical components. Appl. Opt. 2008, 47, 1662–1667. [Google Scholar] [CrossRef] [PubMed]
- Garman, P.D.; Johnson, J.M.; Talesara, V.; Yang, H.; Zhang, D.; Castro, J.; Lu, W.; Hwang, J.; Lee, L.J. Silicon Oxycarbide Accelerated Chemical Vapor Deposition of Graphitic Networks on Ceramic Substrates for Thermal Management Enhancement. ACS Appl. Nano Mater. 2019, 2, 452–458. [Google Scholar] [CrossRef]
- Garman, P.D.; Johnson, J.M.; Talesara, V.; Yang, H.; Du, X.; Pan, J.; Zhang, D.; Yu, J.; Cabrera, E.; Yen, Y.-C.; et al. Dual Silicon Oxycarbide Accelerated Growth of Well-Ordered Graphitic Networks for Electronic and Thermal Applications. Adv. Mater. Technol. 2019. [Google Scholar] [CrossRef]
- De Boer, J.F.; Milner, T.E.; van Gemert, M.J.; Nelson, J.S. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Opt. Lett. 1997, 22, 934–936. [Google Scholar] [CrossRef] [Green Version]
- Pallicity, T.D.; Vu, A.T.; Ramesh, K.; Mahajan, P.; Liu, G.; Dambon, O. Birefringence measurement for validation of simulation of precision glass molding process. J. Am. Ceram. Soc. 2017, 100, 4680–4698. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.; Klocke, F.; Pongs, G.; Yi, A.Y. Numerical Simulation Assisted Curve Compensation in Compression Molding of High Precision Aspherical Glass Lenses. J. Manuf. Sci. Eng. 2009, 131, 011014. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhou, J. Evaluation of Warpage and Residual Stress of Precision Glass Micro-Optics Heated by Carbide-Bonded Graphene Coating in Hot Embossing Process. Nanomaterials 2021, 11, 363. https://doi.org/10.3390/nano11020363
Li L, Zhou J. Evaluation of Warpage and Residual Stress of Precision Glass Micro-Optics Heated by Carbide-Bonded Graphene Coating in Hot Embossing Process. Nanomaterials. 2021; 11(2):363. https://doi.org/10.3390/nano11020363
Chicago/Turabian StyleLi, Lihua, and Jian Zhou. 2021. "Evaluation of Warpage and Residual Stress of Precision Glass Micro-Optics Heated by Carbide-Bonded Graphene Coating in Hot Embossing Process" Nanomaterials 11, no. 2: 363. https://doi.org/10.3390/nano11020363
APA StyleLi, L., & Zhou, J. (2021). Evaluation of Warpage and Residual Stress of Precision Glass Micro-Optics Heated by Carbide-Bonded Graphene Coating in Hot Embossing Process. Nanomaterials, 11(2), 363. https://doi.org/10.3390/nano11020363





