In Situ TEM Observation of Cooperative Grain Rotations and the Bauschinger Effect in Nanocrystalline Palladium
Abstract
:1. Introduction
2. Experimental: Material Synthesis, Methods, Data Acquisition, and Processing
2.1. Specimen Preparation for In Situ TEM Nanomechanics
2.2. In Situ TEM Nanomechanical Experiments
2.3. Quantitative Analysis of ACOM-STEM Data
2.4. Nye Tensor Analysis of Geometrically Necessary Dislocations
3. Results and Discussion
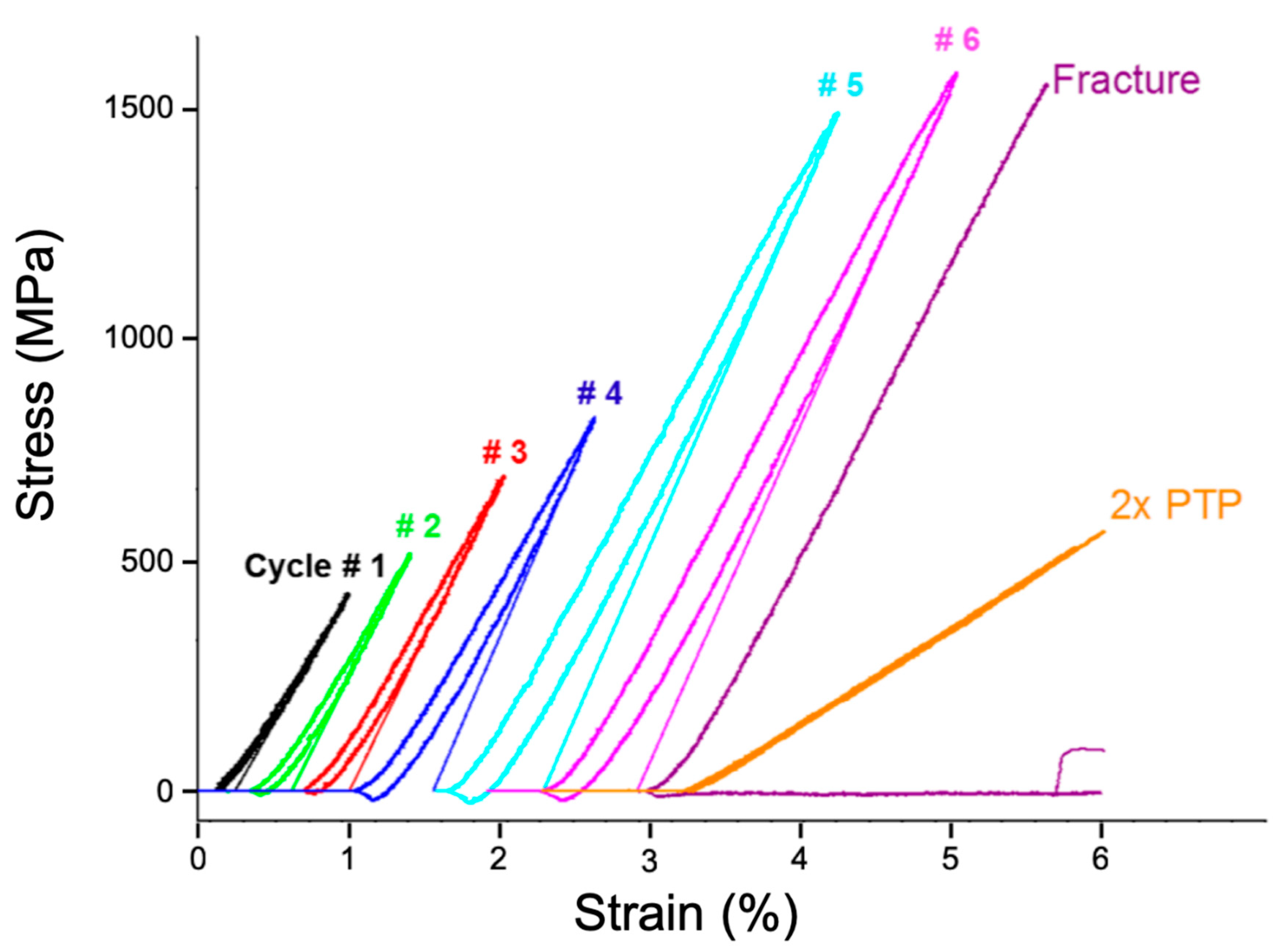
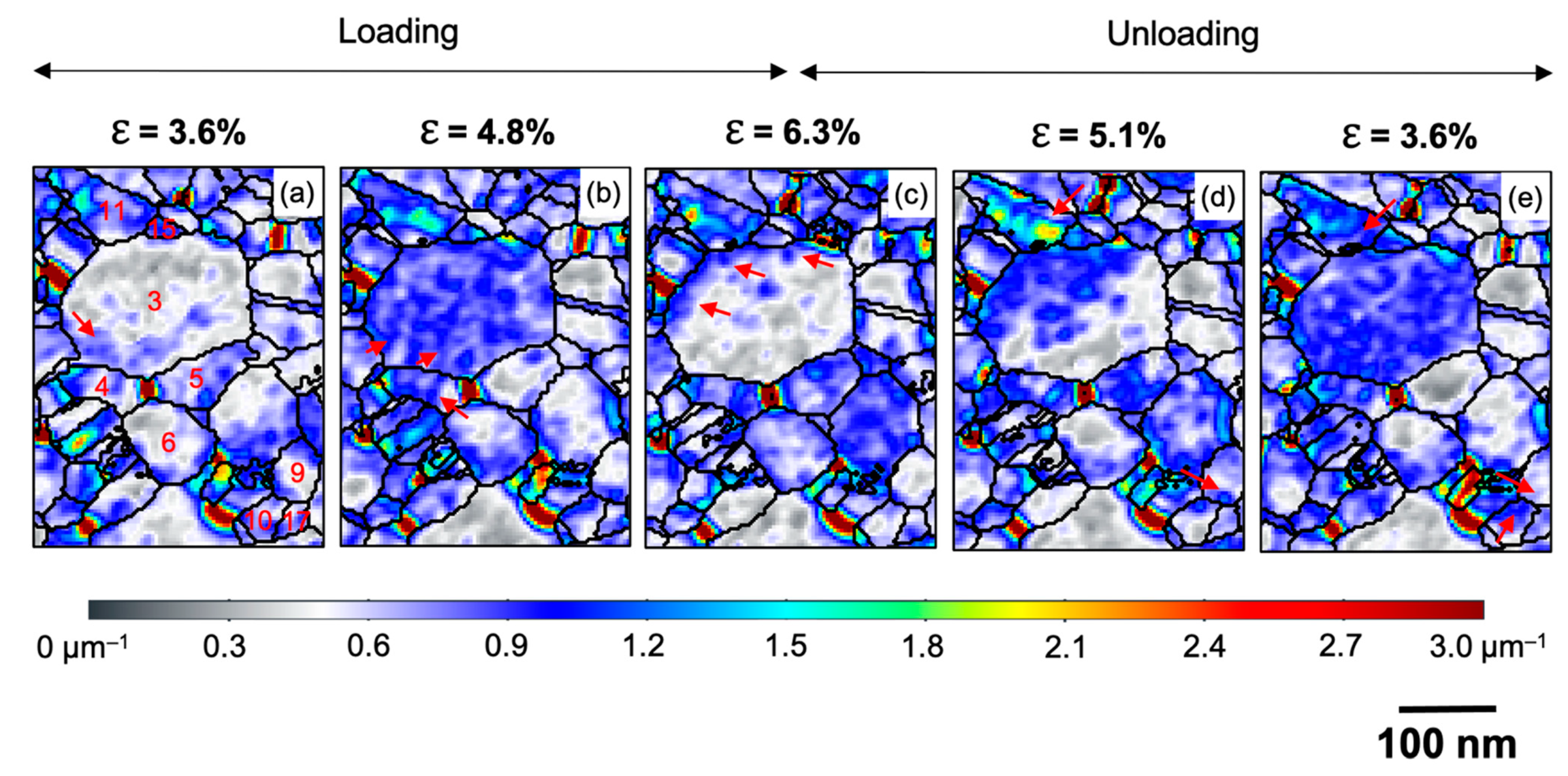
3.1. In Situ Nanomechanical Response: The Bauschinger Effect
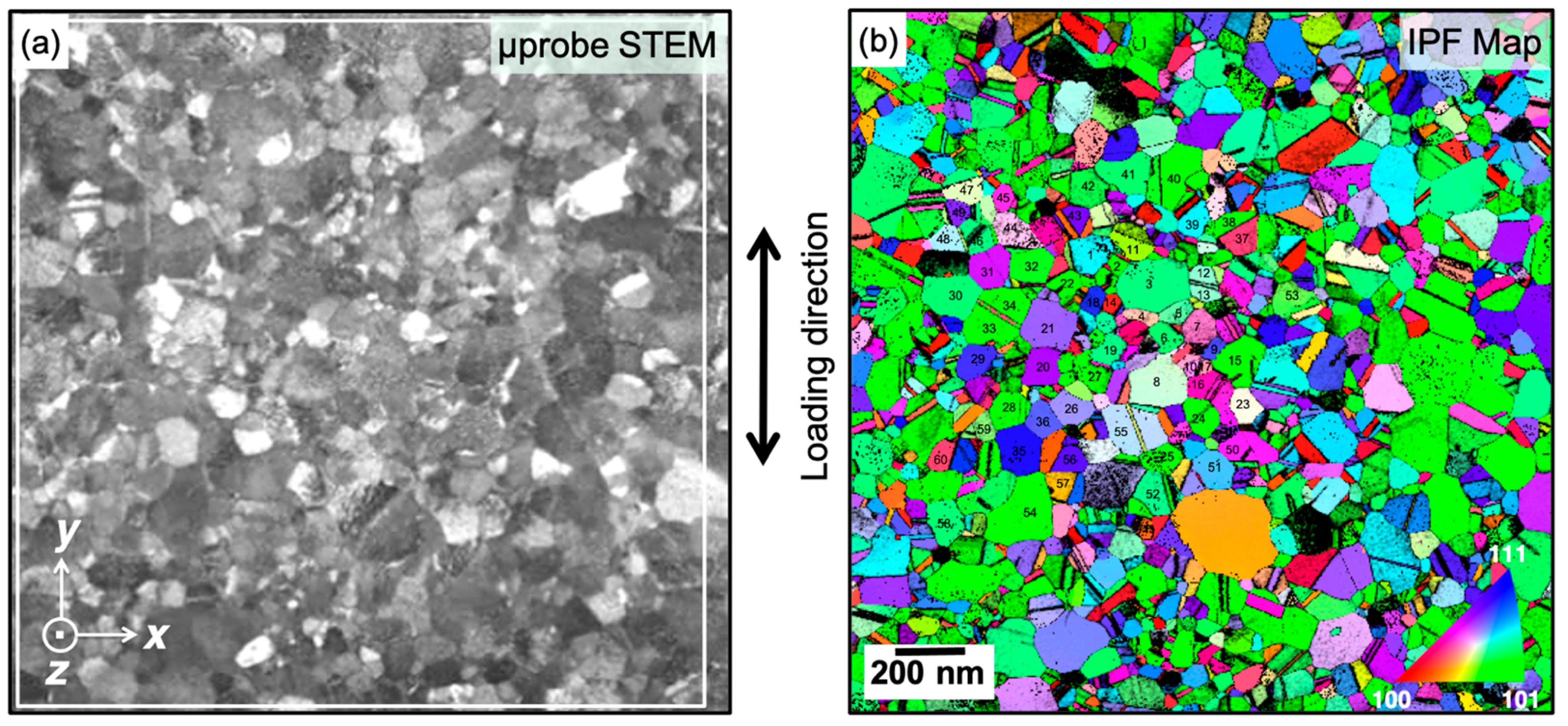
3.2. Structural Observations and Deformation Characteristics of the Nanocrystalline Palladium Film
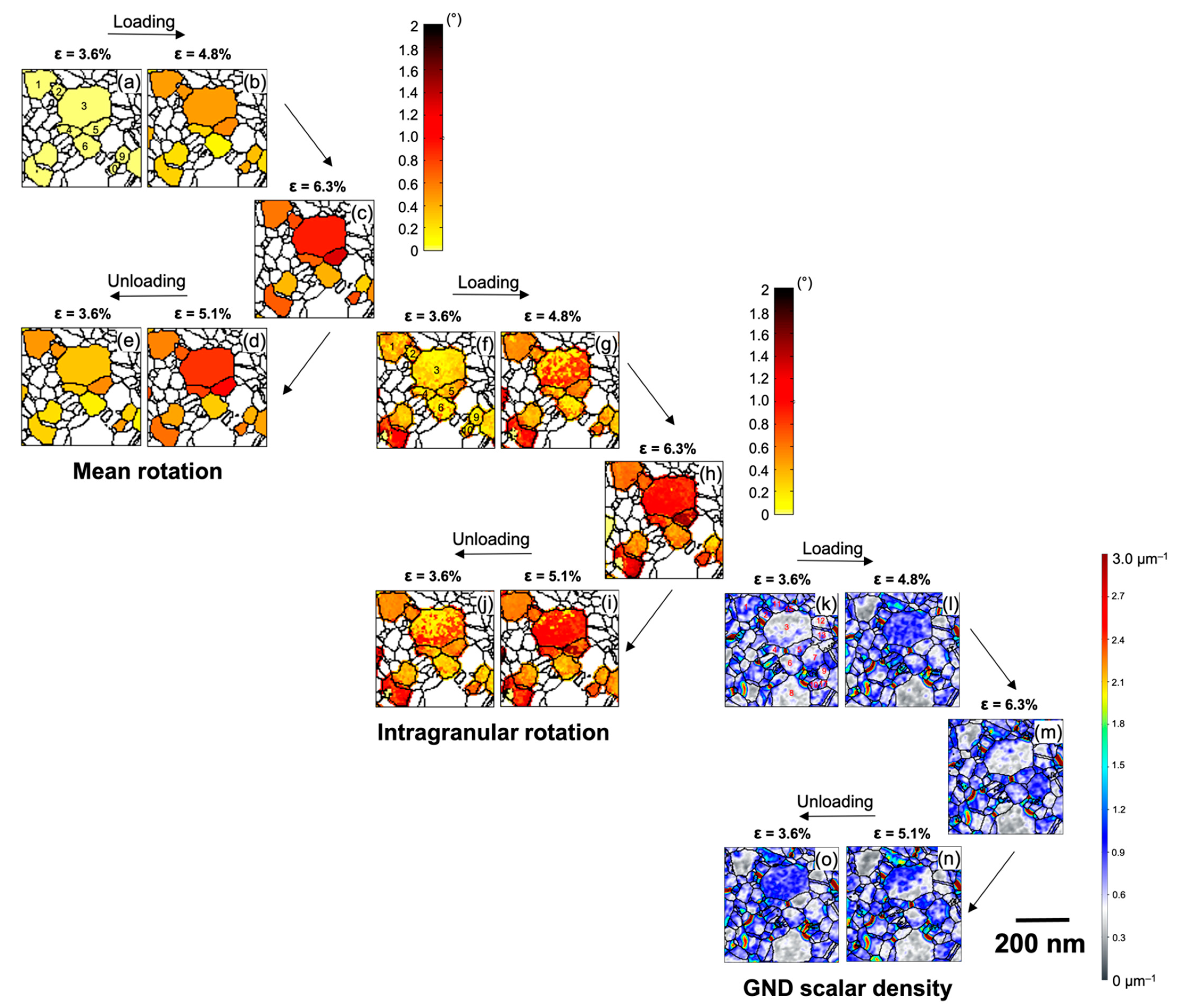
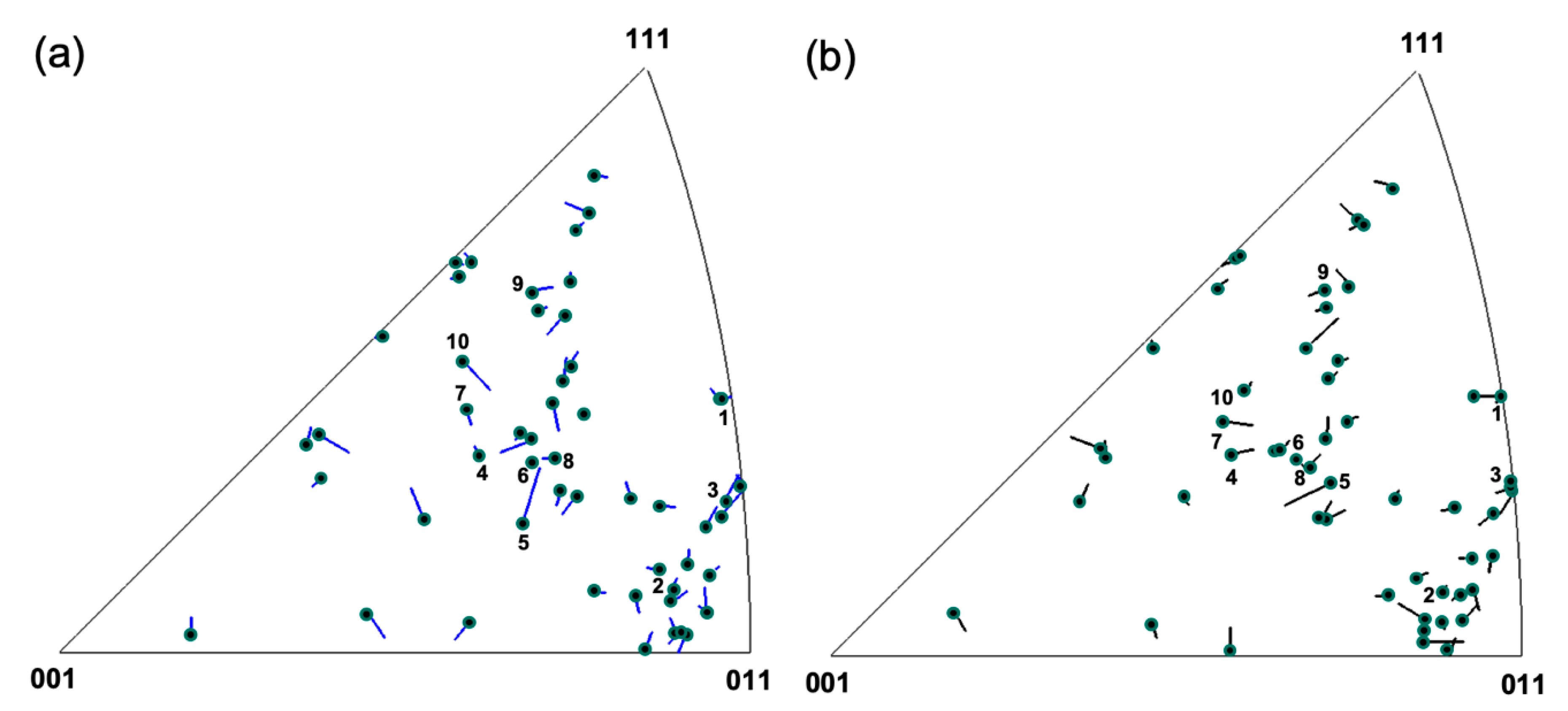
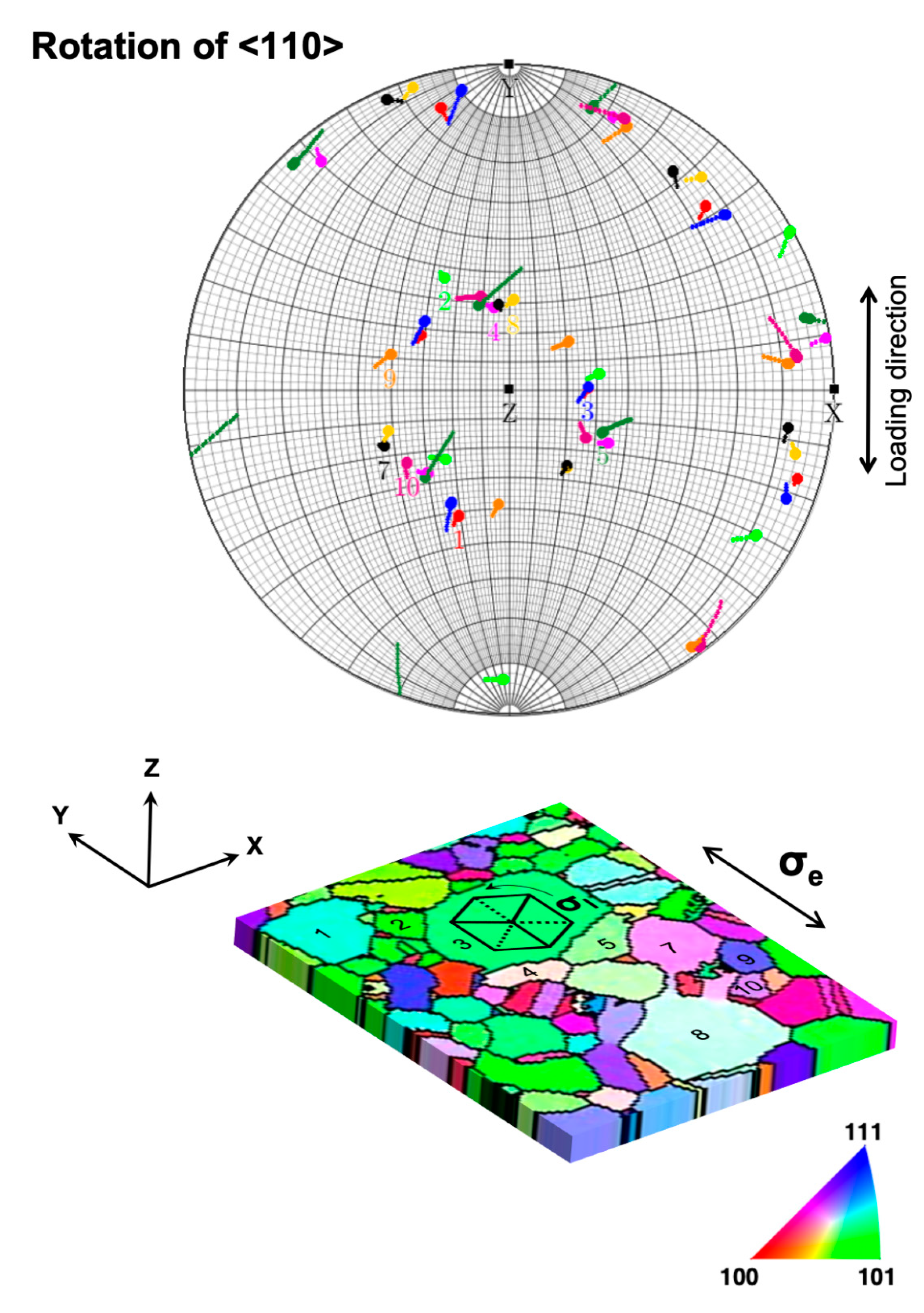
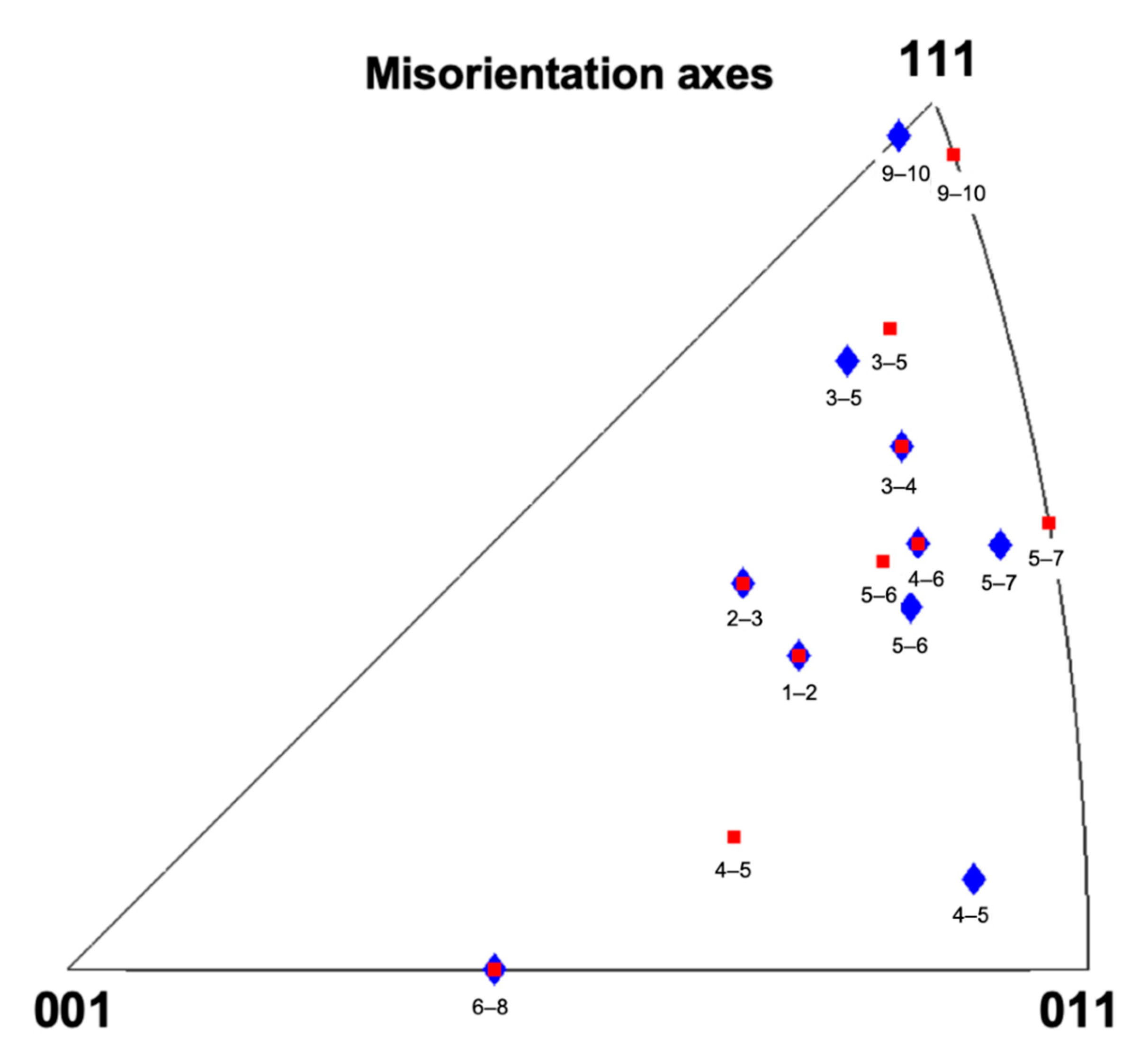
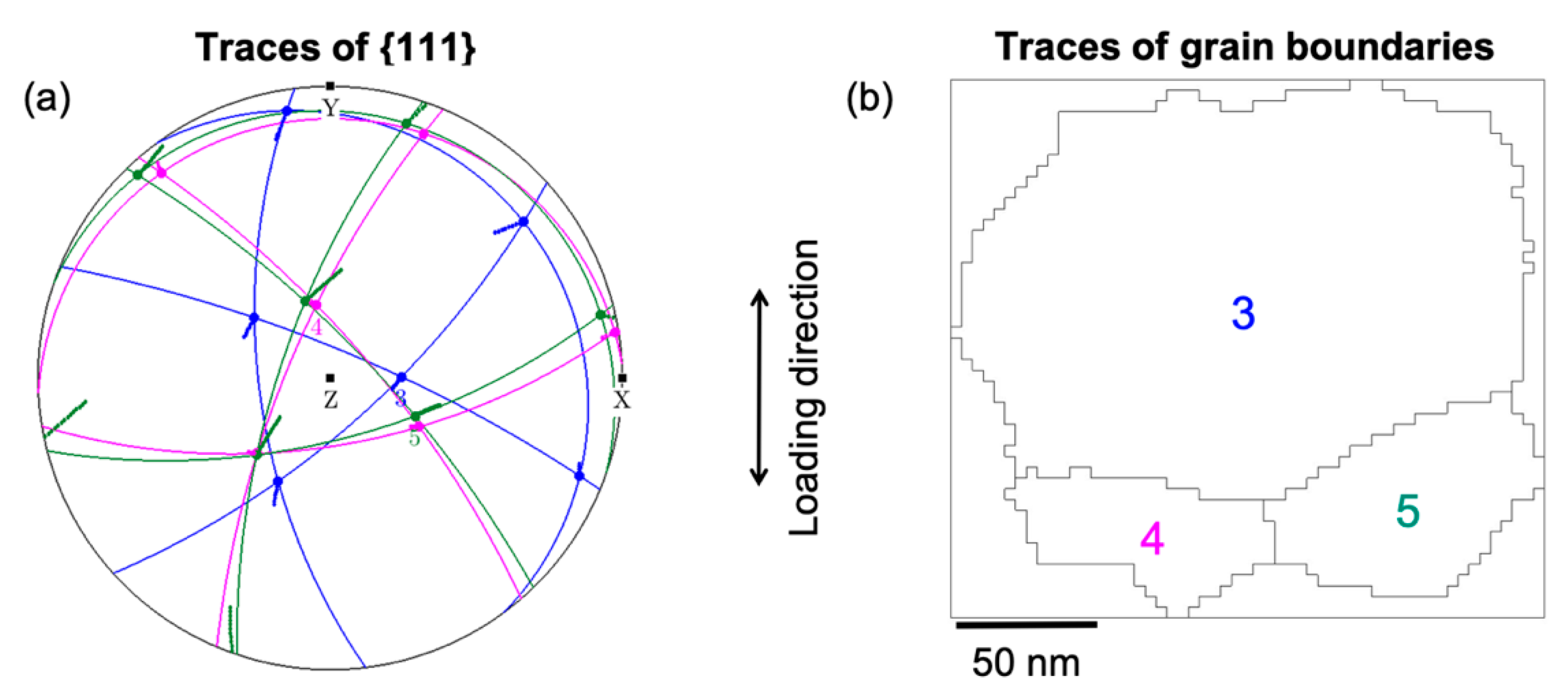
3.3. Cooperative Grain Rotation (CGR)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poulsen, H.F.; Margulies, L.; Schmidt, S.; Winther, G. Lattice Rotations of Individual Bulk Grains. Part I: 3D X-ray Characterization. Acta Mater. 2003, 51, 3821–3830. [Google Scholar] [CrossRef]
- Winther, G.; Margulies, L.; Schmidt, S.; Poulsen, H.F. Lattice Rotations of Individual Bulk Grains Part II: Correlation with Initial Orientation and Model Comparison. Acta Mater. 2004, 52, 2863–2872. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. J. Inst. Metals 1938, 62, 307–324. [Google Scholar]
- Sachs, G.I. Zur Ableitung Einer Fleissbedingun. Z. Ver. Dtsch. Ing. 1928, 72, 734–736. [Google Scholar]
- Hirsch, J.; Lücke, K. Overview No. 76. Mechanism of Deformation and Development of Rolling Textures in Polycrystalline f.c.c. Metals-II. Simulation and Interpretation of Experiments on the Basis of Taylor-Type Theories. Acta Metall. 1988, 36, 2883–2904. [Google Scholar] [CrossRef]
- Ma, E. Watching the Nanograins Roll. Science 2004, 305, 623–624. [Google Scholar] [CrossRef] [PubMed]
- Margulies, L.; Winther, G.; Poulsen, H.F. In Situ Measurement of Grain Rotation during Deformation of Polycrystals. Science 2001, 291, 2392–2394. [Google Scholar] [CrossRef]
- Kocks, U.F. Independent Slip Systems in Crystals. Philos. Mag. 1964, 10, 187–193. [Google Scholar] [CrossRef]
- Bishop, J.F.W.; Hill, R. XLVI. A Theory of the Plastic Distortion of a Polycrystalline Aggregate under Combined Stresses. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 414–427. [Google Scholar] [CrossRef]
- Mao, W. On the Taylor Principles for Plastic Deformation of Polycrystalline Metals. Front. Mater. Sci. 2016, 10, 335–345. [Google Scholar] [CrossRef]
- Mao, W. The Currently Predominant Taylor Principles Should Be Disregarded in the Study of Plastic Deformation of Metals. Front. Mater. Sci. 2018, 12, 322–326. [Google Scholar] [CrossRef]
- Winther, G.; Wright, J.P.; Schmidt, S.; Oddershede, J. Grain Interaction Mechanisms Leading to Intragranular Orientation Spread in Tensile Deformed Bulk Grains of Interstitial-Free Steel. Int. J. Plast. 2017, 88, 108–125. [Google Scholar] [CrossRef] [Green Version]
- Mao, W. Influence of Intergranular Mechanical Interactions on Orientation Stabilities during Rolling of Pure Aluminum. Metals 2019, 9, 477. [Google Scholar] [CrossRef] [Green Version]
- Mu, S.; Tang, F.; Gottstein, G. A Cluster-Type Grain Interaction Deformation Texture Model Accounting for Twinning-Induced Texture and Strain-Hardening Evolution: Application to Magnesium Alloys. Acta Mater. 2014, 68, 310–324. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Seefeldt, M.; Delannay, L. Deformation Texture Prediction: From the Taylor Model to the Advanced Lamel Model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Oddershede, J.; Wright, J.P.; Beaudoin, A.; Winther, G. Deformation-Induced Orientation Spread in Individual Bulk Grains of an Interstitial-Free Steel. Acta Mater. 2015, 85, 301–313. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.S.; Van Swygenhoven, H.; Suresh, S. Mechanical Behavior of Nanocrystalline Metals and Alloys. Acta Mater. 2003, 51, 5743–5774. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical Properties of Nanocrystalline Materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Pande, C.S.; Cooper, K.P. Nanomechanics of Hall-Petch Relationship in Nanocrystalline Materials. Prog. Mater. Sci. 2009, 54, 689–706. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Skrotzki, W.; Chulist, R.; Lippmann, T.; Kurmanaeva, L. Texture Development in a Nanocrystalline Pd-Au Alloy Studied by Synchrotron Radiation. Scr. Mater. 2012, 66, 131–134. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.L.; Jia, N.; Wang, Y.D.; Shen, Y.F.; Choo, H.; Liaw, P.K. Simulations of Texture Evolution in Heavily Deformed Bulk Nanocrystalline Nickel. Mater. Sci. Eng. A 2008, 493, 86–92. [Google Scholar] [CrossRef]
- Madhavan, R.; Suwas, S. Micro-Mechanisms of Deformation Texture Evolution in Nanocrystalline Nickel-Cobalt Alloys. Acta Mater. 2016, 121, 46–58. [Google Scholar] [CrossRef]
- Shan, Z.; Stach, E.A.; Wiezorek, J.M.K.; Knapp, J.A.; Follstaedt, D.M.; Mao, S.X. Grain Boundary-Mediated Plasticity in Nanocrystalline Nickel. Science 2004, 305, 654–657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hahn, H.; Mondal, P.; Padmanabhan, K.A. Plastic Deformation of Nanocrystalline Materials. Nanostruct. Mater. 1997, 9, 603–606. [Google Scholar] [CrossRef]
- Lohmiller, J.; Grewer, M.; Braun, C.; Kobler, A.; Kübel, C.; Schüler, K.; Honkimäki, V.; Hahn, H.; Kraft, O.; Birringer, R.; et al. Untangling Dislocation and Grain Boundary Mediated Plasticity in Nanocrystalline Nickel. Acta Mater. 2014, 65, 295–307. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Kurmanaeva, L.; Weissmueller, J.; Yang, K.; Markmann, J.; Rösner, H.; Scherer, T.; Fecht, H.J. Deformation Mechanisms in Nanocrystalline Palladium at Large Strains1. Acta Mater. 2009, 57, 3391–3401. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Enikeev, N.A.; Yang, K.; Smoliakov, A.; Soloviev, V.P.; Fecht, H.; Hahn, H. Contribution of Grain Boundary Related Strain Accommodation to Deformation of Ultrafine-Grained Palladium. Mater. Sci. Eng. A 2016, 668, 255–262. [Google Scholar] [CrossRef]
- Kobler, A.; Lohmiller, J.; Schäfer, J.; Kerber, M.; Castrup, A.; Kashiwar, A.; Gruber, P.A.; Albe, K.; Hahn, H.; Kübel, C. Deformation-Induced Grain Growth and Twinning in Nanocrystalline Palladium Thin Films. Beilstein J. Nanotechnol. 2013, 4, 554–566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobler, A.; Brandl, C.; Hahn, H.; Kübel, C. In Situ Observation of Deformation Processes in Nanocrystalline Face-Centered Cubic Metals. Beilstein J. Nanotechnol. 2016, 7, 572–580. [Google Scholar] [CrossRef] [Green Version]
- Höppel, H.W.; Kautz, M.; Xu, C.; Murashkin, M.; Langdon, T.G.; Valiev, R.Z.; Mughrabi, H. An Overview: Fatigue Behaviour of Ultrafine-Grained Metals and Alloys. Int. J. Fatigue 2006, 28, 1001–1010. [Google Scholar] [CrossRef]
- Xiang, Y.; Vlassak, J.J. Bauschinger Effect in Thin Metal Films. Scr. Mater. 2005, 53, 177–182. [Google Scholar] [CrossRef]
- Rajagopalan, J.; Han, J.H.; Saif, M.T.A. Bauschinger Effect in Unpassivated Freestanding Nanoscale Metal Films. Scr. Mater. 2008, 59, 734–737. [Google Scholar] [CrossRef]
- Mompiou, F.; Caillard, D.; Legros, M.; Mughrabi, H. In Situ TEM Observations of Reverse Dislocation Motion upon Unloading in Tensile-Deformed UFG Aluminium. Acta Mater. 2012, 60, 3402–3414. [Google Scholar] [CrossRef]
- Izadi, E.; Darbal, A.; Sarkar, R.; Rajagopalan, J. Grain Rotations in Ultrafine-Grained Aluminum Films Studied Using in Situ TEM Straining with Automated Crystal Orientation Mapping. Mater. Des. 2017, 113, 186–194. [Google Scholar] [CrossRef] [Green Version]
- Mompiou, F.; Legros, M. Quantitative Grain Growth and Rotation Probed by In-Situ TEM Straining and Orientation Mapping in Small Grained Al Thin Films. Scr. Mater. 2015, 99, 5–8. [Google Scholar] [CrossRef]
- Kobler, A.; Kashiwar, A.; Hahn, H.; Kübel, C. Combination of in Situ Straining and ACOM TEM: A Novel Method for Analysis of Plastic Deformation of Nanocrystalline Metals. Ultramicroscopy 2013, 128, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Rauch, E.F. DiffGen, NanoMEGAS SPRL. 2016. Available online: https://nanomegas.com/ (accessed on 5 January 2018).
- Rauch, E.F. Index, NanoMEGAS SPRL. 2016. Available online: https://nanomegas.com/ (accessed on 5 January 2018).
- Rauch, E.F. Mapviewer, NanoMEGAS SPRL. 2016. Available online: https://nanomegas.com/ (accessed on 5 January 2018).
- Rauch, E.F.; Véron, M. Automated Crystal Orientation and Phase Mapping in TEM. Mater. Charact. 2014, 98, 1–9. [Google Scholar] [CrossRef]
- Leff, A.C.; Weinberger, C.R.; Taheri, M.L. Estimation of Dislocation Density from Precession Electron Diffraction Data Using the Nye Tensor. Ultramicroscopy 2015, 153, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Kobler, A.; Kübel, C. Challenges in Quantitative Crystallographic Characterization of 3D Thin Films by ACOM-TEM. Ultramicroscopy 2017, 173, 84–94. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX- Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef] [Green Version]
- Beausir, B.; Fundenberger, J.J. Analysis Tools for Electron and X-ray Diffraction, ATEX—Software. Available online: http://www.atex-software.eu/ (accessed on 1 August 2020). Université de Lorraine—Metz 2017.
- Xiang, Y.; Vlassak, J.J. Bauschinger and Size Effects in Thin-Film Plasticity. Acta Mater. 2006, 54, 5449–5460. [Google Scholar] [CrossRef]
- Rajagopalan, J.; Rentenberger, C.; Peter Karnthaler, H.; Dehm, G.; Saif, M.T.A. In Situ TEM Study of Microplasticity and Bauschinger Effect in Nanocrystalline Metals. Acta Mater. 2010, 58, 4772–4782. [Google Scholar] [CrossRef]
- Brandstetter, S.; Van Swygenhoven, H.; Van Petegem, S.; Schmitt, B.; Maaß, R.; Derlet, P.M. From Micro- to Macroplasticity. Adv. Mater. 2006, 18, 1545–1548. [Google Scholar] [CrossRef]
- Thilly, L.; Van Petegem, S.; Renault, P.O.; Lecouturier, F.; Vidal, V.; Schmitt, B.; Van Swygenhoven, H. A New Criterion for Elasto-Plastic Transition in Nanomaterials: Application to Size and Composite Effects on Cu-Nb Nanocomposite Wires. Acta Mater. 2009, 57, 3157–3169. [Google Scholar] [CrossRef]
- Tsuru, T.; Aoyagi, Y.; Kaji, Y.; Shimokawa, T. Heterogeneous Plastic Deformation and Bauschinger Effect in Ultrafine-Grained Metals: Atomistic Simulations. Model. Simul. Mater. Sci. Eng. 2016, 24, 035010. [Google Scholar] [CrossRef]
- Mompiou, F.; Legros, M.; Boé, A.; Coulombier, M.; Raskin, J.P.; Pardoen, T. Inter- and Intragranular Plasticity Mechanisms in Ultrafine-Grained Al Thin Films: An in Situ TEM Study. Acta Mater. 2013, 61, 205–216. [Google Scholar] [CrossRef]
- Farkas, D.; Curtin, W.A. Plastic Deformation Mechanisms in Nanocrystalline Columnar Grain Structures. Mater. Sci. Eng. A 2005, 412, 316–322. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y.; Yang, W.; Gao, H. Competing Grain-Boundary- and Dislocation-Mediated Mechanisms in Plastic Strain Recovery in Nanocrystalline Aluminum. Proc. Natl. Acad. Sci. USA 2009, 106, 16108–16113. [Google Scholar] [CrossRef] [Green Version]
- Hasnaoui, A.; Van Swygenhoven, H.; Derlet, P.M. Cooperative Processes during Plastic Deformation in Nanocrystalline Fcc Metals: A Molecular Dynamics Simulation. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 66, 184112. [Google Scholar] [CrossRef]
- Legros, M.; Gianola, D.S.; Hemker, K.J. In Situ TEM Observations of Fast Grain-Boundary Motion in Stressed Nanocrystalline Aluminum Films. Acta Mater. 2008, 56, 3380–3393. [Google Scholar] [CrossRef]
- Nye, J.F. Some Geometrical Relations in Dislocated Crystals. Acta Metall. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Pantleon, W. Resolving the Geometrically Necessary Dislocation Content by Conventional Electron Backscattering Diffraction. Scr. Mater. 2008, 58, 994–997. [Google Scholar] [CrossRef]
- Toth, L.S.; Gu, C.F.; Beausir, B.; Fundenberger, J.J.; Hoffman, M. Geometrically Necessary Dislocations Favor the Taylor Uniform Deformation Mode in Ultra-Fine-Grained Polycrystals. Acta Mater. 2016, 117, 35–42. [Google Scholar] [CrossRef]
- Vetterick, G.; Leff, A.C.; Marshall, M.; Baldwin, J.K.; Misra, A.; Hattar, K.; Taheri, M.L. Direct Observation of a Coincident Dislocation- and Grain Boundary-Mediated Deformation in Nanocrystalline Iron. Mater. Sci. Eng. A 2018, 709, 339–348. [Google Scholar] [CrossRef]
- Gu, C.F.; Tóth, L.S.; Beausir, B. Modeling of Large Strain Hardening during Grain Refinement. Scr. Mater. 2012, 66, 250–253. [Google Scholar] [CrossRef]
- Winther, G. Slip Systems Extracted from Lattice Rotations and Dislocation Structures. Acta Mater. 2008, 56, 1919–1932. [Google Scholar] [CrossRef]
- Farkas, D.; Spaczer, M. Competing Plastic Deformation Mechanisms in Nanophase Metals. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 60, 22–25. [Google Scholar] [CrossRef]
- Raj, R.; Ashby, M.F. On Grain Boundary Sliding and Diffusional Creep. Metall. Trans. 1971, 2, 1113–1127. [Google Scholar] [CrossRef]
- Harris, K.E.; Singh, V.V.; King, A.H. Grain Rotation in Thin Films of Gold. Acta Mater. 1998, 46, 2623–2633. [Google Scholar] [CrossRef]
- Moldovan, D.; Wolf, D.; Phillpot, S.R. Theory of Diffusion-Accommodated Grain Rotation in Columnar Polycrystalline Microstructures. Acta Mater. 2001, 49, 3521–3532. [Google Scholar] [CrossRef]
- Yang, K.; Fecht, H.J.; Ivanisenko, Y. First Direct in Situ Observation of Grain Boundary Sliding in Ultrafine Grained Noble Metal. Adv. Eng. Mater. 2014, 16, 517–521. [Google Scholar] [CrossRef]
- Gutkin, M.Y.; Ovid’ko, I.A.; Skiba, N.V. Crossover from Grain Boundary Sliding to Rotational Deformation in Nanocrystalline Materials. Acta Mater. 2003, 51, 4059–4071. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.M. Grain-Boundary Sliding in Nanocrystalline Fcc Metals. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 64, 224105. [Google Scholar] [CrossRef]
- Wang, L.; Teng, J.; Liu, P.; Hirata, A.; Ma, E.; Zhang, Z.; Chen, M.; Han, X. Grain Rotation Mediated by Grain Boundary Dislocations in Nanocrystalline Platinum. Nat. Commun. 2014, 5, 4402. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashiwar, A.; Hahn, H.; Kübel, C. In Situ TEM Observation of Cooperative Grain Rotations and the Bauschinger Effect in Nanocrystalline Palladium. Nanomaterials 2021, 11, 432. https://doi.org/10.3390/nano11020432
Kashiwar A, Hahn H, Kübel C. In Situ TEM Observation of Cooperative Grain Rotations and the Bauschinger Effect in Nanocrystalline Palladium. Nanomaterials. 2021; 11(2):432. https://doi.org/10.3390/nano11020432
Chicago/Turabian StyleKashiwar, Ankush, Horst Hahn, and Christian Kübel. 2021. "In Situ TEM Observation of Cooperative Grain Rotations and the Bauschinger Effect in Nanocrystalline Palladium" Nanomaterials 11, no. 2: 432. https://doi.org/10.3390/nano11020432
APA StyleKashiwar, A., Hahn, H., & Kübel, C. (2021). In Situ TEM Observation of Cooperative Grain Rotations and the Bauschinger Effect in Nanocrystalline Palladium. Nanomaterials, 11(2), 432. https://doi.org/10.3390/nano11020432







