Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation
Abstract
1. Introduction
2. Discrete Model
3. Equivalent Continuum Models
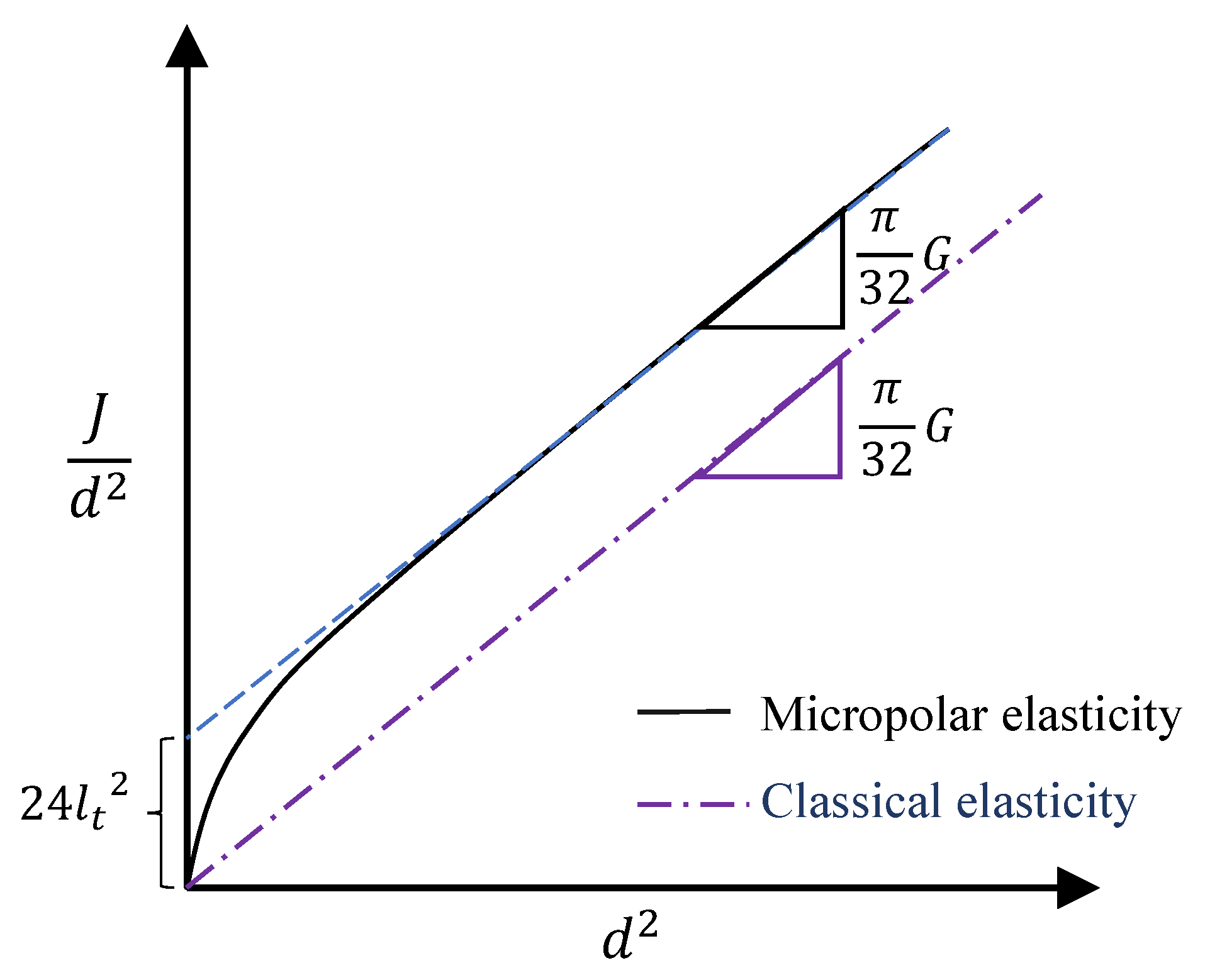
3.1. Micropolar Hollow Circular Cylinder
- : shear modulus
- : coupling number
- : charachteristic lenght for torsion
- : polar ratio
- : Young’s modulus
- : Poisson’s ratio
- : charachteristic lenght for bending
3.2. Micropolar Solid Circular Cylinder
3.3. Couple Stress Theory
4. Identification of Material Parameters and Discussion
4.1. Equivalent Thickness
4.2. Internal Length Parameter
4.3. CNT as Solid Micropolar Cylinder
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Smalley, R.E. Fullerene nanotubes: C 1,000,000 and beyond: Some unusual new molecules—Long, hollow fibers with tantalizing electronic and mechanical properties—Have joined diamonds and graphite in the carbon family. Am. Sci. 1997, 85, 324–337. [Google Scholar]
- Popov, V.N. Carbon nanotubes: Properties and application. Mater. Sci. Eng. R Rep. 2004, 43, 61–102. [Google Scholar] [CrossRef]
- Salvetat, J.P.; Bonard, J.M.; Thomson, N.; Kulik, A.; Forro, L.; Benoit, W.; Zuppiroli, L. Mechanical properties of carbon nanotubes. Appl. Phys. A 1999, 69, 255–260. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.; Rao, A. Carbon Nanotubes. In The Physics of Fullerene-Based and Fullerene-Related Materials; Springer: Berlin/Heidelberg, Germany, 2000; pp. 331–379. [Google Scholar]
- Evazzade, I.; Lobzenko, I.; Golubev, O.; Korznikova, E. Two-phase tension of a carbon nanotube. J. Micromech. Mol. Phys. 2020, 5, 2050001. [Google Scholar] [CrossRef]
- Williams, P.; Papadakis, S.; Patel, A.; Falvo, M.; Washburn, S.; Superfine, R. Fabrication of nanometer-scale mechanical devices incorporating individual multiwalled carbon nanotubes as torsional springs. Appl. Phys. Lett. 2003, 82, 805–807. [Google Scholar] [CrossRef]
- Papadakis, S.; Hall, A.; Williams, P.; Vicci, L.; Falvo, M.; Superfine, R.; Washburn, S. Resonant oscillators with carbon-nanotube torsion springs. Phys. Rev. Lett. 2004, 93, 146101. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, L.F.; Zhang, Y.; Wang, J.; Geng, H.; Zhang, Q. Advances in conceptual electronic nanodevices based on 0D and 1D nanomaterials. Nanomicro Lett. 2014, 6, 1–19. [Google Scholar] [CrossRef]
- Fennimore, A.; Yuzvinsky, T.; Han, W.Q.; Fuhrer, M.; Cumings, J.; Zettl, A. Rotational actuators based on carbon nanotubes. Nature 2003, 424, 408–410. [Google Scholar] [CrossRef]
- Yun, Y.; Shanov, V.; Tu, Y.; Schulz, M.J.; Yarmolenko, S.; Neralla, S.; Sankar, J.; Subramaniam, S. A multi-wall carbon nanotube tower electrochemical actuator. Nano Lett. 2006, 6, 689–693. [Google Scholar] [CrossRef]
- Chopra, S.; McGuire, K.; Gothard, N.; Rao, A.; Pham, A. Selective gas detection using a carbon nanotube sensor. Appl. Phys. Lett. 2003, 83, 2280–2282. [Google Scholar] [CrossRef]
- Andrews, R.; Weisenberger, M. Carbon nanotube polymer composites. Curr. Opin. Solid State Mater. Sci. 2004, 8, 31–37. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Winey, K.I. Polymer nanocomposites containing carbon nanotubes. Macromolecules 2006, 39, 5194–5205. [Google Scholar] [CrossRef]
- Wang, W.; Murthy, N. Characterization of Nanotube-Reinforced Polymer Composites. In Carbon Nanotubes; IntechOpen: Rijeka, Croatia, 2011; Chapter 8. [Google Scholar]
- Rafiee, R. Carbon Nanotube-Reinforced Polymers: From Nanoscale to Macroscale; Micro and Nano Technologies; Elsevier Science: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Haas, H.; Wang, C.Z.; Fähnle, M.; Elsässer, C.; Ho, K.M. Environment-dependent tight-binding model for molybdenum. Phys. Rev. B 1998, 57, 1461–1470. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, K. Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications. Prog. Mater. Sci. 2019, 100, 99–169. [Google Scholar] [CrossRef]
- Rapaport, D. The Art of Molecular Dynamics Simulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Trovalusci, P. Molecular Approaches for Multifield Continua: Origins and Current Developments. In Multiscale Modeling of Complex Materials; Springer: Berlin/Heidelberg, Germany, 2014; pp. 211–278. [Google Scholar]
- Ghavanloo, E.; Rafii-Tabar, H.; Fazelzadeh, S.A. Computational Continuum Mechanics of Nanoscopic Structures; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Kunin, I.A. The Theory of Elastic Media with Microstructure and the Theory of Dislocations. In Mechanics of Generalized Continua; Kröner, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1968; pp. 321–329. [Google Scholar]
- Capriz, G. Continua with Microstructure; Springer Tracts in Natural Philosophy; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Gurtin, M. Configurational Forces as Basis Concept of Continuum Physics; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Eringen, A. Microcontinuum Field Theory; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Trovalusci, P.; Pau, A. Derivation of microstructured continua from lattice systems via principle of virtual works: The case of masonry-like materials as micropolar, second gradient and classical continua. Acta Mech. 2014, 225, 157–177. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Material symmetries in homogenized hexagonal-shaped composites as Cosserat continua. Symmetry 2020, 22, 441. [Google Scholar] [CrossRef]
- Leonetti, L.; Greco, F.; Trovalusci, P.; Luciano, R.; Masiani, R. A multiscale damage analysis of periodic composites using a couple-stress/Cauchy multidomain model: Application to masonry structures. Compos. B Eng. 2018, 141, 50–59. [Google Scholar] [CrossRef]
- Capecchi, D.; Ruta, G.; Trovalusci, P. Voigt and Poincaré’s mechanistic–energetic approaches to linear elasticity and suggestions for multiscale modelling. Arch. Appl. Mech. 2011, 81, 1573–1584. [Google Scholar] [CrossRef]
- Kunin, I. On foundations of the theory of elastic media with microstructure. Int. J. Eng. Sci. 1984, 22, 969–978. [Google Scholar] [CrossRef]
- Maugin, G. Material Inhomogeneities in Elasticity; Applied Mathematics; Taylor & Francis: Abingdon, UK, 1993. [Google Scholar]
- Zhang, Y.; Liu, G.; Wang, J. Small-scale effects on buckling of multiwalled carbon nanotubes under axial compression. Phys. Rev. B 2004, 70, 205430. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, G.; Han, X. Effect of small length scale on elastic buckling of multi-walled carbon nanotubes under radial pressure. Phys. Lett. A 2006, 349, 370–376. [Google Scholar] [CrossRef]
- Khademolhosseini, F.; Rajapakse, R.; Nojeh, A. Torsional buckling of carbon nanotubes based on nonlocal elasticity shell models. Comput. Mater. Sci. 2010, 48, 736–742. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Torsional buckling and postbuckling of double-walled carbon nanotubes by nonlocal shear deformable shell model. Compos. Struct. 2010, 92, 1073–1084. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics. Int. J. Mech. Sci. 2011, 53, 786–792. [Google Scholar] [CrossRef]
- Tuna, M.; Kırca, M. Unification of Eringen’s nonlocal parameter through an optimization-based approach. Mech. Adv. Mater. Struct. 2019, 1–10. [Google Scholar] [CrossRef]
- Eringen, A.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Xie, G.; Long, S. Elastic vibration behaviors oof carbon nanotubes based on micropolar mechanics. Comput. Mater. Contin. 2006, 4, 11. [Google Scholar]
- Sokolowski, M. Theory of Couple-Stresses in Bodies with Constrained Rotations; Number 26 in CISM International Centre for Mechanical Sciences; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar]
- Masiani, R.; Trovalusci, P. Cosserat and Cauchy materials as continuum models of brick masonry. Meccanica 1996, 31, 421–432. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple Stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Buckling analysis of cantilever carbon nanotubes using the strain gradient elasticity and modified couple stress theories. J. Comput. Theor. Nanosci. 2011, 8, 1821–1827. [Google Scholar] [CrossRef]
- Khajueenejad, F.; Ghanbari, J. Internal length parameter and buckling analysis of carbon nanotubes using modified couple stress theory and Timoshenko beam model. Mater. Res. Express 2015, 2, 105009. [Google Scholar] [CrossRef]
- Akbarzadeh Khorshidi, M.; Soltani, D. Nanostructure-dependent dispersion of carbon nanostructures: New insights into the modified couple stress theory. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Liew, K.; Wong, C.; He, X.; Tan, M.; Meguid, S. Nanomechanics of single and multiwalled carbon nanotubes. Phys. Rev. B 2004, 69, 115429. [Google Scholar] [CrossRef]
- Wang, L.; Hu, H.; Guo, W. Validation of the non-local elastic shell model for studying longitudinal waves in single-walled carbon nanotubes. Nanotechnology 2006, 17, 1408. [Google Scholar] [CrossRef]
- Nowacki, W. Theory of Asymmetric Elasticity; Elsevier Science & Technology: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Altenbach, H.; Eremeyev, V. Cosserat Media. In Generalized Continua from the Theory to Engineering Applications; Altenbach, H., Eremeyev, V.A., Eds.; Springer: Vienna, Austria, 2013; pp. 65–130. [Google Scholar]
- Eremeyev, V.A.; Pietraszkiewicz, W. Material symmetry group and constitutive equations of micropolar anisotropic elastic solids. Math. Mech. Solids 2016, 21, 210–221. [Google Scholar] [CrossRef]
- Gauthier, R.; Jahsman, W. A quest for micropolar elastic constants. J. Appl. Mech. 1975, 42, 369–374. [Google Scholar] [CrossRef]
- Lakes, R. Experimental Methods for Study of Cosserat Elastic Solids and Other Generalized Elastic Continua. In Continuum Models for Materials with Microstructure; Muhlhaus, H., Ed.; Wiley: New York, NY, USA, 1995; pp. 1–22. [Google Scholar]
- Arash, B.; Wang, O.; Varadan, V.K. Mechanical properties of carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Frankland, S.; Harik, V.; Odegard, G.; Brenner, D.; Gates, T. The stress-strain behavior of polymer-nanotube composites from molecular dynamics simulation. Compos. Sci. Technol. 2003, 63, 1655–1661. [Google Scholar] [CrossRef]
- Tsai, J.L.; Tzeng, S.H.; Chiu, Y.T. Characterizing elastic properties of carbon nanotubes/polyimide nanocomposites using multi-scale simulation. Compos. B Eng. 2010, 41, 106–115. [Google Scholar] [CrossRef]
- Malagù, M.; Goudarzi, M.; Lyulin, A.; Benvenuti, E.; Simone, A. Diameter-dependent elastic properties of carbon nanotube-polymer composites: Emergence of size effects from atomistic-scale simulations. Compos. B Eng. 2017, 131, 260–281. [Google Scholar] [CrossRef]
- Hamada, N.; Sawada, S.I.; Oshiyama, A. New one-dimensional conductors: Graphitic microtubules. Phys. Rev. Lett. 1992, 68, 1579–1581. [Google Scholar] [CrossRef]
- Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Electronic structure of chiral graphene tubules. Appl. Phys. Lett. 1992, 60, 2204–2206. [Google Scholar] [CrossRef]
- Boumia, L.; Zidour, M.; Benzair, A.; Tounsi, A. A Timoshenko beam model for vibration analysis of chiral single-walled carbon nanotubes. Phys. E Low Dimens. Syst. Nanostruct. 2014, 59, 186–191. [Google Scholar] [CrossRef]
- Rafii-Tabar, H.; Ghavanloo, E.; Fazelzadeh, S.A. Nonlocal continuum-based modeling of mechanical characteristics of nanoscopic structures. Phys. Rep. 2016, 638, 1–97. [Google Scholar] [CrossRef]
- Chowdhury, A. Comprehensive Molecular Dynamics Simulations of Carbon Nanotubes under Axial Force or Torsion or Vibration and New Continuum Models. Ph.D. Thesis, National University of Singapore, Singapore, 2014. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD-Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1996, 117, 1–19. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies in molecular dynamics. I. General method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Studies in molecular dynamics. II. Behavior of a small number of elastic spheres. J. Chem. Phys. 1960, 33, 1439–1451. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. Molecular Dynamics: With Deterministic and Stochastic Numerical Methods; Interdisciplinary Applied Mathematics; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Stuart, S.; Tutein, A.; Harrison, J. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Taliercio, A. Torsion of micropolar hollow circular cylinders. Mech. Res. Commun. 2010, 37, 406–411. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of micropolar elasticity. J. Appl. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Andrews, L. Society of Photo-Optical Instrumentation Engineers. Special Functions of Mathematics for Engineers; Oxford Science Publications, SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Trovalusci, P.; Masiani, R. Material symmetries of micropolar continua equivalent to lattices. Int. J. Solids Struct. 1999, 36, 2091–2108. [Google Scholar] [CrossRef]
- Trovalusci, P.; Masiani, R. Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int. J. Solids Struct. 2003, 40, 1281–1297. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Vodenitcharova, T.; Zhang, L. Effective wall thickness of a single-walled carbon nanotube. Phys. Rev. B 2003, 68, 165401. [Google Scholar] [CrossRef]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programming. In Traces and Emergence of Nonlinear Programming; Springer: Berlin/Heidelberg, Germany, 2014; pp. 247–258. [Google Scholar]
- Khoei, A.; Ban, E.; Banihashemi, P.; Qomi, M.A. Effects of temperature and torsion speed on torsional properties of single-walled carbon nanotubes. Mater. Sci. Eng. C 2011, 31, 452–457. [Google Scholar] [CrossRef]
- Hall, A.; An, L.; Liu, J.; Vicci, L.; Falvo, M.; Superfine, R.; Washburn, S. Experimental measurement of single-wall carbon nanotube torsional properties. Phys. Rev. Lett. 2006, 96, 256102. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E.; Yakobson, B.I. C 2 F, BN, and C nanoshell elasticity from ab initio computations. Phys. Rev. B 2001, 64, 235406. [Google Scholar] [CrossRef]







| Chirality (m,n) | Diameter (Å) | Length L (Å) | Torsional Stiffness K (nN·nm) | Critical Angle (rad) | |
|---|---|---|---|---|---|
| armchair | (5,5) | 6.78 | 32.80 | 10.801 | 0.726 |
| (6,6) | 8.09 | 40.06 | 14.877 | 0.600 | |
| (7,7) | 9.42 | 47.29 | 19.576 | 0.528 | |
| (8,8) | 10.74 | 54.56 | 24.863 | 0.468 | |
| (9,9) | 12.07 | 61.80 | 30.785 | 0.420 | |
| (10,10) | 13.40 | 66.61 | 38.678 | 0.396 | |
| (11,11) | 14.73 | 73.87 | 45.845 | 0.372 | |
| (12,12) | 16.06 | 81.12 | 53.613 | 0.354 | |
| zigzag | (8,0) | 6.33 | 30.62 | 9.511 | 0.798 |
| (10,0) | 7.84 | 39.03 | 13.662 | 0.654 | |
| (12,0) | 9.36 | 47.44 | 18.602 | 0.546 | |
| (14,0) | 10.89 | 53.02 | 25.716 | 0.432 | |
| (16,0) | 12.42 | 61.40 | 32.304 | 0.384 | |
| (18,0) | 13.95 | 68.38 | 40.312 | 0.336 | |
| (20,0) | 15.48 | 78.19 | 47.621 | 0.300 | |
| (21,0) | 16.25 | 82.38 | 51.759 | 0.288 |
| Parameter | G | N | h | norm () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Unit | GPa | Å | - | - | Å | nN | nN | GPa | GPa | - |
| Armchair | 1177 | 2.3 | 1.5 | 0.15 | 1.032 | −43 | 129 | 1152 | 51 | 0.0039 |
| Zigzag | 1016 | 3.7 | 1.49 | 0.19 | 1.035 | −94 | 285 | 979 | 74 | 0.0039 |
| Parameter | G | h | norm () | |
|---|---|---|---|---|
| Unit | GPa | Å | Å | - |
| Armchair | 1168 | 0.6 | 1.14 | 0.02 |
| Zigzag | 1190 | 0.9 | 1.05 | 0.03 |
| Parameter | G | h | norm () |
|---|---|---|---|
| Unit | GPa | Å | - |
| Armchair | 1330 | 1.032 | 0.06 |
| Zigzag | 1278 | 1.035 | 0.11 |
| Parameter | G | N | norm () | ||
|---|---|---|---|---|---|
| Unit | GPa | Å | - | - | - |
| Micropolar | |||||
| Armchair | 214 | 5.5 | 1.4 | 0.7 | 0.0022 |
| Zigzag | 184 | 6 | 1.4 | 0.7 | 0.0043 |
| Couple stress | |||||
| Armchair | 459 | 2.4 | - | - | 0.01 |
| Zigzag | 418 | 2.5 | - | - | 0.012 |
| Cauchy | |||||
| Armchair | 891 | - | - | - | 0.78 |
| Zigzag | 825 | - | - | - | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izadi, R.; Tuna, M.; Trovalusci, P.; Ghavanloo, E. Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials 2021, 11, 453. https://doi.org/10.3390/nano11020453
Izadi R, Tuna M, Trovalusci P, Ghavanloo E. Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials. 2021; 11(2):453. https://doi.org/10.3390/nano11020453
Chicago/Turabian StyleIzadi, Razie, Meral Tuna, Patrizia Trovalusci, and Esmaeal Ghavanloo. 2021. "Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation" Nanomaterials 11, no. 2: 453. https://doi.org/10.3390/nano11020453
APA StyleIzadi, R., Tuna, M., Trovalusci, P., & Ghavanloo, E. (2021). Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials, 11(2), 453. https://doi.org/10.3390/nano11020453







