Optical Spin Hall Effect in Closed Elliptical Plasmonic Nanoslit with Noncircular Symmetry
Abstract
:1. Introduction
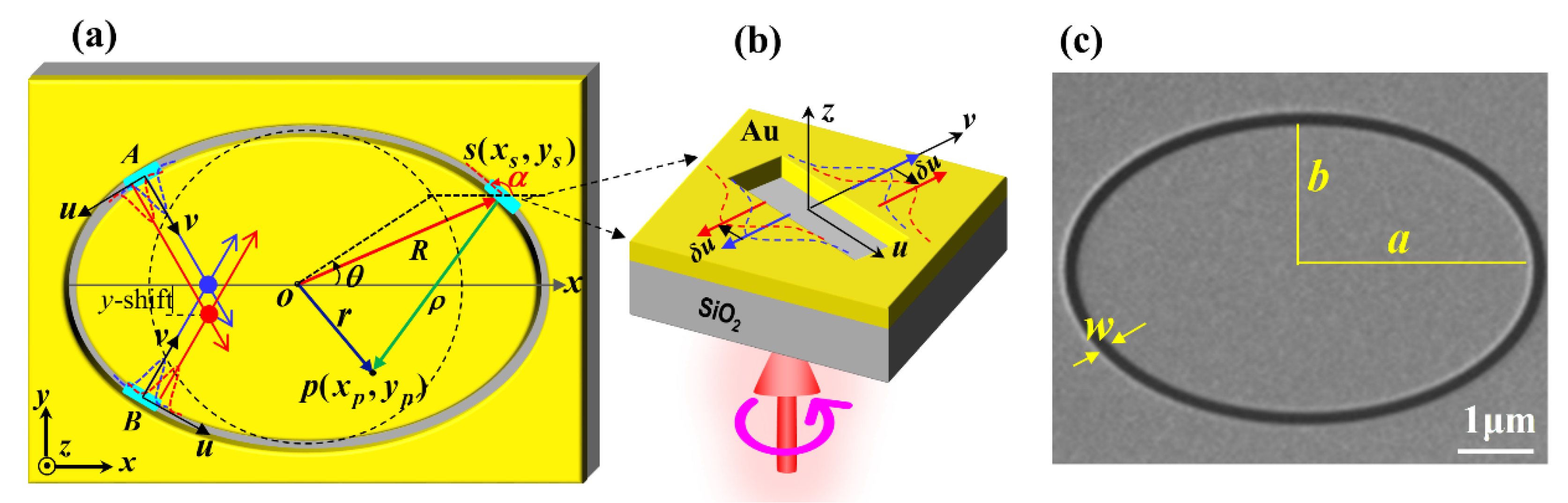
2. Theoretical Analysis of OSHE Produced by an Elliptical Curvilinear Nanoslit
2.1. Plasmonic Wave Field Based on the Incident and Converted Spin Components
2.2. Characteristic Spot Shifts Depending on the Geometric Phase Gradient
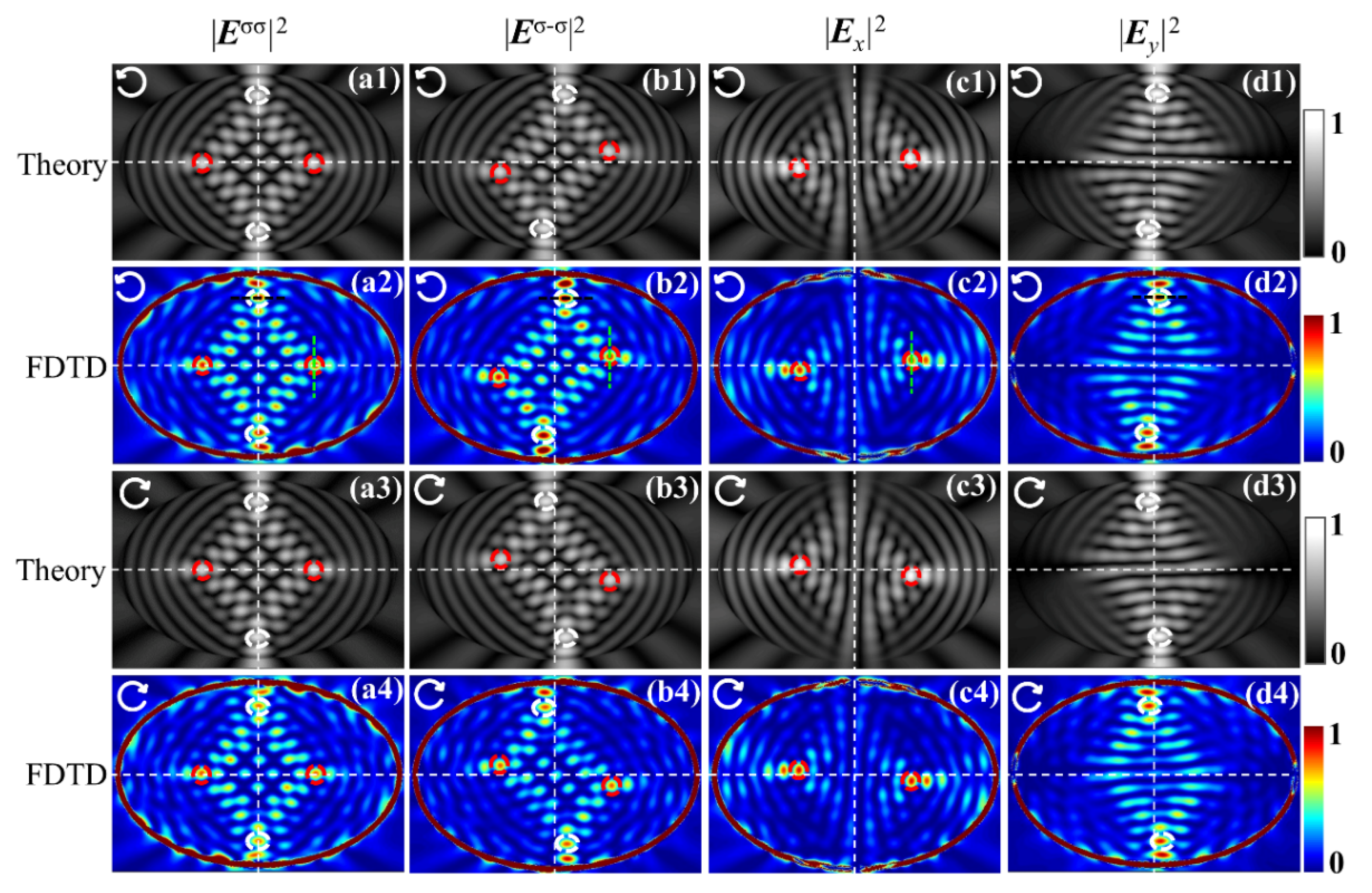
3. Simulations and Discussions
3.1. Centrosymmetric Spot Shifts of OSHE Related to the Noncircular Symmetry of Elliptical Slit
3.2. Conservation of Angular Momentum in SOIs with the Slit
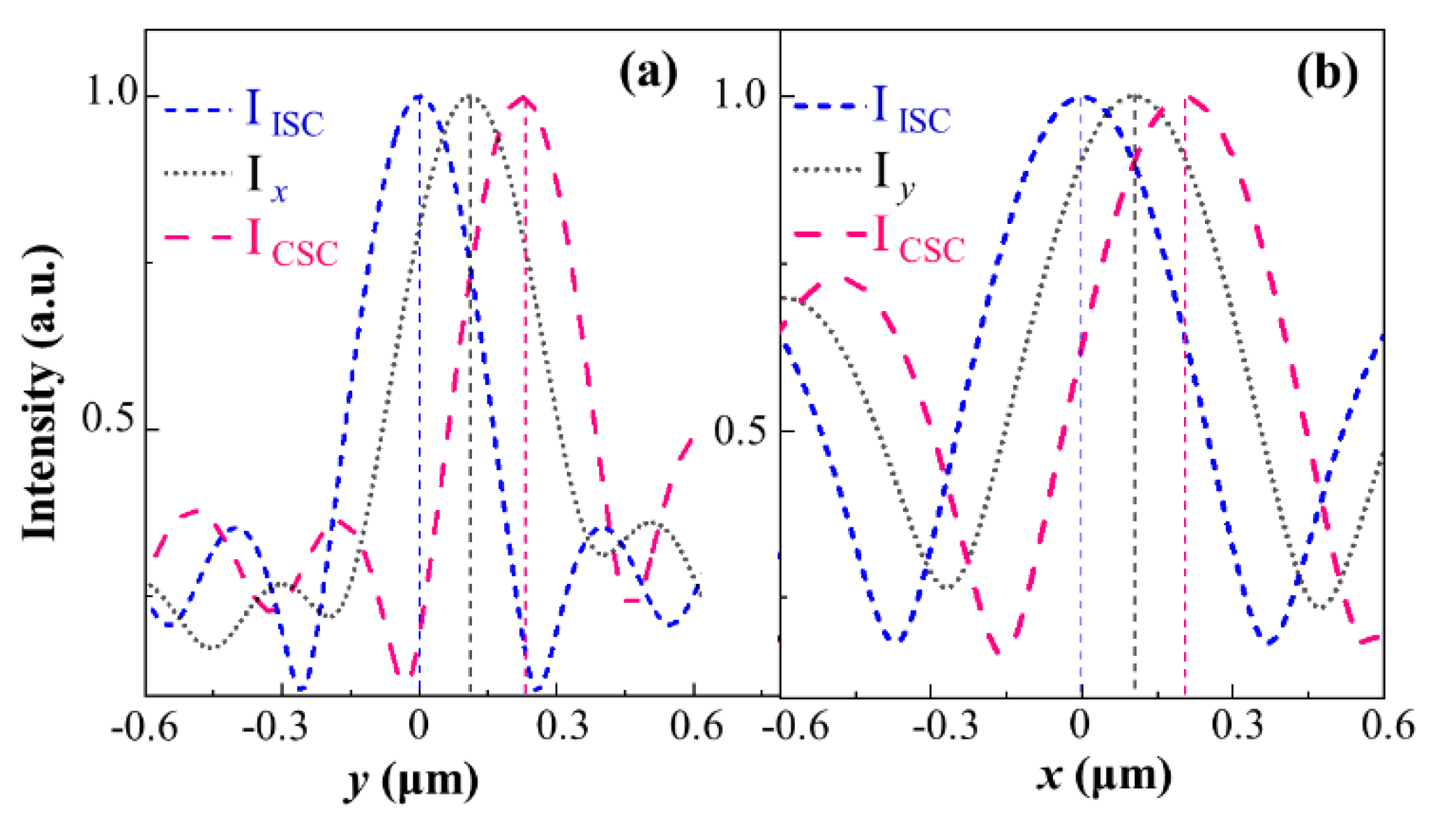
3.3. Variation of the Spots and the Shifts with the Observation Distance
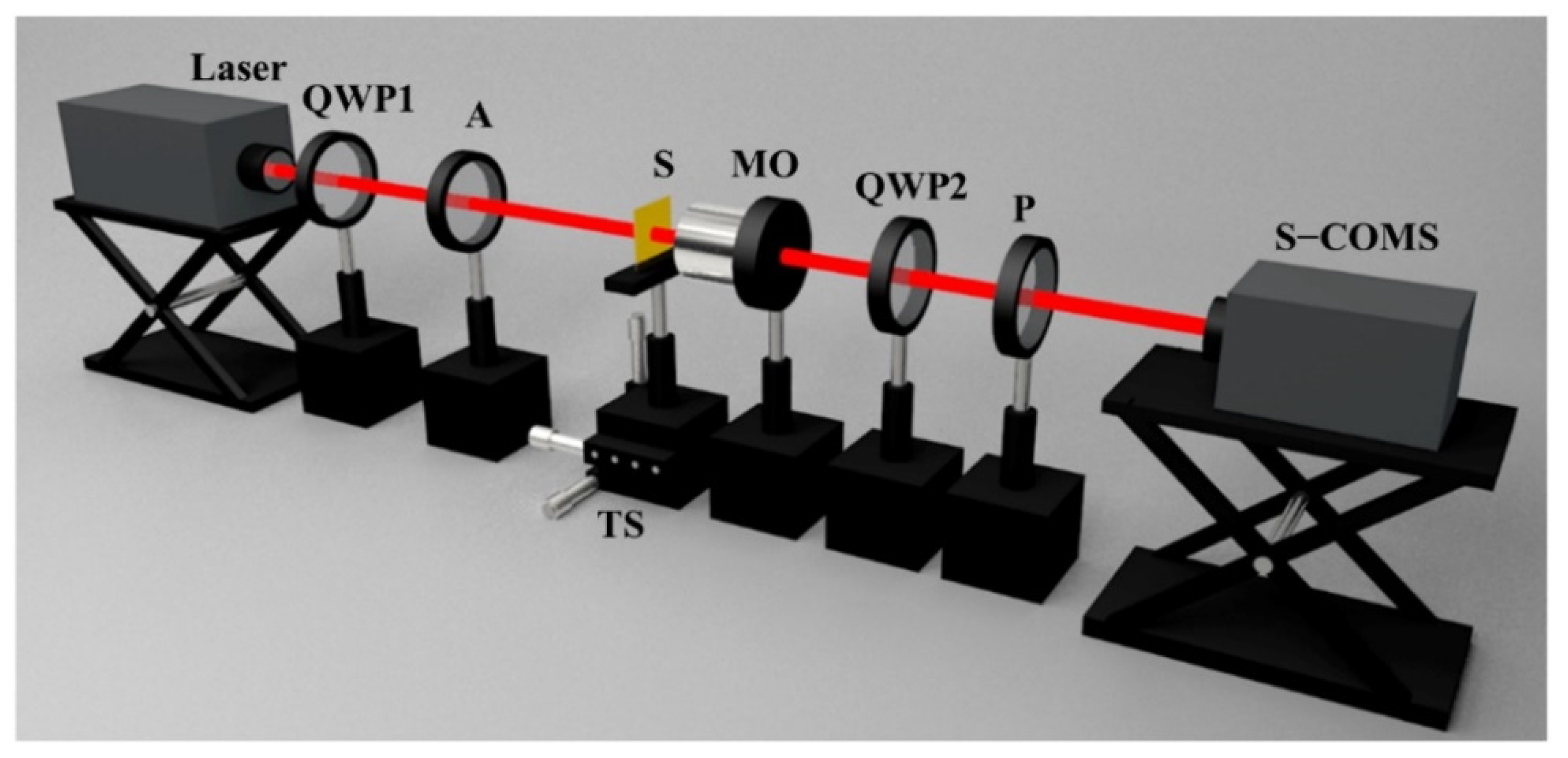
4. Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bliokh, K.Y.; Bliokh, Y.P. Conservation of angular momentum, transverse shift, and spin Hall effect in reflection and refraction of an electromagnetic wave packet. Phys. Rev. Lett. 2006, 96, 073903. [Google Scholar] [CrossRef] [Green Version]
- Kammann, E.; Liew, T.C.; Ohadi, H.; Cilibrizzi, P.; Tsotsis, P.; Hatzopoulos, Z.; Savvidis, P.G.; Kavokin, A.V.; Lagoudakis, P.G. Nonlinear optical spin Hall effect and long-range spin transport in polariton lasers. Phys. Rev. Lett. 2012, 109, 036404. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic spin Hall effect at metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef] [Green Version]
- Shaltout, A.; Liu, J.; Kildishev, A.; Shalaev, V. Photonic spin Hall effect in gap–plasmon metasurfaces for on-chip chiroptical spectroscopy. Optica 2015, 2, 860–863. [Google Scholar] [CrossRef]
- Sharma, D.K.; Kumar, V.; Vasista, A.B.; Chaubey, S.K.; Kumar, G.V.P. Spin-Hall effect in the scattering of structured light from plasmonic nanowire. Opt. Lett. 2018, 43, 2474–2477. [Google Scholar] [CrossRef] [Green Version]
- Bardon-Brun, T.; Delande, D.; Cherroret, N. Spin Hall Effect of light in a random medium. Phys. Rev. Lett. 2019, 123, 043901. [Google Scholar] [CrossRef] [Green Version]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef] [Green Version]
- Chiao, R.Y.; Wu, Y.S. Manifestations of Berry’s topological phase for the photon. Phys. Rev. Lett. 1986, 57, 933–936. [Google Scholar] [CrossRef]
- Berry, M.V. The Adiabatic Phase and Pancharatnam’s Phase for Polarized Light. J. Mod. Opt. 1987, 34, 1401–1407. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef] [Green Version]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Muhlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Song, E.-Y.; Lee, S.-Y.; Hong, J.; Lee, K.; Lee, Y.; Lee, G.-Y.; Kim, H.; Lee, B. A double-lined metasurface for plasmonic complex-field generation. Laser Photonics Rev. 2016, 10, 299–306. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Ke, Y.; Luo, H.; Wen, S. Generation of Airy vortex and Airy vector beams based on the modulation of dynamic and geometric phases. Opt. Lett. 2015, 40, 3193–3196. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Chen, P.; Tang, J.; Duan, W.; Ge, S.-J.; Ma, L.-L.; Wu, R.-X.; Hu, W.; Lu, Y.-Q. Perfect higher-order Poincaré sphere beams from digitalized geometric phases. Phys. Rev. Appl. 2018, 10, 034061. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Ma, L.; Zeng, X.; Li, X.; Zhan, Z.; Ren, X.; He, C.; Liu, C.; Cheng, C. Nanoscale optical lattices of arbitrary orders manipulated by plasmonic metasurfaces combining geometrical and dynamic phases. Nanoscale 2019, 11, 14024–14031. [Google Scholar] [CrossRef]
- Berry, M.V. Interpreting the anholonomy of coiled light. Nature 1987, 326, 277–278. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Coriolis effect in optics: Unified geometric phase and spin-Hall effect. Phys. Rev. Lett. 2008, 101, 030404. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Ge, S.-J.; Duan, W.; Wei, B.-Y.; Cui, G.-X.; Hu, W.; Lu, Y.-Q. Digitalized geometric phases for parallel optical spin and orbital angular momentum encoding. ACS Photonics 2017, 4, 1333–1338. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Zeng, X.Y.; Zhang, R.R.; Zhan, Z.J.; Li, X.; Ma, L.; Liu, C.X.; He, C.W.; Cheng, C.F. Generation of a plasmonic radially polarized vector beam with linearly polarized illumination. Opt. Lett. 2018, 43, 4208–4211. [Google Scholar] [CrossRef]
- Hosten, O.; Kwiat, P. Observation of the spin hall effect of light via weak measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, Y.; Li, Y.; He, H.; Gong, Q. Measurement of spin Hall effect of reflected light. Opt. Lett. 2009, 34, 2551–2553. [Google Scholar] [CrossRef] [PubMed]
- Gorodetski, Y.; Bliokh, K.Y.; Stein, B.; Genet, C.; Shitrit, N.; Kleiner, V.; Hasman, E.; Ebbesen, T.W. 25 Weak measurements of light chirality with a plasmonic slit. Phys. Rev. Lett. 2012, 109, 013901. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.Y.; Niv, A.; Kleiner, V.; Hasman, E. Geometrodynamics of spinning light. Nat. Photonics 2008, 2, 748–753. [Google Scholar] [CrossRef]
- Mei, S.; Huang, K.; Liu, H.; Qin, F.; Mehmood, M.Q.; Xu, Z.; Hong, M.; Zhang, D.; Teng, J.; Danner, A.; et al. On-chip discrimination of orbital angular momentum of light with plasmonic nanoslits. Nanoscale 2016, 8, 2227–2233. [Google Scholar] [CrossRef]
- Ren, H.; Li, X.; Zhang, Q.; Gu, M. On-chip noninterference angular momentum multiplexing of broadband light. Science 2016, 352, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.; Li, X.; Wang, G.; Liu, S.; Zhang, L.; Zeng, C.; Wang, L.; Sun, Q.; Zhao, W.; Zhang, W. Multidimensional manipulation of photonic spin hall effect with a single-layer dielectric metasurface. Adv. Opt. Mater. 2018, 7, 1801365. [Google Scholar] [CrossRef]
- Zhu, T.; Lou, Y.; Zhou, Y.; Zhang, J.; Huang, J.; Li, Y.; Luo, H.; Wen, S.; Zhu, S.; Gong, Q.; et al. generalized spatial differentiation from the spin hall effect of light and its application in image processing of edge detection. Phys. Rev. Appl. 2019, 11, 034043. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Herrera, O.G.; Lara, D.; Bliokh, K.Y.; Ostrovskaya, E.A.; Dainty, C. Optical nanoprobing via spin-orbit interaction of light. Phys. Rev. Lett. 2010, 104, 253601. [Google Scholar] [CrossRef]
- Kruk, S.S.; Decker, M.; Staude, I.; Schlecht, S.; Greppmair, M.; Neshev, D.N.; Kivshar, Y.S. Spin-polarized photon emission by resonant multipolar nanoantennas. ACS Photonics 2014, 1, 1218–1223. [Google Scholar] [CrossRef]
- Luo, X.G.; Pu, M.B.; Li, X.; Ma, X.L. Broadband spin Hall effect of light in single nanoapertures. Light Sci. Appl. 2017, 6, e16276. [Google Scholar] [CrossRef]
- Shitrit, N.; Bretner, I.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Optical spin Hall effects in plasmonic chains. Nano Lett. 2011, 11, 2038–2042. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [Green Version]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yi, X.; Liu, Y.; Ling, X.; Zhou, X.; Ke, Y.; Luo, H.; Wen, S.; Fan, D. Hybrid-order Poincaré sphere. Phys. Rev. A 2015, 91, 023801. [Google Scholar] [CrossRef] [Green Version]
- Gorodetski, Y.; Niv, A.; Kleiner, V.; Hasman, E. Observation of the spin-based plasmonic effect in nanoscale structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef] [Green Version]
- Milione, G.; Evans, S.; Nolan, D.A.; Alfano, R.R. Higher order Pancharatnam-Berry phase and the angular momentum of light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gao, Y.; Jiang, S.; Ma, L.; Liu, C.; Cheng, C. Experimental solution for scattered imaging of the interference of plasmonic and photonic mode waves launched by metal nano-slits. Opt. Express 2015, 23, 3507–3522. [Google Scholar] [CrossRef] [PubMed]
- Ling, X.; Zhou, X.; Yi, X.; Shu, W.; Liu, Y.; Chen, S.; Luo, H.; Wen, S.; Fan, D. Giant photonic spin Hall effect in momentum space in a structured metamaterial with spatially varying birefringence. Light Sci. Appl. 2015, 4, e290. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin–orbit interactions of light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Zeng, X.; Liu, C.; Cheng, C.; Zhang, R.; Zhang, Y.; Zhan, Z.; Kong, Q.; Sun, R.; Cheng, C. Optical Spin Hall Effect in Closed Elliptical Plasmonic Nanoslit with Noncircular Symmetry. Nanomaterials 2021, 11, 851. https://doi.org/10.3390/nano11040851
Ren X, Zeng X, Liu C, Cheng C, Zhang R, Zhang Y, Zhan Z, Kong Q, Sun R, Cheng C. Optical Spin Hall Effect in Closed Elliptical Plasmonic Nanoslit with Noncircular Symmetry. Nanomaterials. 2021; 11(4):851. https://doi.org/10.3390/nano11040851
Chicago/Turabian StyleRen, Xiaorong, Xiangyu Zeng, Chunxiang Liu, Chuanfu Cheng, Ruirui Zhang, Yuqin Zhang, Zijun Zhan, Qian Kong, Rui Sun, and Chen Cheng. 2021. "Optical Spin Hall Effect in Closed Elliptical Plasmonic Nanoslit with Noncircular Symmetry" Nanomaterials 11, no. 4: 851. https://doi.org/10.3390/nano11040851
APA StyleRen, X., Zeng, X., Liu, C., Cheng, C., Zhang, R., Zhang, Y., Zhan, Z., Kong, Q., Sun, R., & Cheng, C. (2021). Optical Spin Hall Effect in Closed Elliptical Plasmonic Nanoslit with Noncircular Symmetry. Nanomaterials, 11(4), 851. https://doi.org/10.3390/nano11040851




