Holey Graphene: Topological Control of Electronic Properties and Electric Conductivity
Abstract
:1. Introduction
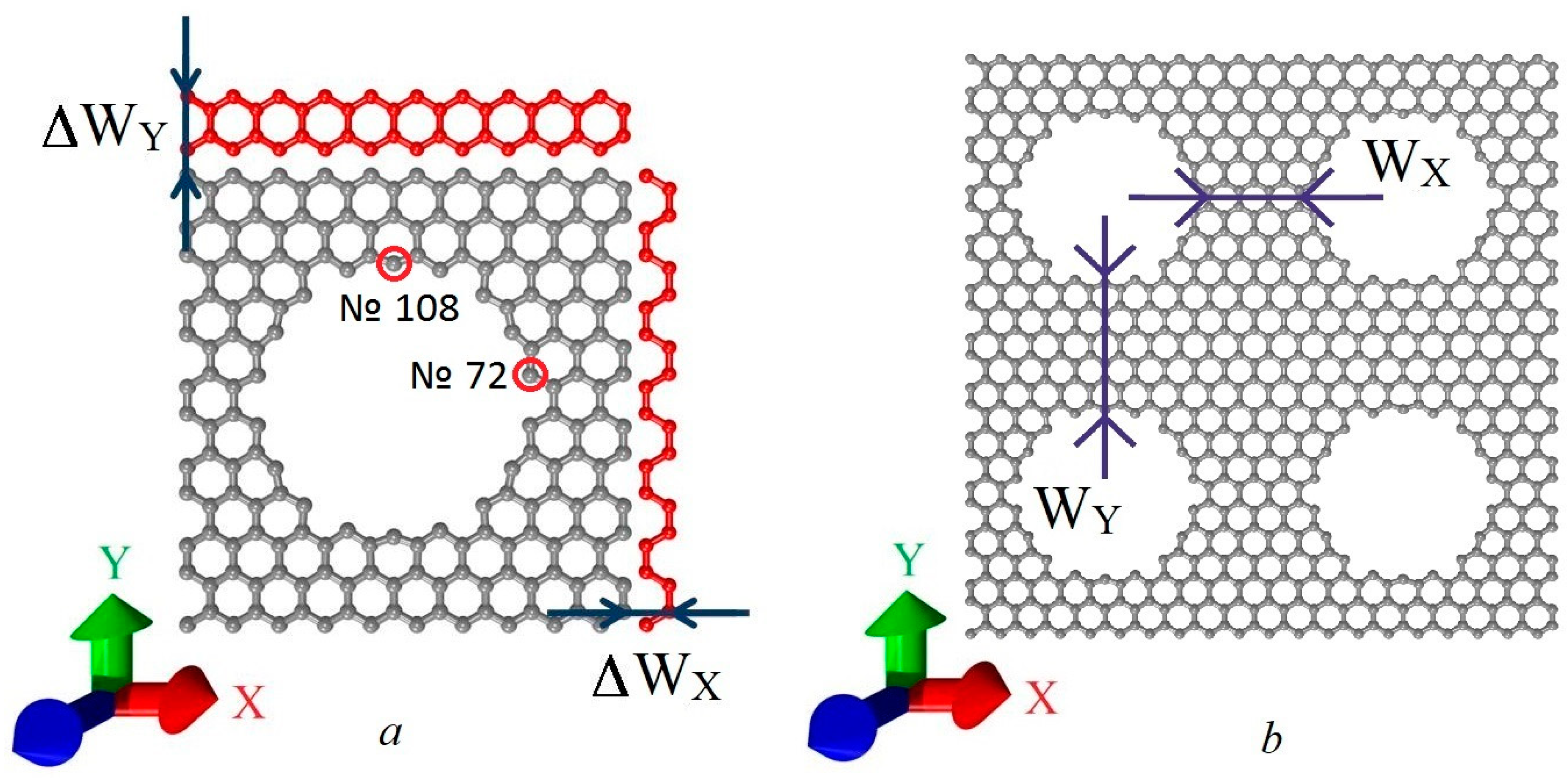
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, Y.; Liao, Y.; Chen, Z.; Connell, J.W. Holey graphene: A unique structural derivative of graphene. Mater. Res. Lett. 2017, 5, 209–234. [Google Scholar] [CrossRef]
- Bai, J.; Zhong, X.; Jiang, S.; Duan, X. Graphene nanomesh. Nat. Nanotechnol. 2010, 5, 190–194. [Google Scholar] [CrossRef]
- Kim, M.; Safron, N.S.; Han, E.; Arnold, M.S.; Gopalan, P. Fabrication and characterization of large-area, semiconducting nanoperforated graphene materials. Nano Lett. 2010, 10, 1125–1131. [Google Scholar] [CrossRef]
- Han, T.H.; Huang, Y.-K.; Tan, A.T.L.; Dravid, V.P.; Huang, J. Steam etched porous graphene oxide network for chemical sensing. J. Am. Chem. Soc. 2011, 133, 15264–15267. [Google Scholar] [CrossRef]
- Zhao, X.; Hayner, C.M.; Kung, M.C.; Kung, H.H. In-plane vacancy-enabled high-power Si-graphene composite electrode for lithium-ion batteries. Adv. Energy Mater. 2011, 1, 1079–1084. [Google Scholar] [CrossRef]
- Han, X.; Funk, M.R.; Shen, F.; Chen, Y.-C.; Li, Y.; Campbell, C.J.; Dai, J.; Yang, X.; Kim, J.-W.; Liao, Y.; et al. Scalable holey graphene synthesis and dense electrode fabrication toward high-performance ultracapacitors. ACS Nano 2014, 8, 8255–8265. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Lin, Z.; Zhong, X.; Huang, X.; Weiss, N.O.; Huang, Y.; Duan, X. Holey graphene frameworks for highly efficient capacitive energy storage. Nat. Commun. 2014, 5, 4554. [Google Scholar] [CrossRef] [PubMed]
- Shim, W.; Kwon, Y.; Jeon, S.; Yu, W.-R. Optimally conductive networks in randomly dispersed CNT: Graphene hybrids. Sci. Rep. 2015, 5, 16568. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Han, X.; Campbell, C.J.; Kim, J.-W.; Zhao, B.; Luo, W.; Dai, J.; Hu, L.; Connell, J.W. Holey graphene nanomanufacturing: Structure, composition, and electrochemical properties. Adv. Funct. Mater. 2015, 25, 2920–2927. [Google Scholar] [CrossRef]
- Peng, Y.-Y.; Liu, Y.-M.; Chang, J.-K.; Wu, C.-H.; Ger, M.-D.; Pu, N.-W.; Chang, C.-L. A facile approach to produce holey graphene and its application in supercapacitors. Carbon 2015, 81, 347–356. [Google Scholar] [CrossRef]
- Yang, C.-H.; Huang, P.-L.; Luo, X.-F.; Wang, C.-H.; Li, C.; Wu, Y.-H.; Chang, J.-K. Holey graphene nanosheets with surface functional groups as high performance supercapacitors in ionic-liquid electrolyte. ChemSusChem 2015, 8, 1779–1786. [Google Scholar] [CrossRef]
- Koenig, S.P.; Wang, L.; Pellegrino, J.; Bunch, J.S. Selective molecular sieving through porous graphene. Nat. Nanotechnol. 2012, 7, 728–732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cohen-Tanugi, D.; Grossman, J.C. Water desalination across nanoporous graphene. Nano Lett. 2012, 12, 3602–3608. [Google Scholar] [CrossRef] [PubMed]
- O’Hern, S.C.; Jang, D.; Bose, S.; Idrobo, J.-C.; Song, Y.; Laoui, T.; Kong, J.; Karnik, R. Nanofiltration across defect-sealed nanoporous monolayer graphene. Nano Lett. 2015, 15, 3254–3260. [Google Scholar] [CrossRef] [Green Version]
- Surwade, S.P.; Smirnov, S.N.; Vlassiouk, I.V.; Unocic, R.R.; Veith, G.M.; Dai, S.; Mahurin, S.M. Water desalination using nanoporous single-layer graphene. Nat. Nanotechnol. 2015, 10, 459–464. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Zhang, Z.; Deng, X.; Fan, Z.; Zeng, Y.; Zhou, J. Improved scaling rules for band gaps in graphene nanomeshs. Carbon 2014, 76, 348–356. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Ragab, T.; Basaran, C. Mechanical and electronic properties of graphene nanomesh heterojunctions. Comput. Mater. Sci. 2018, 153, 64–72. [Google Scholar] [CrossRef]
- Kausar, A. Graphene nanomesh and polymeric material at cutting edge. Polymer-Plast. Technol. Mater. 2019, 58, 803–820. [Google Scholar] [CrossRef]
- Yarifard, M.; Davoodi, J.; Rafii-Tabar, H. In-plane thermal conductivity of graphene nanomesh: A molecular dynamics study. Comput. Mater. Sci. 2016, 111, 247–251. [Google Scholar] [CrossRef]
- Yang, H.X.; Chshiev, M.; Boukhvalov, D.W.; Waintal, X.; Roche, S. Inducing and optimizing magnetism in graphene nanomeshes. Phys. Rev. B 2011, 84, 214404. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.; Ekinci, Y.; Gölzhäuser, A.; Turchanin, A. Freestanding carbon nanomembranes and graphene monolayers nanopatterned via EUV interference lithography. 2D Mater. 2019, 6, 21002. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, C.; Christmann, A.M.; Hu, L.; Fampiou, I.; Muniz, A.R.; Ramasubramaniam, A.; Maroudas, D. Elastic properties of graphene nanomeshes. Appl. Phys. Lett. 2014, 104, 141911. [Google Scholar] [CrossRef]
- Park, J.; Prakash, V. Phonon scattering and thermal conductivity of pillared graphene structures with carbon nanotube-graphene intramolecular junctions. J. Appl. Phys. 2014, 116, 14303. [Google Scholar] [CrossRef]
- Qian, H.-J.; Eres, G.; Irle, S. Quantum chemical molecular dynamics simulation of carbon nanotube–graphene fusion. Mol. Simul. 2017, 43, 1269–1276. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Shmygin, D.S.; Zhang, G.; Glukhova, O.E. Controlling anisotropic electrical conductivity in porous graphene-nanotube thin films. Carbon 2020, 165, 139–149. [Google Scholar] [CrossRef]
- Shunaev, V.V.; Glukhova, O.E. Pillared Graphene Structures Supported by Vertically Aligned Carbon Nanotubes as the Potential Recognition Element for DNA Biosensors. Materials 2020, 13, 5219. [Google Scholar] [CrossRef] [PubMed]
- Keldysh, L.V. Diagram Technique for Nonequilibrium Processes. JETP 1965, 20, 1018–1026. [Google Scholar]
- Datta, S. Quantum Transport: Atom to Transistor, 1st ed.; Cambridge University Press: Cambridge, UK, 2005; p. 404. [Google Scholar]
- Glukhova, O.E. Molecular Dynamics as the Tool for Investigation of Carbon Nanostructures Properties. In Thermal Transport in Carbon-Based Nanomaterials, 1st ed.; Gang, Z., Ed.; Elsiver: Amsterdam, The Netherlands, 2017; Volume 10, pp. 267–290. [Google Scholar]
- Glukhova, O.E. Classification of the Achiral Tubular Nanoclusters. In Carbon Nanotubes: Synthesis and Properties, 1st ed.; Mishra, A.K., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2012; Volume 15, pp. 319–336. [Google Scholar]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Kohn, W. Elektronnaya struktura veshchestva—volnovye funkcii i funkcionaly plotnosti. UFN 2002, 172, 336–348. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry, 3rd ed.; Wiley & Sons: Hoboken, NJ, USA, 2017; p. 620. [Google Scholar]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods, 1st ed.; Cambridge University Press: Cambridge, UK, 2004; p. 640. [Google Scholar]
- Mulliken, R.S. Electronic population analysis on LCAO-MO molecular wave functions. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef] [Green Version]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a Sparse Matrix-Based Implementation of the DFTB Method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barkov, P.V.; Glukhova, O.E. Holey Graphene: Topological Control of Electronic Properties and Electric Conductivity. Nanomaterials 2021, 11, 1074. https://doi.org/10.3390/nano11051074
Barkov PV, Glukhova OE. Holey Graphene: Topological Control of Electronic Properties and Electric Conductivity. Nanomaterials. 2021; 11(5):1074. https://doi.org/10.3390/nano11051074
Chicago/Turabian StyleBarkov, Pavel V., and Olga E. Glukhova. 2021. "Holey Graphene: Topological Control of Electronic Properties and Electric Conductivity" Nanomaterials 11, no. 5: 1074. https://doi.org/10.3390/nano11051074
APA StyleBarkov, P. V., & Glukhova, O. E. (2021). Holey Graphene: Topological Control of Electronic Properties and Electric Conductivity. Nanomaterials, 11(5), 1074. https://doi.org/10.3390/nano11051074






