In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films
Abstract
:1. Introduction
2. Theoretical Models
2.1. A Collection of Mixing Rules
2.2. Thin Film Calculations
2.3. In Situ Photoacoustics
3. Experimental Section
3.1. Porous Silicon Fabrication
Reflectance Spectrometry
4. Results
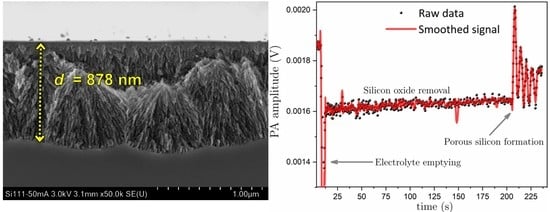
4.1. In Situ Photoacoustic
4.2. Morphological Characterization
4.3. Optical Characterization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. In Situ Photoacoustic Signals during PSi Fabrication


References
- Ramirez-Gutierrez, C.; Castaño-Yepes, J.; Rodriguez-Garcia, M. Porosity and roughness determination of porous silicon thin films by genetic algorithms. Optik 2018, 173, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Cisneros, R.; Pfeiffer, H.; Wang, C. Oxygen Absorption in Free-Standing Porous Silicon: A Structural, Optical and Kinetic Analysis. Nanoscale Res. Lett. 2010, 5, 686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sailor, M.J. Porous Silicon in Practice. In Porous Silicon in Practice; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011; p. 14. [Google Scholar]
- Lujan-Cabrera, I.; Ramirez-Gutierrez, C.; Castaño-Yepes, J.; Rodriguez-Garcia, M. Effects of the interface roughness in the optical response of one-dimensional photonic crystals of porous silicon. Phys. B Condens. Matter 2019, 560, 133–139. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Castaño Yepes, J.D.; Rodriguez-Garcia, M.E. Optical interferometry and photoacoustics as in-situ techniques to characterize the porous silicon formation: A review. Open Mater. Sci. 2018, 4, 23–32. [Google Scholar] [CrossRef]
- Ariza-Flores, A.D.; Gaggero-Sager, L.M.; Agarwal, V. White metal-like omnidirectional mirror from porous silicon dielectric multilayers. Appl. Phys. Lett. 2012, 101, 031119. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Martinez-Hernandez, H.D.; Lujan-Cabrera, I.A.; Rodriguez-García, M.E. Design, fabrication, and optical characterization of one-dimensional photonic crystals based on porous silicon assisted by in-situ photoacoustics. Sci. Rep. 2019, 9, 14732. [Google Scholar] [CrossRef] [PubMed]
- Moretta, R.; De Stefano, L.; Terracciano, M.; Rea, I. Porous Silicon Optical Devices: Recent Advances in Biosensing Applications. Sensors 2021, 21, 1336. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Castaño Yepes, J.D.; Rodriguez-Garcia, M.E. In situ photoacoustic characterization for porous silicon growing: Detection principles. J. Appl. Phys. 2016, 119, 185103. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Gutierrez, C.F.; Castaño-Yepes, J.D.; Rodriguez-García, M.E. Modeling the Photoacoustic Signal During the Porous Silicon Formation. J. Appl. Phys. 2017, 121, 025103. [Google Scholar] [CrossRef] [Green Version]
- Gelloz, B.; Fuwa, H.; Jin, L. Measurement of Optical Constants of Wet Porous Silicon Using In Situ Photoconduction. ECS J. Solid State Sci. Technol. 2016, 5, P190–P196. [Google Scholar] [CrossRef]
- Isaiev, M.; Wang, X.; Termentzidis, K.; Lacroix, D. Thermal transport enhancement of hybrid nanocomposites; impact of confined water inside nanoporous silicon. Appl. Phys. Lett. 2020, 117, 033701. [Google Scholar] [CrossRef]
- Dubyk, K.; Nychyporuk, T.; Lysenko, V.; Termentzidis, K.; Castanet, G.; Lemoine, F.; Lacroix, D.; Isaiev, M. Thermal properties study of silicon nanostructures by photoacoustic techniques. J. Appl. Phys. 2020, 127, 225101. [Google Scholar] [CrossRef]
- Dubyk, K.; Chepela, L.; Lishchuk, P.; Belarouci, A.; Lacroix, D.; Isaiev, M. Features of photothermal transformation in porous silicon based multilayered structures. Appl. Phys. Lett. 2019, 115, 021902. [Google Scholar] [CrossRef] [Green Version]
- Ruíz-Pérez, A.D.; de la Mora, M.B.; Benítez, J.L.; Castañeda-Guzmán, R.; Reyes-Esqueda, J.A.; Villagrán-Muniz, M. In situ study of porous silicon thin films thermal oxidation by pulsed laser photoacoustics. Semicond. Sci. Technol. 2018, 33, 085001. [Google Scholar] [CrossRef]
- Pap, A.E.; Kordás, K.; Vähäkangas, J.; Uusimäki, A.; Leppävuori, S.; Pilon, L.; Szatmári, S. Optical properties of porous silicon. Part III: Comparison of experimental and theoretical results. Opt. Mater. 2006, 28, 506–513. [Google Scholar] [CrossRef]
- Králik, M.; Goraus, M.; Pinčík, E. Optical properties of electrochemically etched N-type silicon wafers for solar cell applications. J. Electr. Eng. 2000, 71, 406–412. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory Principles and Applications; Oxford University Press: Oxford, UK, 2016; pp. 1–24. [Google Scholar]
- Humlicek, J. Data Analysis for Nanomaterials: Effective Medium Approximation, Its Limits and Implementations; Springer: Berlin/Heidelberg, Germany, 2013; pp. 145–178. [Google Scholar]
- Markel, V.A. Introduction to the Maxwell Garnett approximation: Tutorial. J. Opt. Soc. Am. A 2016, 33, 1244–1256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Rep. 2008, 63, 1–30. [Google Scholar] [CrossRef]
- Looyenga, H. Dielectric constants of heterogeneous mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Krzyżanowska, H.; Kulik, M.; Żuk, J. Ellipsometric study of refractive index anisotropy in porous silicon. J. Lumin. 1998, 80, 183–186. [Google Scholar] [CrossRef]
- Arenas, M.C.; Hu, H.; Nava, R.; Del RÍo, J.A. Determination of the complex refractive index of porous silicon layers on crystalline silicon substrates. Int. J. Mod. Phys. B 2010, 24, 4835–4850. [Google Scholar] [CrossRef]
- Lehmann, V.; Stengl, R.; Luigart, A. On the morphology and the electrochemical formation mechanism of mesoporous silicon. Mater. Sci. Eng. B 2000, 69–70, 11–22. [Google Scholar] [CrossRef]
- Guendouz, M.; Joubert, P.; Sarret, M. Effect of crystallographic directions on porous silicon formation on patterned substrates. Mater. Sci. Eng. B 2000, 69–70, 43–47. [Google Scholar] [CrossRef]
- Föll, H.; Carstensen, J.; Christophersen, M.; Hasse, G. A New View of Silicon Electrochemistry. Phys. Status Solidi 2000, 182, 7–16. [Google Scholar] [CrossRef]
- Green, M.A. Self-Consistent Optical Parameters of Intrinsic Silicon at 300K Including Temperature Coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Yan, L.; Chen, B.; Zhang, E.; Zhang, S.; Yang, Y. Precision measurement of refractive index of air based on laser synthetic wavelength interferometry with Edlén equation estimation. Rev. Sci. Instrum. 2015, 86, 085111. [Google Scholar] [CrossRef] [PubMed]
- Mitsas, C.L.; Siapkas, D.I. Generalized matrix method for analysis of coherent and incoherent reflectance and transmittance of multilayer structures with rough surfaces, interfaces, and finite substrates. Appl. Opt. 1995, 34, 1678–1683. [Google Scholar] [CrossRef] [PubMed]
- Missoni, L.L.; Ortiz, G.P.; Martínez Ricci, M.L.; Toranzos, V.J.; Mochán, W.L. Rough 1D photonic crystals: A transfer matrix approach. Opt. Mater. 2020, 109, 110012. [Google Scholar] [CrossRef]
- Poruba, A.; Fejfar, A.; Remeš, Z.; Špringer, J.; Vaněček, M.; Kočka, J.; Meier, J.; Torres, P.; Shah, A. Optical absorption and light scattering in microcrystalline silicon thin films and solar cells. J. Appl. Phys. 2000, 88, 148–160. [Google Scholar] [CrossRef]
- Rosencwaig, A.; Gersho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- Lishchuk, P.; Isaiev, M.; Osminkina, L.; Burbelo, R.; Nychyporuk, T.; Timoshenko, V. Photoacoustic characterization of nanowire arrays formed by metal-assisted chemical etching of crystalline silicon substrates with different doping level. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 107, 131–136. [Google Scholar] [CrossRef]
- Smith, R.L.; Collins, S.D. Porous silicon formation mechanisms. J. Appl. Phys. 1992, 71, R1–R22. [Google Scholar] [CrossRef]
- ImageJ. Available online: https://imagej.net/ParticleSizer (accessed on 11 May 2021).
- Ramirez-Gutierrez, C.F.; Medina-Herrera, A.; Tirado-Mejía, L.; Zubieta-Otero, L.F.; Auciello, O.; Rodriguez-Garcia, M.E. Photoluminescence study of porous p-type silicon: Identification of radiative transitions. J. Lumin. 2018, 201, 11–17. [Google Scholar] [CrossRef]
- Granitzer, P.; Rumpf, K.; Pölt, P.; Reichmann, A.; Krenn, H. Self-assembled mesoporous silicon in the crossover between irregular and regular arrangement applicable for Ni filling. Phys. E Low-Dimens. Syst. Nanostructures 2007, 38, 205–210. [Google Scholar] [CrossRef]
- Golovan, L.A.; Konstantinova, A.F.; Imangazieva, K.B.; Krutkova, E.Y.; Timoshenko, V.Y.; Kashkarov, P.K. Dispersion of optical anisotropy in nanostructurized silicon films. Crystallogr. Rep. 2004. [Google Scholar] [CrossRef]
- Efimova, A.I.; Krutkova, E.Y.; Golovan, L.A.; Timoshenko, V.Y.; Kashkarov, P.K. Effect of form anisotropy of silicon nanocrystals on birefringence and dichroism in porous silicon. Phys. Status Solidi C 2007, 4, 1991–1995. [Google Scholar] [CrossRef]
- Diener, J.; Künzner, N.; Gross, E.; Kovalev, D.; Timoshenko, V.Y.; Fujii, M. The birefringence level of anisotropically nanostructured silicon. Phys. Status Solidi C 2007, 4, 1996–2000. [Google Scholar] [CrossRef]
- Ocier, C.R.; Richards, C.A.; Bacon-Brown, D.A.; Krueger, N.A.; Clawson, M.K.; Soares, J.A.N.T.; Braun, P.V. Optically anisotropic porous silicon microlenses with tunable refractive indexes and birefringence profiles. Opt. Mater. Express 2020, 10, 868–883. [Google Scholar] [CrossRef]










| Sample Name | (mA/cm) | (s) | d (nm) |
|---|---|---|---|
| S5 | 5 | 86.6 | 620 |
| S10 | 10 | 58.0 | 595 |
| S15 | 15 | 46.5 | – |
| S20 | 20 | 39.0 | – |
| S25 | 25 | 29.9 | – |
| S30 | 30 | 29.8 | 804 |
| S35 | 35 | 29.8 | – |
| S40 | 40 | 25.0 | 820 |
| S50 | 50 | 24.0 | 878 |
| S60 | 60 | 23.6 | 720 |
| S70 | 70 | 21.4 | – |
| S80 | 80 | 20.5 | – |
| S90 | 90 | 18.8 | – |
| S100 | 100 | 18.0 | – |
| S110 | 110 | 19.0 | – |
| Sample | EMA Rule | nm | cm | nm | |
|---|---|---|---|---|---|
| S5 | LLL | 0.40 | 622 | 3.3 | 5 |
| BR | 0.42 | 615 | 3.1 | 7 | |
| MG | 0.42 | 606 | 3.4 | 9 | |
| PA | 0.41 | 620 * | - | - | |
| S10 | LLL | 0.39 | 589 | 1.0 | 6 |
| BR | 0.40 | 577 | 0.9 | 9 | |
| MG | 0.40 | 577 | 2.6 | 8 | |
| PA | 0.33 | 595 * | - | - | |
| S30 | LLL | 0.62 | 784 | 3.0 | 9 |
| BR | 0.62 | 783 | 2.6 | 3 | |
| MG | 0.63 | 814 | 2.8 | 10 | |
| PA | 0.61 | 804 * | - | - | |
| S40 | LLL | 0.71 | 810 | 3.5 | 10 |
| BR | 0.69 | 802 | 3.1 | 3 | |
| MG | 0.71 | 821 | 2.8 | 9 | |
| PA | 0.62 | 820 * | |||
| S50 | LLL | 0.77 | 888 | 2.5 | 8 |
| BR | 0.74 | 889 | 3.9 | 3 | |
| MG | 0.78 | 874 | 3.5 | 10 | |
| PA | 0.68 | 878 * | - | - | |
| S60 | LLL | 0.69 | 704 | 2.1 | 3 |
| BR | 0.67 | 723 | 2.4 | 1 | |
| MG | 0.71 | 722 | 4.2 | 10 | |
| PA | 0.58 | 720 * | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez-Gutierrez, C.F.; Lujan-Cabrera, I.A.; Isaza, C.; Anaya Rivera, E.K.; Rodriguez-Garcia, M.E. In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films. Nanomaterials 2021, 11, 1314. https://doi.org/10.3390/nano11051314
Ramirez-Gutierrez CF, Lujan-Cabrera IA, Isaza C, Anaya Rivera EK, Rodriguez-Garcia ME. In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films. Nanomaterials. 2021; 11(5):1314. https://doi.org/10.3390/nano11051314
Chicago/Turabian StyleRamirez-Gutierrez, Cristian Felipe, Ivan Alonso Lujan-Cabrera, Cesar Isaza, Ely Karina Anaya Rivera, and Mario Enrique Rodriguez-Garcia. 2021. "In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films" Nanomaterials 11, no. 5: 1314. https://doi.org/10.3390/nano11051314
APA StyleRamirez-Gutierrez, C. F., Lujan-Cabrera, I. A., Isaza, C., Anaya Rivera, E. K., & Rodriguez-Garcia, M. E. (2021). In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films. Nanomaterials, 11(5), 1314. https://doi.org/10.3390/nano11051314