Structural Disorder and Collective Behavior of Two-Dimensional Magnetic Nanostructures
Abstract
:1. Introduction
2. Methods and Theoretical Background
2.1. Nanostructure Model
2.2. Energy Landscapes
2.3. Kinetic Networks
2.4. Disconnectivity Graphs
2.5. Markovian Dynamics
3. Results
3.1. Weakly-Disordered Square Lattice Ensembles
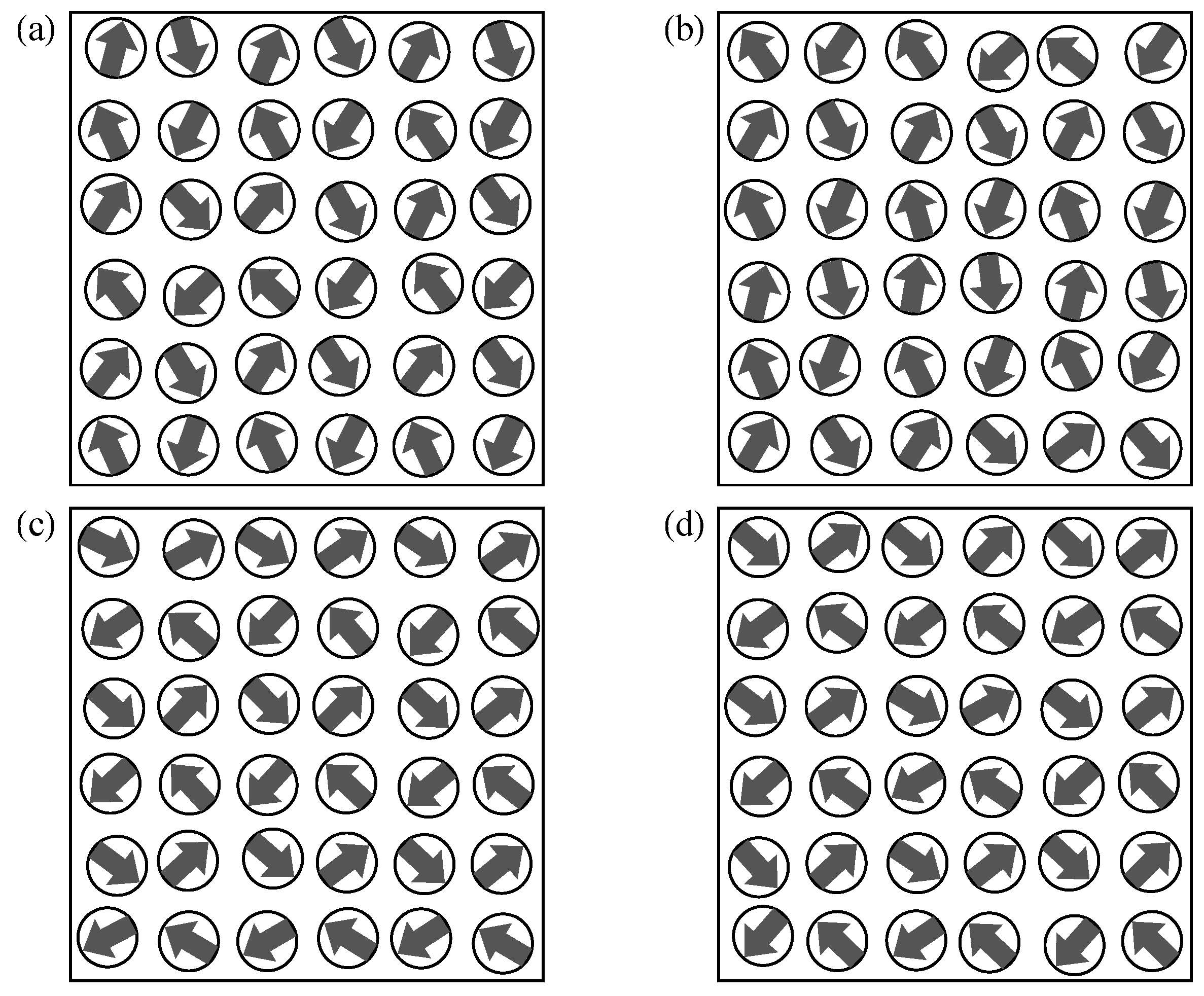
3.1.1. Ground-State Magnetic Order
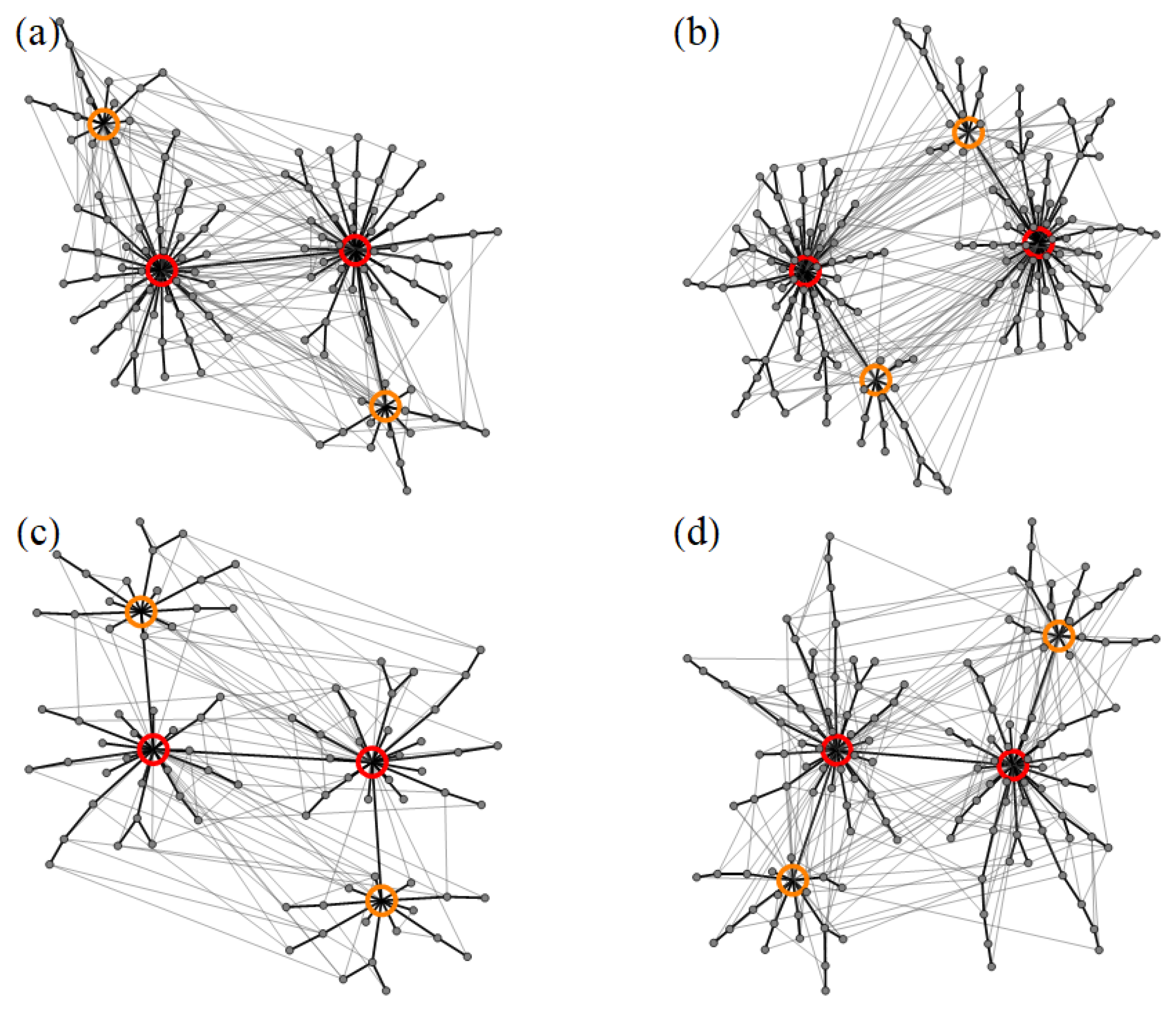
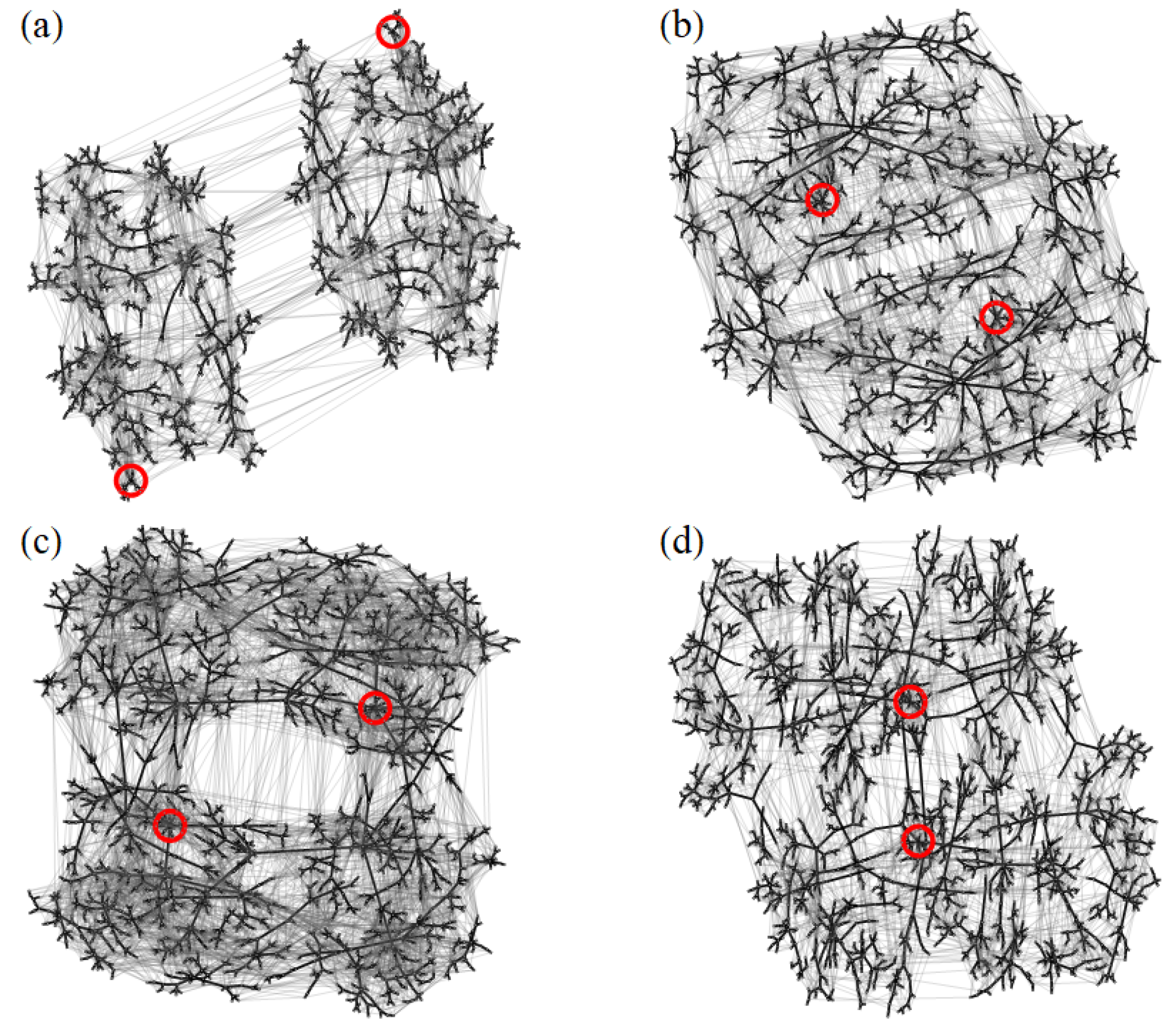
3.1.2. Kinetic Networks
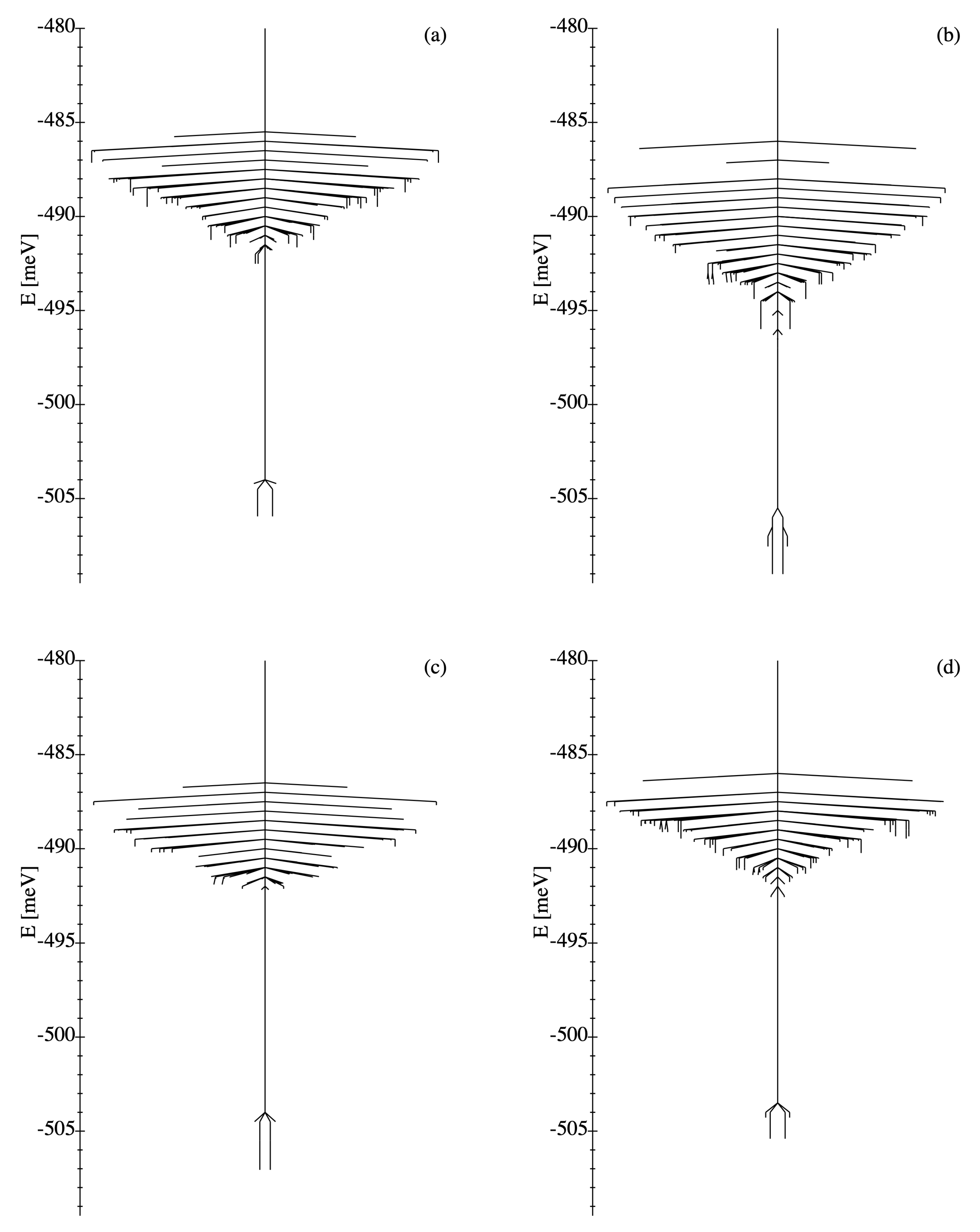
3.1.3. Disconnectivity Graphs
3.1.4. Relaxation Dynamics after Quenching
3.2. Strongly-Disordered Ensembles
3.2.1. Ground-State Magnetic Configurations
3.2.2. Kinetic Networks
3.2.3. Disconnectivity Graphs
3.2.4. Relaxation Dynamics after Saturation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| DG | Disconnectivity graph |
| EL | Energy landscape |
| KN | Kinetic network |
| LM | Local minimum |
| TS | Transition state |
| MEP | Minimum-energy path |
| NP | Nanoparticle |
| MNP | Magnetic nanoparticle |
| RAS | Relaxation after saturation |
| RAQ | Relaxation after quenching |
| SD | Strongly-disordered |
| WDSL | Weakly-disordered square-lattice |
| L-BFGS | Limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm |
References
- Desvaux, C.; Amiens, C.; Fejes, P.; Renaud, P.; Respaud, M.; Lecante, P.; Snoeck, E.; Chaudret, B. Multimillimetre-large superlattices of air-stable iron–cobalt nanoparticles. Nat. Mater. 2005, 4, 750–753. [Google Scholar] [CrossRef]
- Barth, J.V.; Costantini, G.; Kern, K. Engineering atomic and molecular nanostructures at surfaces. Nature 2005, 437, 671–679. [Google Scholar] [CrossRef]
- Jönsson, P.E. Effects of Interparticle Interaction in Ferromagnetic Nanoparticle Systems. J. Nanosci. Nanotechnol. 2010, 10, 6067. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.W.; Mellado, P.; Tchernyshyov, O. Two-Stage Ordering of Spins in Dipolar Spin Ice on the Kagome Lattice. Phys. Rev. Lett. 2011, 106, 207202. [Google Scholar] [CrossRef] [PubMed]
- Farhan, A.; Derlet, P.M.; Kleibert, A.; Balan, A.; Chopdekar, R.V.; Wyss, M.; Anghinolfi, L.; Nolting, F.; Heyderman, L.J. Exploring hyper-cubic energy landscapes in thermally active finite artificial spin-ice systems. Nat. Phys. 2013, 9, 375–382. [Google Scholar] [CrossRef]
- Zhang, S.; Gilbert, I.; Nisoli, C.; Chern, G.W.; Erickson, M.J.; O’Brien, L.; Leighton, C.; Lammert, P.E.; Crespi, V.H.; Schiffer, P. Crystallites of magnetic charges in artificial spin ice. Nature 2013, 500, 553–557. [Google Scholar] [CrossRef] [PubMed]
- Anandakumar, S.; Andrea, T.; Marco, D.; Matteo, P.; Paolo, V. Two-Dimensional Programmable Manipulation of Magnetic Nanoparticles on-Chip. Adv. Mater. 2014, 26, 2384–2390. [Google Scholar]
- Leo, N.; Holenstein, S.; Schildknecht, D.; Sendetskyi, O.; Luetkens, H.; Derlet, P.M.; Scagnioli, V.; Lançon, D.; Margegan, J.R.L.; Prokscha, T.; et al. Collective magnetism in an artificial 2D XY spin system. Nat. Comm. 2018, 9, 2850. [Google Scholar] [CrossRef]
- Streubel, R.; Kent, N.; Dhuey, S.; Scholl, A.; Kevan, S.; Fischer, P. Spatial and Temporal Correlations of XY Macro Spins. Nano Lett. 2018, 18, 7428. [Google Scholar] [CrossRef] [Green Version]
- Sattler, K.; Mühlbach, J.; Recknagel, E. Generation of Metal Clusters Containing from 2 to 500 Atoms. Phys. Rev. Lett. 1980, 45, 821–824. [Google Scholar] [CrossRef]
- Milani, P.; deHeer, W.A. Improved pulsed laser vaporization source for production of intense beams of neutral and ionized clusters. Rev. Sci. Instrum. 1990, 61, 1835. [Google Scholar] [CrossRef]
- Heyderman, L.J.; Solak, H.H.; David, C.; Atkinson, D.; Cowburn, R.P.; Nolting, F. Arrays of nanoscale magnetic dots: Fabrication by x-ray interference lithography and characterization. Appl. Phys. Lett. 2004, 85, 4989. [Google Scholar] [CrossRef] [Green Version]
- Bansmann, J.; Baker, S.H.; Binns, C.; Blackman, J.A.; Bucher, J.P.; Dorantes-Dávila, J.; Dupuis, V.; Favre, L.; Kechrakos, D.; Kleibert, A.; et al. Magnetic and structural properties of isolated and assembled clusters. Surf. Sci. Rep. 2005, 56, 189–275. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Henley, C.L. Ordering due to disorder in dipolar magnets on two-dimensional lattices. Phys. Rev. B 1990, 42, 6574. [Google Scholar] [CrossRef] [PubMed]
- De’Bell, K.; MacIsaac, A.B.; Booth, I.N.; Whitehead, J.P. Dipolar-induced planar anisotropy in ultrathin magnetic films. Phys. Rev. B 1997, 55, 15108. [Google Scholar] [CrossRef]
- Politi, P.; Pini, M.G.; Stamps, R.L. Dipolar ground state of planar spins on triangular lattices. Phys. Rev. B 2006, 73, 020405. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.K.; Minnhagen, P.; Kim, B.J. Kosterlitz-Thouless transition of magnetic dipoles on the two-dimensional plane. Phys. Rev. B 2011, 83, 184409. [Google Scholar] [CrossRef] [Green Version]
- Schildknecht, D.; Heyderman, L.J.; Derlet, P.M. Phase diagram of dipolar-coupled XY moments on disordered square lattices. Phys. Rev. B 2018, 98, 064420. [Google Scholar] [CrossRef] [Green Version]
- Jensen, P.J.; Pastor, G.M. Dipole Coupling Induced Magnetic Ordering in an Ensemble of Nanostructured Islands. Phys. Status Solidi A 2002, 189, 527–531. [Google Scholar] [CrossRef]
- Jensen, P.J.; Pastor, G.M. Low-energy properties of two-dimensional magnetic nanostructures: Interparticle interactions and disorder effects. New J. Phys. 2003, 5, 68. [Google Scholar] [CrossRef]
- Pastor, G.M.; Jensen, P.J. Elementary transitions and magnetic correlations in two-dimensional disordered nanoparticle ensembles. Phys. Rev. B 2008, 78, 134419. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Callaway, J.; Dhar, S. Electronic structure of small iron clusters. Phys. Rev. B 1984, 30, 1724. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Callaway, J.; Wong, K.; Tang, R.; Ziegler, A. Electronic structure of small clusters of nickel and iron. Phys. Rev. B 1985, 31, 1796. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Callaway, J. Electronic structure and magnetism of small V and Cr clusters. Phys. Rev. B 1993, 48, 15358. [Google Scholar] [CrossRef] [PubMed]
- Pastor, G.M.; Dorantes-Dávila, J.; Bennemann, K.H. Size and structural dependence of magnetic properties of small 3d-transition metal clusters. Phys. Rev. B 1989, 40, 7642. [Google Scholar] [CrossRef]
- de Heer, W.A.; Milani, P.; Châtelain, A. Spin relaxation in small free iron clusters. Phys. Rev. Lett. 1990, 65, 488. [Google Scholar] [CrossRef]
- Billas, I.M.L.; Becker, J.A.; Châtelain, A.; de Heer, W.A. Magnetic moments of iron clusters with 25 to 700 atoms and their dependence on temperature. Phys. Rev. Lett. 1993, 71, 4067. [Google Scholar] [CrossRef]
- Bucher, J.P.; Douglas, D.G.; Bloomfield, L.A. Magnetic properties of free cobalt clusters. Phys. Rev. Lett. 1991, 66, 3052. [Google Scholar] [CrossRef]
- Douglass, D.C.; Clox, A.J.; Bucher, J.P.; Bloomfield, L.A. Magnetic properties of free cobalt and gadolinium clusters. Phys. Rev. B 1993, 47, 12874. [Google Scholar] [CrossRef]
- Khanna, S.N.; Linderoth, S. Magnetic behavior of clusters of ferromagnetic transition metals. Phys. Rev. Lett. 1991, 67, 742. [Google Scholar] [CrossRef] [Green Version]
- Pastor, G.M.; Dorantes-Dávila, J.; Pick, S.; Dreyssé, H. Magnetic anisotropy of 3d transition-metal clusters. Phys. Rev. Lett. 1995, 75, 326. [Google Scholar] [CrossRef] [PubMed]
- Guirado-López, R.A.; Dorantes-Dávila, J.; Pastor, G.M. Orbital magnetism in transition-metal clusters: From Hund’s rules to bulk quenching. Phys. Rev. Lett. 2003, 90, 226402. [Google Scholar] [CrossRef] [PubMed]
- Binns, C.; Trohidou, K.N.; Bansmann, J.; Baker, S.H.; Blackman, J.A.; Bucher, J.P.; Kechrakos, D.; Kleibert, A.; Louch, S.; Meiwes-Broer, K.H.; et al. The behaviour of nanostructured materials produced by depositing gas-phase nanoparticles. J. Phys. D Appl. Phys. 2005, 38, R357. [Google Scholar] [CrossRef]
- Dorantes-Dávila, J.; Pastor, G.M. Spin and orbital magnetism in free nanoparticles: Size, composition and temperature effects. In Nanomagnetism: Fundamentals and Applications; Binns, C., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Chapter 2; p. 33. [Google Scholar]
- Phan, M.H.; Alonso, J.; Khurshid, H.; Lampen-Kelley, P.; Chandra, S.; Repa, K.S.; Nemati, Z.; Das, R.; Iglesias, Ó.; Srikanth, H. Exchange Bias Effects in Iron Oxide-Based Nanoparticle Systems. Nanomaterials 2016, 6, 221. [Google Scholar] [CrossRef]
- Dorantes-Dávila, J.; Pastor, G.M. A theoretical perspective to magnetism in nanoalloys. In Nanoalloys: From Fundamentals to Emergent Applications; Calvo, F., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 7; p. 225. [Google Scholar]
- Santos, G.D.; Aparicio, R.; Linares, D.; Miranda, E.N.; Tranchida, J.; Pastor, G.M.; Bringa, E.M. Size and temperature dependent magnetization of iron nanoclusters. Phys. Rev. B 2020, 102, 184426. [Google Scholar] [CrossRef]
- Jonsson, T.; Mattsson, J.; Djurberg, C.; Khan, F.A.; Nordblad, P.; Svedlindh, P. Aging in a Magnetic Particle System. Phys. Rev. Lett. 1995, 75, 4138–4141. [Google Scholar] [CrossRef]
- Sasaki, M.; Jönsson, P.E.; Takayama, H.; Mamiya, H. Aging and memory effects in superparamagnets and superspin glasses. Phys. Rev. B 2005, 71, 104405. [Google Scholar] [CrossRef] [Green Version]
- Parker, D.; Dupuis, V.; Ladieu, F.; Bouchaud, J.P.; Dubois, E.; Perzynski, R.; Vincent, E. Spin-glass behavior in an interacting γ-Fe2O3 nanoparticle system. Phys. Rev. B 2008, 77, 104428. [Google Scholar] [CrossRef] [Green Version]
- Bedanta, S.; Kleemann, W. Supermagnetism. J. Phys. D Appl. Phys. 2009, 42, 013001. [Google Scholar] [CrossRef]
- Suzuki, M.; Fullem, S.I.; Suzuki, I.S.; Wang, L.; Zhong, C.J. Observation of superspin-glass behavior in Fe3O4 nanoparticles. Phys. Rev. B 2009, 79, 024418. [Google Scholar] [CrossRef]
- Margaris, G.; Vasilakaki, M.; Peddis, D.; Trohidou, K.N.; Laureti, S.; Binns, C.; Agostinelli, E.; Rinaldi, D.; Mathieu, R.; Fiorani, D. Superspin glass state in a diluted nanoparticle system stabilized by interparticle interactions mediated by an antiferromagnetic matrix. Nanotechnology 2017, 28, 035701. [Google Scholar] [CrossRef] [PubMed]
- Gallina, D.; Pastor, G.M. Disorder-Induced Transformation of the Energy Landscapes and Magnetization Dynamics in Two-Dimensional Ensembles of Dipole-Coupled Magnetic Nanoparticles. Phys. Rev. X 2020, 10, 021068. [Google Scholar]
- Wales, D.J. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge Molecular Science; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Doye, J.P.K.; Wales, D.J. The effect of the range of the potential on the structure and stability of simple liquids: From clusters to bulk, from sodium to C60. J. Phys. B 1996, 29, 4859. [Google Scholar] [CrossRef]
- Miller, M.A.; Doye, J.P.K.; Wales, D.J. Structural relaxation in Morse clusters: Energy landscapes. J. Chem. Phys. 1998, 110, 328. [Google Scholar] [CrossRef] [Green Version]
- Nocedal, J. Updating Quasi-Newton Matrices with Limited Storage. Math. Comput. 1980, 35, 773. [Google Scholar] [CrossRef]
- Luce, R.D.; Perry, A.D. A method of matrix analysis of group structure. Psychometrika 1949, 14, 95. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Networks; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Becker, O.M.; Karplus, M. The topology of multidimensional potential energy surfaces: Theory and application to peptide structure and kinetics. J. Chem. Phys. 1997, 106, 1495–1517. [Google Scholar] [CrossRef] [Green Version]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 1990, 62, 251. [Google Scholar] [CrossRef]
- Bessarab, P.F.; Uzdin, V.M.; Jónsson, H. Harmonic transition-state theory of thermal spin transitions. Phys. Rev. B 2012, 85, 184409. [Google Scholar] [CrossRef] [Green Version]
- Bessarab, P.F.; Uzdin, V.M.; Jónsson, H. Size and Shape Dependence of Thermal Spin Transitions in Nanoislands. Phys. Rev. Lett. 2013, 110, 020604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Belobrov, P.I.; Gekht, R.S.; Ignatchenko, V.A. Ground state in systems with dipole interaction. Zhurnal Eksp. Teor. Fiz. 1983, 84, 1097. [Google Scholar]
- Schildknecht, D.; Schütt, M.; Heyderman, L.J.; Derlet, P.M. Continuous ground-state degeneracy of classical dipoles on regular lattices. Phys. Rev. B. 2019, 100, 014426. [Google Scholar] [CrossRef] [Green Version]
- Villain, J.; Bidaux, R.; Carton, J.P.; Conte, R. Order as an effect of disorder. J. Phys. 1980, 41, 1263. [Google Scholar] [CrossRef]
- Henley, C.L. Ordering due to disorder in a frustrated vector antiferromagnet. Phys. Rev. Lett. 1989, 62, 2056–2059. [Google Scholar] [CrossRef] [PubMed]
- McClarty, P.A.; Stasiak, P.; Gingras, M.J.P. Order-by-disorder in the X Y pyrochlore antiferromagnet. Phys. Rev. B 2014, 89, 024425. [Google Scholar] [CrossRef] [Green Version]
- Morgan, J.W.R.; Mehta, D.; Wales, D.J. Properties of kinetic transition networks for atomic clusters and glassy solids. Phys. Chem. Chem. Phys. 2017, 19, 25498–25508. [Google Scholar] [CrossRef] [Green Version]
- Miller, M.A.; Wales, D.J. Energy landscape of a model protein. J. Chem. Phys. 1999, 111, 6610–6616. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Berry, R.S. Time autocorrelation function analysis of master equation and its application to atomic clusters. J. Chem. Phys. 2005, 123, 094103. [Google Scholar] [CrossRef]
- Wales, D.J. Decoding head capacity features from the energy landscape. Phys. Rev. E 2017, 95, 030105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rozenbaum, V.M.; Ogenko, V.O.; Chĭko, A.A. Vibrational and orientational states of surface atomic groups. Sov. Phys. Usp. 1991, 34, 883. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Packing Structures and Transitions in Liquids and Solids. Science 1984, 225, 983–989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Souza, V.K.; Wales, D.J. Energy landscapes for diffusion: Analysis of cage-breaking processes. J. Chem. Phys. 2008, 129, 164507. [Google Scholar] [CrossRef] [PubMed]
- De Souza, V.K.; Wales, D.J. Connectivity in the potential energy landscape for binary Lennard-Jones systems. J. Chem. Phys. 2009, 130, 194508. [Google Scholar] [CrossRef] [PubMed]
- Niblett, S.P.; de Souza, V.K.; Stevenson, J.D.; Wales, D.J. Dynamics of a molecular glass former: Energy landscapes for diffusion in ortho-terphenyl. J. Chem. Phys. 2016, 145, 024505. [Google Scholar] [CrossRef] [PubMed]
- Niblett, S.; Biedermann, M.; Wales, D.J.; de Souza, V.K. Pathways for diffusion in the potential energy landscape of the network glass former SiO2. J. Chem. Phys. 2017, 147, 152726. [Google Scholar] [CrossRef] [Green Version]


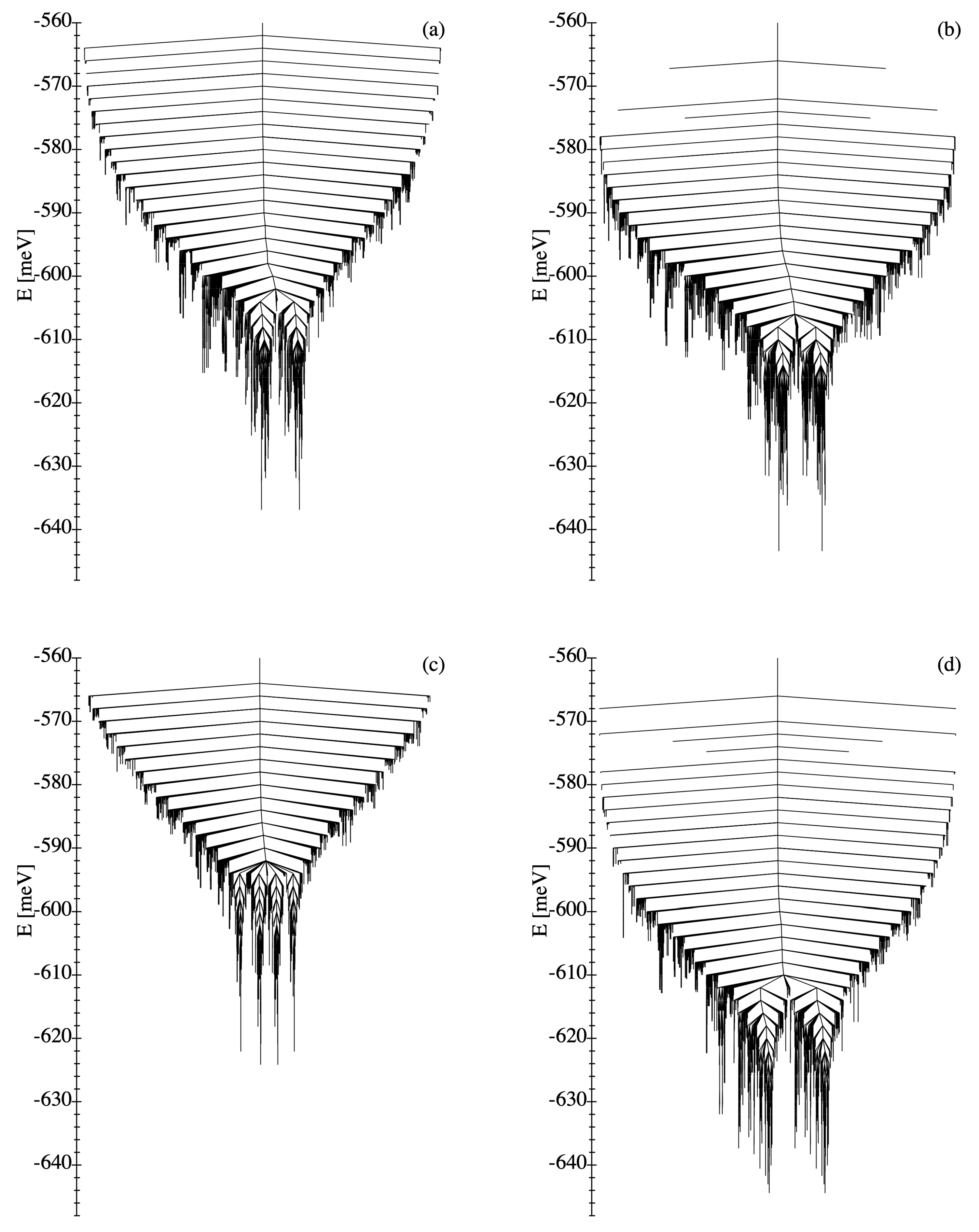
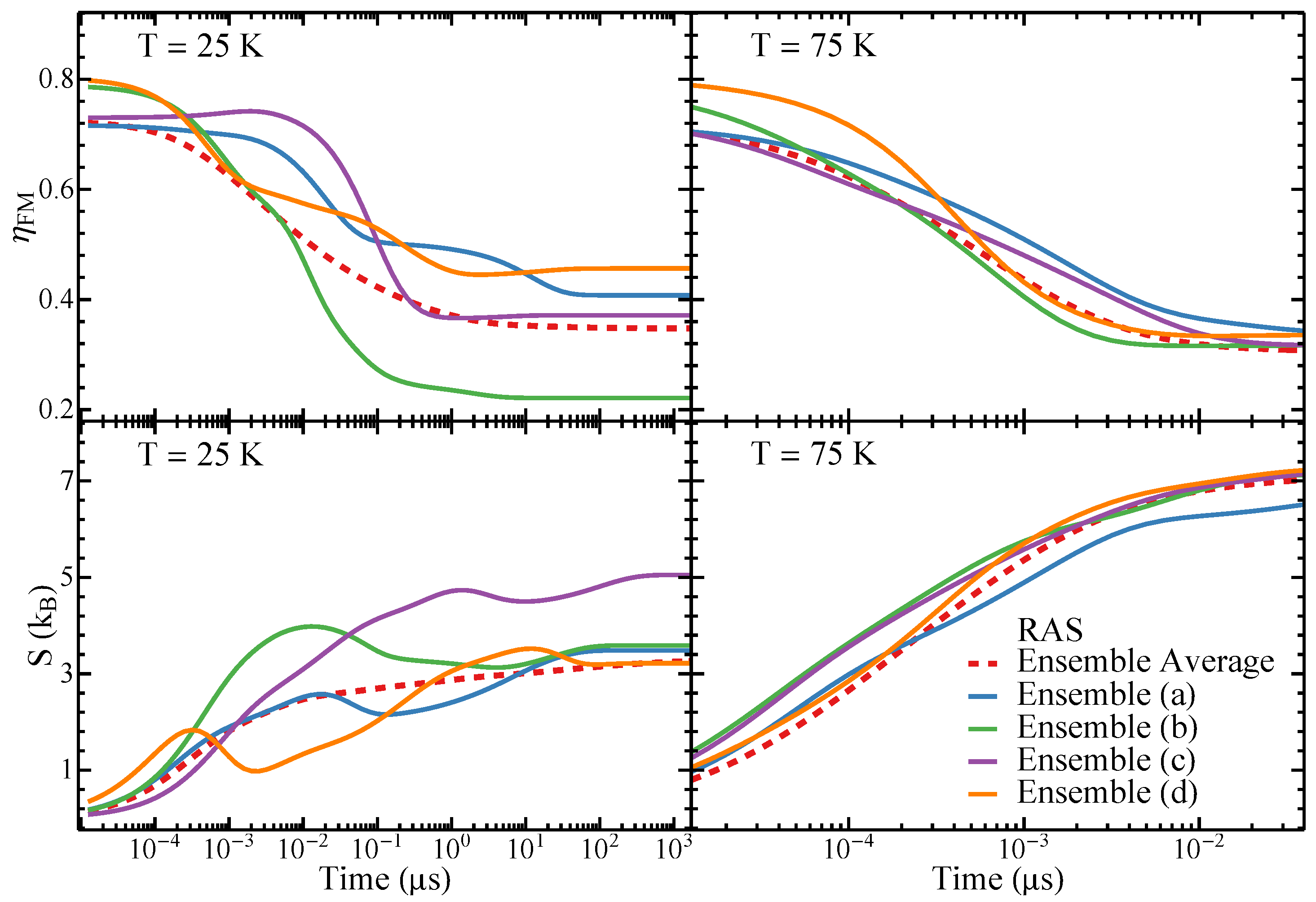
| (a) | (b) | (c) | (d) | ||
|---|---|---|---|---|---|
| 1.04 | 1.09 | 0.68 | 0.55 | ||
| 120 | 148 | 80 | 132 | ||
| 392 | 474 | 254 | 426 |
| (a) | (b) | (c) | (d) | ||
|---|---|---|---|---|---|
| d | 2.51 (3.27) | 2.64 (3.43) | 2.63 (3.27) | 2.67 (3.29) | |
| R | 3.00 (4.06) | 3.00 (4.38) | 3.00 (4.12) | 3.00 (4.04) | |
| D | 5.00 (6.62) | 5.00 (7.14) | 5.00 (7.00) | 5.00 (6.54) | |
| C | 0.08 (0.04) | 0.08 (0.03) | 0.11 (0.05) | 0.09 (0.04) | |
| 0.45 (0.09) | 0.43 (0.09) | 0.40 (0.08) | 0.36 (0.09) |
| (a) | (b) | (c) | (d) | ||
|---|---|---|---|---|---|
| 2276 | 2162 | 2596 | 2532 | ||
| 8876 | 7982 | 11,100 | 9700 | 10,389 ± 4468 |
| (a) | (b) | (c) | (d) | ||
|---|---|---|---|---|---|
| d | 6.54 (4.65) | 5.94 (4.55) | 5.43 (4.31) | 6.57 (4.65) | |
| R | 9.00 (6.00) | 8.00 (6.00) | 7.00 (5.86) | 9.00 (6.00) | |
| D | 14.00 (9.04) | 12.00 (8.90) | 10.00 (8.06) | 14.00 (9.06) | |
| C | 0.11 (0.00) | 0.11 (0.00) | 0.10 (0.00) | 0.14 (0.00) | |
| 0.01 (0.13) | 0.01 (0.13) | 0.01 (0.13) | 0.01 (0.13) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallina, D.; Pastor, G.M. Structural Disorder and Collective Behavior of Two-Dimensional Magnetic Nanostructures. Nanomaterials 2021, 11, 1392. https://doi.org/10.3390/nano11061392
Gallina D, Pastor GM. Structural Disorder and Collective Behavior of Two-Dimensional Magnetic Nanostructures. Nanomaterials. 2021; 11(6):1392. https://doi.org/10.3390/nano11061392
Chicago/Turabian StyleGallina, David, and G. M. Pastor. 2021. "Structural Disorder and Collective Behavior of Two-Dimensional Magnetic Nanostructures" Nanomaterials 11, no. 6: 1392. https://doi.org/10.3390/nano11061392






