Local Morphology Effects on the Photoluminescence Properties of Thin CsPbBr3 Nanocrystal Films
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis of the NCs and Film Preparation
2.2. PL and Time-Resolved PL Measurements
2.3. Investigation of the Morphology and PL Mapping
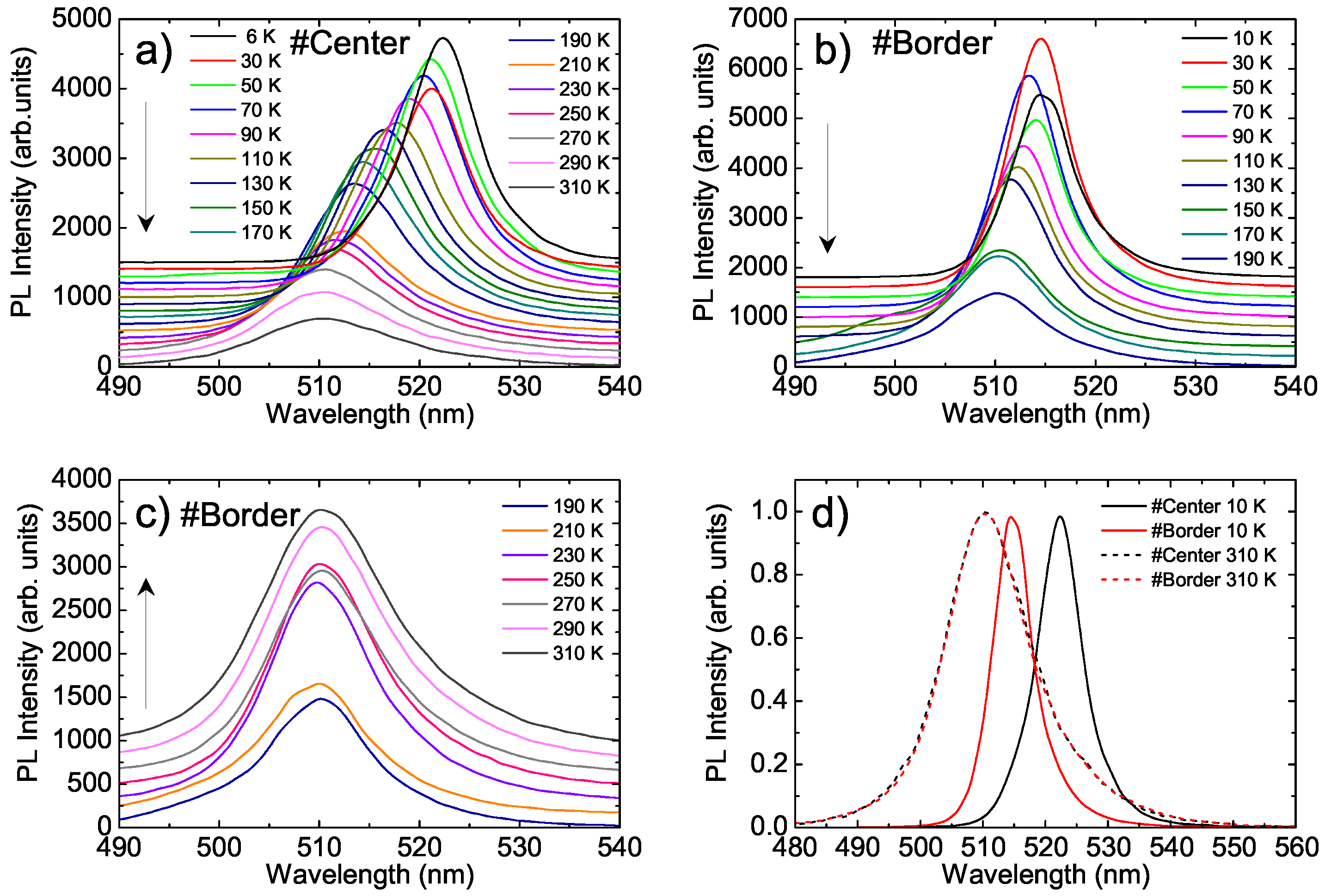
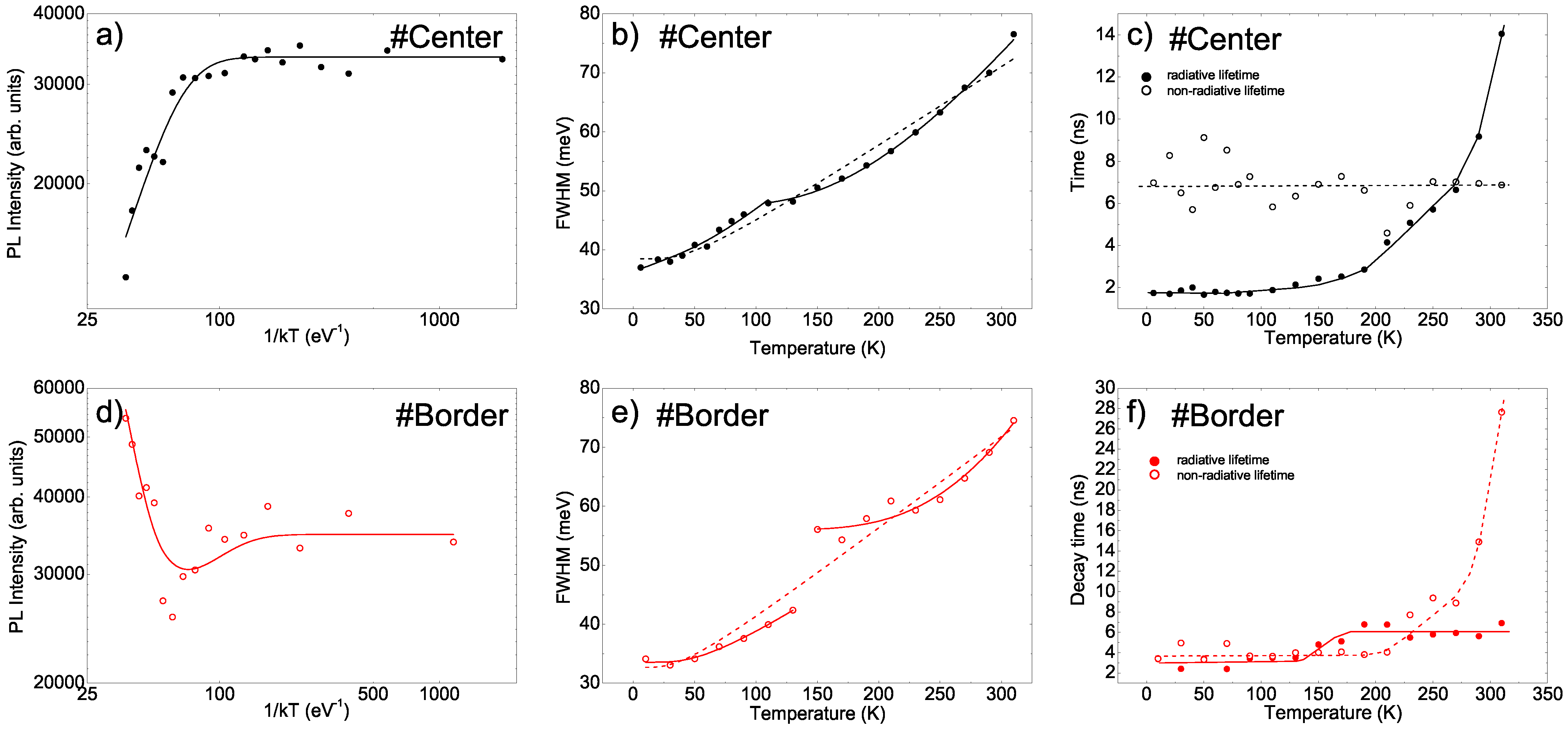
3. Results
4. Discussion
4.1. Conventional Analysis of the Two Points
4.2. Correct Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Note
- Cao, Y.; Wang, N.; Tian, H.; Guo, J.; Wei, Y.; Chen, H.; Miao, Y.; Zou, W.; Pan, K.; He, Y.; et al. Perovskite light-emitting diodes based on spontaneously formed submicrometre-scale structures. Nature 2018, 562, 249–253. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Li, M.N.; Li, Y.; Xie, F.M.; Wu, H.Y.; Zhang, G.H.; Chen, L.; Lee, S.T.; Tang, J.X. Rational Interface Engineering for Efficient Flexible Perovskite Light-Emitting Diodes. ACS Nano 2020, 14, 6107–6116. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. Research Cell Record Efficiency Chart. Available online: https://www.nrel.gov/pv/assets/images/efficiency-chart.png (accessed on 3 May 2021).
- Schileo, G.; Grancini, G. Lead or no lead? Availability, toxicity, sustainability and environmental impact of lead-free perovskite solar cells. J. Mater. Chem. C 2021, 9, 67–76. [Google Scholar] [CrossRef]
- Pham, H.D.; Jain, S.M.; Li, M.; Wang, Z.K.; Manzhos, S.; Feron, K.; Pitchaimuthu, S.; Liu, Z.; Motta, N.; Durrant, J.R.; et al. All-Rounder Low-Cost Dopant-Free D-A-D Hole-Transporting Materials for Efficient Indoor and Outdoor Performance of Perovskite Solar Cells. Adv. Electron. Mater. 2020, 6, 1900884. [Google Scholar] [CrossRef]
- Pham, H.D.; Xianqiang, L.; Li, W.; Manzhos, S.; Kyaw, A.K.K.; Sonar, P. Organic interfacial materials for perovskite-based optoelectronic devices. Energy Environ. Sci. 2019, 12, 1177–1209. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.W.; Jung, H.S.; Shin, H.; Park, N.G. High-Efficiency Perovskite Solar Cells. Chem. Rev. 2020, 120, 7867–7918. [Google Scholar] [CrossRef] [PubMed]
- Yakunin, S.; Protesescu, L.; Krieg, F.; Bodnarchuk, M.I.; Nedelcu, G.; Humer, M.; De Luca, G.; Fiebig, M.; Heiss, W.; Kovalenko, M.V. Low-Threshold Amplified Spontaneous Emission and Lasing from Colloidal Nanocrystals of Caesium Lead Halide Perovskites. Nat. Commun. 2015, 6, 8056. [Google Scholar] [CrossRef] [PubMed]
- Pourdavoud, N.; Mayer, A.; Buchmüller, M.; Brinkmann, K.; Häger, T.; Hu, T.; Heiderhoff, R.; Shutsko, I.; Görrn, P.; Chen, Y.; et al. Distributed Feedback Lasers Based on MAPbBr3. Adv. Mater. Technol. 2018, 3, 1700253. [Google Scholar] [CrossRef]
- De Giorgi, M.L.; Krieg, F.; Kovalenko, M.V.; Anni, M. Amplified Spontaneous Emission Threshold Reduction and Operational Stability Improvement in CsPbBr3 Nanocrystals Films by Hydrophobic Functionalization of the Substrate. Sci. Rep. 2019, 9, 17964. [Google Scholar] [CrossRef]
- De Giorgi, M.L.; Anni, M. Amplified Spontaneous Emission and Lasing in Lead Halide Perovskites: State of the Art and Perspectives. Appl. Sci. 2019, 9, 4591. [Google Scholar] [CrossRef] [Green Version]
- De Giorgi, M.L.; Lippolis, T.; Jamaludin, N.F.; Soci, C.; Bruno, A.; Anni, M. Origin of Amplified Spontaneous Emission Degradation in MAPbBr3 Thin Films under Nanosecond-UV Laser Irradiation. J. Phys. Chem. C 2020, 124, 10696–10704. [Google Scholar] [CrossRef]
- Anni, M.; Cretí, A.; Zhang, Y.; De Giorgi, M.L.; Lomascolo, M. Investigation of the Role of the Environment on the Photoluminescence and the Exciton Relaxation of CsPbBr3 Nanocrystals Thin Films. Appl. Sci. 2020, 10, 2148. [Google Scholar] [CrossRef] [Green Version]
- De Giorgi, M.L.; Milanese, S.; Klini, A.; Anni, M. Environment-Induced Reversible Modulation of Optical and Electronic Properties of Lead Halide Perovskites and Possible Applications to Sensor Development: A Review. Molecules 2021, 26, 705. [Google Scholar] [CrossRef]
- Protesescu, L.; Yakunin, S.; Bodnarchuk, M.I.; Krieg, F.; Caputo, R.; Hendon, C.H.; Yang, R.X.; Walsh, A.; Kovalenko, M.V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, F.; Zhang, Y.; Ding, C.; Kobayashi, S.; Izuishi, T.; Nakazawa, N.; Toyoda, T.; Ohta, T.; Hayase, S.; Minemoto, T.; et al. Highly Luminescent Phase-Stable CsPbI3 Perovskite Quantum Dots Achieving Near 100% Absolute Photoluminescence Quantum Yield. ACS Nano 2017, 11, 10373–10383. [Google Scholar] [CrossRef]
- Koscher, B.A.; Swabeck, J.K.; Bronstein, N.D.; Alivisatos, A.P. Essentially Trap-Free CsPbBr3 Colloidal Nanocrystals by Postsynthetic Thiocyanate Surface Treatment. J. Am. Chem. Soc. 2017, 139, 6566–6569. [Google Scholar] [CrossRef] [Green Version]
- Lozano, G. The Role of Metal Halide Perovskites in Next-Generation Lighting Devices. J. Phys. Chem. Lett. 2018, 9, 3987–3997. [Google Scholar] [CrossRef] [PubMed]
- Protesescu, L.; Yakunin, S.; Kumar, S.; Bär, J.; Bertolotti, F.; Masciocchi, N.; Guagliardi, A.; Grotevent, M.; Shorubalko, I.; Bodnarchuk, M.I.; et al. Dismantling the “Red Wall” of Colloidal Perovskites: Highly Luminescent Formamidinium and Formamidinium-Cesium Lead Iodide Nanocrystals. ACS Nano 2017, 11, 3119–3134. [Google Scholar] [CrossRef] [PubMed]
- Krieg, F.; Ochsenbein, S.T.; Yakunin, S.; ten Brinck, S.; Aellen, P.; Süess, A.; Clerc, B.; Guggisberg, D.; Nazarenko, O.; Shynkarenko, Y.; et al. Colloidal CsPbX3 (X = Cl, Br, I) Nanocrystals 2.0: Zwitterionic Capping Ligands for Improved Durability and Stability. ACS Energy Lett. 2018, 3, 641–646. [Google Scholar] [CrossRef] [Green Version]
- Chiba, T.; Hayashi, Y.; Ebe, H.; Hoshi, K.; Sato, J.; Sato, S.; Pu, Y.J.; Ohisa, S.; Kido, J. Anion-exchange red perovskite quantum dots with ammonium iodine salts for highly efficient light-emitting devices. Nat. Photonics 2018, 12, 681–687. [Google Scholar] [CrossRef]
- Lin, K.; Xing, J.; Quan, L.N.; de Arquer, F.P.G.; Gong, X.; Lu, J.; Xie, L.; Zhao, W.; Zhang, D.; Yan, C.; et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 percent. Nature 2018, 562, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.Y.; Zou, C.; Mao, C.; Corp, K.L.; Yao, Y.C.; Lee, Y.J.; Schlenker, C.W.; Jen, A.K.Y.; Lin, L.Y. CsPbBr3 Perovskite Quantum Dot Vertical Cavity Lasers with Low Threshold and High Stability. ACS Photonics 2017, 4, 2281–2289. [Google Scholar] [CrossRef]
- Dey, A.; Rathod, P.; Kabra, D. Role of Localized States in Photoluminescence Dynamics of High Optical Gain CsPbBr3 Nanocrystals. Adv. Opt. Mater. 2018, 6, 1800109. [Google Scholar] [CrossRef]
- Diroll, B.T.; Nedelcu, G.; Kovalenko, M.V.; Schaller, R.D. High-Temperature Photoluminescence of CsPbX3 (X = Cl, Br, I) Nanocrystals. Adv. Funct. Mater. 2017, 27, 1606750. [Google Scholar] [CrossRef]
- Li, J.; Yuan, X.; Jing, P.; Li, J.; Wei, M.; Hua, J.; Zhao, J.; Tian, L. Temperature-Dependent Photoluminescence of Inorganic Perovskite Nanocrystal Films. RSC Adv. 2016, 6, 78311–78316. [Google Scholar] [CrossRef]
- Woo, H.C.; Choi, J.W.; Shin, J.; Chin, S.H.; Ann, M.H.; Lee, C.L. Temperature-Dependent Photoluminescence of CH3NH3PbBr3 Perovskite Quantum Dots and Bulk Counterparts. J. Phys. Chem. Lett. 2018, 9, 4066–4074. [Google Scholar] [CrossRef]
- Yuan, X.; Hou, X.; Li, J.; Qu, C.; Zhang, W.; Zhao, J.; Li, H. Thermal degradation of luminescence in inorganic perovskite CsPbBr3 nanocrystals. Phys. Chem. Chem. Phys. 2017, 19, 8934–8940. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Pang, G.; Xing, G.; Chen, R. Temperature dependent optical characteristics of all-inorganic CsPbBr3 nanocrystals film. Mater. Tod. Phys. 2020, 15, 100259. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Pan, J.; Yin, J.; Bakr, O.M.; Mohammed, O.F. Room-Temperature Engineering of All-Inorganic Perovskite Nanocrsytals with Different Dimensionalities. Chem. Mat. 2017, 29, 8978–8982. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Yuan, X.; Bo, B.; Li, H.; Zhao, J.; Gao, X. Ultraviolet light induced degradation of luminescence in CsPbBr3 perovskite nanocrystals. MRS Bull. 2018, 102, 86–91. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Peters, J.A.; Liu, Z.; Sebastian, M.; Im, J.; Chasapis, T.C.; Wibowo, A.C.; Chung, D.Y.; Freeman, A.J.; et al. Crystal Growth of the Perovskite Semiconductor CsPbBr3: A New Material for High-Energy Radiation Detection. Cryst. Growth Des. 2013, 13, 2722–2727. [Google Scholar] [CrossRef]
- Diroll, B.T.; Zhou, H.; Schaller, R.D. Low-Temperature Absorption, Photoluminescence, and Lifetime of CsPbX3 (X = Cl, Br, I) Nanocrystals. Adv. Funct. Mater. 2018, 28, 1800945. [Google Scholar] [CrossRef]
- Diroll, B.T.; Guo, P.; Schaller, R.D. Unique Optical Properties of Methylammonium Lead Iodide Nanocrystals below the Bulk Tetragonal-Orthorhombic Phase Transition. Nano Lett. 2018, 18, 846–852. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.H.; Protesescu, L.; Balazs, D.M.; Adjokatse, S.; Kovalenko, M.V.; Loi, M.A. Exciton Recombination in Formamidinium Lead Triiodide: Nanocrystals versus Thin Films. Small 2017, 13, 1700673. [Google Scholar] [CrossRef] [Green Version]
- Papagiorgis, P.; Manoli, A.; Protesescu, L.; Achilleos, C.; Violaris, M.; Nicolaides, K.; Trypiniotis, T.; Bodnarchuk, M.I.; Kovalenko, M.V.; Othonos, A.; et al. Efficient Optical Amplification in the Nanosecond Regime from Formamidinium Lead Iodide Nanocrystals. ACS Photonics 2018, 5, 907–917. [Google Scholar] [CrossRef]
- Tang, B.; Ruan, L.J.; Qin, C.; Shu, A.; He, H.; Ma, Y. High Stability and Temperature-Dependent Photoluminescence of Orthorhombic CsPbI3 Perovskite Nanoparticles. Adv. Opt. Mater. 2020, 8, 2000498. [Google Scholar] [CrossRef]
- De Giorgi, M.L.; Perulli, A.; Yantara, N.; Boix, P.P.; Anni, M. Amplified Spontaneous Emission Properties of Solution Processed CsPbBr3 Perovskite Thin Films. J. Phys. Chem. C 2017, 121, 14772–14778. [Google Scholar] [CrossRef]
- Lee, S.M.; Moon, C.J.; Lim, H.; Lee, Y.; Choi, M.Y.; Bang, J. Temperature-Dependent Photoluminescence of Cesium Lead Halide Perovskite Quantum Dots: Splitting of the Photoluminescence Peaks of CsPbBr3 and CsPb(Br/I)3 Quantum Dots at Low Temperature. J. Phys. Chem. C 2017, 121, 26054–26062. [Google Scholar] [CrossRef]
- Perulli, A.; Balena, A.; Fernandez, M.; Nedelcu, G.; Cretí, A.; Kovalenko, M.V.; Lomascolo, M.; Anni, M. Full-color tuning in binary polymer: Perovskite nanocrystals organic-inorganic hybrid blends. Appl. Phys. Lett. 2018, 112, 171904. [Google Scholar] [CrossRef] [Green Version]
- Akkerman, Q.A.; Gandini, M.; Di Stasio, F.; Rastogi, P.; Palazon, F.; Bertoni, G.; Ball, J.M.; Prato, M.; Petrozza, A.; Manna, L. Strongly emissive perovskite nanocrystal inks for high-voltage solar cells. Nat. Energy 2016, 2, 16194. [Google Scholar] [CrossRef]
- We also observe that the experimental data show intensity fluctuation of about 10% between different temperatures, leading to few points in the low temperature range with higher intensity that the 10 K spectrum. PLQY at 10 K higher than 80% would lead to few points with PLQY very close to, or even higher than, 100%, thus determining unphysical values of the non-radiative decay times. On the contrary lower initial PLQY values would simply act as a scale factor of the extrancted lifetimes, without significantly affecting their temperature dependence, that is the main focus of the current analysis.
- Chirvony, V.S.; Sekerbayev, K.S.; Pashaei Adl, H.; Suarez, I.; Taurbayev, Y.T.; Gualdron-Reyes, A.F.; Mora-Sero, I.; Martinez-Pastor, J.P. Interpretation of the photoluminescence decay kinetics in metal halide perovskite nanocrystals and thin polycrystalline films. J. Lumin. 2020, 221, 117092. [Google Scholar] [CrossRef]
- Yantara, N.; Bhaumik, S.; Yan, F.; Sabba, D.; Dewi, H.A.; Mathews, N.; Boix, P.P.; Demir, H.V.; Mhaisalkar, S. Inorganic Halide Perovskites for Efficient Light-Emitting Diodes. J. Phys. Chem. Lett. 2015, 6, 4360–4364. [Google Scholar] [CrossRef] [PubMed]




| #Point | A | E | ||
|---|---|---|---|---|
| (meV) | (meV/K) | (meV) | (meV) | |
| #Center | 38.5 ± 1.0 | - | 18 ± 7 | 11 ± 4 |
| #Center-LT | 36 ± 7 | - | 25 ± 13 | 20 ± 3 |
| #Center-HT | 47.5 ± 0.6 | - | 214 ± 40 | 57 ± 5 |
| #Border | 33 ±2 | - | 17 ± 13 | 9 ± 6 |
| #Border-LT | 33.5 ± 0.6 | - | 24.6 ± 10 | 15 ± 3 |
| #Border-HT | 56.0 ± 1.1 | - | 1.7 ± 1.2 | 121 ± 18 |
| Film | 24.4 ± 0.7 | - | 60 ± 8 | 19 ± 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anni, M.; Cretí, A.; De Giorgi, M.L.; Lomascolo, M. Local Morphology Effects on the Photoluminescence Properties of Thin CsPbBr3 Nanocrystal Films. Nanomaterials 2021, 11, 1470. https://doi.org/10.3390/nano11061470
Anni M, Cretí A, De Giorgi ML, Lomascolo M. Local Morphology Effects on the Photoluminescence Properties of Thin CsPbBr3 Nanocrystal Films. Nanomaterials. 2021; 11(6):1470. https://doi.org/10.3390/nano11061470
Chicago/Turabian StyleAnni, Marco, Arianna Cretí, Maria Luisa De Giorgi, and Mauro Lomascolo. 2021. "Local Morphology Effects on the Photoluminescence Properties of Thin CsPbBr3 Nanocrystal Films" Nanomaterials 11, no. 6: 1470. https://doi.org/10.3390/nano11061470
APA StyleAnni, M., Cretí, A., De Giorgi, M. L., & Lomascolo, M. (2021). Local Morphology Effects on the Photoluminescence Properties of Thin CsPbBr3 Nanocrystal Films. Nanomaterials, 11(6), 1470. https://doi.org/10.3390/nano11061470








