All-Solid-State Optical Phased Arrays of Mid-Infrared Based Graphene-Metal Hybrid Metasurfaces
Abstract
1. Introduction
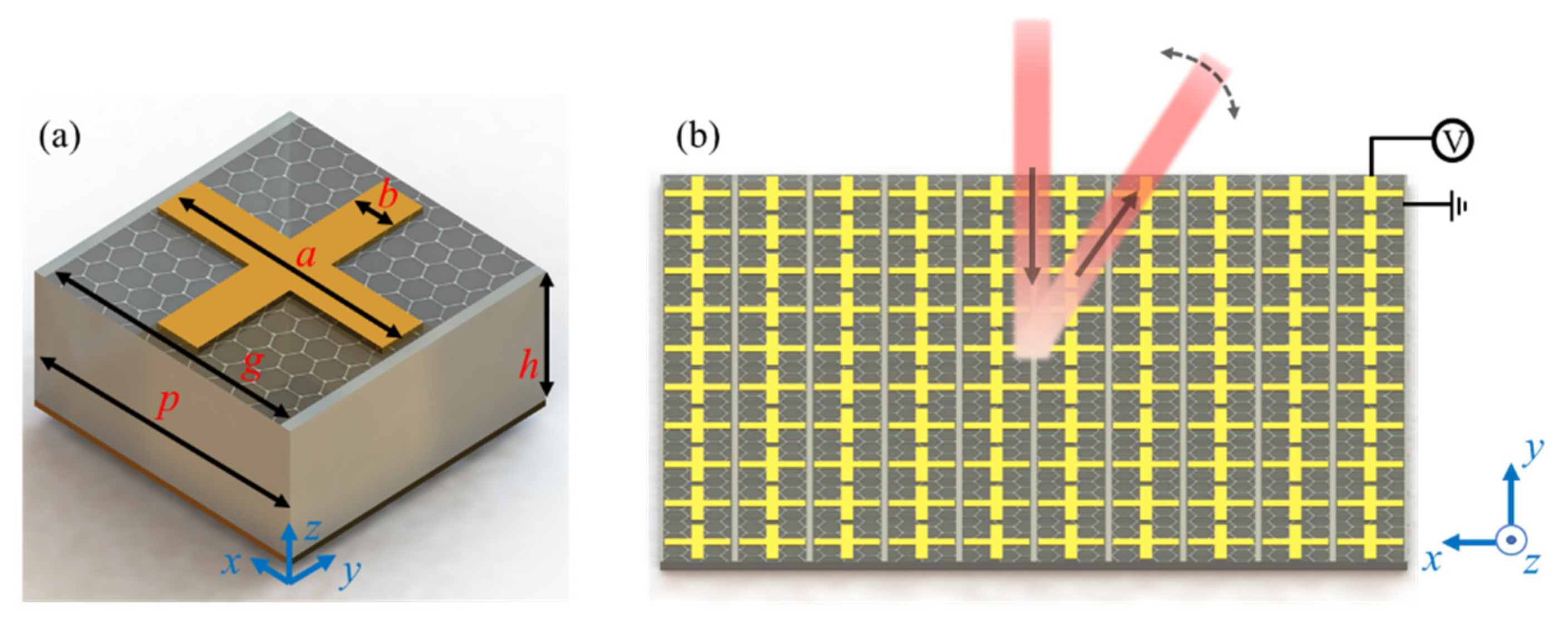
2. Structure and Methods
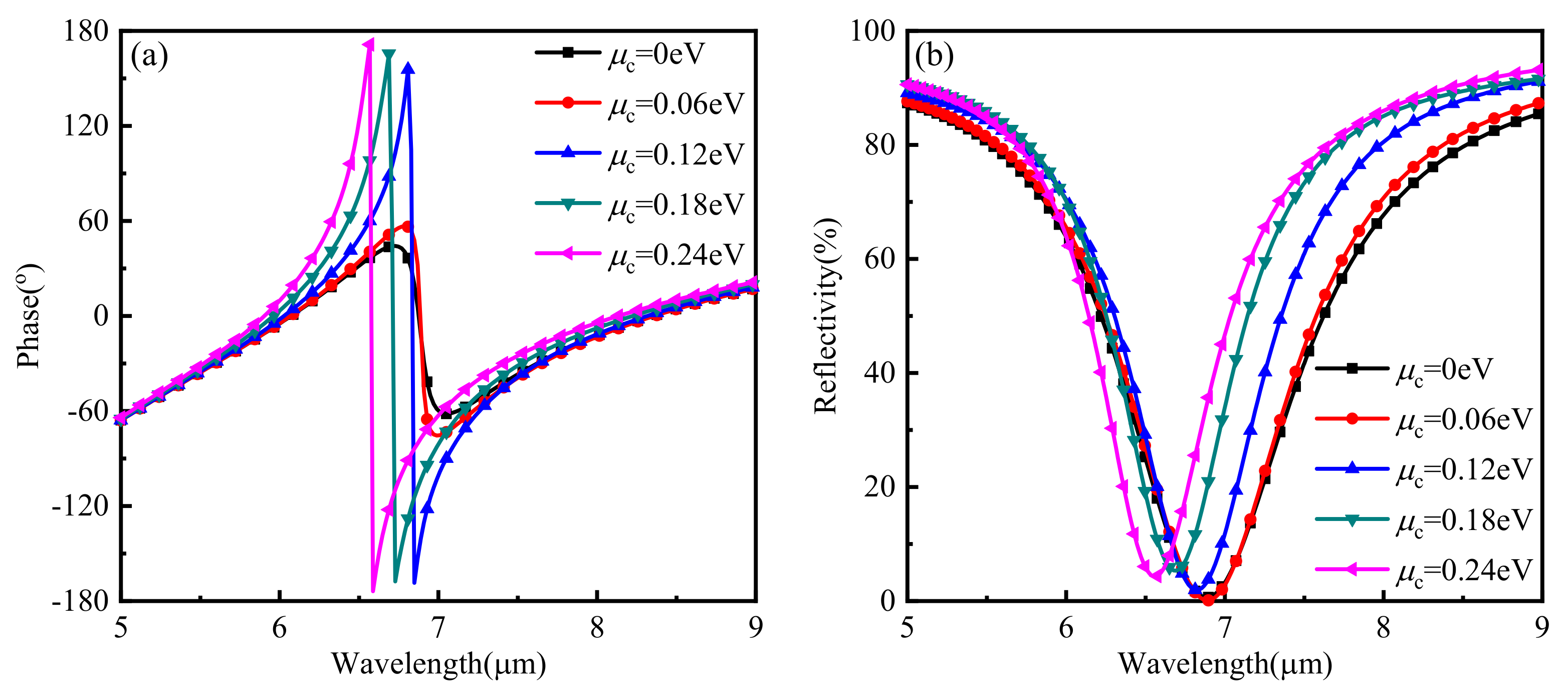
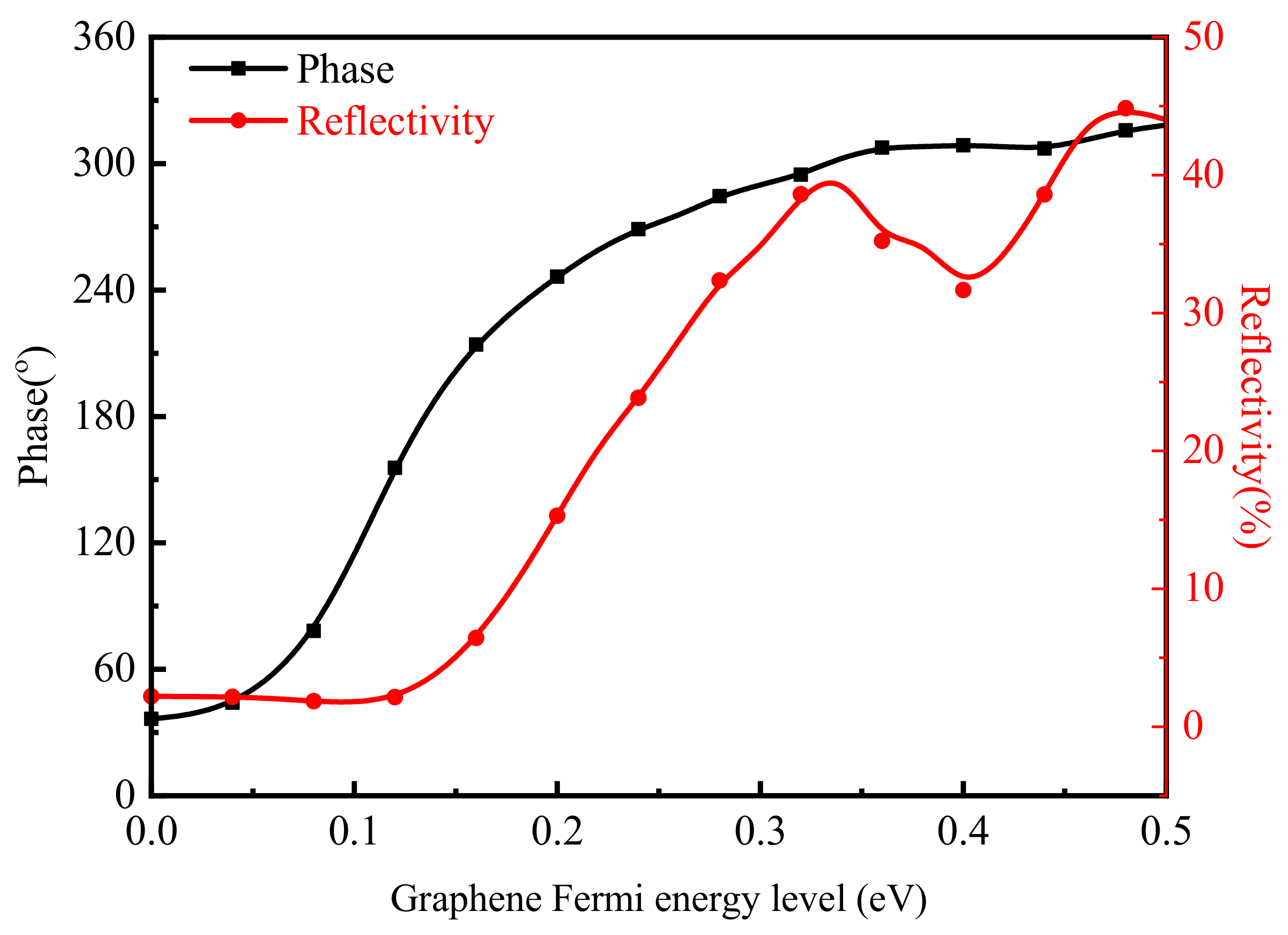
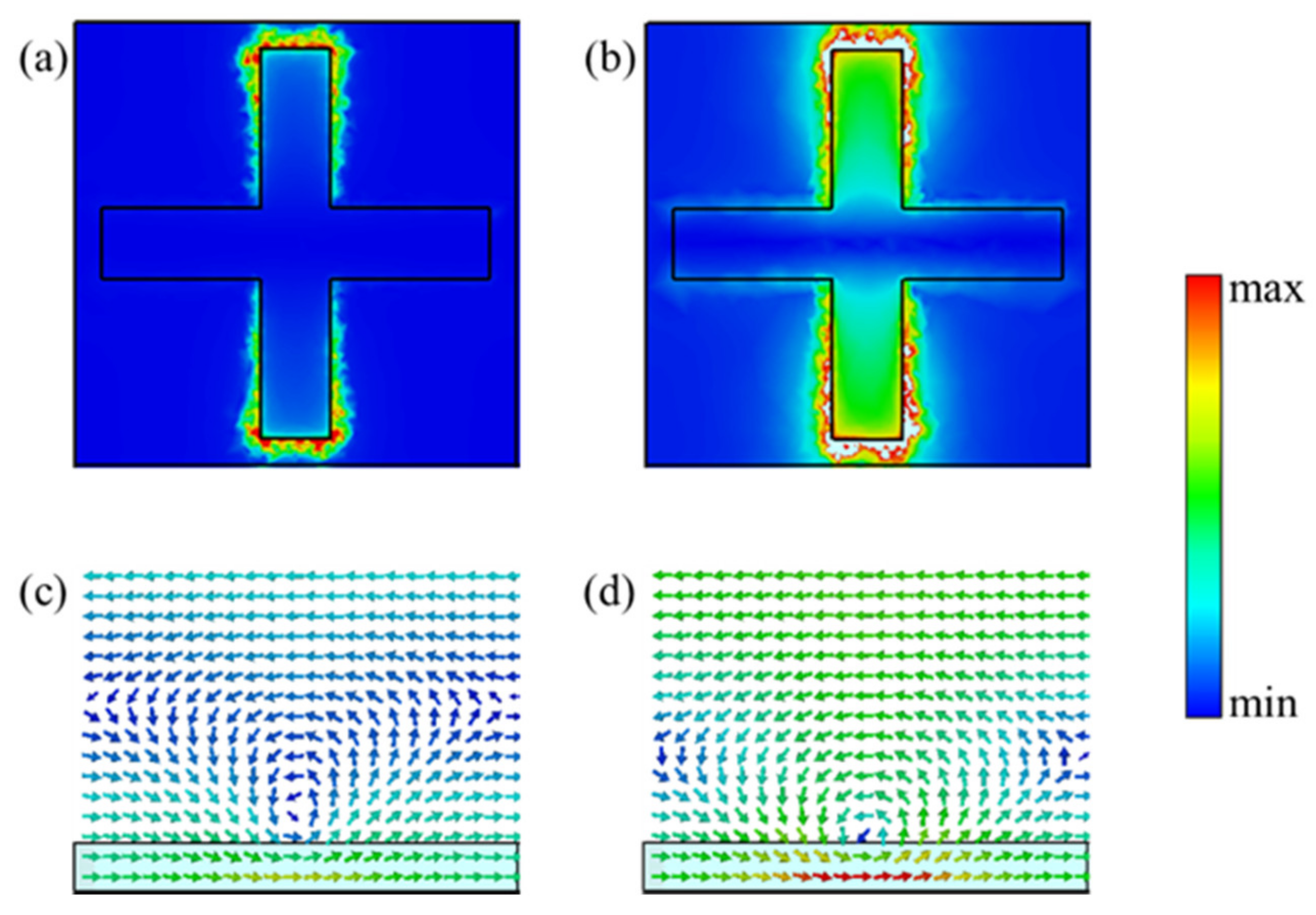
3. Results and Analyses
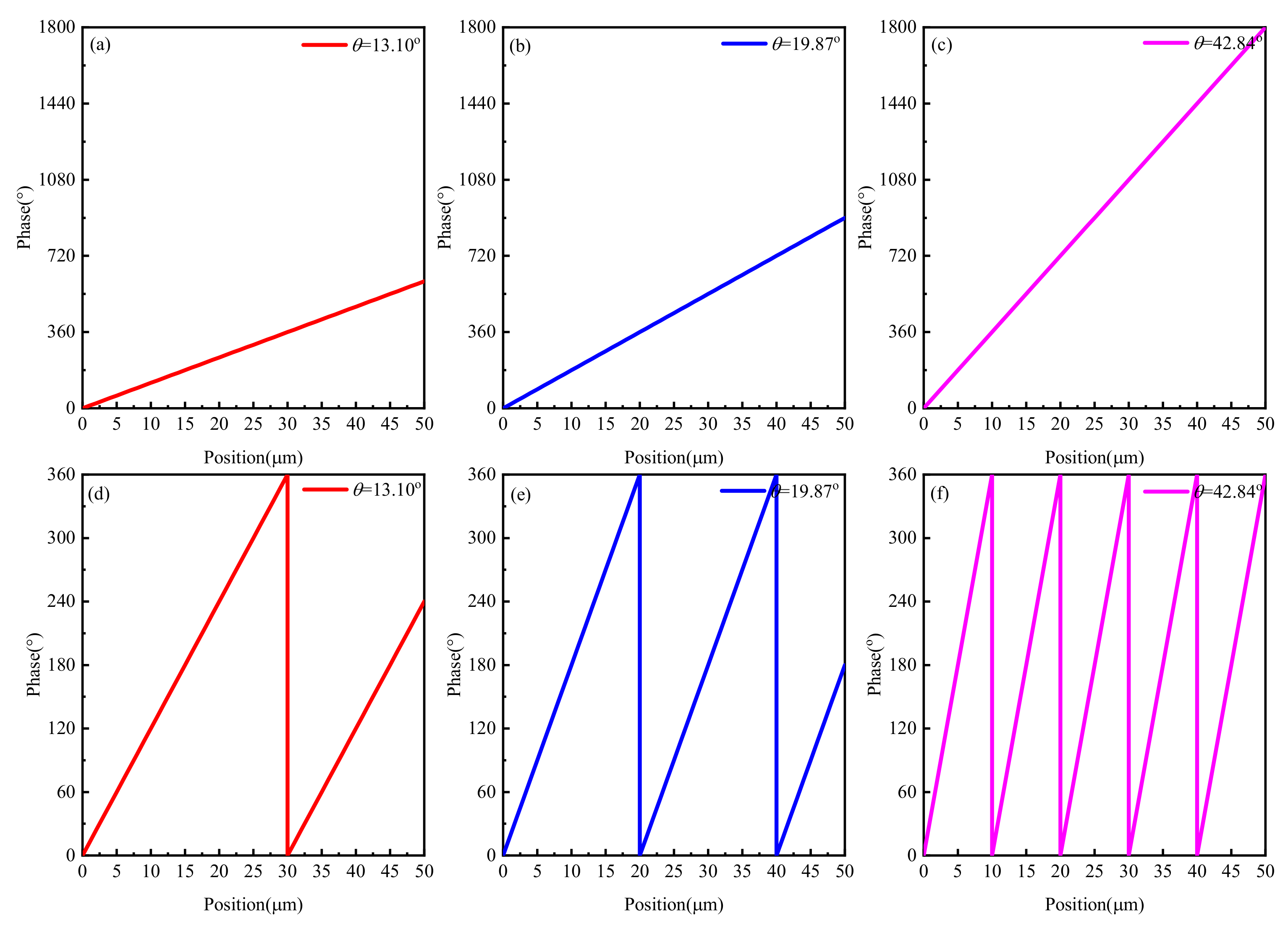
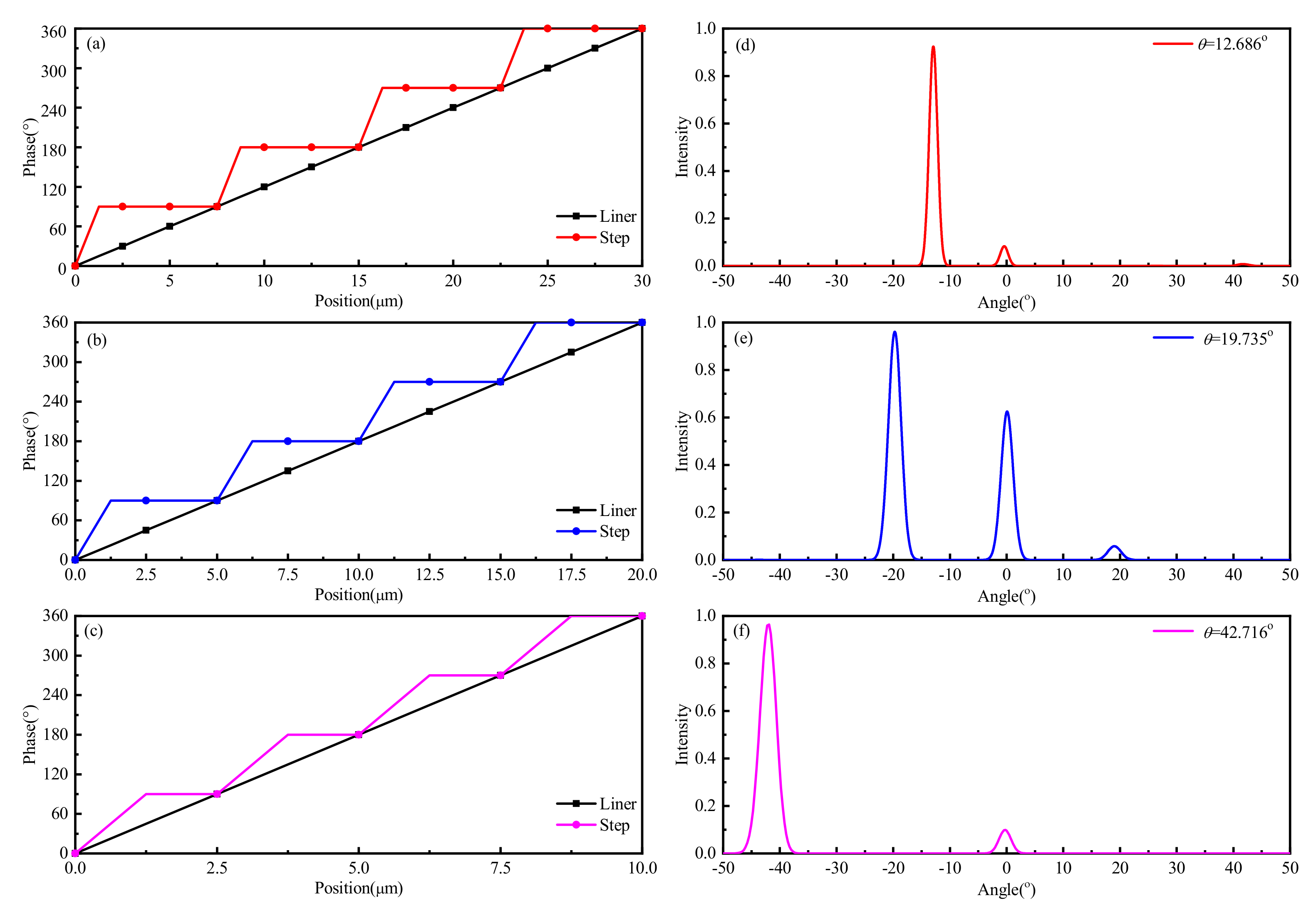
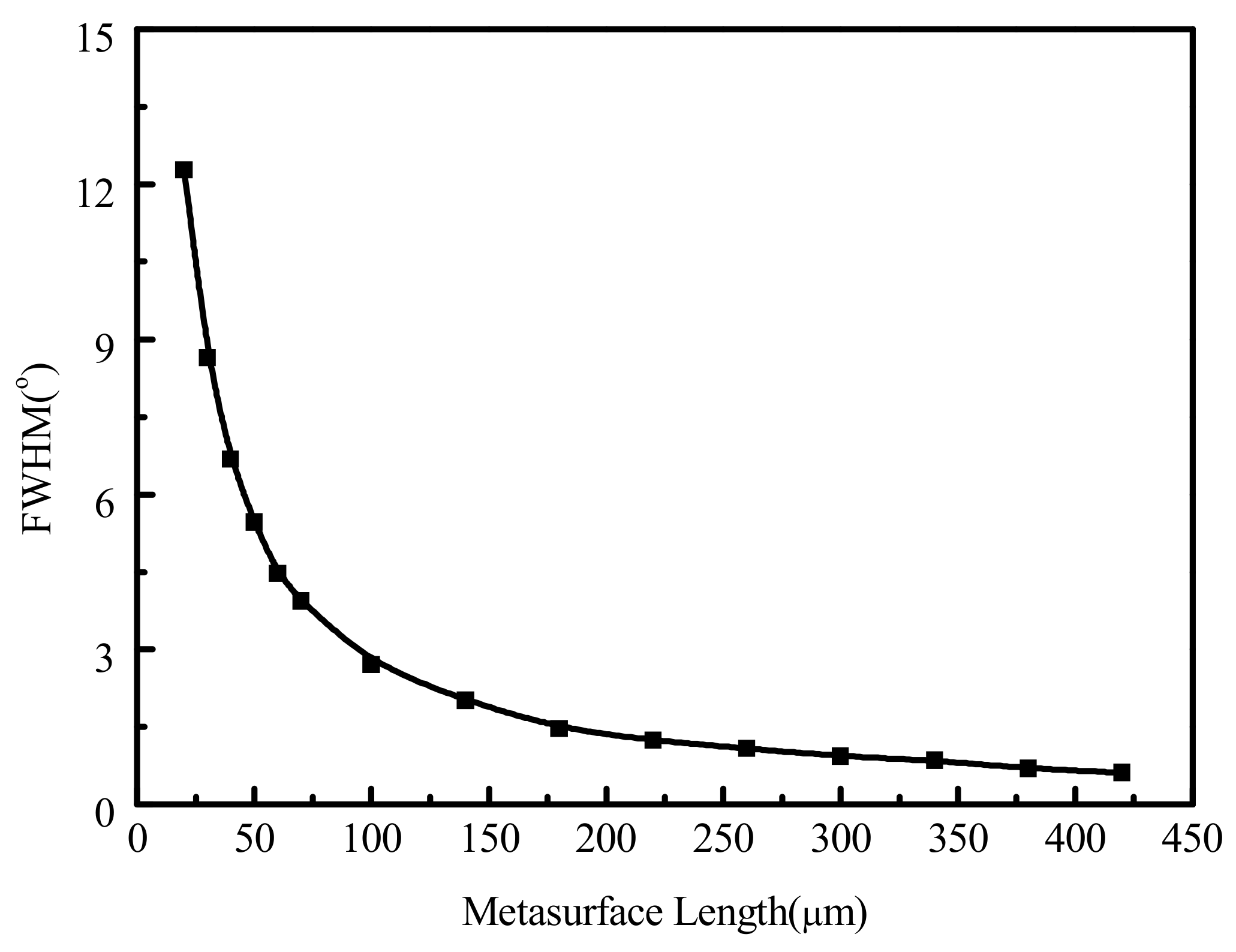
4. Beam Manipulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gozzard, D.R.; Roberts, L.E.; Spollard, J.T.; Sibley, P.G.; Shaddock, D.A. Fast beam steering with an optical phased array. Opt. Lett. 2020, 45, 3793–3796. [Google Scholar] [CrossRef]
- Yoo, B.-W.; Megens, M.; Chan, T.; Sun, T.; Yang, W.; Chang-Hasnain, C.J.; Horsley, D.A.; Wu, M.C. Optical phased array using high contrast gratings for two dimensional beamforming and beamsteering. Opt. Express 2013, 21, 12238–12248. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- McManamon, P.F.; Dorschner, T.A.; Corkum, D.L.; Friedman, L.J.; Hobbs, D.S.; Holz, M.; Liberman, S.; Nguyen, H.Q.; Resler, D.P.; Sharp, R.C.; et al. Optical phased array technology. Proc. IEEE 1996, 84, 268–298. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Bogaerts, W.; Jágerská, J.; Le Thomas, N.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef] [PubMed]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-Insulator. Opt. Express 2010, 18, 13655–13660. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-Scale Silicon Photonic Circuits for Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 264–278. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Abe, H.; Takeuchi, M.; Takeuchi, G.; Ito, H.; Yokokawa, T.; Kondo, K.; Furukado, Y.; Baba, T. Two-dimensional beam-steering device using a doubly periodic Si photonic-crystal waveguide. Opt. Express 2018, 26, 9389–9397. [Google Scholar] [CrossRef]
- Inoue, D.; Ichikawa, T.; Kawasaki, A.; Yamashita, T. Demonstration of a new optical scanner using silicon photonics integrated circuit. Opt. Express 2019, 27, 2499–2508. [Google Scholar] [CrossRef]
- Shirmanesh, G.K.; Sokhoyan, R.; Wu, P.C.; Atwater, H.A. Electro-optically Tunable Multifunctional Metasurfaces. ACS Nano 2020, 14, 6912–6920. [Google Scholar] [CrossRef]
- Zeng, Y.-S.; Qu, S.-W.; Chen, B.-J.; Chan, C.H. All-plasmonic Optical Phased Array Integrated on a Thin-film Platform. Sci. Rep. 2017, 7, 9959. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-Range LiDAR and Free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Wu, L.W.; Ma, H.F.; Wu, R.Y.; Xiao, Q.; Gou, Y.; Wang, M.; Wang, Z.X.; Bao, L.; Wang, H.L.; Qing, Y.M.; et al. Transmission-reflection controls and polarization controls of electromagnetic holograms by a reconfigurable anisotropic digital coding metasurface. Adv. Opt. Mater. 2020, 8, 2001065. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.; Yang, J.; Sun, B.; Zhao, B.; Luo, X. Reconfigurable Metasurface for multifunctional control of electromagnetic waves. Adv. Opt. Mater. 2017, 5, 6. [Google Scholar] [CrossRef]
- Yan, X.; Chen, J.; Dai, D.; Shi, Y. Polarization multiplexing silicon-photonic optical phased array for 2D wide-angle optical beam steering. IEEE Photonics J. 2021, 13, 1–6. [Google Scholar] [CrossRef]
- Kazemian, A.; Wang, P.; Zhuang, Y.; Yi, Y. Optimization of the silicon-based aperiodic optical phased array antenna. Opt. Lett. 2021, 46, 801–804. [Google Scholar] [CrossRef]
- Clevenson, H.A.; Spector, S.J.; Benney, L.; Moebius, M.G.; Brown, J.; Hare, A.; Huang, A.; Mlynarczyk, J.; Poulton, C.V.; Hosseini, E.; et al. Incoherent light imaging using an optical phased array. Appl. Phys. Lett. 2020, 116, 031105. [Google Scholar] [CrossRef]
- Schliesser, A.; Picqué, N.; Hänsch, T.W. Mid-infrared frequency combs. Nat. Photonics 2012, 6, 440–449. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Horie, Y.; Kamali, S.M.; Faraon, A. Planar metasurface retroreflector. Nat. Photonics 2017, 11, 415–420. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.; Shalaev, V.M. Metasurface holograms for visible light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Metasurface optics for full-color computational imaging. Sci. Adv. 2018, 4, eaar2114. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Khorasaninejad, M.; Huang, Y.-W.; Roques-Carmes, C.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Ding, Z.-W.; Tamagnone, M.; Chaudhary, K.; et al. Single-layer metasurface with controllable multiwavelength functions. Nano Lett. 2018, 18, 2420–2427. [Google Scholar] [CrossRef] [PubMed]
- Qin, F.; Ding, L.; Zhang, L.; Monticone, F.; Chum, C.C.; Deng, J.; Mei, S.; Li, Y.; Teng, J.; Hong, M.; et al. Hybrid bilayer plasmonic metasurface efficiently manipulates visible light. Sci. Adv. 2016, 2, e1501168. [Google Scholar] [CrossRef]
- Wang, S.; Lai, J.; Wu, T.; Chen, C.; Sun, J. Wide-band achromatic flat focusing lens based on all-dielectric subwavelength metasurface. Opt. Express 2017, 25, 7121–7130. [Google Scholar] [CrossRef]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically Tunable Metasurface Perfect Absorbers for Ultrathin Mid-Infrared Optical Modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef]
- Komar, A.; Paniagua-Domínguez, R.; Miroshnichenko, A.E.; Yu, Y.F.; Kivshar, Y.S.; Kuznetsov, A.I.; Neshev, D.N. Dynamic beam switching by liquid crystal tunable dielectric metasurfaces. ACS Photonics 2018, 5, 1742–1748. [Google Scholar] [CrossRef]
- Komar, A.; Fang, Z.; Bohn, J.; Sautter, J.; Decker, M.; Miroshnichenko, A.; Pertsch, T.; Brener, I.; Kivshar, Y.S.; Staude, I.; et al. Electrically tunable all-dielectric optical metasurfaces based on liquid crystals. Appl. Phys. Lett. 2017, 110, 071109. [Google Scholar] [CrossRef]
- Luo, Z.; Long, J.; Chen, X.; Sievenpiper, D. Electrically tunable metasurface absorber based on dissipating behavior of embedded varactors. Appl. Phys. Lett. 2016, 109, 071107. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y.; Cheng, Z. Design of a photo-excited switchable broadband reflective linear polarization conversion metasurface for terahertz waves. IEEE Photonics J. 2018, 10, 1–10. [Google Scholar] [CrossRef]
- Masyukov, M.; Vozianova, A.; Grebenchukov, A.; Gubaidullina, K.; Zaitsev, A.; Khodzitsky, M. Optically tunable terahertz chiral metasurface based on multi-layered graphene. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Xie, Z.; Sun, W.; Wang, X.; Ji, Y.; Wang, S.; Lin, Y.; Zhang, Y. Terahertz tunable metasurface lens based on vanadium dioxide phase transition. Plasmonics 2016, 11, 1285–1290. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.; Faraon, A. MEMS-tunable dielectric metasurface lens. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Colburn, S.; Majumdar, A.; Böhringer, K.F. MEMS-actuated metasurface Alvarez lens. Microsyst. Nanoeng. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Park, J.; Gil Jeong, B.; Kim, S.I.; Lee, D.; Kim, J.; Shin, C.; Lee, C.B.; Otsuka, T.; Kyoung, J.; Kim, S.; et al. All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional LiDAR applications. Nat. Nanotechnol. 2021, 16, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Sturmberg, B.C.P.; Lin, K.-T.; Yang, Y.; Zheng, X.; Chong, T.K.; De Sterke, C.M.; Jia, B. A 90-nm-thick graphene metamaterial for strong and extremely broadband absorption of unpolarized light. Nat. Photonics 2019, 13, 270–276. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef]
- Shi, C.; He, X.; Peng, J.; Xiao, G.; Liu, F.; Lin, F.; Zhang, H. Tunable terahertz hybrid graphene-metal patterns metamaterials. Opt. Laser Technol. 2019, 114, 28–34. [Google Scholar] [CrossRef]
- Zeng, F.; Ye, L.; Li, L.; Wang, Z.; Zhao, W.; Zhang, Y. Tunable mid-infrared dual-band and broadband cross-polarization converters based on U-shaped graphene metamaterials. Opt. Express 2019, 27, 33826–33839. [Google Scholar] [CrossRef]
- Lesina, A.C.; Goodwill, D.; Bernier, E.; Ramunno, L.; Berini, P. Tunable plasmonic metasurfaces for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1. [Google Scholar] [CrossRef]
- Savo, S.; Shrekenhamer, D.; Padilla, W.J. Liquid Crystal Metamaterial Absorber Spatial Light Modulator for THz Applications. Adv. Opt. Mater. 2014, 2, 275–279. [Google Scholar] [CrossRef]
- Orazbayev, B.; Beruete, M.; Khromova, I. Tunable beam steering enabled by graphene metamaterials. Opt. Express 2016, 24, 8848–8861. [Google Scholar] [CrossRef] [PubMed]
- AbdollahRamezani, S.; Arik, K.; Farajollahi, S.; Khavasi, A.; Kavehvash, Z. Beam manipulating by gate-tunable graphene-based metasurfaces. Opt. Lett. 2015, 40, 5383–5386. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Huang, Z.; Bai, X.; Zhan, P.; Liu, Y. Dual-band light focusing using stacked graphene metasurfaces. ACS Photonics 2017, 4, 1770–1775. [Google Scholar] [CrossRef]
- Hosseininejad, S.E.; Rouhi, K.; Neshat, M.; Cabellos-Aparicio, A.; Abadal, S.; Alarcon, E. Digital metasurface based on graphene: An application to beam steering in terahertz plasmonic antennas. IEEE Trans. Nanotechnol. 2019, 18, 734–746. [Google Scholar] [CrossRef]
- Su, Z.; Chen, X.; Yin, J.; Zhao, X. Graphene-based terahertz metasurface with tunable spectrum splitting. Opt. Lett. 2016, 41, 3799–3802. [Google Scholar] [CrossRef]
- Fallahi, A.; Perruisseau-Carrier, J. Design of tunable biperiodic graphene metasurfaces. Phys. Rev. B 2012, 86, 195408. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; Yang, G.; Li, Q.; Zhang, Y.; Yan, S.; Wang, C. All-Solid-State Optical Phased Arrays of Mid-Infrared Based Graphene-Metal Hybrid Metasurfaces. Nanomaterials 2021, 11, 1552. https://doi.org/10.3390/nano11061552
Wang Y, Wang Y, Yang G, Li Q, Zhang Y, Yan S, Wang C. All-Solid-State Optical Phased Arrays of Mid-Infrared Based Graphene-Metal Hybrid Metasurfaces. Nanomaterials. 2021; 11(6):1552. https://doi.org/10.3390/nano11061552
Chicago/Turabian StyleWang, Yue, Yu Wang, Guohui Yang, Qingyan Li, Yu Zhang, Shiyu Yan, and Chunhui Wang. 2021. "All-Solid-State Optical Phased Arrays of Mid-Infrared Based Graphene-Metal Hybrid Metasurfaces" Nanomaterials 11, no. 6: 1552. https://doi.org/10.3390/nano11061552
APA StyleWang, Y., Wang, Y., Yang, G., Li, Q., Zhang, Y., Yan, S., & Wang, C. (2021). All-Solid-State Optical Phased Arrays of Mid-Infrared Based Graphene-Metal Hybrid Metasurfaces. Nanomaterials, 11(6), 1552. https://doi.org/10.3390/nano11061552





