3.1. TiO2 (Anatase)-ZnO Interface
Anatase TiO2 and hexagonal ZnO have at ambient temperature similar bandgaps of 3.2 eV (indirect) and 3.3 eV (direct at Γ point), respectively. For ZnO the (110) surface is nonpolar, and has dimensions of 5.628 and 5.207 Å; anatase TiO2 also has (001) as nonpolar surface (even though it is not the most stable one); and its supercell has parameters a = b = 5.342 Å. Thus the epitaxial misfits are of 5% or lower, which justifies considering this interface.
These bulk structures were relaxed with the PBE functional, keeping in the valence space 6, 10 and 12 electrons for O, Ti and Zn, respectively. This resulted in conventional cell sizes of a = b = 3.808 Å and c = 9.703 Å (for anatase) and a = b = 3.288 Å and c = 5.305 Å (for ZnO; β = 120°). These cell lengths are a bit larger than the experimental ones, as is typical of the PBE functional. With these values, the experimental bandgaps of both semiconductors can be reproduced using the hybrid HSE06 functional if the Fock exchange mixing α is α = 0.20 (for anatase) and α = 0.37 (for ZnO). Note that if one had to use the same α value in both cases it would be impossible to obtain bandgap values equal to the experimental ones. The Hartree potential profiles averaged in planes parallel to the said interfaces, as well as the positions of the VB and CB relative to them, are given for both materials in
Figure 1. Throughout this article the VB will always be represented in a red colour, the CB in a blue colour, and the relevant positions of the Hartree potential profile in a black colour. Note that the minima appear at the position of the nuclei; therefore it has been chosen to use as reference for the VB and CB the maximum position, corresponding to the planes between the nuclei. If the integration had been carried out near the nuclei it might have been subjected to important integration grid-related inaccuracies. This criterion will be followed in the rest of this article.
For the models implying semiconductor slabs facing the vacuum, symmetric slabs involving 9 cations layers and 11 cation layers were chosen for anatase and ZnO, respectively. For determining the number of layers to use, the best criterion is that in the central region of all the slabs the potential profiles are converged enough, at least in the planes between the atomic layers; this applies also to the alternating slabs method, and the criterion will be kept throughout this article. The corresponding Hartree potential profiles, after relaxing atom coordinates with fixed cell size, are given in
Figure 2 together with the positions of the VB and CB transferred from the hybrid functional calculations displayed in
Figure 1. In all cases only half of the unit cell is represented, since both interfaces are equivalent by symmetry. This allows the band alignment resulting from the slabs-versus-vacuum model to be inferred.
For the model with the alternating slabs, the structure obtained after full relaxation yielded lateral dimensions of 5.496 Å × 5.361 Å; intermediate, as expected, between those of the individual phases. This structure, again showing only half of the symmetric cell, is presented in
Figure 3, together with the resulting Hartree potential profile and the positions of the VB and CB transferred from the hybrid functional calculations carried out for the bulk systems, so that the band alignment predicted by this other model can be evaluated.
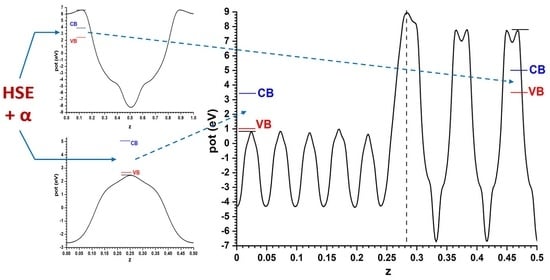
The comparison of both models shows that, although the difference is not large (just 0.1 eV), the prediction of the sign of the CB offset, shown in
Figure 4, is opposite: in the slabs/vacuum case the CB of ZnO is predicted to lie a bit higher than that of anatase, while in the alternating slab model the reverse happens. The outcome of the latter case agrees with the result that the present author reported in an earlier work [
40], also using the alternating slabs model (even though in that case a different software was used: the CRYSTAL program, based on atom-centred basis sets), which explained the then recent result [
41] that a ZnO-based dye sensitized photovoltaic cell improved its efficiency if a very thin layer of anatase TiO
2 was deposited on the ZnO nanoparticles, which was interpreted there assuming that anatase formed with its CB a barrier preventing the recombination of the excited electrons with the hole remaining in the dye. Now it is seen that the model using slabs against vacuum would have given different results.
It is worthwhile trying to understand this difference between both models. One way could be to examine the Hartree potential profile for the alternating slabs model and obtain the difference between it and the sum of the Hartree profiles of the individual slabs, while keeping the same cell size and atomic positions. The difference, shown in
Figure 5, is not large, it is certainly much smaller than the values of the full profile shown in
Figure 3; but one finds that the Hartree potential imbalance between one phase and the other shown in
Figure 5 (0.33 eV) is clearly higher than the difference in results between both models (just 0.1 eV). Some other effects must be at work. Very probably the reason is that while in the slabs versus vacuum model there will be a spill of electronic density towards the vacuum side which may reach different distances in the ZnO and TiO
2 cases (and note that this will appear as well in the alternating slabs model, with fixed atomic positions involved in the said subtraction of Hartree potential profiles), this is not possible in the alternating slabs case, where in addition the Pauli exclusion principle will force a rearrangement of the individual wavefunctions. The mentioned Hartree potential difference is thus not useful to understand the difference between both methods of estimating the band offset. In the following, this difference of Hartree potential will not be considered further.
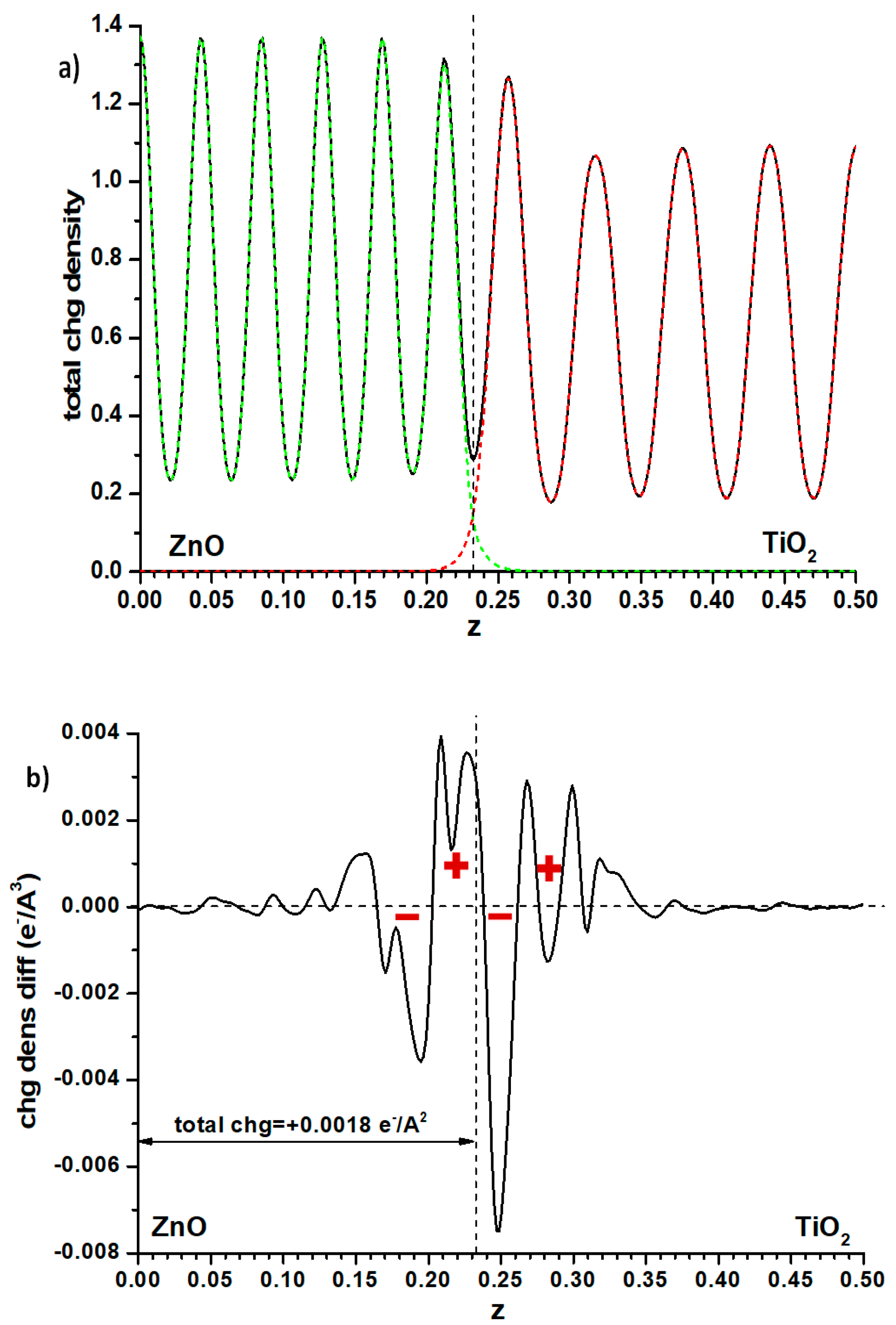
Another possibility is to examine the plane-averaged profile of electronic density and subtract from it the sum of the individual slabs that remain unchanged, as for the Hartree profile, the cell size and atomic positions. This may reveal some flow of electron density between both phases, perhaps explaining the effect. Again, as seen in
Figure 6 where the full electronic density given by the PAW method is compared with the said difference, the effect is small. The integration of this difference, measured (somewhat arbitrarily) up to the point of the minimum in total electron density at the interface position (marked with a dashed line in that figure), implies that a small charge (0.0018 e
−/Å
2) has flown from anatase to ZnO. This should raise the electron levels in ZnO, contrarily to what one could think by looking at the difference between both methods of calculation of the band offsets (
Figure 4). However, examining the electron density difference curve more closely, one observes that the electron density distribution implies the presence, at both sides of the interface, of a significant dipole (marked with red signs in
Figure 6b) accumulating electronic density more towards the anatase side; it may be this dipole, rather than the net amount of charge transferred, which causes the electron levels of the anatase side to rise.
Finally, one can examine the Bader charges at the atoms in one and another side of the alternating slab model of the interface. Here of course the situation of slabs versus vacuum is not taken into account. One then finds that a net electronic charge of 0.006 e
−/Å
2 is transferred to the anatase side. The difference with the result found when considering the electronic density difference (
Figure 6) may be due to different factors. The Bader charges use basins of electronic density the frontiers of which may not coincide with the interface plane. Furthermore, Bader charges are just single values that do not take into account the possibility that the Bader basins may include an uneven distribution of electronic density, i.e., may have dipoles which influence the Hartree potential profiles; for this reason, in the rest of the cases presented here, the profile of electronic density differences will still be shown, to verify whether they may present the dipole effect shown in
Figure 6.
In any case, what may be at the root of the charge transfer revealed by the Bader charges is the difference in averaged electronegativities between ZnO and TiO
2; whether calculated in the Pauling or Allred–Rochow scales [
42] and with arithmetic or geometric means, it is evaluated to be 0.15–0.3 units higher for TiO
2 than for ZnO. This explains that there may be some transfer of electronic density from ZnO to TiO
2 when joining both materials, so that the electronic levels of TiO
2 are raised; this of course cannot be taken into account in the slabs-versus-vacuum method of calculating band offsets.
Finally, it is worth verifying if the distortions induced in the alternating slab model lead to a significant change in the bandgaps of these materials. For this, distorted bulk structures were obtained from the centre of the fully relaxed alternating slabs, and their electronic structures were evaluated keeping the same cell dimensions and atomic coordinates deduced from these central regions and using the same α values as for the bulk phases. Bandgaps of 3.17 and 3.24 eV were obtained for anatase and ZnO, respectively, indicating that the distortions, while slightly decreasing the bandgaps (by 30 meV in both cases), are probably not enough to reverse the sign of the band offsets.
In summary, any comparison between the results of both models, slabs versus vacuum and alternating slabs, may require a very detailed discussion. In the rest of this paper, other semiconductor pairs will be addressed; only the results similar to those of
Figure 4 will be presented in the main text, while the structures and potential or electron density profiles will always be given in the
Supplementary Materials.
3.2. ZnS-CuGaS2 Interface
ZnS and CuGaS2 have bandgaps of 3.54 and 2.38 eV, respectively. Both materials have their atoms in tetrahedral coordination, the first one with a fcc arrangement and the second one with a tetragonal chalcopyrite structure; in both cases their (110) planes are nonpolar. According to experimental data, the lattice dimensions of these planes (doubled in the ZnS case) are 7.65 Å × 10.82 Å and 7.58 Å × 10.49 Å, respectively. The misfit is 3% or smaller; one can therefore consider studying interfaces built from these planes.
Their bulk structures were relaxed with the PBE functional, keeping in the valence space 6, 11, 12 and 3 electrons for S, Cu, Zn and Ga, respectively. Relaxing ZnS leads to dimensions in these planes of 7.704 and 10.895 Å; its experimental bandgap is obtained with the HSE06 hybrid functional using α = 0.307. Relaxing equally CuGaS
2 leads to (110) plane dimensions of 7.582 and 10.622 Å; in this case the experimental bandgap is obtained with HSE06 using α = 0.315. The very similar α values here could be expected since the CuGaS
2 structure can be derived from that of ZnS simply by changing the neighbours closest to Zn in the periodic table. The structures seen parallel to the (110) planes, as well as the Hartree profiles including the positions of the bands relative to them as deduced from the mentioned HSE06 calculations, are presented for both materials in
Figure S1 of the Supplementary Materials.
The structures chosen for the slab/vacuum model include 10 cation layers for each material; thanks to the centred symmetry of both structures the number of atoms can be halved.
Figure S2 presents the structures of these slabs once relaxed in atomic positions (not in cell size), together with the Hartree potential profiles and the positions of the VB and CB transferred from the bulk results given in
Figure S1. As in
Figure 2 above, this allows for the determining of the band offsets within the slab/vacuum model.
The alternating slab model including both materials, with the same amount of cation planes, was built and relaxed as in case I above. The resulting lateral dimensions, as expected, were intermediate between those of the individual phases. The Hartree potential profile was obtained and the positions of the VB and CB were transferred so that the band offsets deduced from this model can be obtained.
Figure S3 presents those data.
The comparison of both models is presented in
Figure 7. Here, we see that the band offsets, although always with the same sign (leading to a type II band alignment), are more different than in
Figure 4 above, i.e., the difference amounts to ca. 0.3 eV. Again, it is worthwhile to try to understand the reason why. As before, the differences of the Hartree potential profiles give no clue, due to the spill of the electronic density towards the vacuum. One may then look at the distribution of electronic density. In this case the density difference curve, presented in
Figure S4, does not reveal any significant electron density transfer (its integral up to the minimum of total density amounts only to 0.0002 e
−/Å
2); and no dipole seems to have developed. One explanation for the difference between both methods appears when one looks at the Bader charges of the different atoms; they reveal that there is a net transfer of 0.001 e
−/Å
2 from ZnS to CuGaS
2, which may explain at least in part the rise in the levels of the latter material when the two phases are put in contact. Additionally, the averaged electronegativities of CuGaS
2 are higher by ca. 0.1 units than those of ZnS, which, together with the probably higher softness of (at least) the anions, explains again that some electronic density may have been transferred from ZnS to CuGaS
2.
3.3. A Related System: The Interface between CdS and CuGaS2
CdS has a bandgap of 2.3 eV, and since its structure is the same as that of ZnS the (110) surface is again nonpolar. Due to the larger size of Cd the dimensions of that plane, which will be used again to build the interface, are now (once doubled) 8.248 × 11.664 Å, i.e., ca. 9% and 11% larger than those of CuGaS2; this may allow to see to what extent the distortions induced when forming the interface in the mixed slab method may alter the results.
CdS, with 12 electrons kept in the valence space of Cd, gave after relaxation at the PBE level a cubic lattice constant of 5.933 Å, implying lateral dimensions of 8.39 × 11.866 Å for the doubled (110) surface. Its bandgap could be reproduced with the HSE06 functional using α = 0.30.
Figure S5 presents the Hartree potential profile, together with the positions of VB and CB provided by VASP; the figure given in
Section 2.2 for CuGaS
2 is reproduced here as well, to ease the comparisons. The Hartree potential profile found for both phases within the slab/vacuum model using the same scheme as above is presented, as well as the positions of VB and CB, in
Figure S6; this, together with the previous results found for CuGaS
2, allows obtaining the band offsets within this model.
The alternating slab model was also undertaken; after full relaxation of the structure at the PBE level the lateral dimensions were 7.95 × 11.04 Å, implying significant distortions of these phases. In any case the joint Hartree profile was obtained; it is presented in
Figure S7 together with the positions of the VB and CB of both phases as deduced from the hybrid functional calculations of the bulk solids.
This would allow the comparison of the results of both models. However here, due to the larger epitaxial misfit and the ensuing lattice distortions, it is convenient to verify whether there is a change in the positions of the VB and CB which may affect to the band alignments. One way to check this is to build (as said in the anatase|ZnO case), from the innermost regions of both alternating slabs, bulk structures with the same cell periodicity and atom positions of these inner regions, of course with no relaxation at all; and then carry out HSE06 calculations for these distorted bulk phases using the same α value as for the fully relaxed bulks. The result of that calculation, including the Hartree potential profile as well as the band positions, is given in
Figure S8a). One can see that the bandgaps have decreased significantly, especially for CuGaS
2, for which the distorted structure leads to a bandgap even lower than 2.0 eV. If these new band positions are translated to the same Hartree potential profile already obtained for the alternating slab model, the result is given in
Figure S8b).
Figure 8 presents a summary of these results. While the slabs versus vacuum model (
Figure 8a) gives nearly the same band offset as the alternating slabs model when the distortions are disregarded (
Figure 8b), once the latter are taken into account (
Figure 8c) the band alignment is severely altered; although a type II band alignment still appears, the band offset is reduced by ca. 0.5 eV.
Of course, these distortions will never happen in the real world. Interfaces implying the (110) planes of both materials may indeed occur, but the two phases will try to develop the lattice constants producing in all cases the energy minima; this will result in any type of defects (e.g., stacking faults) which may allow those minima to be approached. For such systems one might study with important cell misfit, as in the CdS|CuGaS2 case presented here, the electron density distribution in the mixed slabs model, as well as the corresponding electron density transfer; but no useful information may be gained from this, as these distortions will never be real. Even the result of the Bader analysis, yielding here a (rather small) transfer of atomic charge from CdS to CuGaS2 of 0.0005 e−/Å2, which is in agreement again with the prediction considering the averaged electronegativities, must be used with caution.
In the end, the most convenient way of handling a problem such as the one found here may consist in developing larger supercells in the directions parallel to the desired interface which allow for a smaller overall strain, even if this implies a larger number of defects or unsatisfied bonds at the interface; this was performed for example in ref. [
43]. Indeed, the contacting phases, especially if they are not present as ultrathin films, will manage to grow in such a way that their bandgaps are not disturbed much from the natural ones. This may take place by contact through different crystal planes, developing stacking faults (or other defect types) and accumulating impurities at the interface, etc.
3.4. The Rutile TiO2-PbTe Interface
Rutile-type TiO
2 has a bandgap of 3.0 eV, much larger than that of PbTe (0.27 eV [
44]). TiO
2, with tetragonal structure, has a = b = 4.594 Å and c = 2.959 Å; PbTe, when the symmetry of its fcc structure is decreased to centred tetragonal, has a = b = 4.569 Å. Since both (001) planes are nonpolar (although it is well known that for rutile TiO
2 the most stable surface is the (110) one), they provide a nice example of near-perfect epitaxy (the misfit is ~0.5%).
These structures were relaxed with the PBE functional, keeping in the valence space 6, 10, 14 and 24 electrons for O, Ti, Pb and Te, respectively. In the case of PbTe it is necessary to include the spin-orbit relativistic interaction, due to the especially heavy nature of the Pb cation. The fully relaxed PbTe, including the spin-orbit coupling (henceforth mentioned as S.-O. coupling), has (in the tetragonal setting) a = 4.627 Å; its bandgap is reproduced with HSE06 functional using α = 0.115. Here it is found that, if the S.-O. coupling is not included, the hybrid calculation with the same α value yields a gap of 1.00 eV. The situation is thus similar to that well known in the case of the nowadays much studied methylammonium lead iodide perovskite, which also includes divalent Pb; in that case, neglect of the S.-O. coupling leads to a bandgap 0.9 eV higher [
45].
In order to be consistent, one also has to apply the spin-orbit interaction to the rutile case (although doing so negligibly changes its bandgap), as well as to all the other calculations in this section. After the PBE relaxation (including S.-O. coupling), rutile TiO
2 has a = 4.601 Å and c = 2.953 Å. Its bandgap can be reproduced with HSE06 functional (including again S.-O. coupling) using α = 0.21. The resulting Hartree potential profiles for both semiconductors in the direction perpendicular to the (001) plane are given in
Figure S9, including also the positions of VB and CB relative to them.
As in the preceding cases,
Figure S10 presents the Hartree potential profiles of the TiO
2 and PbTe (001) slabs contiguous to the vacuum, relaxed in atomic coordinates but with the dimensions parallel to the surface fixed to the bulk values; the positions of the VB and CB relative to them, as transferred from the respective hybrid calculations carried out for the bulk phases, are also included, so that the band offsets resulting from this model can be obtained. Note that in this case the number of cation planes of the rutile phase (17) had to be significantly higher than that chosen for the PbTe phase (9); not because of the shorter interplanar spacing in the first case, but mainly due to the oscillating nature of the Hartree profile found for the rutile, which required ensuring a converged enough profile in this case.
For the alternating slabs model, the resulting Hartree potential profile, again with the same number of cation layers, is presented in
Figure S11 together with the corresponding positions of the VBs and CBs. The band offsets resulting from this model can thus be estimated.
The comparison of both models is presented in
Figure 9. It can be seen that the difference in band offsets is ca. 0.20 eV. This is clearly smaller than the band offset itself (over 1.00 eV), but is not insignificant. As in the preceding cases, the total electronic density distribution is almost the same as the sum of the densities of the separated slabs; the relevant quantity is the difference in electron densities, which is presented in
Figure S12 together with the full electron density profile of the compound slab. This difference is not really large, and amounts, up to the point of minimum density between slabs, to a transfer from PbTe to TiO
2 of 0.002 e
−/Å
2. There is some hint of a dipole at both sides of the interface, with higher amount of electronic density, in both sides, towards the side of PbTe. If one looks at the Bader charges, it can be seen however that that the amount of charge transferred from PbTe to TiO
2 is 0.0086 e
−/Å
2. This agrees with the difference in electronegativity of both materials, which is higher in TiO
2 by 0.6–1.0 units (depending on the way it is estimated).
3.5. The Interface between the (111) Planes of Diamond and α-Tin
C in the diamond form and the semiconducting α-tin form (also called gray tin) have cubic fcc structures with a = 3.567 and 6.489 Å, respectively. The ratio between these values is 1.819, thus differing only 5% from
= 1.732. This implies that a
supercell of the (111) plane in diamond, with a = 4.368 Å, can be combined with the (111) plane of α-tin (where a = 4.588 Å). Their bandgaps are certainly very different: for diamond the bandgap is 5.44 eV, while for α-tin it is only ~0.1 eV [
46].
The structures were relaxed with the PBE functional, keeping in the valence space 4 and 14 electrons for C and Sn, respectively. For the Sn primitive cell this resulted in a = 4.707 Å for the (111) surface (therefore a = 6.656 Å for the conventional cell), and its bandgap could be reproduced with the HSE06 functional using α = 0.20. It was verified that including the spin-orbit coupling, together with this α value, did not lead to a significant change in the bandgap. For the primitive lattice of diamond-type C this relaxation resulted in a = 2.527 Å (therefore a = 3.574 Å for the conventional cell), so that
times this value implies 4.377 Å; its bandgap could be reproduced with HSE06 using α = 0.27. For both cases the Hartree potential profiles in the direction perpendicular to the (111) plane were obtained; they are presented, together with the positions of the VB and CB, in
Figure S13.
When working with the slabs, care was taken in this case to use spin-polarized calculations, since one should take into account, especially for diamond, the possibility of having dangling bonds containing unpaired electrons. For both materials, slabs facing the vacuum with interfaces parallel to the (111) plane and containing nine planes, having the lateral dimensions fixed at the values of the bulk, were built and relaxed in the internal atomic coordinates; the resulting Hartree potential profiles are shown in
Figure S14 together with the positions of VB and CB as transferred from the results in
Figure S13. One may note the significant distortion of the profile for the outermost layer in the α-tin. Additionally, spin densities appear in the C slab joining vacuum: the values projected inside the PAW sphere amount to 0.45 for those C atoms presenting dangling bonds, and there are also values of 0.12 in some deeper C atoms. This is compatible with the minimum gap computed here at the PBE level for this slab: 2.06 eV, indicating that a metallic character is not present. In the Sn slab facing the vacuum, however, no net spin density is found for any atom, not even those which might have dangling bonds. Probably, although such bonds may be present, a metallic behaviour occurs in this case, with equal population of up and down spins in all atoms. However, these results probably do not reflect the real experimental situation; see below the comments on known reconstructions of these surfaces.
The structure of the completely relaxed compound slab including the same number of atomic layers is presented in
Figure S15, together with the Hartree potential profile and the corresponding positions of the VB and CB. Here, however, no spin density is found on any atom; this might be due to the metallic character of the Sn-C interface, which affects the overall spin density distribution equaling for all atoms the population of up and down spins. Note also that the distortion of atomic positions revealed in
Figure S13 is not present here.
The comparison of both calculation methods is presented in
Figure 10. Here, the difference in band offsets is higher, almost 0.3 eV, although this does not alter the character of the band alignment that remains of type 1. The analysis of the electron density distribution, shown in
Figure S16, indicates an electron density transfer from Sn to C of 0.006 e
−/Å
2, while the Bader analysis indicates that there is a relatively large transfer of electrons from Sn to C of 0.06 e
−/Å
2, in agreement with the difference of average electronegativities (ca. 0.6/0.8 units in the Pauling/Allred–Rochow scales, respectively).
However, it turns out that for diamond-type C it was reported that a 2 × 1 reconstruction exists for the (111) surface [
47]. For Sn (111), two reconstructions are known (at least for 50 ML thin films): a (3 × 3) one existing at ambient temperature and a (2 × 2) one appearing in the interval between 50 and 150 °C, being followed at higher temperature by a (1 × 1) structure, shortly before fusion [
48]. All these reconstructions, of course, were identified for interfaces between these materials and vacuum. It makes no sense trying to study them, since what one wants to study here is the band offset appearing when both materials are joined, and due to the electronegativity difference one can foresee that a significant electron density transfer from Sn to C will then appear. The main issue here then is that one cannot know which reconstructions might arise at an interface between Sn and C (111) surfaces; they might be quite different from those experimentally observed for the individual surfaces.