Beyond Charge Transfer: The Impact of Auger Recombination and FRET on PL Quenching in an rGO-QDs System
Abstract
:1. Introduction
2. Materials and Methods
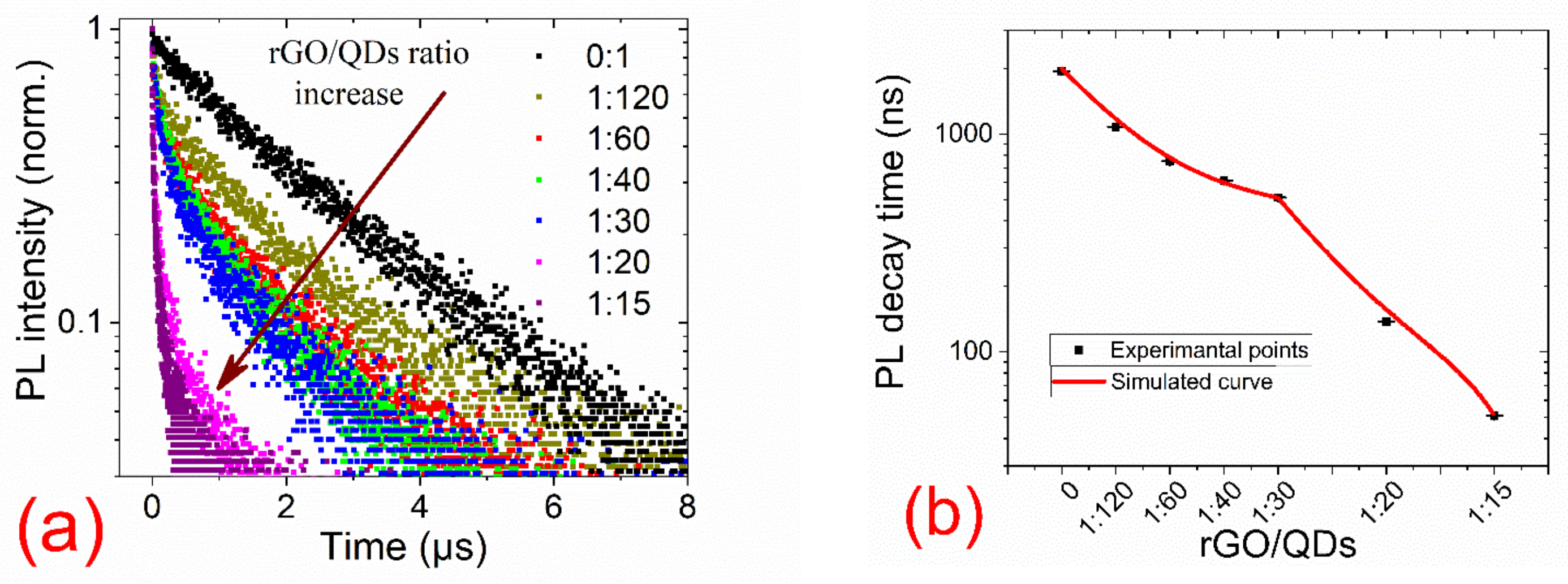
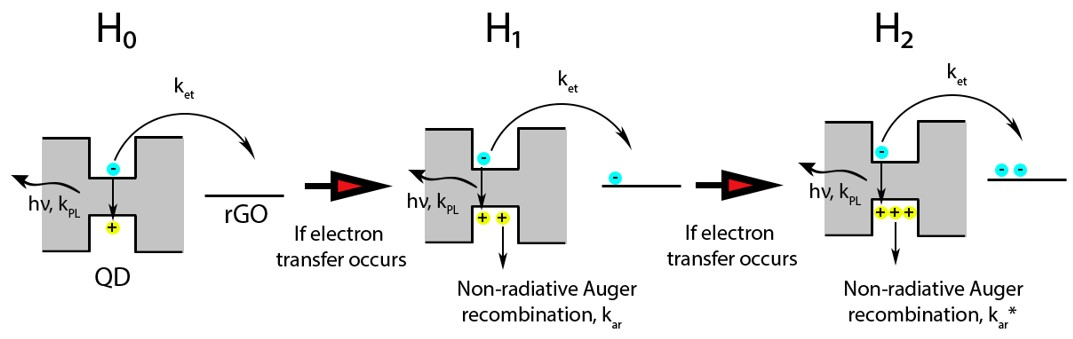
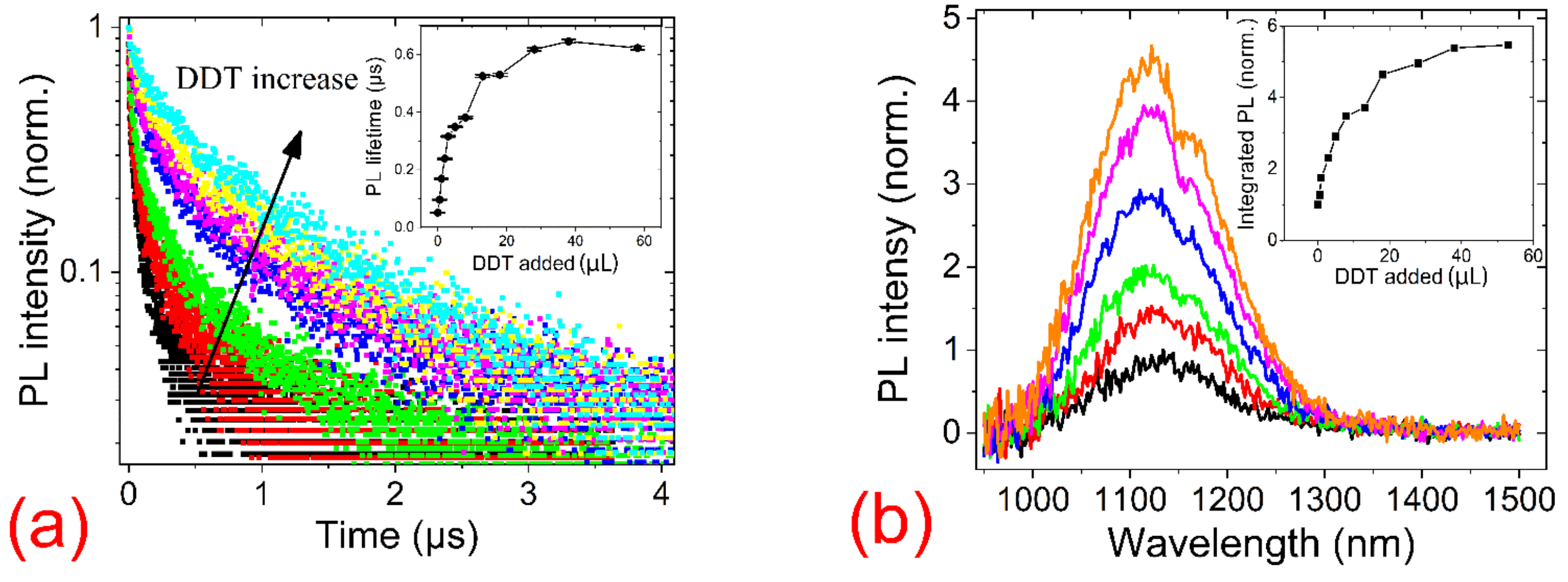
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Nozik, A.J.; Beard, M.C.; Luther, J.M.; Law, M.; Ellingson, R.J.; Johnson, J.C. Semiconductor quantum dots and quantum dot arrays and applications of multiple exciton generation to third-generation photovoltaic solar cells. Chem. Rev. 2010, 110, 6873–6890. [Google Scholar] [CrossRef] [PubMed]
- Omata, T. Colloidal semiconductor quantum dots; syntheses, properties and applications. J. Ceram. Soc. Jpn. 2015, 123, 1–8. [Google Scholar] [CrossRef]
- Sargent, E.H. Colloidal quantum dot solar cells. Nat. Photonics 2012, 6, 133–135. [Google Scholar] [CrossRef]
- Keuleyan, S.; Lhuillier, E.; Brajuskovic, V.; Guyot-Sionnest, P. Mid-infrared HgTe colloidal quantum dot photodetectors. Nat. Photonics 2011, 5, 489–493. [Google Scholar] [CrossRef]
- Litvin, A.P.; Martynenko, I.V.; Purcell-Milton, F.; Baranov, A.V.; Fedorov, A.V.; Gun’Ko, Y.K. Colloidal quantum dots for optoelectronics. J. Mater. Chem. A 2017, 5, 13252–13275. [Google Scholar] [CrossRef]
- Probst, C.E.; Zrazhevskiy, P.; Bagalkot, V.; Gao, X. Quantum dots as a platform for nanoparticle drug delivery vehicle design. Adv. Drug Deliv. Rev. 2013, 65, 703–718. [Google Scholar] [CrossRef]
- Wang, R.; Shang, Y.; Kanjanaboos, P.; Zhou, W.; Ning, Z.; Sargent, E.H. Colloidal quantum dot ligand engineering for high performance solar cells. Energy Environ. Sci. 2016, 9, 1130–1143. [Google Scholar] [CrossRef]
- Brown, P.R.; Kim, D.; Lunt, R.R.; Zhao, N.; Bawendi, M.G.; Grossman, J.C.; Bulović, V. Energy level modification in lead sulfide quantum dot thin films through ligand exchange. ACS Nano 2014, 8, 5863–5872. [Google Scholar] [CrossRef] [PubMed]
- Kumawat, N.K.; Swarnkar, A.; Nag, A.; Kabra, D. Ligand Engineering to Improve the Luminance Efficiency of CsPbBr3 Nanocrystal Based Light-Emitting Diodes. J. Phys. Chem. C 2018, 122, 13767–13773. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Tang, J.; Tang, W. Surface ligands engineering of semiconductor quantum dots for chemosensory and biological applications. Mater. Today 2017, 20, 360–376. [Google Scholar] [CrossRef]
- Litvin, A.P.; Babaev, A.A.; Parfenov, P.S.; Dubavik, A.; Cherevkov, S.A.; Baranov, M.A.; Bogdanov, K.V.; Reznik, I.A.; Ilin, P.O.; Zhang, X.; et al. Ligand-assisted formation of graphene/quantum dot monolayers with improved morphological and electrical properties. Nanomaterials 2020, 10, 723. [Google Scholar] [CrossRef]
- Sokolov, P.M.; Zvaigzne, M.A.; Krivenkov, V.A.; Litvin, A.P.; Baranov, A.V.; Fedorov, A.V.; Samokhvalov, P.S.; Nabiev, I.R. Graphene–quantum dot hybrid nanostructures with controlled optical and photoelectric properties for solar cell applications. Russ. Chem. Rev. 2019, 88, 370–386. [Google Scholar] [CrossRef]
- Martín-García, B.; Bi, Y.; Prato, M.; Spirito, D.; Krahne, R.; Konstantatos, G.; Moreels, I. Reduction of moisture sensitivity of PbS quantum dot solar cells by incorporation of reduced graphene oxide. Sol. Energy Mater. Sol. Cells 2018, 183, 1–7. [Google Scholar] [CrossRef]
- Babaev, A.A.; Parfenov, P.S.; Onishchuk, D.A.; Dubavik, A.; Cherevkov, S.A.; Rybin, A.V.; Baranov, M.A.; Baranov, A.V.; Litvin, A.P.; Fedorov, A.V. Functionalized rGO interlayers improve the fill factor and current density in PbS QDs-based solar cells. Materials 2019, 12, 4221. [Google Scholar] [CrossRef] [PubMed]
- Martín-García, B.; Polovitsyn, A.; Prato, M.; Moreels, I. Efficient charge transfer in solution-processed PbS quantum dot-reduced graphene oxide hybrid materials. J. Mater. Chem. C 2015, 3, 7088–7095. [Google Scholar] [CrossRef]
- Lightcap, I.V.; Kamat, P.V. Fortification of CdSe quantum dots with graphene oxide. Excited state interactions and light energy conversion. J. Am. Chem. Soc. 2012, 134, 7109–7116. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Zhang, K.; Chen, W.; Liu, Y.; Geng, Z.; Zeng, J.; Pan, N.; Yan, L.; Wang, X.; Hou, J.G. Dramatically enhanced photoresponse of reduced graphene oxide with linker-free anchored CdSe nanoparticles. ACS Nano 2010, 4, 3033–3038. [Google Scholar] [CrossRef]
- Pham, C.V.; Eck, M.; Krueger, M. Thiol functionalized reduced graphene oxide as a base material for novel graphene-nanoparticle hybrid composites. Chem. Eng. J. 2013, 231, 146–154. [Google Scholar] [CrossRef]
- Jung, M.H.; Chu, M.J. Comparative experiments of graphene covalently and physically binding CdSe quantum dots to enhance the electron transport in flexible photovoltaic devices. Nanoscale 2014, 6, 9241–9249. [Google Scholar] [CrossRef]
- Wei, X.N.; Ou, C.L.; Guan, X.X.; Peng, Z.K.; Zheng, X.C. Facile assembly of CdS-reduced graphene oxide heterojunction with enhanced elimination performance for organic pollutants in wastewater. Appl. Surf. Sci. 2019, 469, 666–673. [Google Scholar] [CrossRef]
- Zedan, A.F.; Sappal, S.; Moussa, S.; El-Shall, M.S. Ligand-controlled microwave synthesis of cubic and hexagonal cdse nanocrystals supported on graphene. Photoluminescence quenching by graphene. J. Phys. Chem. C 2010, 114, 19920–19927. [Google Scholar] [CrossRef]
- Babaev, A.; Dubavik, A.; Cherevkov, S.; Parfenov, P.; Ushakova, E.; Baranov, M.; Nabiev, I.; Baranov, A.; Litvin, A. Optical properties of PBS-GO and PBS-RGO system for solar cells fabrication. In Proceedings of the 10th Anniversary International Conference on Nanomaterials-Research and Application (NANOCON 2018), Brno, Czech Republic, 17–19 October 2018; pp. 24–29. [Google Scholar]
- Do Nascimento, R.F.; Silva, A.C.A.; Sales, T.O.; Sonsin, A.F.; Da Silva Fonseca, E.J.; Souza, S.T.; De Oliveira, Y.M.; De Abreu, F.C.; Dantas, N.O. Tuning the Optical and Electrical Properties of rGO-CdSe/CdS Ultrasmall Quantum Dot Nanocomposites. J. Phys. Chem. C 2021, 125, 6805–6811. [Google Scholar] [CrossRef]
- Efros, A.L. Nanocrystals: Almost always bright. Nat. Mater. 2008, 7, 612–613. [Google Scholar] [CrossRef] [PubMed]
- Efros, A.L.; Nesbitt, D.J. Origin and control of blinking in quantum dots. Nat. Nanotechnol. 2016, 11, 661–671. [Google Scholar] [CrossRef]
- Ushakova, E.V.; Litvin, A.P.; Parfenov, P.S.; Fedorov, A.V.; Artemyev, M.; Prudnikau, A.V.; Rukhlenko, I.D.; Baranov, A.V. Anomalous size-dependent decay of low-energy luminescence from PbS quantum dots in colloidal solution. ACS Nano 2012, 6, 8913–8921. [Google Scholar] [CrossRef] [PubMed]
- Hines, M.A.; Scholes, G.D. Colloidal PbS Nanocrystals with Size-Tunable Near-Infrared Emission: Observation of Post-Synthesis Self-Narrowing of the Particle Size Distribution. Adv. Mater. 2003, 15, 1844–1849. [Google Scholar] [CrossRef]
- Wu, J.; Ling, L.; Xie, J.; Ma, G.; Wang, B. Surface modification of nanosilica with 3-mercaptopropyl trimethoxysilane: Experimental and theoretical study on the surface interaction. Chem. Phys. Lett. 2014, 591, 227–232. [Google Scholar] [CrossRef]
- An, Y.; Chen, M.; Xue, Q.; Liu, W. Preparation and self-assembly of carboxylic acid-functionalized silica. J. Colloid Interface Sci. 2007, 311, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wang, S.; Zhang, D.; Li, Z.; Fang, Y.; Qiu, X. Control of carrier type and density in exfoliated graphene by interface engineering. ACS Nano 2011, 5, 408–412. [Google Scholar] [CrossRef]
- Huang, N.J.; Xia, Q.Q.; Zhang, Z.H.; Zhao, L.; Zhang, G.D.; Gao, J.F.; Tang, L.C. Simultaneous improvements in fire resistance and alarm response of GO paper via one-step 3-mercaptopropyltrimethoxysilane functionalization for efficient fire safety and prevention. Compos. Part. A Appl. Sci. Manuf. 2020, 131, 105797. [Google Scholar] [CrossRef]
- Senkevich, J.J.; Mitchell, C.J.; Yang, G.R.; Lu, T.M. Surface chemistry of mercaptan and growth of pyridine short-chain alkoxy silane molecular layers. Langmuir 2002, 18, 1587–1594. [Google Scholar] [CrossRef]
- Skurlov, I.D.; Onishchuk, D.A.; Parfenov, P.S.; Litvin, A.P. An Experimental Setup for Analysis of Weak Photoluminescence in the Near-Infrared Spectral Region. Opt. Spectrosc. 2018, 125, 756–759. [Google Scholar] [CrossRef]
- Parfenov, P.S.; Litvin, A.P.; Ushakova, E.V.; Fedorov, A.V.; Baranov, A.V.; Berwick, K. Note: Near infrared spectral and transient measurements of PbS quantum dots luminescence. Rev. Sci. Instrum. 2013, 84, 116104. [Google Scholar] [CrossRef]
- Parfenov, P.S.; Litvin, A.P.; Baranov, A.V.; Ushakova, E.V.; Fedorov, A.V.; Prudnikov, A.V.; Artemyev, M.V. Measurement of the luminescence decay times of PbS quantum dots in the near-IR spectral range. Opt. Spectrosc. 2012, 112, 868–873. [Google Scholar] [CrossRef]
- Chistyakov, A.A.; Zvaigzne, M.A.; Nikitenko, V.R.; Tameev, A.R.; Martynov, I.L.; Prezhdo, O.V. Optoelectronic Properties of Semiconductor Quantum Dot Solids for Photovoltaic Applications. J. Phys. Chem. Lett. 2017, 8, 4129–4139. [Google Scholar] [CrossRef]
- Lightcap, I.V.; Kosel, T.H.; Kamat, P.V. Anchoring semiconductor and metal nanoparticles on a two-dimensional catalyst mat. storing and shuttling electrons with reduced graphene oxide. Nano Lett. 2010, 10, 577–583. [Google Scholar] [CrossRef]
- Peterson, J.J.; Krauss, T.D. Fluorescence spectroscopy of single lead sulfide quantum dots. Nano Lett. 2006, 6, 510–514. [Google Scholar] [CrossRef]
- Galland, C.; Ghosh, Y.; Steinbrück, A.; Sykora, M.; Hollingsworth, J.A.; Klimov, V.I.; Htoon, H. Two types of luminescence blinking revealed by spectroelectrochemistry of single quantum dots. Nature 2011, 479, 203–207. [Google Scholar] [CrossRef]
- Litvin, A.P.; Parfenov, P.S.; Ushakova, E.V.; Vorsina, T.A.; Simões Gamboa, A.L.; Fedorov, A.V.; Baranov, A.V. FRET-Activated Delayed Fluorescence in Densely Packed PbS Quantum-Dot Ensembles. J. Phys. Chem. C 2015. [Google Scholar] [CrossRef]
- De Geyter, B.; Justo, Y.; Moreels, I.; Lambert, K.; Smet, P.F.; Van Thourhout, D.; Houtepen, A.J.; Grodzinska, D.; De Mello Donega, C.; Meijerink, A.; et al. The different nature of band edge absorption and emission in colloidal PbSe/CdSe core/shell quantum dots. ACS Nano 2011, 5, 58–66. [Google Scholar] [CrossRef]
- Zhao, H.; Liang, H.; Gonfa, B.A.; Chaker, M.; Ozaki, T.; Tijssen, P.; Vidal, F.; Ma, D. Investigating photoinduced charge transfer in double- and single-emission PbS@CdS core@shell quantum dots. Nanoscale 2014, 6, 215–225. [Google Scholar] [CrossRef] [PubMed]

| Sample | A1 | t1, ns | A2 | t2, ns | A3 | t3, ns | Average PL Lifetime, ns |
|---|---|---|---|---|---|---|---|
| 0:1 | 0.13 ± 0.01 | 147 ± 14 | 0.870 ± 0.003 | 2212 ± 10 | 1950 ± 14 | ||
| 1:120 | 0.38 ± 0.01 | 62 ± 3 | 0.26 ± 0.03 | 840 ± 80 | 0.35 ± 0.03 | 2343 ± 88 | 1080 ± 12 |
| 1:60 | 0.40 ± 0.01 | 33 ± 2 | 0.20 ± 0.01 | 369 ± 20 | 0.33 ± 0.01 | 1939 ± 32 | 750 ± 8 |
| 1:40 | 0.39 ± 0.01 | 33 ± 1 | 0.33 ± 0.01 | 324 ± 10 | 0.280 ± 0.005 | 1744 ± 23 | 610 ± 5 |
| 1:30 | 0.31 ± 0.02 | 28 ± 2 | 0.39 ± 0.01 | 170 ± 8 | 0.300 ± 0.004 | 1437 ± 18 | 510 ± 5 |
| 1:20 | 0.64 ± 0.01 | 13.0 ± 1 | 0.280 ± 0.005 | 123 ± 3 | 0.080 ± 0.002 | 1149 ± 23 | 138 ± 1 |
| 1:15 | 0.51 ± 0.01 | 4.0 ± 1 | 0.37 ± 0.01 | 39 ± 1 | 0.120 ± 0.003 | 281 ± 7 | 51 ± 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babaev, A.A.; Sokolova, A.V.; Cherevkov, S.A.; Berwick, K.; Baranov, A.V.; Fedorov, A.V.; Litvin, A.P. Beyond Charge Transfer: The Impact of Auger Recombination and FRET on PL Quenching in an rGO-QDs System. Nanomaterials 2021, 11, 1623. https://doi.org/10.3390/nano11061623
Babaev AA, Sokolova AV, Cherevkov SA, Berwick K, Baranov AV, Fedorov AV, Litvin AP. Beyond Charge Transfer: The Impact of Auger Recombination and FRET on PL Quenching in an rGO-QDs System. Nanomaterials. 2021; 11(6):1623. https://doi.org/10.3390/nano11061623
Chicago/Turabian StyleBabaev, Anton A., Anastasiia V. Sokolova, Sergei A. Cherevkov, Kevin Berwick, Alexander V. Baranov, Anatoly V. Fedorov, and Aleksandr P. Litvin. 2021. "Beyond Charge Transfer: The Impact of Auger Recombination and FRET on PL Quenching in an rGO-QDs System" Nanomaterials 11, no. 6: 1623. https://doi.org/10.3390/nano11061623







