Synthetic Data in Quantitative Scanning Probe Microscopy
Abstract
:1. Introduction
2. Artificial SPM Data
2.1. Geometrical Shapes and Patterns
2.2. Deposition and Roughening
2.3. Order and Disorder
2.4. Instrument Influence
2.5. Further Methods
3. Synthetic Data Applications
3.1. Impact of Tip on SPM Results
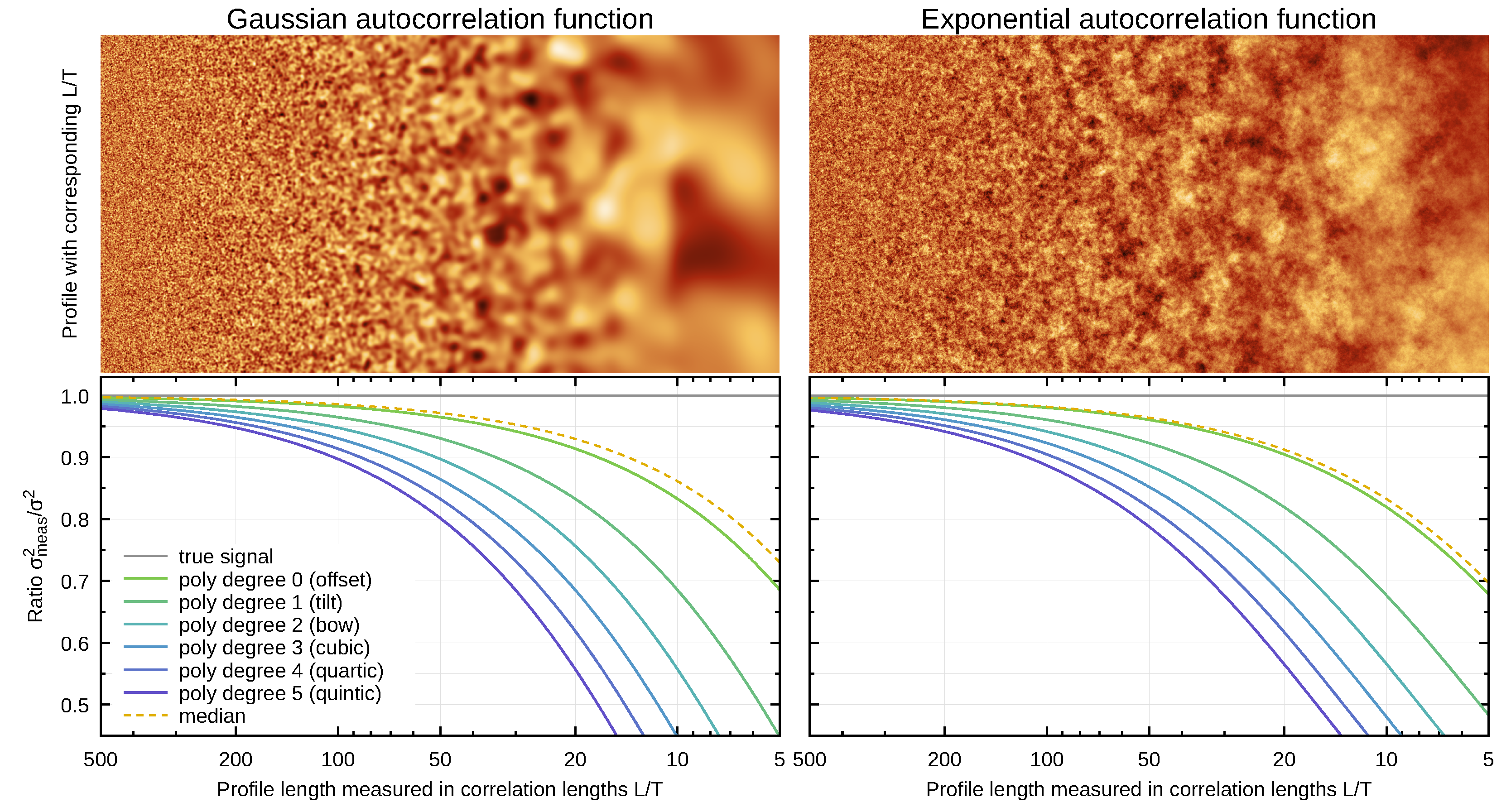
3.2. Levelling, Preprocessing, and Background Removal
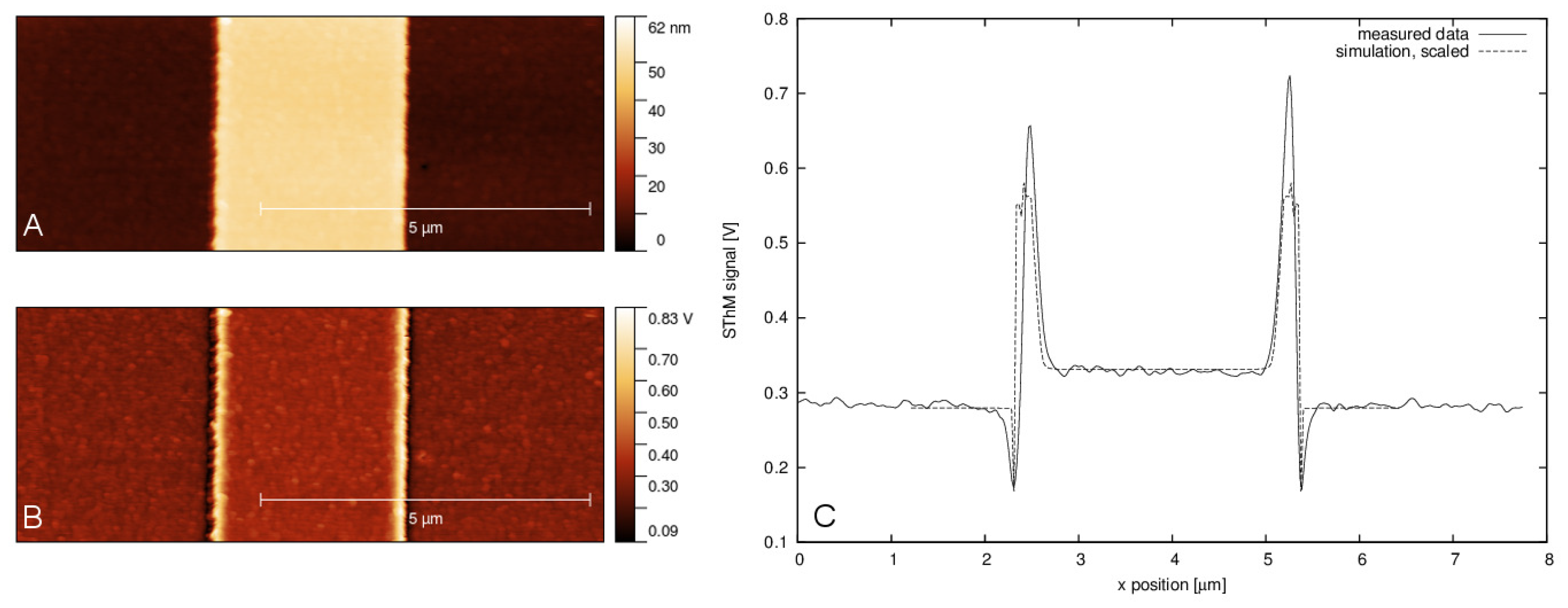
3.3. Non-Topographical SPM Quantities
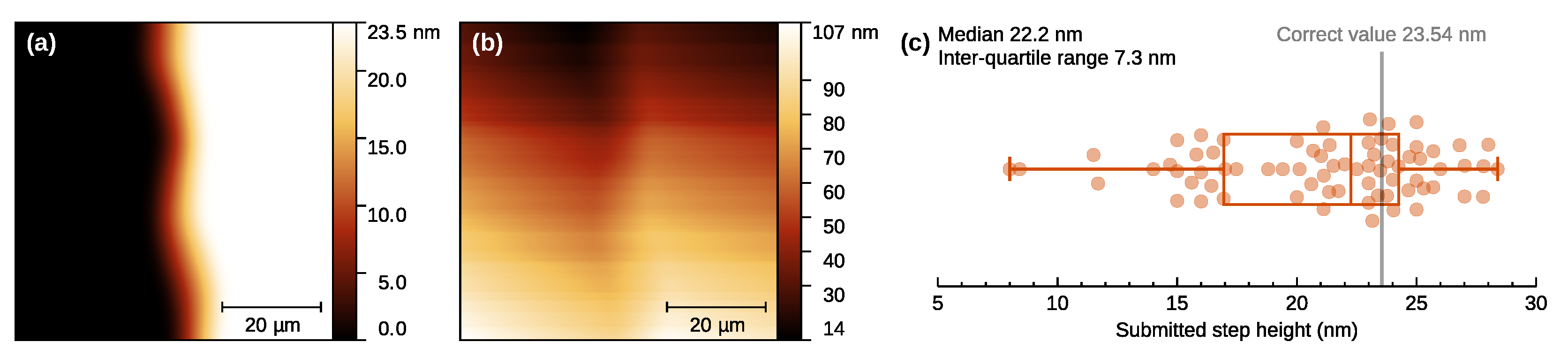
3.4. Use of Synthetic Data for Better Sampling
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| C-AFM | Conductive Atomic Force Microscopy |
| DDA | Deposition, Diffusion and Aggregation |
| DFT | Density Functional Theory |
| DLA | Diffusion-Limited Aggregation |
| EDT | Euclidean Distance Transform |
| FDM | Finite Difference Model |
| FEM | Finite Element Method |
| FFT | Fast Fourier Transform |
| GUM | Guide to the expression of Uncertainty in Measurement |
| KLT | Kessler–Levine–Tu |
| KPZ | Kardar–Parisi–Zhang |
| LALI | Local Activation and Long-range Inhibition |
| MC | Monte Carlo |
| MEMS | Microelectromechanical systems |
| MFM | Magnetic Force Microscopy |
| PDE | Partial Differential Equation |
| PID | Proportional-Integral-Derivative |
| RGB | Red, Green and Blue |
| SPM | Scanning Probe Microscopy |
| SThM | Scanning Thermal Microscopy |
| STM | Scanning Tunnelling Microscopy |
References
- Voigtländer, B. Scanning Probe Microscopy; NanoScience and Technology; Springer: Berlin, Germany, 2013. [Google Scholar]
- Meyer, E.; Hug, H.J.; Bennewitz, R. Scanning Probe Microscopy: The Lab on the Tip; Advanced Texts in Physics; Springer: Berlin, Germany, 2004. [Google Scholar]
- Klapetek, P. Quantitative Data Processing in Scanning Probe Microscopy, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Ceria, P.; Ducourtieux, S.; Boukellal, Y. Estimation of the measurement uncertainty of LNE’s metrological Atomic Force Microscope using virtual instrument modeling and Monte Carlo Method. In Proceedings of the 17th International Congress of Metrology, Paris, France, 21–24 September 2015; p. 14007. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Dziomba, T.; Koenders, L. Modelling and simulating scanning force microscopes for estimating measurement uncertainty: A virtual scanning force microscope. Meas. Sci. Technol. 2011, 22, 094004. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Gwyddion Developers. Gwyddion. Available online: http://gwyddion.net/ (accessed on 1 July 2021).
- Klapetek, P.; Yacoot, A.; Grolich, P.; Valtr, M.; Nečas, D. Gwyscan: A library to support non-equidistant Scanning Probe Microscope measurements. Meas. Sci. Technol. 2017, 28, 034015. [Google Scholar] [CrossRef]
- Yang, C.; Wang, W.; Chen, Y. Contour-oriented automatic tracking based on Gaussian processes for atomic force microscopy. Measurement 2019, 148, 106951. [Google Scholar] [CrossRef]
- Ren, M.J.; Cheung, C.F.; Xiao, G.B. Gaussian Process Based Bayesian Inference System for Intelligent Surface Measurement. Sensors 2018, 18, 4069. [Google Scholar] [CrossRef] [Green Version]
- Payton, O.; Champneys, A.; Homer, M.; Picco, L.; Miles, M. Feedback-induced instability in tapping mode atomic force microscopy: Theory and experiment. Proc. R. Soc. A 2011, 467, 1801. [Google Scholar] [CrossRef] [Green Version]
- Koops, R.; van Veghel, M.; van de Nes, A. A dedicated calibration standard for nanoscale areal surface texture measurements. Microelectron. Eng. 2015, 141, 250–255. [Google Scholar] [CrossRef]
- Babij, M.; Majstrzyk, W.; Sierakowski, A.; Janus, P.; Grabiec, P.; Ramotowski, Z.; Yacoot, A.; Gotszalk, T. Electromagnetically actuated MEMS generator for calibration of AFM. Meas. Sci. Technol. 2021, 32, 065903. [Google Scholar] [CrossRef]
- Marino, A.; Desii, A.; Pellegrino, M.; Pellegrini, M.; Filippeschi, C.; Mazzolai, B.; Mattoli, V.; Ciofani, G. Nanostructured Brownian Surfaces Prepared through Two-Photon Polymerization: Investigation of Stem Cell Response. ACS Nano 2014, 8, 11869–11882. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, T.; Huang, W. Focused Ion Beam Fabrication and Atomic Force Microscopy Characterization of Micro/Nanoroughness Artifacts With Specified Statistic Quantities. IEEE Trans. Nanotechnol. 2014, 13, 563–573. [Google Scholar] [CrossRef]
- Hemmleb, M.; Berger, D.; Dziomba, T. Focused Ion Beam fabrication of defined scalable roughness structures. In Proceedings of the European Microscopy Congress, Lyon, France, 28 August–2 September 2016. [Google Scholar] [CrossRef]
- Bontempi, M.; Visani, A.; Benini, M.; Gambardella, A. Assessing conformal thin film growth under nonstochastic deposition conditions: Application of a phenomenological model of roughness replication to synthetic topographic images. J. Microsc. 2020, 280, 270–279. [Google Scholar] [CrossRef]
- Klapetek, P.; Ohlídal, I. Theoretical analysis of the atomic force microscopy characterization of columnar thin films. Ultramicroscopy 2003, 94, 19–29. [Google Scholar] [CrossRef]
- Klapetek, P.; Ohlídal, I.; Bílek, J. Influence of the atomic force microscope tip on the multifractal analysis of rough surfaces. Ultramicroscopy 2004, 102, 51–59. [Google Scholar] [CrossRef]
- Mwema, F.; Akinlabi, E.T.; Oladijo, O. Demystifying Fractal Analysis of Thin Films: A Reference for Thin Film Deposition Processes. In Trends in Mechanical and Biomedical Design; Springer: Singapore, 2020; pp. 213–222. [Google Scholar] [CrossRef]
- Klapetek, P.; Valtr, M.; Nečas, D.; Salyk, O.; Dzik, P. Atomic force microscopy analysis of nanoparticles in non-ideal conditions. Nanoscale Res. Lett. 2011, 6, 514. [Google Scholar] [CrossRef] [Green Version]
- Vekinis, A.A.; Constantoudis, V. Neural network evaluation of geometric tip-sample effects in AFM measurements. Micro Nano Eng. 2020, 8, 100057. [Google Scholar] [CrossRef]
- Wang, W.; Whitehouse, D. Application of neural networks to the reconstruction of scanning probe microscope images distorted by finite-size tips. Nanotechnology 1995, 6, 45–51. [Google Scholar] [CrossRef]
- Wang, Y.F.; Kilpatrick, J.I.; Jarvis, S.P.; Boland, F.; Kokaram, A.; Corrigan, D. Double-Tip Artefact Removal from Atomic Force Microscopy Images. IEEE Trans. Image Process. 2016, 25, 2774–2788. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, T.; Huang, W. Improving Dimensional Measurement From Noisy Atomic Force Microscopy Images by Non-Local Means Filtering. Scanning 2016, 38, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, T.D.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. One-dimensional autocorrelation and power spectrum density functions of irregular regions. Ultramicroscopy 2013, 124, 13–19. [Google Scholar] [CrossRef]
- Hu, C.; Cai, J.; Li, Y.; Bi, C.; Gu, Z.; Zhu, J.; Zang, J.; Zheng, W. In situ growth of ultra-smooth or super-rough thin films by suppression of vertical or horizontal growth of surface mounds. J. Mat. Chem. C 2020, 8, 3248–3257. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P.; Valtr, M. Estimation of roughness measurement bias originating from background subtraction. Meas. Sci. Technol. 2020, 31, 094010. [Google Scholar] [CrossRef] [Green Version]
- Garnæs, J.; Nečas, D.; Nielsen, L.; Madsen, M.H.; Torras-Rosell, A.; Zeng, G.; Klapetek, P.; Yacoot, A. Algorithms for using silicon steps for scanning probe microscope evaluation. Metrologia 2020, 57, 064002. [Google Scholar] [CrossRef]
- Huang, Q.; Gonda, S.; Misumi, I.; Keem, T.; Kurosawa, T. Research on pitch analysis methods for calibration of one-dimensional grating standard based on nanometrological AFM. Proc. SPIE 2006, 6280, 628007. [Google Scholar]
- Ghosal, S.; Salapaka, M. Fidelity imaging for Atomic Force Microscopy. Appl. Phys. Lett. 2015, 106, 013113. [Google Scholar] [CrossRef]
- Chen, Y. Data fusion for accurate microscopic rough surface metrology. Ultramicroscopy 2016, 165, 15–25. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Study of user influence in routine SPM data processing. Meas. Sci. Technol. 2017, 28, 034014. [Google Scholar] [CrossRef]
- Kawashima, E.; Fujii, M.; Yamashita, K. Simulation of Conductive Atomic Force Microscopy of Organic Photovoltaics by Dynamic Monte Carlo Method. Chem. Lett. 2019, 48, 513–516. [Google Scholar] [CrossRef]
- Klapetek, P.; Martinek, J.; Grolich, P.; Valtr, M.; Kaur, N.J. Graphics cards based topography artefacts simulations in Scanning Thermal Microscopy. Int. J. Heat Mass Transfe 2017, 108, 841–850. [Google Scholar] [CrossRef]
- Klapetek, P.; Campbell, A.C.; Buršíková, V. Fast mechanical model for probe-sample elastic deformation estimation in scanning probe microscopy. Ultramicroscopy 2019, 201, 18–27. [Google Scholar] [CrossRef]
- Kato, A.; Burger, S.; Scholze, F. Analytical modeling and three-dimensional finite element simulation of line edge roughness in scatterometry. Appl. Opt. 2012, 51, 6457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zong, W.; Wu, D.; He, C. Radius and angle determination of diamond Berkovich indenter. Measurement 2017, 104, 243–252. [Google Scholar] [CrossRef]
- Argento, C.; French, R. Parametric tip model and force–distance relation for Hamaker constant determination from atomic force microscopy. J. Appl. Phys. 1996, 80, 6081–6090. [Google Scholar] [CrossRef] [Green Version]
- Alderighi, M.; Ierardi, V.; Allegrini, M.; Fuso, F.; Solaro, R. An Atomic Force Microscopy Tip Model for Investigating the Mechanical Properties of Materials at the Nanoscale. J. Nanosci. Nanotechnol. 2008, 8, 2479–2482. [Google Scholar] [CrossRef]
- Patil, S.; Dharmadhikari, C. Investigation of the electrostatic forces in scanning probe microscopy at low bias voltages. Surf. Interf. Anal. 2002, 33, 155–158. [Google Scholar] [CrossRef]
- Albonetti, C.; Chiodini, S.; Annibale, P.; Stoliar, P.; Martinez, V.; Garcia, R.; Biscarini, F. Quantitative phase-mode electrostatic force microscopy on silicon oxide nanostructures. J. Microsc. 2020, 280, 252–269. [Google Scholar] [CrossRef]
- Yang, L.; song Tu, Y.; li Tan, H. Influence of atomic force microscope (AFM) probe shape on adhesion force measured in humidity environment. Appl. Math. Mech. 2014, 35, 567–574. [Google Scholar] [CrossRef]
- Belikov, S.; Erina, N.; Huang, L.; Su, C.; Prater, C.; Magonov, S.; Ginzburg, V.; McIntyre, B.; Lakrout, H.; Meyers, G. Parametrization of atomic force microscopy tip shape models for quantitative nanomechanical measurements. J. Vac. Sci. Technol. 2008, 27, 984–992. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, D.; Zhang, F.H.; Gan, Y. AFM characterization of patterned sapphire substrate with dense cone arrays: Image artifacts and tip-cone convolution effect. Appl. Surf. Sci. 2018, 433, 358–366. [Google Scholar] [CrossRef]
- Villarrubia, J.S. Algorithms for Scanned Probe Microscope Image Simulation, Surface Reconstruction, and Tip Estimation. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 425–454. [Google Scholar] [CrossRef]
- Canet-Ferrer, J.; Coronado, E.; Forment-Aliaga, A.; Pinilla-Cienfuegos, E. Correction of the tip convolution effects in the imaging of nanostructures studied through scanning force microscopy. Nanotechnology 2014, 25, 395703. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Luo, J.; Doudevski, I.; Erten, S.; Kim, S.H. Atomic Force Microscopy (AFM) Analysis of an Object Larger and Sharper than the AFM Tip. Microsc. Microanal. 2019, 25, 1106–1111. [Google Scholar] [CrossRef] [PubMed]
- Consultative Committee for Length. Mise en Pratique for the Definition of the Metre in the SI. 2019. Available online: https://www.bipm.org/utils/en/pdf/si-mep/SI-App2-metre.pdf (accessed on 6 May 2021).
- Consultative Committee for Length. Recommendations of CCL/WG-N on: Realization of SI Metre Using Height of Monoatomic Steps of Crystalline Silicon Surfaces. 2019. Available online: https://www.bipm.org/utils/common/pdf/CC/CCL/CCL-GD-MeP-3.pdf (accessed on 6 May 2021).
- Gloystein, A.; Nilius, N.; Goniakowski, J.; Noguera, C. Nanopyramidal Reconstruction of Cu2O(111): A Long-Standing Surface Puzzle Solved by STM and DFT. J. Phys. Chem. C 2020, 124, 26937–26943. [Google Scholar] [CrossRef]
- Vrubel, I.I.; Yudin, D.; Pervishko, A.A. On the origin of the electron accumulation layer at clean InAs(111) surfaces. Phys. Chem. Chem. Phys 2021, 23, 4811–4817. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Silveira, O.J.; Alldritt, B.; Krejčí, O.; Foster, A.S.; Liljeroth, P. Synthesis and Local Probe Gating of a Monolayer Metal-Organic Framework. Adv. Func. Mater. 2021, 31, 2100519. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D. Theory of the scanning tunneling microscope. Phys. Rev. B 1985, 31, 805–813. [Google Scholar] [CrossRef]
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 1974, 10, 266–271. [Google Scholar]
- Delaunay, B. Sur la sphère vide. Izvestia Akademii Nauk SSSR Otdelenie Matematicheskikh i Estestvennykh Nauk 1934, 7, 793–800. (In Russian) [Google Scholar]
- De Berg, M.; Otfried, C.; van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications, 3rd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. J. Reine Angew. Math. 1907, 133, 97–178. (In French) [Google Scholar]
- Williams, J.A.; Le, H.R. Tribology and MEMS. J. Phys. D Appl. Phys 2006, 39, R201–R214. [Google Scholar] [CrossRef]
- Cresti, A.; Pala, M.G.; Poli, S.; Mouis, M.; Ghibaudo, G. A Comparative Study of Surface-Roughness-Induced Variability in Silicon Nanowire and Double-Gate FETs. IEEE T. Electron. Dev. 2011, 58, 2274–2281. [Google Scholar] [CrossRef]
- Pala, M.G.; Cresti, A. Increase of self-heating effects in nanodevices induced by surface roughness: A full-quantum study. J. Appl. Phys. 2015, 117, 084313. [Google Scholar] [CrossRef]
- Bruzzone, A.A.G.; Costa, H.L.; Lonardo, P.M.; Lucca, D.A. Advances in engineered surfaces for functional performance. CIRP Ann. Manuf. Technol. 2008, 57, 750–769. [Google Scholar] [CrossRef]
- Bhushan, B. Biomimetics inspired surfaces for drag reduction and oleophobicity/philicity. Beilstein J. Nanotechnol. 2011, 2, 66–84. [Google Scholar] [CrossRef] [Green Version]
- Barabási, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Levi, A.C.; Kotrla, M. Theory and simulation of crystal growth. J. Phys. Condens. Matter 1997, 9, 299–344. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wio, H.S.; Escudero, C.; Revelli, J.A.; Deza, R.R.; de la Lama, M.S. Recent developments on the Kardar–Parisi–Zhang surface-growth equation. Philos. T. Roy. Soc. A 2011, 369, 396–411. [Google Scholar] [CrossRef] [PubMed]
- Ales, A.; Lopez, J.M. Faceted patterns and anomalous surface roughening driven by long-range temporally correlated noise. Phys. Rev. E 2019, 99, 062139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kessler, D.A.; Levine, H.; Tu, Y. Interface fluctuations in random media. Phys. Rev. A 1991, 43, 4551(R). [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Mollick, S.A.; Saini, M.; Guha, P.; Som, T. Experimental and simulation studies on temporal evolution of chemically etched Si surface: Tunable light trapping and cold cathode electron emission properties. J. Appl. Phys. 2019, 125, 164302. [Google Scholar] [CrossRef]
- Weeks, J.D.; Gilmer, G.H.; Jackson, K.A. Analytical theory of crystal growth. J. Chem. Phys. 1976, 65, 712–720. [Google Scholar] [CrossRef]
- Meakin, P.; Jullien, R. Simple Ballistic Deposition Models For The Formation Of Thin Films. In Modeling of Optical Thin Films; SPIE: Bellingham, WA, USA, 1988; Volume 0821, pp. 45–55. [Google Scholar]
- Russ, J.C. Fractal Surfaces; Springer Science: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Vold, M.J. A numerical approach to the problem of sediment volume. J. Coll. Sci. 1959, 14, 168–174. [Google Scholar] [CrossRef]
- Sarma, S.D.; Tamborenea, P. A new universality class for kinetic growth: One-dimensional molecular-beam epitaxy. Phys. Rev. Lett. 1991, 66, 325–328. [Google Scholar] [CrossRef]
- Wolf, D.E.; Villain, J. Growth with surface diffusion. Europhys. Lett. 1990, 13, 389–394. [Google Scholar] [CrossRef]
- Drotar, J.T.; Zhao, Y.P.; Lu, T.M.; Wang, G.C. Surface roughening in shadowing growth and etching in 2+1 dimensions. Phys. Rev. B 2000, 62, 2118–2125. [Google Scholar] [CrossRef] [Green Version]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Schwoebel, R.; Shipsey, E. Step motion on crystal surfaces. J. Appl. Phys. 1966, 37, 3682–3686. [Google Scholar] [CrossRef]
- Schwoebel, R. Step motion on crystal surfaces 2. J. Appl. Phys. 1969, 40, 614–618. [Google Scholar] [CrossRef]
- Haußer, F.; Voigt, A. Ostwald ripening of two-dimensional homoepitaxial islands. Phys. Rev. B 2005, 72, 035437. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.W.; Thiel, P.A.; Bartelt, M. Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds. Surf. Sci. Rep. 2006, 61, 1–128. [Google Scholar] [CrossRef]
- Lai, K.C.; Han, Y.; Spurgeon, P.; Huang, W.; Thiel, P.A.; Liu, D.J.; Evans, J.W. Reshaping, Intermixing, and Coarsening for Metallic Nanocrystals: Nonequilibrium Statistical Mechanical and Coarse-Grained Modeling. Chem. Rev. 2019, 119, 6670–6768. [Google Scholar] [CrossRef] [Green Version]
- Chiodini, S.; Straub, A.; Donati, S.; Albonetti, C.; Borgatti, F.; Stoliar, P.; Murgia, M.; Biscarini, F. Morphological Transitions in Organic Ultrathin Film Growth Imaged by In Situ Step-by-Step Atomic Force Microscopy. J. Phys. Chem. C 2020, 124, 14030–14042. [Google Scholar] [CrossRef]
- Allen, M.P. Computational Soft Matter: From Synthetic Polymers to Proteins. In NIC Series; Attig, N., Binder, K., Grubmüller, H., Kremer, K., Eds.; John von Neumann Institute for Computing: Jülich, Germany, 2004; pp. 1–28. [Google Scholar]
- Miyamoto, S.; Kollamn, P.A. SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comp. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Meron, E. Pattern-formation in excitable media. Phys. Rep. 1992, 218, 1–66. [Google Scholar] [CrossRef]
- Winfree, A.T. Spiral Waves of Chemical Activity. Science 1972, 175, 634–636. [Google Scholar] [CrossRef]
- Merzhanov, A.; Rumanov, E. Physics of reaction waves. Rev. Mod. Phys. 1999, 71, 1173–1211. [Google Scholar] [CrossRef]
- Fernandez-Oto, C.; Escaff, D.; Cisternas, J. Spiral vegetation patterns in high-altitude wetlands. Ecol. Complex. 2019, 37, 38–46. [Google Scholar] [CrossRef]
- Scott, S.K.; Wang, J.; Showalter, K. Modelling studies of spiral waves and target patterns in premixed flames. J. Chem. Soc. Faraday T. 1997, 93, 1733–1739. [Google Scholar] [CrossRef]
- Christoph, J.; Chebbok, M.; Richter, C.; Schröder-Schetelig, J.; Bittihn, P.; Stein, S.; Uzelac, I.; Fenton, F.H.; Hasenfuß, G.; Gilmour, R.F., Jr.; et al. Electromechanical vortex filaments during cardiac fibrillation. Nature 2018, 555, 667–672. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. Roy. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Green, J.B.A.; Sharpe, J. Positional information and reaction-diffusion: Two big ideas in developmental biology combine. Development 2015, 142, 1203–1211. [Google Scholar] [CrossRef] [Green Version]
- Kondo, S. An updated kernel-based Turing model for studying the mechanisms of biological pattern formation. J. Theor. Biol. 2017, 414, 120–127. [Google Scholar] [CrossRef]
- Vock, S.; Sasvári, Z.; Bran, C.; Rhein, F.; Wolff, U.; Kiselev, N.S.; Bogdanov, A.N.; Schultz, L.; Hellwig, O.; Neu, V. Quantitative Magnetic Force Microscopy Study of the Diameter Evolution of Bubble Domains in a Co/Pd Multilayer. IEEE Trans. Magn. 2011, 47, 2352–2355. [Google Scholar] [CrossRef]
- Vock, S.; Hengst, C.; Wolf, M.; Tschulik, K.; Uhlemann, M.; Sasvári, Z.; Makarov, D.; Schmidt, O.G.; Schultz, L.; Neu, V. Magnetic vortex observation in FeCo nanowires by quantitative magnetic force microscopy. Appl. Phys. Lett. 2014, 105, 172409. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P.; Neu, V.; Havlíček, M.; Puttock, R.; Kazakova, O.; Hu, X.; Zajíčková, L. Determination of tip transfer function for quantitative MFM using frequency domain filtering and least squares method. Sci. Rep. 2019, 9, 3880. [Google Scholar] [CrossRef]
- Hu, X.; Dai, G.; Sievers, S.; Fernández-Scarioni, A.; Corte-León, H.; Puttock, R.; Barton, C.; Kazakova, O.; Ulvr, M.; Klapetek, P.; et al. Round robin comparison on quantitative nanometer scale magnetic field measurements by magnetic force microscopy. J. Magn. Magn. Mater. 2020, 511, 166947. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik 1925, 31, 253–258. (In German) [Google Scholar] [CrossRef]
- Peierls, R. On Ising’s model of ferromagnetism. Math. Proc. Camb. Philos. Soc. 1936, 32, 477–481. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1; Pergamon: New York, NY, USA, 1980. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1989. [Google Scholar]
- Rothman, D.H.; Zaleski, S. Lattice-gas models of phase separation: Interfaces, phase transitions, and multiphase flow. Rev. Mod. Phys. 1994, 66, 1417–1479. [Google Scholar] [CrossRef] [Green Version]
- De With, G. Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Frost, J.M.; Cheynis, F.; Tuladhar, S.M.; Nelson, J. Influence of Polymer-Blend Morphology on Charge Transport and Photocurrent Generation in Donor–Acceptor Polymer Blends. Nano Lett. 2006, 6, 1674–1681. [Google Scholar] [CrossRef] [PubMed]
- Ibarra-García-Padilla, E.; Malanche-Flores, C.G.; Poveda-Cuevas, F.J. The hobbyhorse of magnetic systems: The Ising model. Eur. J. Phys. 2016, 37, 065103. [Google Scholar] [CrossRef] [Green Version]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [Green Version]
- Meinhardt, H.; Gierer, A. Pattern formation by local self-activation and lateral inhibition. BioEssays 2000, 22, 753–760. [Google Scholar] [CrossRef]
- Liehr, A.W. Dissipative Solitons in Reaction Diffusion Systems. Mechanism, Dynamics, Interaction; Springer Series in Synergetics; Springer: Berlin, Germany, 2013; Volume 70. [Google Scholar]
- Pismen, L.M.; Monine, M.I.; Tchernikov, G.V. Patterns and localized structures in a hybrid non-equilibrium Ising model. Physica D 2004, 199, 82–90. [Google Scholar] [CrossRef]
- Horvát, S.; Hantz, P. Pattern formation induced by ion-selective surfaces: Models and simulations. J. Chem. Phys. 2005, 123, 034707. [Google Scholar] [CrossRef]
- De Gomensoro Malheiros, M.; Walter, M. Pattern formation through minimalist biologically inspired cellular simulation. In Proceedings of the Graphics Interface 2017, Edmonton, Alberta, 16–19 May 2017; pp. 148–155. [Google Scholar]
- Marinello, F.; Balcon, M.; Schiavuta, P.; Carmignato, S.; Savio, E. Thermal drift study on different commercial scanning probe microscopes during the initial warming-up phase. Meas. Sci. Technol. 2011, 22, 094016. [Google Scholar] [CrossRef]
- Han, C.; Chung, C.C. Reconstruction of a scanned topographic image distorted by the creep effect of a Z scanner in atomic force microscopy. Rev. Sci. Instrum. 2011, 82, 053709. [Google Scholar] [CrossRef]
- Klapetek, P.; Nečas, D.; Campbellová, A.; Yacoot, A.; Koenders, L. Methods for determining and processing 3D errors and uncertainties for AFM data analysis. Meas. Sci. Technol. 2011, 22, 025501. [Google Scholar] [CrossRef]
- Klapetek, P.; Grolich, P.; Nezval, D.; Valtr, M.; Šlesinger, R.; Nečas, D. GSvit—An open source FDTD solver for realistic nanoscale optics simulations. Comput. Phys. Commun 2021, 265, 108025. [Google Scholar] [CrossRef]
- Labuda, A.; Bates, J.R.; Grütter, P.H. The noise of coated cantilevers. Nanotechnology 2012, 23, 025503. [Google Scholar] [CrossRef]
- Boudaoud, M.; Haddab, Y.; Gorrec, Y.L.; Lutz, P. Study of thermal and acoustic noise interferences in low stiffness AFM cantilevers and characterization of their dynamic properties. Rev. Sci. Instrum. 2012, 83, 013704. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.X.; Fei, Y.T.; Gonda, S.; Misumi, I.; Sato, O.; Keem, T.; Kurosawa, T. The interference effect in an optical beam deflection detection system of a dynamic mode AFM. Meas. Sci. Technol. 2005, 17, 1417–1423. [Google Scholar] [CrossRef]
- Méndez-Vilas, A.; González-Martín, M.; Nuevo, M. Optical interference artifacts in contact atomic force microscopy images. Ultramicroscopy 2002, 92, 243–250. [Google Scholar] [CrossRef]
- Legleiter, J. The effect of drive frequency and set point amplitude on tapping forces in atomic force microscopy: Simulation and experiment. Nanotechnology 2009, 20, 245703. [Google Scholar] [CrossRef] [Green Version]
- Shih, F.Y. Image Processing and Mathematical Morphology (Fundamentals and Applications); Taylor & Francis: London, UK, 2009. [Google Scholar]
- Perlin, K. A Unified Texture/Reflectance Model. In Proceedings of the SIGGRAPH ’84 Advanced Image Synthesis Course Notes, Minneapolis, MN, USA, 23–27 July 1984. [Google Scholar]
- Lagae, A.; Lefebvre, S.; Cook, R.; DeRose, T.; Drettakis, G.; Ebert, D.; Lewis, J.; Perlin, K.; Zwicker, M. A Survey of Procedural Noise Functions. Comput. Graph. Forum 2010, 29, 2579–2600. [Google Scholar] [CrossRef] [Green Version]
- Fournier, A.; Fussell, D.; Carpenter, L. Computer rendering of stochastic models. Commun. ACM 1982, 25, 371–384. [Google Scholar] [CrossRef]
- Berry, M.; Lewis, Z. On the Weierstrass–Mandelbrot fractal function. Proc. R. Soc. A 1980, 370, 459–484. [Google Scholar]
- Buldyrev, S.V.; Barabási, A.L.; Caserta, F.; Havlin, S.; Stanley, H.E.; Vicsek, T. Anomalous interface roughening in porous media: Experiment and model. Phys. Rev. A 1992, 45, R8313–R8316. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Modelling Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Ding, W.; Dai, C.; Yu, T.; Xu, J.; Fu, Y. Grinding performance of textured monolayer CBN wheels: Undeformed chip thickness nonuniformity modeling and ground surface topography prediction. Int. J. Mach. Tool. Manu. 2017, 122, 66–80. [Google Scholar] [CrossRef]
- Der Weeen, P.V.; Zimer, A.M.; Pereira, E.C.; Mascaro, L.H.; Bruno, O.M.; Baets, B.D. Modeling pitting corrosion by means of a 3D discrete stochastic model. Corros. Sci. 2014, 82, 133–144. [Google Scholar] [CrossRef]
- Werner, B.T. Eolian dunes: Computer simulations and attractor interpretation. Geology 1995, 23, 1107–1110. [Google Scholar] [CrossRef]
- Pech, A.; Hingston, P.; Masek, M.; Lam, C.P. Evolving Cellular Automata for Maze Generation. In Artificial Life and Computational Intelligence; Lecture Notes in Artificial Intelligence; Chalup, S., Blair, A., Randall, M., Eds.; Springer: Cham, Switzerland, 2015; Volume 8955, pp. 112–124. [Google Scholar]
- Iben, H.N.; O’Brien, J.F. Generating surface crack patterns. Graph. Models 2009, 71, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Desbenoit, B.; Galin, E.; Akkouche, S. Simulating and modeling lichen growth. Comput. Graph. Forum 2004, 23, 341–350. [Google Scholar] [CrossRef]
- Efros, A.A.; Freeman, W.T. Image Quilting for Texture Synthesis and Transfer. In Proceedings of the SIGGRAPH 2001 Conference Proceedings, Computer Graphics, Los Angeles, CA, USA, 12–17 August 2001; pp. 341–346. [Google Scholar]
- Lefebvre, S.; Hoppe, H. Parallel controllable texture synthesis. ACM Trans. Graph. 2005, 24, 777–786. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Lefebvre, S.; Kwatra, V.; Turk, G. State of the Art in Example-based Texture Synthesis. In Eurographics 2009 State of The Art Reports; Pauly, M., Greiner, G., Eds.; Eurographics Association: Munich, Germany, 2009; p. 3. [Google Scholar]
- Nečas, D.; Valtr, M.; Klapetek, P. How levelling and scan line corrections ruin roughness measurement and how to prevent it. Sci. Rep. 2020, 10, 15294. [Google Scholar] [CrossRef] [PubMed]
- Eifler, M.; Seewig, F.S.J.; Kirsch, B.; Aurich, J.C. Manufacturing of new roughness standards for the linearity of the vertical axis—Feasibility study and optimization. Eng. Sci. Technol. Intl. J. 2016, 19, 1993–2001. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Ràfols, F.; Almqvist, A. Generating randomly rough surfaces with given height probability distribution and power spectrum. Tribol. Int. 2019, 131, 591–604. [Google Scholar] [CrossRef]
- Klapetek, P.; Ohlídal, I.; Bílek, J. Atomic force microscope tip influence on the fractal and multi-fractal analyses of the properties of ndomly rough surfaces. In Nanoscale Calibration Standards and Methods; Wilkening, G., Koenders, L., Eds.; Wiley VCH: Weinheim, Germany, 2005; p. 452. [Google Scholar]
- Consultative Committee for Length. Recommendations of CCL/WG-N on: Realization of SI Metre Using Silicon Lattice and Transmission Electron Microscopy for Dimensional Nanometrology. 2019. Available online: https://www.bipm.org/utils/common/pdf/CC/CCL/CCL-GD-MeP-2.pdf (accessed on 6 May 2021).
- Zhao, Y.; Wang, G.C.; Lu, T.M. Characterization of Amorphous and Crystalline Rough Surface—Principles and Applications; Experimental Methods in the Physical Sciences; Academic Press: San Diego, CA, USA, 2000; Volume 37. [Google Scholar]
- Sadewasser, S.; Leendertz, C.; Streicher, F.; Lux-Steiner, M. The influence of surface topography on Kelvin probe force microscopy. Nanotechnology 2009, 20, 505503. [Google Scholar] [CrossRef] [PubMed]
- Fenwick, O.; Latini, G.; Cacialli, F. Modelling topographical artifacts in scanning near-field optical microscopy. Synth. Met. 2004, 147, 171–173. [Google Scholar] [CrossRef]
- Martin, O.; Girard, C.; Dereux, A. Dielectric versus topographic contrast in near-field microscopy. J. Opt. Soc. Am 1996, 13, 1802–1808. [Google Scholar] [CrossRef] [Green Version]
- Gucciardi, P.G.; Bachelier, G.; Allegrini, M.; Ahn, J.; Hong, M.; Chang, S.; Jhe, W.; Hong, S.C.; Baek, S.H. Artifacts identification in apertureless near-field optical microscopy. J. Appl. Phys. 2007, 101, 064303. [Google Scholar] [CrossRef]
- Biscarini, F.; Ong, K.Q.; Albonetti, C.; Liscio, F.; Longobardi, M.; Mali, K.S.; Ciesielski, A.; Reguera, J.; Renner, C.; Feyter, S.D.; et al. Quantitative Analysis of Scanning Tunneling Microscopy Images of Mixed-Ligand-Functionalized Nanoparticles. Langmuir 2013, 29, 13723–13734. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, L.; Xu, L.; Chen, W. Finite Element Modelling of Single Cell Based on Atomic Force Microscope Indentation Method. Comput. Math. Method Med. 2019, 2019, 7895061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugimoto, Y.; Pou, P.; Abe, M.; Jelinek, P.; Perez, R.; Morita, S.; Custance, O. Chemical identification of individual surface atoms by atomic force microscopy. Nature 2007, 446, 64–67. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Hatano, T.; Tien, T.; Herrmann, G.; Edwards, C.; Burgess, S.C.; Miles, M. An adaptive non-raster scanning method in atomic force microscopy for simple sample shapes. Meas. Sci. Technol. 2015, 26, 035401. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Lv, L.; Yang, G.; Niu, Y. Super-resolution AFM imaging based on compressive sensing. Appl. Surf. Sci. 2020, 508, 145231. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008 Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement. Available online: http://bipm.org/ (accessed on 6 May 2021).
- Wiener, N. The Homogeneous Chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Augustin, F.; Gilg, A.; Paffrath, M.; Rentrop, P.; Wever, U. A survey in mathematics for industry polynomial chaos for the approximation of uncertainties: Chances and limits. Eur. J. Appl. Math. 2008, 19, 149–190. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Amyot, R.; Flechsig, H. BioAFMviewer: An interactive interface for simulated AFM scanning of biomolecular structures and dynamics. PLoS Comput. Biol. 2020, 16, e1008444. [Google Scholar] [CrossRef] [PubMed]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nečas, D.; Klapetek, P. Synthetic Data in Quantitative Scanning Probe Microscopy. Nanomaterials 2021, 11, 1746. https://doi.org/10.3390/nano11071746
Nečas D, Klapetek P. Synthetic Data in Quantitative Scanning Probe Microscopy. Nanomaterials. 2021; 11(7):1746. https://doi.org/10.3390/nano11071746
Chicago/Turabian StyleNečas, David, and Petr Klapetek. 2021. "Synthetic Data in Quantitative Scanning Probe Microscopy" Nanomaterials 11, no. 7: 1746. https://doi.org/10.3390/nano11071746
APA StyleNečas, D., & Klapetek, P. (2021). Synthetic Data in Quantitative Scanning Probe Microscopy. Nanomaterials, 11(7), 1746. https://doi.org/10.3390/nano11071746






