Anomalous Terminal Shear Viscosity Behavior of Polycarbonate Nanocomposites Containing Grafted Nanosilica Particles
Abstract
:1. Introduction
2. Theoretical Background
2.1. Viscosity Behaviour
- = 2.5; , , ... = 0 for dilute solutions (Einstein relation) [27].
2.2. Definition of Rheological Properties
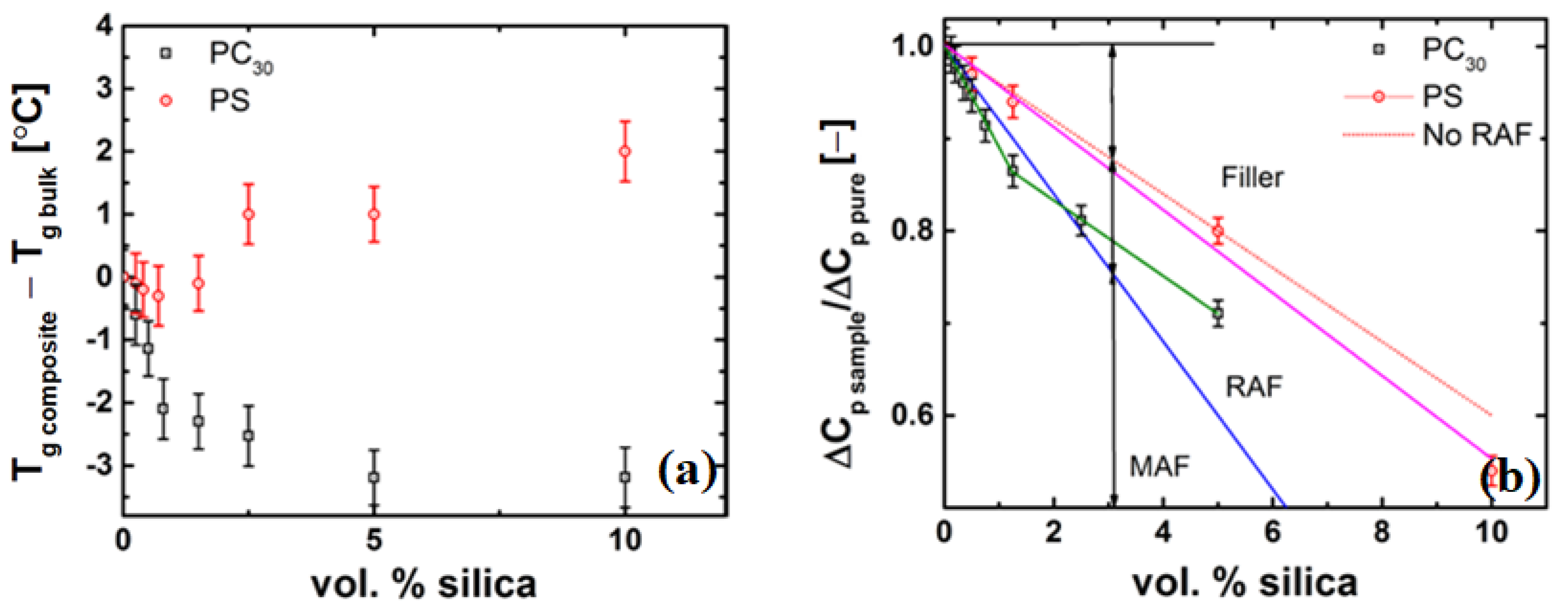
2.3. Definition of Thermal Properties
3. Materials and Methods
3.1. Preparation of Nanocomposites and Samples for Testing
Sample Preparation for FTIR and XPS
3.2. Characterization of Samples
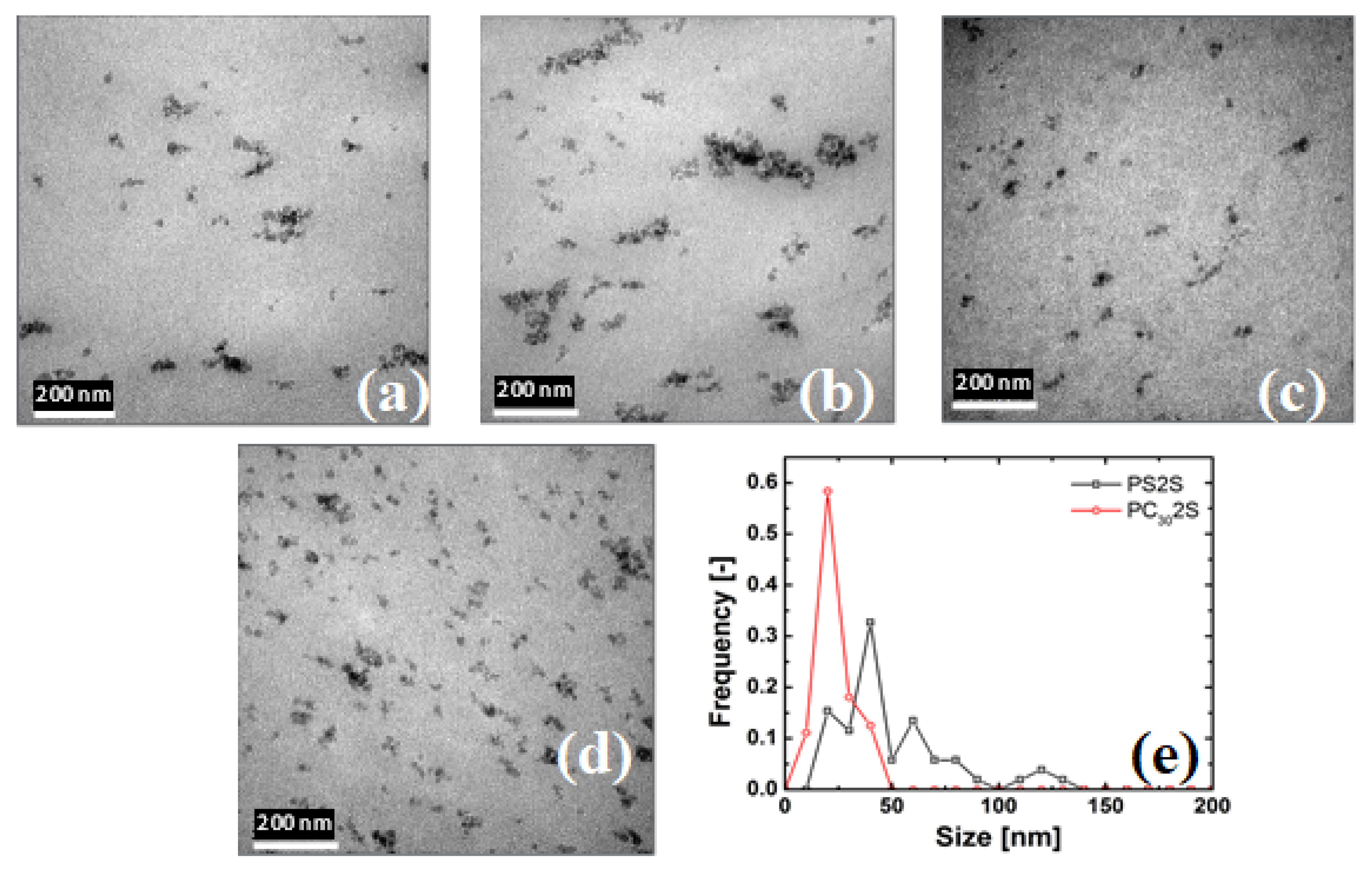
3.2.1. Transmission Electron Microscopy (TEM)
3.2.2. Size Exclusion Chromatography (SEC)
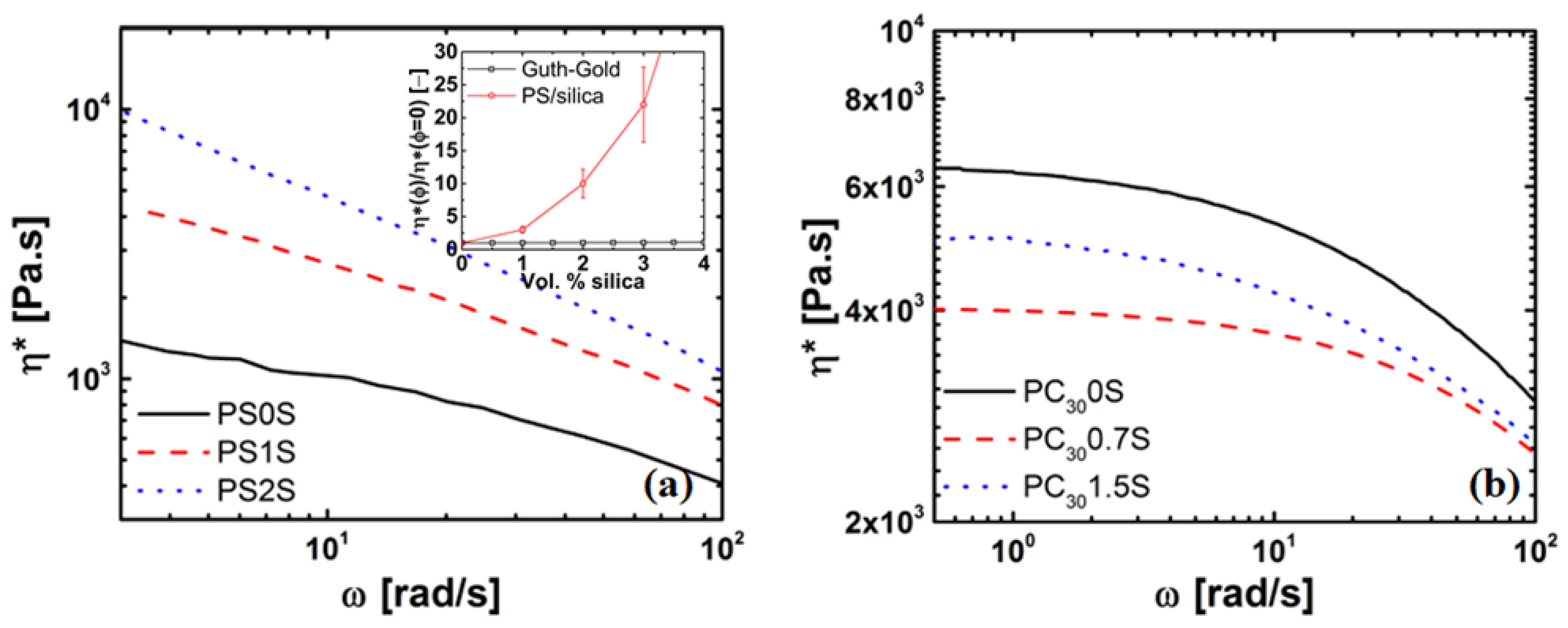
3.2.3. Melt Rheology
3.2.4. Differential Scanning Calorimetry (DSC)
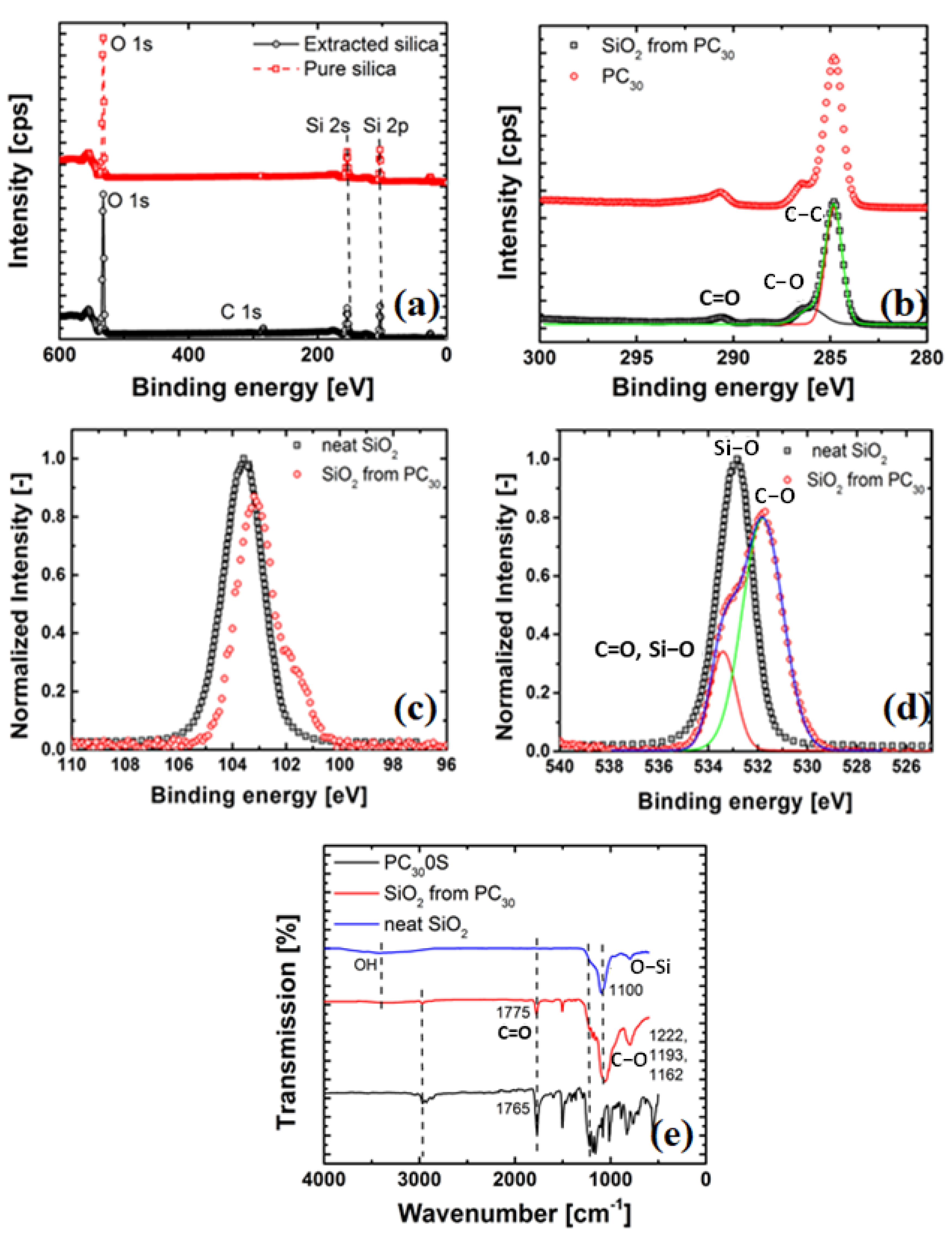
3.2.5. X-ray Photoelectron Spectroscopy (XPS)
3.2.6. Fourier Transform Infrared (FTIR) Spectroscopy
4. Results and Discussion
4.1. State of Dispersion
4.2. Evidence of Grafting
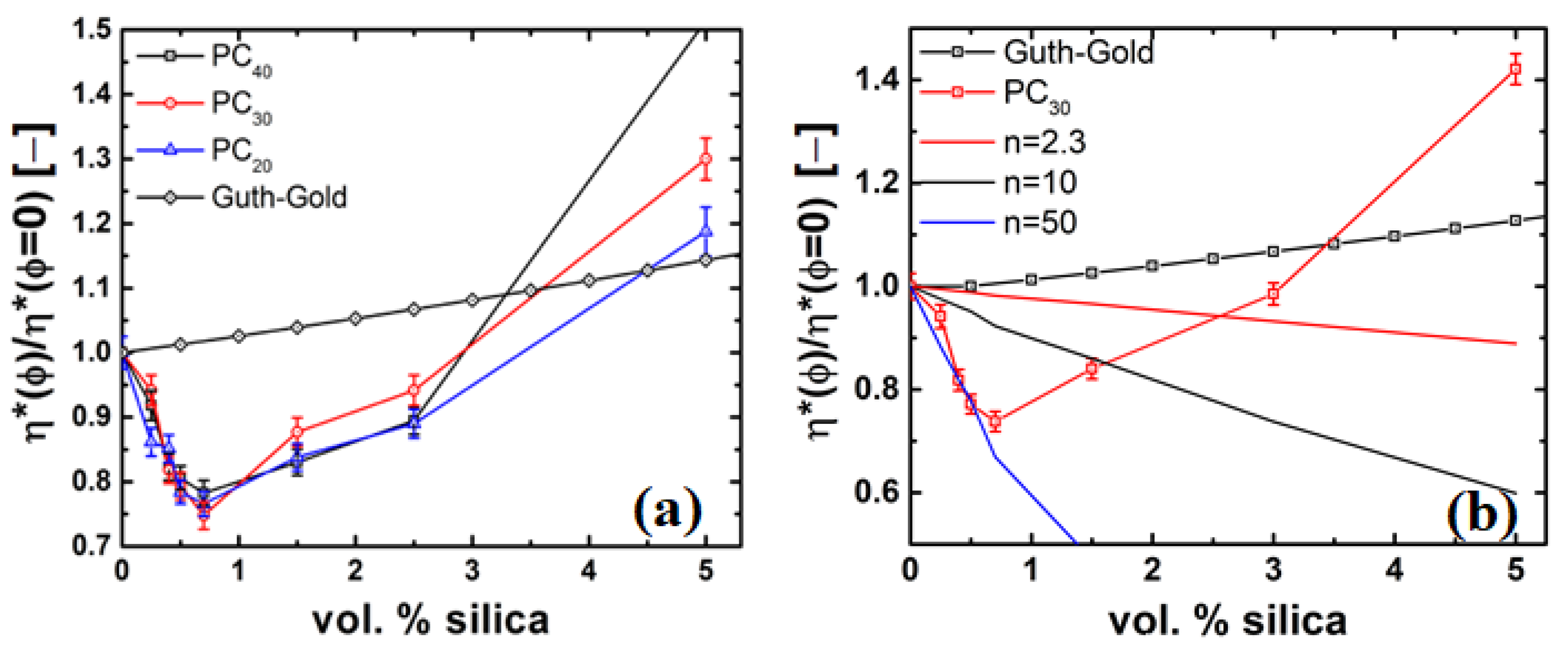
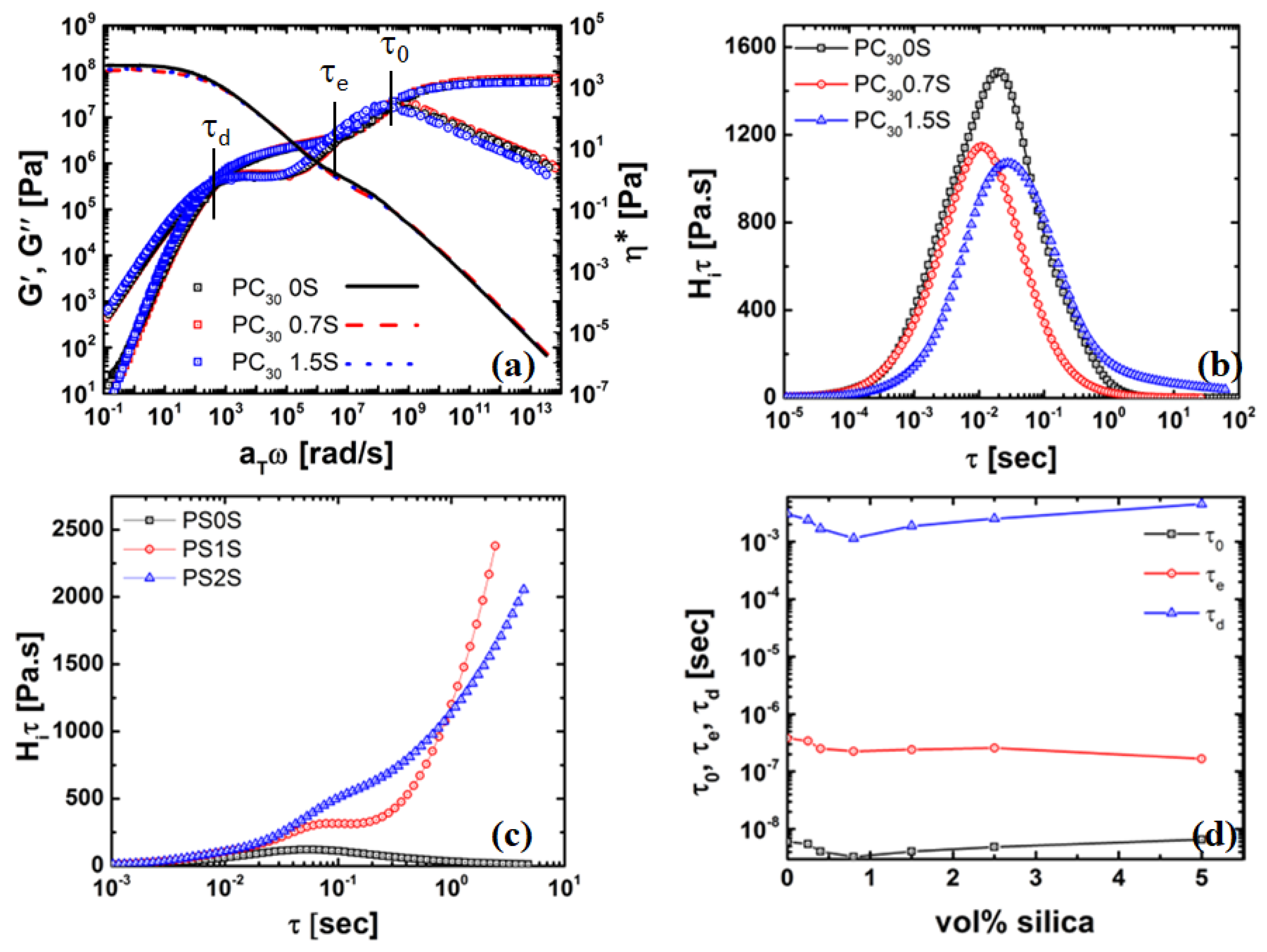
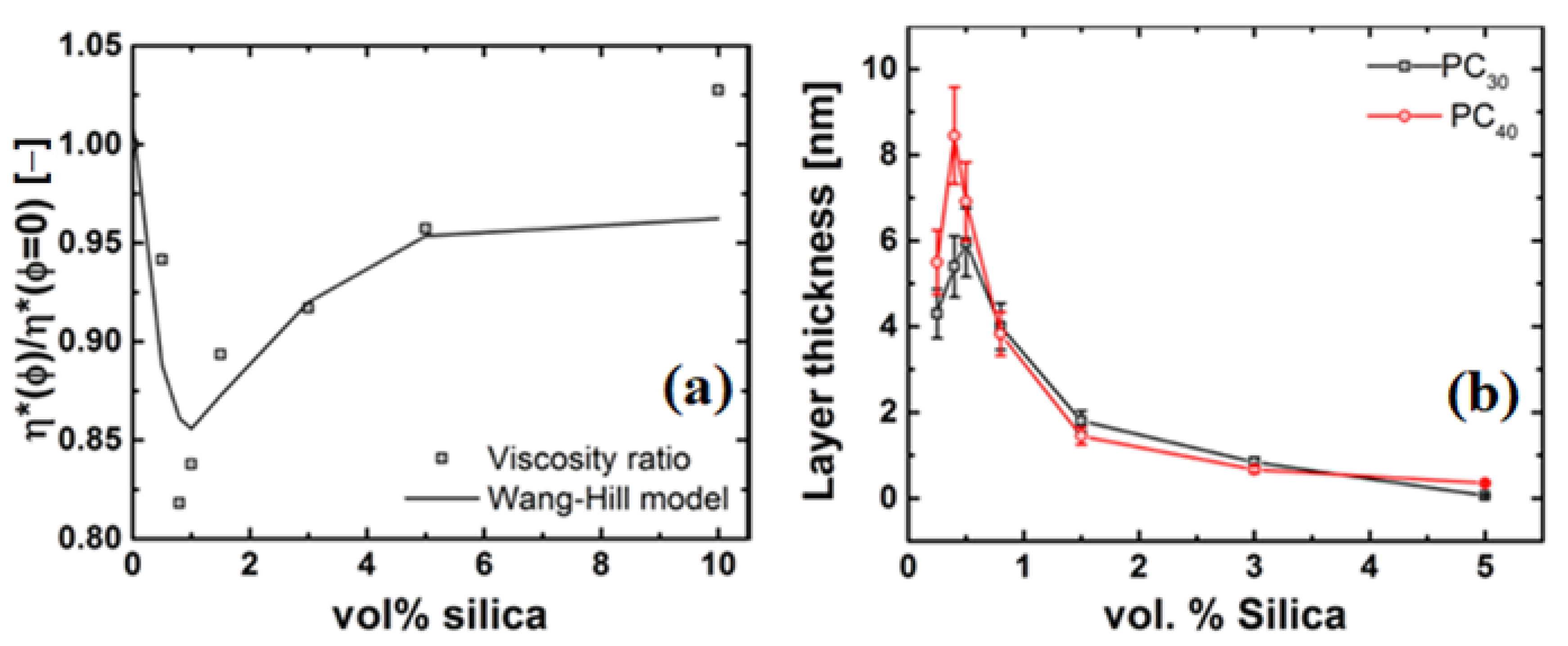
4.3. Rheology of Silica Nanocomposites
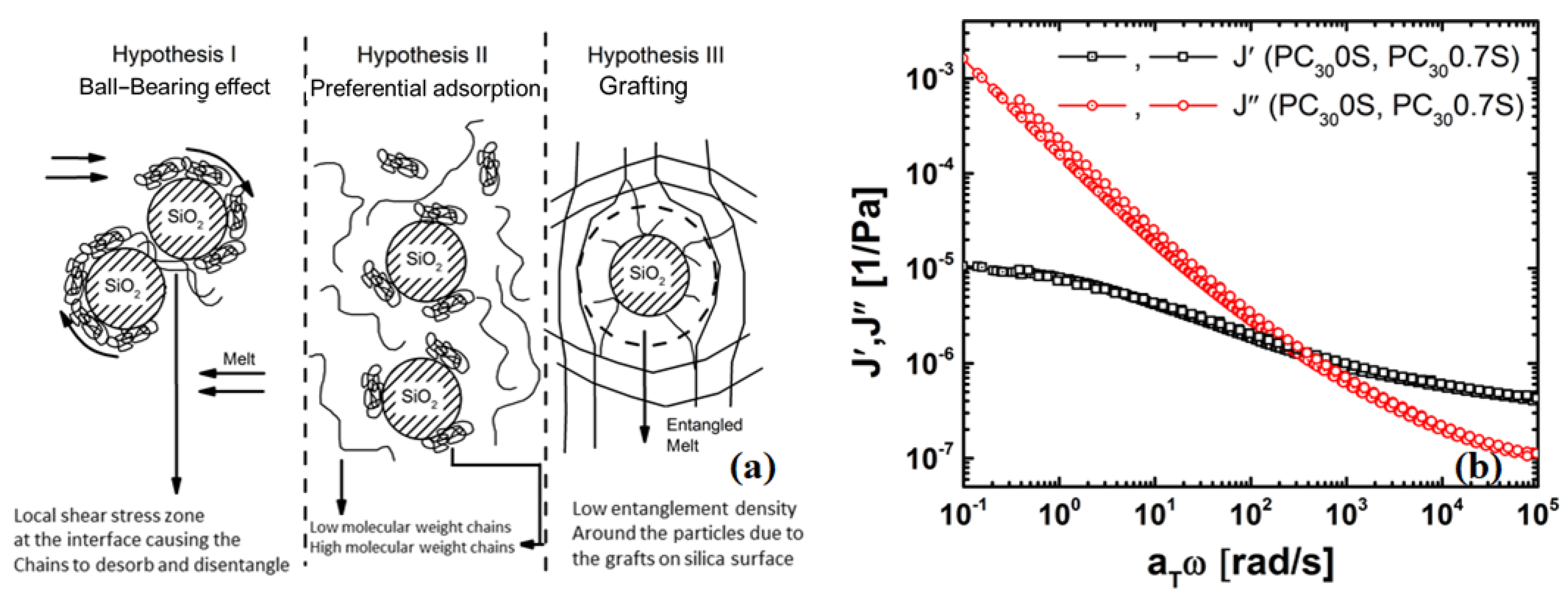
4.4. Possible Mechanisms of Viscosity Reduction
4.4.1. Chain Grafting Causing Disentanglement at the Interface Enabling Faster Modes of Relaxation
4.4.2. Thickness of the Grafted Layer of the Polymer Chain around the Particle
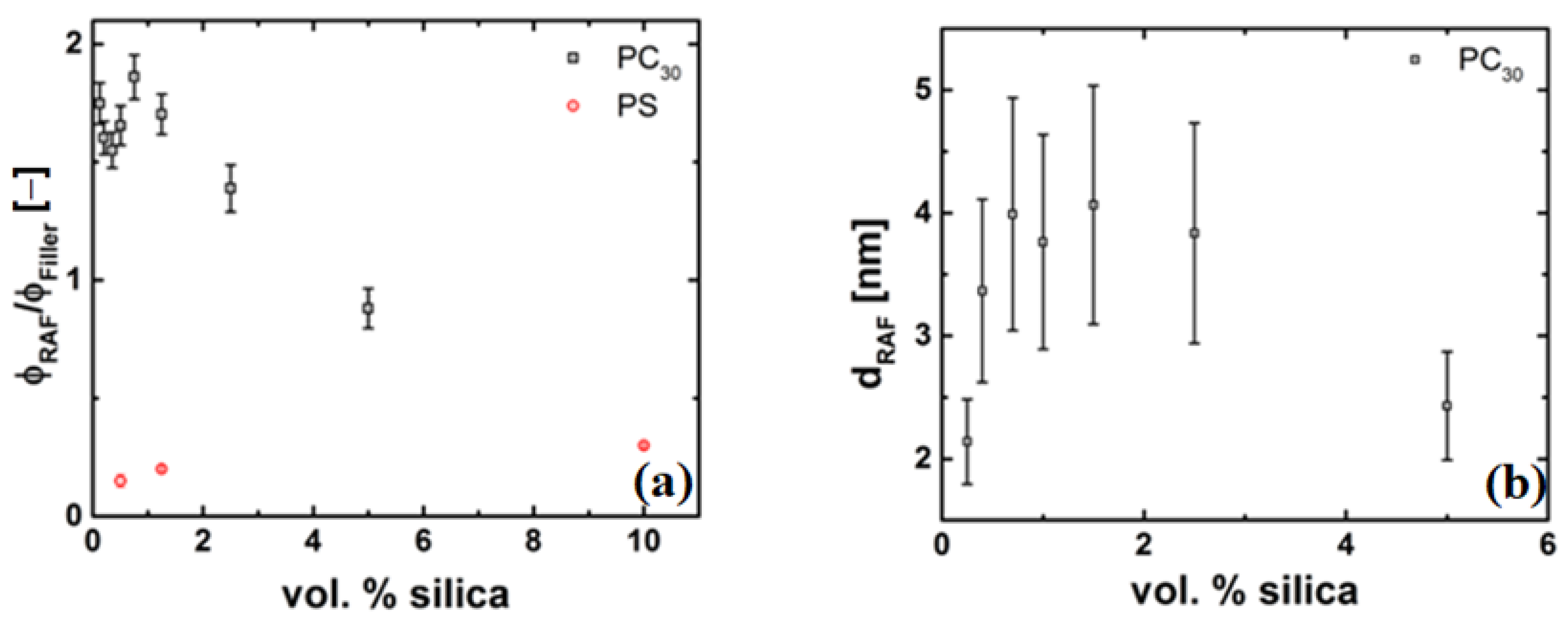
4.4.3. Evidence of a Low-Viscosity Layer
- , (short time scales), where b is the Kuhn length.
- (long times scales)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaia, R.A.; Giannelis, E.P. Polymer nanocomposites: Status and opportunities. MRS Bull. 2001, 26, 394–401. [Google Scholar] [CrossRef]
- Nusser, K.; Schneider, G.J.; Pyckhout-Hintzen, W.; Richter, D. Viscosity Decrease and Reinforcement in Polymer-Silsesquioxane Composites. Macromolecules 2011, 44, 7820–7830. [Google Scholar] [CrossRef]
- Termonia, Y. Chain confinement in polymer nanocomposites and its effect on polymer bulk properties. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 687–692. [Google Scholar] [CrossRef]
- Hussain, F.; Hojjati, M.; Okamoto, M.; Gorga, R. Review article: Polymer-matrix nanocomposites, processing, manufacturing, and application: An overview. J. Compos. Mater. 2006, 40, 1511–1575. [Google Scholar] [CrossRef]
- Handbook of Polycarbonate Science and Technology; LeGrand, D.G.; Bendler, J.T. (Eds.) Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Akcora, P.; Kumar, S.K.; Moll, J.; Lewis, S.; Schadler, L.S.; Li, Y.; Benicewicz, B.C.; Sandy, A.; Narayanan, S.; Ilavsky, J.; et al. “Gel-like” mechanical reinforcement in polymer nanocomposite melts. Macromolecules 2009, 43, 1003–1010. [Google Scholar] [CrossRef]
- Cho, J.; Paul, D. Nylon 6 nanocomposites by melt compounding. Polymer 2001, 42, 1083–1094. [Google Scholar] [CrossRef]
- Heinrich, G.; Klüppel, M.; Vilgis, T.A. Reinforcement of elastomers. Curr. Opin. Solid State Mater. Sci. 2002, 6, 195–203. [Google Scholar] [CrossRef]
- Kraus, G. Reinforcement of Elastomer; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Nusser, K.; Schneider, G.J.; Richter, D. Rheology and anomalous flow properties of poly (ethylene-alt-propylene)–silica nanocomposites. Macromolecules 2013, 46, 6263–6272. [Google Scholar] [CrossRef]
- Riggleman, R.A.; Toepperwein, G.; Papakonstantopoulos, G.J.; Barrat, J.L.; de Pablo, J.J. Entanglement network in nanoparticle reinforced polymers. J. Chem. Phys. 2009, 130, 244903. [Google Scholar] [CrossRef]
- Mackay, M.E.; Dao, T.T.; Tuteja, A.; Ho, D.L.; Van Horn, B.; Kim, H.C.; Hawker, C.J. Nanoscale effects leading to non-Einstein-like decrease in viscosity. Nat. Mater. 2003, 2, 762–766. [Google Scholar] [CrossRef] [PubMed]
- Mackay, M.E.; Tuteja, A.; Duxbury, P.M.; Hawker, C.J.; Van Horn, B.; Guan, Z.; Chen, G.; Krishnan, R. General strategies for nanoparticle dispersion. Science 2006, 311, 1740–1743. [Google Scholar] [CrossRef] [PubMed]
- Tuteja, A.; Mackay, M.E.; Hawker, C.J.; Van Horn, B. Effect of ideal, organic nanoparticles on the flow properties of linear polymers: Non-Einstein-like behavior. Macromolecules 2005, 38, 8000–8011. [Google Scholar] [CrossRef]
- Tuteja, A.; Duxbury, P.M.; Mackay, M.E. Multifunctional nanocomposites with reduced viscosity. Macromolecules 2007, 40, 9427–9434. [Google Scholar] [CrossRef]
- Tuteja, A.; Mackay, M.E.; Narayanan, S.; Asokan, S.; Wong, M.S. Breakdown of the continuum Stokes-Einstein relation for nanoscale inclusions in polymer melts. Nano Lett. 2007, 7, 1276–1281. [Google Scholar] [CrossRef]
- Tuteja, A.; Duxbury, P.M.; Mackay, M.E. Polymer chain swelling induced by dispersed nanoparticles. Phys. Rev. Lett. 2008, 100, 077801. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Goossens, J.G.P.; Peters, G.W.M.; van Duin, M.; Lemstra, P.J. Strong decrease in viscosity of nanoparticle-filled polymer melts through selective adsorption. Soft Matter 2008, 4, 1848–1854. [Google Scholar] [CrossRef]
- Mangal, R.; Srivastava, S.; Archer, L.A. Phase stability and dynamics of entangled polymer–nanoparticle composites. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lai, B.; Ni, X. Rheological Behavior and Interaction of Polycarbonate/Barium Sulfate Composites. J. Macromol. Sci. Part B 2008, 47, 1028–1038. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J.; He, J. Increased flow property of polycarbonate by adding hollow glass beads. Polym. Eng. Sci. 2005, 45, 1119–1131. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, G.; Wang, X.; Li, G.; Zhang, Z. Rheology enhancement of polycarbonate/calcium carbonate nanocomposites prepared by melt-compounding. Mater. Lett. 2006, 60, 1035–1038. [Google Scholar] [CrossRef]
- Jin, S.H.; Choi, D.K.; Lee, D.S. Electrical and rheological properties of polycarbonate/multiwalled carbon nanotube nanocomposites. Colloids Surfaces A Physicochem. Eng. Asp. 2008, 313–314, 242–245. [Google Scholar] [CrossRef]
- Shenoy, A.V. Rheology of Filled Polymer Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Eggers, H.; Schummer, P. Reinforcement mechanisms in carbon black and silica loaded rubber melts at low stresses. Rubber Chem. Technol. 1996, 69, 253–265. [Google Scholar] [CrossRef]
- Kopesky, E.T.; Haddad, T.S.; McKinley, G.H.; Cohen, R.E. Miscibility and viscoelastic properties of acrylic polyhedral oligomeric silsesquioxane–poly (methyl methacrylate) blends. Polymer 2005, 46, 4743–4752. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Zur Theorie der Brownschen Bewegung. Ann. Der. Phys. 1906, 324, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Guth, E.; Gold, O. On the hydrodynamical theory of the viscosity of suspensions. Phys. Rev. 1938, 53, 322. [Google Scholar]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Roberts, C.; Cosgrove, T.; Schmidt, R.G.; Gordon, G.V. Diffusion of Poly(dimethylsiloxane) Mixtures with Silicate Nanoparticles. Macromolecules 2001, 34, 538–543. [Google Scholar] [CrossRef]
- Liu, C.; He, J.; Van Ruymbeke, E.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef] [Green Version]
- Lipatov, Y.S.; Privalko, V. Glass transition in filled polymer systems. Polym. Sci. USSR 1972, 14, 1843–1848. [Google Scholar] [CrossRef]
- Kalfus, J.; Jancar, J. Relaxation processes in PVAc-HA nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 1380–1388. [Google Scholar] [CrossRef]
- Arrighi, V.; McEwen, I.; Qian, H.; Prieto, M.S. The glass transition and interfacial layer in styrene-butadiene rubber containing silica nanofiller. Polymer 2003, 44, 6259–6266. [Google Scholar] [CrossRef]
- Miwa, Y.; Drews, A.R.; Schlick, S. Detection of the direct effect of clay on polymer dynamics: The case of spin-labeled poly (methyl acrylate)/clay nanocomposites studied by ESR, XRD, and DSC. Macromolecules 2006, 39, 3304–3311. [Google Scholar] [CrossRef]
- Jiang, T.; Zukoski, C.F. Role of Particle Size and Polymer Length in Rheology of Colloid–Polymer Composites. Macromolecules 2012, 45, 9791–9803. [Google Scholar] [CrossRef]
- Kirst, K.U.; Kremer, F.; Litvinov, V.M. Broad-band dielectric spectroscopy on the molecular dynamics of bulk and adsorbed poly (dimethylsiloxane). Macromolecules 1993, 26, 975–980. [Google Scholar] [CrossRef]
- Lin, W.Y.; Blum, F.D. Segmental dynamics of bulk and silica-adsorbed poly(methyl acrylate)-d 3 by deuterium NMR: The effect of molecular weight. Macromolecules 1998, 31, 4135–4142. [Google Scholar] [CrossRef]
- Mammeri, F.; Rozes, L.; Le Bourhis, E.; Sanchez, C. Elaboration and mechanical characterization of nanocomposites thin films: Part II. Correlation between structure and mechanical properties of SiO2-PMMA hybrid materials. J. Eur. Ceram. Soc. 2006, 26, 267–272. [Google Scholar] [CrossRef]
- Vieweg, S.; Unger, R.; Hempel, E.; Donth, E. Kinetic structure of glass transition in polymer interfaces between filler and SBR matrix. J. Non-Cryst. Solids 1998, 235, 470–475. [Google Scholar] [CrossRef]
- Menczel, J.; Wunderlich, B. Heat capacity hysteresis of semicrystalline macromolecular glasses. J. Polym. Sci. Polym. Lett. Ed. 1981, 19, 261–264. [Google Scholar] [CrossRef]
- Sargsyan, A. Quantification of the Immobilized Fraction in Polymer Inorganic Nanocomposites. Ph.D. Thesis, University of Rostock, Rostock, Germany, 2007. [Google Scholar]
- Wurm, A.; Ismail, M.; Kretzschmar, B.; Pospiech, D.; Schick, C. Retarded crystallization in polyamide/layered silicates nanocomposites caused by an immobilized interphase. Macromolecules 2010, 43, 1480–1487. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Milner, S.T.; Graessley, W.W. Packing length influence in linear polymer melts on the entanglement, critical, and reptation molecular weights. Macromolecules 1999, 32, 6847–6851. [Google Scholar] [CrossRef]
- Wang, F.; Meng, X.; Xu, X.; Wen, B.; Qian, Z.; Gao, X.; Ding, Y.; Zhang, S.; Yang, M. Inhibited transesterification of PET/PBT blends filled with silica nanoparticles during melt processing. Polym. Degrad. Stab. 2008, 93, 1397–1404. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Harsiny, S.; Goossens, J.G.; Hoeks, T.L.; Peters, G.W. Physical aging in polycarbonate nanocomposites containing grafted nanosilica particles: A comparison between enthalpy and yield stress evolution. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2069–2081. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Cox, W.; Merz, E. Rheology of polymer melts. A correlation of dynamic and steady-flow measurement. Am. Soc. Test. Mater. Spec. Tech. Publ. 1958, 247, 178–188. [Google Scholar]
- Sun, C. Controlling the Rheology of Polymer/Silica Nanocomposites. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2010. [Google Scholar]
- Goel, V.; Chatterjee, T.; Bombalski, L.; Yurekli, K.; Matyjaszewski, K.; Krishnamoorti, R. Viscoelastic properties of silica-grafted poly(styrene–acrylonitrile) nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2014–2023. [Google Scholar] [CrossRef]
- Ren, J.; Krishnamoorti, R. Nonlinear viscoelastic properties of layered-silicate-based intercalated nanocomposites. Macromolecules 2003, 36, 4443–4451. [Google Scholar] [CrossRef]
- Pissis, P.; Kotsilkova, R. Thermoset Nanocomposites for Engineering Applications; Smithers Rapra Technology: Shrewsbury, UK, 2007. [Google Scholar]
- Graham, M.D. Wall slip and the nonlinear dynamics of large amplitude oscillatory shear flows. J. Rheol. 1995, 39, 697–712. [Google Scholar] [CrossRef]
- Mackay, M.; Henson, D. The effect of molecular mass and temperature on the slip of polystyrene melts at low stress levels. J. Rheol. 1998, 42, 1505–1517. [Google Scholar] [CrossRef]
- Henson, D.J.; Mackay, M.E. Effect of gap on the viscosity of monodisperse polystyrene melts: Slip effects. J. Rheol. 1995, 39, 359–373. [Google Scholar] [CrossRef]
- Schulze, D.; Trinkle, S.; Mülhaupt, R.; Friedrich, C. Rheological evidence of modifications of polypropylene by beta-irradiation. Rheol. Acta 2003, 42, 251–258. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, S.Q. Exfoliation and yield behavior in nanodispersions of organically modified montmorillonite clay. J. Rheol. 2003, 47, 483–495. [Google Scholar] [CrossRef]
- Jouault, N.; Vallat, P.; Dalmas, F.; Said, S.; Jestin, J.; Boué, F. Well-Dispersed Fractal Aggregates as Filler in Polymer- Silica Nanocomposites: Long-Range Effects in Rheology. Macromolecules 2009, 42, 2031–2040. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Srivastava, S.; Narayanan, S.; Archer, L.A. Polymer nanocomposites: Polymer and particle dynamics. Soft Matter 2012, 8, 10813–10818. [Google Scholar] [CrossRef]
- Cosgrove, T.; Roberts, C.; Garasanin, T.; Schmidt, R.G.; Gordon, G.V. NMR Spin- Spin Relaxation Studies of Silicate-Filled Low Molecular Weight Poly(dimethylsiloxane)s. Langmuir 2002, 18, 10080–10085. [Google Scholar] [CrossRef]
- Graessley, W.; Edwards, S. Entanglement interactions in polymers and the chain contour concentration. Polymer 1981, 22, 1329–1334. [Google Scholar] [CrossRef]
- Nakajima, N.; Okuno, S. Effect of rubber–plasticizer interaction on temperature and concentration dependence of viscoelastic properties. J. Rheol. 1994, 38, 541–553. [Google Scholar] [CrossRef]
- Robertson, J.E. Thermal Degradation Studies of Polycarbonate. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VR, USA, 2001. [Google Scholar]
- Aho, J. Rheological Characterization of Polymer Melts in Shear and Extension: Measurement Reliability and Data for Practical Processing. Ph.D. Thesis, Julkaisu-Tampere University of Technology, Tampere, Finland, 2011. [Google Scholar]
- Sen, S.; Xie, Y.; Kumar, S.K.; Yang, H.; Bansal, A.; Ho, D.L.; Hall, L.; Hooper, J.B.; Schweizer, K.S. Chain conformations and bound-layer correlations in polymer nanocomposites. Phys. Rev. Lett. 2007, 98, 128302. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.J.; Zukoski, C.F. Rheology and microstructure of entangled polymer nanocomposite melts. Macromolecules 2009, 42, 8370–8384. [Google Scholar] [CrossRef]
- Lakdawala, K.; Salovey, R. Rheology of polymers containing carbon black. Polym. Eng. Sci. 1987, 27, 1035–1042. [Google Scholar] [CrossRef]
- Liang, J.Z. Toughening and reinforcing in rigid inorganic particulate filled poly (propylene): A review. J. Appl. Polym. Sci. 2002, 83, 1547–1555. [Google Scholar] [CrossRef]
- Dealy, J.M.; Larson, R.G. Structure and Rheology of Molten Polymers; Hanser: Munich, Germany, 2006. [Google Scholar]
- Masnada, E.; Merabia, S.; Couty, M.; Barrat, J.L. Entanglement-induced reinforcement in polymer nanocomposites. Soft Matter 2013, 9, 10532–10544. [Google Scholar] [CrossRef]
- Akcora, P.; Liu, H.; Kumar, S.K.; Moll, J.; Li, Y.; Benicewicz, B.C.; Schadler, L.S.; Acehan, D.; Panagiotopoulos, A.Z.; Pryamitsyn, V.; et al. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Chevigny, C.; Dalmas, F.; Di Cola, E.; Gigmes, D.; Bertin, D.; Boué, F.; Jestin, J. Polymer-grafted-nanoparticles nanocomposites: Dispersion, grafted chain conformation, and rheological behavior. Macromolecules 2011, 44, 122–133. [Google Scholar] [CrossRef]
- Sen, S.; Xie, Y.; Bansal, A.; Yang, H.; Cho, K.; Schadler, L.; Kumar, S. Equivalence between polymer nanocomposites and thin polymer films: Effect of processing conditions and molecular origins of observed behavior. Eur. Phys. J. Spec. Top. 2007, 141, 161–165. [Google Scholar] [CrossRef]
- Giovino, M.; Pribyl, J.; Benicewicz, B.; Kumar, S.; Schadler, L. Linear rheology of polymer nanocomposites with polymer-grafted nanoparticles. Polymer 2017, 131, 104–110. [Google Scholar] [CrossRef]
- Yagfarov, M.S.; Ionkin, V.; Gizatullina, Z. Study of the low-temperature thermal behaviour of filled polydimethylsiloxanes. Polym. Sci. USSR 1969, 11, 2626–2632. [Google Scholar] [CrossRef]
- Schick, C.; Donth, E. Characteristic length of glass transition: Experimental evidence. Phys. Scr. 1991, 43, 423. [Google Scholar] [CrossRef]
- Picu, R.; Rakshit, A. Dynamics of free chains in polymer nanocomposites. J. Chem. Phys. 2007, 126, 144909. [Google Scholar] [CrossRef]
- Ganesan, V.; Pryamitsyn, V.; Surve, M.; Narayanan, B. Noncontinuum effects in nanoparticle dynamics in polymers. J. Chem. Phys. 2006, 124, 221102. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Hill, R.J. Anomalous bulk viscosity of polymer-nanocomposite melts. Soft Matter 2009, 5, 3940–3953. [Google Scholar] [CrossRef]
- Brown, D.; Marcadon, V.; Mele, P.; Alberola, N. Effect of filler particle size on the properties of model nanocomposites. Macromolecules 2008, 41, 1499–1511. [Google Scholar] [CrossRef]
- Brown, D.; Mele, P.; Marceau, S.; Alberola, N. A molecular dynamics study of a model nanoparticle embedded in a polymer matrix. Macromolecules 2003, 36, 1395–1406. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D.; Li, L.; Byutner, O. A molecular dynamics simulation study of the viscoelastic properties of polymer nanocomposites. J. Chem. Phys. 2002, 117, 9478–9489. [Google Scholar] [CrossRef]
- Starr, F.W.; Schrøder, T.B.; Glotzer, S.C. Effects of a nanoscopic filler on the structure and dynamics of a simulated polymer melt and the relationship to ultrathin films. Phys. Rev. E 2001, 64, 021802. [Google Scholar] [CrossRef] [Green Version]
- Termonia, Y. Monte-Carlo modeling of dense polymer melts near nanoparticles. Polymer 2009, 50, 1062–1066. [Google Scholar] [CrossRef]
- Wyart, F.B.; De Gennes, P. Viscosity at small scales in polymer melts. Eur. Phys. J. E 2000, 1, 93–97. [Google Scholar] [CrossRef]
- Cai, L.H.; Panyukov, S.; Rubinstein, M. Mobility of nonsticky nanoparticles in polymer liquids. Macromolecules 2011, 44, 7853–7863. [Google Scholar] [CrossRef] [Green Version]
- Schneider, G.J.; Nusser, K.; Neueder, S.; Brodeck, M.; Willner, L.; Farago, B.; Holderer, O.; Briels, W.J.; Richter, D. Anomalous chain diffusion in unentangled model polymer nanocomposites. Soft Matter 2013, 9, 4336–4348. [Google Scholar] [CrossRef] [Green Version]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Entanglements in polymer nanocomposites containing spherical nanoparticles. Soft Matter 2016, 12, 2567–2574. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Kröger, M.; Liu, W.K. Dynamic structure of unentangled polymer chains in the vicinity of non-attractive nanoparticles. Soft Matter 2014, 10, 1723–1737. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Nanoparticle effect on the dynamics of polymer chains and their entanglement network. Phys. Rev. Lett. 2012, 109, 118001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamamoto, U.; Schweizer, K.S. Theory of entanglements and tube confinement in rod–sphere nanocomposites. ACS Macro Lett. 2013, 2, 955–959. [Google Scholar] [CrossRef]


| Material | [Kg/mol] | PDI | [nm] | [nm] | [°C] |
|---|---|---|---|---|---|
| 21.3 | 2.3 | 6.4 | 3.8 | 142 | |
| 31.5 | 2.5 | 7.6 | 3.8 | 148 | |
| 39.3 | 3.2 | 8.5 | 3.8 | 149 | |
| PS | 300 | 2.6 | 14.5 | 8.4 | 100 |
| Material | [] | Layer Thickness [nm] |
|---|---|---|
| 0S, 0S, 0S | 0 | - |
| 0.7S | −13 | 6 |
| 3S | −1.4 | 1 |
| 0.7S | −13 | 7 |
| 3S | −1.4 | 0.8 |
| 0.7S | −16 | 8 |
| 3S | −2.7 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramakrishnan, V.; Goossens, J.G.P.; Hoeks, T.L.; Peters, G.W.M. Anomalous Terminal Shear Viscosity Behavior of Polycarbonate Nanocomposites Containing Grafted Nanosilica Particles. Nanomaterials 2021, 11, 1839. https://doi.org/10.3390/nano11071839
Ramakrishnan V, Goossens JGP, Hoeks TL, Peters GWM. Anomalous Terminal Shear Viscosity Behavior of Polycarbonate Nanocomposites Containing Grafted Nanosilica Particles. Nanomaterials. 2021; 11(7):1839. https://doi.org/10.3390/nano11071839
Chicago/Turabian StyleRamakrishnan, Vaidyanath, Johannes G. P. Goossens, Theodorus L. Hoeks, and Gerrit W. M. Peters. 2021. "Anomalous Terminal Shear Viscosity Behavior of Polycarbonate Nanocomposites Containing Grafted Nanosilica Particles" Nanomaterials 11, no. 7: 1839. https://doi.org/10.3390/nano11071839
APA StyleRamakrishnan, V., Goossens, J. G. P., Hoeks, T. L., & Peters, G. W. M. (2021). Anomalous Terminal Shear Viscosity Behavior of Polycarbonate Nanocomposites Containing Grafted Nanosilica Particles. Nanomaterials, 11(7), 1839. https://doi.org/10.3390/nano11071839







