Ballistic Heat Transport in Nanocomposite: The Role of the Shape and Interconnection of Nanoinclusions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Studied Configurations
2.2. Equilibrium Molecular Dynamics
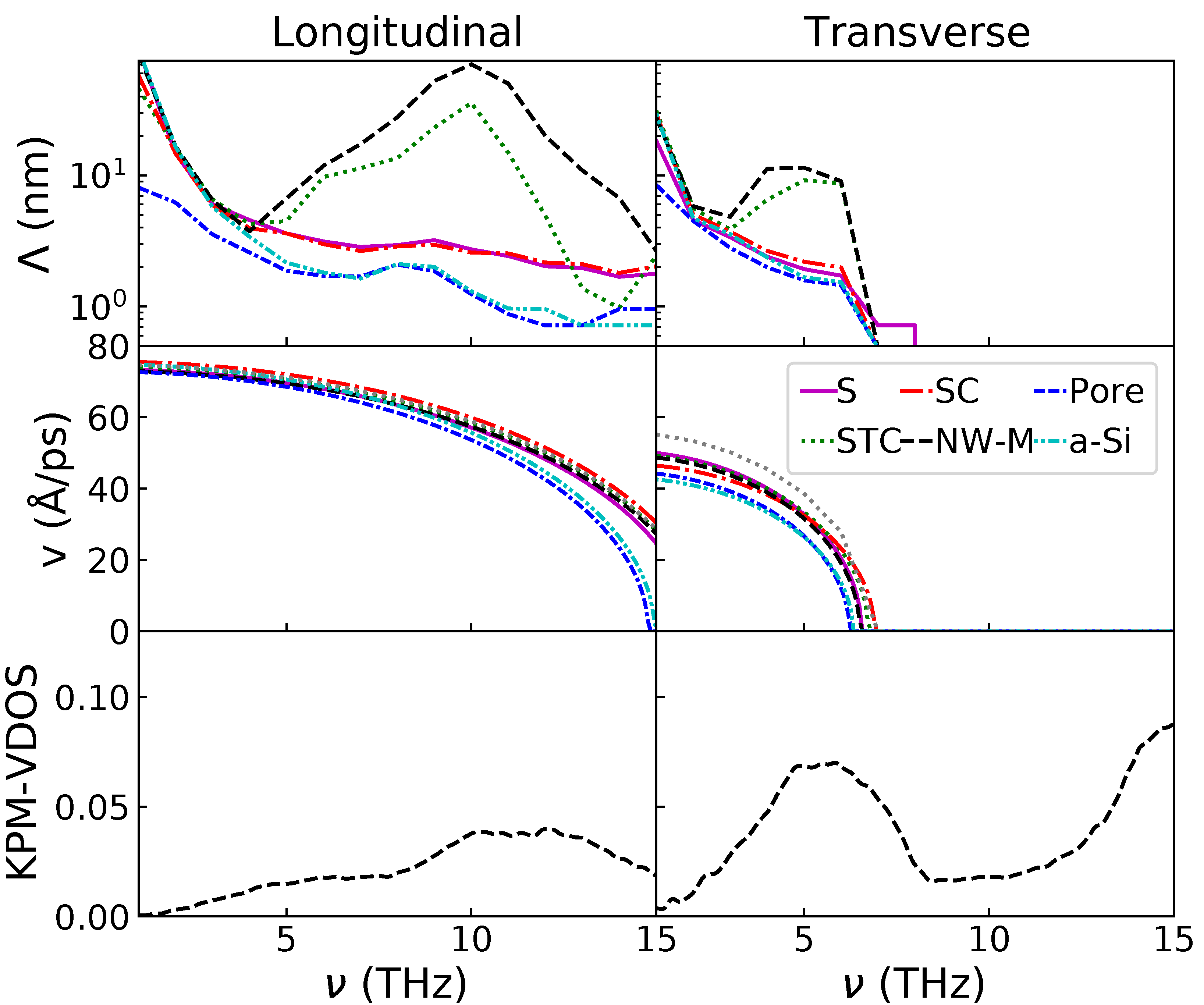
2.3. Thermal Conductivity from the Kinetic Theory
2.4. Wave Packet Propagation
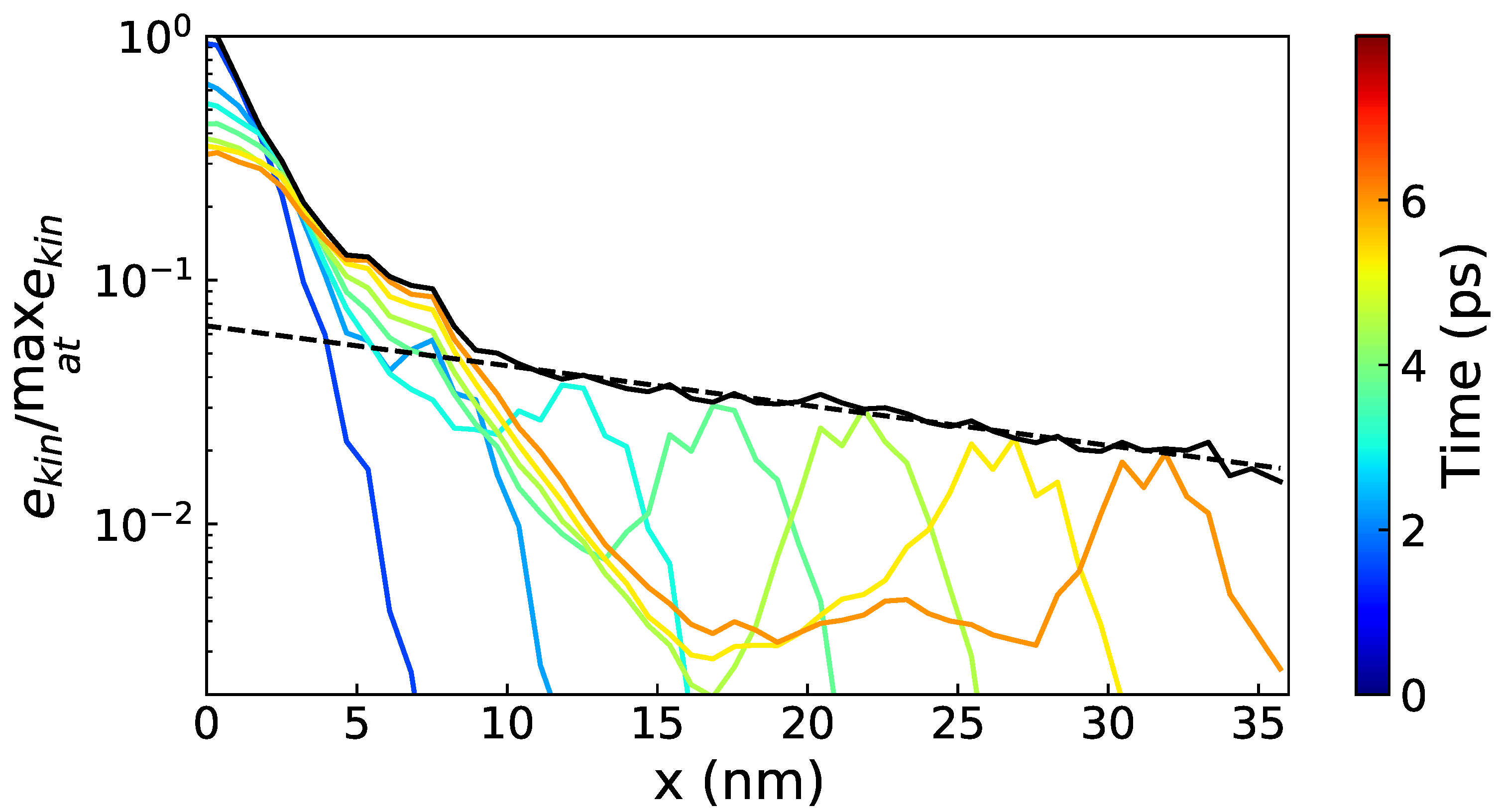
2.5. Lifetime Estimation and Temperature Effect
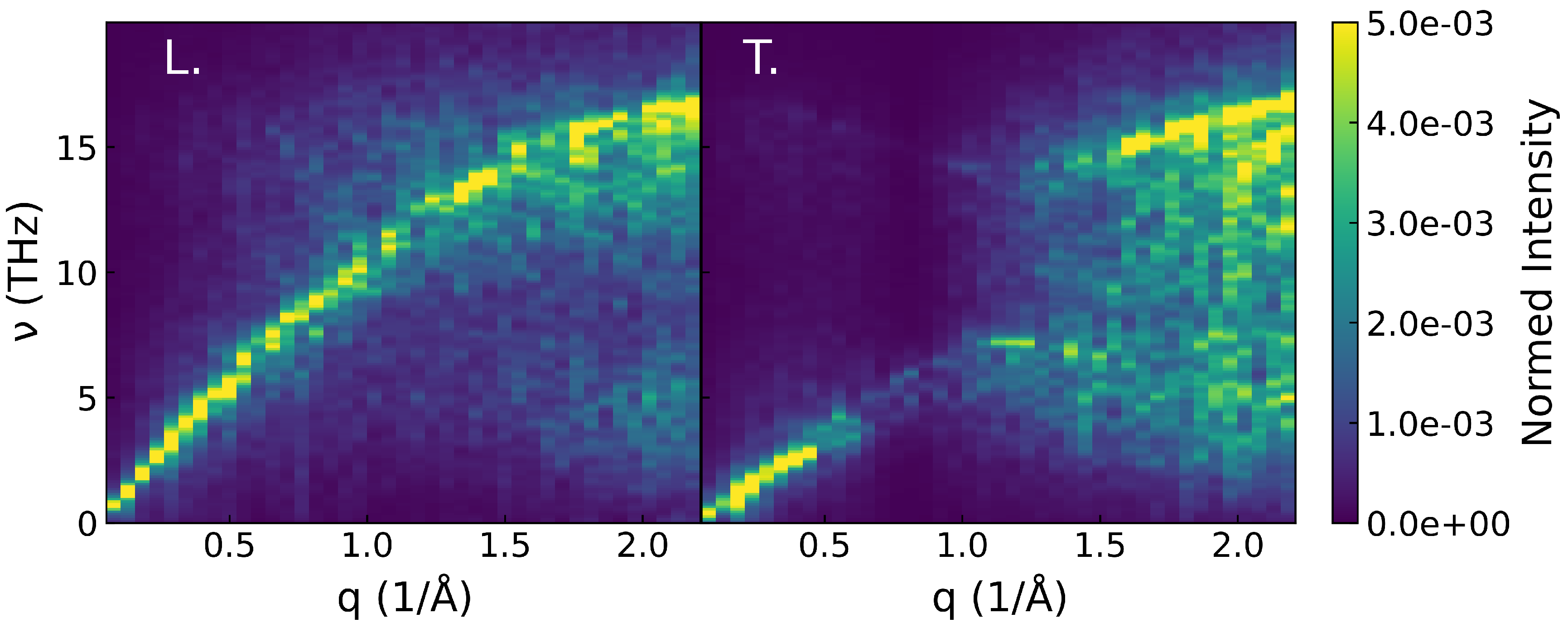
2.6. Group Velocity through the Dynamical Structure Factor
2.7. Vibrational Density of States
3. Results
3.1. Ballisticity through Wave-Packet Simulations
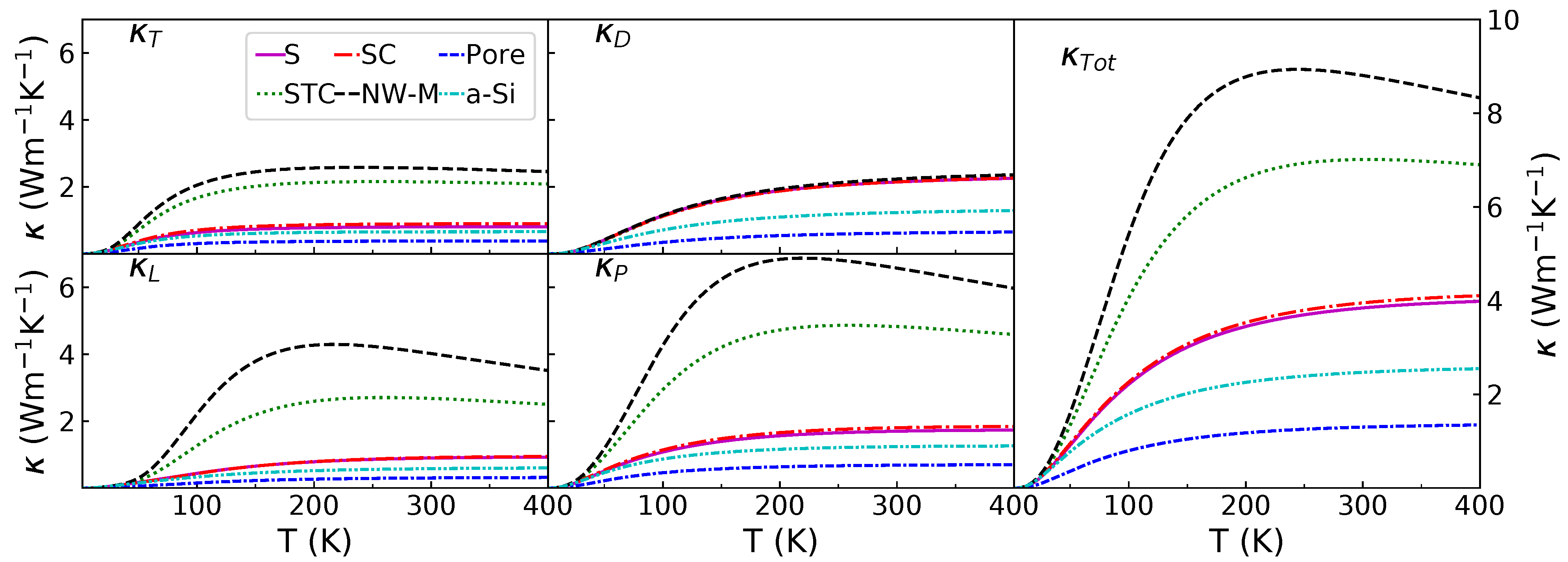
3.2. Diffusive and Propagative Contributions to the Thermal Conductivity
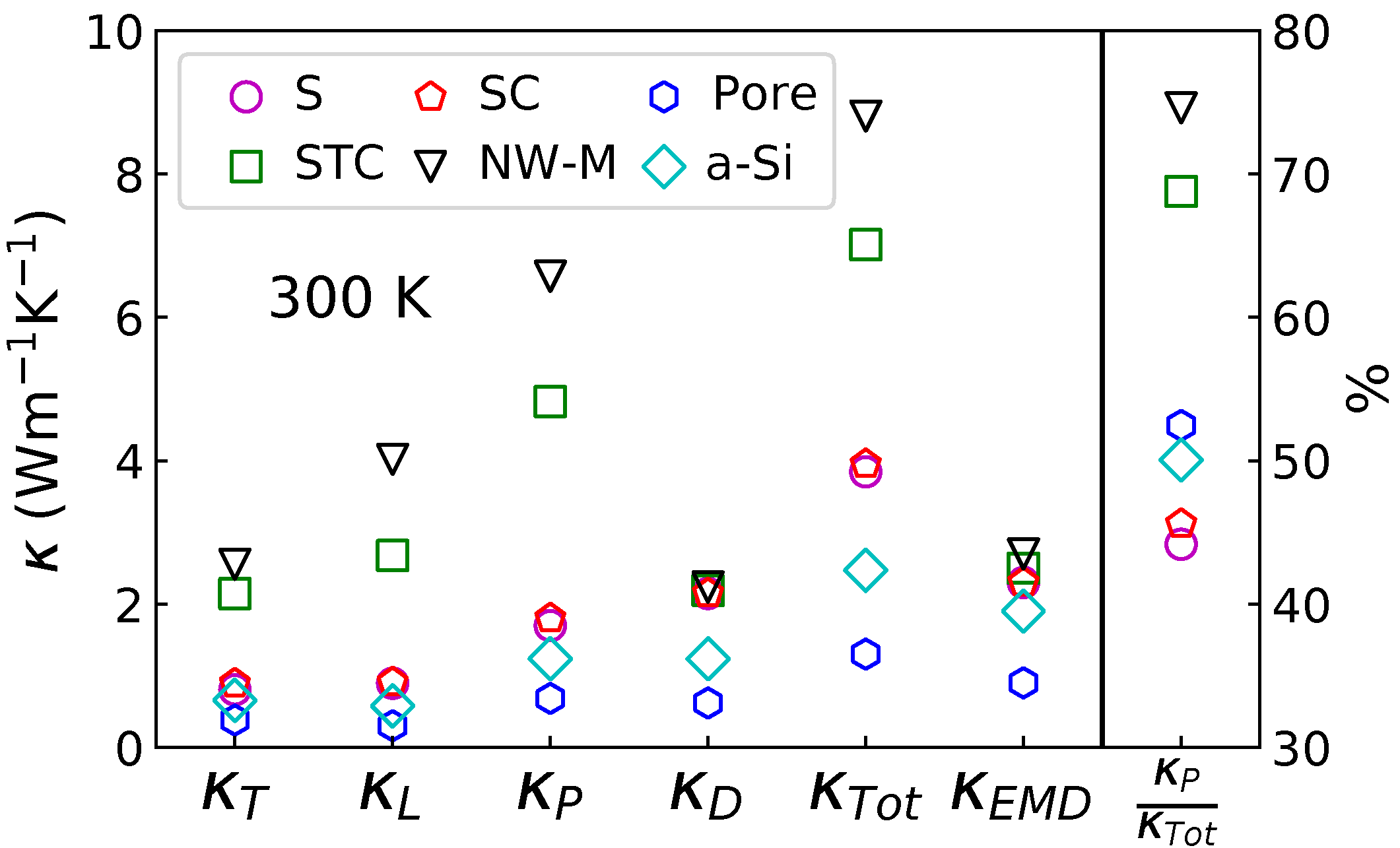
3.3. Global Estimation of the Thermal Conductivity
4. Discussion
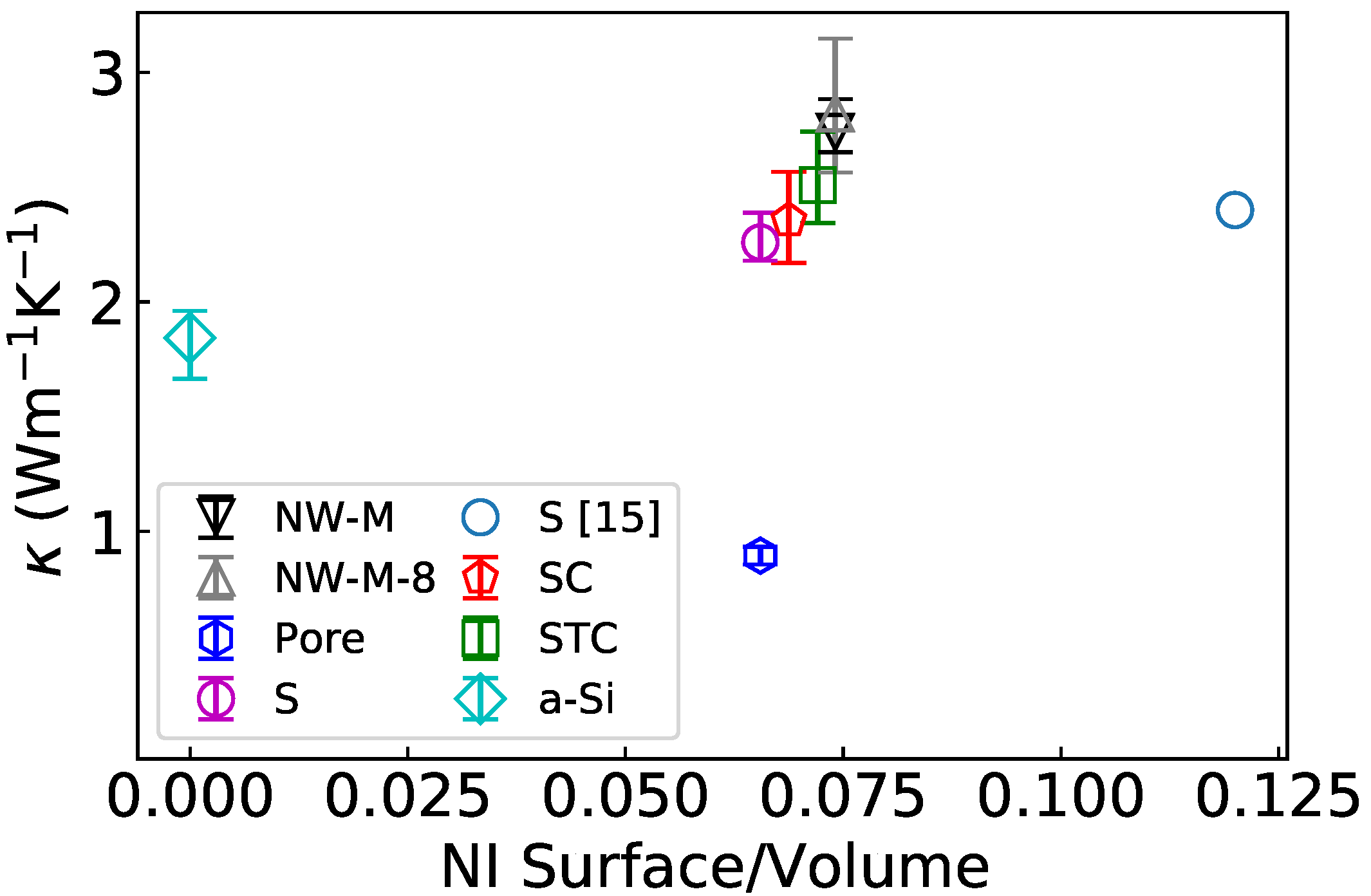
4.1. Thermal Conductivity
4.2. Ballistic and Diffusive Transport
4.3. Validity of the Hypothesis Made
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Damped Harmonic Oscillator

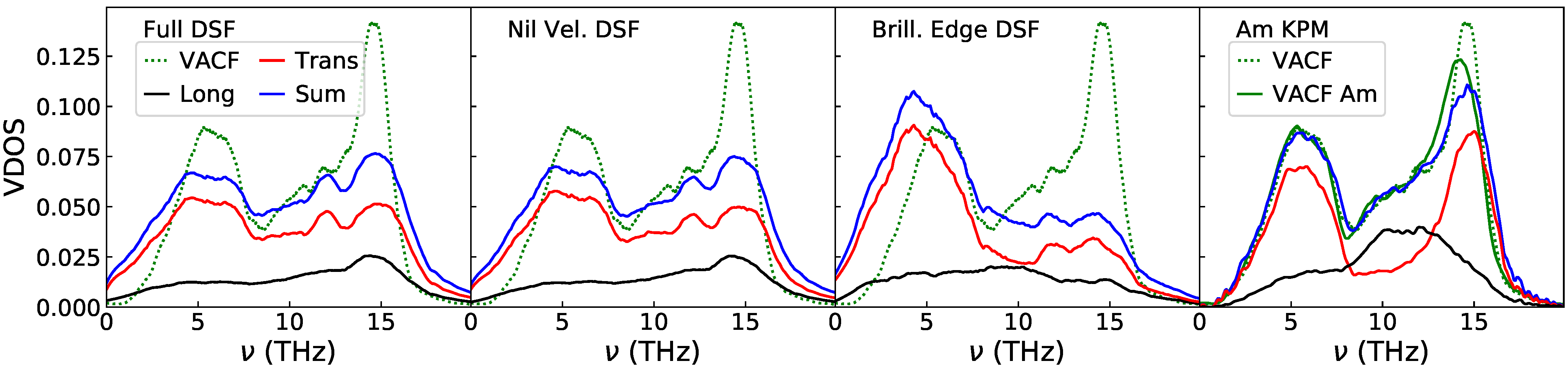
Appendix B. VDOS Estimated with DSF, VACF or KPM
References
- Kim, W.; Zide, J.; Gossard, A.; Klenov, D.; Stemmer, S.; Shakouri, A.; Majumdar, A. Thermal Conductivity Reduction and Thermoelectric Figure of Merit Increase by Embedding Nanoparticles in Crystalline Semiconductors. Phys. Rev. Lett. 2006, 96, 045901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, T.J.; Yan, F.; Zhao, X.B.; Zhang, S.N.; Chen, Y.; Yang, S.H. Preparation and thermoelectric properties of bulkin situnanocomposites with amorphous/nanocrystal hybrid structure. J. Phys. D Appl. Phys. 2007, 40, 6094–6097. [Google Scholar] [CrossRef]
- Murray, D.B.; Saviot, L. Phonons in an inhomogeneous continuum: Vibrations of an embedded nanoparticle. Phys. Rev. B 2004, 69, 094305. [Google Scholar] [CrossRef] [Green Version]
- Damart, T.; Giordano, V.M.; Tanguy, A. Nanocrystalline inclusions as a low-pass filter for thermal transport in a-Si. Phys. Rev. B 2015, 92, 094201. [Google Scholar] [CrossRef] [Green Version]
- Allen, P.B.; Feldman, J.L. Thermal conductivity of disordered harmonic solids. Phys. Rev. B 1993, 48, 12581–12588. [Google Scholar] [CrossRef]
- Allen, P.B.; Feldman, J.L.; Fabian, J.; Wooten, F. Diffusons, locons and propagons: Character of atomie yibrations in amorphous Si. Philos. Mag. B 1999, 79, 1715–1731. [Google Scholar] [CrossRef]
- Seyf, H.R.; Henry, A. A method for distinguishing between propagons, diffusions, and locons. J. Appl. Phys. 2016, 120, 025101. [Google Scholar] [CrossRef] [Green Version]
- Beltukov, Y.M.; Kozub, V.I.; Parshin, D.A. Ioffe-Regel criterion and diffusion of vibrations in random lattices. Phys. Rev. B 2013, 87, 134203. [Google Scholar] [CrossRef] [Green Version]
- Larkin, J.M.; McGaughey, A.J.H. Thermal conductivity accumulation in amorphous silica and amorphous silicon. Phys. Rev. B 2014, 89, 144303. [Google Scholar] [CrossRef] [Green Version]
- DeAngelis, F.; Muraleedharan, M.G.; Moon, J.; Seyf, H.R.; Minnich, A.J.; McGaughey, A.J.H.; Henry, A. Thermal Transport in Disordered Materials. Nanoscale Microscale Thermophys. Eng. 2019, 23, 81–116. [Google Scholar] [CrossRef]
- Sääskilahti, K.; Oksanen, J.; Tulkki, J.; McGaughey, A.J.H.; Volz, S. Vibrational mean free paths and thermal conductivity of amorphous silicon from non-equilibrium molecular dynamics simulations. AIP Adv. 2016, 6, 121904. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Gravouil, A.; Giordano, V.; Tanguy, A. Thermal Transport in a 2D Nanophononic Solid: Role of bi-Phasic Materials Properties on Acoustic Attenuation and Thermal Diffusivity. Nanomaterials 2019, 9, 1471. [Google Scholar] [CrossRef] [Green Version]
- Termentzidis, K.; Giordano, V.M.; Katsikini, M.; Paloura, E.; Pernot, G.; Verdier, M.; Lacroix, D.; Karakostas, I.; Kioseoglou, J. Enhanced thermal conductivity in percolating nanocomposites: A molecular dynamics investigation. Nanoscale 2018, 10, 21732–21741. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Minnich, A.J. The best nanoparticle size distribution for minimum thermal conductivity. Sci. Rep. 2015, 5, 8995. [Google Scholar] [CrossRef] [Green Version]
- Tlili, A.; Giordano, V.M.; Beltukov, Y.M.; Desmarchelier, P.; Merabia, S.; Tanguy, A. Enhancement and anticipation of the Ioffe–Regel crossover in amorphous/nanocrystalline composites. Nanoscale 2019, 11, 21502–21512. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Pan, N. Predictions of effective physical properties of complex multiphase materials. Mater. Sci. Eng. R Rep. 2008, 63, 1–30. [Google Scholar] [CrossRef]
- Fang, K.C.; Weng, C.I.; Ju, S.P. An investigation into the structural features and thermal conductivity of silicon nanoparticles using molecular dynamics simulations. Nanotechnology 2006, 17, 3909–3914. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Hofmeister, H.; Tan, G.; Dubiel, M. Shape and internal structure of silver nanoparticles embedded in glass. J. Mater. Res. 2005, 20, 1551–1562. [Google Scholar] [CrossRef]
- Vasudevan, S.; Fullerton-Shirey, S.K. Effect of Nanoparticle Shape on the Electrical and Thermal Properties of Solid Polymer Electrolytes. J. Phys. Chem. C 2019, 123, 10720–10726. [Google Scholar] [CrossRef]
- Jabbari, F.; Rajabpour, A.; Saedodin, S. Thermal conductivity and viscosity of nanofluids: A review of recent molecular dynamics studies. Chem. Eng. Sci. 2017, 174, 67–81. [Google Scholar] [CrossRef]
- Miura, A.; Zhou, S.; Nozaki, T.; Shiomi, J. Crystalline—Amorphous Silicon Nanocomposites with Reduced Thermal Conductivity for Bulk Thermoelectrics. ACS Appl. Mater. Interfaces 2015, 7, 13484–13489. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, Y.; Isogawa, M.; Ueda, T.; Yamasaka, S.; Matsui, H.; Kikkawa, J.; Ikeuchi, S.; Oyake, T.; Hori, T.; Shiomi, J.; et al. Anomalous reduction of thermal conductivity in coherent nanocrystal architecture for silicon thermoelectric material. Nano Energy 2015, 12, 845–851. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, Y. Nanostructure design for drastic reduction of thermal conductivity while preserving high electrical conductivity. Sci. Technol. Adv. Mater. 2018, 19, 31–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Hu, J.; Yao, Y.; Zeng, X.; Sun, J.; Pan, G.; Sun, R.; Xu, J.B.; Wong, C.P. Manipulating Orientation of Silicon Carbide Nanowire in Polymer Composites to Achieve High Thermal Conductivity. Adv. Mater. Interfaces 2017, 4, 1700446. [Google Scholar] [CrossRef]
- Car, D.; Wang, J.; Verheijen, M.A.; Bakkers, E.P.A.M.; Plissard, S.R. Rationally Designed Single-Crystalline Nanowire Networks. Adv. Mater. 2014, 26, 4875–4879. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Ding, H.; Meng, H.; Feng, L.; Wu, Y.; Shiomi, J.; Yang, N. Nano-cross-junction effect on phonon transport in silicon nanowire cages. Phys. Rev. B 2016, 94, 165434. [Google Scholar] [CrossRef] [Green Version]
- Verdier, M.; Lacroix, D.; Termentzidis, K. Thermal transport in two- and three-dimensional nanowire networks. Phys. Rev. B 2018, 98, 155434. [Google Scholar] [CrossRef] [Green Version]
- Kimmer, C.; Aubry, S.; Skye, A.; Schelling, P.K. Scattering of phonons from a high-energy grain boundary in silicon: Dependence on angle of incidence. Phys. Rev. B 2007, 75, 144105. [Google Scholar] [CrossRef]
- Yang, L.; Minnich, A.J. Thermal transport in nanocrystalline Si and SiGe by ab initio based Monte Carlo simulation. Sci. Rep. 2017, 7, 44254. [Google Scholar] [CrossRef] [PubMed]
- Hori, T.; Shiomi, J.; Dames, C. Effective phonon mean free path in polycrystalline nanostructures. Appl. Phys. Lett. 2015, 106, 171901. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Maras, E.; Trushin, O.; Stukowski, A.; Ala-Nissila, T.; Jónsson, H. Global transition path search for dislocation formation in Ge on Si(001). Comput. Phys. Commun. 2016, 205, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Vink, R.; Barkema, G.; van der Weg, W.; Mousseau, N. Fitting the Stillinger—Weber potential to amorphous silicon. J. Non-Cryst. Solids 2001, 282, 248–255. [Google Scholar] [CrossRef]
- France-Lanord, A.; Merabia, S.; Albaret, T.; Lacroix, D.; Termentzidis, K. Thermal properties of amorphous/crystalline silicon superlattices. J. Phys. Condens. Matter 2014, 26, 355801. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Surblys, D.; Matsubara, H.; Kikugawa, G.; Ohara, T. Application of atomic stress to compute heat flux via molecular dynamics for systems with many-body interactions. Phys. Rev. E 2019, 99, 051301. [Google Scholar] [CrossRef] [Green Version]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Phonon wave-packet dynamics at semiconductor interfaces by molecular-dynamics simulation. Appl. Phys. Lett. 2002, 80, 2484–2486. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; HOLT, Rinehart and Winston: New York, NY, USA; London, UK, 1976; Volume 2005. [Google Scholar]
- Larkin, J.M.; McGaughey, A.J.H. Predicting alloy vibrational mode properties using lattice dynamics calculations, molecular dynamics simulations, and the virtual crystal approximation. J. Appl. Phys. 2013, 114, 023507. [Google Scholar] [CrossRef] [Green Version]
- Beltukov, Y.M.; Fusco, C.; Parshin, D.A.; Tanguy, A. Boson peak and Ioffe-Regel criterion in amorphous siliconlike materials: The effect of bond directionality. Phys. Rev. E 2016, 93, 023006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beltukov, Y.M.; Parshin, D.A.; Giordano, V.M.; Tanguy, A. Propagative and diffusive regimes of acoustic damping in bulk amorphous material. Phys. Rev. E 2018, 98, 023005. [Google Scholar] [CrossRef] [Green Version]
- Callaway, J. Model for Lattice Thermal Conductivity at Low Temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Yang, F.; Dames, C. Mean free path spectra as a tool to understand thermal conductivity in bulk and nanostructures. Phys. Rev. B 2013, 87, 035437. [Google Scholar] [CrossRef]
- Boon, J.P.; Yip, S. Molecular Hydrodynamics; Courier Corporation: North Chelmsford, MA, USA, 1991. [Google Scholar]
- Dove, M.T. Time correlation functions. In Introduction to Lattice Dynamics; Cambridge Topics in Mineral Physics and Chemistry; Cambridge University Press: Cambridge, UK, 1993; pp. 229–232. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Beltukov, Y.M.; Fusco, C.; Tanguy, A.; Parshin, D.A. Transverse and longitudinal vibrations in amorphous silicon. J. Phys. Conf. Ser. 2015, 661, 012056. [Google Scholar] [CrossRef]
- Weiße, A.; Wellein, G.; Alvermann, A.; Fehske, H. The kernel polynomial method. Rev. Mod. Phys. 2006, 78, 275–306. [Google Scholar] [CrossRef] [Green Version]
- Rycroft, C.H. Multiscale Modeling in Granular Flow. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Chantrenne, P.; Termentzidis, K. Prediction of the thermal conductivity of SiC nanowires with kinetic theory of gases. Phys. Status Solidi A 2012, 209, 2492–2498. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936. [Google Scholar] [CrossRef]
- Zeller, R.C.; Pohl, R.O. Thermal Conductivity and Specific Heat of Noncrystalline Solids. Phys. Rev. B 1971, 4, 2029–2041. [Google Scholar] [CrossRef]
- Cahill, D.G.; Pohl, R.O. Lattice Vibrations and Heat Transport in Crystals and Glasses. Annu. Rev. Phys. Chem. 1988, 39, 93–121. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Scandolo, S. Thermal conductivity of solid argon from molecular dynamics simulations. J. Chem. Phys. 2004, 120, 3765–3769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef] [Green Version]
- Lv, W.; Henry, A. Direct calculation of modal contributions to thermal conductivity via Green–Kubo modal analysis. New J. Phys. 2016, 18, 013028. [Google Scholar] [CrossRef] [Green Version]
- Minnich, A.; Chen, G. Modified effective medium formulation for the thermal conductivity of nanocomposites. Appl. Phys. Lett. 2007, 91, 073105. [Google Scholar] [CrossRef]
- Termentzidis, K.; Isaiev, M.; Salnikova, A.; Belabbas, I.; Lacroix, D.; Kioseoglou, J. Impact of screw and edge dislocations on the thermal conductivity of individual nanowires and bulk GaN: A molecular dynamics study. Phys. Chem. Chem. Phys. 2018, 20, 5159–5172. [Google Scholar] [CrossRef] [Green Version]
- Cahill, D.G.; Katiyar, M.; Abelson, J.R. Thermal conductivity of a-Si:H thin films. Phys. Rev. B 1994, 50, 6077–6081. [Google Scholar] [CrossRef]
- Isaiev, M.; Newby, P.J.; Canut, B.; Tytarenko, A.; Lishchuk, P.; Andrusenko, D.; Gomès, S.; Bluet, J.M.; Fréchette, L.G.; Lysenko, V.; et al. Thermal conductivity of partially amorphous porous silicon by photoacoustic technique. Mater. Lett. 2014, 128, 71–74. [Google Scholar] [CrossRef]
- Massoud, A.M.; Chapuis, P.O.; Canut, B.; Bluet, J.M. Thermal conductivity of irradiated porous silicon down to the oxide limit investigated by Raman thermometry and scanning thermal microscopy. J. Appl. Phys. 2020, 128, 175109. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Cui, Z.; Gerboth, M.; Zhao, Y.; Xu, T.T.; Walker, D.G.; Li, D. Ballistic Phonon Penetration Depth in Amorphous Silicon Dioxide. Nano Lett. 2017, 17, 7218–7225. [Google Scholar] [CrossRef]
- Yang, L.; Latour, B.; Minnich, A.J. Phonon transmission at crystalline-amorphous interfaces studied using mode-resolved atomistic Green’s functions. Phys. Rev. B 2018, 97, 205306. [Google Scholar] [CrossRef] [Green Version]
- Desmarchelier, P.; Tanguy, A.; Termentzidis, K. Thermal rectification in asymmetric two-phase nanowires. Phys. Rev. B 2021, 103, 014202. [Google Scholar] [CrossRef]
- Zou, J.; Balandin, A. Phonon heat conduction in a semiconductor nanowire. J. Appl. Phys. 2001, 89, 2932–2938. [Google Scholar] [CrossRef] [Green Version]
- Kargar, F.; Debnath, B.; Kakko, J.P.; Säynätjoki, A.; Lipsanen, H.; Nika, D.L.; Lake, R.K.; Balandin, A.A. Direct observation of confined acoustic phonon polarization branches in free-standing semiconductor nanowires. Nat. Commun. 2016, 7, 13400. [Google Scholar] [CrossRef]
- Volz, S.G.; Chen, G. Molecular dynamics simulation of thermal conductivity of silicon nanowires. Appl. Phys. Lett. 1999, 75, 2056–2058. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Hyżorek, K. Role of the phonon confinement effect and boundary scattering in reducing the thermal conductivity of argon nanowire. J. Chem. Phys. 2021, 154, 054702. [Google Scholar] [CrossRef]
- Klemens, P. Thermal Conductivity and Lattice Vibrational Modes; Solid State Physics; Academic Press: New York, NY, USA, 1958; Volume 7, pp. 1–98. [Google Scholar] [CrossRef]
- Luh, D.A.; Miller, T.; Paggel, J.J.; Chiang, T.C. Large Electron-Phonon Coupling at an Interface. Phys. Rev. Lett. 2002, 88, 256802. [Google Scholar] [CrossRef] [PubMed]

| Pore | Sphere | SC | STC | NW-M |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |
| a-Si | Pore | Sphere | SC | STC | NW-M | |
|---|---|---|---|---|---|---|
 |  |  |  |  |  | |
| Time |  | Longitudinal | 2 THz |  | ||
| 0.6 ps | 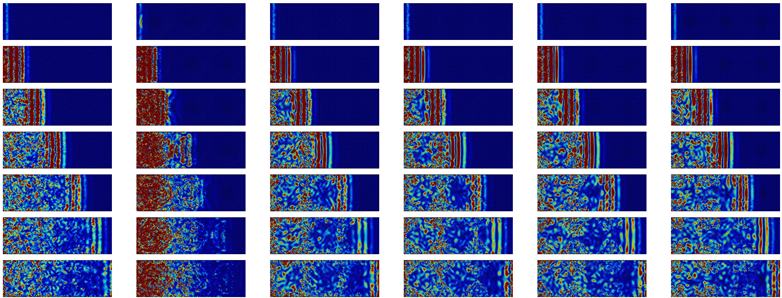 | |||||
| 1.5 ps | ||||||
| 2.4 ps | ||||||
| 3.3 ps | ||||||
| 4.2 ps | ||||||
| 5.1 ps | ||||||
| 6.0 ps | ||||||
| Time |  | Transverse | 2 THz |  | ||
| 0.6 ps | 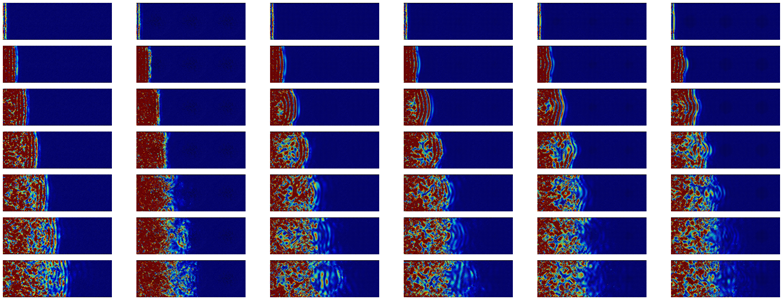 | |||||
| 1.5 ps | ||||||
| 2.4 ps | ||||||
| 3.3 ps | ||||||
| 4.2 ps | ||||||
| 5.1 ps | ||||||
| 6.0 ps | ||||||
| a-Si | Pore | Sphere | SC | STC | NW-M | |
|---|---|---|---|---|---|---|
 |  |  |  |  |  | |
| Time |  | Longitudinal | 10 THz |  | ||
| 0.6 ps | 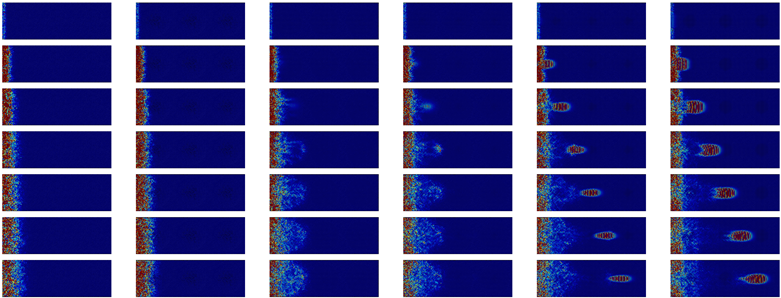 | |||||
| 1.5 ps | ||||||
| 2.4 ps | ||||||
| 3.3 ps | ||||||
| 4.2 ps | ||||||
| 5.1 ps | ||||||
| 6.0 ps | ||||||
| Time |  | Transverse | 4 THz |  | ||
| 0.6 ps | 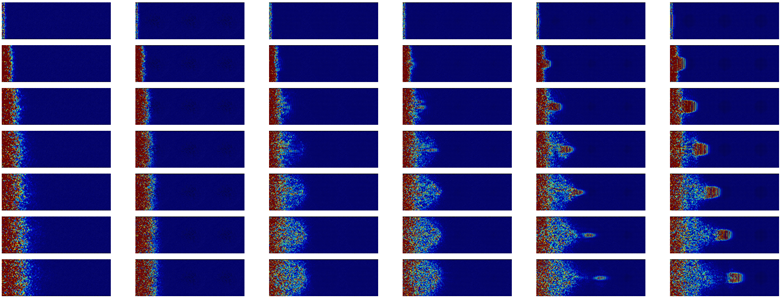 | |||||
| 1.5 ps | ||||||
| 2.4 ps | ||||||
| 3.3 ps | ||||||
| 4.2 ps | ||||||
| 5.1 ps | ||||||
| 6.0 ps | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desmarchelier, P.; Carré, A.; Termentzidis, K.; Tanguy, A. Ballistic Heat Transport in Nanocomposite: The Role of the Shape and Interconnection of Nanoinclusions. Nanomaterials 2021, 11, 1982. https://doi.org/10.3390/nano11081982
Desmarchelier P, Carré A, Termentzidis K, Tanguy A. Ballistic Heat Transport in Nanocomposite: The Role of the Shape and Interconnection of Nanoinclusions. Nanomaterials. 2021; 11(8):1982. https://doi.org/10.3390/nano11081982
Chicago/Turabian StyleDesmarchelier, Paul, Alice Carré, Konstantinos Termentzidis, and Anne Tanguy. 2021. "Ballistic Heat Transport in Nanocomposite: The Role of the Shape and Interconnection of Nanoinclusions" Nanomaterials 11, no. 8: 1982. https://doi.org/10.3390/nano11081982
APA StyleDesmarchelier, P., Carré, A., Termentzidis, K., & Tanguy, A. (2021). Ballistic Heat Transport in Nanocomposite: The Role of the Shape and Interconnection of Nanoinclusions. Nanomaterials, 11(8), 1982. https://doi.org/10.3390/nano11081982





