Triple-Band Anisotropic Perfect Absorbers Based on α-Phase MoO3 Metamaterials in Visible Frequencies
Abstract
:1. Introduction
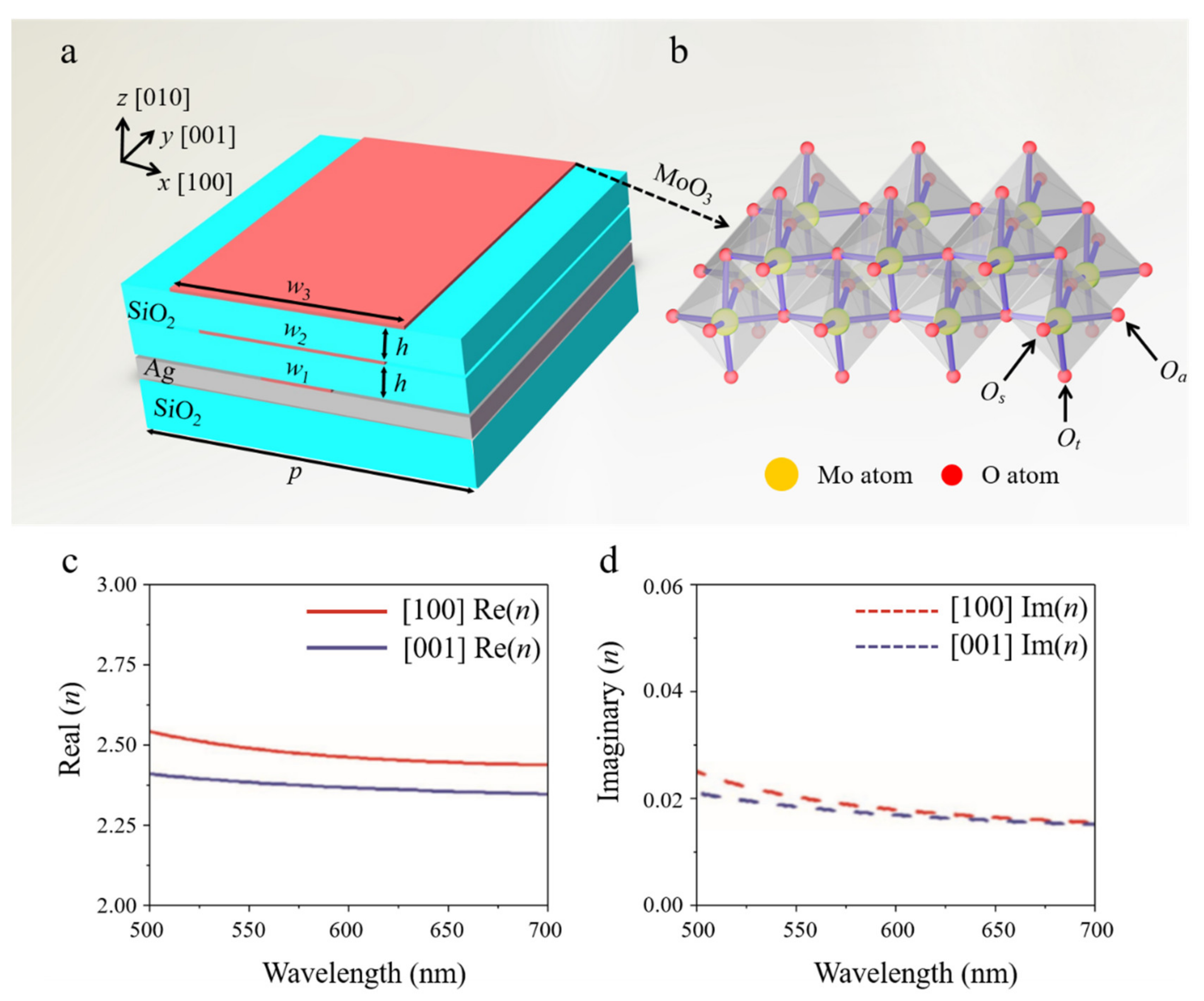
2. Materials and Methods
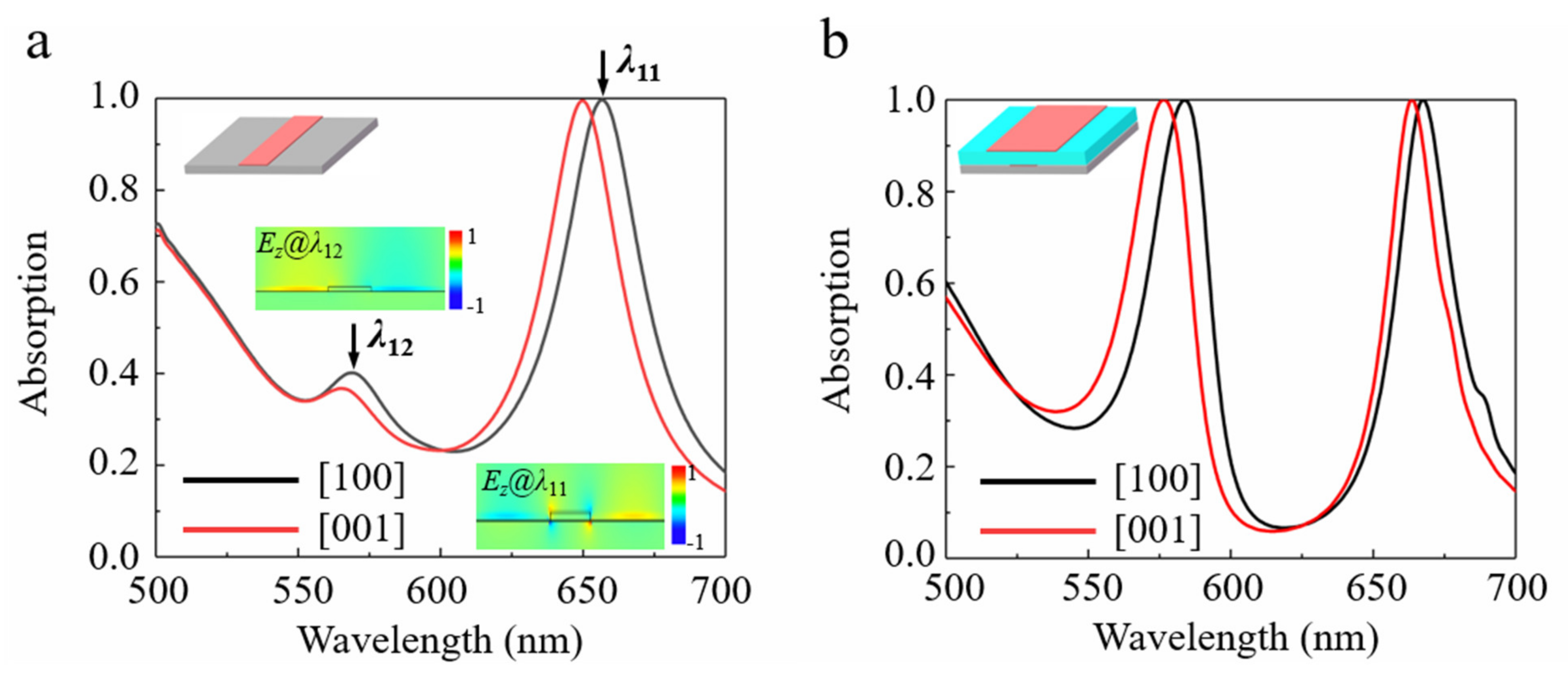
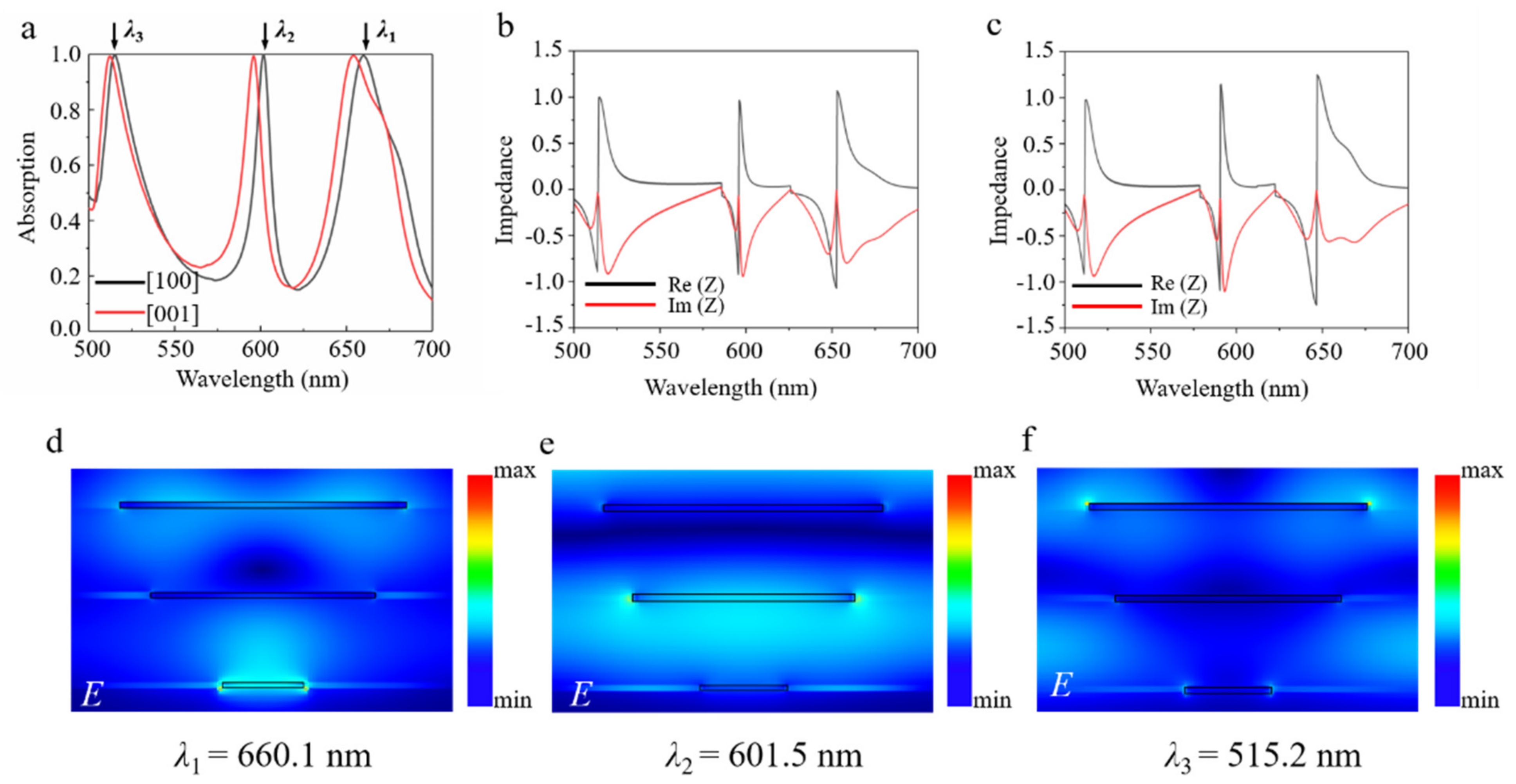
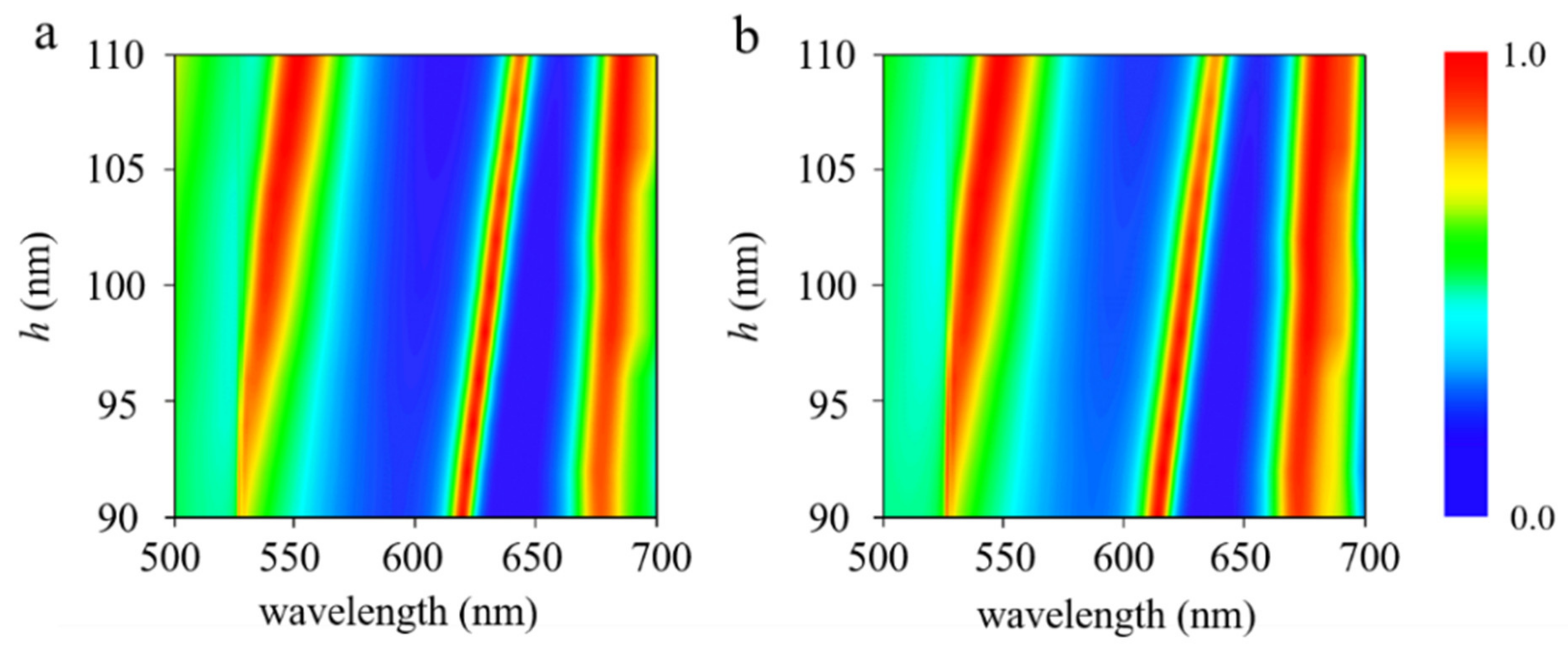
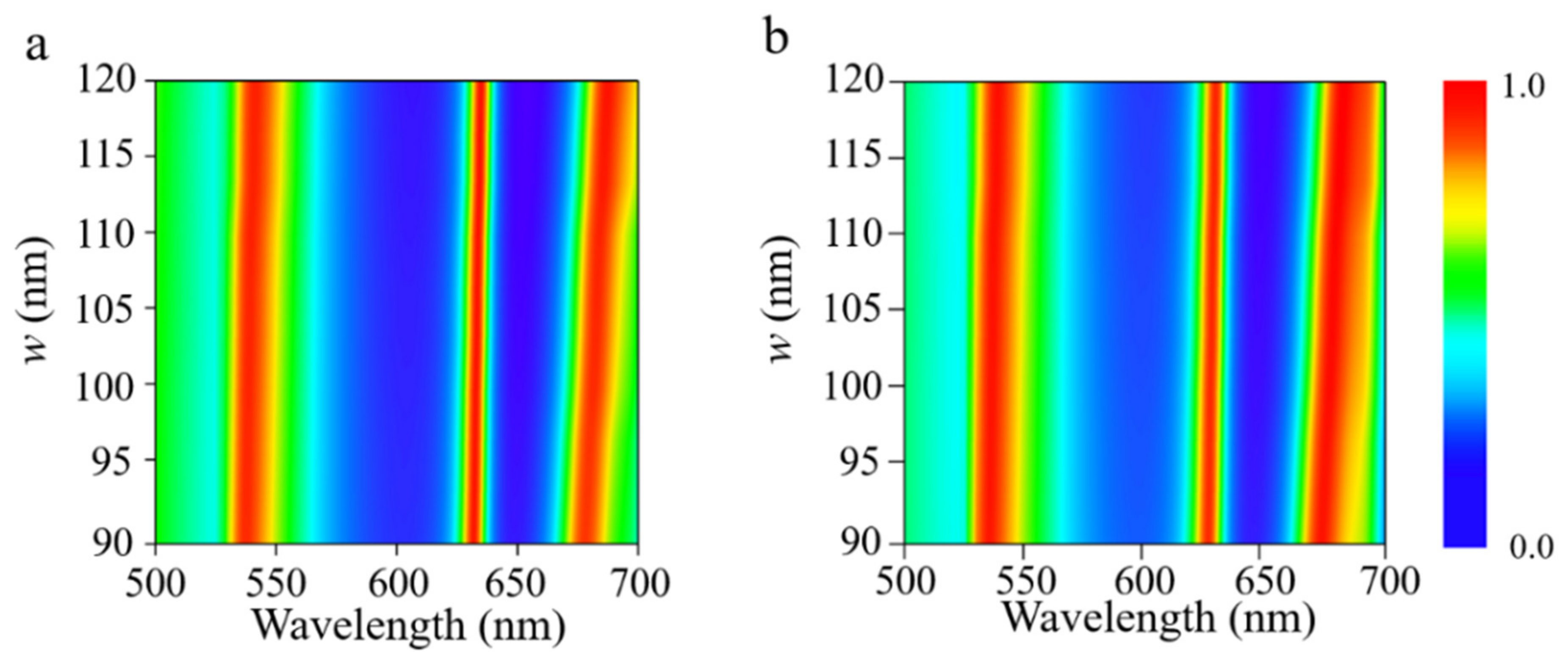
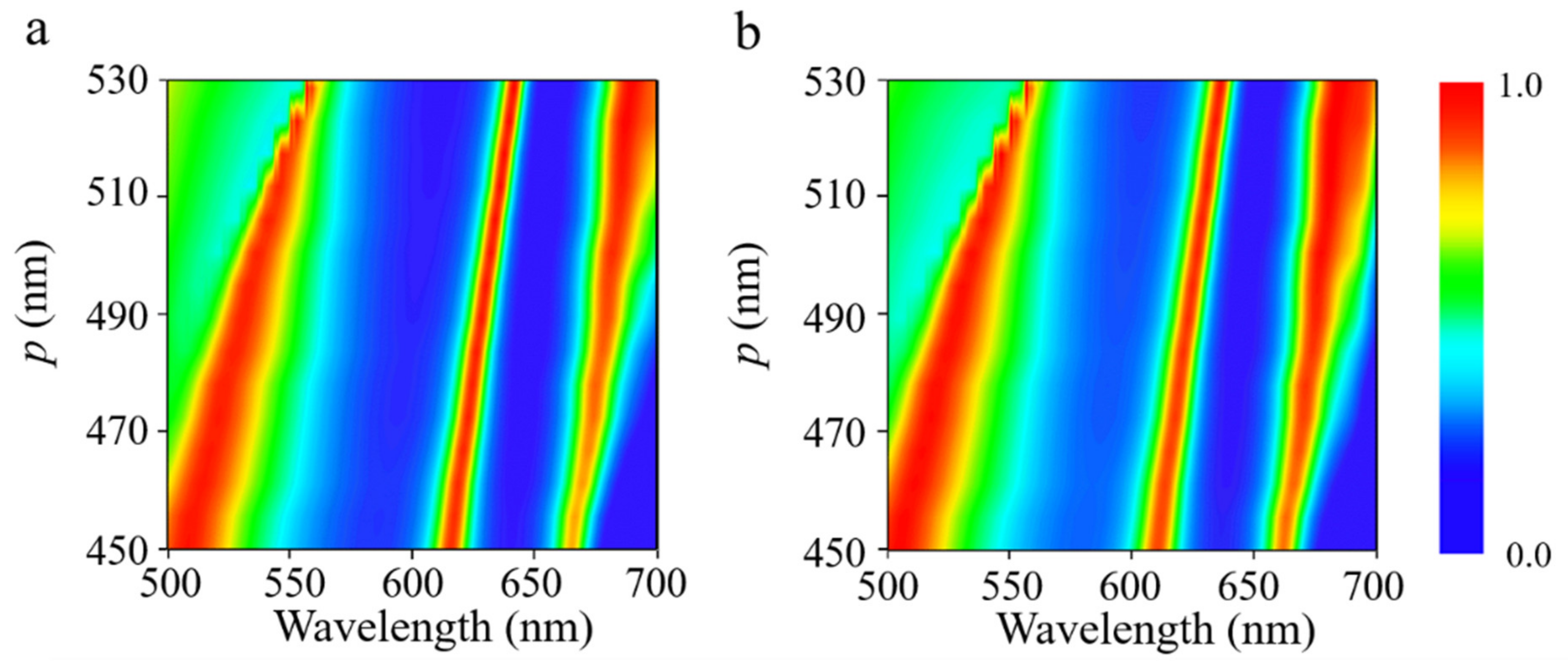
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Feng, Y.; Zhao, J. Graphene-enabled tunable multifunctional metamaterial for dynamical polarization manipulation of broadband terahertz wave. Carbon 2020, 163, 244–252. [Google Scholar] [CrossRef]
- Song, L.; Ci, L.; Lu, H.; Sorokin, P.B.; Jin, C.; Ni, J.; Kvashnin, A.G.; Kvashnin, D.G.; Lou, J.; Yakobson, B.I.; et al. Large scale growth and characterization of atomic hexagonal boron nitride layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.; Song, X.; Dereshgi, S.A.; Xu, H.; Aydin, K. Tunable multi-wavelength absorption in mid-IR region based on a hybrid patterned graphene-hBN structure. Opt. Express 2019, 27, 23576–23584. [Google Scholar] [CrossRef]
- Min, B.K.; Nguyen, V.-T.; Kim, S.J.; Yi, Y.; Choi, C.-G. Surface Plasmon Resonance-Enhanced Near-Infrared Absorption in Single-Layer MoS2 with Vertically Aligned Nanoflakes. ACS Appl. Mater. Interfaces 2020, 12, 14476–14483. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Aydin, K. Localized Surface Plasmons in Nanostructured Monolayer Black Phosphorus. Nano Lett. 2016, 16, 3457–3462. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Yang, N.; Huang, L.; Su, J.; Jiang, C. Tunable Anisotropic Perfect Enhancement Absorption in Black Phosphorus-Based Metasurfaces. IEEE Photon. J. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Xiong, F.; Zhang, J.; Zhu, Z.; Yuan, X.; Qin, S. Strong anisotropic perfect absorption in monolayer black phosphorous and its application as tunable polarizer. J. Opt. 2017, 19, 075002. [Google Scholar] [CrossRef]
- Jia, Z.; Huang, L.; Su, J.; Tang, B. Tunable plasmon-induced transparency based on monolayer black phosphorus by bright-dark mode coupling. Appl. Phys. Express 2020, 13, 072006. [Google Scholar] [CrossRef]
- Ajayan, P.; Kim, P.; Banerjee, K. Two-dimensional van der Waals materials. Phys. Today 2016, 69, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Alonso-Gonzalez, P.; Li, S.; Nikitin, A.Y.; Yuan, J.; Martin-Sanchez, J.; Taboada-Gutierrez, J.; Amenabar, I.; Li, P.; Velez, S.; et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 2018, 562, 557–562. [Google Scholar] [CrossRef] [Green Version]
- Taboada-Gutierrez, J.; Alvarez-Perez, G.; Duan, J.; Ma, W.; Crowley, K.; Prieto, I.; Bylinkin, A.; Autore, M.; Volkova, H.; Kimura, K.; et al. Broad spectral tuning of ultra-low-loss polaritons in a van der Waals crystal by intercalation. Nat. Mater. 2020, 19, 964–968. [Google Scholar] [CrossRef]
- Lajaunie, L.; Boucher, F.; Dessapt, R.; Moreau, P. Strong anisotropic influence of local-field effects on the dielectric response of α-MoO3. Phys. Rev. B 2013, 88, 115141. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Abedini Dereshgi, S.; Song, X.; Murthy, A.; Dravid, V.P.; Cao, T.; Aydin, K. Polarization Reflector/Color Filter at Visible Frequencies via Anisotropic α-MoO3. Adv. Opt. Mater. 2020, 8, 2000088. [Google Scholar] [CrossRef]
- Hu, G.; Ou, Q.; Si, G.; Wu, Y.; Wu, J.; Dai, Z.; Krasnok, A.; Mazor, Y.; Zhang, Q.; Bao, Q. Observation of topological polaritons and photonic magic angles in twisted van der Waals bi-layers. Nature 2020, 582, 209–213. [Google Scholar] [CrossRef]
- Abedini Dereshgi, S.; Folland, T.G.; Murthy, A.A.; Song, X.; Tanriover, I.; Dravid, V.P.; Caldwell, J.D.; Aydin, K. Lithography-free IR polarization converters via orthogonal in-plane phonons in alpha-MoO3 flakes. Nat. Commun. 2020, 11, 5771–5779. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Zhu, Y.; Zhou, X.; Huang, L.; Lang, X. Wide-Angle Polarization-Independent Broadband Absorbers Based on Concentric Multisplit Ring Arrays. IEEE Photon. J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, L.; Guo, J.; Dai, X.; Xiang, Y.; Wen, S. Turnable perfect absorption at infrared frequencies by a Graphene-hBN Hyper Crystal. Opt. Express 2016, 24, 17103–17114. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Qu, L.; Qu, L.; Zhang, Y.; Zhang, H.; Cao, M. Tunable broadband terahertz metamaterial absorber using multi-layer black phosphorus and vanadium dioxide. J. Phys. D 2020, 53, 145105. [Google Scholar] [CrossRef]
- Huang, X.; He, W.; Yang, F.; Ran, J.; Gao, B.; Zhang, W.-L. Polarization-independent and angle-insensitive broadband absorber with a target-patterned graphene layer in the terahertz regime. Opt. Express 2018, 26, 25558–25566. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.; Yang, J.; Yin, Z. Broadband terahertz metamaterial absorber based on tantalum nitride. Appl. Opt. 2017, 56, 2449–2454. [Google Scholar] [CrossRef] [PubMed]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, Y.; Luo, H. Temperature Tunable Narrow-Band Terahertz Metasurface Absorber Based on InSb Micro-Cylinder Arrays for Enhanced Sensing Application. IEEE Access 2020, 8, 82981–82988. [Google Scholar] [CrossRef]
- Khonina, S.N.; Butt, M.A.; Kazanskiy, N.L. Numerical investigation of metasurface narrowband perfect absorber and a plasmonic sensor for a near-infrared wavelength range. J. Opt. 2021, 23, 065102. [Google Scholar] [CrossRef]
- Aydin, K.; Ferry, V.E.; Briggs, R.M.; Atwater, H.A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2011, 2, 1–7. [Google Scholar] [CrossRef]
- Sang, T.; Qi, H.; Wang, X.; Yin, X.; Li, G.; Niu, X.; Ma, B.; Jiao, H. Ultrabroadband Absorption Enhancement via Hybridization of Localized and Propagating Surface Plasmons. Nanomaterials 2020, 10, 1625. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.; Palacios, E.; Liu, Z.; Butun, S.; Aydin, K. Chiral-selective plasmonic metasurface absorbers operating at visible frequencies. IEEE Photon. Technol. Lett. 2017, 29, 295–298. [Google Scholar] [CrossRef]
- Yi, Z.; Li, J.; Lin, J.; Qin, F.; Chen, X.; Yao, W.; Liu, Z.; Cheng, S.; Wu, P.; Li, H. Broadband polarization-insensitive and wide-angle solar energy absorber based on tungsten ring-disc array. Nanoscale 2020, 12, 23077–23083. [Google Scholar] [CrossRef]
- Huang, S.; Xie, Z.; Chen, W.; Lei, J.; Wang, F.; Liu, K.; Li, L. Metasurface with multi-sized structure for multi-band coherent perfect absorption. Opt. Express 2018, 26, 7066–7078. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Dong, G.; Hao, Y.; Lei, M.; Bi, K. Multi-band terahertz metasurface absorber. Mod. Phys. Lett. B 2017, 31, 1750354. [Google Scholar] [CrossRef]
- Kokilavani, S.; Syed, A.; Thomas, A.M.; Elgorban, A.M.; Al-Rashed, S.; Raju, L.L.; Khan, S.S. Integrating Ag2WO4 on VS4 nanoplates with synergy of plasmonic photocatalysis and boosted visible-light harvesting and its antibacterial applications. J. Alloy. Compd. 2021, 865, 158810. [Google Scholar] [CrossRef]
- Jiang, K.; Sun, X.; Zhang, Z.-H.; Ben, J.; Che, J.; Shi, Z.; Jia, Y.; Chen, Y.; Zhang, S.; Lv, W.; et al. Polarization-enhanced AlGaN solar-blind ultraviolet detectors. Photonics Res. 2020, 8, 1243–1252. [Google Scholar] [CrossRef]
- Kanté, B.; de Lustrac, A.; Lourtioz, J.-M.; Burokur, S.N. Infrared cloaking based on the electric response of split ring resonators. Opt. Express 2008, 16, 9191–9198. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Liu, Z.; Wang, L.; Liu, J.; Lin, Q. Tunable ultra-narrowband and wide-angle graphene-based perfect absorber in the optical communication region. Appl. Phys. Express 2018, 11, 105102. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, B.; Jiang, C. Tunable ultra-broadband anisotropic absorbers based on multi-layer black phosphorus ribbons. Appl. Phys. Express 2019, 12, 032009. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, B.; Yang, N.; Lang, X.; Su, J.; Li, Z. Tunable wide-angle perfect absorber based on black phosphorous-dielectric-metallic hybrid architecture. Phys. E Low Dimens. Syst. Nanostruct. 2021, 126, 114449. [Google Scholar] [CrossRef]
- Qi, H.; Sang, T.; Yin, X.; Wang, X.; Li, G. Dual-band absorption enhancement of monolayer molybdenum disulfide by a tapered metamaterial waveguide slab. Appl. Phys. Express 2020, 13, 065001. [Google Scholar] [CrossRef]
- Deng, G.; Dereshgi, S.A.; Song, X.; Wei, C.; Aydin, K. Phonon-polariton assisted broadband resonant absorption in anisotropic α-phase MoO3 nanostructures. Phys. Rev. B 2020, 102, 035408. [Google Scholar] [CrossRef]
- Dong, D.; Liu, Y.; Fu, Y. Critical Coupling and Perfect Absorption Using α-MoO3 Multilayers in the Mid-Infrared. Ann. Der Phys. 2021, 533, 2000512. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys. 2005, 71, 036617. [Google Scholar] [CrossRef] [Green Version]
- Byelobrov, V.O.; Zinenko, T.L.; Kobayashi, K.; Nosich, A.I. Periodicity Matters: Grating or lattice resonances in the scattering by sparse arrays of subwavelength strips and wires. IEEE Antennas Propag. Mag. 2015, 57, 34–45. [Google Scholar] [CrossRef]
| Polarization | ε∞ | ωpj [cm−1] | ω0 [cm−1] | γj [cm−1] |
|---|---|---|---|---|
| x | 5.065 | 21,672 | 27,019 | 1342.2 |
| y | 4.502 | 29,078 | 32,271 | 2027.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Yang, N.; Song, X.; Jin, G.; Su, J. Triple-Band Anisotropic Perfect Absorbers Based on α-Phase MoO3 Metamaterials in Visible Frequencies. Nanomaterials 2021, 11, 2061. https://doi.org/10.3390/nano11082061
Tang B, Yang N, Song X, Jin G, Su J. Triple-Band Anisotropic Perfect Absorbers Based on α-Phase MoO3 Metamaterials in Visible Frequencies. Nanomaterials. 2021; 11(8):2061. https://doi.org/10.3390/nano11082061
Chicago/Turabian StyleTang, Bin, Neigang Yang, Xianglian Song, Gui Jin, and Jiangbin Su. 2021. "Triple-Band Anisotropic Perfect Absorbers Based on α-Phase MoO3 Metamaterials in Visible Frequencies" Nanomaterials 11, no. 8: 2061. https://doi.org/10.3390/nano11082061
APA StyleTang, B., Yang, N., Song, X., Jin, G., & Su, J. (2021). Triple-Band Anisotropic Perfect Absorbers Based on α-Phase MoO3 Metamaterials in Visible Frequencies. Nanomaterials, 11(8), 2061. https://doi.org/10.3390/nano11082061







