Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Description of Shell-Foundation Interaction Model
2.2. Nonlinear Structural Model in the Presence of a PF
3. Solution Procedure
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nat. Cell Biol. 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Xie, S.; Li, W.; Pan, Z.; Chang, B.; Sun, L. Mechanical and physical properties on carbon nanotube. J. Phys. Chem. Solids 2000, 61, 1153–1158. [Google Scholar] [CrossRef]
- Curtin, W.A.; Sheldon, B.W. CNT-reinforced ceramics and metals. Mater. Today 2004, 7, 44–49. [Google Scholar] [CrossRef]
- Esawi, A.M.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling Behavior of FG-CNT Reinforced Composite Conical Shells Subjected to a Combined Loading. Nanomaterials 2020, 10, 419. [Google Scholar] [CrossRef] [Green Version]
- Silvestre, J.; Silvestre, N.; De Brito, J. Polymer nanocomposites for structural applications: Recent trends and new perspectives. Mech. Adv. Mater. Struct. 2016, 23, 1263–1277. [Google Scholar] [CrossRef]
- Park, S.-H.; Bae, J. Polymer Composite Containing Carbon Nanotubes and their Applications. Recent Patents Nanotechnol. 2017, 11, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Liew, K.M.; Pan, Z.; Zhang, L.-W. The recent progress of functionally graded CNT reinforced composites and structures. Sci. China Ser. G Phys. Mech. Astron. 2019, 63, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.-S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Methods Appl. Mech. Eng. 2011, 213–216, 196–205. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, L.; Liew, K. Vibration analysis of CNT-reinforced functionally graded rotating cylindrical panels using the element-free kp-Ritz method. Compos. Part B Eng. 2015, 77, 291–303. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, B.; Shi, D.; Liang, Q. A semi-analytical method for vibration analysis of functionally graded carbon nanotube reinforced composite double-curved panels and shells of revolution. Compos. Struct. 2017, 174, 87–109. [Google Scholar] [CrossRef]
- Wang, Q.; Cui, X.; Qin, B.; Liang, Q. Vibration analysis of the functionally graded carbon nanotube reinforced composite shallow shells with arbitrary boundary conditions. Compos. Struct. 2017, 182, 364–379. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Free vibration analysis of carbon nanotube-reinforced functionally graded composite shell structures. Appl. Math. Model. 2018, 53, 132–155. [Google Scholar] [CrossRef]
- Sobhy, M. Magneto-electro-thermal bending of FG-graphene reinforced polymer double-curved shallow shells with piezoelectromagnetic faces. Compos. Struct. 2018, 203, 844–860. [Google Scholar] [CrossRef]
- Radwan, A.F.; Sobhy, M. Transient instability analysis of viscoelastic sandwich CNTs-reinforced microplates exposed to 2D magnetic field and hygrothermal conditions. Compos. Struct. 2020, 245, 112349. [Google Scholar] [CrossRef]
- Vu, V.T.; Tran, H.Q.; Tran, M.T. Free vibration analysis of laminated functionally graded carbon nanotube-reinforced composite doubly curved shallow shell panels using a new four-variable refined theory. J. Compos. Sci. 2019, 3, 104. [Google Scholar]
- Sofiyev, A.H.; Mammadov, Z.; Dimitri, R.; Tornabene, F. Vibration analysis of shear deformable carbon nanotubes-based functionally graded conical shells resting on elastic foundations. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M. Geometrically nonlinear analysis of functionally graded shallow curved tubes in thermal environment. Thin-Walled Struct. 2018, 132, 48–57. [Google Scholar] [CrossRef]
- Nguyen, P.D.; Quang, V.D.; Anh, V.T.T.; Duc, N.D. Nonlinear Vibration of Carbon Nanotube Reinforced Composite Truncated Conical Shells in Thermal Environment. Int. J. Struct. Stab. Dyn. 2019, 19. [Google Scholar] [CrossRef]
- Khoa, N.D.; Anh, V.M.; Duc, N.D. Nonlinear dynamic response and vibration of functionally graded nanocomposite cylindrical panel reinforced by carbon nanotubes in thermal environment. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Avey, M.; Yusufoglu, E. On the solution of large-amplitude vibration of carbon nanotube-based double-curved shallow shells. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.; Shen, H.S. Nonlinear vibration of temperature-dependent FG-CNTRC laminated plates with negative Poisson’s ratio. Thin-Wall Struct. 2020, 148, 106514. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Large deflection response-based geometrical nonlinearity of nanocomposite structures reinforced with carbon nanotubes. Appl. Math. Mech. 2020, 41, 1227–1250. [Google Scholar] [CrossRef]
- Shahmohammadi, M.A.; Abdollahi, P.; Salehipour, H. Geometrically nonlinear analysis of doubly curved imperfect shallow shells made of functionally graded carbon nanotube reinforced composite (FG_CNTRC). Mech. Based Des. Struct. Mach. 2020, 1–25. [Google Scholar] [CrossRef]
- Pasternak, P.L. On a new method of analysis of an elastic foundation by means of two foundation constants. Gos. Izd. Lib. Po Stroit. Arkhitekture Mosc. 1054, 1, 1–56. (In Russian) [Google Scholar]
- Kerr, A.D. Elastic and Viscoelastic Foundation Models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Reddy, J. Winkler–Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos. Part B Eng. 2013, 57, 269–296. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Shojaei, M. Faghih Vibrational analysis of functionally graded carbon nanotube-reinforced composite spherical shells resting on elastic foundation using the variational differential quadrature method. Euro J. Mech. A-Solids 2016, 60, 166–182. [Google Scholar] [CrossRef]
- Zhang, L.; Liew, K.M. Large deflection analysis of FG-CNT reinforced composite skew plates resting on Pasternak foundations using an element-free approach. Compos. Struct. 2015, 132, 974–983. [Google Scholar] [CrossRef]
- Dinh, D.N.; Nguyen, P.D. The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations. Materials 2017, 10, 1194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, H.-S.; He, X.-Q. Large amplitude free vibration of nanotube-reinforced composite doubly curved panels resting on elastic foundations in thermal environments. J. Vib. Control. 2015, 23, 2672–2689. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Large amplitude free vibration analysis of shear deformable FGM shallow arches on nonlinear elastic foundation. Thin-Walled Struct. 2019, 144, 106237. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet reinforced composite double-curved shallow shells on elastic foundations. Steel Compos. Struct. 2019, 133, 195–208. [Google Scholar]
- Sofiyev, A.H.; Pirmamedov, I.T.; Kuruoglu, N. Influence of elastic foundations and carbon nanotube reinforcement on the hydrostatic buckling pressure of truncated conical shells. Appl. Math. Mech. 2020, 41, 1011–1026. [Google Scholar] [CrossRef]
- Sofiyev, A.; Kuruoglu, N. Buckling analysis of shear deformable composite conical shells reinforced by CNTs subjected to combined loading on the two-parameter elastic foundation. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Volmir, A.S. The Nonlinear Dynamics of Plates and Shells; Sci Edit: Moscow, Russia, 1972. [Google Scholar]
- Grigolyuk, E.I. On vibrations of a shallow circular cylindrical panel experiencing finite deflections. App. Math. Mech. 1955, 19, 382–386. [Google Scholar]
- Alijani, F.; Amabili, M.; Karagiozis, K.; Bakhtiari-Nejad, F. Nonlinear vibrations of functionally graded doubly curved shallow shells. J. Sound Vib. 2010, 330, 1432–1454. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K.; Lo, S.H.; Au, F.T.K. Three-dimensional vibration analysis of rectangular thick plates on Pasternak foundation. Int. J. Numer. Methods Eng. 2004, 59, 1313–1334. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Shi, X. A modified solution for the free vibration analysis of moderately thick orthotropic rectangular plates with general boundary conditions, internal line supports and resting on elastic foundation. Meccanica 2015, 51, 1985–2017. [Google Scholar] [CrossRef]


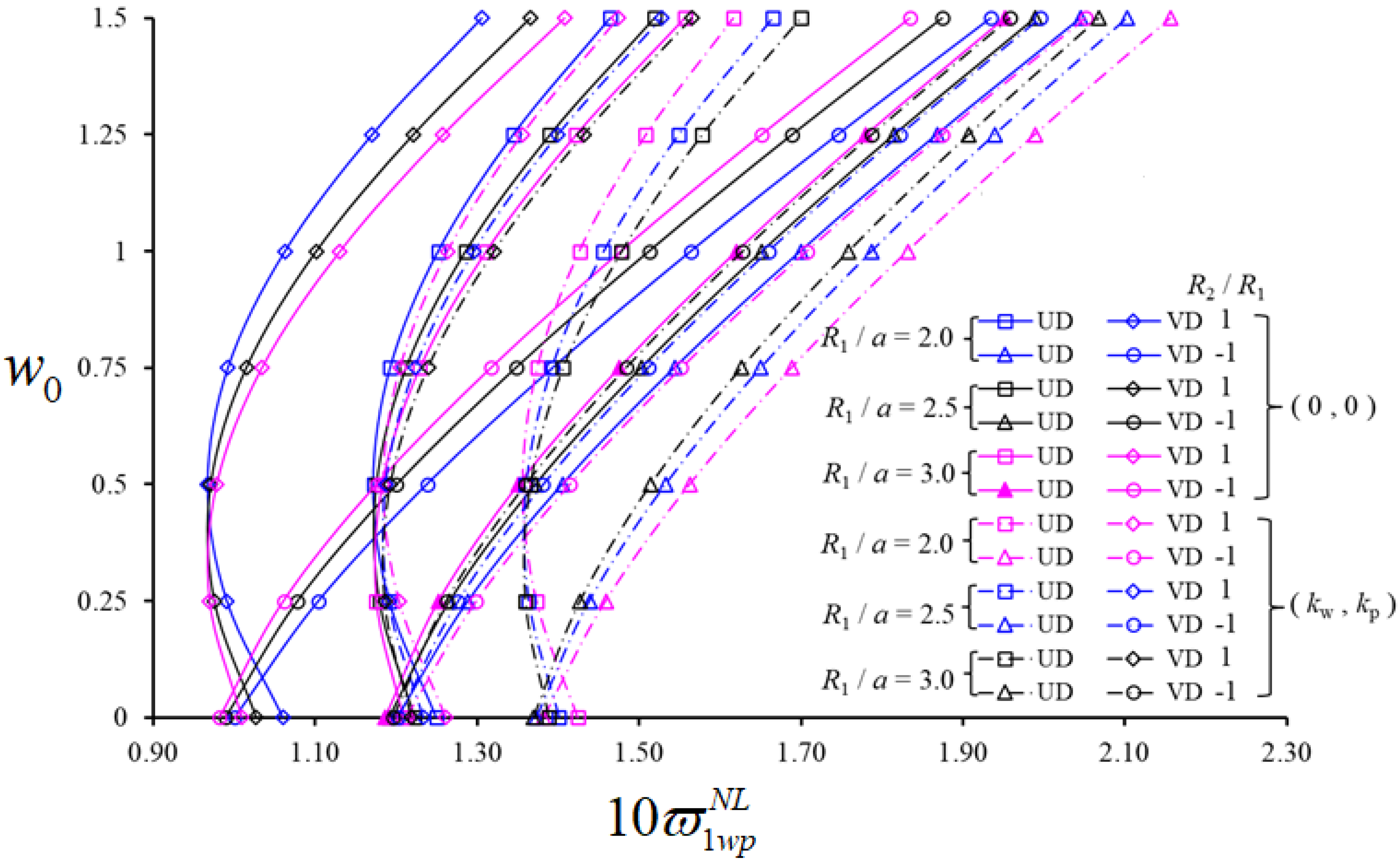
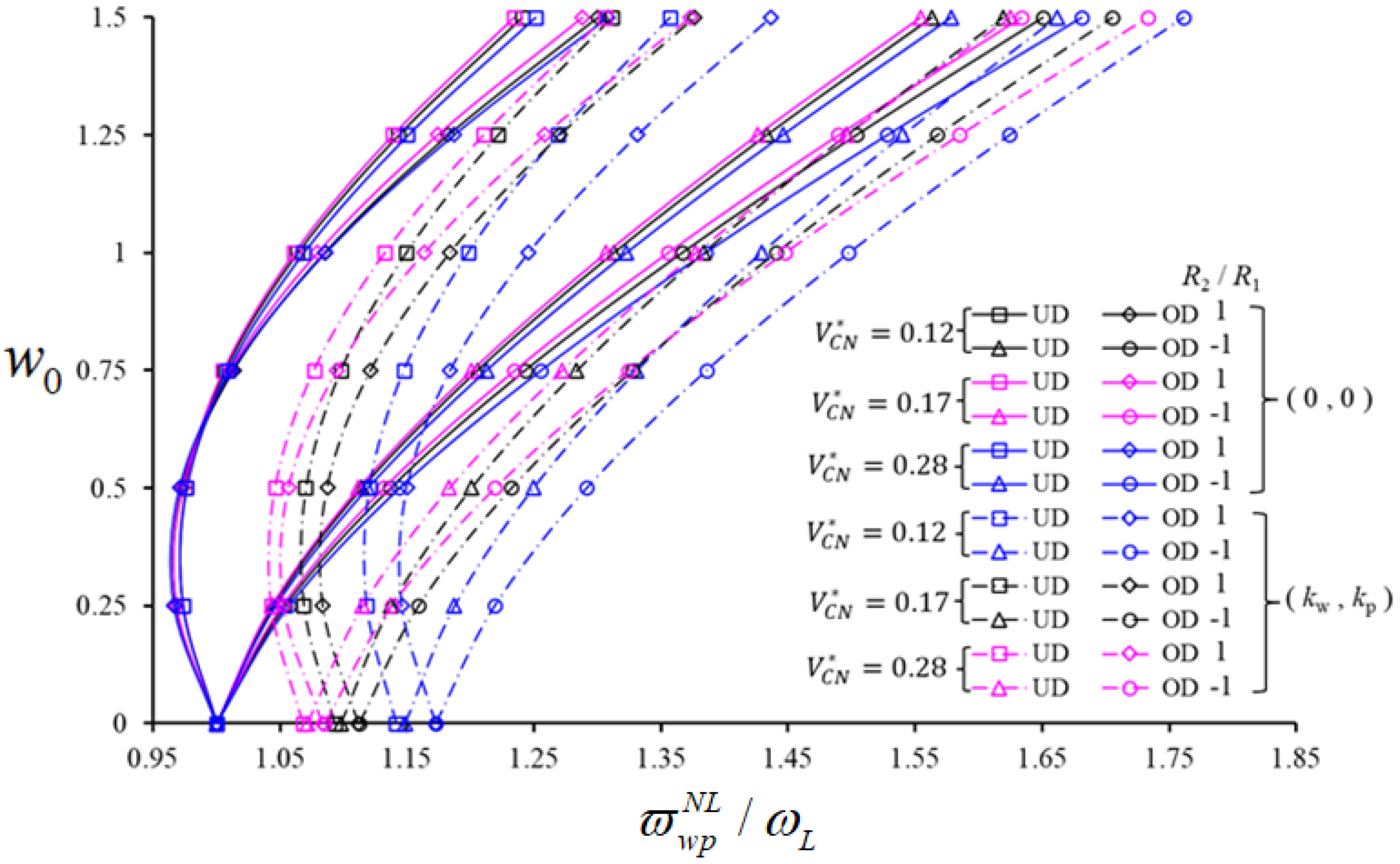
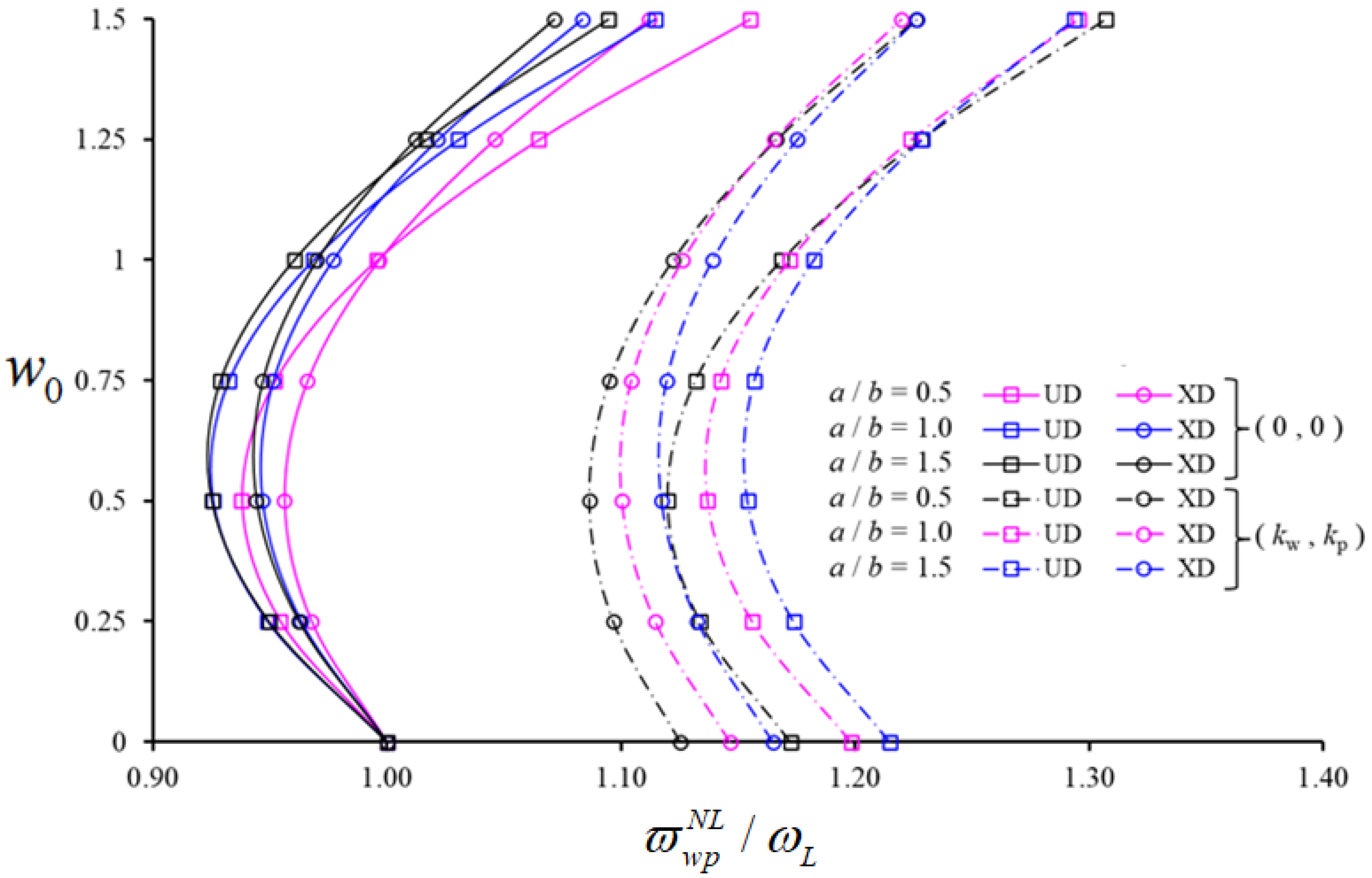
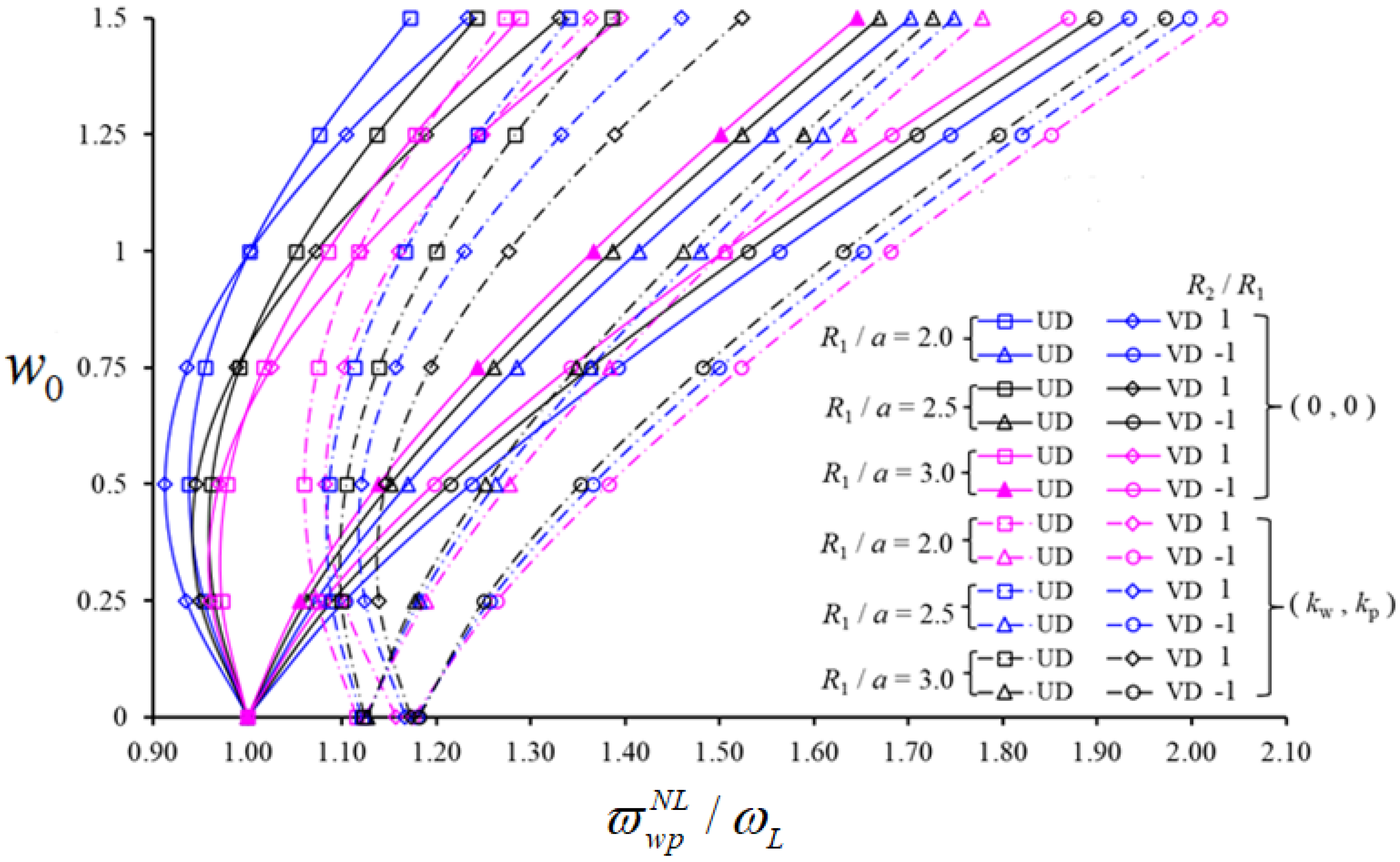
| Structural Members | ||||
|---|---|---|---|---|
| Alijani [38] | Present Study | |||
| Spherical shell | 0.5 | 0.5 | 0.0779 | 0.0781 |
| Hypar shell | 0.5 | −0.5 | 0.0597 | 0.0600 |
| Studies | Mode Number | ||
|---|---|---|---|
| Zhou et al. [39] | 2.6551 | 5.5717 | 5.5717 |
| Wang et al. [40] | 2.6551 | 5.5717 | 5.5717 |
| Present study | 2.6557 | 5.5761 | 5.5761 |
| 0.12 | 0.137 | 1.022 | 0.715 |
| 0.17 | 0.142 | 1.626 | 1.138 |
| 0.28 | 0.141 | 1.585 | 1.109 |
| 0.12 | 0.17 | 0.28 | |||||||||||
| 0.445 | 0.388 | 0.362 | 0.540 | 0.569 | 0.506 | 0.476 | 0.680 | 0.615 | 0.517 | 0.493 | 0.782 | ||
| 0.503 | 0.452 | 0.431 | 0.589 | 0.614 | 0.557 | 0.530 | 0.719 | 0.656 | 0.566 | 0.544 | 0.815 | ||
| 0.526 | 0.478 | 0.457 | 0.608 | 0.633 | 0.577 | 0.551 | 0.735 | 0.673 | 0.586 | 0.564 | 0.829 | ||
| 0.548 | 0.502 | 0.482 | 0.627 | 0.651 | 0.597 | 0.572 | 0.750 | 0.690 | 0.605 | 0.584 | 0.843 | ||
| 0.583 | 0.540 | 0.522 | 0.658 | 0.681 | 0.629 | 0.605 | 0.776 | 0.717 | 0.636 | 0.66 | 0.685 | ||
| 0.602 | 0.561 | 0.544 | 0.676 | 0.697 | 0.647 | 0.624 | 0.791 | 0.733 | 0.653 | 0.634 | 0.878 | ||
| 0.622 | 0.581 | 0.565 | 0.693 | 0.714 | 0.665 | 0.642 | 0.805 | 0.748 | 0.670 | 0.652 | 0.891 | ||
| 0.599 | 0.557 | 0.540 | 0.672 | 0.694 | 0.644 | 0.621 | 0.788 | 0.730 | 0.650 | 0.631 | 0.876 | ||
| 0.618 | 0.578 | 0.561 | 0.690 | 0.711 | 0.662 | 0.639 | 0.803 | 0.745 | 0.667 | 0.649 | 0.889 | ||
| 0.637 | 0.598 | 0.581 | 0.706 | 0.727 | 0.679 | 0.657 | 0.817 | 0.760 | 0.684 | 0.666 | 0.901 | ||
| 0.615 | 0.574 | 0.557 | 0.687 | 0.708 | 0.659 | 0.636 | 0.800 | 0.743 | 0.664 | 0.646 | 0.886 | ||
| 0.634 | 0.594 | 0.578 | 0.703 | 0.724 | 0.676 | 0.654 | 0.815 | 0.758 | 0.681 | 0.663 | 0.899 | ||
| 0.652 | 0.614 | 0.598 | 0.720 | 0.740 | 0.693 | 0.671 | 0.829 | 0.773 | 0.698 | 0.680 | 0.912 | ||
| 0.911 | 0.878 | 0.878 | 0.960 | 1.095 | 1.055 | 1.055 | 1.155 | 1.376 | 1.325 | 1.324 | 1.453 | ||
| 0.941 | 0.909 | 0.909 | 0.988 | 1.119 | 1.080 | 1.080 | 1.178 | 1.395 | 1.345 | 1.344 | 1.471 | ||
| 0.953 | 0.921 | 0.922 | 1.000 | 1.129 | 1.091 | 1.091 | 1.188 | 1.403 | 1.353 | 1.352 | 1.479 | ||
| 0.965 | 0.934 | 0.934 | 1.012 | 1.140 | 1.101 | 1.101 | 1.198 | 1.411 | 1.361 | 1.361 | 1.486 | ||
| 0.986 | 0.955 | 0.955 | 1.031 | 1.157 | 1.119 | 1.119 | 1.214 | 1.425 | 1.375 | 1.375 | 1.499 | ||
| 0.997 | 0.967 | 0.967 | 1.043 | 1.167 | 1.129 | 1.129 | 1.223 | 1.433 | 1.384 | 1.383 | 1.507 | ||
| 1.009 | 0.979 | 0.979 | 1.054 | 1.177 | 1.139 | 1.140 | 1.233 | 1.440 | 1.392 | 1.391 | 1.514 | ||
| 0.995 | 0.965 | 0.965 | 1.041 | 1.165 | 1.127 | 1.128 | 1.122 | 1.431 | 1.382 | 1.382 | 1.505 | ||
| 1.007 | 0.977 | 0.977 | 1.052 | 1.175 | 1.138 | 1.138 | 1.231 | 1.439 | 1.390 | 1.390 | 1.513 | ||
| 1.018 | 0.989 | 0.989 | 1.063 | 1.185 | 1.148 | 1.148 | 1.240 | 1.447 | 1.398 | 1.398 | 1.520 | ||
| 1.005 | 0.975 | 0.975 | 1.050 | 1.173 | 1.136 | 1.136 | 1.229 | 1.438 | 1.389 | 1.388 | 1.512 | ||
| 1.016 | 0.987 | 0.987 | 1.061 | 1.183 | 1.146 | 1.146 | 1.239 | 1.445 | 1.397 | 1.396 | 1.519 | ||
| 1.028 | 0.999 | 0.999 | 1.072 | 1.193 | 1.156 | 1.156 | 1.248 | 1.453 | 1.405 | 1.405 | 1.527 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmure, A.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials 2021, 11, 2090. https://doi.org/10.3390/nano11082090
Mahmure A, Tornabene F, Dimitri R, Kuruoglu N. Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials. 2021; 11(8):2090. https://doi.org/10.3390/nano11082090
Chicago/Turabian StyleMahmure, Avey, Francesco Tornabene, Rossana Dimitri, and Nuri Kuruoglu. 2021. "Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity" Nanomaterials 11, no. 8: 2090. https://doi.org/10.3390/nano11082090
APA StyleMahmure, A., Tornabene, F., Dimitri, R., & Kuruoglu, N. (2021). Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials, 11(8), 2090. https://doi.org/10.3390/nano11082090








