Formation of Fe-Ni Nanoparticle Strands in Macroscopic Polymer Composites: Experiment and Simulation
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Effect of Particle Size Distribution
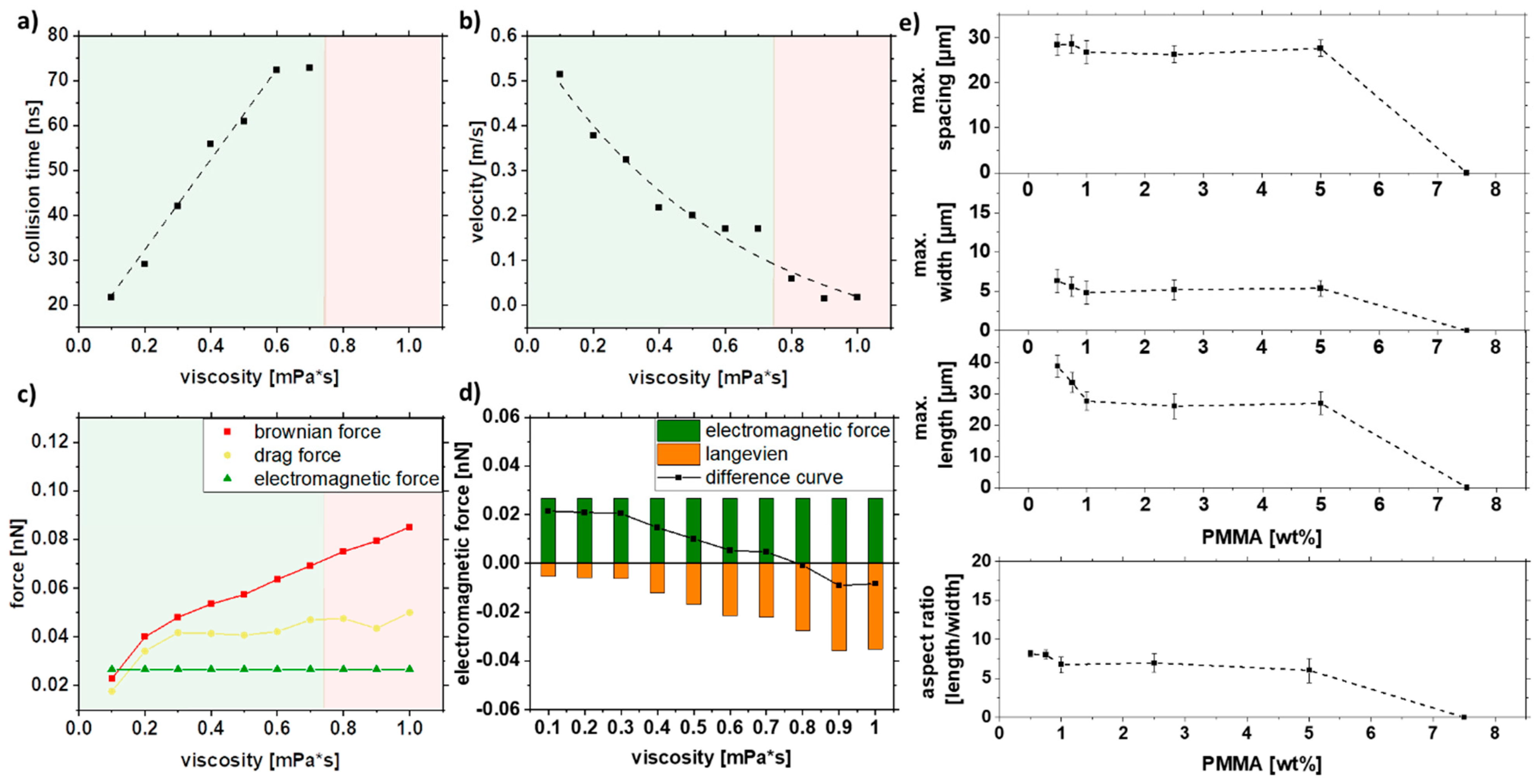
3.2. Effect of Polymer Viscosity during Formation
3.3. Effect of the External Magnetic Field
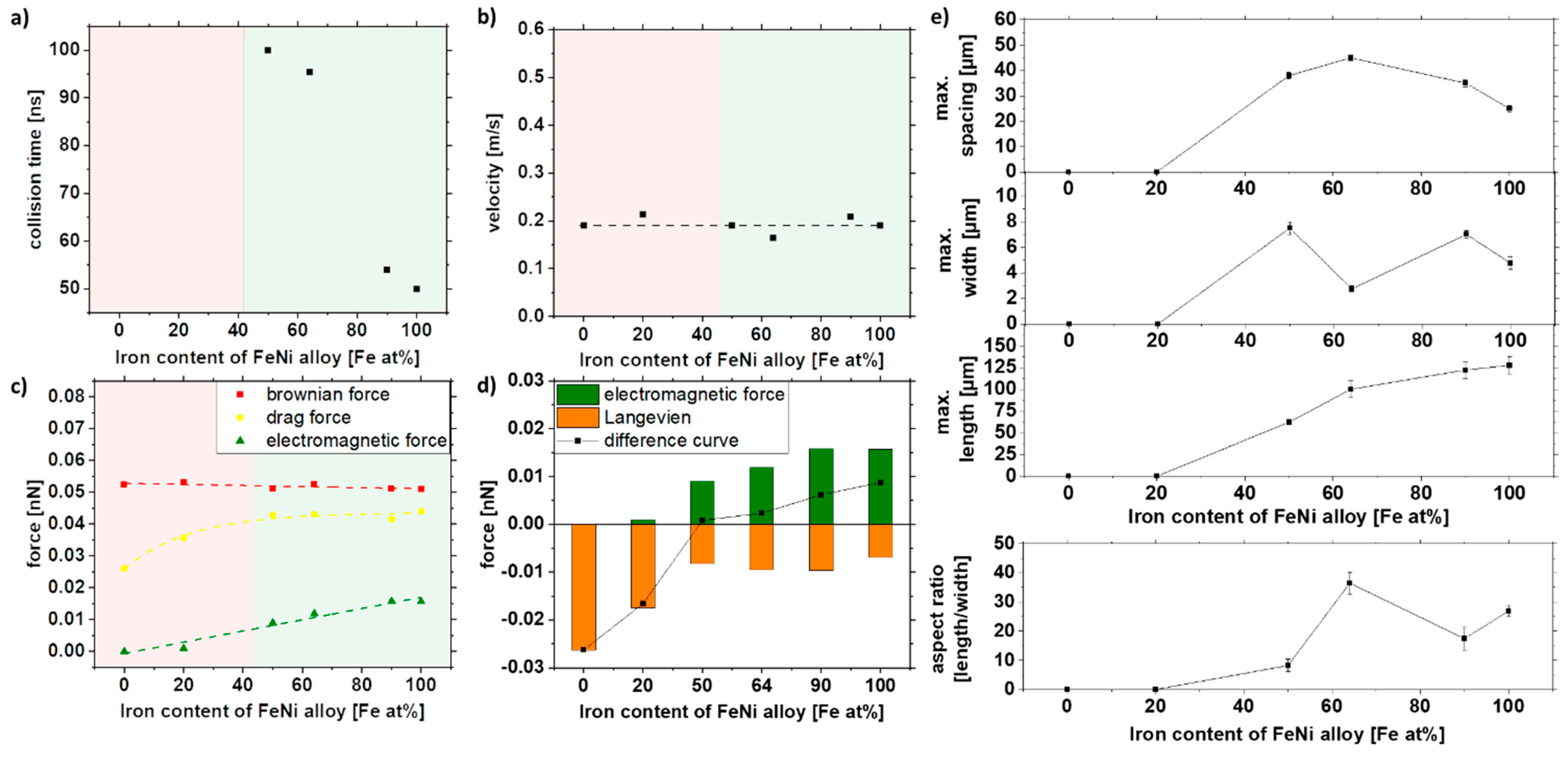
3.4. Effect of the Nanomaterial Composition
3.5. Magnetic Properties of the Composite
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Dijith, K.S.; Aiswarya, R.; Praveen, M.; Pillai, S.; Surendran, K.P. Polyol derived Ni and NiFe alloys for effective shielding of electromagnetic interference. Mater. Chem. Front. 2018, 2, 1829–1841. [Google Scholar] [CrossRef]
- Bhingardive, V.; Suwas, S.; Bose, S. New physical insights into the electromagnetic shielding efficiency in PVDF nanocomposites containing multiwall carbon nanotubes and magnetic nanoparticles. Rsc. Adv. 2015, 5, 79463–79472. [Google Scholar] [CrossRef]
- Lu, X.G.; Liu, Q.R.; Huo, G.; Liang, G.Y.; Sun, Q.J.; Song, X.P. CTAB-mediated synthesis of iron-nickel alloy nanochains and their magnetic properties. Colloid Surf. A 2012, 407, 23–28. [Google Scholar] [CrossRef]
- Menon, A.V.; Madras, G.; Bose, S. Magnetic Alloy-MWNT Heterostructure as Efficient Electromagnetic Wave Suppressors in Soft Nanocomposites. ChemistrySelect 2017, 2, 7831–7844. [Google Scholar] [CrossRef]
- Cai, N.; Yang, H.P.; Zhang, X.; Xia, S.W.; Yao, D.D.; Bartocci, P.; Fantozzi, F.; Chen, Y.Q.; Chen, H.P.; Williams, P.T. Bimetallic carbon nanotube encapsulated Fe-Ni catalysts from fast pyrolysis of waste plastics and their oxygen reduction properties. Waste Manag. 2020, 109, 119–126. [Google Scholar] [CrossRef]
- Huo, J.J.; Chen, Y.L.; Liu, Y.; Guo, J.J.; Lu, L.; Li, W.X.; Wang, Y.; Liu, H. Bifunctional iron nickel phosphide nanocatalysts supported on porous carbon for highly efficient overall water splitting. Sustain. Mater. Technol. 2019, 22, e00117. [Google Scholar] [CrossRef]
- Liu, Y.; Chi, Y.; Shan, S.; Yin, J.; Luo, J.; Zhong, C.-J. Characterization of magnetic NiFe nanoparticles with controlled bimetallic composition. J. Alloy. Compd. 2014, 587, 260–266. [Google Scholar] [CrossRef]
- Zhen, L.; Gong, Y.X.; Jiang, J.T.; Shao, W.Z. Electromagnetic properties of FeNi alloy nanoparticles prepared by hydrogen-thermal reduction method. J. Appl. Phys. 2008, 104, 034312. [Google Scholar] [CrossRef]
- Paraskevas, I.; Caps, V.; Tsang, S.C. Syntheses of carbon encapsulated magnetic FeNi nanoparticle via decompositions of methane and benzene. Carbon 2006, 44, 820–823. [Google Scholar] [CrossRef]
- Castrillon, M.; Mayoral, A.; Magen, C.; Meier, J.G.; Marquina, C.; Irusta, S.; Santamaria, J. Synthesis and characterization of ultra-small magnetic FeNi/G and NiCo/G nanoparticles. Nanotechnology 2012, 23, 085601. [Google Scholar] [CrossRef]
- Dong, X.L.; Zhang, Z.D.; Zhao, X.G.; Chuang, Y.C.; Jin, S.R.; Sun, W.M. The preparation and characterization of ultrafine Fe–Ni particles. J. Mater. Res. 2011, 14, 398–406. [Google Scholar] [CrossRef]
- Li, X.G.; Chiba, A.; Takahashi, S. Preparation and magnetic properties of ultrafine particles of Fe Ni alloys. J. Magn. Magn. Mater. 1997, 170, 339–345. [Google Scholar] [CrossRef]
- Zhang, H.T.; Ding, J.; Chow, G.M. Synthesis and characterizations of Ni–Fe@spinel oxide core–shell nanoparticles. Mater. Res. Bull. 2009, 44, 1195–1199. [Google Scholar] [CrossRef]
- Zhang, D.; Gökce, B.; Barcikowski, S. Laser Synthesis and Processing of Colloids: Fundamentals and Applications. Chem. Rev. 2017, 117, 3990–4103. [Google Scholar] [CrossRef]
- Fazio, E.; Gökce, B.; De Giacomo, A.; Meneghetti, M.; Compagnini, G.; Tommasini, M.; Waag, F.; Lucotti, A.; Zanchi, C.G.; Ossi, P.M.; et al. Nanoparticles Engineering by Pulsed Laser Ablation in Liquids: Concepts and Applications. Nanomaterials 2020, 10, 2317. [Google Scholar] [CrossRef]
- Amendola, V.; Meneghetti, M. What controls the composition and the structure of nanomaterials generated by laser ablation in liquid solution? Phys. Chem. Chem. Phys. 2013, 15, 3027–3046. [Google Scholar] [CrossRef]
- Gökce, B.; Amendola, V.; Barcikowski, S. Opportunities and Challenges for Laser Synthesis of Colloids. Chemphyschem 2017, 18, 983–985. [Google Scholar] [CrossRef] [PubMed]
- Streubel, R.; Barcikowski, S.; Gökce, B. Continuous multigram nanoparticle synthesis by high-power, high-repetition-rate ultrafast laser ablation in liquids. Opt. Lett. 2016, 41, 1486–1489. [Google Scholar] [CrossRef] [PubMed]
- Streubel, R.; Bendt, G.; Gökce, B. Pilot-scale synthesis of metal nanoparticles by high-speed pulsed laser ablation in liquids. Nanotechnology 2016, 27, 205602. [Google Scholar] [CrossRef] [PubMed]
- Archana, V.N.; Mani, M.; Johny, J.; Vinayasree, S.; Mohanan, P.; Garza-Navarro, M.A.; Shaji, S.; Anantharaman, M.R. On the microwave absorption of magnetic nanofluids based on barium hexaferrite in the S and X bands prepared by pulsed laser ablation in liquid. AIP Adv. 2019, 9, 035035. [Google Scholar] [CrossRef]
- Zhang, H.-w.; Liu, Y.; Sun, S.-h. Synthesis and assembly of magnetic nanoparticles for information and energy storage applications. Front. Phys. China 2010, 5, 347–356. [Google Scholar] [CrossRef]
- Beck, G.; Barcikowski, S.; Chakravadhanula, V.S.K.; Comesana-Hermo, M.; Deng, M.; Farle, M.; Hilgendorff, M.; Jakobi, J.; Janek, J.; Kienle, L.; et al. An approach for transparent and electrically conducting coatings: A transparent plastic varnish with nanoparticulate magnetic additives. Thin Solid Films 2015, 595, 96–107. [Google Scholar] [CrossRef]
- Hupfeld, T.; Wegner, A.; Blanke, M.; Donate-Buendia, C.; Sharov, V.; Nieskens, S.; Piechotta, M.; Giese, M.; Barcikowski, S.; Gökce, B. Plasmonic Seasoning: Giving Color to Desktop Laser 3D Printed Polymers by Highly Dispersed Nanoparticles. Adv. Optical Mater. 2020, 8, 2000473. [Google Scholar] [CrossRef]
- Hupfeld, T.; Salamon, S.; Landers, J.; Sommereyns, A.; Donate-Buendia, C.; Schmidt, J.; Wende, H.; Schmidt, M.; Barcikowski, S.; Gökce, B. 3D printing of magnetic parts by laser powder bed fusion of iron oxide nanoparticle functionalized polyamide powders. J. Mater. Chem. C 2020, 8, 12204–12217. [Google Scholar] [CrossRef]
- Nadarajah, R.; Landers, J.; Salamon, S.; Koch, D.; Tahir, S.; Donate-Buendia, C.; Zingsem, B.; Dunin-Borkowski, R.E.; Donner, W.; Farle, M.; et al. Towards laser printing of magnetocaloric structures by inducing a magnetic phase transition in iron-rhodium nanoparticles. Sci. Rep. 2021, 11, 13719. [Google Scholar] [CrossRef]
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle polymer composites: Where two small worlds meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Gökce, B. Perspective of laser-prototyping nanoparticle-polymer composites. Appl Surf. Sci. 2017, 392, 991–1003. [Google Scholar] [CrossRef]
- Maurer, E.; Barcikowski, S.; Gökce, B. Process Chain for the Fabrication of Nanoparticle Polymer Composites by Laser Ablation Synthesis. Chem. Eng. Technol. 2017, 40, 1535–1543. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, H.E.; You, B.K.; Cho, S.B.; Mishra, R.; Kang, I.S.; Lee, K.J. Flexible Crossbar-Structured Phase Change Memory Array via Mo-Based Interfacial Physical Lift-Off. Adv. Funct. Mater. 2019, 29, 1806338. [Google Scholar] [CrossRef]
- Barcikowski, S.; Baranowski, T.; Durmus, Y.; Wiedwald, U.; Gökce, B. Solid solution magnetic FeNi nanostrand-polymer composites by connecting-coarsening assembly. J. Mater. Chem. C 2015, 3, 10699–10704. [Google Scholar] [CrossRef]
- Spasova, M.; Salgueiriño-Maceira, V.; Schlachter, A.; Hilgendorff, M.; Giersig, M.; Liz-Marzán, L.M.; Farle, M. Magnetic and optical tunable microspheres with a magnetite/gold nanoparticle shell. J. Mater. Chem. 2005, 15, 2095–2098. [Google Scholar] [CrossRef]
- Fang, W.X.; He, Z.H.; Xu, X.Q.; Mao, Z.Q.; Shen, H. Magnetic-field-induced chain-like assembly structures of Fe3O4 nanoparticles. Europhys. Lett. 2007, 77, 68004. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Q. Synthesis of magnetosome chain-like structures. Nanotechnology 2008, 19, 475603. [Google Scholar] [CrossRef] [PubMed]
- Korth, B.D.; Keng, P.; Shim, I.; Bowles, S.E.; Tang, C.; Kowalewski, T.; Nebesny, K.W.; Pyun, J. Polymer-coated ferromagnetic colloids from well-defined macromolecular surfactants and assembly into nanoparticle chains. J. Am. Chem. Soc. 2006, 128, 6562–6563. [Google Scholar] [CrossRef]
- Lalatonne, Y.; Richardi, J.; Pileni, M.P. Van der Waals versus dipolar forces controlling mesoscopic organizations of magnetic nanocrystals. Nat. Mater. 2004, 3, 121–125. [Google Scholar] [CrossRef]
- Xiong, Y.; Chen, Q.; Tao, N.; Ye, J.; Tang, Y.; Feng, J.; Gu, X. The formation of legume-like structures of Co nanoparticles through a polymer-assisted magnetic-field-induced assembly. Nanotechnology 2007, 18, 345301. [Google Scholar] [CrossRef]
- Kou, Z.; Liu, E.; Yue, J.; Sui, Y.; Huang, Z.; Zhang, D.; Wang, Y.; Zhai, Y.; Du, J.; Zhai, H. The magnetic properties of well-aligned nickel nanochains synthesized by magnetic field-induced assembly approach. J. Appl. Phys. 2015, 117, 17E709. [Google Scholar] [CrossRef]
- Imahori, H.; Norieda, H.; Yamada, H.; Nishimura, Y.; Yamazaki, I.; Sakata, Y.; Fukuzumi, S. Light-harvesting and photocurrent generation by gold electrodes modified with mixed self-assembled monolayers of boron-dipyrrin and ferrocene-porphyrin-fullerene triad. J. Am. Chem. Soc. 2001, 123, 100–110. [Google Scholar] [CrossRef]
- Lu, H.B.; Liao, L.; Li, J.C.; Shuai, M.; Liu, Y.L. Hematite nanochain networks: Simple synthesis, magnetic properties, and surface wettability. Appl. Phys. Lett. 2008, 92, 093102. [Google Scholar] [CrossRef]
- Morimoto, H.; Maekawa, T. Cluster structures and cluster-cluster aggregations in a two-dimensional ferromagnetic colloidal system. J. Phys. A Math. Gen. 2000, 33, 247–258. [Google Scholar] [CrossRef]
- Ytreberg, F.M.; McKay, S.R. Calculated properties of field-induced aggregates in ferrofluids. Phys. Rev. E 2000, 61, 4107–4110. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, P.; Yang, G.W. Fabrication of One-Dimensional Chain of Iron-Based Bimetallic Alloying Nanoparticles with Unique Magnetizations. Cryst Growth Des. 2014, 14, 5847–5855. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, P.; Xiao, J.; Li, H.B.; Wang, C.X.; Yang, G.W. A general strategy for one-step fabrication of one-dimensional magnetic nanoparticle chains based on laser ablation in liquid. Laser Phys. Lett. 2014, 11, 056001. [Google Scholar] [CrossRef]
- Fragouli, D.; Torre, B.; Bertoni, G.; Buonsanti, R.; Cingolani, R.; Athanassiou, A. Formation and microscopic investigation of iron oxide aligned nanowires into polymeric nanocomposite films. Microsc. Res. Tech. 2010, 73, 952–958. [Google Scholar] [CrossRef]
- Conde-Leborán, I.; Serantes, D.; Baldomir, D. Orientation of the magnetization easy axes of interacting nanoparticles: Influence on the hyperthermia properties. J. Magn. Magn. Mater. 2015, 380, 321–324. [Google Scholar] [CrossRef]
- Ilg, P.; Kroger, M. Anisotropic self-diffusion in ferrofluids studied via Brownian dynamics simulations. Phys. Rev. E 2005, 72, 031504. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Li, J.; Gao, R. The structural force arising from magnetic interactions in polydisperse ferrofluids. Appl. Phys. Lett. 2009, 94, 212501. [Google Scholar] [CrossRef]
- Sahoo, Y.; Cheon, M.; Wang, S.; Luo, H.; Furlani, E.P.; Prasad, P.N. Field-Directed Self-Assembly of Magnetic Nanoparticles. J. Phys. Chem. B 2004, 108, 3380–3383. [Google Scholar] [CrossRef]
- Nikov, R.G.; Nedyalkov, N.N.; Karashanova, D.B. Laser ablation of Ni in the presence of external magnetic field: Selection of microsized particles. Appl. Surf. Sci. 2020, 518, 146211. [Google Scholar] [CrossRef]
- Lu, H.; Gou, J.; Leng, J.; Du, S. Synergistic effect of carbon nanofiber and sub-micro filamentary nickel nanostrand on the shape memory polymer nanocomposite. Smart Mater. Struct. 2011, 20, 035017. [Google Scholar] [CrossRef]
- Kamp, M.; Tymoczko, A.; Popescu, R.; Schürmann, U.; Nadarajah, R.; Gökce, B.; Rehbock, C.; Gerthsen, D.; Barcikowski, S.; Kienle, L. Composition and structure of magnetic high-temperature-phase, stable Fe–Au core–shell nanoparticles with zero-valent bcc Fe core. Nanoscale Adv. 2020, 2, 3912–3920. [Google Scholar] [CrossRef]
- Nadarajah, R.; Tahir, S.; Landers, J.; Koch, D.; Semisalova, A.S.; Wiemeler, J.; El-Zoka, A.; Kim, S.H.; Utzat, D.; Moller, R.; et al. Controlling the Oxidation of Magnetic and Electrically Conductive Solid-Solution Iron-Rhodium Nanoparticles Synthesized by Laser Ablation in Liquids. Nanomaterials 2020, 10, 2362. [Google Scholar] [CrossRef]
- Nilsson, F.; Karlsson, M.; Pallon, L.; Giacinti, M.; Olsson, R.T.; Venturi, D.; Gedde, U.W.; Hedenqvist, M.S. Influence of water uptake on the electrical DC-conductivity of insulating LDPE/MgO nanocomposites. Compos. Sci. Technol. 2017, 152, 11–19. [Google Scholar] [CrossRef]
- Massaro, A.; Spano, F.; Athanassiou, A.; Cingolani, R. FEM modeling of conductivity and electrical coupling in polymeric nanocomposite material. In Proceedings of the 2011 Numerical Simulation of Optoelectronic Devices, Rome, Italy, 5–8 September 2011; pp. 85–86. [Google Scholar]
- Manta, A.; Gresil, M.; Soutis, C. Predictive Model of Graphene Based Polymer Nanocomposites: Electrical Performance. Appl. Compos. Mater. 2016, 24, 281–300. [Google Scholar] [CrossRef]
- Cricrì, G.; Garofalo, E.; Naddeo, F.; Incarnato, L. Stiffness constants prediction of nanocomposites using a periodic 3D-FEM model. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 207–220. [Google Scholar] [CrossRef]
- Wang, H.W.; Zhou, H.W.; Peng, R.D.; Mishnaevsky, L. Nanoreinforced polymer composites: 3D FEM modeling with effective interface concept. Compos. Sci. Technol. 2011, 71, 980–988. [Google Scholar] [CrossRef]
- Chwał, M.; Muc, A. FEM micromechanical modeling of nanocomposites with carbon nanotubes. Rev. Adv. Mater. Sci. 2021, 60, 342–351. [Google Scholar] [CrossRef]
- Uth, N.; Mueller, J.; Smucker, B.; Yousefi, A.M. Validation of scaffold design optimization in bone tissue engineering: Finite element modeling versus designed experiments. Biofabrication 2017, 9, 015023. [Google Scholar] [CrossRef] [PubMed]
- Hassanzadeh-Aghdam, M.K.; Ansari, R. A Micromechanical Model for Effective Thermo-elastic Properties of Nanocomposites with Graded Properties of Interphase. Iran. J. Sci. Technol. Trans. Mech. Eng. 2016, 41, 141–147. [Google Scholar] [CrossRef]
- Jafarpour, A.; Safarabadi Farahani, M.; Haghighi-Yazdi, M. Numerical investigation of oriented CNFs effects on thermo-mechanical properties and curing residual stresses field of polymeric nanocomposites. Mech. Mater. 2019, 138, 103176. [Google Scholar] [CrossRef]
- Shu, W.; Stanciulescu, I. Fully coupled thermo-mechanical cohesive zone model with thermal softening: Application to nanocomposites. Int. J. Solids Struct. 2020, 188-189, 1–11. [Google Scholar] [CrossRef]
- Hsissou, R.; Bekhta, A.; Dagdag, O.; El Bachiri, A.; Rafik, M.; Elharfi, A. Rheological properties of composite polymers and hybrid nanocomposites. Heliyon 2020, 6, e04187. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Liu, Y.; Gai, D.; Dikin, D.A.; Putz, K.W.; Chen, W.; Catherine Brinson, L.; Burkhart, C.; Poldneff, M.; Jiang, B.; et al. Utilizing real and statistically reconstructed microstructures for the viscoelastic modeling of polymer nanocomposites. Compos. Sci. Technol. 2012, 72, 1725–1732. [Google Scholar] [CrossRef]
- Sanei, S.H.R.; Doles, R.; Ekaitis, T. Effect of Nanocomposite Microstructure on Stochastic Elastic Properties: An Finite Element Analysis Study. ASCE-ASME J. Risk Uncert. Eng. Syst. Part B Mech. Eng. 2019, 5, 030903. [Google Scholar] [CrossRef]
- Miles, J.J.; Chantrell, R.W.; Parker, M.R. Model of magnetic-field-induced ordering in dispersions of fine paramagnetic particles. J. Appl. Phys. 1985, 57, 4271–4273. [Google Scholar] [CrossRef]
- Bertoni, G.; Torre, B.; Falqui, A.; Fragouli, D.; Athanassiou, A.; Cingolani, R. Nanochains Formation of Superparamagnetic Nanoparticles. J. Phys. Chem. C 2011, 115, 7249–7254. [Google Scholar] [CrossRef]
- Zhao, Z.; Torres-Díaz, I.; Vélez, C.; Arnold, D.; Rinaldi, C. Brownian Dynamics Simulations of Magnetic Nanoparticles Captured in Strong Magnetic Field Gradients. J. Phys. Chem. C 2016, 121, 801–810. [Google Scholar] [CrossRef]
- Hucht, A.; Buschmann, S.; Entel, P. Molecular dynamics simulations of the dipolar-induced formation of magnetic nanochains and nanorings. Europhys. Lett. 2007, 77, 57003. [Google Scholar] [CrossRef][Green Version]
- Zhang, W.G.; Jin, Z.G. Research on successive preparation of nano-FeNi alloy and its ethanol sol by pulsed laser ablation. Sci. China Ser. B 2004, 47, 159–165. [Google Scholar] [CrossRef]
- Shih, C.Y.; Streubel, R.; Heberle, J.; Letzel, A.; Shugaev, M.V.; Wu, C.; Schmidt, M.; Gökce, B.; Barcikowski, S.; Zhigilei, L.V. Two mechanisms of nanoparticle generation in picosecond laser ablation in liquids: The origin of the bimodal size distribution. Nanoscale 2018, 10, 6900–6910. [Google Scholar] [CrossRef]
- Lin, Q.; Nadarajah, R.; Hoglund, E.; Semisalova, A.; Howe, J.M.; Gökce, B.; Zangari, G. Towards Synthetic L10-FeNi: Detecting the Absence of Cubic Symmetry in Laser-Ablated Fe-Ni Nanoparticles. Appl. Surf. Sci. 2021, 567, 150664. [Google Scholar] [CrossRef]
- Liu, K.; Schuch, F.; Kiran, E. High-pressure viscosity and density of poly(methyl methacrylate) plus acetone and poly(methyl methacrylate) plus acetone plus CO2 systems. J. Supercrit. Fluid 2006, 39, 89–101. [Google Scholar] [CrossRef]
- Zhang, J.; Oko, D.N.; Garbarino, S.; Imbeault, R.; Chaker, M.; Tavares, A.C.; Guay, D.; Ma, D. Preparation of PtAu Alloy Colloids by Laser Ablation in Solution and Their Characterization. J. Phys. Chem. C 2012, 116, 13413–13420. [Google Scholar] [CrossRef]
- Marzun, G.; Levish, A.; Mackert, V.; Kallio, T.; Barcikowski, S.; Wagener, P. Laser synthesis, structure and chemical properties of colloidal nickel-molybdenum nanoparticles for the substitution of noble metals in heterogeneous catalysis. J. Colloid Interface Sci. 2017, 489, 57–67. [Google Scholar] [CrossRef] [PubMed]
- Wack, M.; Volk, M.; Wei, Q. Magnetic Properties of the Iron–Nickel System: Pressure, Composition, and Grain Size. In Magnetic Fields in the Solar System: Planets, Moons and Solar Wind Interactions; Lühr, H., Wicht, J., Gilder, S.A., Holschneider, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 383–406. [Google Scholar]
- Scheunert, G.; Heinonen, O.; Hardeman, R.; Lapicki, A.; Gubbins, M.; Bowman, R.M. A review of high magnetic moment thin films for microscale and nanotechnology applications. Appl. Phys. Rev. 2016, 3, 011301. [Google Scholar] [CrossRef]
- Neumeister, A.; Jakobi, J.; Rehbock, C.; Moysig, J.; Barcikowski, S. Monophasic ligand-free alloy nanoparticle synthesis determinants during pulsed laser ablation of bulk alloy and consolidated microparticles in water. Phys. Chem. Chem. Phys. 2014, 16, 23671–23678. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.D.; Pinski, F.J.; Staunton, J.B. The Slater–Pauling curve: First principles calculations of the moments of Fe1−cNic and V1−cFec. J. Appl. Phys. 1987, 61, 3715–3717. [Google Scholar] [CrossRef]

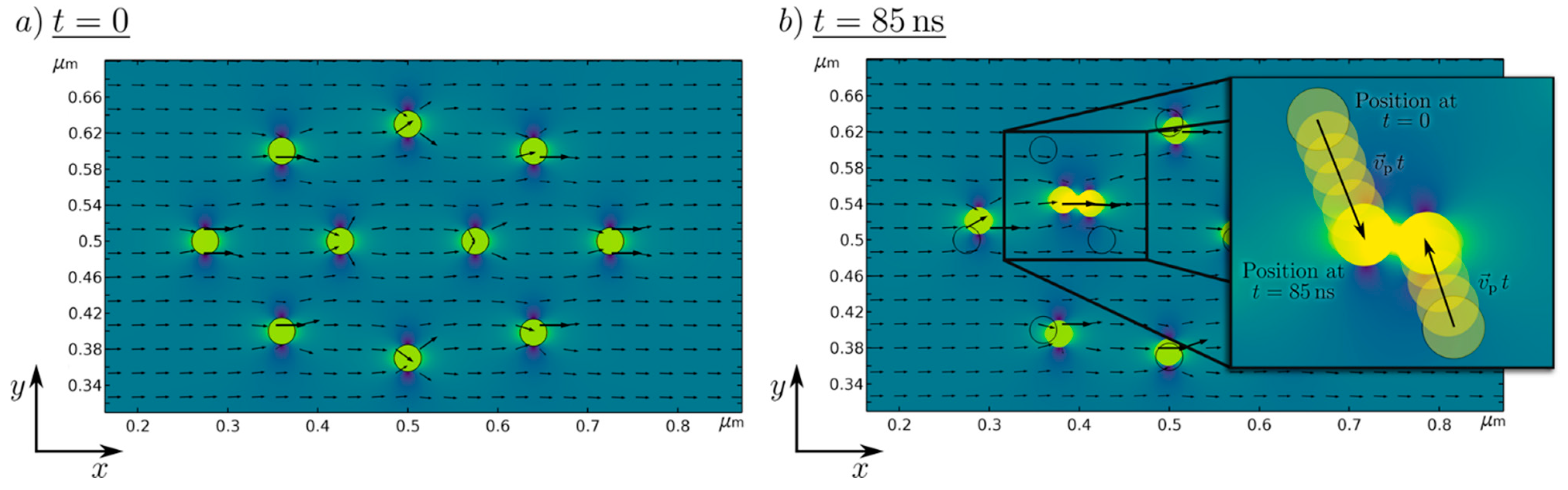

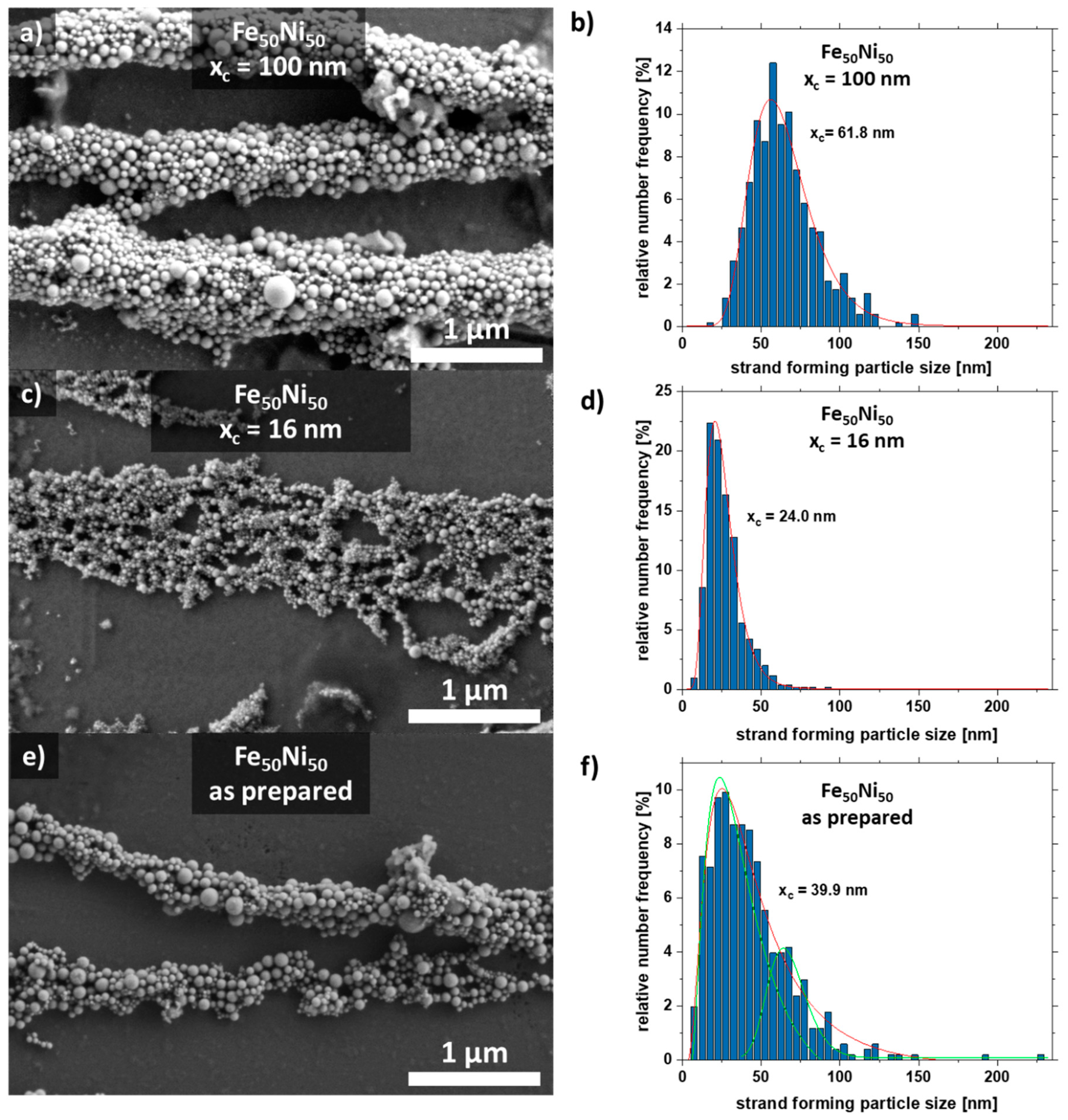
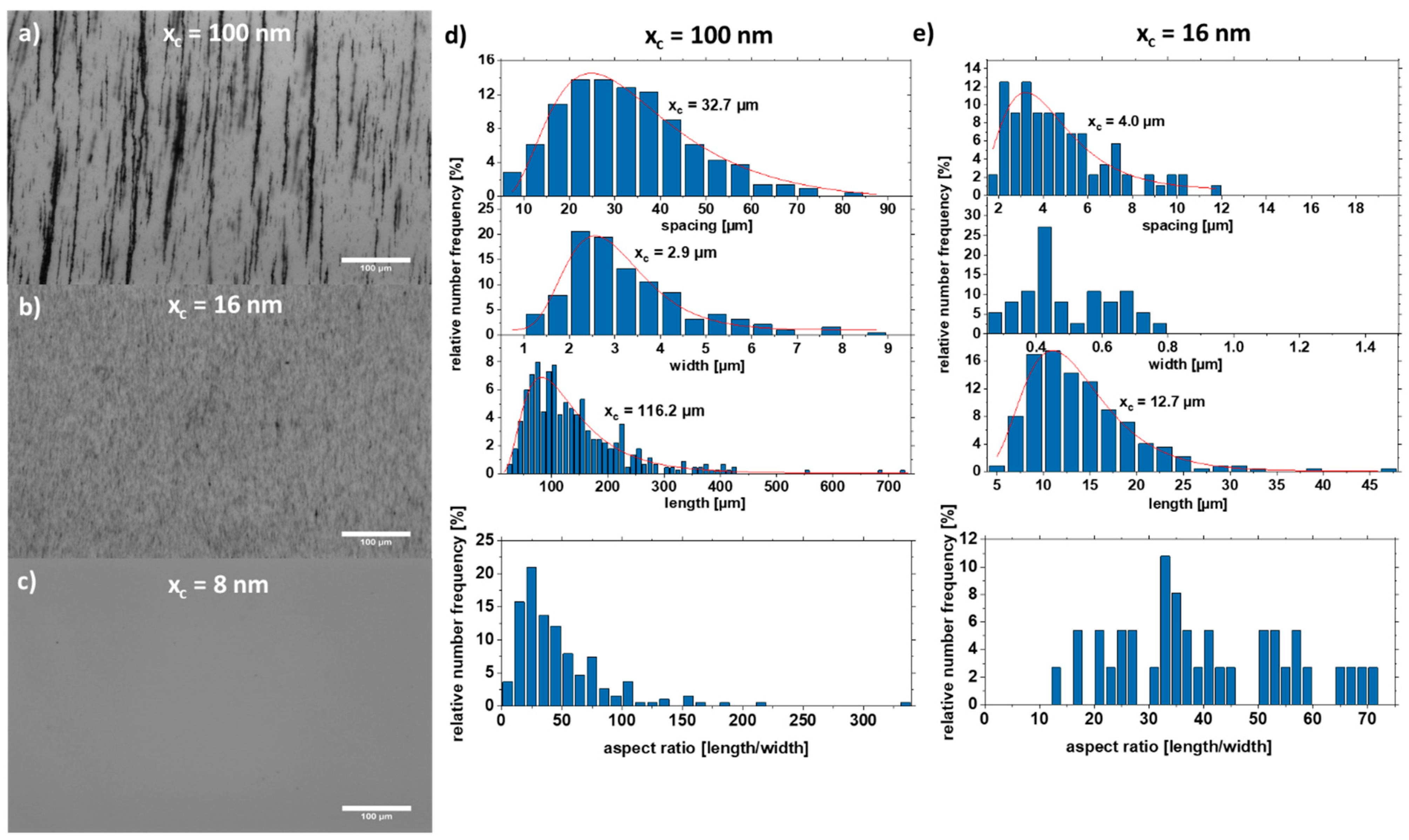
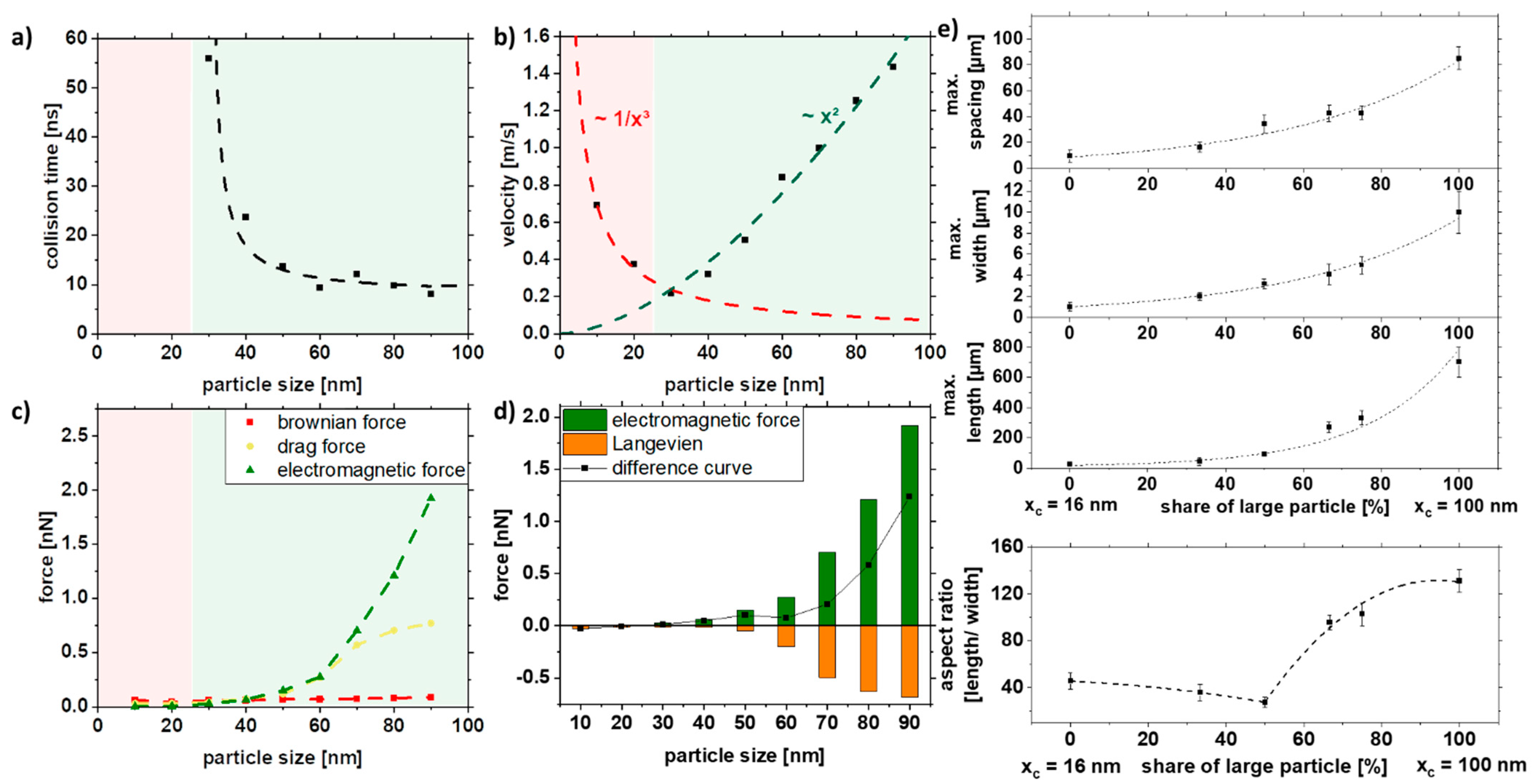


| Size | Step | Volume (mL) | RPM | Time (min) | Description |
|---|---|---|---|---|---|
| x < 10 nm | i | 50 | 2000 | 36 | use supernatant for second step |
| ii | 2 | 18,000 | 20 | collect supernatant | |
| 10 nm > x > 50 nm | i | 50 | 2000 | 36 | use supernatant for second step |
| ii | 2 | 18,000 | 20 | collect pellet | |
| x > 50 nm | i | 50 | 4000 | 9 | centrifuged 7 times and collect pellet |
| Material | ρ (g/cm³) | Mean Size (nm) | M1T (Am2/kg) | M170mT (Am2/kg) | Hc (mT) | Mr (Am2/kg) |
|---|---|---|---|---|---|---|
| Ni | 8.91 | 13.6 ± 9.4 | 1.1 | 0.17 | −0.6 | 0.001 |
| Fe20Ni80 | 8.70 | 17.8 ± 13.4 | 11.7 | 6.8 | −0.7 | 0.03 |
| Fe50Ni50 | 8.40 | 13.1 ± 9.0 | 34.5 | 20.8 | −0.9 | 0.6 |
| Fe64Ni36 | 8.25 | 11.9 ± 5.7 | 46.1 | 24.7 | −3.3 | 1.6 |
| Fe90Ni10 | 7.98 | 14.5 ± 7.7 | 54.7 | 28.3 | −6.0 | 2.3 |
| Fe | 7.87 | 16.5 ± 8.5 | 50.5 | 24.9 | −7.1 | 2.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadarajah, R.; Tasdemir, L.; Thiel, C.; Salamon, S.; Semisalova, A.S.; Wende, H.; Farle, M.; Barcikowski, S.; Erni, D.; Gökce, B. Formation of Fe-Ni Nanoparticle Strands in Macroscopic Polymer Composites: Experiment and Simulation. Nanomaterials 2021, 11, 2095. https://doi.org/10.3390/nano11082095
Nadarajah R, Tasdemir L, Thiel C, Salamon S, Semisalova AS, Wende H, Farle M, Barcikowski S, Erni D, Gökce B. Formation of Fe-Ni Nanoparticle Strands in Macroscopic Polymer Composites: Experiment and Simulation. Nanomaterials. 2021; 11(8):2095. https://doi.org/10.3390/nano11082095
Chicago/Turabian StyleNadarajah, Ruksan, Leyla Tasdemir, Christian Thiel, Soma Salamon, Anna S. Semisalova, Heiko Wende, Michael Farle, Stephan Barcikowski, Daniel Erni, and Bilal Gökce. 2021. "Formation of Fe-Ni Nanoparticle Strands in Macroscopic Polymer Composites: Experiment and Simulation" Nanomaterials 11, no. 8: 2095. https://doi.org/10.3390/nano11082095
APA StyleNadarajah, R., Tasdemir, L., Thiel, C., Salamon, S., Semisalova, A. S., Wende, H., Farle, M., Barcikowski, S., Erni, D., & Gökce, B. (2021). Formation of Fe-Ni Nanoparticle Strands in Macroscopic Polymer Composites: Experiment and Simulation. Nanomaterials, 11(8), 2095. https://doi.org/10.3390/nano11082095







