Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet
Abstract
:1. Introduction
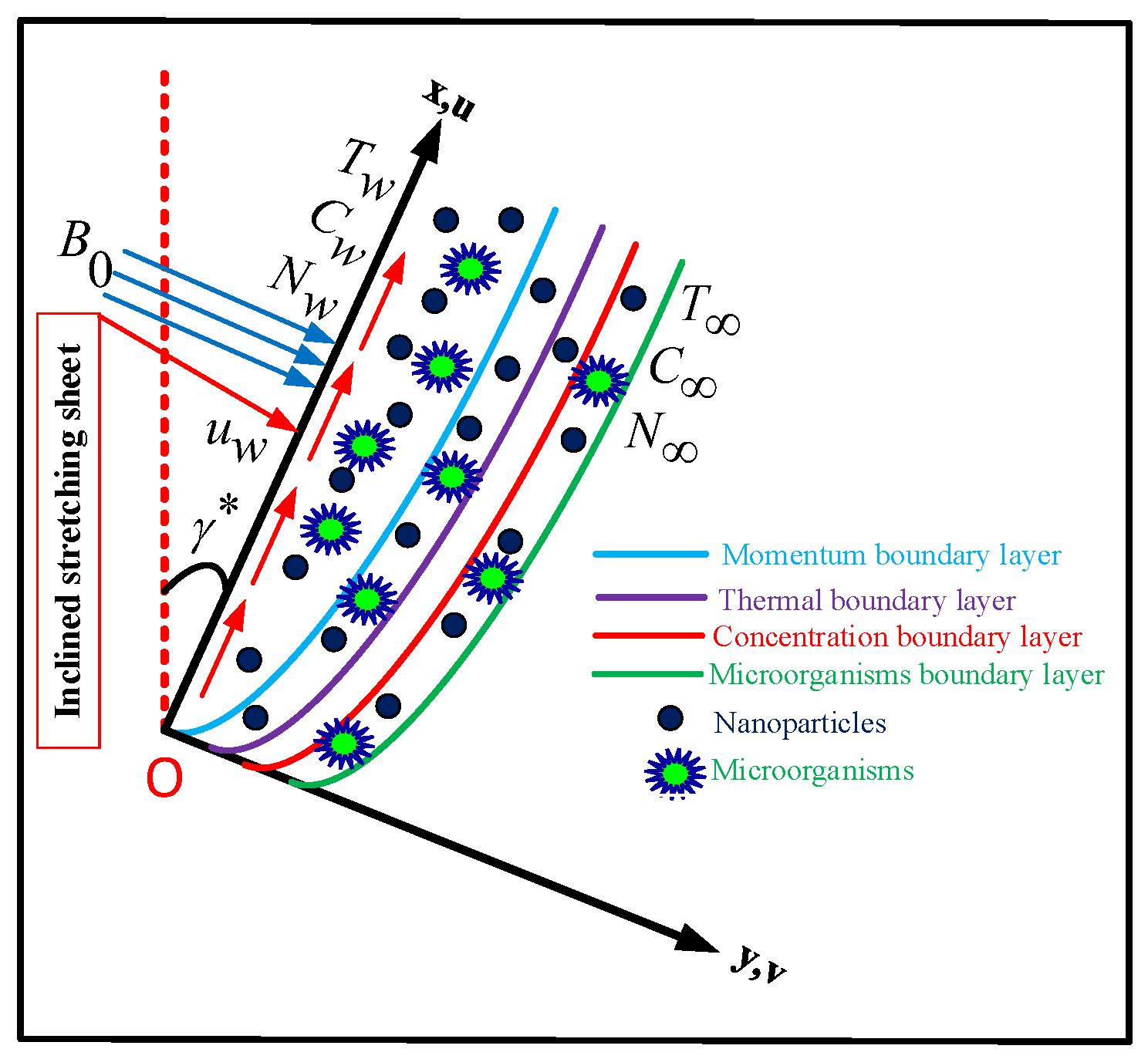
2. Mathematical Formulation
3. Physical Quantities
4. Solution Procedure
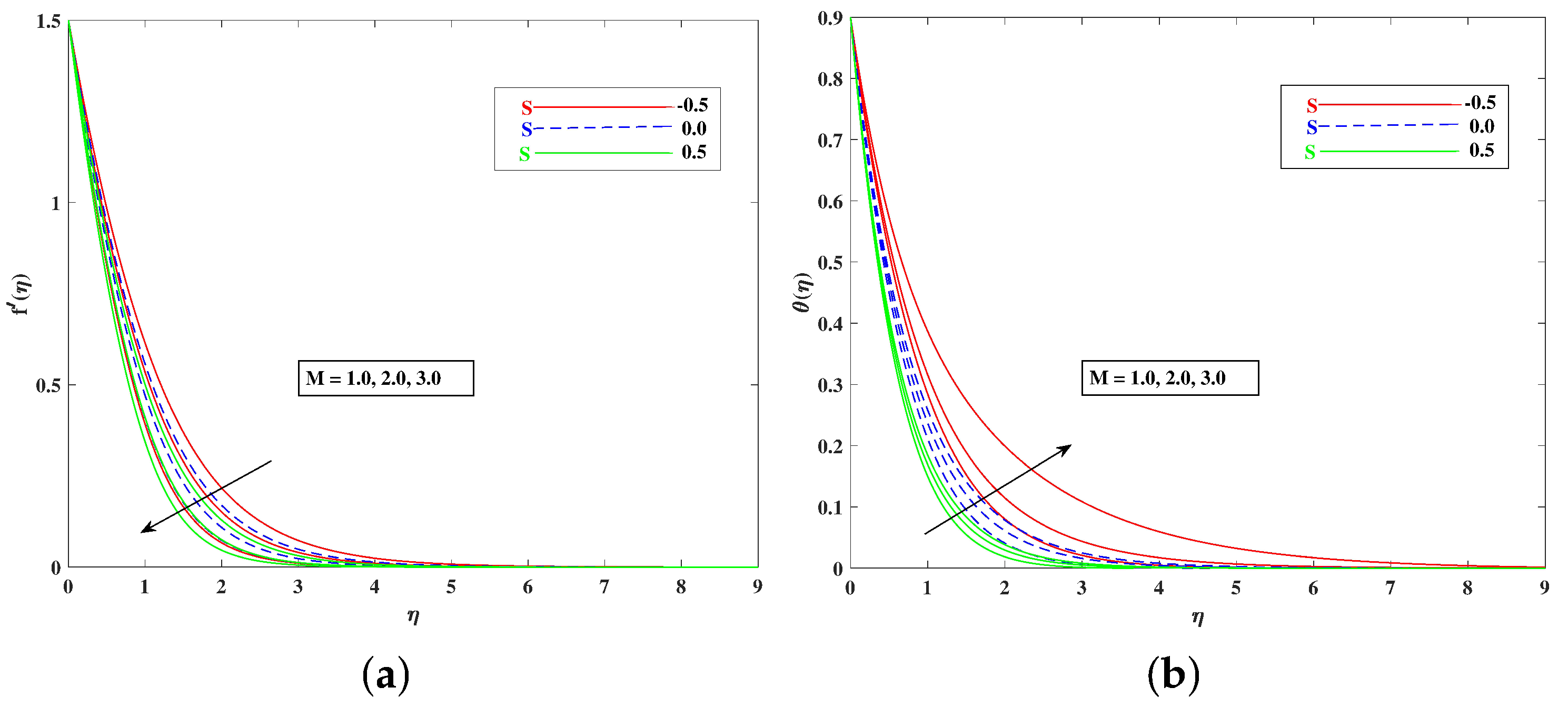
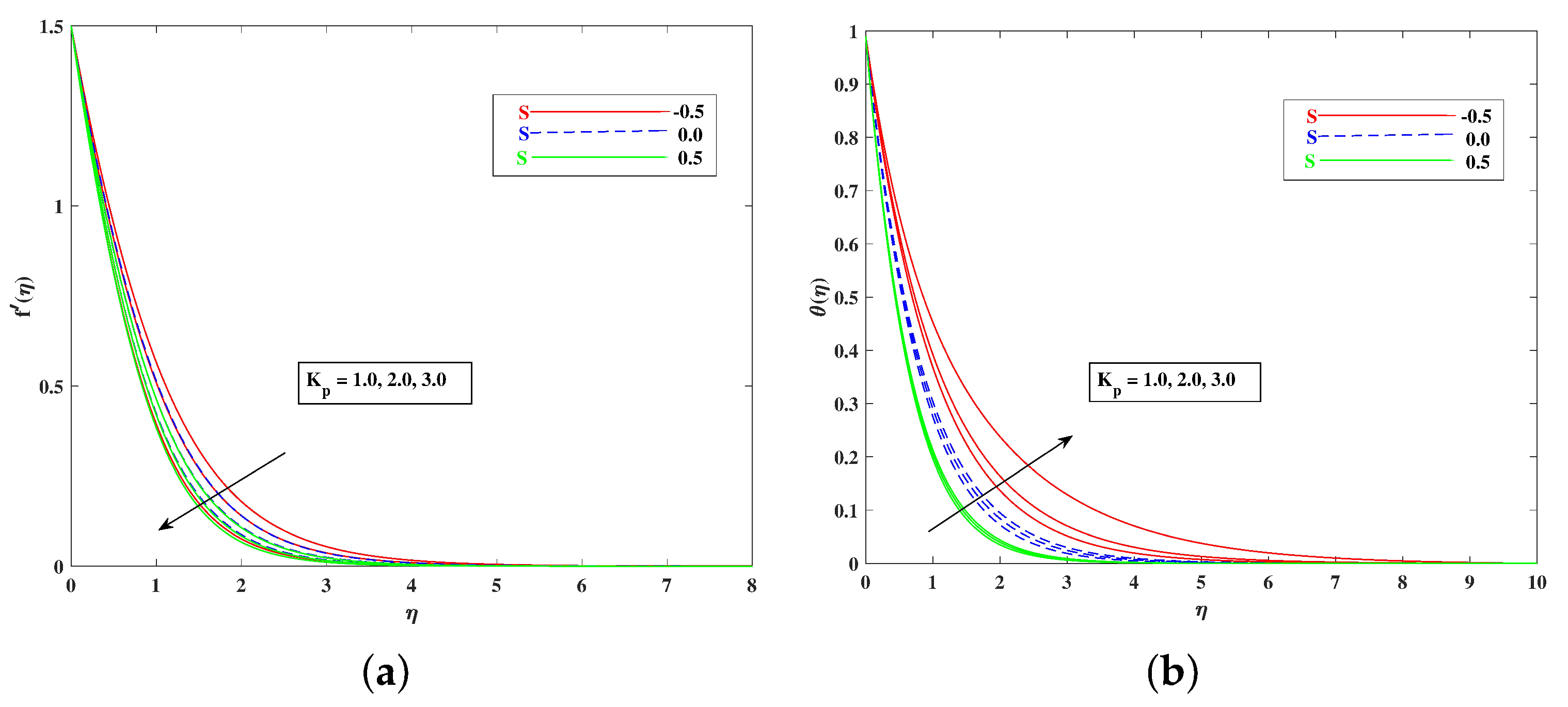
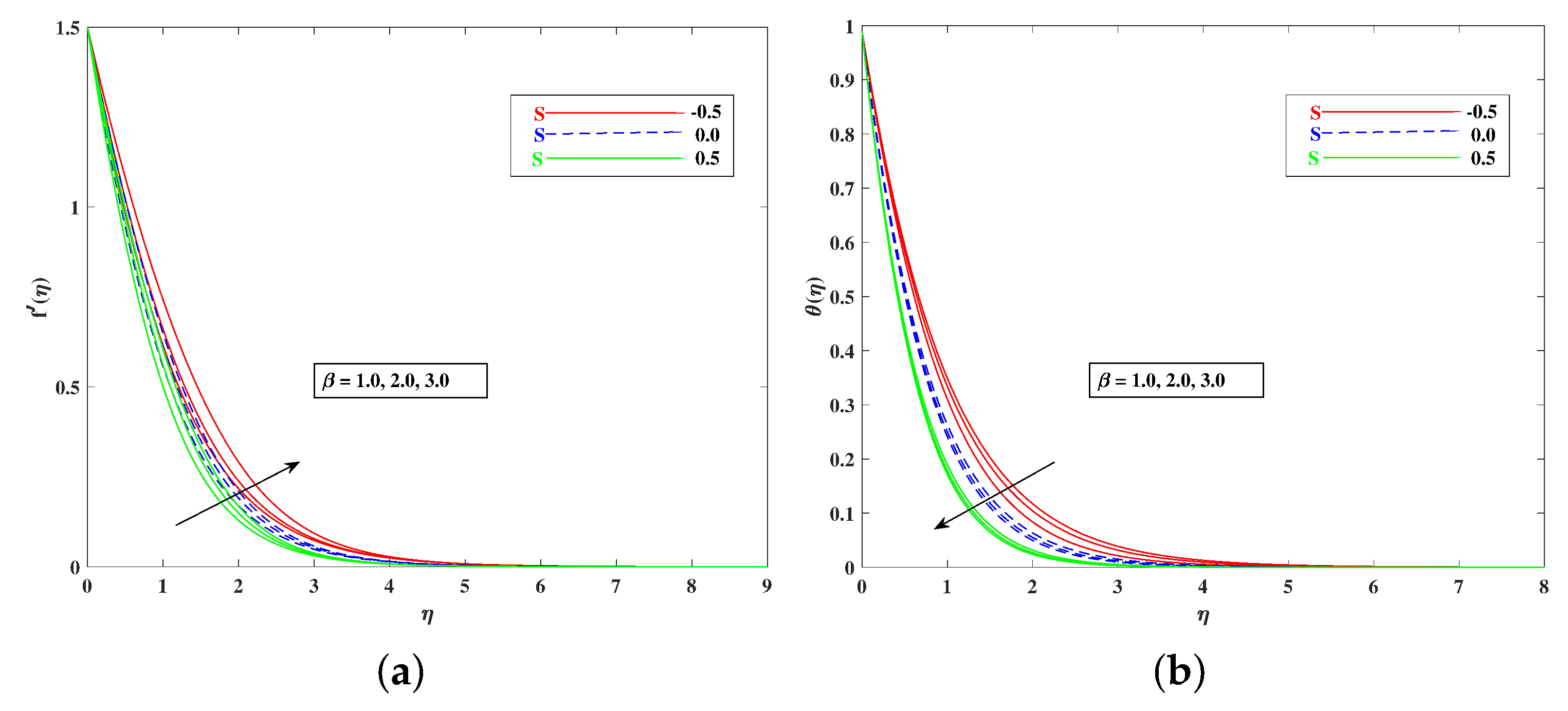
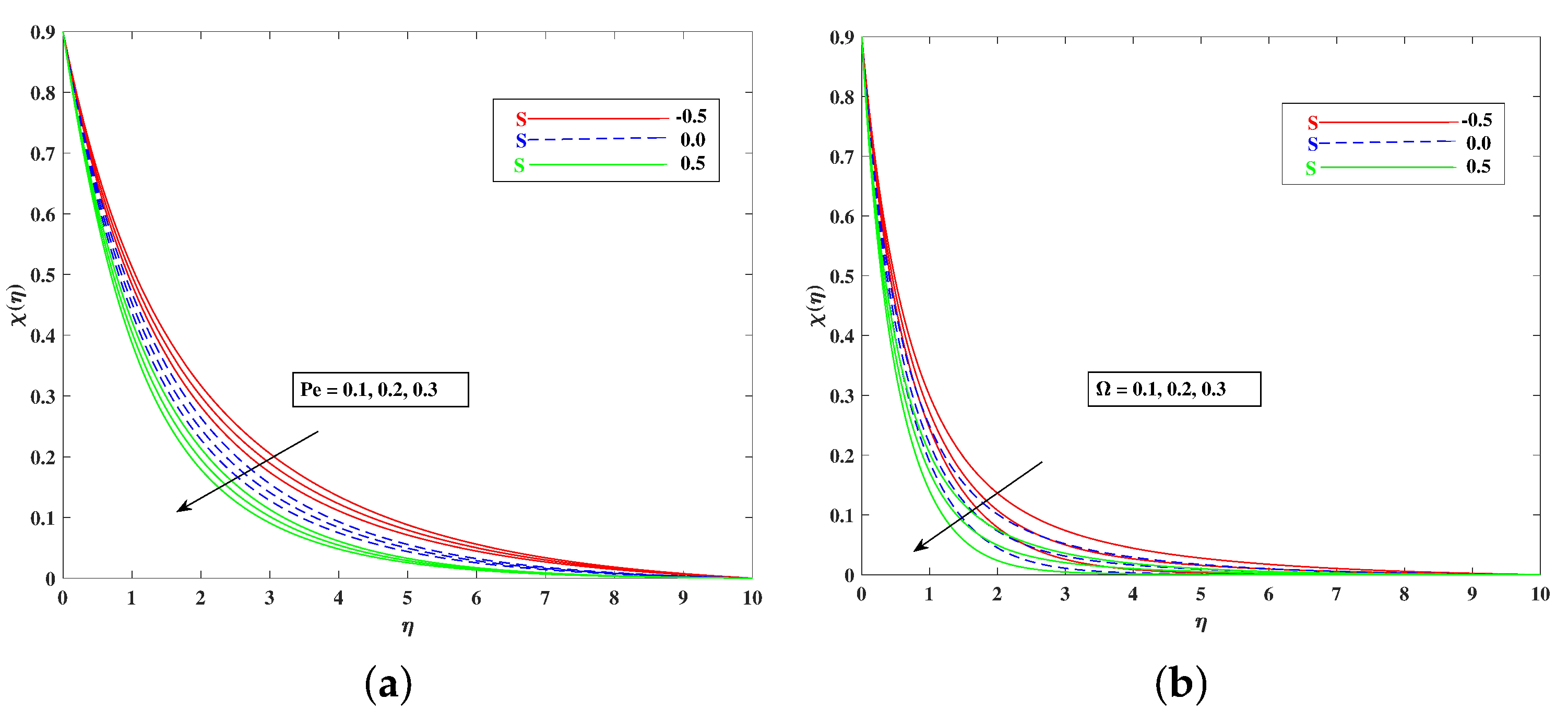
5. Results and Discussion
6. Conclusions
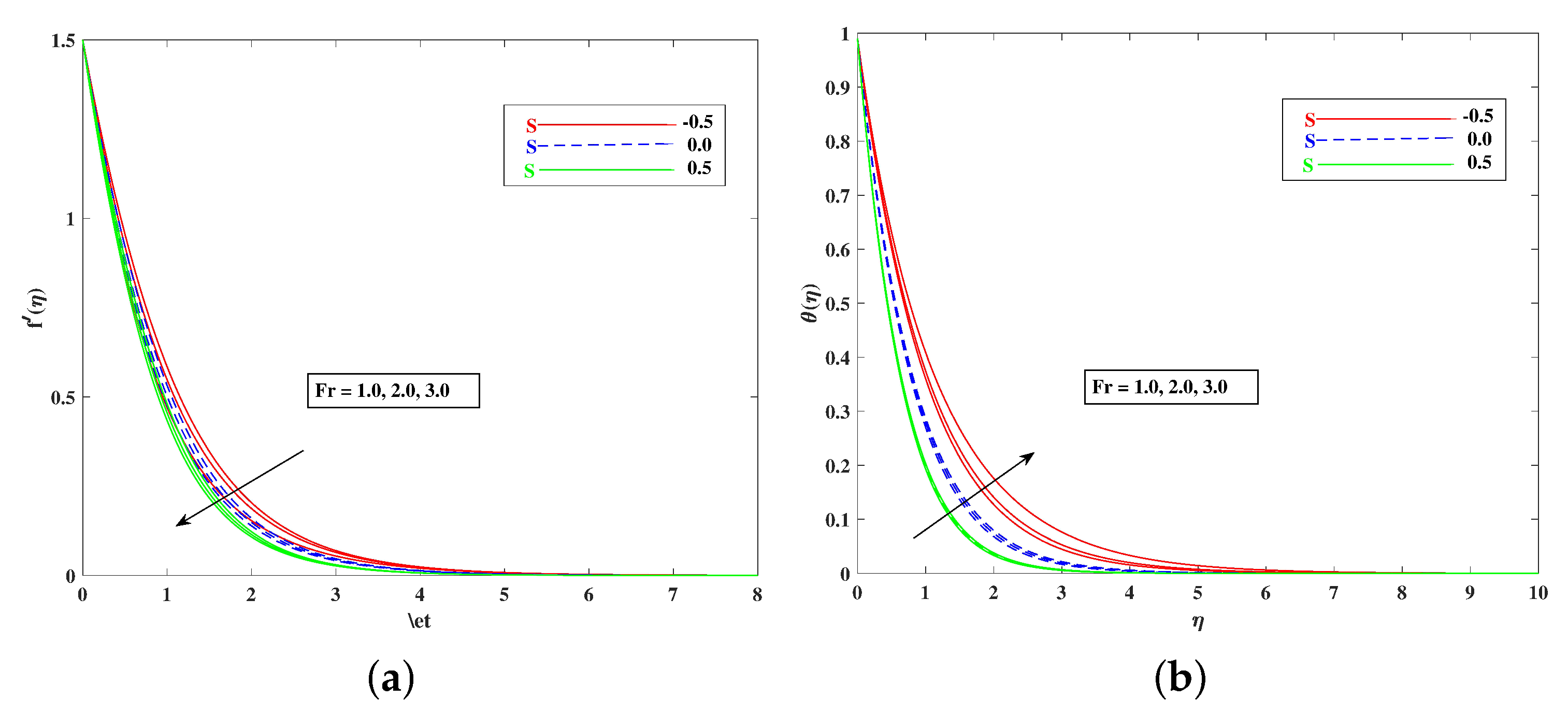
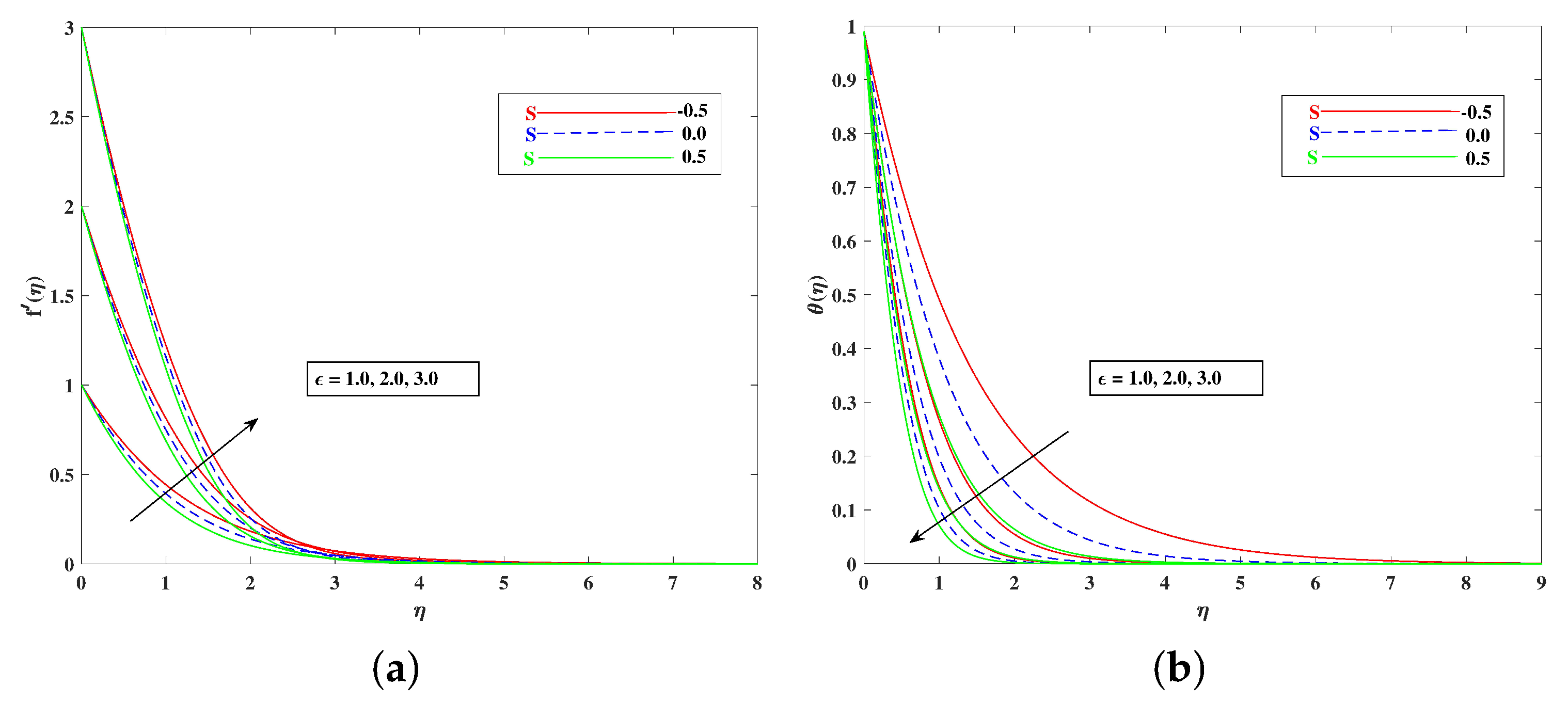
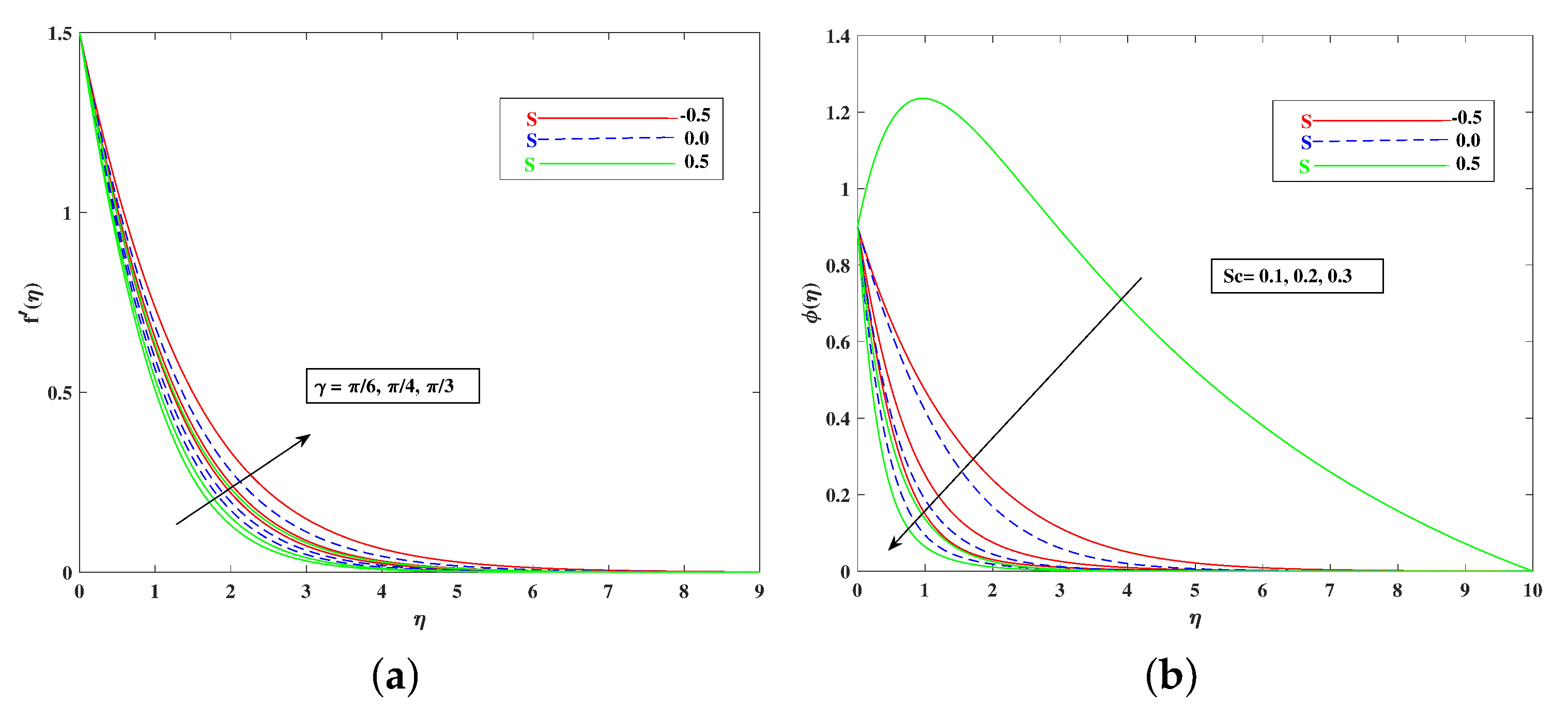
- The fluid velocity improved with improving , , , , and , and it diminished against M, , and ;
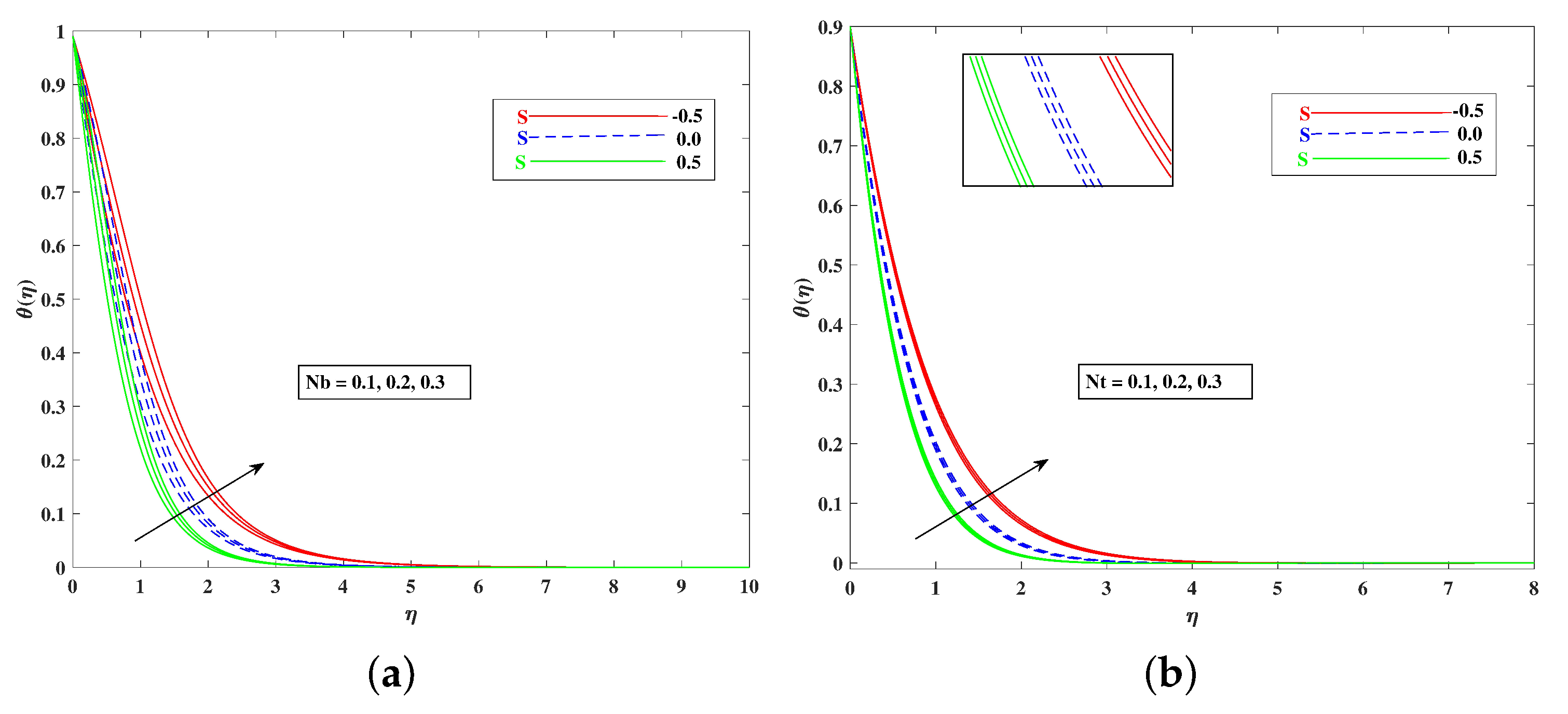
- The Temperature increased against the larger values of the thermophoresis parameters and Brownian motion , as well as the temperature rose with the increasing values of and M, and it reduced when the mixed convection parameter improved;
- The concentration of the nanoparticles lowered when rose;
- Graphs of the dependent quantities velocity, temperature, concentration, and bioconvection profile were determined for three cases of mass transport ;
- The microorganisms’ diffusion decreased when the values of the parameters , , and increased;
- The skin friction was enhanced with , and and diminished against ;
- The results were compared with the past literature to validate the results;
- The Nusselt number decreased against , , and , and it increased in magnitude directly with ;
- The increment in and resulted in a decline in the motile density number .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Fluid velocity components along the | |
| Density of the motile microorganisms | |
| Fluid velocity components along the | |
| Concentration at the surface | |
| g | Gravitational acceleration |
| Brownian diffusion coefficient | |
| Fluid density | |
| Diffusivity of the microorganisms | |
| Mass density of the nanoparticles | |
| Thermophoretic diffusion coefficient | |
| Skin friction | |
| Temperature at the surface | |
| Nusselt number | |
| Sherwood number | |
| Dynamic viscosity | |
| Kinematic viscosity | |
| Thermophoresis parameter | |
| Density of the motile microorganisms at the surface | |
| Thermophoretic diffusion coefficient | |
| Ambient temperature | |
| Specific heat | |
| Uniform magnetic field | |
| Fluid parameters | |
| Ambient concentration | |
| k | Porous medium permeability |
| Ambient motile microorganisms | |
| Nanoparticles’ concentration | |
| Constant maximum cell swimming speed | |
| Similarity variable | |
| Dimensionless stream function | |
| Dimensionless velocity profile | |
| Dimensionless nanofluid temperature | |
| Dimensionless nanofluid concentration | |
| Dimensionless density of the motile microorganisms |
References
- Alshomrani, A.S. Numerical investigation for bioconvection flow of viscoelastic nanofluid with magnetic dipole and motile microorganisms. Arab. J. Sci. Eng. 2021, 46, 5945–5956. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, M.I.; Khan, N.B.; Kadry, S.; Khan, S.U.; Tlili, I.; Nayak, M. Significance of activation energy, bioconvection and magnetohydrodynamic in flow of third grade fluid (non-Newtonian) towards stretched surface: A Buongiorno model analysis. Int. Commun. Heat Mass Transf. 2020, 118, 104893. [Google Scholar] [CrossRef]
- Dey, D.; Chutia, B. Dusty nanofluid flow with bioconvection past a vertical stretching surface. J. King Saud-Univ.-Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Ferdows, M.; Zaimi, K.; Rashad, A.M.; Nabwey, H.A. MHD bioconvection flow and heat transfer of nanofluid through an exponentially stretchable sheet. Symmetry 2020, 12, 692. [Google Scholar] [CrossRef]
- Irfan, M.; Farooq, M.A.; Mushtaq, A.; Shamsi, Z.H. Unsteady MHD bionanofluid flow in a porous medium with thermal radiation near a stretching/shrinking sheet. Math. Probl. Eng. 2020, 2020, 8822999. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Bhaumik, A.; Kumam, P.; Thounthong, P.; Amiri, I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci. Rep. 2020, 10, 1–26. [Google Scholar] [CrossRef]
- Abbasi, A.; Mabood, F.; Farooq, W.; Batool, M. Bioconvective flow of viscoelastic Nanofluid over a convective rotating stretching disk. Int. Commun. Heat Mass Transf. 2020, 119, 104921. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ur Rehman, S.; Ahmadian, A.; Salahshour, S.; Salimi, M. First Solution of Fractional Bioconvection with Power Law Kernel for a Vertical Surface. Mathematics 2021, 9, 1366. [Google Scholar] [CrossRef]
- Oyelakin, I.; Mondal, S.; Sibanda, P. Nonlinear radiation in bioconvective Casson nanofluid flow. Int. J. Appl. Comput. Math. 2019, 5, 1–20. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids With Nanoparticles; Technical Report; Argonne National Lab.: Lemont, IL, USA, 1995.
- Hayat, T.; Khan, W.; Abbas, S.; Nadeem, S.; Ahmad, S. Impact of induced magnetic field on second-grade nanofluid flow past a convectively heated stretching sheet. Appl. Nanosci. 2020, 10, 3001–3009. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Ahmad, B. Entropy generation minimization: Darcy–Forchheimer nanofluid flow due to curved stretching sheet with partial slip. Int. Commun. Heat Mass Transf. 2020, 111, 104445. [Google Scholar] [CrossRef]
- Sudarsana Reddy, P.; Sreedevi, P. Impact of chemical reaction and double stratification on heat and mass transfer characteristics of nanofluid flow over porous stretching sheet with thermal radiation. Int. J. Ambient. Energy 2020. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S.; Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1–15. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Rehman, A.U.; Abdal, S. Variable viscosity effects on unsteady MHD an axisymmetric nanofluid flow over a stretching surface with thermo-diffusion: Fem approach. Symmetry 2020, 12, 234. [Google Scholar] [CrossRef] [Green Version]
- Shoaib, M.; Raja, M.A.Z.; Sabir, M.T.; Islam, S.; Shah, Z.; Kumam, P.; Alrabaiah, H. Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]
- Ghosh, R.; Agbaje, T.M.; Mondal, S.; Shaw, S. Bio-convective viscoelastic Casson nanofluid flow over a stretching sheet in the presence of induced magnetic field with Cattaneo-Christov double diffusion. Int. J. Biomath. 2021, 2150099. [Google Scholar] [CrossRef]
- Khan, S.A.; Ali, B.; Eze, C.; Lau, K.T.; Ali, L.; Chen, J.; Zhao, J. Magnetic dipole and thermal radiation impacts on stagnation point flow of micropolar based nanofluids over a vertically stretching sheet: Finite element approach. Processes 2021, 9, 1089. [Google Scholar] [CrossRef]
- Ali, L.; Wang, Y.; Ali, B.; Liu, X.; Din, A.; Al Mdallal, Q. The function of nanoparticle’s diameter and Darcy–Forchheimer flow over a cylinder with effect of magnetic field and thermal radiation. Case Stud. Therm. Eng. 2021, 28, 101392. [Google Scholar] [CrossRef]
- Sadiq, K.; Jarad, F.; Siddique, I.; Ali, B. Soret and radiation effects on mixture of ethylene glycol-water (50%–50%) based Maxwell nanofluid flow in an upright channel. Complexity 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Yahya, A.U.; Salamat, N.; Habib, D.; Ali, B.; Hussain, S.; Abdal, S. Implication of Bio-convection and Cattaneo-Christov heat flux on Williamson Sutterby nanofluid transportation caused by a stretching surface with convective boundary. Chin. J. Phys. 2021, 73, 706–718. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Hussain, S.; Ali, B.; Abdal, S. Significance of Stephen blowing and Lorentz force on dynamics of Prandtl nanofluid via Keller box approach. Int. Commun. Heat Mass Transf. 2021, 128, 105599. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Hussain, S.; Ali, L.; Baleanu, D. Boger nanofluid: Significance of Coriolis and Lorentz forces on dynamics of rotating fluid subject to suction/injection via finite element simulation. Sci. Rep. 2022, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sarpkaya, T. Flow of non-Newtonian fluids in a magnetic field. AIChE J. 1961, 7, 324–328. [Google Scholar] [CrossRef]
- Nagaraja, B.; Gireesha, B. Exponential space-dependent heat generation impact on MHD convective flow of Casson fluid over a curved stretching sheet with chemical reaction. J. Therm. Anal. Calorim. 2021, 143, 4071–4079. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Bahar, A.; Salah, F. Slip role for unsteady MHD mixed convection of nanofluid over stretching sheet with thermal radiation and electric field. Indian J. Phys. 2020, 94, 195–207. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple slip effects on MHD unsteady viscoelastic nano-fluid flow over a permeable stretching sheet with radiation using the finite element method. SN Appl. Sci. 2020, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Shateyi, S.; Muzara, H. On the Numerical Analysis of Unsteady MHD Boundary Layer Flow of Williamson Fluid over a Stretching Sheet and Heat and Mass Transfers. Computation 2020, 8, 55. [Google Scholar] [CrossRef]
- Yasmin, A.; Ali, K.; Ashraf, M. Study of heat and mass transfer in MHD flow of micropolar fluid over a curved stretching sheet. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Jabeen, K.; Mushtaq, M.; Akram Muntazir, R. Analysis of MHD fluids around a linearly stretching sheet in porous media with thermophoresis, radiation, and chemical reaction. Math. Probl. Eng. 2020, 2020, 9685482. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negera, M. MHD slip flow of upper-convected Maxwell nanofluid over a stretching sheet with chemical reaction. J. Egypt. Math. Soc. 2020, 28, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Nayak, M.K.; Shaw, S.; Khan, M.I.; Makinde, O.; Chu, Y.M.; Khan, S.U. Interfacial layer and shape effects of modified Hamilton’s Crosser model in entropy optimized Darcy–Forchheimer flow. Alex. Eng. J. 2021, 60, 4067–4083. [Google Scholar] [CrossRef]
- Nayak, M.K.; Agbaje, T.M.; Mondal, S.; Sibanda, P.; Makanda, G. Entropy minimized MHD microrotations of Cross nanomaterials with cubic autocatalytic chemical reaction. Heat Transf. 2022, 51, 490–533. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kannan, T.; DasaradhaRamaiah, K.; Sakthivel, G. Boundary layer flow of nanofluids to analyse the heat absorption/generation over a stretching sheet with variable suction/injection in the presence of viscous dissipation. Int. J. Ambient. Energy 2020, 41, 969–980. [Google Scholar] [CrossRef]
- Razzaghi, M.; Baharifard, F.; Parand, K. Numerical Simulation of Flow over Non-Linearly Stretching Sheet Considering Chemical Reaction and Magnetic Field. Mathematics 2020, 8, 1496. [Google Scholar] [CrossRef]
- Rehman, S.; Rehman, S.U.; Khan, A.; Khan, Z. The effect of flow distribution on heat and mass transfer of MHD thin liquid film flow over an unsteady stretching sheet in the presence of variational physical properties with mixed convection. Phys. A Stat. Mech. Its Appl. 2020, 551, 124120. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Heat and Mass Transfer of a Non-Newtonian Jeffrey Nanofluid over An Extrusion Stretching Sheet with Thermal Radiation and Nonuniform Heat Source/sink. Comput. Therm. Sci. Int. J. 2020, 12, 163–178. [Google Scholar] [CrossRef]
- Kairi, R.R.; Shaw, S.; Roy, S.; Raut, S. Thermosolutal marangoni impact on bioconvection in suspension of gyrotactic microorganisms over an inclined stretching sheet. J. Heat Transf. 2021, 143, 031201. [Google Scholar] [CrossRef]
- Mkhatshwa, M.P.; Motsa, S.; Sibanda, P. MHD bioconvective radiative flow of chemically reactive Casson nanofluid from a vertical surface with variable transport properties. Int. J. Ambient. Energy 2020. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Lee, C. Peristaltic flow of a Prandtl fluid model in an asymmetric channel. Int. J. Phys. Sci. 2012, 7, 687–695. [Google Scholar]
- Bilal, M.; Nazeer, M. Numerical analysis for the non-Newtonian flow over stratified stretching/shrinking inclined sheet with the aligned magnetic field and nonlinear convection. Arch. Appl. Mech. 2021, 91, 949–964. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Ur Rehman, S.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T. MHD Williamson Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.; Hussain, A.; Malik, M.; Mukhtar, S. On magnetohydrodynamics Prandtl fluid flow in the presence of stratification and heat generation. Phys. A Stat. Mech. Appl. 2020, 540, 123008. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar]
- Waini, I.; Zainal, N.A.; Khashi’ie, N.S. Aligned magnetic field effects on flow and heat transfer of the upper-convected Maxwell fluid over a stretching/shrinking sheet. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 97, p. 01078. [Google Scholar]
- Bhattacharyya, K. Effects of heat source/sink on MHD flow and heat transfer over a shrinking sheet with mass suction. Chem. Eng. Res. Bull. 2011, 15, 12–17. [Google Scholar] [CrossRef]



| Abel [47] | Iskandar [48] | Bilal [43] | Our Results | |
|---|---|---|---|---|
| 0.0 | −0.999962 | −1.00000005 | −1.0000000 | −1.0000002 |
| 0.2 | −1.051948 | −1.05188989 | −1.0518899 | −1.0518896 |
| 0.4 | −1.101850 | −1.10190327 | −1.1019044 | −1.1019027 |
| 0.6 | −1.150163 | −1.15013734 | −1.1501382 | −1.1501488 |
| 0.8 | −1.196692 | −1.19671125 | −1.1967134 | −1.1967110 |
| 1.2 | −1.285257 | −1.28536326 | −1.2863640 | −1.2863740 |
| S | Bhattacharyya [49] | Iskandar [48] | Bilal [43] | (Our Results) |
|---|---|---|---|---|
| 2.0 | 2.414300 | 2.41421357 | 2.41421369 | 2.41423 |
| 3.0 | 3.302750 | 3.30277563 | 3.30277621 | 3.30278 |
| 4.0 | 4.236099 | 4.23606797 | 4.23606814 | 4.23607 |
| M | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.3 | 2.0 | 1.0 | 1.0 | 0.1 | 0.3 | 0.2 | 0.5154 |
| 2.0 | 0.6645 | |||||||
| 3.0 | 0.8036 | |||||||
| 0.3 | 0.5154 | |||||||
| 0.4 | 0.5234 | |||||||
| 0.5 | 0.5314 | |||||||
| 2.0 | 0.5154 | |||||||
| 3.0 | 0.5954 | |||||||
| 4.0 | 0.6641 | |||||||
| 1.0 | 0.5154 | |||||||
| 2.0 | 0.5159 | |||||||
| 3.0 | 0.5163 | |||||||
| 1.0 | 0.5154 | |||||||
| 2.0 | 0.5214 | |||||||
| 3.0 | 0.5274 | |||||||
| 0.1 | 0.5154 | |||||||
| 0.2 | 0.5037 | |||||||
| 0.3 | 0.4843 | |||||||
| 0.3 | 0.5154 | |||||||
| 0.4 | 0.5537 | |||||||
| 0.5 | 0.5922 | |||||||
| 0.2 | 0.5154 | |||||||
| 0.3 | 0.5188 | |||||||
| 0.4 | 0.5223 |
| 0.8 | 0.1 | 0.1 | 0.3 | 0.5944 |
| 0.9 | 0.6647 | |||
| 1.0 | 0.7350 | |||
| 0.1 | 0.5944 | |||
| 0.2 | 0.5949 | |||
| 0.3 | 0.5904 | |||
| 0.1 | 0.5944 | |||
| 0.2 | 0.5754 | |||
| 0.3 | 0.5559 | |||
| 0.3 | 0.5944 | |||
| 0.4 | 0.5116 | |||
| 0.5 | 0.4292 |
| 0.1 | 0.3 | 0.1 | 0.2838 |
| 0.2 | 0.3047 | ||
| 0.3 | 0.3258 | ||
| 0.3 | 0.2838 | ||
| 0.4 | 0.3246 | ||
| 0.5 | 0.3593 | ||
| 0.1 | 0.2838 | ||
| 0.2 | 0.2853 | ||
| 0.3 | 0.2868 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Mustafa, Z.; Siddique, I.; Ajmal, M.; Jaradat, M.M.M.; Rehman, S.U.; Ali, B.; Ali, H.M. Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet. Nanomaterials 2022, 12, 1791. https://doi.org/10.3390/nano12111791
Wang J, Mustafa Z, Siddique I, Ajmal M, Jaradat MMM, Rehman SU, Ali B, Ali HM. Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet. Nanomaterials. 2022; 12(11):1791. https://doi.org/10.3390/nano12111791
Chicago/Turabian StyleWang, Jianfeng, Zead Mustafa, Imran Siddique, Muhammad Ajmal, Mohammed M. M. Jaradat, Saif Ur Rehman, Bagh Ali, and Hafiz Muhammad Ali. 2022. "Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet" Nanomaterials 12, no. 11: 1791. https://doi.org/10.3390/nano12111791
APA StyleWang, J., Mustafa, Z., Siddique, I., Ajmal, M., Jaradat, M. M. M., Rehman, S. U., Ali, B., & Ali, H. M. (2022). Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy–Forchheimer Flow across an Inclined Sheet. Nanomaterials, 12(11), 1791. https://doi.org/10.3390/nano12111791









