Nature of the Poynting Vector Field Singularities in Resonant Light Scattering by Nanoparticles
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
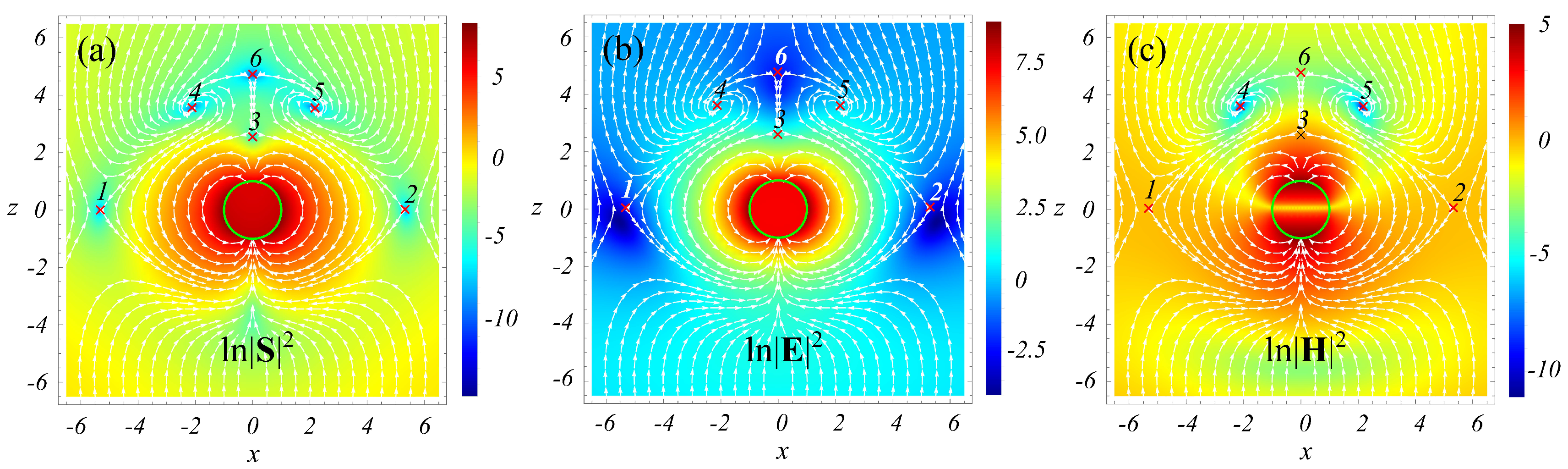
3.1. Sphere
- (i)
- does vanish at all singular points;
- (ii)
- vanishes at the foci owing to vector vanishing;
- (iii)
- in contrast, at the saddle-type singular points neither nor turn to zero.
3.2. Cylinder
4. Conclusions
- The geometric and Poincaré criteria for singularities give rise to the same condition: at singular points.
- In 3D problems optical vortices are field-induced singularities, while saddles are polarization-induced.
- In the vicinity of any 3D generic singularity, regardless of its specific type, the universal condition (11) must hold.
- If a field-induced singularity lies in an invariant plane, which is parallel to the plane of oscillations of vector E, the singularity is H-field-induced. If the invariant plane is parallel to the plane of vector H oscillations, the singularity is E-field-induced.
- In 2D problems, the condition div reduces the types of possible non-degenerate singularities only to saddles and centers.
- In 3D problems, optical vortices in non-dissipative media have a focus-saddle structure. Importantly, for a stable focus, the saddle is unstable and vice versa. Moreover, the modulus of the contraction (expansion) index in the direction transversal to the plane of the focus is twice as much as that for the in-plane streamlines.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| MDPI | Multidisciplinary Digital Publishing Institute |
| r.h.s. | right-hand side |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
References
- Al Zoubi, W.; Allaf, A.W.; Assfour, B.; Ko, Y.G. Concurrent Oxidation-Reduction Reactions in a Single System Using a Low-Plasma Phenomenon: Excellent Catalytic Performance and Stability in the Hydrogenation Reaction. ACS Appl. Mater. Interfaces 2022, 14, 6740–6753. [Google Scholar] [CrossRef] [PubMed]
- Al Zoubi, W.; Nashrah, N.; Kurnia Putri, R.A.; Allaf, A.W.; Assfour, B.; Ko, Y.G. Strong dual-metal-support interactions induced by low-temperature plasma phenomenon. Mater. Today Nano 2022, 100213. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Z.; Yang, H.; Wen, L.; Yi, Z.; Zhou, Z.; Dai, B.; Zhang, J.; Wu, X.; Wu, P. Multi-mode surface plasmon resonance absorber based on dart-type single-layer graphene. RSC Adv. 2022, 12, 7821–7829. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Luo, Y.; Yang, H.; Yi, Z.; Zhang, J.; Song, Q.; Yang, W.; Liu, C.; Wu, X.; Wu, P. Thermal tuning of terahertz metamaterial absorber properties based on VO2. Phys. Chem. Chem. Phys. 2022, 24, 8846–8853. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Yang, X.; Wang, Y.; Zhang, J.; Li, J. Graphitic encapsulation and electronic shielding of metal nanoparticles to achieve metal–carbon interfacial superlubricity. ACS Appl. Mater. Interfaces 2021, 13, 3397–3407. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Youji, L.; Feitai, C.; Peng, X.; Ming, L. Facile synthesis of mesoporous titanium dioxide doped by Ag-coated graphene with enhanced visible-light photocatalytic performance for methylene blue degradation. RSC Adv. 2017, 7, 25314–25324. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Cai, R.; Long, F.; Wang, J. Development and application of tetrabromobisphenol A imprinted electrochemical sensor based on graphene/carbon nanotubes three-dimensional nanocomposites modified carbon electrode. Talanta 2015, 134, 435–442. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Luk’yanchuk, B.; Hong, M.; Lin, Y.; Chong, T. Energy flow around a small particle investigated by classical Mie theory. Phys. Rev. B 2004, 70, 035418. [Google Scholar] [CrossRef]
- Bashevoy, M.; Fedotov, V.; Zheludev, N. Optical whirlpool on an absorbing metallic nanoparticle. Opt. Express 2005, 13, 8372–8379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luk’yanchuk, B.; Tribel’skiĭ, M.; Ternovskiĭ, V. Light scattering at nanoparticles close to plasmon resonance frequencies. J. Opt. Technol. 2006, 73, 371–377. [Google Scholar] [CrossRef]
- Tribelsky, M.I.; Luk’yanchuk, B.S. Anomalous light scattering by small particles. Phys. Rev. Lett. 2006, 97, 263902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novitsky, A.V.; Barkovsky, L.M. Poynting singularities in optical dynamic systems. Phys. Rev. A 2009, 79, 033821. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Hanson, S.G.; Mokhun, I.I.; Vasnetsov, M.V.; Wang, W. Editorial: Singular and Correlation Optics. Front. Phys. 2021, 9, 651964. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.N.; Dhama, R.; Jiang, C.; Minin, O.V.; Minin, I.V.; Wang, Z. Full three-dimensional Poynting vector flow analysis of great field-intensity enhancement in specifically sized spherical-particles. Sci. Rep. 2019, 9, 20224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, D.; Novitsky, A.; Zhang, T.; Cheong, F.C.; Gao, L.; Lim, C.T.; Luk’yanchuk, B.; Qiu, C.W. Unveiling the correlation between non-diffracting tractor beam and its singularity in Poynting vector. Laser Photonics Rev. 2014, 9, 75–82. [Google Scholar] [CrossRef]
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Chapter 5 Singular Optics: Optical Vortices and Polarization Singularities. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2009; Volume 53, pp. 293–363. [Google Scholar] [CrossRef]
- Mokhun, I.; Khrobatin, R.; Mokhun, A.; Viktorovskaya, J. The behavior of the Poynting vector in the area of elementary polarization singularities. Opt. Appl. 2007, 37, 261–277. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; WILEY-VCH Verlag: Weinheim, Germany, 1998. [Google Scholar]
- Landau, L.D.; Bell, J.; Kearsley, M.; Pitaevskii, L.; Lifshitz, E.; Sykes, J. Electrodynamics of Continuous Media; Elsevier: Amsterdam, The Netherlands, 2013; Volume 8. [Google Scholar]
- Polyanskiy, M. Refractive Index Database. Available online: http://refractiveindex.info/ (accessed on 5 May 2022).
- Bohren, C.F. How can a particle absorb more than the light incident on it? Am. J. Phys. 1983, 51, 323–327. [Google Scholar] [CrossRef]
- Tribelsky, M.I.; Miroshnichenko, A.E. Resonant scattering of electromagnetic waves by small metal particles: A new insight into the old problem. Physics-Uspekhi 2022, 65, 40–61. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tribelsky, M.I.; Rubinstein, B.Y. Nature of the Poynting Vector Field Singularities in Resonant Light Scattering by Nanoparticles. Nanomaterials 2022, 12, 1878. https://doi.org/10.3390/nano12111878
Tribelsky MI, Rubinstein BY. Nature of the Poynting Vector Field Singularities in Resonant Light Scattering by Nanoparticles. Nanomaterials. 2022; 12(11):1878. https://doi.org/10.3390/nano12111878
Chicago/Turabian StyleTribelsky, Michael I., and Boris Y. Rubinstein. 2022. "Nature of the Poynting Vector Field Singularities in Resonant Light Scattering by Nanoparticles" Nanomaterials 12, no. 11: 1878. https://doi.org/10.3390/nano12111878
APA StyleTribelsky, M. I., & Rubinstein, B. Y. (2022). Nature of the Poynting Vector Field Singularities in Resonant Light Scattering by Nanoparticles. Nanomaterials, 12(11), 1878. https://doi.org/10.3390/nano12111878






