Tailoring Polarization Conversion in Achiral All-Dielectric Metasurfaces by Using Quasi-Bound States in the Continuum
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation of the Stokes Parameters
2.2. Nanodisk Array Implementation
3. Results and Discussion
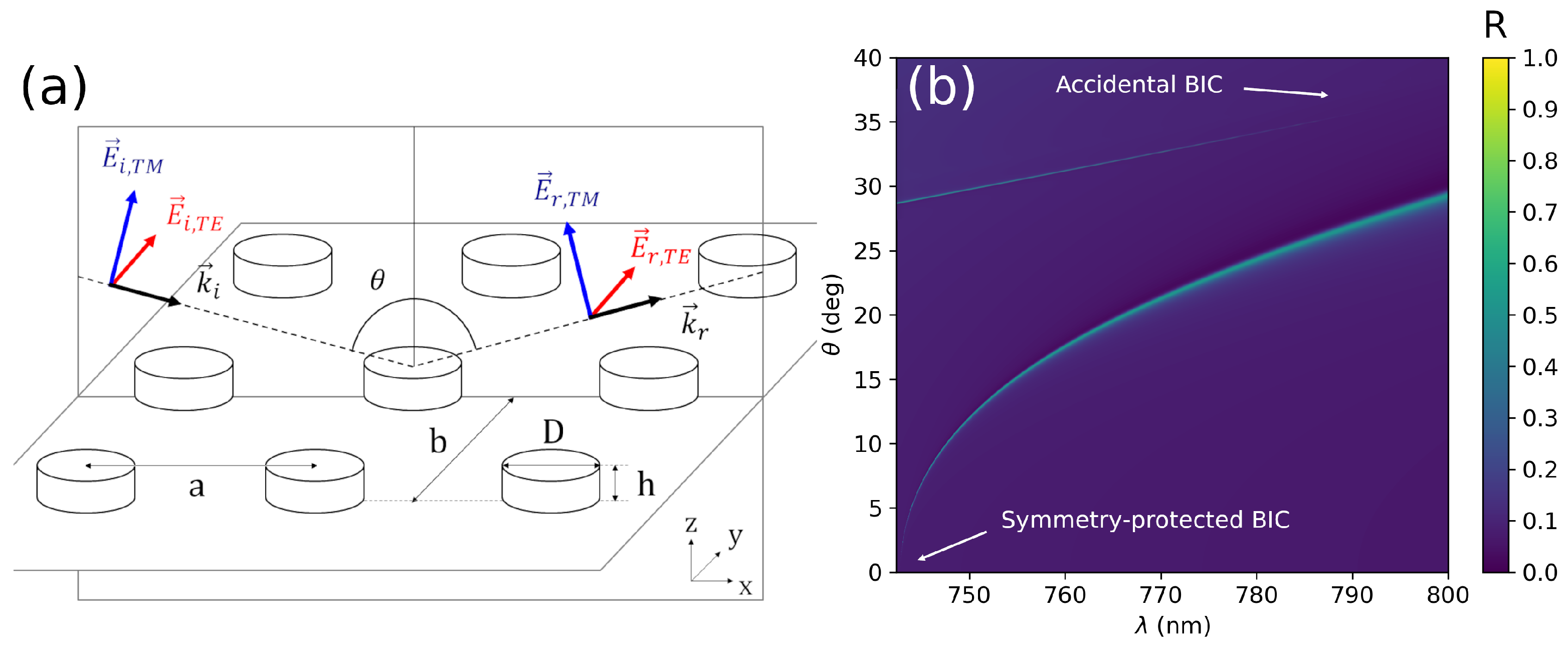
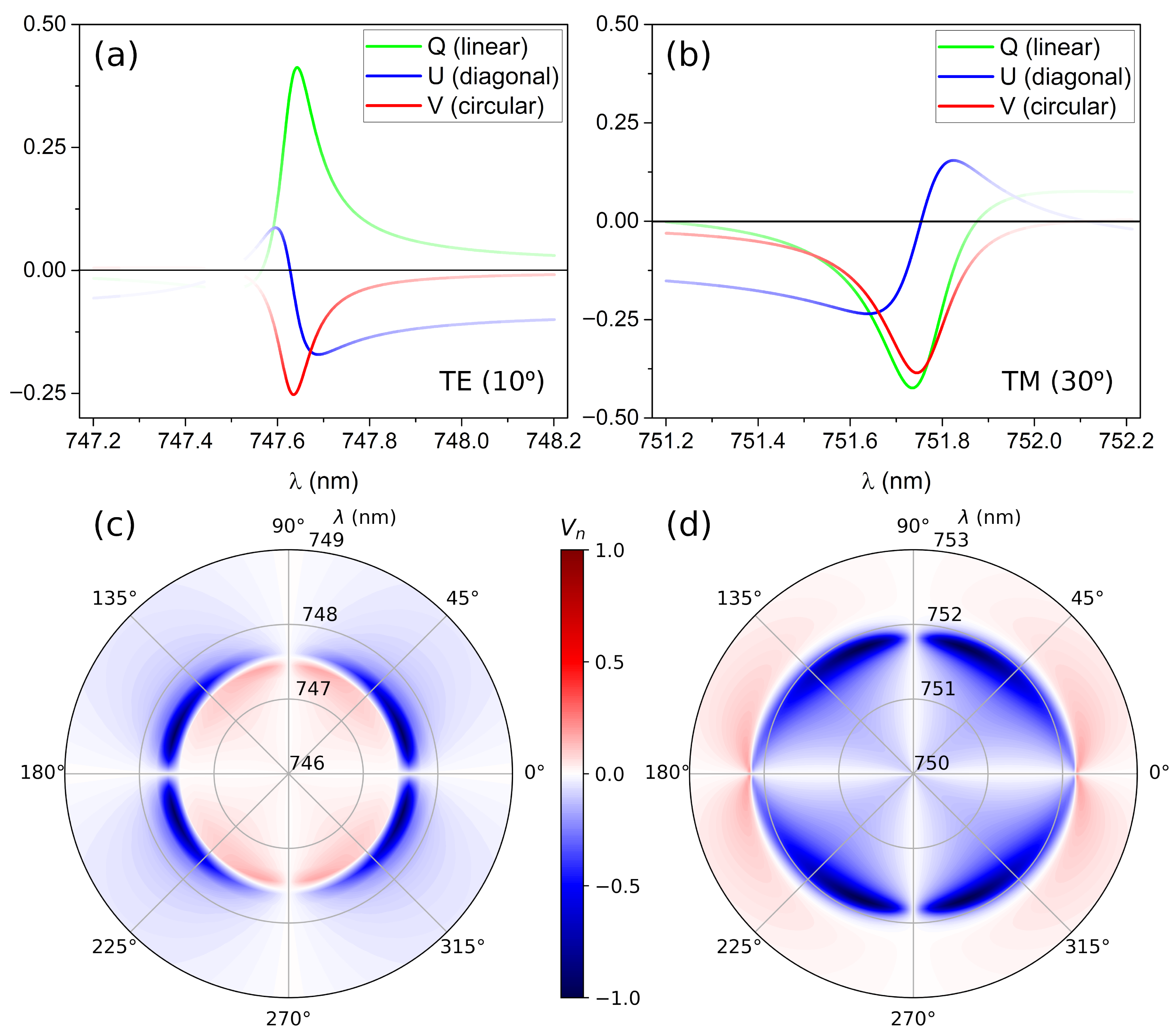
3.1. Single BICs
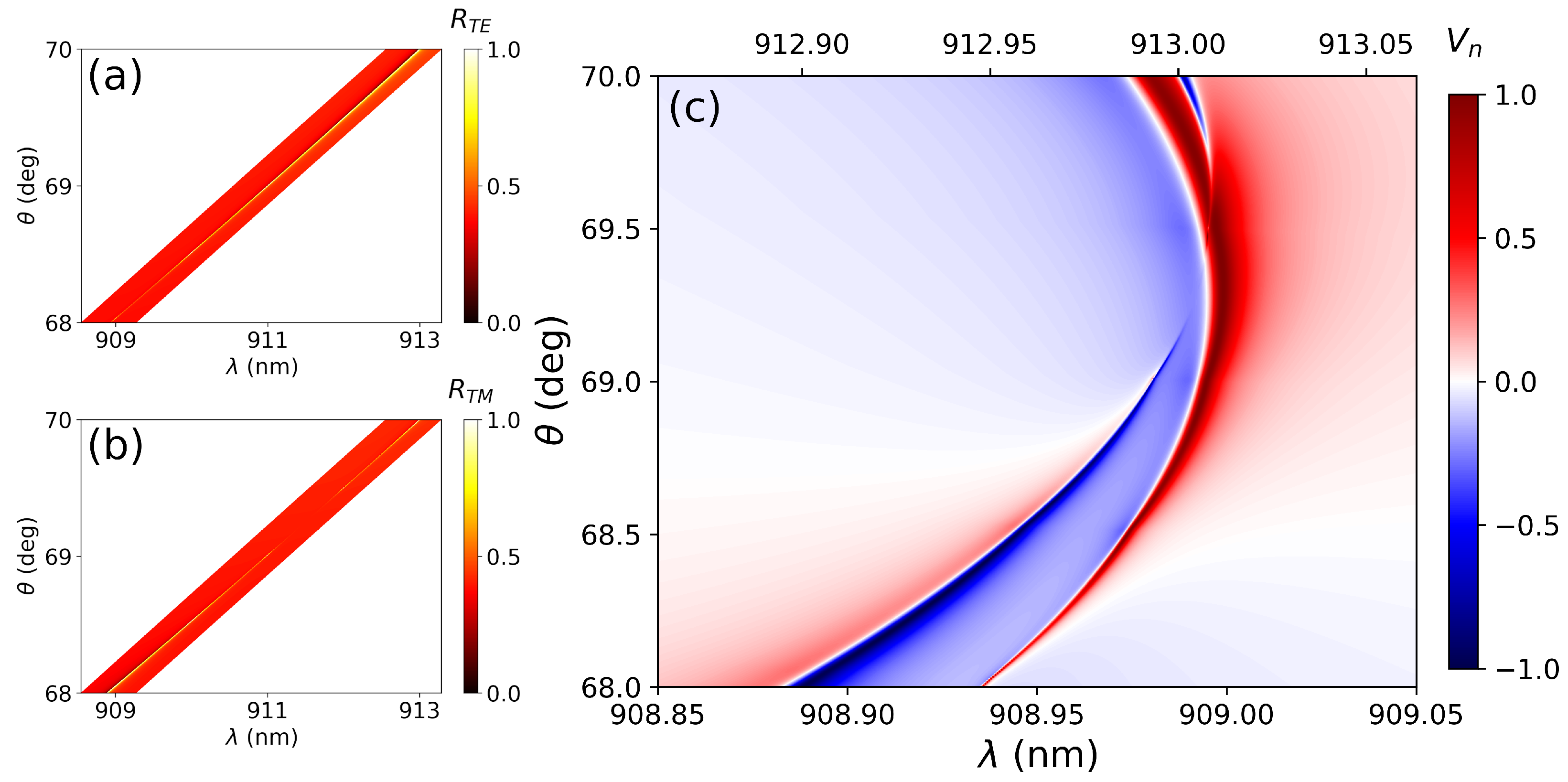
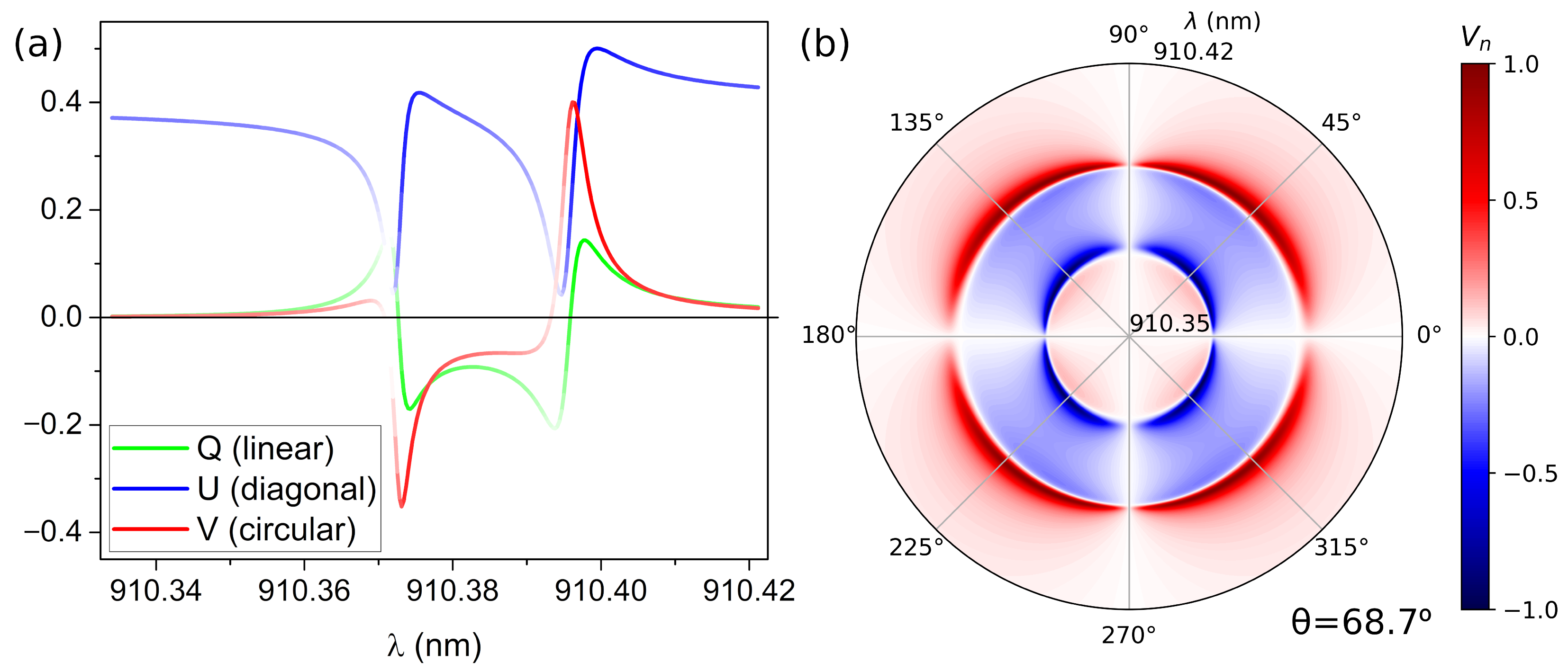
3.2. Double Accidental BIC
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MTS | Metasurfaces |
| BIC | Bound state in the continuum |
| aBIC | Accidental BIC |
| CEMD | Coupled electric & magnetic dipole |
| TE | Transversal electric |
| TM | Transversal magnetic |
| RCP | Right-handed polarization |
| LCP | Left-handed polarization |
References
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 76401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheben, P.; Halir, R.; Schmid, J.H.; Atwater, H.A.; Smith, D.R. Subwavelength integrated photonics. Nature 2018, 560, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef]
- Zhu, A.Y.; Chen, W.T.; Zaidi, A.; Huang, Y.W.; Khorasaninejad, M.; Sanjeev, V.; Qiu, C.W.; Capasso, F. Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 2018, 7, 17158. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Pu, M.; Li, X.; Gao, P.; Ma, X.; Luo, J.; Yu, H.; Luo, X. All-Dielectric Metasurfaces for Simultaneous Giant Circular Asymmetric Transmission and Wavefront Shaping Based on Asymmetric Photonic Spin–Orbit Interactions. Adv. Funct. Mater. 2017, 27, 1704295. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Y.; Li, Y.; Gong, Y.; Maier, S.A.; Hong, M. All-dielectric planar chiral metasurface with gradient geometric phase. Opt. Express 2018, 26, 6067–6078. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Liu, M.; Kruk, S.; Xu, Y.; Srivastava, Y.K.; Singh, R.; Han, J.; Kivshar, Y.; Shadrivov, I.V. Polarization-Sensitive Dielectric Membrane Metasurfaces. Adv. Opt. Mater. 2020, 8, 2000555. [Google Scholar] [CrossRef]
- Kim, J.; Choudhury, S.; DeVault, C.; Zhao, Y.; Kildishev, A.V.; Shalaev, V.M.; Alù, A.; Boltasseva, A. Controlling the Polarization State of Light with Plasmonic Metal Oxide Metasurface. ACS Nano 2016, 10, 9326–9333. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, M.; Liao, T.; Cui, X. Design of beam deflector, splitters, wave plates and metalens using photonic elements with dielectric metasurface. Opt. Commun. 2018, 411, 93–100. [Google Scholar] [CrossRef]
- Wei, S.; Yang, Z.; Zhao, M. Design of ultracompact polarimeters based on dielectric metasurfaces. Opt. Lett. 2017, 42, 1580–1583. [Google Scholar] [CrossRef]
- Guo, K.; Xu, H.; Peng, Z.; Liu, X.; Guo, Z. High-Efficiency Full-Vector Polarization Analyzer Based on GaN Metasurface. IEEE Sens. J. 2019, 19, 3654–3659. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Crozier, K.B. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat. Commun. 2014, 5, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, J.; Qian, H.; Chen, C.F.; Zhao, J.; Li, G.; Wu, Q.; Luo, H.; Wen, S.; Liu, Z. Optical edge detection based on high-efficiency dielectric metasurface. Proc. Natl. Acad. Sci. USA 2019, 166, 11137–11140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, Y.; Li, Y.; Liu, J.; Zhang, X.; Cai, Y.; Chen, Y.; Chen, S.; Fan, D. Switchable phase and polarization singular beams generation using dielectric metasurfaces. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Yoon, G.; Lee, D.; Nam, K.T.; Rho, J. “Crypto-Display” in Dual-Mode Metasurfaces by Simultaneous Control of Phase and Spectral Responses. ACS Nano 2018, 12, 6421–6428. [Google Scholar] [CrossRef]
- Gao, S.; Park, C.S.; Lee, S.S.; Choi, D.Y. A Highly Efficient Bifunctional Dielectric Metasurface Enabling Polarization-Tuned Focusing and Deflection for Visible Light. Adv. Opt. Mater. 2019, 7, 1801337. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, X.; Luo, X.; Ou, X.; Li, L.; Chen, Y.; Yang, P.; Wang, S.; Duan, H. All-dielectric metasurfaces for polarization manipulation: Principles and emerging applications. Nanophotonics 2020, 9, 3755–3780. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound States in the Continuum in Photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Maksimov, D.N. Topological Bound States in the Continuum in Arrays of Dielectric Spheres. Phys. Rev. Lett. 2017, 118, 267401. [Google Scholar] [CrossRef]
- Ha, S.T.; Fu, Y.H.; Emani, N.K.; Pan, Z.; Bakker, R.M.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Directional lasing in resonant semiconductor nanoantenna arrays. Nat. Nanotechnol. 2018, 13, 1042–1047. [Google Scholar] [CrossRef]
- Doeleman, H.M.; Monticone, F.; den Hollander, W.; Alù, A.; Koenderink, A.F. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photonics 2018, 12, 397–401. [Google Scholar] [CrossRef]
- Abujetas, D.R.; van Hoof, N.; ter Huurne, S.; Gómez Rivas, J.; Sánchez-Gil, J.A. Spectral and temporal evidence of robust photonic bound states in the continuum on terahertz metasurfaces. Optica 2019, 6, 996. [Google Scholar] [CrossRef] [Green Version]
- Koshelev, K.L.; Bogdanov, A.; Kivshar, Y.S. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Pitchappa, P.; Wang, W.; Srivastava, Y.K.; Rybin, M.V.; Singh, R. Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2002001. [Google Scholar] [CrossRef]
- Kang, M.; Zhang, S.; Xiao, M.; Xu, H. Merging Bound States in the Continuum at Off-High Symmetry Points. Phys. Rev. Lett. 2021, 126, 117402. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Olmos-Trigo, J.; Sánchez-Gil, J.A. Tailoring Accidental Double Bound States in the Continuum in All-Dielectric Metasurfaces. Adv. Opt. Mater. 2022, 2200301. [Google Scholar] [CrossRef]
- Taghizadeh, A.; Chung, I.S. Quasi bound states in the continuum with few unit cells of photonic crystal slab. Appl. Phys. Lett. 2017, 111, 031114. [Google Scholar] [CrossRef] [Green Version]
- Koshelev, K.L.; Lepeshov, S.; Liu, M.; Bogdanov, A.A.; Kivshar, Y.S. Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Zhou, C.; Liu, T.; Xiao, S. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-Protected Dual Bound States in the Continuum in Metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Barreda, Á.; Moreno, F.; Sáenz, J.J.; Litman, A.; Geffrin, J.M.; Sánchez-Gil, J.A. Brewster quasi bound states in the continuum in all-dielectric metasurfaces from single magnetic-dipole resonance meta-atoms. Sci. Rep. 2019, 9, 16048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorkunov, M.V.; Antonov, A.A.; Kivshar, Y.S. Metasurfaces with Maximum Chirality Empowered by Bound States in the Continuum. Phys. Rev. Lett. 2020, 125, 093903. [Google Scholar] [CrossRef]
- Overvig, A.; Yu, N.; Alù, A. Chiral Quasi-Bound States in the Continuum. Phys. Rev. Lett. 2021, 126, 073001. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, W.; Zhao, M.; Wang, J.; Zhang, Y.; Chen, A.; Guan, F.; Liu, X.; Shi, L.; Zi, J. Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum. Nat. Photonics 2020, 14, 623–628. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, Y.; Ma, X.; Fang, W.; Zhang, W.; Gao, W. Polarization conversion in anisotropic dielectric metasurfaces originating from bound states in the continuum. Opt. Lett. 2021, 46, 4120. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Sánchez-Gil, J.A.; Sáenz, J.J. Generalized Brewster effect in high-refractive-index nanorod-based metasurfaces. Opt. Express 2018, 26, 31523. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Olmos-Trigo, J.; Sáenz, J.J.; Sánchez-Gil, J.A. Coupled electric and magnetic dipole formulation for planar arrays of particles: Resonances and bound states in the continuum for all-dielectric metasurfaces. Phys. Rev. B Condens. Matter Mater. Phys. 2020, 102, 125411. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Sánchez-Gil, J.A. Near-Field Excitation of Bound States in the Continuum in All-Dielectric Metasurfaces through a Coupled Electric/Magnetic Dipole Model. Nanomaterials 2021, 11, 998. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 45404. [Google Scholar] [CrossRef] [Green Version]
- Sersic, I.; van de Haar, M.A.; Arango, F.B.; Koenderink, A.F. Ubiquity of Optical Activity in Planar Metamaterial Scatterers. Phys. Rev. Lett. 2012, 108, 223903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swiecicki, S.D.; Sipe, J.E. Surface-lattice resonances in two-dimensional arrays of spheres: Multipolar interactions and a mode analysis. Phys. Rev. B Condens. Matter Mater. Phys. 2017, 95, 195406. [Google Scholar] [CrossRef] [Green Version]
- Babicheva, V.E.; Evlyukhin, A.B. Resonant Lattice Kerker Effect in Metasurfaces With Electric and Magnetic Optical Responses. Laser Photon. Rev. 2017, 11, 1700132. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, Y.; Femius Koenderink, A. General point dipole theory for periodic metasurfaces: Magnetoelectric scattering lattices coupled to planar photonic structures. Opt. Express 2017, 25, 21358. [Google Scholar] [CrossRef] [Green Version]
- Baur, S.; Sanders, S.; Manjavacas, A. Hybridization of Lattice Resonances. ACS Nano 2018, 12, 1618–1629. [Google Scholar] [CrossRef]
- Murai, S.; Abujetas, D.R.; Castellanos, G.W.; Sánchez-Gil, J.A.; Zhang, F.; Rivas, J.G. Bound States in the Continuum in the Visible Emerging from out-of-Plane Magnetic Dipoles. ACS Photonics 2020, 7, 2204–2210. [Google Scholar] [CrossRef]
- Reid, M.T.H.; Johnson, S.G. Efficient Computation of Power, Force, and Torque in BEM Scattering Calculations. IEEE Trans. Antennas Propag. 2015, 63, 3588–3598. [Google Scholar] [CrossRef] [Green Version]
- Babicheva, V.E.; Evlyukhin, A.B. Metasurfaces with Electric Quadrupole and Magnetic Dipole Resonant Coupling. ACS Photonics 2018, 5, 2022–2033. [Google Scholar] [CrossRef] [Green Version]
- Babicheva, V.E.; Evlyukhin, A.B. Analytical model of resonant electromagnetic dipole-quadrupole coupling in nanoparticle arrays. Phys. Rev. B 2019, 99, 195444. [Google Scholar] [CrossRef] [Green Version]
| R | /nm | /nm | Q-Factor | |||
|---|---|---|---|---|---|---|
| TE (10°) | 0.145 | 0.567 | 0.433 | 747.588 | 0.139 | 5375 |
| TM (30°) | 0.397 | 0.490 | 0.510 | 751.795 | 0.314 | 2391 |
| aBIC RCP | 0.410 | 5 × 10 | 0.999995 | 911.119 | 0.006 | 158,016 |
| aBIC LCP | 0.375 | 10 × 10 | 0.999990 | 909.339 | 0.008 | 113,667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pura, J.L.; Kabonire, R.; Abujetas, D.R.; Sánchez-Gil, J.A. Tailoring Polarization Conversion in Achiral All-Dielectric Metasurfaces by Using Quasi-Bound States in the Continuum. Nanomaterials 2022, 12, 2252. https://doi.org/10.3390/nano12132252
Pura JL, Kabonire R, Abujetas DR, Sánchez-Gil JA. Tailoring Polarization Conversion in Achiral All-Dielectric Metasurfaces by Using Quasi-Bound States in the Continuum. Nanomaterials. 2022; 12(13):2252. https://doi.org/10.3390/nano12132252
Chicago/Turabian StylePura, Jose Luis, Ruhinda Kabonire, Diego R. Abujetas, and José A. Sánchez-Gil. 2022. "Tailoring Polarization Conversion in Achiral All-Dielectric Metasurfaces by Using Quasi-Bound States in the Continuum" Nanomaterials 12, no. 13: 2252. https://doi.org/10.3390/nano12132252







