On Capacitance and Energy Storage of Supercapacitor with Dielectric Constant Discontinuity
Abstract
:1. Introduction
2. Model and Method
3. Results and Discussion
4. Summary
- (i)
- The low solution value greatly reduces both the value and the value under certain electrode potential, but at the same time, significantly increases the saturation voltage, beyond which the value does not further increase with the voltage applied, which significantly increases the saturation value because of the approximate proportional relation between the energy storage and square of the voltage in comparison to the proportional relation between the energy storage and the value.
- (ii)
- Because of the low solution value, influence of electrolyte bulk concentration on is rather small except when the electrode potential is around the ZCP; consequently, the energy storage curves are rather insensitive to the electrolyte bulk concentration.
- (iii)
- Higher counter-ion valency or smaller counter-ion size help in raising the and values. The enhancing effect of the counter-ion valency reduces greatly with dropping of the value; whereas the counter-ion size effect remains significant enough for low value.
- (iv)
- Both the and values increase monotonously with the electrode dielectric constant decreasing for all voltages considered; the increase rate with the dropping of the value rises faster with the voltages, and for voltage strength of 2 V the value increase rate up to 15% can be achieved by reducing the value from to 5. For small enough pore the value effect gets unobservable when the value differs from that corresponding to dielectric electrode.
- (v)
- Both the and the values are positively correlated with the pore size; but for the low value considered the pore size effect on the value gets more and more significant with the voltage applied.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rogers, W.B. A mean-field model of linker-mediated colloidal interactions. J. Chem. Phys. 2020, 153, 124901. [Google Scholar] [CrossRef] [PubMed]
- Carrique, F.; Ruiz-Reina, E.; Arroyo, F.J.; Delgado, A.V. Influence of ion size effects on the electrokinetics of aqueous salt-free colloids in alternating electric fields. Phys. Rev. E 2020, 102, 032614. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Li, W.; Wang, R. Conformation of a single polyelectrolyte in poor solvents. J. Chem. Phys. 2020, 153, 064901. [Google Scholar] [CrossRef] [PubMed]
- Nikam, R.; Xu, X.; Kanduč, M.; Dzubiella, J. Competitive sorption of monovalent and divalent ions by highly charged globular macromolecules. J. Chem. Phys. 2020, 153, 044904. [Google Scholar] [CrossRef]
- Semenyuk, P.I.; Efimova, A.A.; Lentin, I.I.; Le-Deygen, I.M.; Izumrudov, V.A. Interaction of Ionenes with Lipid Membrane: Unusual Impact of Charge Density. Langmuir 2020, 36, 14717–14727. [Google Scholar] [CrossRef]
- Shen, G.; Sun, Y.; Wang, Y.; Lu, X.; Ji, X. Interfacial structure and differential capacitance of ionic liquid/graphite interface: A perturbed-chain SAFT density functional theory study. J. Mol. Liq. 2020, 310, 113199. [Google Scholar] [CrossRef]
- Heo, M.; Shin, G.R.; Kim, S.-C. Capacitance of electrolytes with hydration-mediated interaction in planar electric double layers. Mol. Phys. 2019, 118, e1610196. [Google Scholar] [CrossRef]
- Chenn, I.; Sigal, I.M. On Derivation of the Poisson–Boltzmann Equation. J. Stat. Phys. 2020, 180, 954–1001. [Google Scholar] [CrossRef]
- Antonova, A.; Barbero, G.; Evangelista, L.R.; Tilli, P. Ambipolar diffusion in the low frequency impedance response of electrolytic cells. J. Stat. Mech. Theory Exp. 2020, 2020, 043202. [Google Scholar] [CrossRef]
- Razmkhah, M. Effects of carboxylic group on bulk and electrical double layer properties of amino acid ionic liquid. J. Mol. Liq. 2019, 299, 112158. [Google Scholar] [CrossRef]
- Elisea-Espinoza, J.J.; González-Tovar, E.; Martínez-González, J.A.; Peña, C.G.G.; Guerrero-García, G.I. On the non-dominance of counterions in the 1:z planar electrical double layer of point-ions. Mol. Phys. 2021, 119. [Google Scholar] [CrossRef]
- Arun, L.; Karthikeyan, C.; Philip, D.; Unni, C. Optical, magnetic, electrical, and chemo-catalytic properties of bio-synthesized CuO/NiO nanocomposites. J. Phys. Chem. Solids 2020, 136, 109155. [Google Scholar] [CrossRef]
- Zhao, R.; Remsing, R.C.; Weeks, J.D. Response Theory for Static and Dynamic Solvation of Ionic and Dipolar Solutes in Water. J. Stat. Phys. 2020, 180, 721–738. [Google Scholar] [CrossRef]
- Li, D.-D.; Yang, Y.-R.; Wang, X.-D.; Feng, G. Electrical Double Layer of Linear Tricationic Ionic Liquids at Graphite Electrode. J. Phys. Chem. C 2020, 124, 15723–15729. [Google Scholar] [CrossRef]
- Šamaj, L. Attraction of Like-Charged Walls with Counterions Only: Exact Results for the 2D Cylinder Geometry. J. Stat. Phys. 2020, 181, 1699–1729. [Google Scholar] [CrossRef]
- Gupta, A.; Rajan, A.G.; Carter, E.A.; Stone, H.A. Thermodynamics of Electrical Double Layers with Electrostatic Correlations. J. Phys. Chem. C 2020, 124, 26830–26842. [Google Scholar] [CrossRef]
- Šamaj, L. Short-Distance Symmetry of Pair Correlations in Two-Dimensional Jellium. J. Stat. Phys. 2019, 178, 247–264. [Google Scholar] [CrossRef] [Green Version]
- Khademi, M.; Barz, D.P.J. Structure of the Electrical Double Layer Revisited: Electrode Capacitance in Aqueous Solutions. Langmuir 2020, 36, 4250–4260. [Google Scholar] [CrossRef]
- Wickramaarachchi, K.; Minakshi, M.; Aravindh, S.A.; Dabare, R.; Gao, X.; Jiang, Z.-T.; Wong, K.W. Repurposing N-Doped Grape Marc for the Fabrication of Supercapacitors with Theoretical and Machine Learning Models. Nanomaterials 2022, 12, 1847. [Google Scholar] [CrossRef]
- Sharma, P.; Singh, D.; Minakshi, M.; Quadsia, S.; Ahuja, R. Activation-Induced Surface Modulation of Biowaste-Derived Hierarchical Porous Carbon for Supercapacitors. ChemPlusChem 2022, 87, e202200126. [Google Scholar] [CrossRef]
- Reščič, J.; Linse, P. Potential of mean force between charged colloids: Effect of dielectric discontinuities. J. Chem. Phys. 2008, 129, 114505. [Google Scholar] [CrossRef] [PubMed]
- Seijo, M.; Pohl, M.; Ulrich, S.; Stoll, S. Dielectric discontinuity effects on the adsorption of a linear polyelectrolyte at the surface of a neutral nanoparticle. J. Chem. Phys. 2009, 131, 174704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markovich, T.; Andelman, D.; Orland, H. Ionic profiles close to dielectric discontinuities: Specific ion-surface interactions. J. Chem. Phys. 2016, 145, 134704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, H.; Li, H.; Solis, F.J.; de la Cruz, M.O.; Luijten, E. Asymmetric electrolytes near structured dielectric interfaces. J. Chem. Phys. 2018, 149, 164701. [Google Scholar] [CrossRef] [Green Version]
- Abdelaal, M.; Hung, T.-C.; Mohamed, S.; Yang, C.-C.; Huang, H.-P.; Hung, T.-F. A Comparative Study of the Influence of Nitrogen Content and Structural Characteristics of NiS/Nitrogen-Doped Carbon Nanocomposites on Capacitive Performances in Alkaline Medium. Nanomaterials 2021, 11, 1867. [Google Scholar] [CrossRef]
- Wannasen, L.; Mongkolthanaruk, W.; Swatsitang, E.; Pavasant, P.; Pinitsoontorn, S. Co2P2O7 Microplate/Bacterial Cellulose-Derived Carbon Nanofiber Composites with Enhanced Electrochemical Performance. Nanomaterials 2021, 11, 2015. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, R.; Tian, C. Impacts of solvent electric dipole and ion valency on energy storage in ultrananoporous supercapacitor: An ising model study. J. Phys. Chem. Solids 2021, 157, 110188. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, R. Ising model study on effects of solvent electric dipole on ultrananoporous supercapacitor. Chin. J. Phys. 2021, 73, 391–405. [Google Scholar] [CrossRef]
- Tergolina, V.B.; dos Santos, A.P. Effect of dielectric discontinuity on a spherical polyelectrolyte brush. J. Chem. Phys. 2017, 147, 114103. [Google Scholar] [CrossRef] [Green Version]
- Guerrero García, G.I.; Olvera de la Cruz, M. Polarization Effects of Dielectric Nanoparticles in Aqueous Charge-Asymmetric Electrolytes. J. Phys. Chem. B 2014, 118, 8854–8862. [Google Scholar] [CrossRef]
- Korobko, A.V.; Marques, C.M.; Schöps, M.; Schädler, V.; Wiesner, U.; Mendes, E. Dielectric discontinuity in equilibrium block copolymer micelles. Soft Matter 2015, 11, 7081–7085. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, A.P.; Bakhshandeh, A.; Levin, Y. Effects of the dielectric discontinuity on the counterion distribution in a colloidal suspension. J. Chem. Phys. 2011, 135, 044124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P. Electrostatic attraction between ionic reverse micelles with dielectric discontinuity. J. Chem. Phys. 2002, 117, 9460–9464. [Google Scholar] [CrossRef]
- Wernersson, E.; Kjellander, R. Image Charges and Dispersion Forces in Electric Double Layers: The Dependence of Wall−Wall Interactions on Salt Concentration and Surface Charge Density. J. Phys. Chem. B 2007, 111, 14279–14284. [Google Scholar] [CrossRef] [PubMed]
- Jho, Y.S.; Park, G.; Chang, C.S.; Pincus, P.A.; Kim, M.W. Effects of dielectric discontinuities on two charged plates. Phys. Rev. E 2007, 76, 011920. [Google Scholar] [CrossRef]
- Wernersson, E.; Kjellander, R. Ion correlation forces between uncharged dielectric walls. J. Chem. Phys. 2008, 129, 144701. [Google Scholar] [CrossRef] [Green Version]
- Téllez, G.; Trizac, E. A Two-Dimensional One Component Plasma and a Test Charge: Polarization Effects and Effective Potential. J. Stat. Phys. 2012, 146, 832–849. [Google Scholar] [CrossRef]
- Curtis, R.; Lue, L. Depletion forces due to image charges near dielectric discontinuities. Curr. Opin. Colloid Interface Sci. 2015, 20, 19–23. [Google Scholar] [CrossRef] [Green Version]
- Varela, L.; Téllez, G.; Trizac, E. One-dimensional colloidal model with dielectric inhomogeneity. Phys. Rev. E 2021, 103, 042603. [Google Scholar] [CrossRef]
- Odinaev, S.; Akdodov, D.M.; Makhmadbegov, R.S. Makhmadbegov, study of the frequency dispersion of dielectric permittivity and dielectric loss coefficient for aqueous potassium iodide solutions. J. Struct. Chem. 2022, 63, 964–975. [Google Scholar] [CrossRef]
- Evans, R. Nature of the liquid-vapor interface and other topics in the statistical mechanics of nonuniform classical fluids. Adv. Phys. 1979, 28, 143. [Google Scholar] [CrossRef]
- Henderson, D. (Ed.) Fundamentals of Inhomogeneous Fluids; Marcel Dekker: New York, NY, USA, 1992. [Google Scholar]
- Vergara, E.L.C.; Kontogeorgis, G.M.; Liang, X. Gas Adsorption and Interfacial Tension with Classical Density Functional Theory. Ind. Eng. Chem. Res. 2019, 58, 5650–5664. [Google Scholar] [CrossRef]
- Marshall, B.D. A theoretical analysis on the separation of mixtures by extractive adsorption. Chem. Eng. Sci. 2021, 235, 116460. [Google Scholar] [CrossRef]
- Kolesnikov, A.L.; Budkov, Y.A.; Gor, G.Y. Adsorption-induced deformation of mesoporous materials with corrugated cylindrical pores. J. Chem. Phys. 2020, 153, 194703. [Google Scholar] [CrossRef]
- Eller, J.; Gross, J. Free-Energy-Averaged Potentials for Adsorption in Heterogeneous Slit Pores Using PC-SAFT Classical Density Functional Theory. Langmuir 2021, 37, 3538–3549. [Google Scholar] [CrossRef] [PubMed]
- Myhal, V.; Derzhko, O. Wetting in the presence of the electric field: The classical density functional theory study for a model system. Phys. A Stat. Mech. Its Appl. 2017, 474, 293–300. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S. Wetting Transition of Nonpolar Neutral Molecule System on a Neutral and Atomic Length Scale Roughness Substrate. J. Stat. Phys. 2018, 170, 979–998. [Google Scholar] [CrossRef]
- Kundu, P.; Mishra, P.; Jaiswal, A.; Ram, J. Structures and phase transition in a two-dimensional system of Gay-Berne molecules. J. Mol. Liq. 2019, 296, 111769. [Google Scholar] [CrossRef]
- Morfe, P.S. Surface Tension and Gamma-Convergence of Van der Waals-Cahn-Hilliard Phase Transitions in Stationary Ergodic Media. J. Stat. Phys. 2020, 181, 2225–2256. [Google Scholar] [CrossRef]
- Gußmann, F.; Dietrich, S.; Roth, R. Toward a density-functional theory for the Jagla fluid. Phys. Rev. E 2020, 102, 062112. [Google Scholar] [CrossRef]
- Kim, H.; Schimmele, L.; Dietrich, S. Wetting behavior of a colloidal particle trapped at a composite liquid-vapor interface of a binary liquid mixture. Phys. Rev. E 2021, 103, 042802. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A. Configuraional Entropy of a parabolic potential system: A density functional approach. Phys. Scr. 2020, 96, 025703. [Google Scholar] [CrossRef]
- Gurin, P.; Odriozola, G.; Varga, S. Enhanced two-dimensional nematic order in slit-like pores. New J. Phys. 2021, 23, 063053. [Google Scholar] [CrossRef]
- Forsman, J.; Nordholm, S. Polyelectrolyte Mediated Interactions in Colloidal Dispersions: Hierarchical Screening, Simulations, and a New Classical Density Functional Theory. Langmuir 2012, 28, 4069–4079. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S. Inter-surface effective electrostatic interactions in the presence of surface charge discreteness and solvent granularity. Mol. Phys. 2020, 118, e1778807. [Google Scholar] [CrossRef]
- Zhou, S. On the statistical mechanics investigation of structure and effective electrostatic force between two solid surfaces in electrolyte dissolved in non-polar solvent. J. Stat. Mech. Theory Exp. 2020, 2020, 073210. [Google Scholar] [CrossRef]
- Balzer, C.; Jiang, J.; Marson, R.L.; Ginzburg, V.V.; Wang, Z.-G. Nonelectrostatic Adsorption of Polyelectrolytes and Mediated Interactions between Solid Surfaces. Langmuir 2021, 37, 5483–5493. [Google Scholar] [CrossRef]
- Haertel, A. Structure of electric double layers in capacitive systems and to what extent (classical) density functional theory describes it. J. Phys. Condens. Mat. 2017, 29, 423002. [Google Scholar] [CrossRef]
- Faramarzi, E.; Maghari, A. The effect of dispersion interactions on the structure and performance of electrical double layer of ionic liquids. J. Mol. Liq. 2017, 246, 325–331. [Google Scholar] [CrossRef]
- Neal, J.N.; Wesolowski, D.J.; Henderson, D.; Wu, J. Electric double layer capacitance for ionic liquids in nanoporous electrodes: Effects of pore size and ion composition. J. Mol. Liq. 2018, 270, 145–150. [Google Scholar] [CrossRef]
- Yang, G.; Prasianakis, N.I.; Churakov, S.V. Comparative Modeling of Ions and Solvent Properties in Ca-Na Montmorillonite by Atomistic Simulations and Fluid Density Functional Theory. Clays Clay Miner. 2020, 68, 100–114. [Google Scholar] [CrossRef]
- Yang, J.; Ding, Y.; Lian, C.; Ying, S.; Liu, H. Theoretical Insights into the Structures and Capacitive Performances of Confined Ionic Liquids. Polymers 2020, 12, 722. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, J.; Ginzburg, V.V.; Wang, Z.-G. On the origin of oscillatory interactions between surfaces mediated by polyelectrolyte solution. J. Chem. Phys. 2019, 151, 214901. [Google Scholar] [CrossRef] [PubMed]
- Vrugt, M.T.; Löwen, H.; Wittkowski, R. Classical dynamical density functional theory: From fundamentals to applications. Adv. Phys. 2020, 69, 121–247. [Google Scholar] [CrossRef]
- Binder, K.; A Egorov, S.; Milchev, A.; Nikoubashman, A. Understanding the properties of liquid-crystalline polymers by computational modeling. J. Phys. Mater. 2020, 3, 032008. [Google Scholar] [CrossRef]
- Lutsko, J.F.; Lam, J. Classical density functional theory, unconstrained crystallization, and polymorphic behavior. Phys. Rev. E 2018, 98, 012604. [Google Scholar] [CrossRef] [Green Version]
- Somerville, W.R.C.; Stokes, J.L.; Adawi, A.M.; Horozov, T.S.; Archer, A.J.; A Buzza, D.M. Density functional theory for the crystallization of two-dimensional dipolar colloidal alloys. J. Phys. Condens. Matter 2018, 30, 405102. [Google Scholar] [CrossRef] [Green Version]
- Lutsko, J.F.; Schoonen, C. Classical density-functional theory applied to the solid state. Phys. Rev. E 2020, 102, 062136. [Google Scholar] [CrossRef]
- Ney, E.M.; Hou, C.-H.; Taboada-Serrano, P. Calculation of Electrical Double Layer Potential Profiles in Nanopores from Grand Canonical Monte Carlo Simulations. J. Chem. Eng. Data 2018, 63, 2557–2566. [Google Scholar] [CrossRef]
- Heo, M.; Shin, G.R.; Kim, S.-C. Differential capacitance of uniformly charged hard-sphere ions in planar electric double layers. J. Stat. Mech. Theory Exp. 2019, 2019, 083207. [Google Scholar] [CrossRef]
- Islam, S.; Lamperski, S.; Islam, M.; Henderson, D.; Bhuiyan, L.B. Temperature dependence of differential capacitance in the electric double layer.Symmetric valency 1:1 electrolytes. J. Chem. Phys. 2020, 152, 204702. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S. A statistical mechanics study on relationship between nanopore size and energy storage in supercapacitors. J. Phys. Chem. Solids 2020, 148, 109705. [Google Scholar] [CrossRef]
- Zhou, S. Solvent granularity in the differential electrical capacitance of supercapacitor and mechanism analysis. Phys. A Stat. Mech. Appl. 2019, 533, 121905. [Google Scholar] [CrossRef]
- Sato, T.; Sasaki, T.; Ohnuki, J.; Umezawa, K.; Takano, M. Hydrophobic Surface Enhances Electrostatic Interaction in Water. Phys. Rev. Lett. 2018, 121, 206002. [Google Scholar] [CrossRef] [PubMed]
- Alawneh, M.; Henderson, D.; Outhwaite, C.; Bhuiyan, L. The effect of dielectric polarization of the electrode on anomalous temperature effects in the electrical double layer. Mol. Simul. 2008, 34, 501–507. [Google Scholar] [CrossRef]
- Zhou, S.; Lamperski, S.; Zydorczak, M. Properties of a planar electric double layer under extreme conditions investigated by classical density functional theory and Monte Carlo simulations. J. Chem. Phys. 2014, 141, 64701. [Google Scholar] [CrossRef]
- Zhou, S.; Lamperski, S.; Sokołowska, M. Classical density functional theory and Monte Carlo simulation study of electric double layer in the vicinity of a cylindrical electrode. J. Stat. Mech. Theory Exp. 2017, 2017, 073207. [Google Scholar] [CrossRef]
- Lamperski, S.; Zhou, S. Structural and electrical properties of an electric double layer formed inside a cylindrical pore investigated by Monte Carlo and classical density functional theory. Microfluid. Nanofluid. 2019, 23, 20. [Google Scholar] [CrossRef]
- Zhou, S.; Lamperski, S. Unusual properties of the electric double layer in an extremely narrow nanotube. A grand canonical Monte Carlo and classical DFT study. J. Phys. Chem. Solids 2021, 161, 110440. [Google Scholar] [CrossRef]
- Zhou, S. Capacitance of electrical double layer formed inside a single infinitely long cylindrical pore. J. Stat. Mech. Theory Exp. 2018, 2018, 103203. [Google Scholar] [CrossRef]
- Yang, C.; Chen, J.; Qing, T.; Fan, X.; Sun, W.; von Cresce, A.; Ding, M.S.; Borodin, O.; Vatamanu, J.; Schroeder, M.; et al. 4.0 V Aqueous Li-Ion Batteries. Joule 2017, 1, 122–132. [Google Scholar] [CrossRef] [Green Version]
- Lee, A.A.; Vella, D.; Goriely, A.; Kondrat, S. Capacitance-Power-Hysteresis Trilemma in Nanoporous Supercapacitors. Phys. Rev. X 2016, 6, 021034. [Google Scholar] [CrossRef]
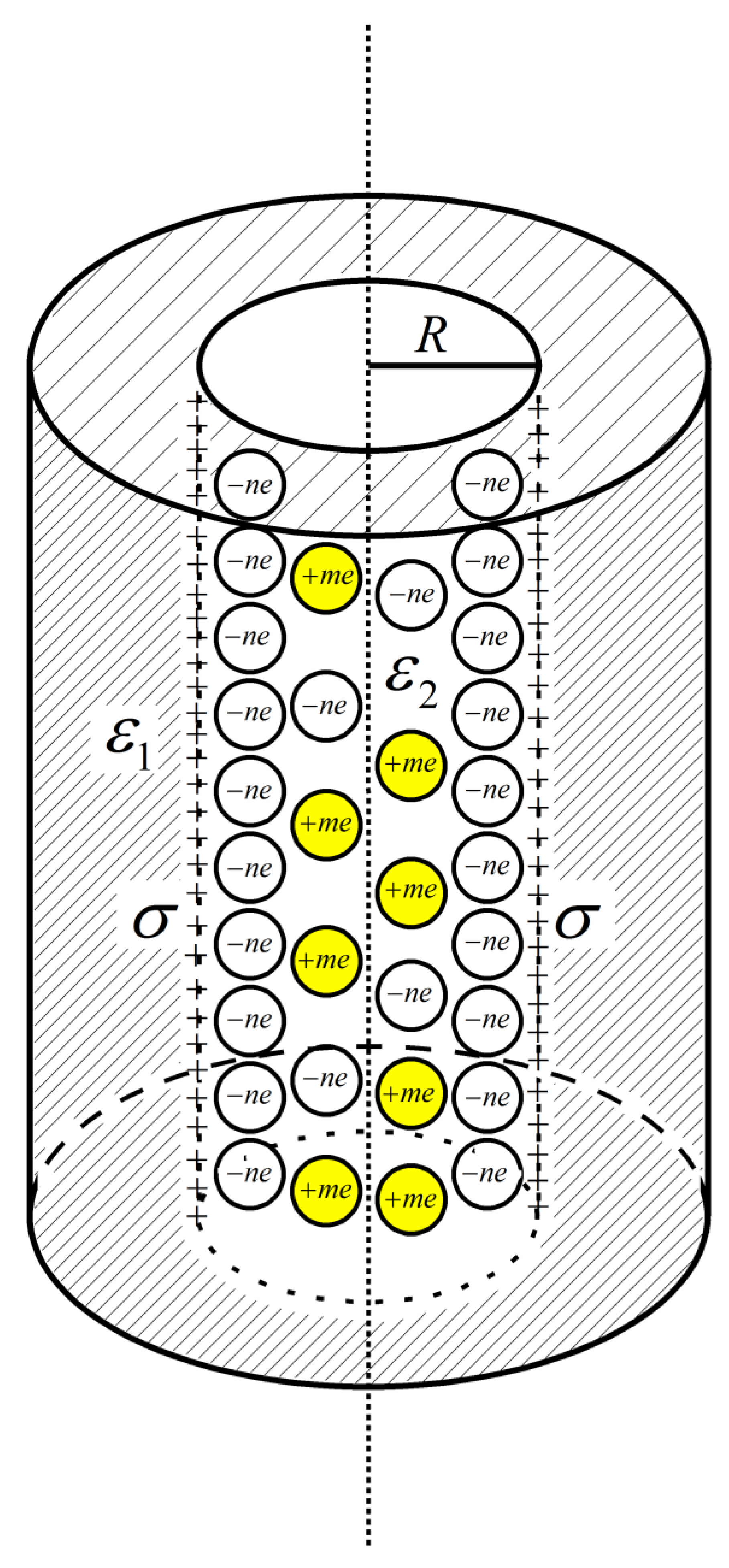
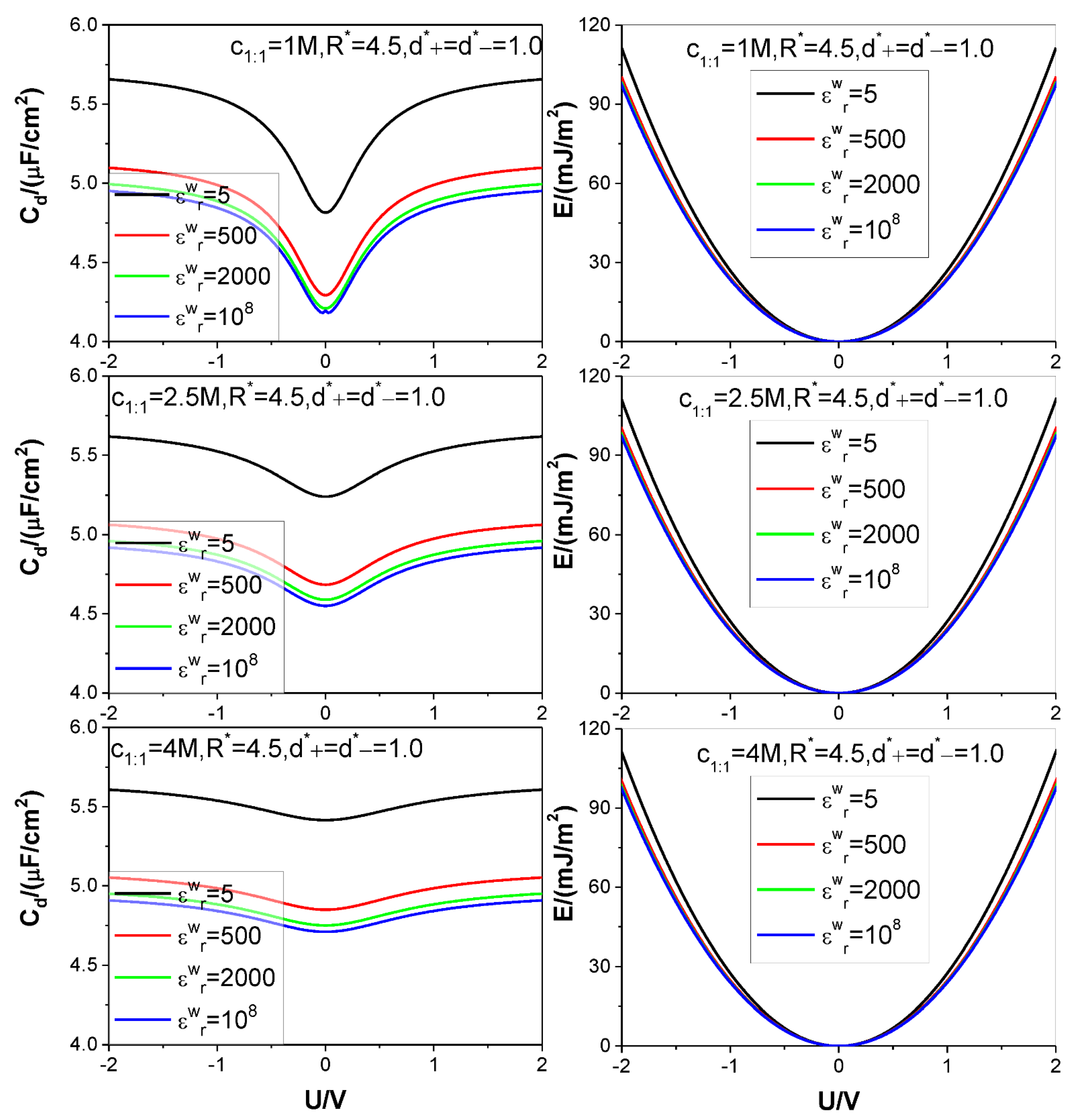
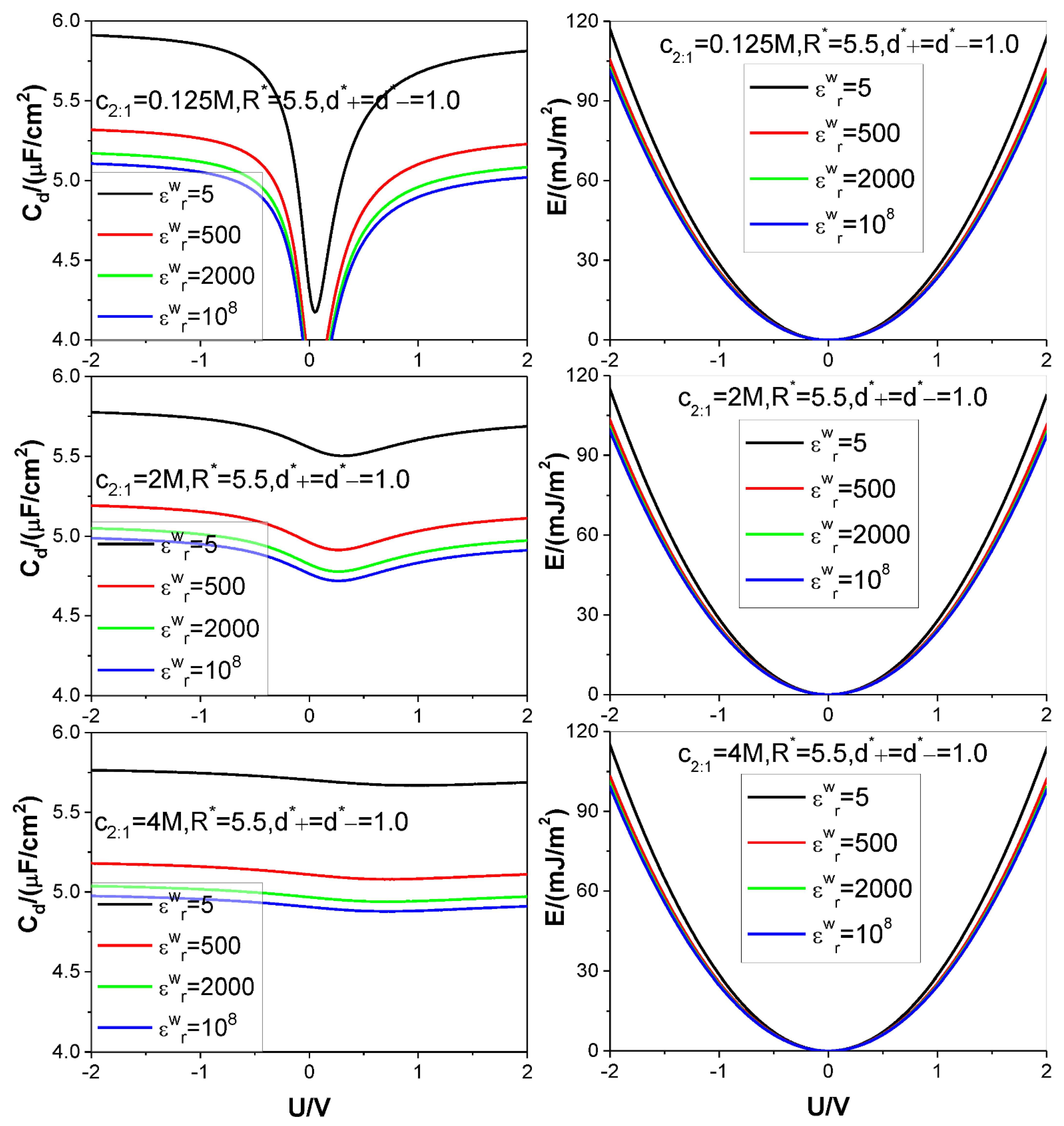
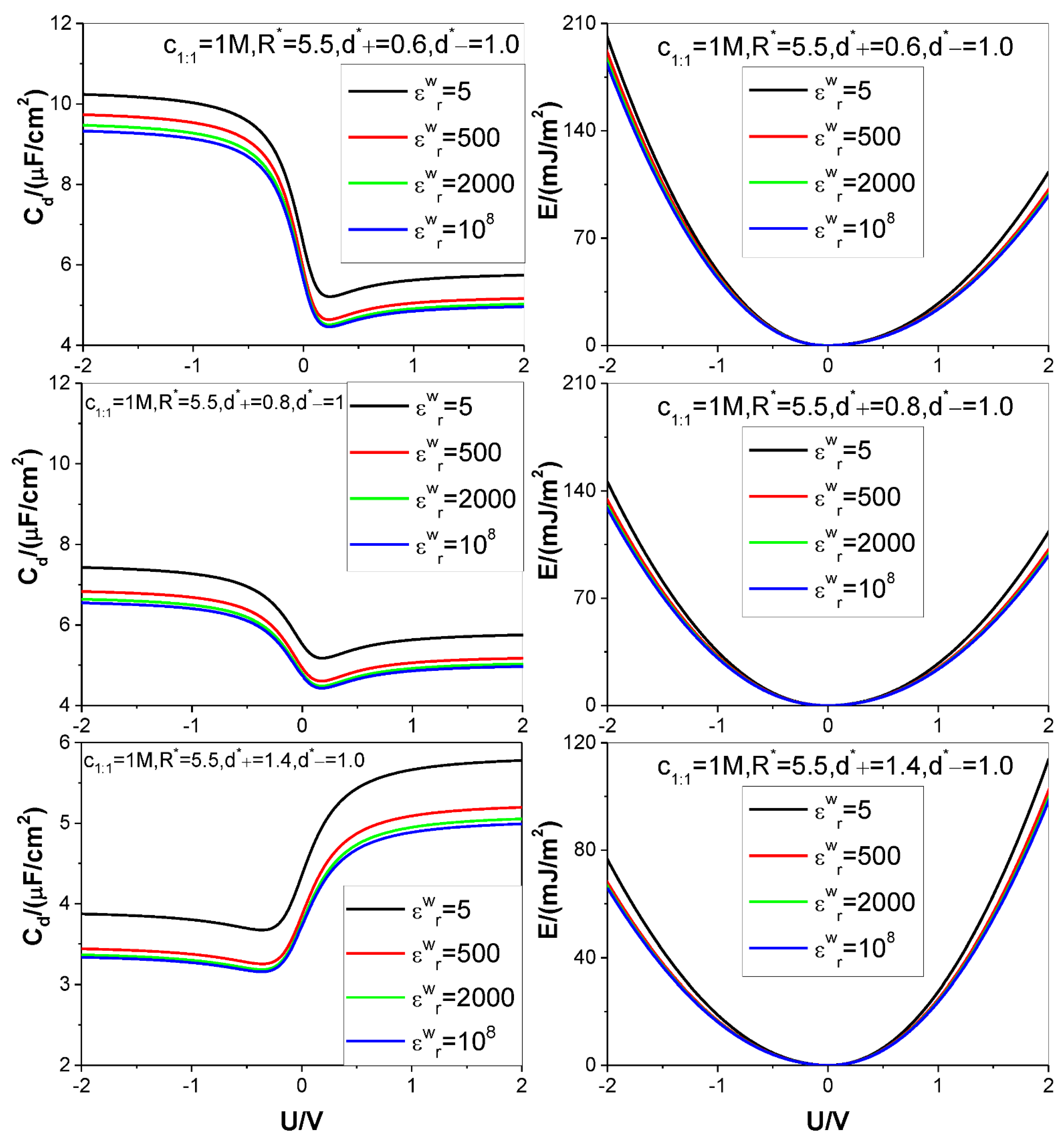
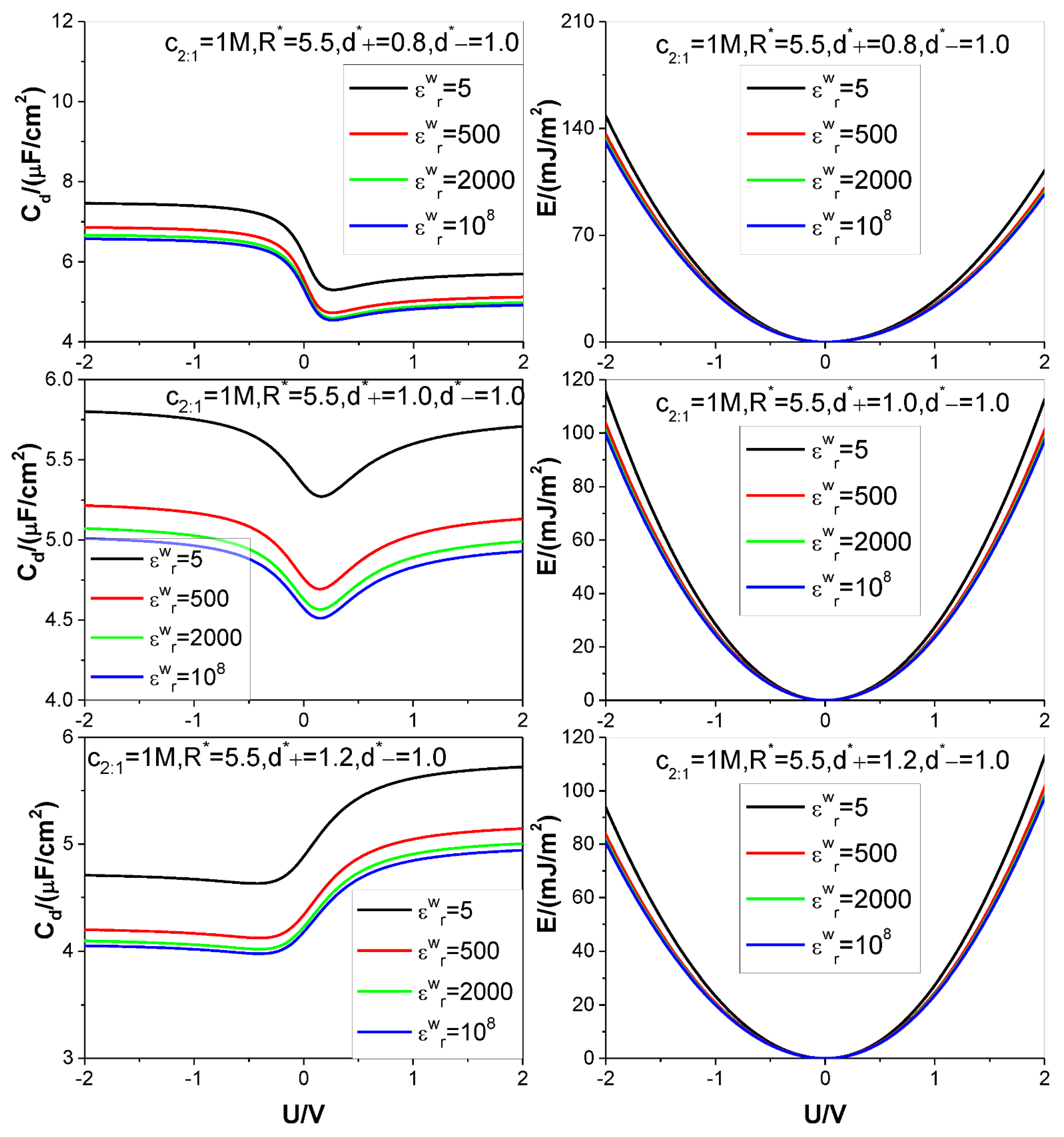
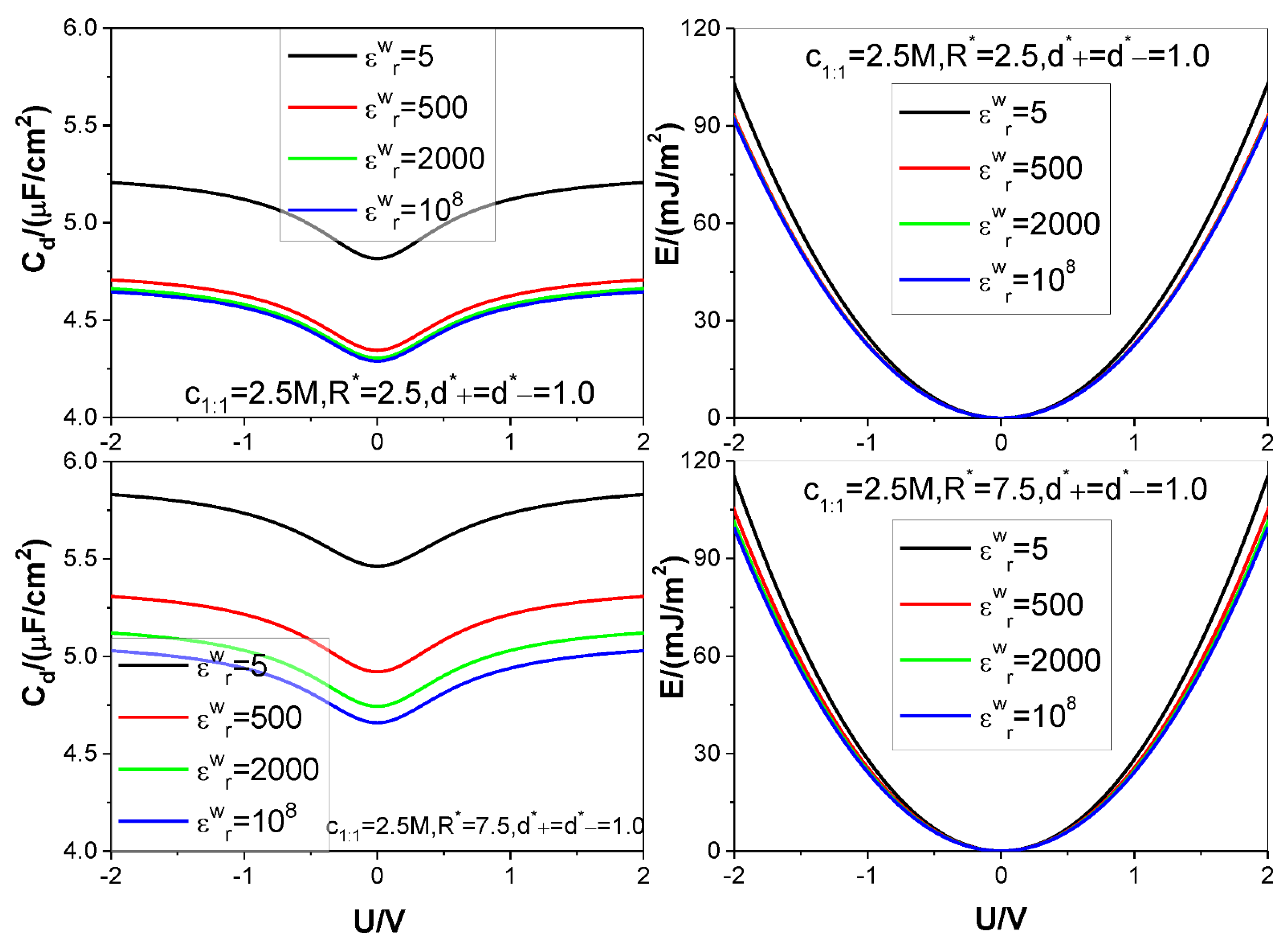
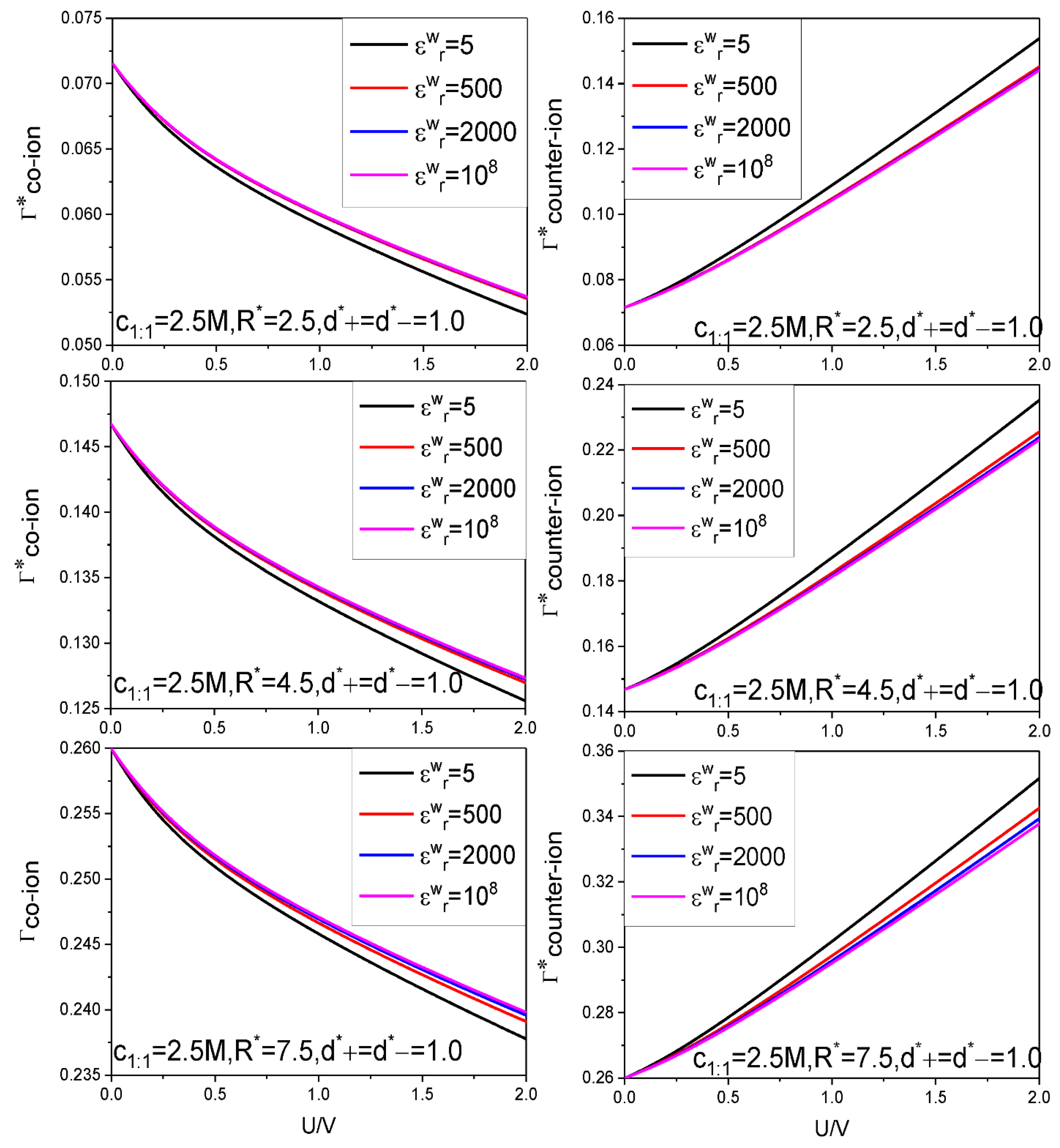
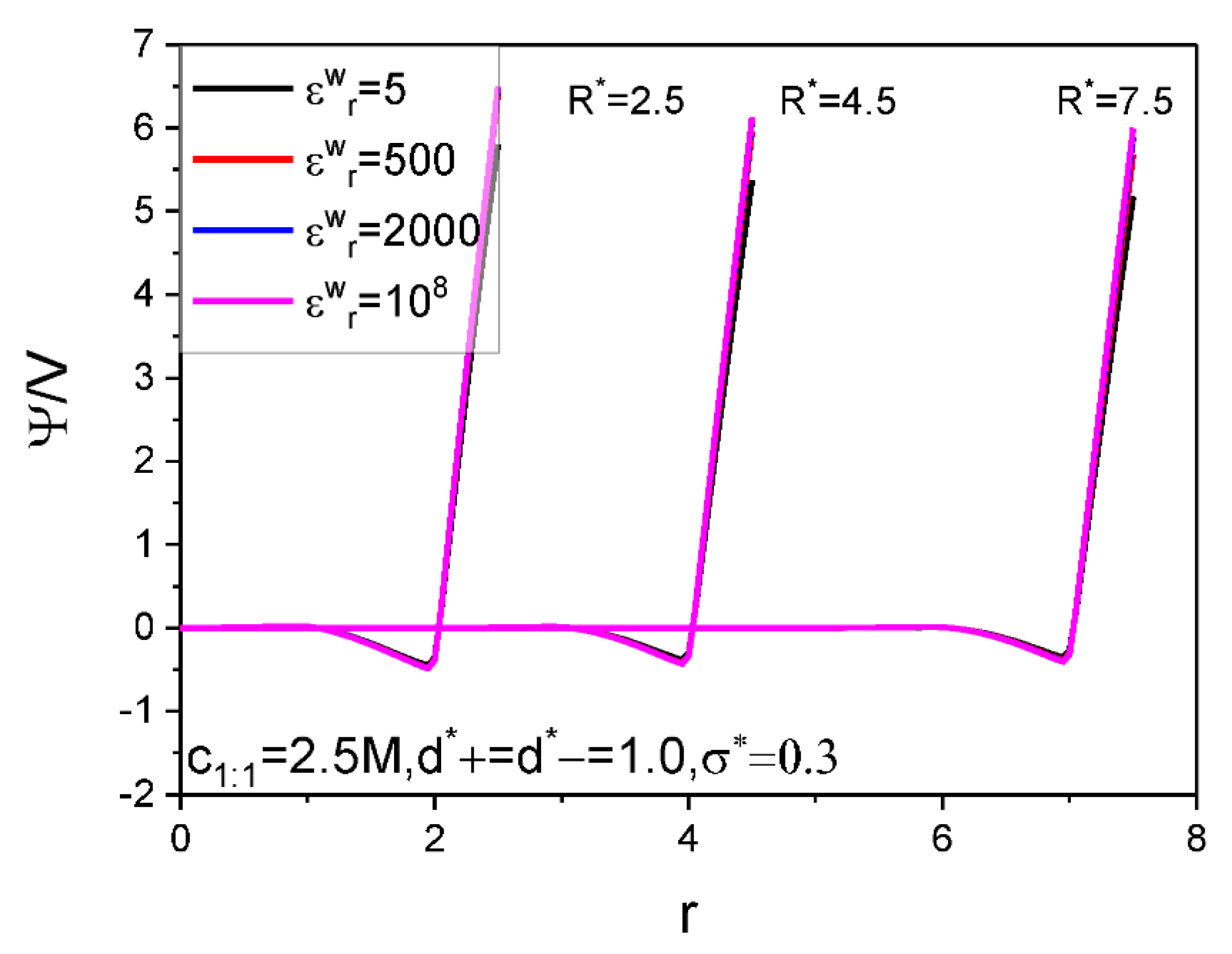
| Figure No | c/mol L−1 | m:n | ||||||
|---|---|---|---|---|---|---|---|---|
| Figure 2 | 1.0 | 5, 500, 2000, 108 | 4.5 | 1 | 1 | 1:1 | 298.15 | 10 |
| 2.5 | ||||||||
| 4.0 | ||||||||
| Figure 3 | 0.125 | 5, 500, 2000, 108 | 5.5 | 1 | 1 | 2:1 | 298.15 | 10 |
| 2.0 | ||||||||
| 4.0 | ||||||||
| Figure 4 | 1.0 | 5, 500, 2000, 108 | 5.5 | 0.6 | 1 | 1:1 | 298.15 | 10 |
| 0.8 | ||||||||
| 1.4 | ||||||||
| Figure 5 | 1.0 | 5, 500, 2000, 108 | 5.5 | 0.8 | 1 | 2:1 | 298.15 | 10 |
| 1.0 | ||||||||
| 1.2 | ||||||||
| Figure 6 | 2.5 | 5, 500, 2000, 108 | 2.5 7.5 | 1 | 1 | 1:1 | 298.15 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S. On Capacitance and Energy Storage of Supercapacitor with Dielectric Constant Discontinuity. Nanomaterials 2022, 12, 2534. https://doi.org/10.3390/nano12152534
Zhou S. On Capacitance and Energy Storage of Supercapacitor with Dielectric Constant Discontinuity. Nanomaterials. 2022; 12(15):2534. https://doi.org/10.3390/nano12152534
Chicago/Turabian StyleZhou, Shiqi. 2022. "On Capacitance and Energy Storage of Supercapacitor with Dielectric Constant Discontinuity" Nanomaterials 12, no. 15: 2534. https://doi.org/10.3390/nano12152534
APA StyleZhou, S. (2022). On Capacitance and Energy Storage of Supercapacitor with Dielectric Constant Discontinuity. Nanomaterials, 12(15), 2534. https://doi.org/10.3390/nano12152534





