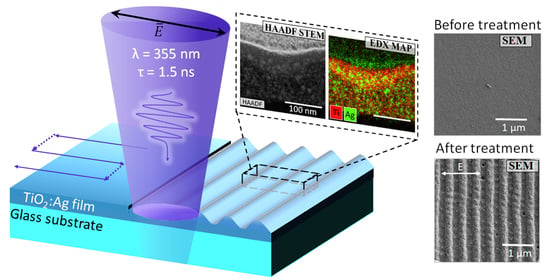
Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings
Abstract
:1. Introduction
2. Materials and Methods
3. Results
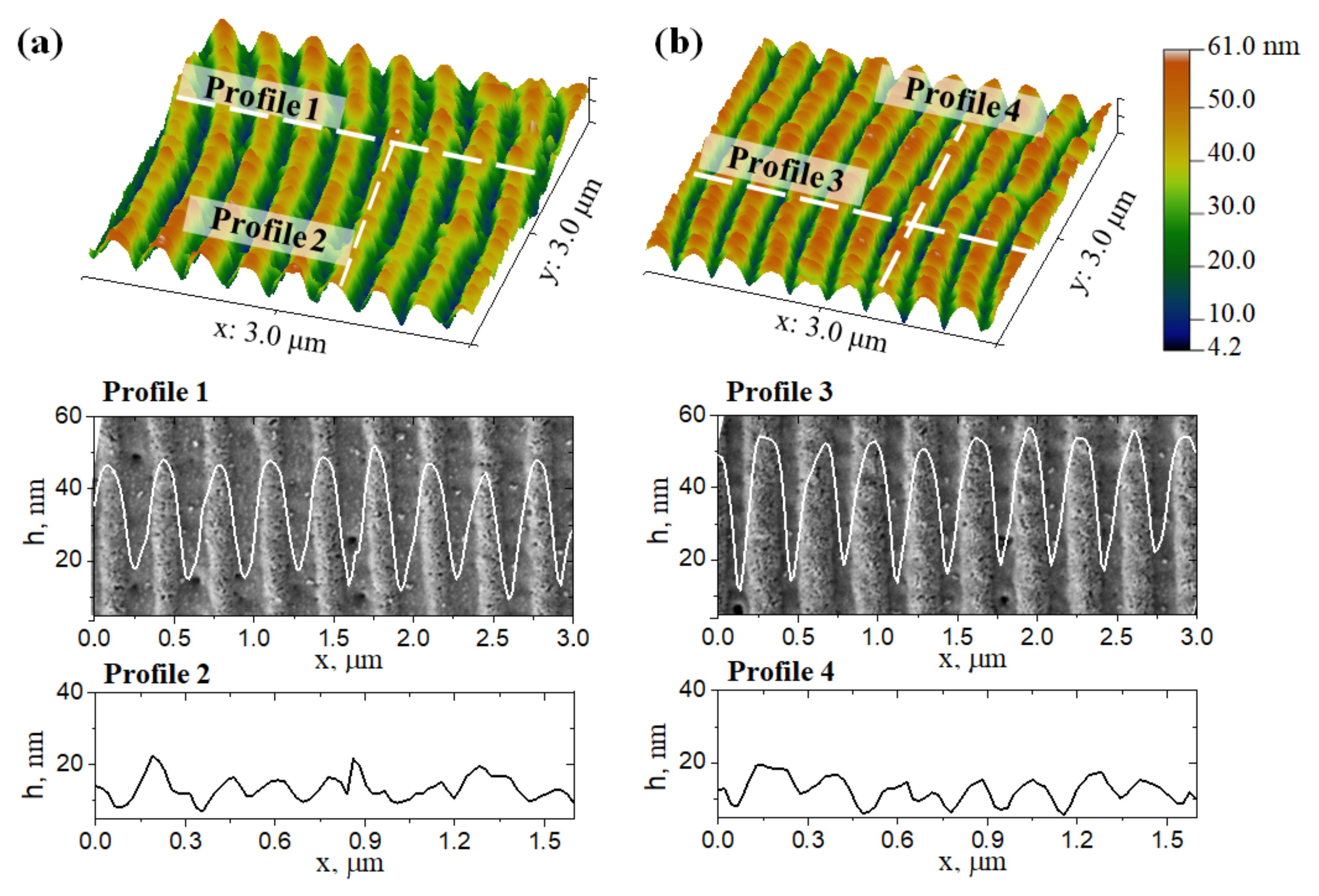
3.1. Laser Fabrication of Nanocomposite Gratings
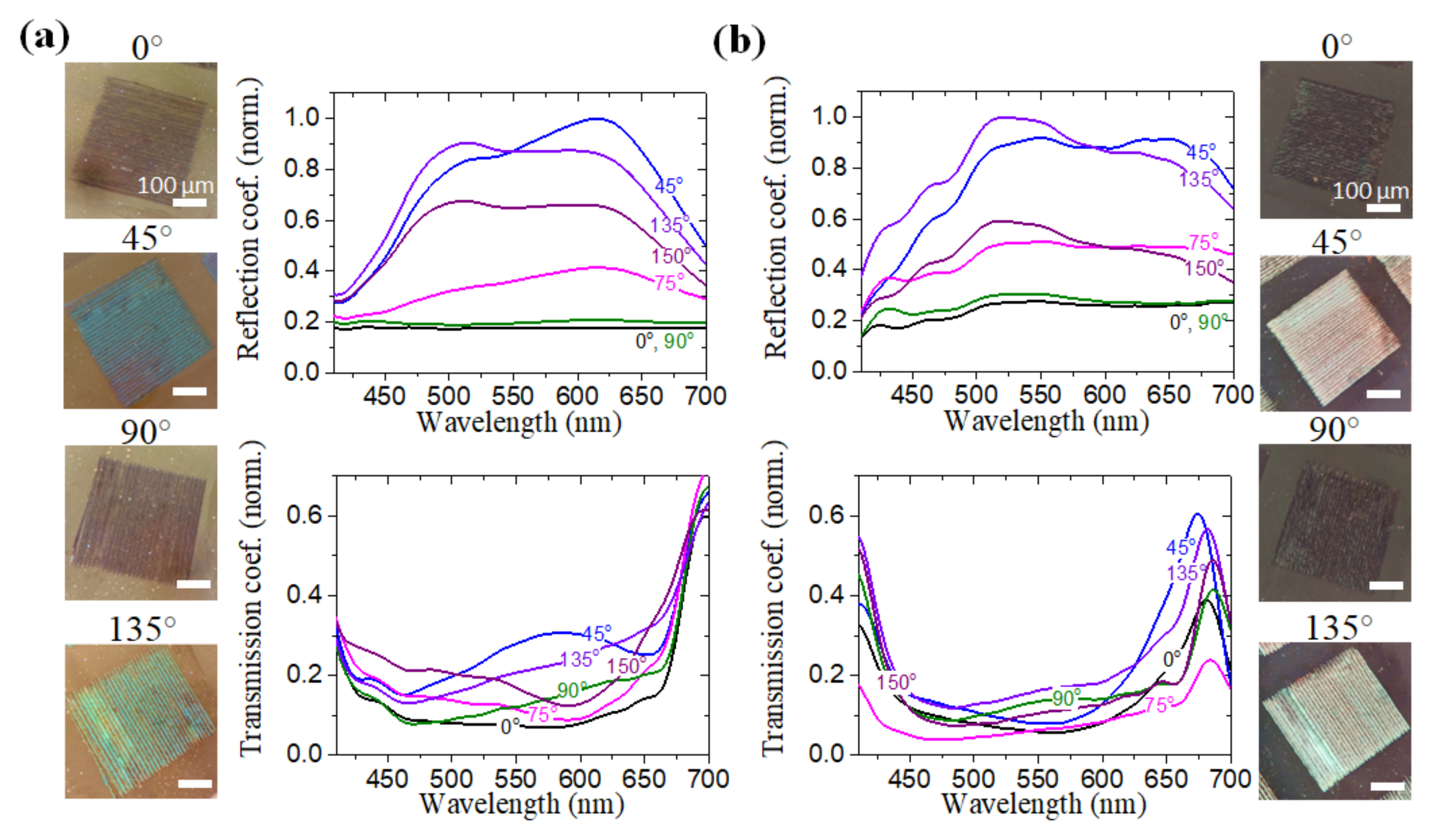
3.2. Optical Properties and Applications
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| SEM | Scanning electron microscopy |
| HAADF STEM | High-angle annular dark-field scanning transmission electron microscopy |
| EDX | Energy-dispersive X-ray spectroscopy |
| LIPSS | Laser-indused periodic surface structures |
| SPP | Surface plasmon-polariton |
Appendix A. Statistical Analysis of the Period and DLOA of the Nanocomposite Gratings
| N, Pulses | F, mJ/cm2 | d, nm () | DLOA , | D, nm () |
|---|---|---|---|---|
| 54 | 27 | 335 | 19 | 179 |
| 54 | 30 | 331 | 12 | 184 |
| 54 | 36 | 335 | 18 | 171 |
| 54 | 27 | 333 | 16 | 187 |
| 60 | 30 | 330 | 10 | 194 |
| 60 | 36 | 342 | 12 | 198 |
| 60 | 45 | 342 | 8 | 181 |
| 60 | 52 | 330 | 14 | |
| 60 | 67 | 328 | 15 | 192 |
| 77 | 27 | 337 | 13 | |
| 77 | 28 | 327 | 8 | 190 |
| 90 | 27 | 326 | 6 | |
| 90 | 37 | 302 | 14 | |
| 108 | 23 | 326 | 11 | |
| 108 | 28 | 329 | 15 | |
| 108 | 31 | 321 | 16 | |
| 135 | 25 | 330 | 14 | |
| 135 | 28 | 303 | 16 | |
| 180 | 23 | 332 | 17 | |
| 180 | 25 | 340 | 15 | |
| 180 | 28 | 324 | 8 | |
| 270 | 23 | 324 | 17 | |
| 270 | 28 | 315 | 16 | |
| 540 | 21 | 324 | 8 | 192 |
| 540 | 23 | 316 | 15 | |
| 540 | 25 | 316 | 7 |
Appendix B. Optical Properties Estimations for the Irradiated Material
References
- Papadopoulos, A.; Skoulas, E.; Mimidis, A.; Perrakis, G.; Kenanakis, G.; Tsibidis, G.D.; Stratakis, E. Biomimetic omnidirectional antireflective glass via direct ultrafast laser nanostructuring. Adv. Mater. 2019, 31, 1901123. [Google Scholar] [CrossRef] [PubMed]
- Sinev, D.A.; Yuzhakova, D.S.; Moskvin, M.K.; Veiko, V.P. Formation of the submicron oxidative LIPSS on thin titanium films during nanosecond laser recording. Nanomaterials 2020, 10, 2161. [Google Scholar] [CrossRef] [PubMed]
- Prosa, M.; Bolognesi, M.; Fornasari, L.; Grasso, G.; Lopez-Sanchez, L.; Marabelli, F.; Toffanin, S. Nanostructured organic/hybrid materials and components in miniaturized optical and chemical sensors. Nanomaterials 2020, 10, 480. [Google Scholar] [CrossRef] [PubMed]
- Dostovalov, A.; Bronnikov, K.; Korolkov, V.; Babin, S.; Mitsai, E.; Mironenko, A.; Tutov, M.; Zhang, D.; Sugioka, K.; Maksimovic, J.; et al. Hierarchical anti-reflective laser-induced periodic surface structures (LIPSSs) on amorphous si films for sensing applications. Nanoscale 2020, 12, 13431–13441. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Liang, G.; Gheno, A.; Vedraine, S.; Ratier, B.; Ho, H.P.; Yu, N. Plasmonic metasensors based on 2D hybrid atomically thin perovskite nanomaterials. Nanomaterials 2020, 10, 1289. [Google Scholar] [CrossRef] [PubMed]
- Kalachyova, Y.; Mares, D.; Lyutakov, O.; Kostejn, M.; Lapcak, L.; Svorcik, V. Surface plasmon polaritons on silver gratings for optimal SERS response. J. Phys. Chem. 2015, 119, 9506–9512. [Google Scholar] [CrossRef]
- Colnită, A.; Marconi, D.; Dina, N.E.; Brezeștean, I.; Bogdan, D.; Turcu, I. 3D silver metallized nanotrenches fabricated by nanoimprint lithography as flexible SERS detection platform. Spectrochim. Acta Part Mol. Biomol. Spectrosc. 2022, 276, 121232. [Google Scholar] [CrossRef]
- Dalloz, N.; Le, V.D.; Hebert, M.; Eles, B.; Flores Figueroa, M.A.; Hubert, C.; Ma, H.; Sharma, N.; Vocanson, F.; Ayala, S.; et al. Anti-Counterfeiting White Light Printed Image Multiplexing by Fast Nanosecond Laser Processing. Adv. Mater. 2022, 34, 2104054. [Google Scholar] [CrossRef]
- Zhu, C.; Tian, L.; Liao, J.; Zhang, X.; Gu, Z. Fabrication of bioinspired hierarchical functional structures by using honeycomb films as templates. Adv. Funct. Mater. 2018, 28, 1803194. [Google Scholar] [CrossRef]
- Liu, M.; Li, M.T.; Xu, S.; Yang, H.; Sun, H.B. Bioinspired superhydrophobic surfaces via laser-structuring. Front. Chem. 2020, 8, 835. [Google Scholar] [CrossRef]
- Demirhan, Y.; Alaboz, H.; Ozyuzer, L.; Nebioğlu, M.A.; Takan, T.A.Y.L.A.N.; Altan, H.; Sabah, C. Metal mesh filters based on Ti, ITO and Cu thin films for terahertz waves. Opt. Quantum Electron. 2016, 48, 170. [Google Scholar] [CrossRef]
- Oh, D.K.; Lee, S.; Lee, S.H.; Lee, W.; Yeon, G.; Lee, N.; Han, K.S.; Jung, S.; Kim, D.H.; Lee, D.Y.; et al. Tailored Nanopatterning by Controlled Continuous Nanoinscribing with Tunable Shape, Depth, and Dimension. ACS Nano 2019, 13, 11194–11202. [Google Scholar] [CrossRef]
- Ahn, S.H.; Guo, L.J. Spontaneous formation of periodic nanostructures by localized dynamic wrinkling. Nano Lett. 2010, 10, 4228–4234. [Google Scholar] [CrossRef]
- Lee, K.M.; Bunning, T.J.; White, T.J.; McConney, M.E.; Godman, N.P. Tunable reflective colors in holographically patterned liquid crystal gels. In Liquid Crystals XXV; SPIE: Washington, DC, USA, 2021; p. 1180705. [Google Scholar]
- Zola, R.S.; Bisoyi, H.K.; Wang, H.; Urbas, A.M.; Bunning, T.J.; Li, Q. Dynamic Control of Light Direction Enabled by Stimuli-Responsive Liquid Crystal Gratings. Adv. Mater. 2018, 31, 1806172. [Google Scholar] [CrossRef]
- Lu, C.; Lipson, R. Interference lithography: A powerful tool for fabricating periodic structures. Laser Photonics Rev. 2010, 4, 568–580. [Google Scholar] [CrossRef]
- Gedvilas, M.; Voisiat, B.; Indrišiūnas, S.; Račiukaitis, G.; Veiko, V.; Zakoldaev, R.; Sinev, D.; Shakhno, E. Thermo-chemical microstructuring of thin metal films using multi-beam interference by short (nano-& picosecond) laser pulses. Thin Solid Film. 2017, 634, 134–140. [Google Scholar]
- Ushkov, A.A.; Verrier, I.; Kampfe, T.; Jourlin, Y. Subwavelength diffraction gratings with macroscopic moiré patterns generated via laser interference lithography. Opt. Express 2020, 28, 16453–16468. [Google Scholar] [CrossRef]
- Torres-Torres, D.; Torres-Torres, C.; Vega-Becerra, O.; Cheang-Wong, J.C.; Rodríguez-Fernández, L.; Crespo-Sosa, A.; Oliver, A. Structured strengthening by two-wave optical ablation in silica with gold nanoparticles. Opt. Laser Technol. 2015, 75, 115–122. [Google Scholar] [CrossRef]
- Martynas Beresna, M.G.; Kazansky, P.G. Ultrafast laser direct writing and nanostructuring in transparent materials. Adv. Opt. Photonics 2014, 6, 293–339. [Google Scholar] [CrossRef]
- Bonse, J.; Krüger, J.; Höhm, S.; Rosenfeld, A. Femtosecond laser-induced periodic surface structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Vorobyev, A.; Makin, V.; Guo, C. Periodic ordering of random surface nanostructures induced by femtosecond laser pulses on metals. J. Appl. Phys. 2007, 101, 034903. [Google Scholar] [CrossRef]
- Liu, Y.H.; Tseng, Y.K.; Cheng, C.W. Direct fabrication of rotational femtosecond laser-induced periodic surface structure on a tilted stainless steel surface. Opt. Laser Technol. 2021, 134, 106648. [Google Scholar] [CrossRef]
- Le Harzic, R.; Dörr, D.; Sauer, D.; Neumeier, M.; Epple, M.; Zimmermann, H.; Stracke, F. Large-area, uniform, high-spatial-frequency ripples generated on silicon using a nanojoule-femtosecond laser at high repetition rate. Opt. Lett. 2011, 36, 229–231. [Google Scholar] [CrossRef]
- Gnilitskyi, I.; Derrien, T.J.Y.; Levy, Y.; Bulgakova, N.M.; Mocek, T.; Orazi, L. High-speed manufacturing of highly regular femtosecond laser-induced periodic surface structures: Physical origin of regularity. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Bonse, J.; Gräf, S. Maxwell Meets Marangoni–A Review of Theories on Laser-Induced Periodic Surface Structures. Laser Photonics Rev. 2020, 14, 2000215. [Google Scholar] [CrossRef]
- Varlamova, O.; Costache, F.; Ratzke, M.; Reif, J. Control parameters in pattern formation upon femtosecond laser ablation. Appl. Surf. Sci. 2007, 253, 7932–7936. [Google Scholar] [CrossRef]
- Bonse, J.; Krüger, J. Pulse number dependence of laser-induced periodic surface structures for femtosecond laser irradiation of silicon. J. Appl. Phys. 2010, 108, 034903. [Google Scholar] [CrossRef]
- De La Cruz, A.R.; Lahoz, R.; Siegel, J.; De La Fuente, G.; Solis, J. High speed inscription of uniform, large-area laser-induced periodic surface structures in Cr films using a high repetition rate fs laser. Opt. Lett. 2014, 39, 2491–2494. [Google Scholar] [CrossRef]
- Zuev, D.A.; Makarov, S.V.; Mukhin, I.S.; Milichko, V.A.; Starikov, S.V.; Morozov, I.A.; Shishkin, I.I.; Krasnok, A.E.; Belov, P.A. Fabrication of Hybrid Nanostructures via Nanoscale Laser-Induced Reshaping for Advanced Light Manipulation. Adv. Mater. 2016, 28, 3087–3093. [Google Scholar] [CrossRef]
- Sun, Y.; Sinev, I.; Zalogina, A.; Ageev, E.; Shamkhi, H.; Komissarenko, F.; Morozov, I.; Lepeshov, S.; Milichko, V.; Makarov, S.; et al. Reconfigurable Near-field Enhancement with Hybrid Metal-Dielectric Oligomers. Laser Photonics Rev. 2019, 13, 1800274. [Google Scholar] [CrossRef]
- Guo, R.; Rusak, E.; Staude, I.; Dominguez, J.; Decker, M.; Rockstuhl, C.; Brener, I.; Neshev, D.N.; Kivshar, Y.S. Multipolar coupling in hybrid metal–dielectric metasurfaces. Acs Photonics 2016, 3, 349–353. [Google Scholar] [CrossRef]
- Vijayakanth, T.; Liptrot, D.J.; Gazit, E.; Boomishankar, R.; Bowen, C.R. Recent Advances in Organic and Organic–Inorganic Hybrid Materials for Piezoelectric Mechanical Energy Harvesting. Adv. Funct. Mater. 2022, 32, 2109492. [Google Scholar] [CrossRef]
- Sharma, V.; Sharma, H.; Singh, S.K.; Kumar, R.; Kumari, Y.; Sachdev, K. Organic–Inorganic Hybrid Structure as a Conductive and Transparent Layer for Energy and Optoelectronic Applications. ACS Appl. Electron. Mater. 2021, 3, 1601–1609. [Google Scholar] [CrossRef]
- Tomita, Y.; Aoi, T.; Hasegawa, S.; Xia, F.; Wang, Y.; Oshima, J. Very high contrast volume holographic gratings recorded in photopolymerizable nanocomposite materials. Opt. Express 2020, 28, 28366–28382. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.; Dai, H.; Liu, C. Influence of thermal growth of Au nanoparticles in the coupling efficiency of Au/SiO2 nanocomposite grating coupler. Nanotechnology 2021, 32, 315302. [Google Scholar] [CrossRef]
- Destouches, N.; Sharma, N.; Vangheluwe, M.; Dalloz, N.; Vocanson, F.; Bugnet, M.; Hébert, M.; Siegel, J. Laser-Empowered Random Metasurfaces for White Light Printed Image Multiplexing. Adv. Funct. Mater. 2021, 31, 2010430. [Google Scholar] [CrossRef]
- Gutha, R.R.; Sadeghi, S.M.; Wing, W.J. Ultrahigh refractive index sensitivity and tunable polarization switching via infrared plasmonic lattice modes. Appl. Phys. Lett. 2017, 110, 153103. [Google Scholar] [CrossRef]
- Utyushev, A.D.; Zakomirnyi, V.I.; Rasskazov, I.L. Collective lattice resonances: Plasmonics and beyond. Rev. Phys. 2021, 6, 100051. [Google Scholar] [CrossRef]
- Wing, W.J.; Sadeghi, S.M.; Gutha, R.R. Polarization switching from plasmonic lattice mode to multipolar localized surface plasmon resonances in arrays of large nanoantennas. J. Appl. Phys. 2016, 120, 234301. [Google Scholar] [CrossRef]
- Andreeva, Y.; Koval, V.; Sergeev, M.; Veiko, V.P.; Destouches, N.; Vocanson, F.; Ma, H.; Loshachenko, A.; Itina, T.E. Picosecond laser writing of Ag- SiO2 nanocomposite nanogratings for optical filtering. Opt. Lasers Eng. 2020, 124, 105840. [Google Scholar] [CrossRef]
- Nadar, L.; Sayah, R.; Vocanson, F.; Crespo-Monteiro, N.; Boukenter, A.; Sao Joao, S.; Destouches, N. Influence of reduction processes on the colour and photochromism of amorphous mesoporous TiO2 thin films loaded with a silver salt. Photochem. Photobiol. Sci. 2011, 10, 1810–1816. [Google Scholar] [CrossRef]
- Liu, Z.; Destouches, N.; Vitrant, G.; Lefkir, Y.; Epicier, T.; Vocanson, F.; Bakhti, S.; Fang, Y.; Bandyopadhyay, B.; Ahmed, M. Understanding the growth mechanisms of Ag nanoparticles controlled by plasmon-induced charge transfers in Ag-TiO2 films. J. Phys. Chem. 2015, 119, 9496–9505. [Google Scholar] [CrossRef]
- Destouches, N.; Crespo-Monteiro, N.; Vitrant, G.; Lefkir, Y.; Reynaud, S.; Epicier, T.; Liu, Y.; Vocanson, F.; Pigeon, F. Self-organized growth of metallic nanoparticles in a thin film under homogeneous and continuous-wave light excitation. J. Mater. Chem. 2014, 2, 6256–6263. [Google Scholar] [CrossRef]
- Sharma, N.; Vangheluwe, M.; Vocanson, F.; Cazier, A.; Bugnet, M.; Reynaud, S.; Vermeulin, A.; Destouches, N. Laser-driven plasmonic gratings for hiding multiple images. Mater. Horizons 2019, 6, 978–983. [Google Scholar] [CrossRef]
- Liu, Z.; Siegel, J.; Garcia-Lechuga, M.; Epicier, T.; Lefkir, Y.; Reynaud, S.; Bugnet, M.; Vocanson, F.; Solis, J.; Vitrant, G.; et al. Three-dimensional self-organization in nanocomposite layered systems by ultrafast laser pulses. ACS Nano 2017, 11, 5031–5040. [Google Scholar] [CrossRef]
- Sokolowski-Tinten, K.; von der Linde, D. Generation of dense electron-hole plasmas in silicon. Phys. Rev. B 2000, 61, 2643. [Google Scholar] [CrossRef]
- Siefke, T.; Kroker, S.; Pfeiffer, K.; Puffky, O.; Dietrich, K.; Franta, D.; Ohlídal, I.; Szeghalmi, A.; Kley, E.B.; Tünnermann, A. Materials pushing the application limits of wire grid polarizers further into the deep ultraviolet spectral range. Adv. Opt. Mater. 2016, 4, 1780–1786. [Google Scholar] [CrossRef]
- Das, S.K.; Dasari, K.; Rosenfeld, A.; Grunwald, R. Extended-area nanostructuring of TiO2 with femtosecond laser pulses at 400 nm using a line focus. Nanotechnology 2010, 21, 155302. [Google Scholar] [CrossRef]
- Lin, C.P.; Chen, H.; Nakaruk, A.; Koshy, P.; Sorrell, C. Effect of annealing temperature on the photocatalytic activity of TiO2 thin films. Energy Procedia 2013, 34, 627–636. [Google Scholar] [CrossRef]
- Dintinger, J.; Martin, O.J. Channel and wedge plasmon modes of metallic V-grooves with finite metal thickness. Opt. Express 2009, 17, 2364–2374. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1976, 6, 4370. [Google Scholar] [CrossRef]
- Hutley, M.; Maystre, D. The total absorption of light by a diffraction grating. Opt. Commun. 1976, 19, 431–436. [Google Scholar] [CrossRef]
- Rotenberg, N.; Caspers, J.N.; van Driel, H.M. Tunable ultrafast control of plasmonic coupling to gold films. Phys. Rev. B 2009, 80, 245420. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreeva, Y.; Suvorov, A.; Grigoryev, E.; Khmelenin, D.; Zhukov, M.; Makin, V.; Sinev, D. Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings. Nanomaterials 2022, 12, 2811. https://doi.org/10.3390/nano12162811
Andreeva Y, Suvorov A, Grigoryev E, Khmelenin D, Zhukov M, Makin V, Sinev D. Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings. Nanomaterials. 2022; 12(16):2811. https://doi.org/10.3390/nano12162811
Chicago/Turabian StyleAndreeva, Yaroslava, Alexander Suvorov, Evgeniy Grigoryev, Dmitry Khmelenin, Mikhail Zhukov, Vladimir Makin, and Dmitry Sinev. 2022. "Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings" Nanomaterials 12, no. 16: 2811. https://doi.org/10.3390/nano12162811
APA StyleAndreeva, Y., Suvorov, A., Grigoryev, E., Khmelenin, D., Zhukov, M., Makin, V., & Sinev, D. (2022). Laser Fabrication of Highly Ordered Nanocomposite Subwavelength Gratings. Nanomaterials, 12(16), 2811. https://doi.org/10.3390/nano12162811