Charge Transport in UV-Oxidized Graphene and Its Dependence on the Extent of Oxidation
Abstract
:1. Introduction
2. Experimental
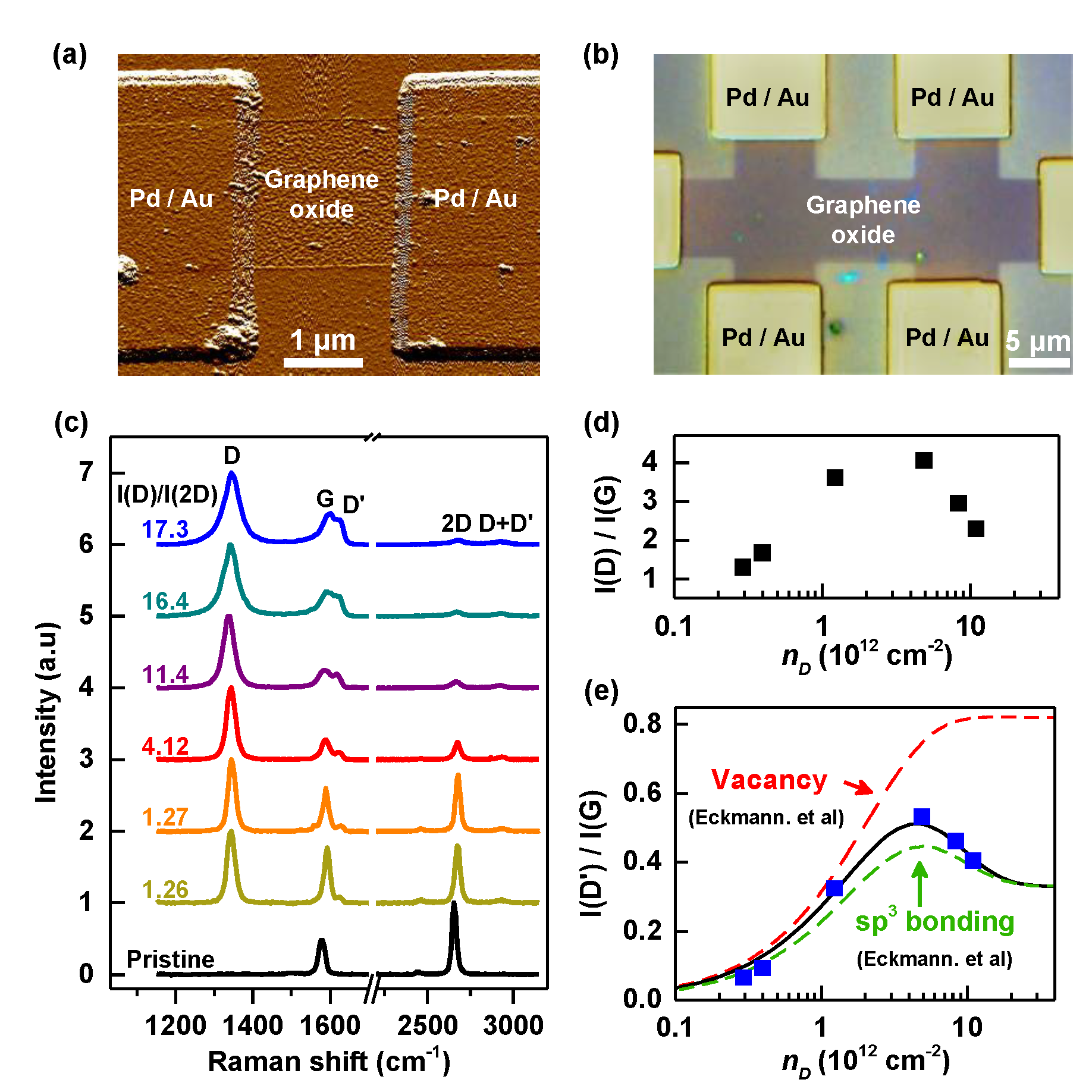
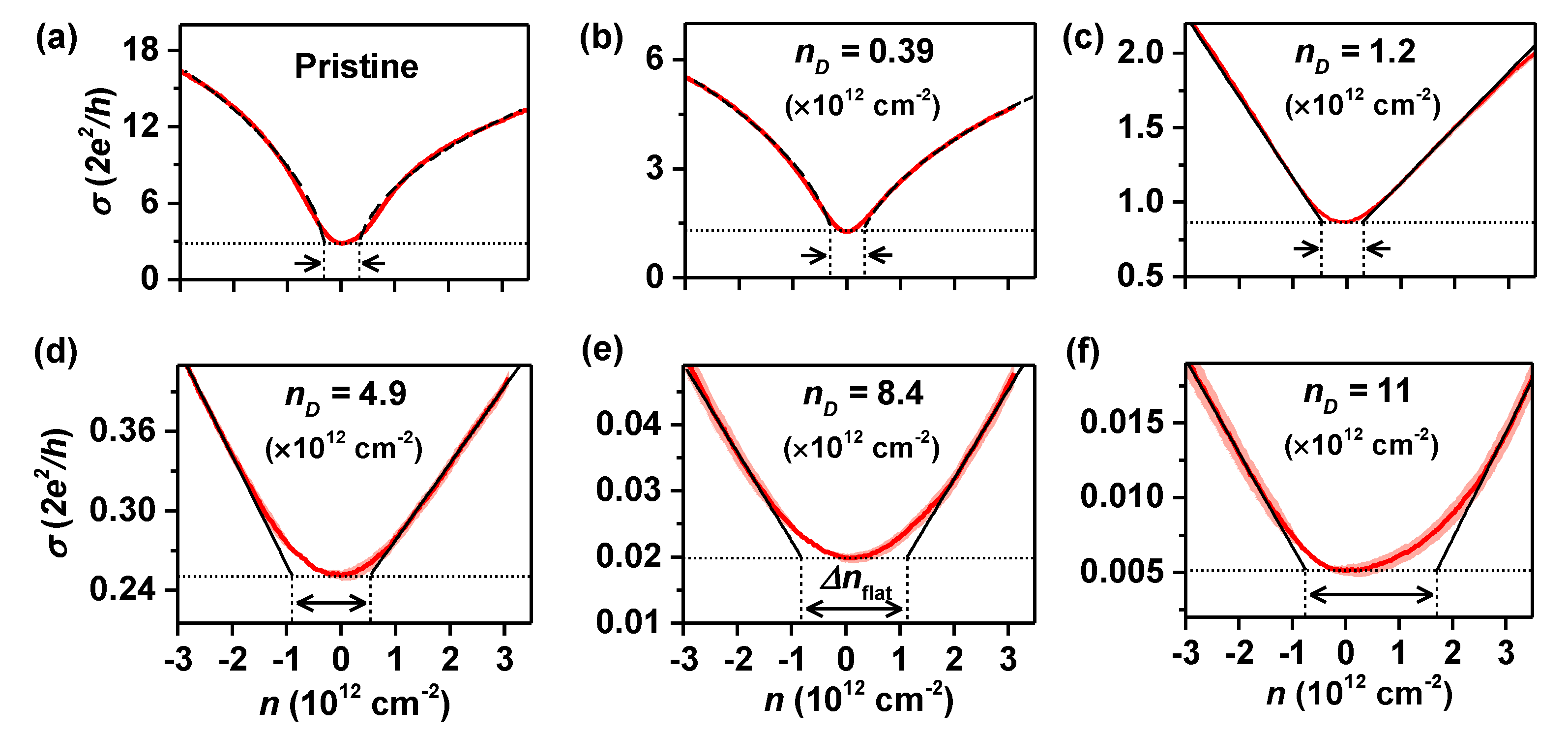
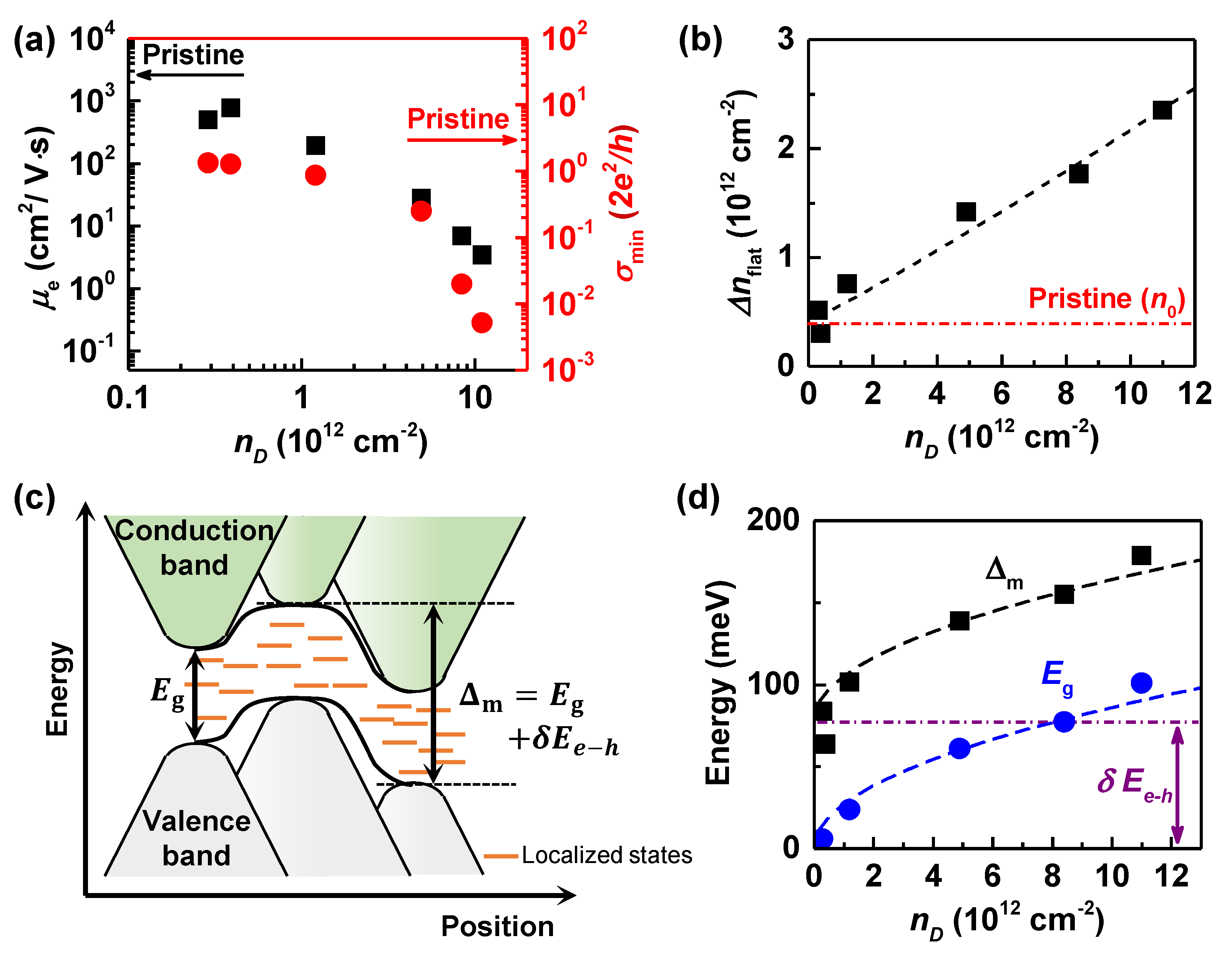
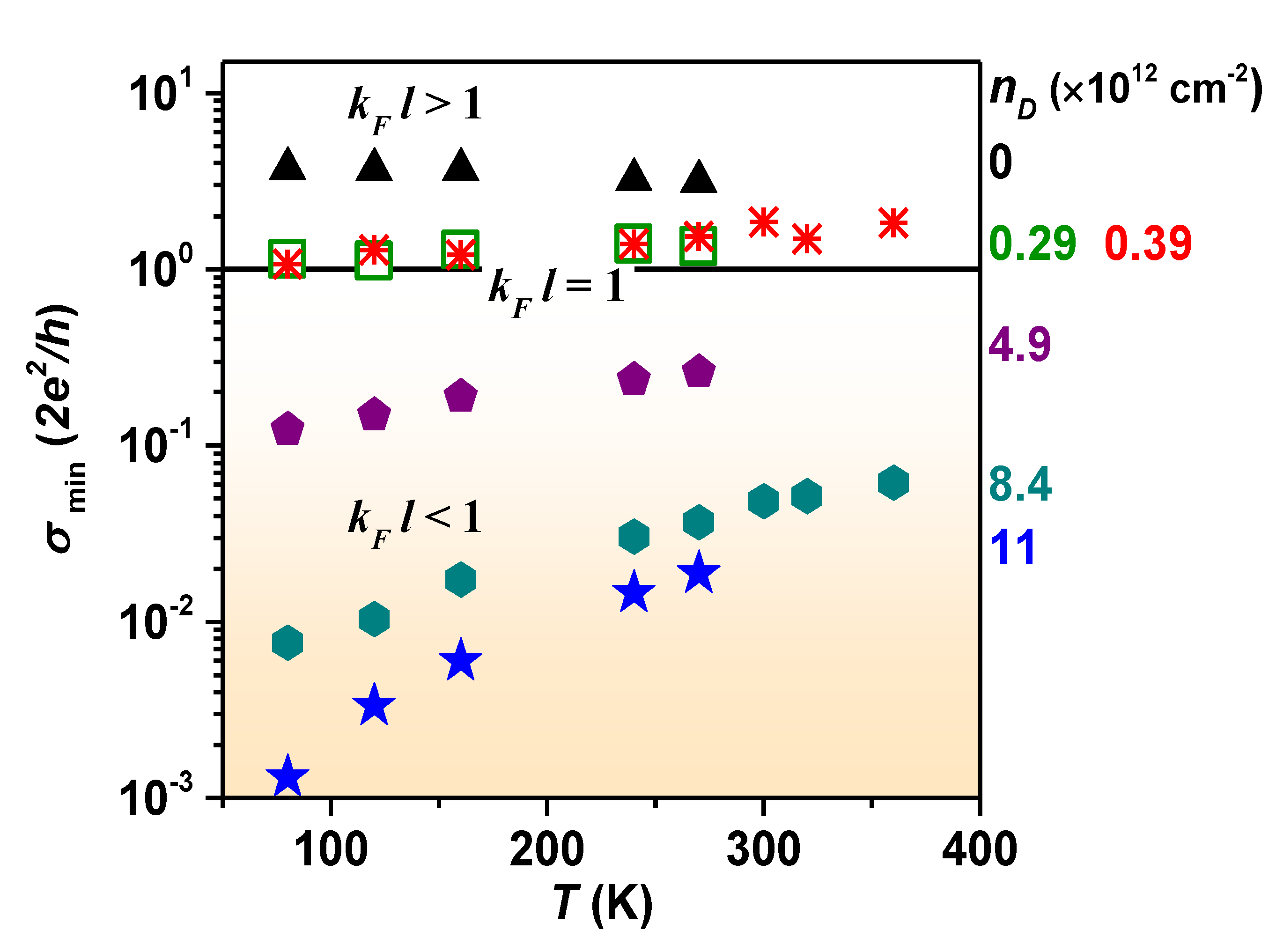
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Morozov, S.; Novoselov, K.; Katsnelson, M.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A. Giant intrinsic carrier mobilities in graphene and its bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Shi, Y.; Wang, X. Synthesis, charge transport and device applications of graphene nanoribbons. Synth. Met. 2015, 210, 109–122. [Google Scholar] [CrossRef]
- Craciun, M.; Khrapach, I.; Barnes, M.; Russo, S. Properties and applications of chemically functionalized graphene. J. Phys. Condens. Matter 2013, 25, 423201. [Google Scholar] [CrossRef]
- Ahmad, Y.; Batisse, N.; Chen, X.; Dubois, M. Preparation and Applications of Fluorinated Graphenes. C 2021, 7, 20. [Google Scholar] [CrossRef]
- Whitener, K.E., Jr. Hydrogenated graphene: A user’s guide. J. Vac. Sci. Technol. A Vacuum Surf. Film. 2018, 36, 05G401. [Google Scholar] [CrossRef]
- Jin, Y.; Zheng, Y.; Podkolzin, S.G.; Lee, W. Band gap of reduced graphene oxide tuned by controlling functional groups. J. Mater. Chem. C 2020, 8, 4885–4894. [Google Scholar] [CrossRef]
- Yan, J.A.; Xian, L.; Chou, M. Structural and electronic properties of oxidized graphene. Phys. Rev. Lett. 2009, 103, 086802. [Google Scholar] [CrossRef]
- Nourbakhsh, A.; Cantoro, M.; Vosch, T.; Pourtois, G.; Clemente, F.; van der Veen, M.H.; Hofkens, J.; Heyns, M.M.; De Gendt, S.; Sels, B.F. Bandgap opening in oxygen plasma-treated graphene. Nanotechnology 2010, 21, 435203. [Google Scholar] [CrossRef]
- Lundie, M.; Šljivančanin, Ž.; Tomić, S. Analysis of energy gap opening in graphene oxide. J. Phys. Conf. Ser. 2014, 526, 012003. [Google Scholar]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
- Pei, S.; Cheng, H.M. The reduction of graphene oxide. Carbon 2012, 50, 3210–3228. [Google Scholar] [CrossRef]
- Eda, G.; Mattevi, C.; Yamaguchi, H.; Kim, H.; Chhowalla, M. Insulator to semimetal transition in graphene oxide. J. Phys. Chem. C 2009, 113, 15768–15771. [Google Scholar] [CrossRef]
- Negishi, R.; Akabori, M.; Ito, T.; Watanabe, Y.; Kobayashi, Y. Band-like transport in highly crystalline graphene films from defective graphene oxides. Sci. Rep. 2016, 6, 28936. [Google Scholar] [CrossRef]
- Liu, L.; Xie, D.; Wu, M.; Yang, X.; Xu, Z.; Wang, W.; Bai, X.; Wang, E. Controlled oxidative functionalization of monolayer graphene by water-vapor plasma etching. Carbon 2012, 50, 3039–3044. [Google Scholar] [CrossRef]
- Mulyana, Y.; Uenuma, M.; Ishikawa, Y.; Uraoka, Y. Reversible oxidation of graphene through ultraviolet/ozone treatment and its nonthermal reduction through ultraviolet irradiation. J. Phys. Chem. C 2014, 118, 27372–27381. [Google Scholar] [CrossRef]
- Haidari, M.M.; Kim, H.; Kim, J.H.; Park, M.; Lee, H.; Choi, J.S. Doping effect in graphene-graphene oxide interlayer. Sci. Rep. 2020, 10, 8258. [Google Scholar] [CrossRef]
- Osofsky, M.; Hernández, S.; Nath, A.; Wheeler, V.; Walton, S.; Krowne, C.; Gaskill, D. Functionalized graphene as a model system for the two-dimensional metal-insulator transition. Sci. Rep. 2016, 6, 19939. [Google Scholar] [CrossRef]
- Ryu, G.H.; Lee, J.; Kang, D.; Jo, H.J.; Shin, H.S.; Lee, Z. Effects of dry oxidation treatments on monolayer graphene. 2D Mater. 2017, 4, 024011. [Google Scholar] [CrossRef]
- Yang, X.; Yan, M. Removing contaminants from transferred CVD graphene. Nano Res. 2020, 13, 599–610. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Verzhbitskiy, I.; Davey, R.; Casiraghi, C. Raman study on defective graphene: Effect of the excitation energy, type, and amount of defects. Phys. Rev. B 2013, 88, 035426. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef]
- Anno, Y.; Takeuchi, M.; Matsuoka, M.; Takei, K.; Akita, S.; Arie, T. Effect of defect-induced carrier scattering on the thermoelectric power of graphene. Appl. Phys. Lett. 2017, 110, 263501. [Google Scholar] [CrossRef]
- Childres, I.; Jauregui, L.A.; Tian, J.; Chen, Y.P. Effect of oxygen plasma etching on graphene studied using Raman spectroscopy and electronic transport measurements. New J. Phys. 2011, 13, 025008. [Google Scholar] [CrossRef]
- Pollard, A.J.; Brennan, B.; Stec, H.; Tyler, B.J.; Seah, M.P.; Gilmore, I.S.; Roy, D. Quantitative characterization of defect size in graphene using Raman spectroscopy. Appl. Phys. Lett. 2014, 105, 253107. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, Q.; Eigler, S. Room-temperature transport properties of graphene with defects derived from oxo-graphene. Chem.- Eur. J. 2020, 26, 6484–6489. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.H.; Zhang, J.; Jin, X.; Liu, J.Y.; Li, Q.; Li, M.H.; Cai, W.; Wu, D.Y.; Zhan, D.; Ren, B. Quantitative correlation between defect density and heterogeneous electron transfer rate of single layer graphene. J. Am. Chem. Soc. 2014, 136, 16609–16617. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Hone, J.; Stormer, H.; Kim, P. Temperature-dependent transport in suspended graphene. Phys. Rev. Lett. 2008, 101, 096802. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A. Graphene Schottky diodes: An experimental review of the rectifying graphene/semiconductor heterojunction. Phys. Rep. 2016, 606, 1–58. [Google Scholar] [CrossRef]
- Chen, J.H.; Cullen, W.G.; Jang, C.; Fuhrer, M.; Williams, E.D. Defect scattering in graphene. Phys. Rev. Lett. 2009, 102, 236805. [Google Scholar] [CrossRef]
- Chen, J.H.; Jang, C.; Adam, S.; Fuhrer, M.; Williams, E.D.; Ishigami, M. Charged-impurity scattering in graphene. Nat. Phys. 2008, 4, 377–381. [Google Scholar] [CrossRef]
- Moser, J.; Tao, H.; Roche, S.; Alzina, F.; Torres, C.S.; Bachtold, A. Magnetotransport in disordered graphene exposed to ozone: From weak to strong localization. Phys. Rev. B 2010, 81, 205445. [Google Scholar] [CrossRef]
- Eigler, S.; Enzelberger-Heim, M.; Grimm, S.; Hofmann, P.; Kroener, W.; Geworski, A.; Dotzer, C.; Röckert, M.; Xiao, J.; Papp, C.; et al. Wet chemical synthesis of graphene. Adv. Mater. 2013, 25, 3583–3587. [Google Scholar] [CrossRef]
- Abanin, D.A.; Shytov, A.; Levitov, L. Peierls-type instability and tunable band gap in functionalized graphene. Phys. Rev. Lett. 2010, 105, 086802. [Google Scholar] [CrossRef]
- Sehrawat, P.; Islam, S.; Mishra, P.; Ahmad, S. Reduced graphene oxide (rGO) based wideband optical sensor and the role of Temperature, Defect States and Quantum Efficiency. Sci. Rep. 2018, 8, 3537. [Google Scholar]
- Adam, S.; Hwang, E.; Galitski, V.; Sarma, S.D. A self-consistent theory for graphene transport. Proc. Natl. Acad. Sci. USA 2007, 104, 18392–18397. [Google Scholar] [CrossRef]
- Gallagher, P.; Todd, K.; Goldhaber-Gordon, D. Disorder-induced gap behavior in graphene nanoribbons. Phys. Rev. B 2010, 81, 115409. [Google Scholar] [CrossRef]
- Stampfer, C.; Güttinger, J.; Hellmüller, S.; Molitor, F.; Ensslin, K.; Ihn, T. Energy gaps in etched graphene nanoribbons. Phys. Rev. Lett. 2009, 102, 056403. [Google Scholar] [CrossRef]
- Adam, S.; Cho, S.; Fuhrer, M.; Sarma, S.D. Density inhomogeneity driven percolation metal-insulator transition and dimensional crossover in graphene nanoribbons. Phys. Rev. Lett. 2008, 101, 046404. [Google Scholar] [CrossRef]
- Sarma, S.D.; Hwang, E. Two-dimensional metal-insulator transition as a strong localization induced crossover phenomenon. Phys. Rev. B 2014, 89, 235423. [Google Scholar] [CrossRef]
- Vianelli, A.; Candini, A.; Treossi, E.; Palermo, V.; Affronte, M. Observation of different charge transport regimes and large magnetoresistance in graphene oxide layers. Carbon 2015, 89, 188–196. [Google Scholar] [CrossRef]
- Chen, J.H.; Li, L.; Cullen, W.G.; Williams, E.D.; Fuhrer, M.S. Tunable Kondo effect in graphene with defects. Nat. Phys. 2011, 7, 535–538. [Google Scholar] [CrossRef]
- Hilke, M.; Massicotte, M.; Whiteway, E.; Yu, V. Weak localization in graphene: Theory, simulations, and experiments. Sci. World J. 2014, 2014, 737296. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.Y.; Haidari, M.M.; Kee, E.H.; Choi, J.S.; Park, B.H.; Campbell, E.E.B.; Jhang, S.H. Charge Transport in UV-Oxidized Graphene and Its Dependence on the Extent of Oxidation. Nanomaterials 2022, 12, 2845. https://doi.org/10.3390/nano12162845
Lee HY, Haidari MM, Kee EH, Choi JS, Park BH, Campbell EEB, Jhang SH. Charge Transport in UV-Oxidized Graphene and Its Dependence on the Extent of Oxidation. Nanomaterials. 2022; 12(16):2845. https://doi.org/10.3390/nano12162845
Chicago/Turabian StyleLee, Hwa Yong, Mohd Musaib Haidari, Eun Hee Kee, Jin Sik Choi, Bae Ho Park, Eleanor E. B. Campbell, and Sung Ho Jhang. 2022. "Charge Transport in UV-Oxidized Graphene and Its Dependence on the Extent of Oxidation" Nanomaterials 12, no. 16: 2845. https://doi.org/10.3390/nano12162845
APA StyleLee, H. Y., Haidari, M. M., Kee, E. H., Choi, J. S., Park, B. H., Campbell, E. E. B., & Jhang, S. H. (2022). Charge Transport in UV-Oxidized Graphene and Its Dependence on the Extent of Oxidation. Nanomaterials, 12(16), 2845. https://doi.org/10.3390/nano12162845





