On the Critical Heat Flux Assessment of Micro- and Nanoscale Roughened Surfaces
Abstract
:1. Introduction
| Sr. | Ref. | CHF Prediction Method |
|---|---|---|
| 1 | [3] | Bubble interference model |
| 2 | [4,5,6] | Hydrodynamic instability model |
| 3 | [7,8] | Extended hydrodynamic theory |
| 4 | [9] | Macro layer dryout model |
| 5 | [10,11] | Hot/dry spot model |
| 6 | [12,13] | Interfacial lift-off model |
| 7 | [14] | Dimensional analysis |
| 8 | [15,16,17,18,19,20] | Correlations with effect of orientation at 1 atm. |
| 9 | [1,11,21,22] | Correlations with effects of orientation and contact angle at 1 atm. |
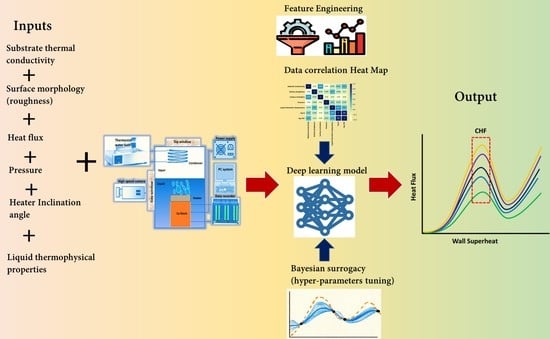
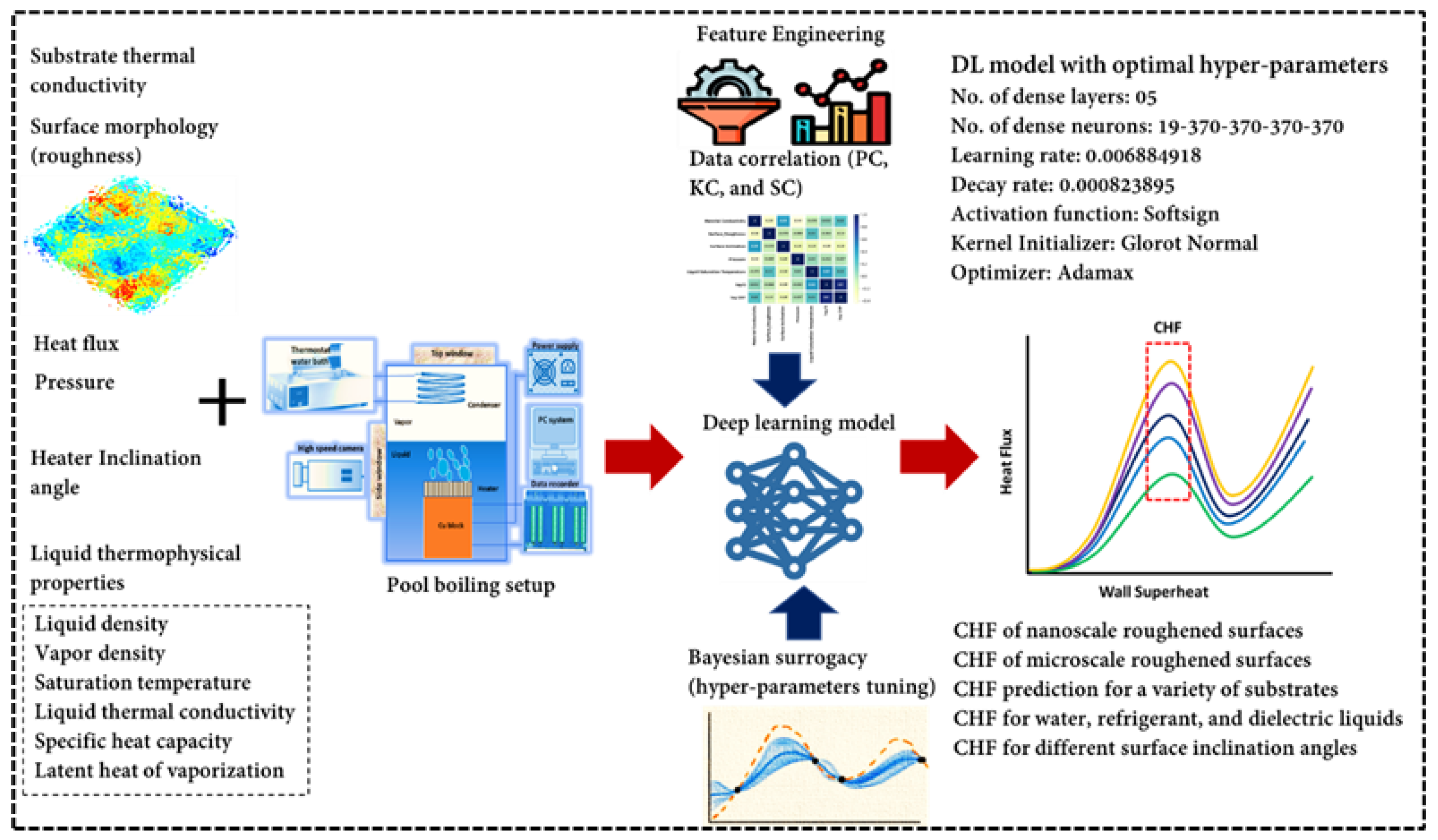
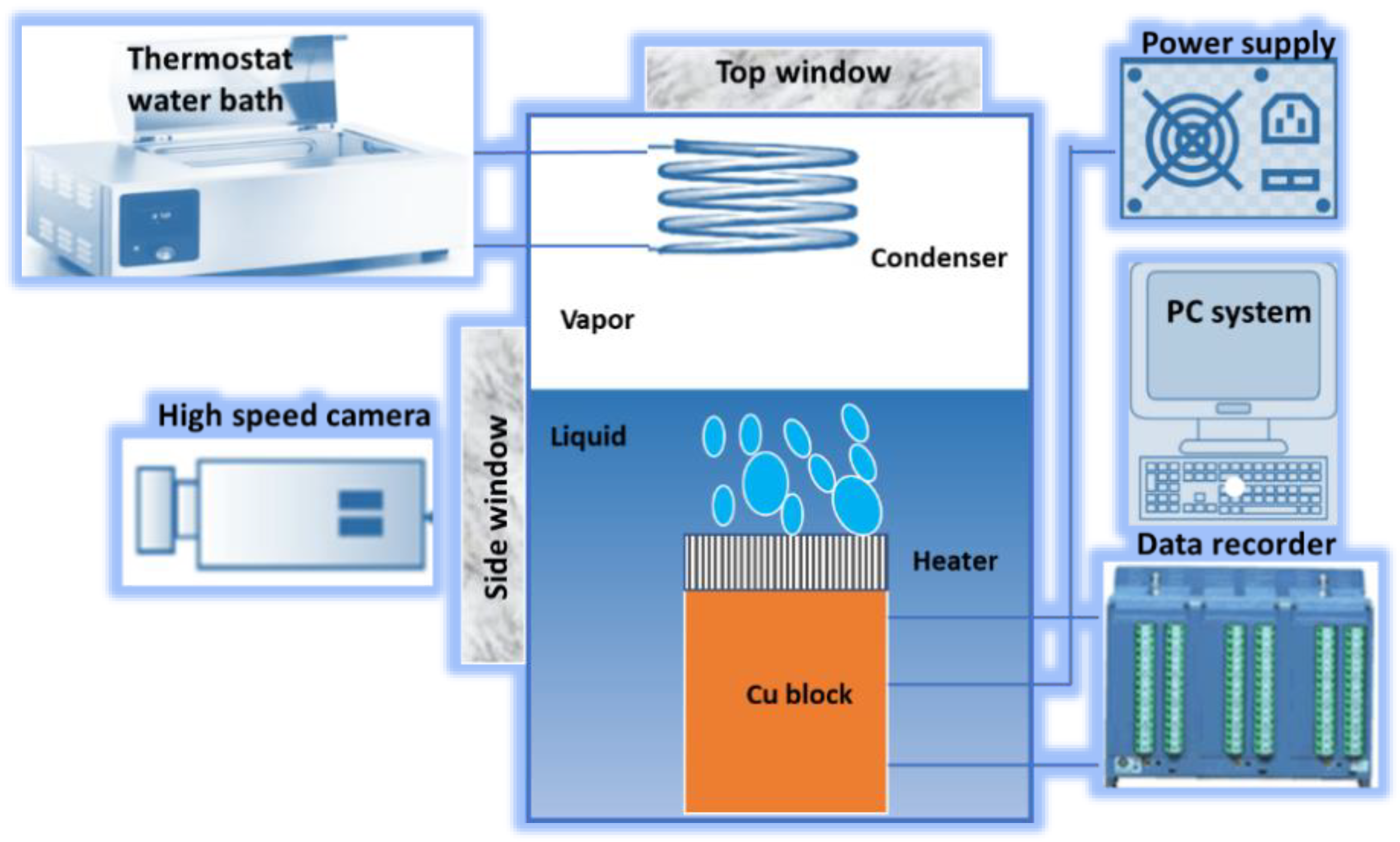
2. Methodology
3. Results and Discussion
4. Conclusions
- 1-
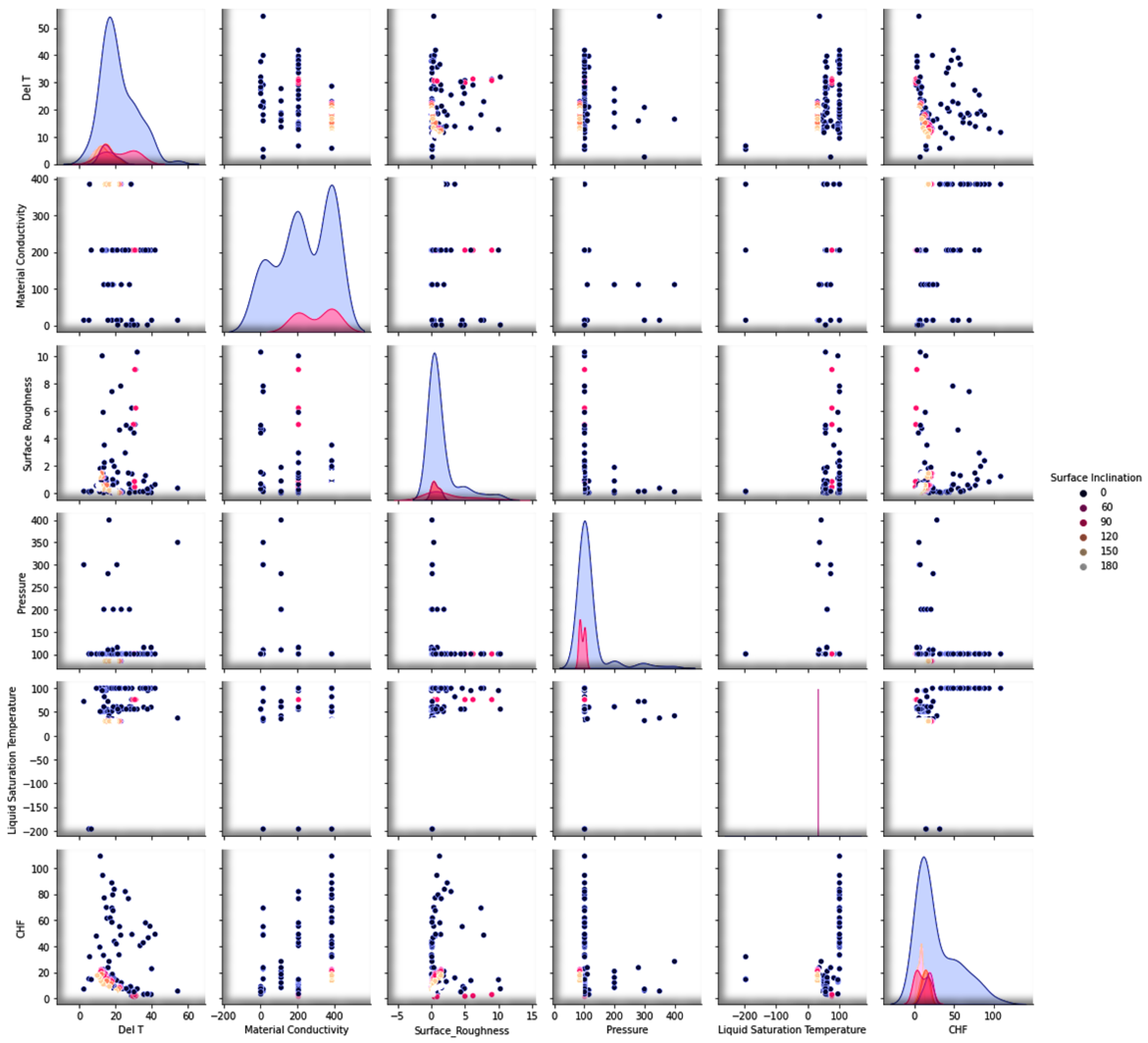
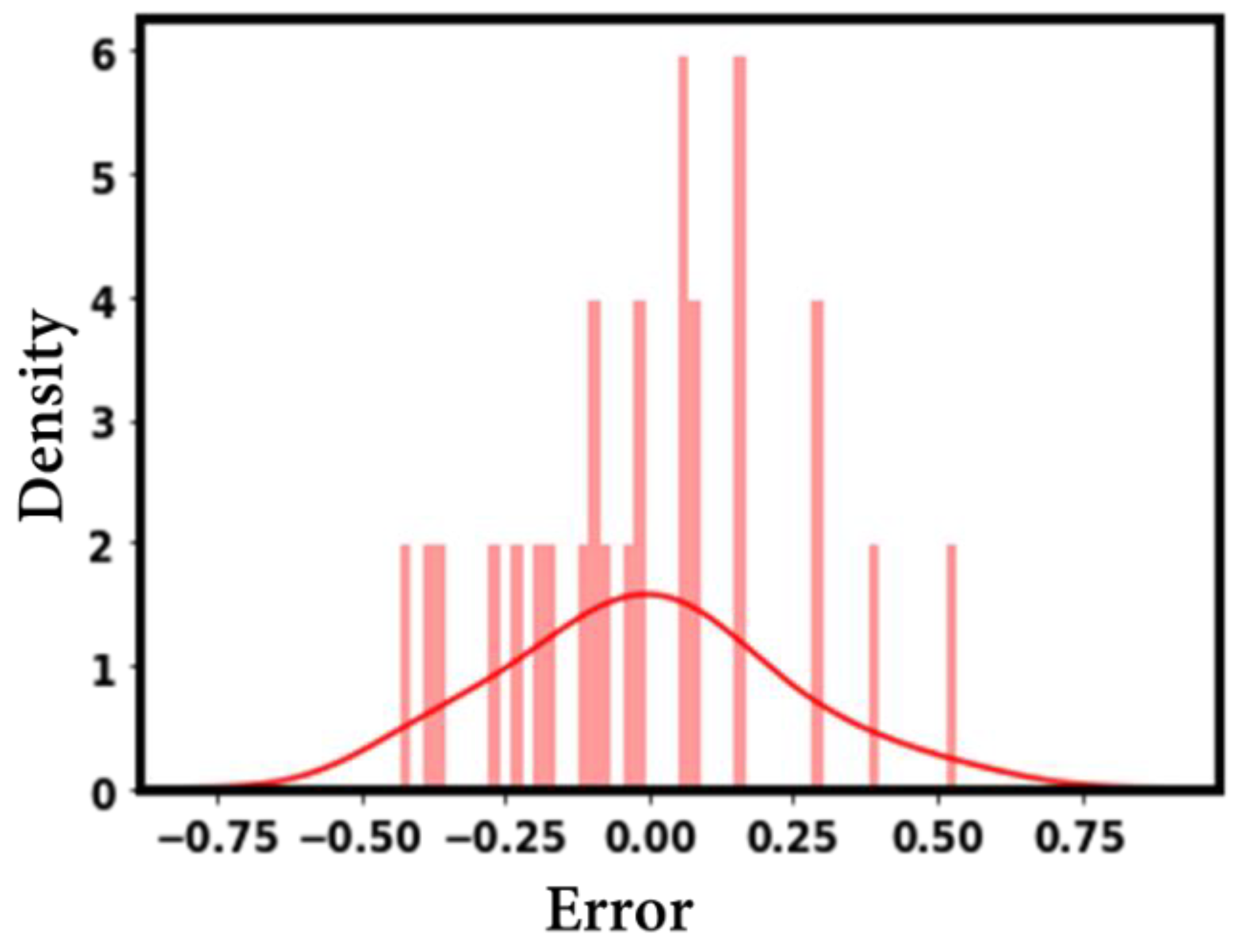
- With feature engineering (by using logarithmic transformation), different inputs (such as liquid thermophysical properties, surface morphology, and testing conditions) could be better correlated with the pool-boiling CHF. For instance, when log is applied to CHF and heat flux, a high accuracy (R2 = 0.971) is achieved.
- 2-
- Different correlations such as Pearson, Spearman, and Kendal correlations can be helpful in finding the degree and direction of association between the investigated features.
- 3-
- For hyper-parameters’ optimization, the RF model yields a relatively better accuracy compared to the GP and GBRT.
- 4-
- The optimal model (with 05 dense layers of 19-370-370-370-370 neurons, learning and decay rates of 0.006884918 and 0.000823895, and with the activation function, kernel initializer, and optimizer as softsign, glorot normal, and adamax, respectively) could achieve an accuracy of R2 = 0.971, RD = 0.1%, MSE = 0.0541, and MAE = 0.185.
- 5-
- The developed method is able to predict the CHF for a wide range of surface morphologies (nanoscale roughness in nm to microscale roughness in µm), substrate materials (copper, aluminum, stainless steel, etc.), and working fluids (refrigerants, dielectric liquids, and water). The investigated CHF ranges between 80 and 2079 kW/m2.
- 6-
- The CHF prediction model’s accuracy is valid for different heater inclination angles and operating pressures.
Author Contributions
Funding
Conflicts of Interest
References
- Kandlikar, S.G. A theoretical model to predict pool boiling CHF incorporating effects of contact angle and orientation. J. Heat Transf. 2001, 123, 1071–1079. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Pool boiling critical heat flux (CHF)—Part 1: Review of mechanisms, models, and correlations. Int. J. Heat Mass Transf. 2018, 117, 1352–1367. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Griffith, P. Correlation of Maximum Heat Flux Data for Boiling of Saturated Liquids; Massachusetts Institute of Technology, Division of Industrial Cooperation: Cambridge, MA, USA, 1955. [Google Scholar]
- Zuber, N. On the stability of boiling heat transfer. Trans. Am. Soc. Mech. Eng. 1958, 80, 711–714. [Google Scholar] [CrossRef]
- Zuber, N. Hydrodynamic Aspects of Boiling Heat Transfer; United States Atomic Energy Commission, Technical Information Service: Washington, DC, USA, 1959.
- Zuber, N. The hydrodynamic crisis in pool boiling of saturated and subcooled liquids. Int. Dev. Heat Transf. 1961, 27, 230–236. [Google Scholar]
- Linehard, J.; Dhir, V.K. Extended Hydrodynamic Theory of the Peak and Minimum Pool Boiling Heat Fluxes; NASA: Washington, DC, USA, 1973.
- Lienhard, J.; Dhir, V. Hydrodynamic prediction of peak pool-boiling heat fluxes from finite bodies. J. Heat Transf. 1973, 95, 152–158. [Google Scholar] [CrossRef]
- Haramura, Y.; Katto, Y. A new hydrodynamic model of critical heat flux, applicable widely to both pool and forced convection boiling on submerged bodies in saturated liquids. Int. J. Heat Mass Transf. 1983, 26, 389–399. [Google Scholar] [CrossRef]
- Yagov, V.V. Is a crisis in pool boiling actually a hydrodynamic phenomenon? Int. J. Heat Mass Transf. 2014, 73, 265–273. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Dinh, T.-N. High heat flux boiling and burnout as microphysical phenomena: Mounting evidence and opportunities. Multiph. Sci. Technol. 2006, 18, 251–276. [Google Scholar] [CrossRef]
- Mudawar, I.; Howard, A.H.; Gersey, C.O. An analytical model for near-saturated pool boiling critical heat flux on vertical surfaces. Int. J. Heat Mass Transf. 1997, 40, 2327–2339. [Google Scholar] [CrossRef]
- Guan, C.-K.; Klausner, J.F.; Mei, R. A new mechanistic model for pool boiling CHF on horizontal surfaces. Int. J. Heat Mass Transf. 2011, 54, 3960–3969. [Google Scholar] [CrossRef]
- Kutateladze, S. On the transition to film boiling under natural convection. Kotloturbostroenie 1948, 3, 10–12. [Google Scholar]
- El-Genk, M.S.; Bostanci, H. Saturation boiling of HFE-7100 from a copper surface, simulating a microelectronic chip. Int. J. Heat Mass Transf. 2003, 46, 1841–1854. [Google Scholar] [CrossRef]
- Vishnev, I. Effect of orienting the hot surface with respect to the gravitational field on the critical nucleate boiling of a liquid. J. Eng. Phys. 1973, 24, 43–48. [Google Scholar] [CrossRef]
- Arik, M.; Bar-Cohen, A. Ebullient cooling of integrated circuits by Novec fluids. In Proceedings of the Pacific Rim Intersociety, Electronics Packaging Conference, Kauai, HI, USA, 8–13 July 2001. [Google Scholar]
- Brusstar, M.J.; Merte, H., Jr. Effects of heater surface orientation on the critical heat flux—II. A model for pool and forced convection subcooled boiling. Int. J. Heat Mass Transf. 1997, 40, 4021–4030. [Google Scholar]
- Brusstar, M.J.; Merte, H., Jr. Effects of buoyancy on the critical heat flux in forced convection. J. Thermophys. Heat Transf. 1994, 8, 322–328. [Google Scholar] [CrossRef]
- Chang, J.; You, S. Heater orientation effects on pool boiling of micro-porous-enhanced surfaces in saturated FC-72. J. Heat Transf. 1996, 118, 937–943. [Google Scholar] [CrossRef]
- Kirichenko, Y.A.; Chernyakov, P. Determination of the first critical thermal flux on flat heaters. J. Eng. Phys. 1971, 20, 699–703. [Google Scholar] [CrossRef]
- Liao, L.; Bao, R.; Liu, Z. Compositive effects of orientation and contact angle on critical heat flux in pool boiling of water. Heat Mass Transf. 2008, 44, 1447–1453. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Pool boiling critical heat flux (CHF)–Part 2: Assessment of models and correlations. Int. J. Heat Mass Transf. 2018, 117, 1368–1383. [Google Scholar] [CrossRef]
- Cerjan, B.; Gerislioglu, B.; Link, S.; Nordlander, P.; Halas, N.J.; Griep, M. Towards scalable plasmonic Fano-resonant metasurfaces for colorimetric sensing. Nanotechnology 2022, 33, 405201. [Google Scholar] [CrossRef]
- Sajjad, U.; Abbas, A.; Sadeghianjahromi, A.; Abbas, N.; Liaw, J.S.; Wang, C.C. Enhancing corrosion resistance of Al 5050 alloy based on surface roughness and its fabrication methods; an experimental investigation. J. Mater. Res. Technol. 2021, 11, 1859–1867. [Google Scholar] [CrossRef]
- Abbas, N.; Shad, M.R.; Hussain, M.; Mehdi, S.M.Z.; Sajjad, U. Fabrication and characterization of silver thin films using physical vapor deposition, and the investigation of annealing effects on their structures. Mater. Res. Express 2019, 6, 116437. [Google Scholar] [CrossRef]
- Mehdi, S.; Shah, Y.; Mondal, A.; Kim, N.-H. Bubble dynamics of R-134a boiling in enhanced surfaces having pores on sub-tunnels. Int. J. Heat Mass Transf. 2020, 155, 119753. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, X.; Yin, L. Research on image classification method based on improved multi-scale relational network. PeerJ Comput. Sci. 2021, 7, e613. [Google Scholar] [CrossRef]
- Ma, Z.; Zheng, W.; Chen, X.; Yin, L. Joint embedding VQA model based on dynamic word vector. PeerJ Comput. Sci. 2021, 7, e353. [Google Scholar] [CrossRef]
- Ban, Y.; Liu, M.; Wu, P.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Depth Estimation Method for Monocular Camera Defocus Images in Microscopic Scenes. Electronics 2022, 11, 2012. [Google Scholar] [CrossRef]
- Bai, Y.; Nardi, D.C.; Zhou, X.; Picón, R.A.; Flórez-López, J. A new comprehensive model of damage for flexural subassemblies prone to fatigue. Comput. Struct. 2021, 256, 106639. [Google Scholar] [CrossRef]
- Zhao, W.; Suo, H.; Wang, S.; Ma, L.; Wang, L.; Wang, Q.; Zhang, Z. Mg gas infiltration for the fabrication of MgB2 pellets using nanosized and microsized B powders. J. Eur. Ceram. Soc. 2022, in press. [CrossRef]
- Wu, Y.; Zhao, Y.; Han, X.; Jiang, G.; Shi, J.; Liu, P.; Khan, M.Z.; Huhtinen, H.; Zhu, J.; Jin, Z.; et al. Ultra-fast growth of cuprate superconducting films: Dual-phase liquid assisted epitaxy and strong flux pinning. Mater. Today Phys. 2021, 18, 100400. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, R. Isolated Ni atoms induced edge stabilities and equilibrium shapes of CVD-prepared hexagonal boron nitride on Ni (111) surface. New J. Chem. 2022. [Google Scholar] [CrossRef]
- Ji, B.; Gou, J.; Zheng, Y.; Zhou, X.; Kidkhunthod, P.; Wang, Y.; Tang, Q.; Tang, Y. Metalloid-cluster ligands enabling stable and active FeN4-Ten motifs for oxygen reduction reaction. Adv. Mater. 2022, 34, 2202714. [Google Scholar] [CrossRef] [PubMed]
- Sajjad, U.; Hussain, I.; Hamid, K.; Bhat, S.A.; Ali, H.M.; Wang, C.-C. A deep learning method for estimating the boiling heat transfer coefficient of porous surfaces. J. Therm. Anal. Calorim. 2021, 145, 1911–1923. [Google Scholar] [CrossRef]
- Sajjad, U.; Hussain, I.; Wang, C.-C. A high-fidelity approach to correlate the nucleate pool boiling data of roughened surfaces. Int. J. Multiph. Flow 2021, 142, 103719. [Google Scholar] [CrossRef]
- Sajjad, U.; Hussain, I.; Imran, M.; Sultan, M.; Wang, C.-C.; Alsubaie, A.S.; Mahmoud, K.H. Boiling Heat Transfer Evaluation in Nanoporous Surface Coatings. Nanomaterials 2021, 11, 3383. [Google Scholar] [CrossRef]
- Sajjad, U.; Hussain, I.; Hamid, K.; Ali, H.M.; Wang, C.-C.; Yan, W.-M. Liquid-to-vapor phase change heat transfer evaluation and parameter sensitivity analysis of nanoporous surface coatings. Int. J. Heat Mass Transf. 2022, 194, 123088. [Google Scholar] [CrossRef]
- Sajjad, U.; Kumar, A.; Wang, C.-C. Nucleate pool boiling OF sintered coated porous surfaces with dielectric liquid, HFE-7200. J. Enhanc. Heat Transf. 2020, 27, 767–784. [Google Scholar] [CrossRef]
- Sajjad, U.; Sadeghianjahromi, A.; Wang, C.-C. Enhancing boiling heat transfer for electronics cooling by embedding an array of microgrooves into sandblasted surfaces. Heat Transf. Res. 2021, 52, 71–89. [Google Scholar] [CrossRef]
- Pearson, E.S. The test of significance for the correlation coefficient. J. Am. Stat. Assoc. 1931, 26, 128–134. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1948. [Google Scholar]
- Spearman, C. Demonstration of formulae for true measurement of correlation. Am. J. Psychol. 1907, 18, 161–169. [Google Scholar] [CrossRef]
- Asfahan, H.M.; Sajjad, U.; Sultan, M.; Hussain, I.; Hamid, K.; Ali, M.; Wang, C.-C.; Shamshiri, R.R.; Khan, M.U. Artificial intelligence for the prediction of the thermal performance of evaporative cooling systems. Energies 2021, 14, 3946. [Google Scholar] [CrossRef]
- Sajjad, U.; Hussain, I.; Sultan, M.; Mehdi, S.; Wang, C.-C.; Rasool, K.; Saleh, S.M.; Elnaggar, A.Y.; Hussein, E.E. Determining the factors affecting the boiling heat transfer coefficient of sintered coated porous surfaces. Sustainability 2021, 13, 12631. [Google Scholar] [CrossRef]



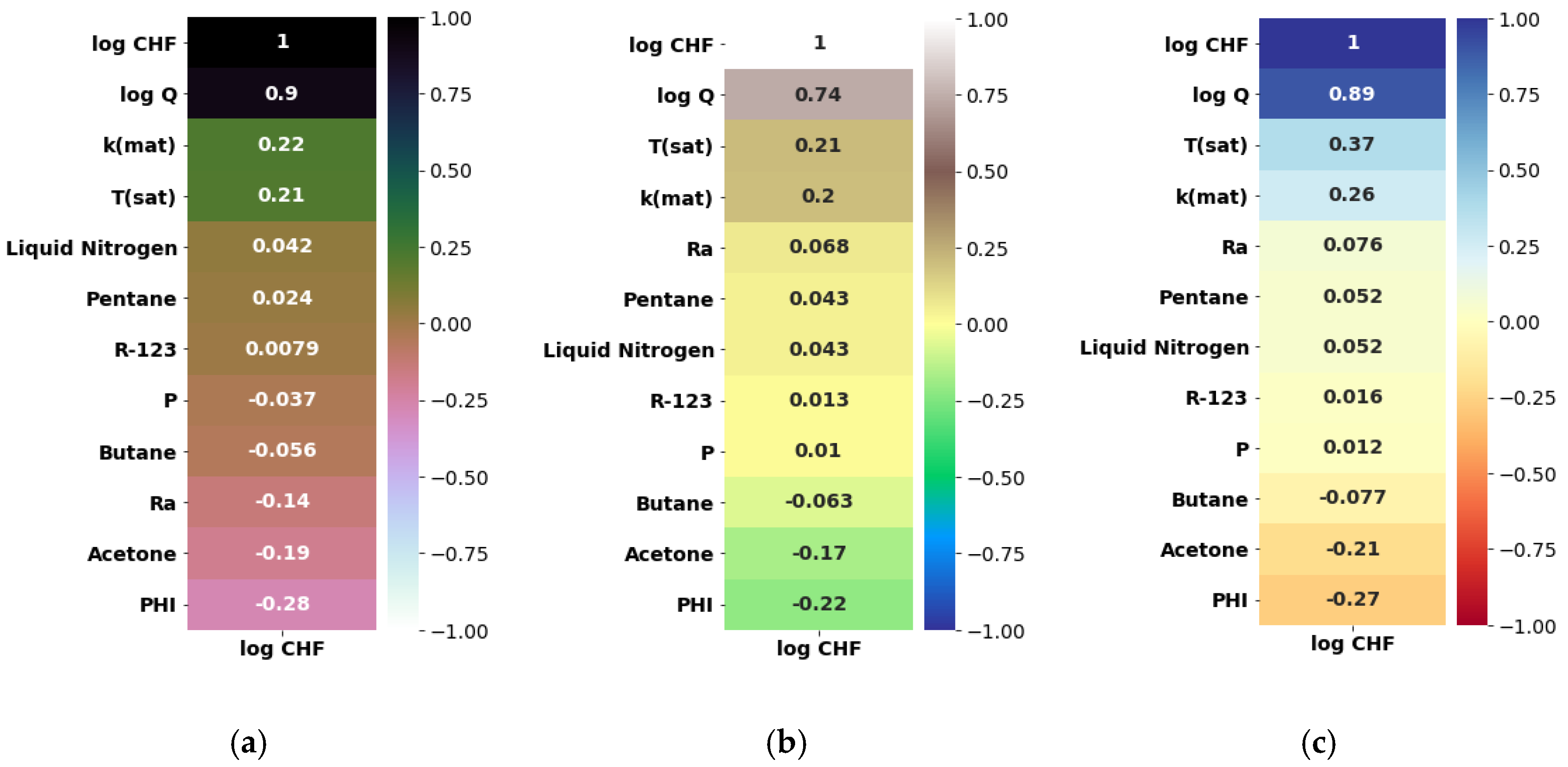
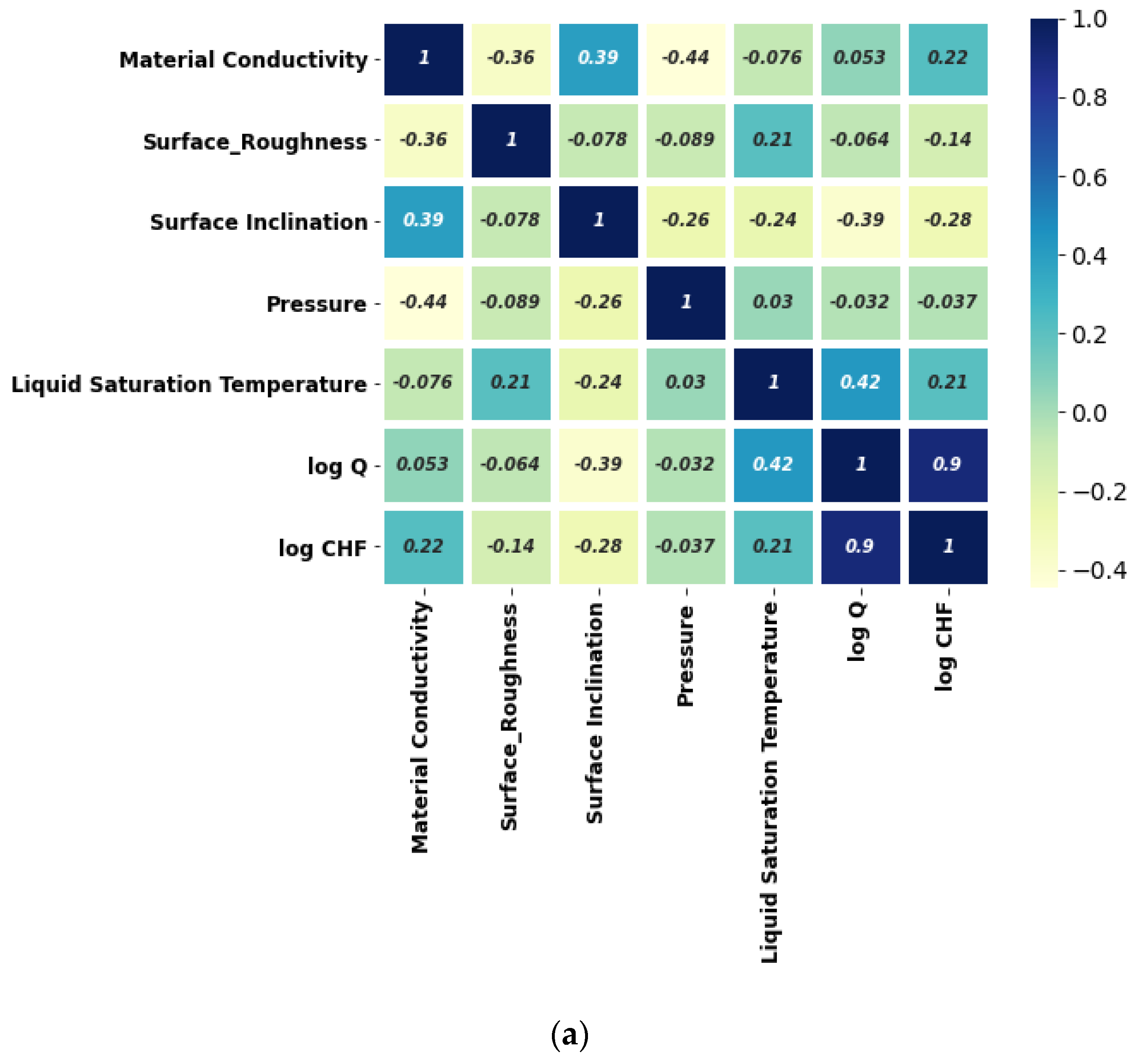

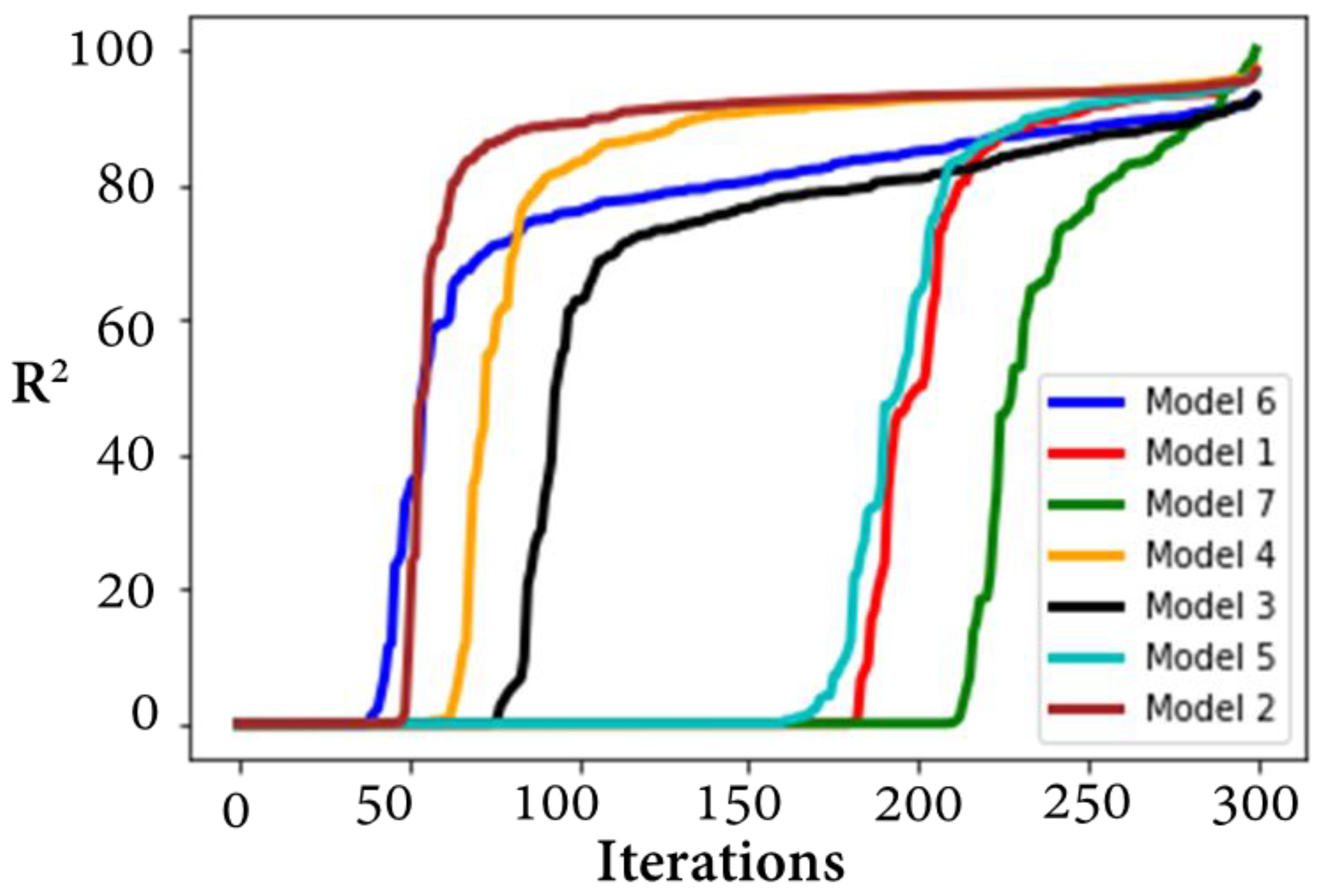
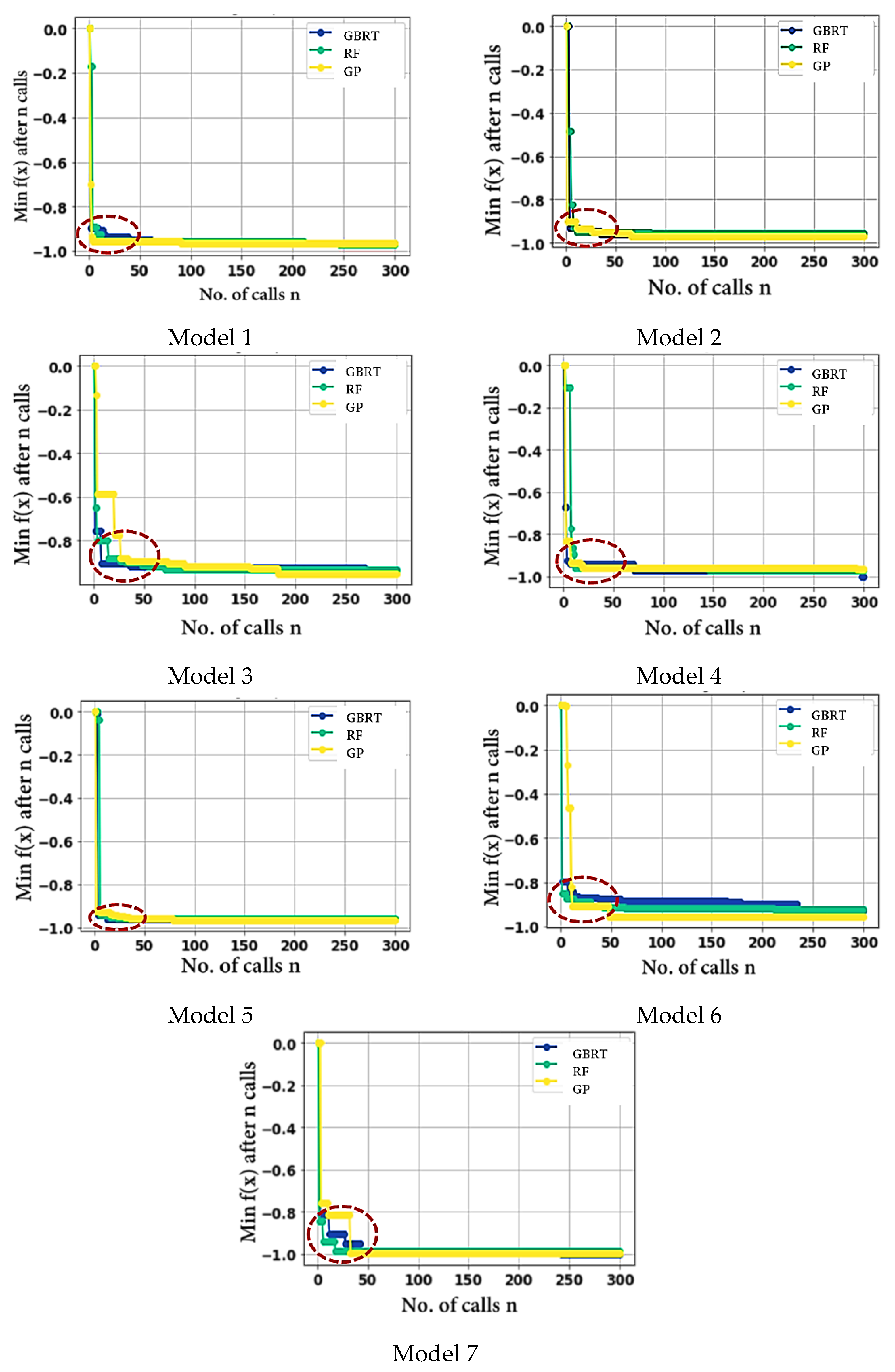
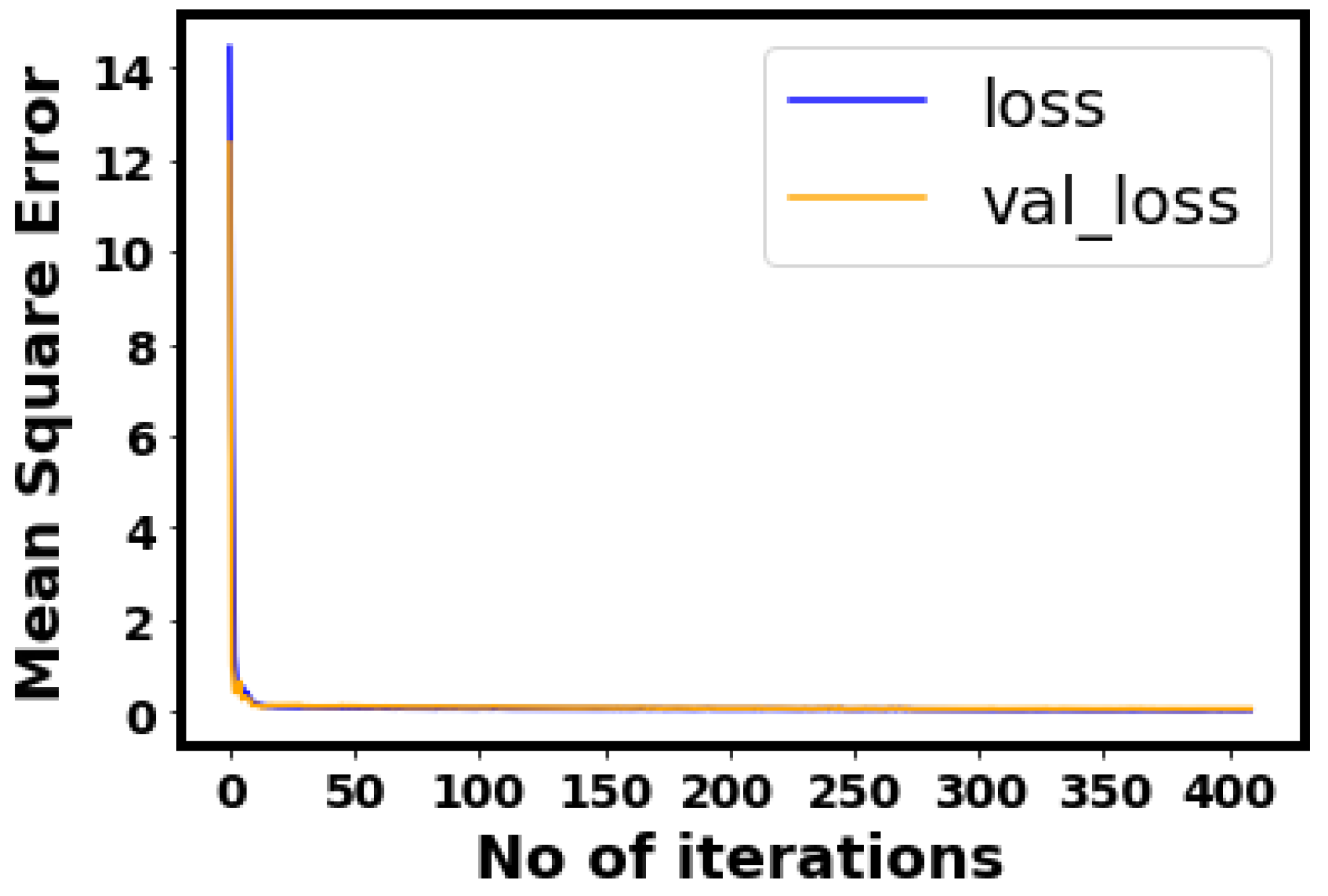
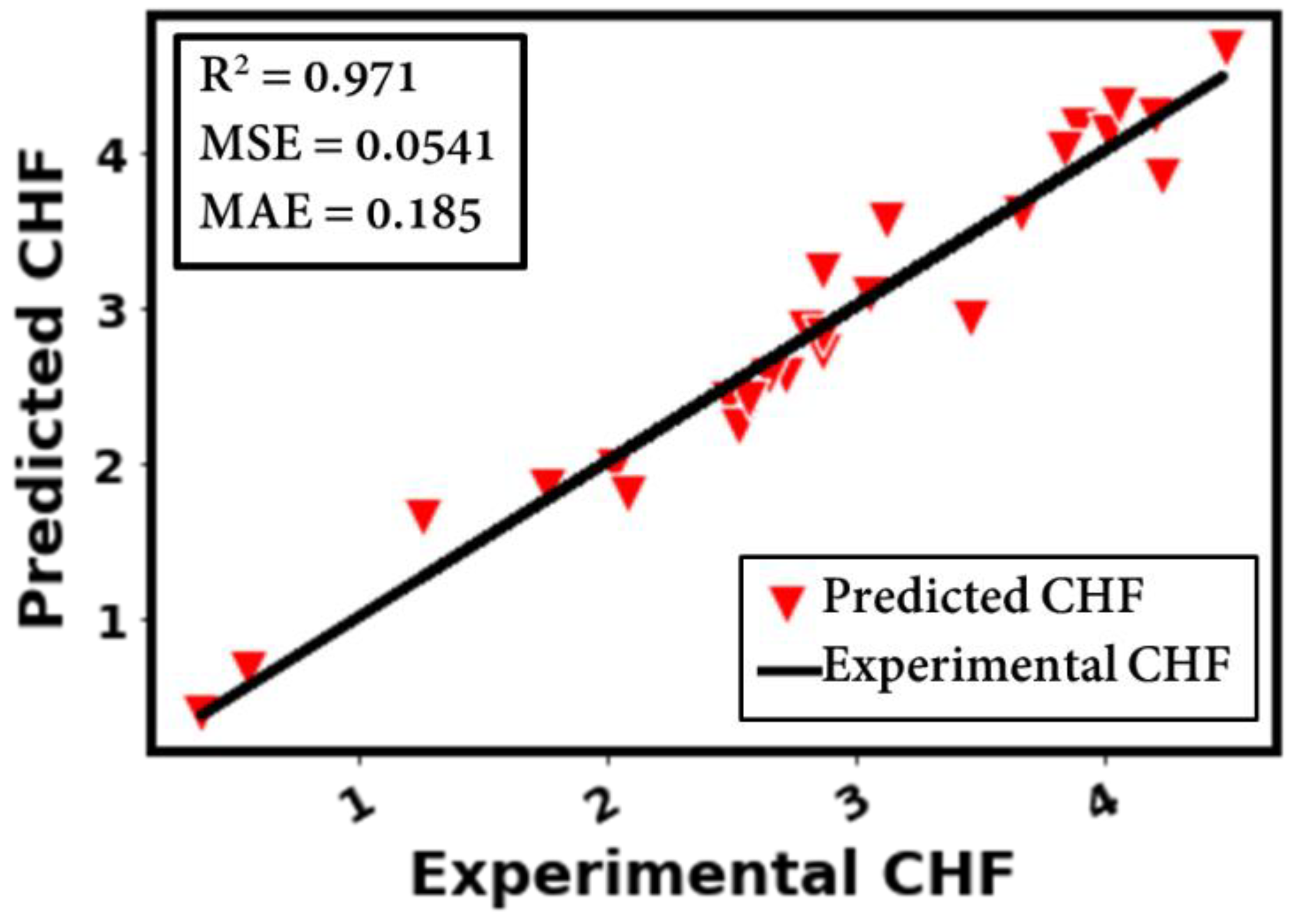
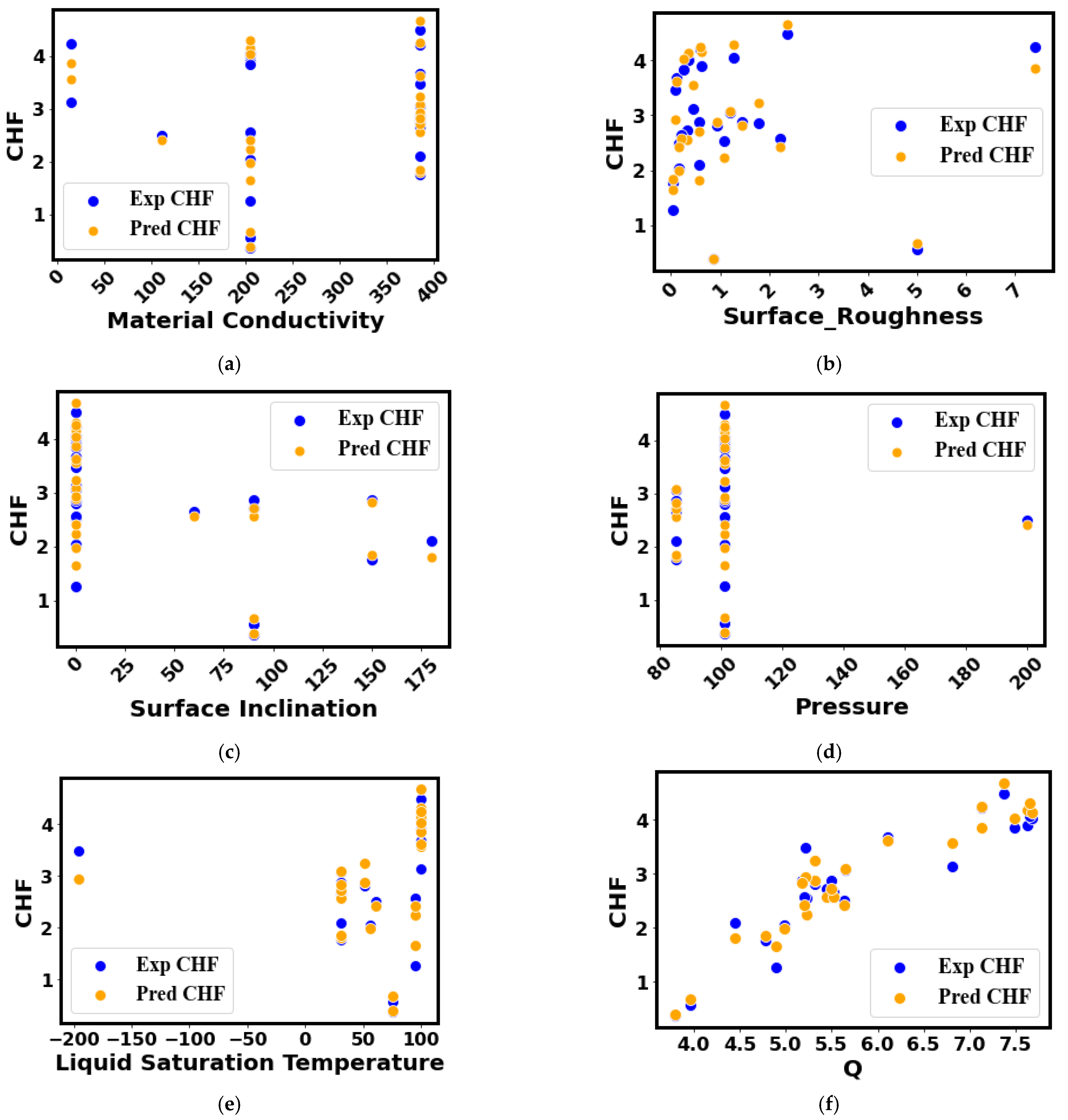
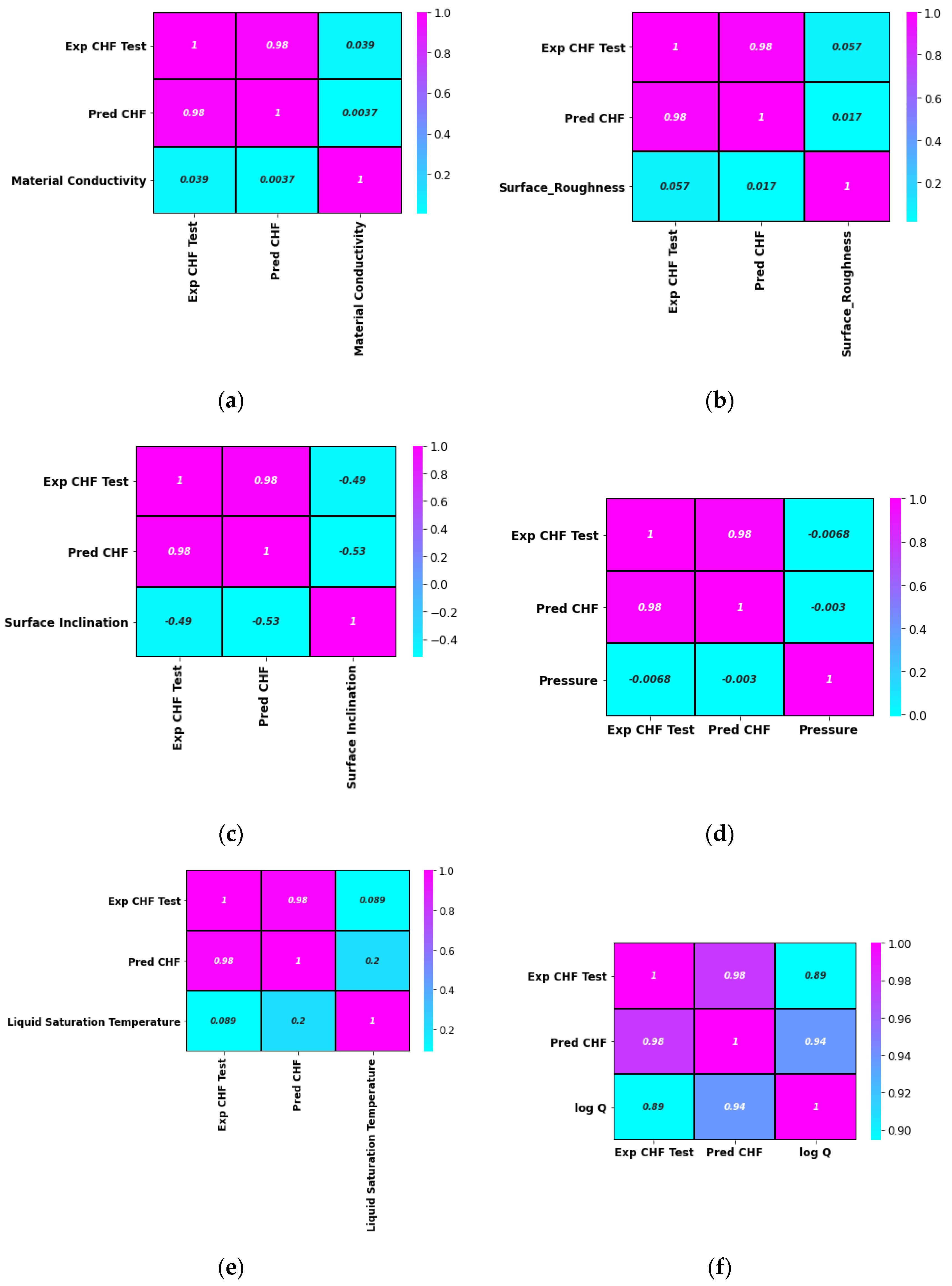
| Sr. | Description | R2 of Bayesian Surrogate Models | ||
|---|---|---|---|---|
| RF | GP | GBRT | ||
| 1 | Q is dropped, log is applied to CHF and Del T | 96.95 | 95.57 | 95.12 |
| 2 | Log is applied to all input features | 95.03 | 96.92 | 94.69 |
| 3 | Del T is dropped | 93.11 | 91.11 | 92.13 |
| 4 | Del T is dropped, log is applied to CHF and Q | 97.14 | 97.05 | 97.06 |
| 5 | Del T is dropped, log is applied to CHF | 96.22 | 95.44 | 96.40 |
| 6 | Q is dropped | 92.17 | 90.23 | 93.10 |
| 7 | All features are included | 98.5 | 100 | 99.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajjad, U.; Hussain, I.; Raza, W.; Sultan, M.; Alarifi, I.M.; Wang, C.-C. On the Critical Heat Flux Assessment of Micro- and Nanoscale Roughened Surfaces. Nanomaterials 2022, 12, 3256. https://doi.org/10.3390/nano12183256
Sajjad U, Hussain I, Raza W, Sultan M, Alarifi IM, Wang C-C. On the Critical Heat Flux Assessment of Micro- and Nanoscale Roughened Surfaces. Nanomaterials. 2022; 12(18):3256. https://doi.org/10.3390/nano12183256
Chicago/Turabian StyleSajjad, Uzair, Imtiyaz Hussain, Waseem Raza, Muhammad Sultan, Ibrahim M. Alarifi, and Chi-Chuan Wang. 2022. "On the Critical Heat Flux Assessment of Micro- and Nanoscale Roughened Surfaces" Nanomaterials 12, no. 18: 3256. https://doi.org/10.3390/nano12183256
APA StyleSajjad, U., Hussain, I., Raza, W., Sultan, M., Alarifi, I. M., & Wang, C.-C. (2022). On the Critical Heat Flux Assessment of Micro- and Nanoscale Roughened Surfaces. Nanomaterials, 12(18), 3256. https://doi.org/10.3390/nano12183256