The Impacts of Viscoelastic Behavior on Electrokinetic Energy Conversion for Jeffreys Fluid in Microtubes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analytical Solutions of the Velocity Field
2.2. Resolution Procedure
2.3. Analytical Solution of the Streaming Potential
2.4. Electric Energy Conversion Efficiency
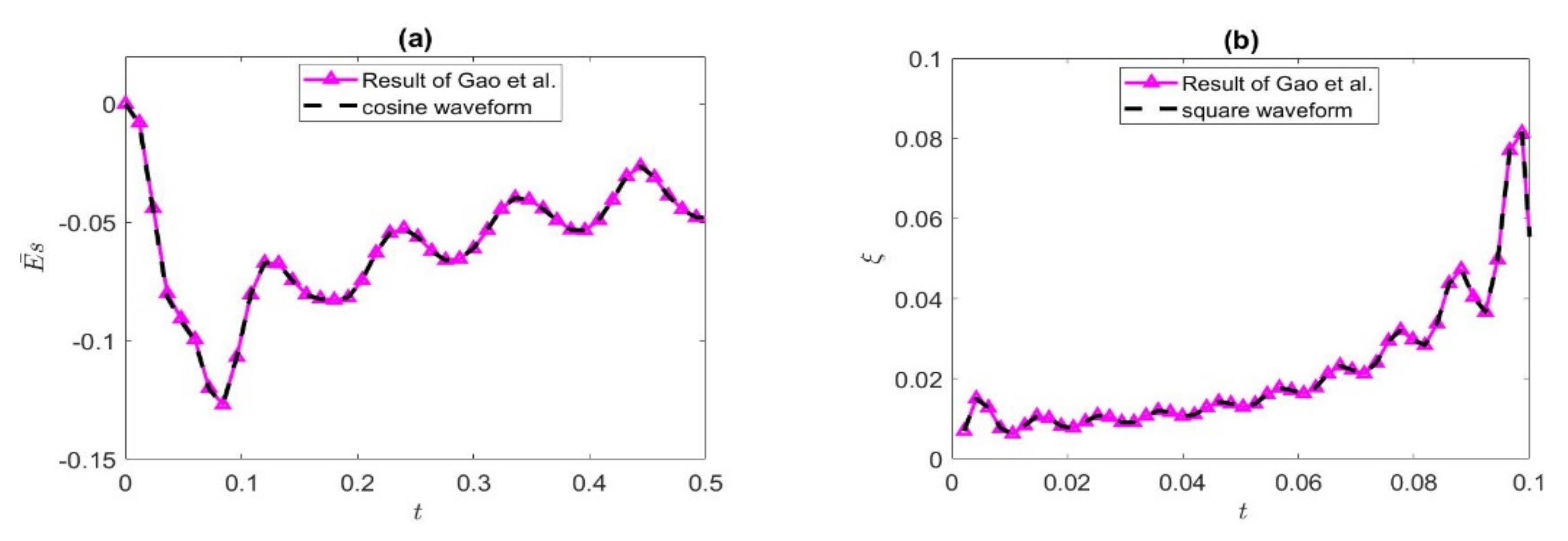
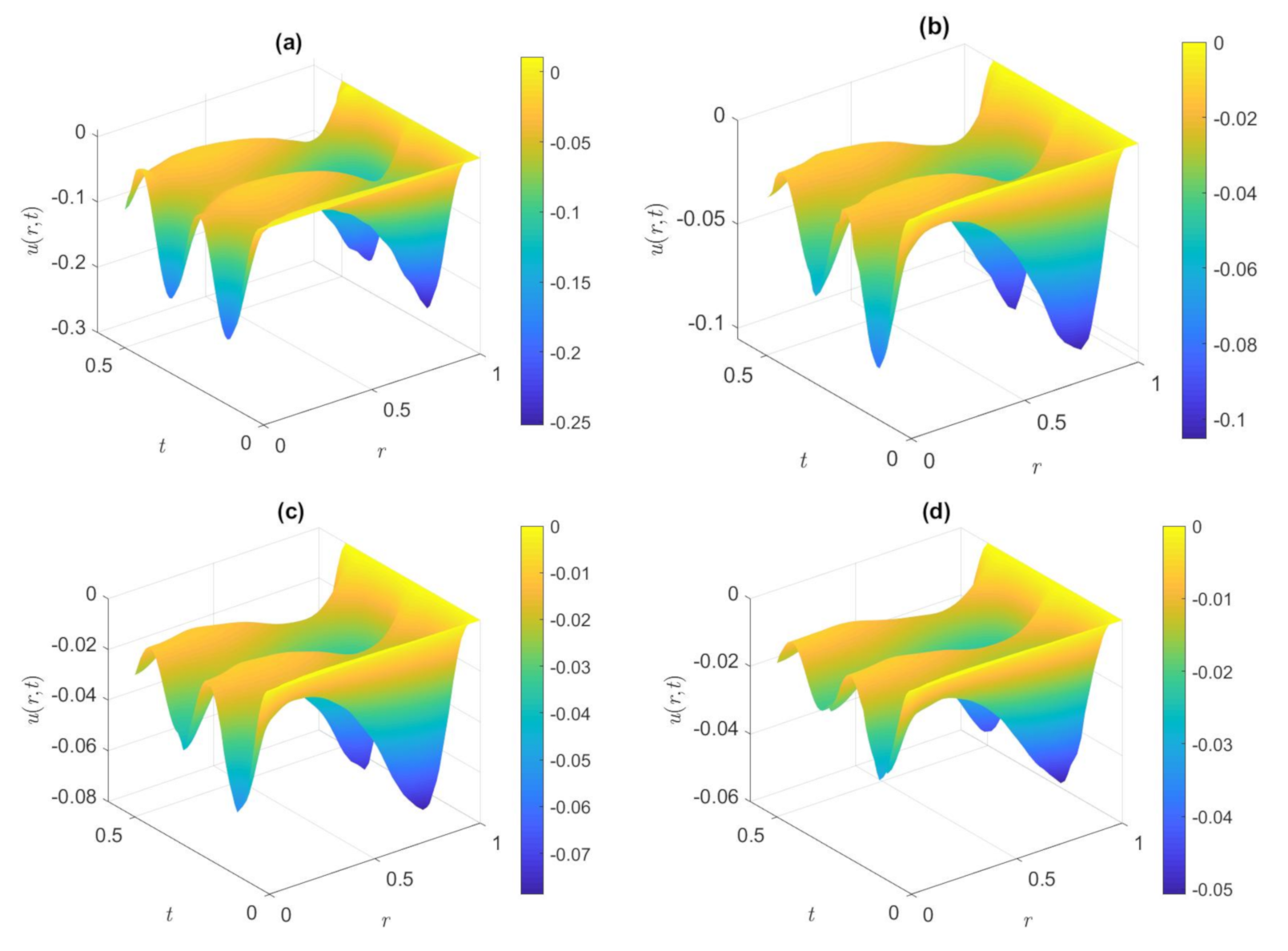
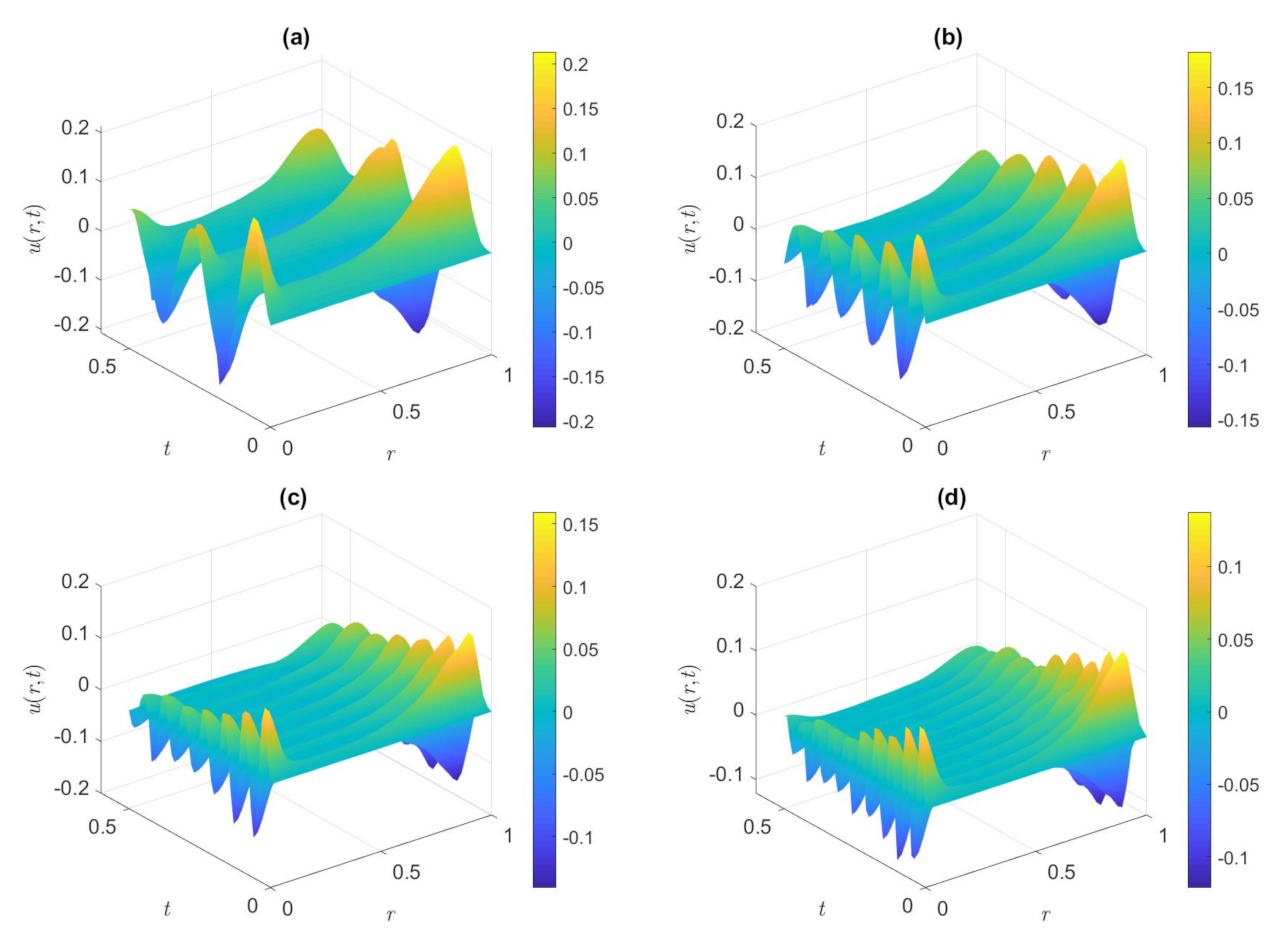
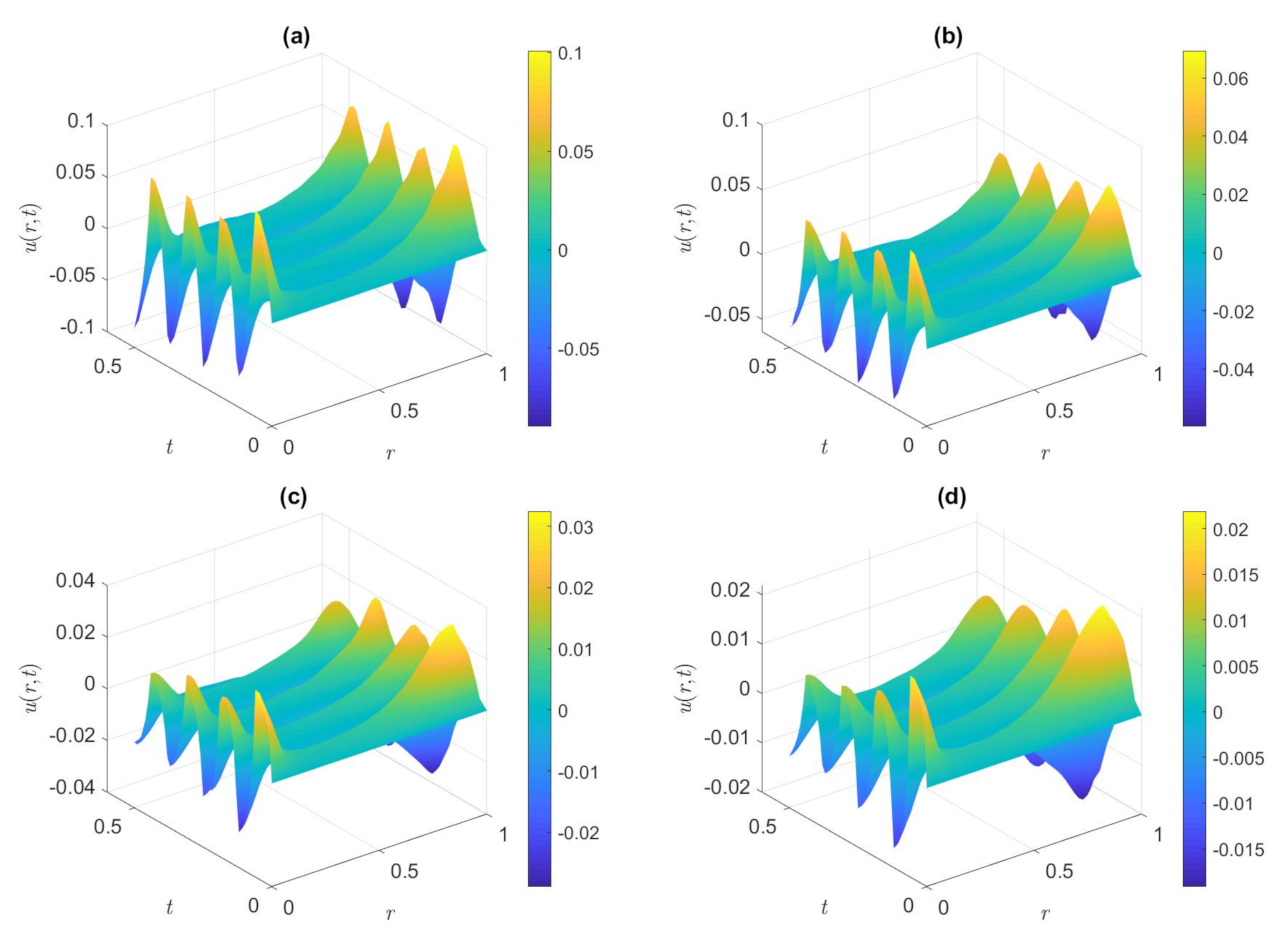
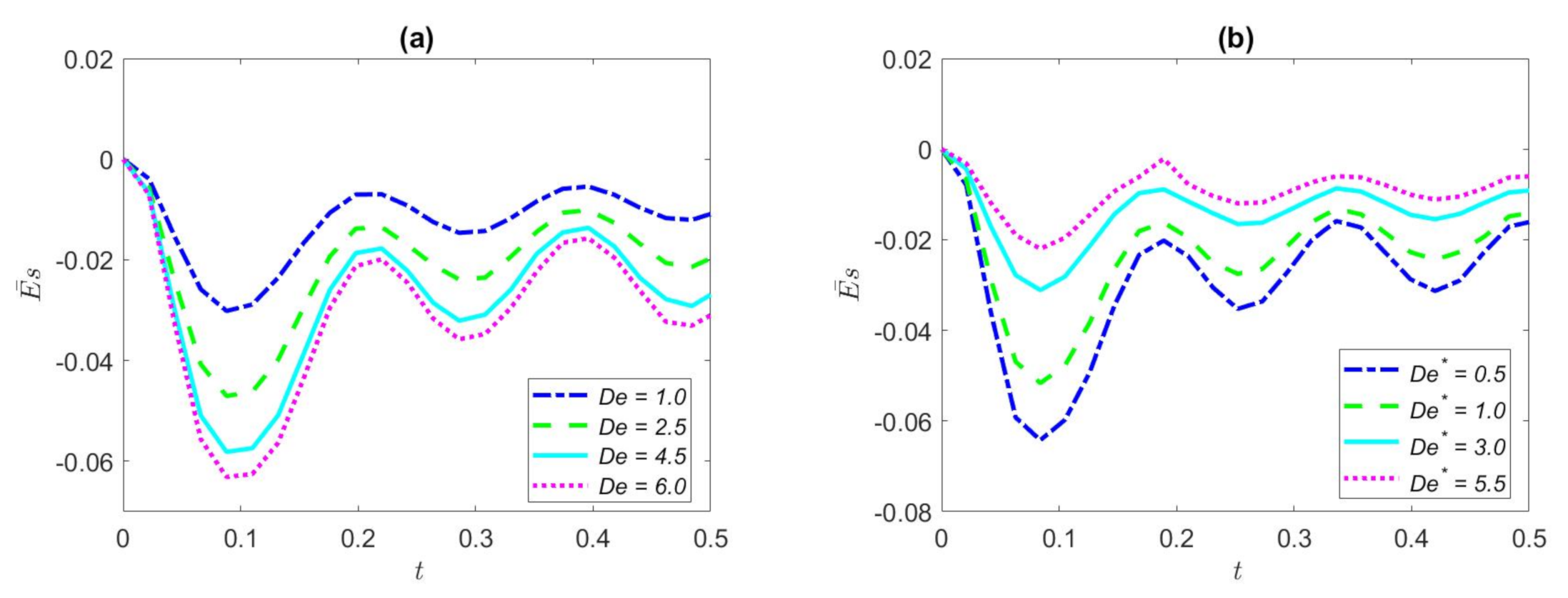
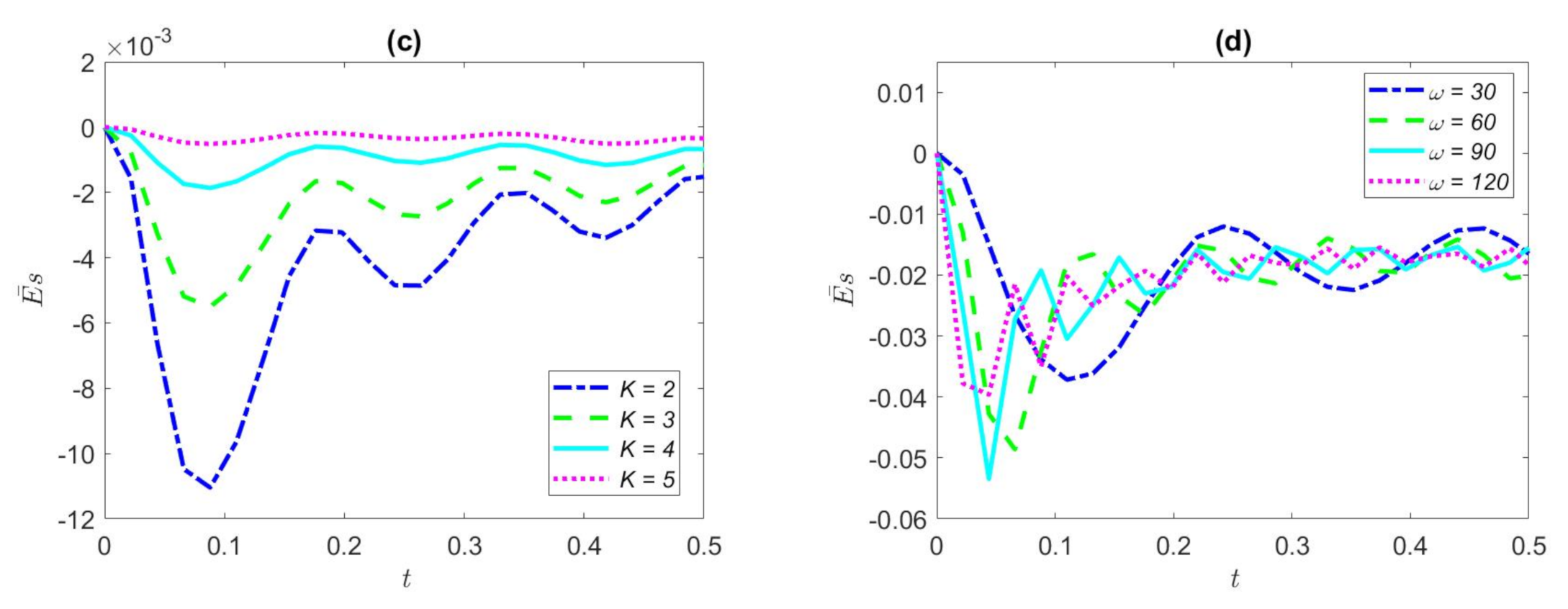
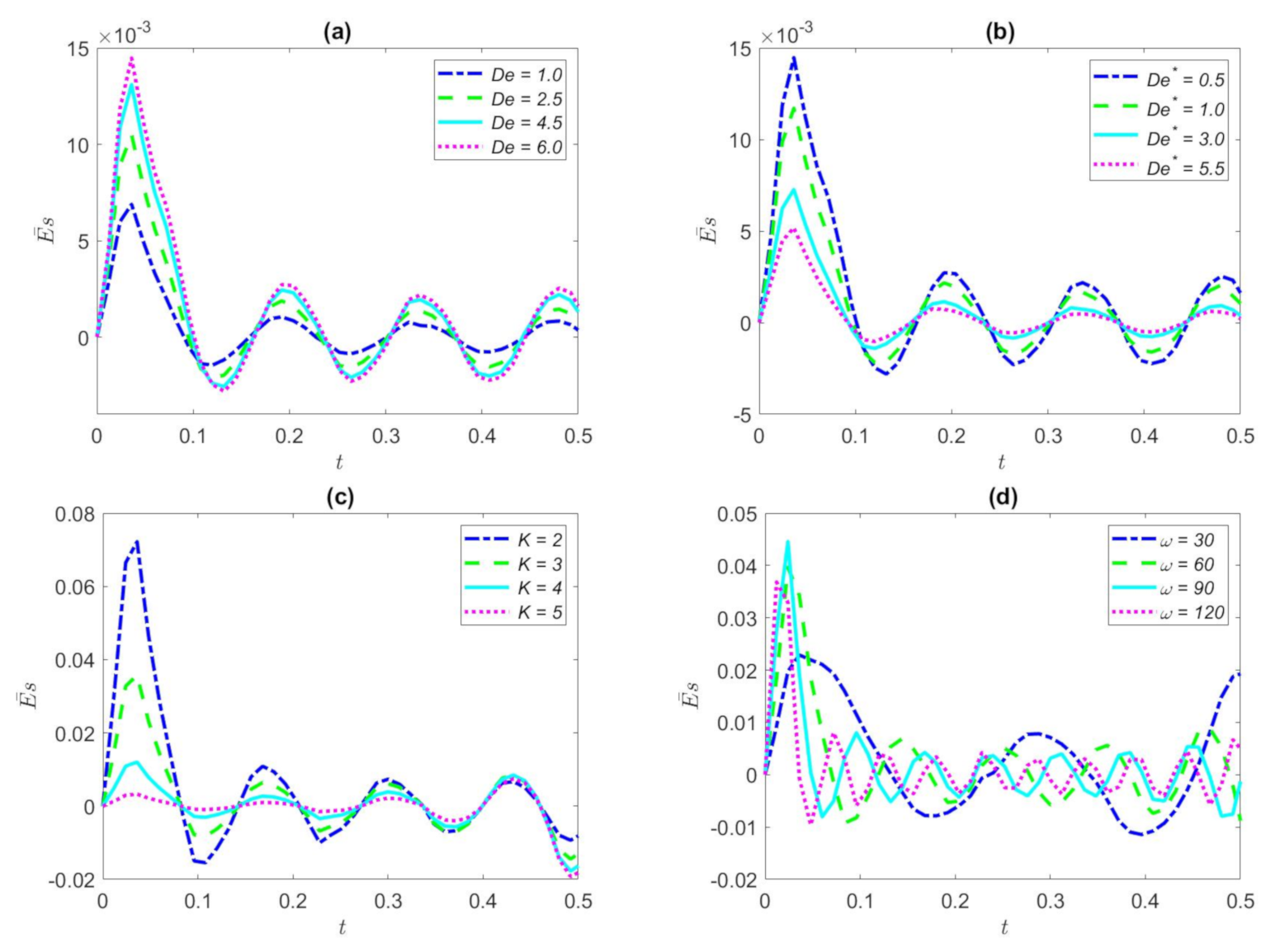
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shao, C.; Chi, J.; Shang, L.; Fan, Q.; Ye, F. Droplet microfluidics-based biomedical microcarriers. Acta. Biomater. 2022, 138, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Li, S.; Guo, Y.; Zeng, X.; Liu, B.-F. A review on microfluidics manipulation of the extracellular chemical microenvironment and its emerging application to cell analysis. Anal. Chim. Acta. 2020, 1125, 94–113. [Google Scholar] [CrossRef] [PubMed]
- Luni, C.; Gagliano, O.; Elvassore, N. Derivation and Differentiation of Human Pluripotent Stem Cells in Microfluidic Devices. Annu. Rev. Biomed Eng. 2022, 24, 231–248. [Google Scholar] [CrossRef] [PubMed]
- Karthik, V.; Karuna, B.; Kumar, P.S.; Saravanan, S.; Hemavathy, R.V. Development of lab-on-chip biosensor for the detection of toxic heavy metals: A review. Chemosphere 2022, 299, 134427. [Google Scholar] [CrossRef] [PubMed]
- Le, H.T.; Haque, R.I.; Ouyang, Z.; Lee, S.W.; Fried, S.I.; Zhao, D.; Qiu, M.; Han, A. MEMS inductor fabrication and emerging applications in power electronics and neurotechnologies. Microsyst. Nanoeng. 2021, 7, 59. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Li, Z.; Tang, Q.; Chen, J.; Huang, Y.; Hu, C.; Guo, H.; Peng, Y.; Wang, Z.L. A Mobile and Self-Powered Micro-Flow Pump Based on Triboelectricity Driven Electroosmosis. Adv. Mater. 2021, 33, e2102765. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, S.; Liu, Y.; Yang, T.; Tong, Z.; Shan, X.; Fu, H. Precise monodisperse droplet generation by pressure-driven microfluidic flows. Chem. Eng. Sci. 2022, 248, 117206. [Google Scholar] [CrossRef]
- Calver, S.N.; Gaffney, E.A.; Walsh, E.J.; Durham, W.M.; Oliver, J.M. On the thin-film asymptotics of surface tension driven microfluidics. J. Fluid 2020, 901, 1–28. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Jian, Y.J. Electrokinetic energy conversion of nanofluids in MHD-based microtube. Energy 2020, 212, 118711. [Google Scholar] [CrossRef]
- Zhao, G.P.; Jian, Y.J.; Long, C.; Mandula, B. Magnetohydrodynamic flow of generalized Maxwell fluids in a rectangular micro pump under an AC electric field. J. Magn. Magn. Mater. 2015, 387, 111–117. [Google Scholar] [CrossRef]
- Zhao, G.P.; Zhang, J.L.; Wang, Z.Q.; Jian, Y.J. Electrokinetic energy conversion of electro-magneto-hydro-dynamic nanofluids through a microannulus under the time-periodic excitation. Appl. Math. Mech. 2021, 42, 1029–1046. [Google Scholar] [CrossRef]
- Bimalendu, M.; Aditya, B. Effect of skimming layer in an electroosmotically driven viscoelastic fluid flow over charge modulated walls. Electrophoresis 2021, 43, 724–731. [Google Scholar]
- Bimalendu, M.; Aditya, B. Microconfined electroosmotic flow of a complex fluid with asymmetric charges: Interplay of fluid rheology and physicochemical heterogeneity. J. Non-Newton. Fluid 2021, 289, 104479. [Google Scholar]
- Sujit, S.; Balaram, K. Electroosmotic pressure-driven oscillatory flow and mass transport of Oldroyd-B fluid under high zeta potential and slippage conditions in microchannels. Colloid Surf. A 2022, 647, 129070. [Google Scholar]
- Zhang, J.L.; Zhao, G.P.; Gao, X.; Li, N.; Jian, Y.J. Streaming potential and electrokinetic energy conversion of nanofluids in a parallel plate microchannel under the time-periodic excitation. Chin. J. Phys. 2022, 75, 55–68. [Google Scholar] [CrossRef]
- Xie, Z.Y. Electrokinetic energy conversion of core-annular flow in a slippery nanotube. Colloid Surf. A 2022, 642, 128723. [Google Scholar] [CrossRef]
- Long, R.; Wu, F.; Chen, X.; Liu, Z.; Liu, W. Temperature-depended ion concentration polarization in electrokinetic energy conversion. Int. J. Heat Mass Transf. 2021, 168, 120842. [Google Scholar] [CrossRef]
- Jian, Y.J. Electrokinetic energy conversion of fluids with pressure-dependent viscosity in nanofluidic channels. Int. J. Eng. Sci. 2022, 170, 103590. [Google Scholar] [CrossRef]
- Jian, Y.J.; Li, F.Q.; Liu, Y.B.; Chang, L.; Liu, Q.S.; Yang, L.G. Electrokinetic energy conversion efficiency of viscoelastic fluids in a polyelectrolyte-grafted nanochannel. Colloid Surf. B 2017, 156, 405–413. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Jian, Y.J. Electrokinetic energy conversion of power-law fluids in a slit nanochannel beyond Debye-Hückel linearization. Energy 2022, 252, 124029. [Google Scholar] [CrossRef]
- Chu, X.; Jian, Y.J. Electrokinetic energy conversion through cylindrical microannulus with periodic heterogeneous wall potentials. J. Phys. D 2022, 55, 1–22. [Google Scholar] [CrossRef]
- Buren, M.; Jian, Y.J.; Zhao, Y.C.; Chang, L.; Liu, Q.S. Effects of surface charge and boundary slip on time-periodic pressure-driven flow and electrokinetic energy conversion in a nanotube. Beilstein J. Nanotech. 2019, 10, 1628–1635. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Oztop, H.F. Investigation of MHD and applied electric field effects in a conduit cramed with nanofluids. Int. Commun. Heat Mass Transf. 2021, 121, 105097. [Google Scholar] [CrossRef]
- Zhao, G.P.; Wang, Z.Q.; Jian, Y.J. Heat transfer of the MHD nanofluid in porous microtubes under the electrokinetic effects. Int. J. Heat Mass Transf. 2019, 130, 821–830. [Google Scholar] [CrossRef]
- Hashimoto, S.; Harada, M.; Higuchi, Y.; Matsunaga, T. Enhancement mechanism of convective heat transfer via nanofluid: An analysis by means of synchrotron radiation imaging. Int. J. Heat Mass Transf. 2020, 159, 120081. [Google Scholar] [CrossRef]
- Pouyan, T.; Amin, S.; Davood, T.; Pouya, B. An experimental investigation for study the rheological behavior of water–carbon nanotube/magnetite nanofluid subjected to a magnetic field. Physical A 2019, 534, 122129. [Google Scholar]
- Izza, A.I.; Mohd, Z.Y.; Firas, B.I.; Prem, G. Heat transfer enhancement with nano-fluids: A review of recent applications and experiments. Int. J. Heat Technol. 2018, 36, 1350–1361. [Google Scholar]
- Zhang, D.; He, Z.; Guan, J.; Tang, S.; Shen, C. Heat transfer and flow visualization of pulsating heat pipe with silica nanofluid: An experimental study. Int. J. Heat Mass Transf. 2022, 183, 122100. [Google Scholar] [CrossRef]
- Habibishandiz, M.; Saghir, Z. MHD mixed convection heat transfer of nanofluid containing oxytactic microorganisms inside a vertical annular porous cylinder. Int. J. Thermo Fluid 2022, 14, 100151. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.Y.; Wang, B.X. Effect of nanoparticle aggregation on the thermal radiation properties of nanofluids: An experimental and theoretical study. Int. J. Heat Mass Transf. 2020, 154, 119690. [Google Scholar] [CrossRef]
- Chao, Y.; Zhang, H.N.; Li, Y.K.; Li, X.B.; Wu, J.; Li, F.C. Nonlinear effects of viscoelastic fluid flows and applications in microfluidics: A review. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2020, 234, 4390–4414. [Google Scholar]
- Dalir, N.; Dehsar, M.; Nourazar, S.S. Entropy analysis for magnetohydrodynamic flow and heat transfer of a Jeffrey nanofluid over a stretching sheet. Energy 2015, 79, 351–362. [Google Scholar] [CrossRef]
- An, S.J.; Tian, K.; Ding, Z.; Jian, Y. Electroosmotic and pressure-driven slip flow of fractional viscoelastic fluids in microchannels. Appl. Math. Comput. 2022, 425, 125073. [Google Scholar] [CrossRef]
- Saleem, S.; Subia, G.S.; Nazeer, M.; Hussain, F.; Hameed, M.K. Theoretical study of electro-osmotic multiphase flow of Jeffrey fluid in a divergent channel with lubricated walls. Int. Commun. Heat Mass Transf. 2021, 127, 105548. [Google Scholar] [CrossRef]
- Padmaa, R.; Tamil Selvi, R.; Ponalagusamy, R. Effects of slip and magnetic field on the pulsatile flow of a Jeffrey fluid with magnetic nanoparticles in a stenosed artery. Eur. Phys. J. Plus. 2019, 134, 1–15. [Google Scholar] [CrossRef]
- Peralta, M.; Arcos, J.; Méndez, F.; Bautista, O. Mass transfer through a concentric-annulus microchannel driven by an oscillatory electroosmotic flow of a Maxwell fluid. J. Non-Newton. Fluid 2019, 266, 46–58. [Google Scholar]
- Rafiq, M.; Sajid, M.; Sharifa, E.A.; Khan, M.I.; Essam, R.E. MHD electroosmotic peristaltic flow of Jeffrey nanofluid with slip conditions and chemical reaction. Alex. Eng. J. 2022, 61, 9977–9992. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Mustafa, M.; Alsaedi, A. Three-dimensional flow of Jeffrey fluid with Cattaneo–Christov heat flux: An application to non-Fourier heat flux theory. Chin. J. Phys. 2017, 55, 1067–1077. [Google Scholar] [CrossRef]
- Christiaan, L.R. On Flows of Viscoelastic Fluids of Oldroyd Type with Wall Slip. J. Math. Fluid Mech. 2014, 16, 335–350. [Google Scholar]
- Baranovskii, E.S. On steady motion of viscoelastic fluid of Oldroyd type. Sb. Math. 2014, 205, 763–776. [Google Scholar] [CrossRef]
- Antony, N.B. Continuum mechanics modeling of complex fluid systems following Oldroyd’s seminal 1950 work. J. Non-Newton. Fluid 2021, 298, 104677. [Google Scholar]
- Baranovskii, E.S.; Artemov, M.A. Global Existence Results for Oldroyd Fluids with Wall Slip. Acta Appl. Math. 2017, 147, 197–210. [Google Scholar] [CrossRef]
- Hinch, J.; Harlen, O. Oldroyd B, and not A? J. Non-Newton. Fluid 2021, 298, 104668. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Steady flows of an oldroyd fluid with threshold slip. Commun. Pure Appl. Anal. 2019, 18, 735–750. [Google Scholar] [CrossRef]
- Angiolo, F.; Lorenzo, F.; Fabio, R.; Giuseppe, S. Creep, recovery and vibration of an incompressible viscoelastic material of the rate type: Simple tension case. Int. J. Nonlin. Mech. 2022, 138, 103851. [Google Scholar]
- Kaushik, P.; Abhimanyu, P.; Mondal, P.K.; Chakraborty, S. Confinement effects on the rotational microflows of a viscoelastic fluid under electrical double layer phenomenon. J. Non-Newton. Fluid 2017, 244, 123–137. [Google Scholar] [CrossRef]
- Alvi, N.; Latif, T.; Hussain, Q.; Asghar, S. Peristalsis of nonconstant viscosity Jeffrey fluid with nanoparticles. Results Phys. 2016, 6, 1109–1125. [Google Scholar] [CrossRef]
- Hira, M.; Khadija, M.; Hameed, U.; Majeed, S.A. Computational analysis of an axisymmetric flow of Jeffrey fluid in a permeable micro channel. Appl. Math. Comput. 2022, 418, 126826. [Google Scholar]
- Li, P.; Abbasi, A.; El-Zahar, E.R.; Farooq, W.; Hussain, Z.; Khan, S.U.; Khan, M.I.; Farooq, S.; Malik, M.Y.; Wang, F. Hall effects and viscous dissipation applications in peristaltic transport of Jeffrey nanofluid due to wave frame. Colloid Interface Sci. Commun. 2022, 47, 100593. [Google Scholar] [CrossRef]
- Mederos, G.; Arcos, J.; Bautista, O.; Méndez, F. Hydrodynamics rheological impact of an oscillatory electroosmotic flowon a mass transfer process in a microcapillary with a reversible wall reaction. Phys. Fluids 2020, 32, 122003. [Google Scholar] [CrossRef]
- Koner, P.; Bera, S.; Ohshima, H. Effect of ion partitioning on an oscillatory electro-osmotic flow on solute transport process of fractional Jeffrey fluid through polyelectrolyte-coated nanopore with reversible wall reaction. Phys. Fluids 2022, 34, 062016. [Google Scholar] [CrossRef]
- Liu, Q.S.; Yang, L.G.; Su, J. Transient electroosmotic flow of general Jeffrey fluid between two micro-parallel plates. Acta Phys. Sin. 2013, 14, 144702. [Google Scholar]
- Ishtiaq, F.; Ellahi, R.; Bhatti, M.M.; Alamri, S.Z. Insight in Thermally Radiative Cilia-Driven Flow of Electrically Conducting Non-Newtonian Jeffrey Fluid under the Influence of Induced Magnetic Field. Mathematics 2022, 10, 2007. [Google Scholar] [CrossRef]
- Ambreen, A.; Sajid, M.; Rana, M.A.; Mahmood, K. Numerical simulation of heat transfer features in oblique stagnation-point flow of Jeffrey fluid. Ambreen. Aip Adv. 2018, 8, 105111. [Google Scholar]
- Gao, X.; Zhao, G.P.; Li, N.; Zhang, J.L.; Jian, Y.J. The electrokinetic energy conversion analysis of viscoelastic fluid under the periodic pressure in microtubes. Colloid Surf. A 2022, 646, 128976. [Google Scholar] [CrossRef]
- Ding, Z.D.; Jian, Y.J. Resonance behaviors in periodic viscoelastic electrokinetic flows: A universal Deborah number. Phys. Fluids 2021, 33, 032023. [Google Scholar] [CrossRef]
- Byron, B.R.; Robert, C.A.; Ole, H. The General Linear Viscoelastic Fluid. In Dynamics of Polymeric Liquids; A Wiley-Interscience Publication: Toronto, ON, Canada, 1987; Volume 1, pp. 255–283. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhao, G.; Gao, X.; Zhang, Y.; Jian, Y. The Impacts of Viscoelastic Behavior on Electrokinetic Energy Conversion for Jeffreys Fluid in Microtubes. Nanomaterials 2022, 12, 3355. https://doi.org/10.3390/nano12193355
Li N, Zhao G, Gao X, Zhang Y, Jian Y. The Impacts of Viscoelastic Behavior on Electrokinetic Energy Conversion for Jeffreys Fluid in Microtubes. Nanomaterials. 2022; 12(19):3355. https://doi.org/10.3390/nano12193355
Chicago/Turabian StyleLi, Na, Guangpu Zhao, Xue Gao, Ying Zhang, and Yongjun Jian. 2022. "The Impacts of Viscoelastic Behavior on Electrokinetic Energy Conversion for Jeffreys Fluid in Microtubes" Nanomaterials 12, no. 19: 3355. https://doi.org/10.3390/nano12193355




