Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics
Abstract
1. Introduction
2. Heat Dissipation Model of TIMs Used in High-Power Electronics
2.1. Thermal Resistance Models
2.2. Thermal Conductivity Models
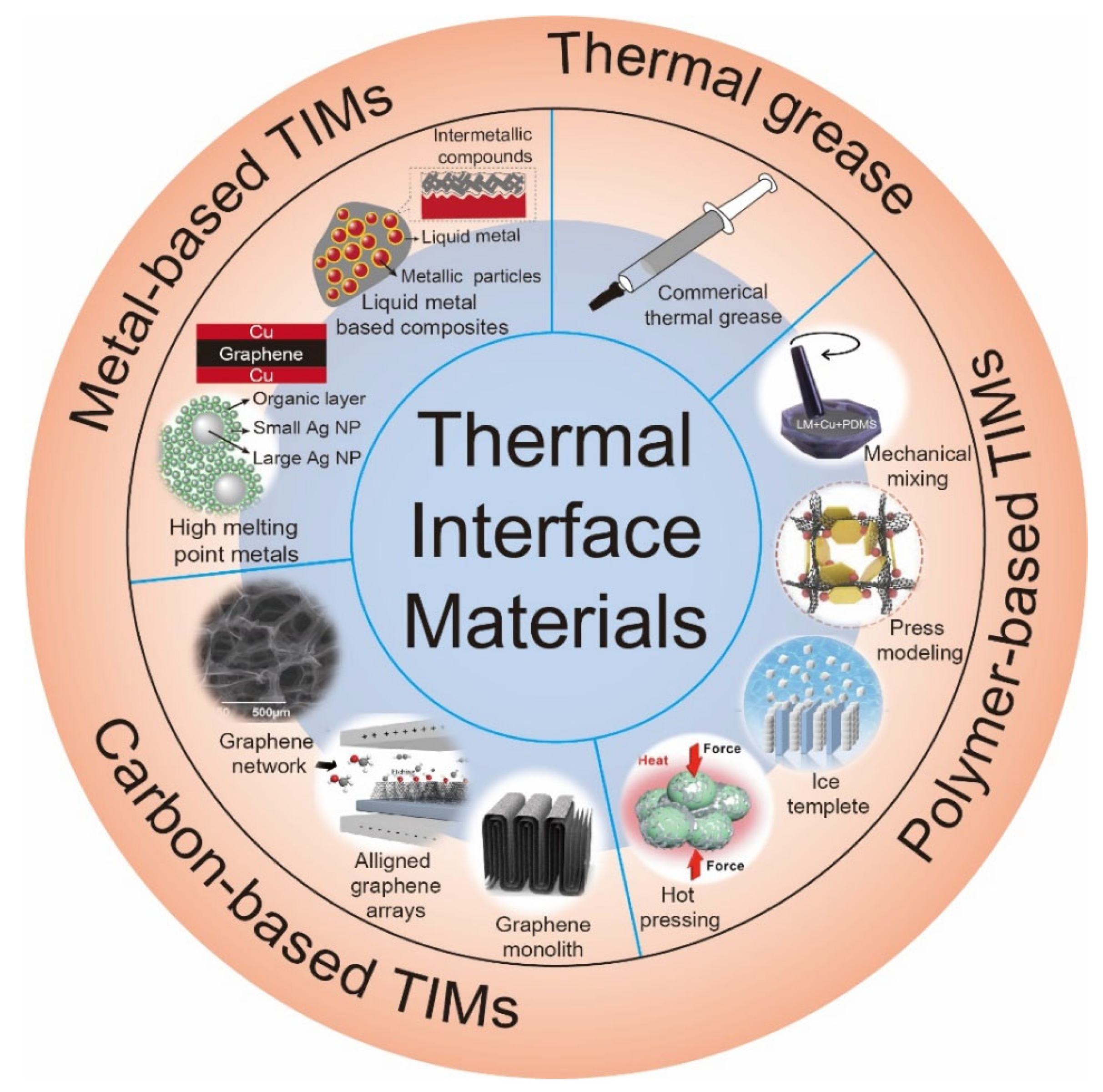
3. Types of Advanced Thermal Interface Materials for High-Power Electronics
3.1. Thermal Grease
3.2. Metal-Based Thermal Interface Materials
3.3. Carbon-Based Thermal Interface Materials
3.4. Polymer-Based Thermal Interface Materials
3.5. Methods of Thermal Measurement for Advanced Thermal Interface Materials
4. Overview and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.; Chen, X.; Lu, G.-Q. Reliability of High-Power Light Emitting Diode Attached with Different Thermal Interface Materials. J. Electron. Packag. 2010, 132, 031011. [Google Scholar] [CrossRef]
- Jones, E.A.; de Rooij, M. High-Power-Density GaN-Based Converters: Thermal Management Considerations. IEEE Power Electron. Mag. 2019, 6, 22–29. [Google Scholar] [CrossRef]
- Cui, Y.; Li, M.; Hu, Y. Emerging interface materials for electronics thermal management: Experiments, modeling, and new opportunities. J. Mater. Chem. C 2020, 8, 10568–10586. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, X.; Xiao, G.D.; Zhang, K.; He, X.; Xin, S.; Liu, X.; Zhong, A.; Chai, Y. Thermal interface material with graphene enhanced sintered copper for high temperature power electronics. Nanotechnology 2021, 32, 31011. [Google Scholar] [CrossRef]
- McGlen, R.J.; Jachuck, R.; Lin, S. Integrated thermal management techniques for high power electronic devices. Appl. Therm. Eng. 2004, 24, 1143–1156. [Google Scholar] [CrossRef]
- Otiaba, K.C.; Ekere, N.N.; Bhatti, R.S.; Mallik, S.; Alam, M.O.; Amalu, E.H. Thermal interface materials for automotive electronic control unit: Trends, technology and R&D challenges. Microelectron. Reliab. 2011, 51, 2031–2043. [Google Scholar] [CrossRef]
- Suresh, R.; Bloschock, K.P.; Bar-Cohen, A. Advanced thermal management technologies for defense electronics. In Proceedings of the Defense Transformation and Net-Centric Systems 2012, Baltimore, MD, USA, 23–27 April 2012. [Google Scholar]
- Yoonjin, W.; Jungwan, C.; Agonafer, D.; Asheghi, M.; Goodson, K.E. Fundamental Cooling Limits for High Power Density Gallium Nitride Electronics. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 737–744. [Google Scholar] [CrossRef]
- Schulz, M.; Allen, S.T.; Pohl, W. The crucial influence of thermal interface material in power electronic design. In Proceedings of the IEEE Semiconductor Thermal Measurement & Management Symposium, San Jose, CA, USA, 17–21 March 2013. [Google Scholar]
- Qinglin, T.; Dongcheng, L.; Yanping, Z.; Xin, L.; Lihua, Z. Research on the uniform temperature of heat dissipation for the reverse oblique microchannel. In Proceedings of the 2021 22nd International Conference on Electronic Packaging Technology (ICEPT), Xiamen, China, 14–17 September 2021. [Google Scholar]
- Kang, T.; Ye, Y.X.; Jia, Y.C.; Kong, Y.M.; Jiao, B.B. Enhanced Thermal Management of GaN Power Amplifier Electronics with Micro-Pin Fin Heat Sinks. Electronics 2020, 9, 1778. [Google Scholar] [CrossRef]
- Lumbreras, D.; Vilella, M.; Zaragoza, J.; Berbel, N.; Jorda, J.; Collado, A. Effect of the Heat Dissipation System on Hard-Switching GaN-Based Power Converters for Energy Conversion. Energies 2021, 14, 6287. [Google Scholar] [CrossRef]
- Sarvar, F.; Whalley, D.; Conway, P. Thermal Interface Materials—A Review of the State of the Art. Electron. Syst. Technol. Conf. 2006, 2, 1292–1302. [Google Scholar]
- Zhou, J.; Li, B.-W. The physics of heat dissipation in micro-nano-scale devices. Wuli 2013, 42, 89–99. [Google Scholar] [CrossRef]
- Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial thermal resistance: Past, present, and future. Rev. Mod. Phys. 2022, 94, 025002. [Google Scholar] [CrossRef]
- Zhang, P.; Yuan, P.; Jiang, X.; Zhai, S.P.; Zeng, J.H.; Xian, Y.Q.; Qin, H.B.; Yang, D.G. A Theoretical Review on Interfacial Thermal Transport at the Nanoscale. Small 2018, 14, 1702769. [Google Scholar] [CrossRef] [PubMed]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Prasher, R. Acoustic mismatch model for thermal contact resistance of van der Waals contacts. Appl. Phys. Lett. 2009, 94, 041905. [Google Scholar] [CrossRef]
- Hopkins, P.E.; Norris, P.M. Effects of joint vibrational states on thermal boundary conductance. Nanoscale Microscale Thermophys. Eng. 2007, 11, 247–257. [Google Scholar] [CrossRef]
- Belmabrouk, H.; Rezgui, H.; Nasri, F.; Aissa, M.F.B.; Guizani, A.A. Interfacial heat transport across multilayer nanofilms in ballistic–diffusive regime. Eur. Phys. J. Plus 2020, 135, 109. [Google Scholar] [CrossRef]
- Stevens, R.J.; Zhigilei, L.V.; Norris, P.M. Effects of temperature and disorder on thermal boundary conductance at solid-solid interfaces: Nonequilibrium molecular dynamics simulations. Int. J. Heat Mass Transf. 2007, 50, 3977–3989. [Google Scholar] [CrossRef]
- Dai, J.; Tian, Z. Rigorous formalism of anharmonic atomistic Green’s function for three-dimensional interfaces. Phys. Rev. B 2020, 101, 041301. [Google Scholar] [CrossRef]
- Shahil, K.M.F.; Balandin, A.A. Graphene-Multilayer Graphene Nanocomposites as Highly Efficient Thermal Interface Materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef]
- Prasher, R.S.; Matayabas, J.C. Thermal contact resistance of cured gel polymeric thermal interface material. IEEE Trans. Compon. Packag. Technol. 2004, 24, 702–709. [Google Scholar] [CrossRef]
- Prasher, R. Thermal interface materials: Historical perspective, status, and future directions. Proc. IEEE 2006, 94, 1571–1586. [Google Scholar] [CrossRef]
- Hu, X.; Govindasamy, S.; Goodson, K.E. Two-Medium Model for the Bond Line Thickness of Particle Filled Thermal Interface Materials. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, Anaheim, CA, USA, 13–19 November 2004. [Google Scholar]
- Prasher, R.S. Surface chemistry and characteristics based model for the thermal contact resistance of fluidic interstitial thermal interface materials. J. Heat Transf.-Trans. Asme 2001, 123, 969–975. [Google Scholar] [CrossRef]
- Wang, H.; Feng, J.Y.; Hu, X.J.; Ng, K.M. Reducing thermal contact resistance using a bilayer aligned CNT thermal interface material. Chem. Eng. Sci. 2010, 65, 1101–1108. [Google Scholar] [CrossRef]
- Giordanengo, B.; Benazzi, N.; Vinckel, J.; Gasser, J.G.; Roubi, L. Thermal conductivity of liquid metals and metallic alloys. J. Non-Cryst. Solids 1999, 250, 377–383. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.J.; Weng, G.J.; Su, Y. The effects of temperature and alignment state of nanofillers on the thermal conductivity of both metal and nonmetal based graphene nanocomposites. Acta Mater. 2020, 185, 461–473. [Google Scholar] [CrossRef]
- Xu, J.Z.; Gao, B.Z.; Kang, F.Y. A reconstruction of Maxwell model for effective thermal conductivity of composite materials. Appl. Therm. Eng. 2016, 102, 972–979. [Google Scholar] [CrossRef]
- Hasselman, D.P.H.; Johnson, L.F. Effective Thermal Conductivity of Composites with Interfacial Thermal Barrier Resistance. J. Compos. Mater. 1989, 21, 508–515. [Google Scholar] [CrossRef]
- Molina, J.M.; Rodriguez-Guerrero, A.; Louis, E.; Rodriguez-Reinoso, F.; Narciso, J. Porosity Effect on Thermal Properties of Al-12 wt % Si/Graphite Composites. Materials 2017, 10, 177. [Google Scholar] [CrossRef]
- Caccia, M.; Rodriguez, A.; Narciso, J. Diamond Surface Modification to Enhance Interfacial Thermal Conductivity in Al/Diamond Composites. JOM 2014, 66, 920–925. [Google Scholar] [CrossRef]
- Prieto, R.; Molina, J.M.; Narciso, J.; Louis, E. Thermal conductivity of graphite flakes-SiC particles/metal composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1970–1977. [Google Scholar] [CrossRef]
- Yang, X.T.; Liang, C.B.; Ma, T.B.; Guo, Y.Q.; Kong, J.; Gu, J.W.; Chen, M.J.; Zhu, J.H. A review on thermally conductive polymeric composites: Classification, measurement, model and equations, mechanism and fabrication methods. Adv. Compos. Hybrid Mater. 2018, 1, 207–230. [Google Scholar] [CrossRef]
- Pietrak, K.; Wiśniewski, T.S. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2014, 95, 14–24. [Google Scholar]
- Li, H.K.; Zheng, W.D. Enhanced thermal conductivity of epoxy/alumina composite through multiscale-disperse packing. J. Compos. Mater. 2021, 55, 17–25. [Google Scholar] [CrossRef]
- Jung, J.; Jeong, S.H.; Hjort, K.; Ryu, S. Investigation of thermal conductivity for liquid metal composites using the micromechanics-based mean-field homogenization theory. Soft Matter 2020, 16, 5840–5847. [Google Scholar] [CrossRef]
- Kochetov, R.; Korobko, A.V.; Andritsch, T.; Morshuis, P.H.F.; Picken, S.J.; Smit, J.J. Modelling of the thermal conductivity in polymer nanocomposites and the impact of the interface between filler and matrix. J. Phys. D Appl. Phys. 2011, 44, 395401. [Google Scholar] [CrossRef]
- Liang, L.H.; Wei, Y.G.; Li, B. Thermal conductivity of composites with nanoscale inclusions and size-dependent percolation. J. Phys. Condens. Matter 2008, 20, 365201. [Google Scholar] [CrossRef]
- Slack, G.A. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321–335. [Google Scholar] [CrossRef]
- Ziambaras, E.; Hyldgaard, P. Thermal transport in SiC nanostructures. Mater. Sci. Eng. C Biomim. Supramol. Syst. 2005, 25, 635–640. [Google Scholar] [CrossRef][Green Version]
- Mehra, N.; Mu, L.W.; Ji, T.; Yang, X.T.; Kong, J.; Gu, J.W.; Zhu, J.H. Thermal transport in polymeric materials and across composite interfaces. Appl. Mater. Today 2018, 12, 92–130. [Google Scholar] [CrossRef]
- Agari, Y.; Uno, T. Estimation on thermal conductivities of filled polymers. J. Appl. Polym. Sci. 1986, 32, 5705–5712. [Google Scholar] [CrossRef]
- Zha, J.W.; Zhu, Y.H.; Li, W.K.; Bai, J.; Dang, Z.M. Low dielectric permittivity and high thermal conductivity silicone rubber composites with micro-nano-sized particles. Appl. Phys. Lett. 2012, 101, 062905. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Met. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Weber, L.; Tavangar, R. Diamond-based metal matrix composites for thermal management made by liquid metal infiltration—Potential and limits. Adv. Mater. Res. 2008, 59, 111–115. [Google Scholar] [CrossRef]
- Tavangar, R.; Molina, J.M.; Weber, L. Assessing predictive schemes for thermal conductivity against diamond-reinforced silver matrix composites at intermediate phase contrast. Scr. Mater. 2007, 56, 357–360. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 27–40. [Google Scholar] [CrossRef]
- Lewis, T.B.; Nielsen, L.E. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970, 14, 1449–1471. [Google Scholar] [CrossRef]
- Cheng, S.C.; Vachon, R.I. A technique for predicting the thermal conductivity of suspensions, emulsions and porous materials. Int. J. Heat Mass Transf. 1970, 13, 537–546. [Google Scholar] [CrossRef]
- Cheng, S.C.; Vachon, R.I. The prediction of the thermal conductivity of two and three phase solid heterogeneous mixtures. Int. J. Heat Mass Transf. 1969, 12, 249–264. [Google Scholar] [CrossRef]
- Fletcher, L.S. A review of thermal enhancement techniques for electronic systems. IEEE Trans. Compon. Hybrids Manuf. Technol. 1990, 13, 1012–1021. [Google Scholar] [CrossRef]
- Kusuma, W.J.; Fadarina; Hasan, A.; Polytechn Sriwijaya, P.S.S.I. Sodium Silicate Composite Filled by Zinc Oxide as Low Resistance Thermal Grease. J. Phys. Conf. Ser. 2019, 1167, 012045. [Google Scholar] [CrossRef]
- Naghibi, S.; Kargar, F.; Wright, D.; Huang, C.Y.T.; Mohammadzadeh, A.; Barani, Z.; Salgado, R.; Balandin, A.A. Noncuring Graphene Thermal Interface Materials for Advanced Electronics. Adv. Electron. Mater. 2020, 6, 1901303. [Google Scholar] [CrossRef]
- Uppal, A.; Kong, W.; Rana, A.; Wang, R.Y.; Rykaczewski, K. Enhancing Thermal Transport in Silicone Composites via Bridging Liquid Metal Fillers with Reactive Metal Co-Fillers and Matrix Viscosity Tuning. ACS Appl. Mater. Interfaces 2021, 13, 43348–43355. [Google Scholar] [CrossRef] [PubMed]
- Wunderle, B.; May, D.; Heilmann, J.; Arnold, J.; Hirscheider, J.; Li, Y.; Bauer, J.; Schacht, R.; Ras, M.A. Accelerated Pump Out Testing for Thermal Greases. In Proceedings of the 2019 20th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Hannover, Germany, 24–27 March 2019. [Google Scholar]
- Jiang, B.; Wang, H.; Wen, G.; Wang, E.; Fang, X.; Liu, G.; Zhou, W. Copper–graphite–copper sandwich: Superior heat spreader with excellent heat-dissipation ability and good weldability. RSC Adv. 2016, 6, 25128–25136. [Google Scholar] [CrossRef]
- Kong, W.; Wang, Z.; Wang, M.; Manning, K.C.; Uppal, A.; Green, M.D.; Wang, R.Y.; Rykaczewski, K. Oxide-Mediated Formation of Chemically Stable Tungsten-Liquid Metal Mixtures for Enhanced Thermal Interfaces. Adv. Mater. 2019, 31, e1904309. [Google Scholar] [CrossRef] [PubMed]
- Xing, W.; Chen, S.; Wang, H.; Liu, W.; Zheng, J.; Zheng, F.; Li, X.; Tao, P.; Shang, W.; Fu, B.; et al. Construction of 3D Conductive Network in Liquid Gallium with Enhanced Thermal and Electrical Performance. Adv. Mater. Technol. 2021, 7, 2100970. [Google Scholar] [CrossRef]
- Wang, H.; Xing, W.; Chen, S.; Song, C.; Dickey, M.D.; Deng, T. Liquid Metal Composites with Enhanced Thermal Conductivity and Stability Using Molecular Thermal Linker. Adv. Mater. 2021, 33, e2103104. [Google Scholar] [CrossRef]
- Zeng, C.; Ma, C.; Shen, J. High thermal conductivity in diamond induced carbon fiber-liquid metal mixtures. Compos. Part B Eng. 2022, 238, 109902. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Li, X.; Mei, Y.H.; Lu, G.Q. Novel interface material used in high power electronic die-attaching on bare Cu substrates. J. Mater. Sci. Mater. Electron. 2016, 27, 10941–10950. [Google Scholar] [CrossRef]
- Li, M.; Xiao, Y.; Zhang, Z.; Yu, J. Bimodal sintered silver nanoparticle paste with ultrahigh thermal conductivity and shear strength for high temperature thermal interface material applications. ACS Appl. Mater. Interfaces 2015, 7, 9157–9168. [Google Scholar] [CrossRef]
- Yeh, C.T.; Qiu, W.C.; Ji, J.D.; Pan, J.A.; Hsiao, C.S. Advanced nano-Ag thermal interface material for high thermal flip chip BGA. In Proceedings of the 2016 11th International Microsystems Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 26–28 October 2016. [Google Scholar]
- Xing, W.; Wang, H.; Chen, S.; Tao, P.; Shang, W.; Fu, B.; Song, C.; Deng, T. Gallium-Based Liquid Metal Composites with Enhanced Thermal and Electrical Performance Enabled by Structural Engineering of Filler. Adv. Eng. Mater. 2022, 24, 2101678. [Google Scholar] [CrossRef]
- Mao, D.; Chen, J.; Ren, L.; Zhang, K.; Yuen, M.M.F.; Zeng, X.; Sun, R.; Xu, J.-B.; Wong, C.-P. Spherical core-shell Al@Al2O3 filled epoxy resin composites as high-performance thermal interface materials. Compos. Part A Appl. Sci. Manuf. 2019, 123, 260–269. [Google Scholar] [CrossRef]
- Anithambigai, P.; Shanmugan, S.; Mutharasu, D.; Zahner, T.; Lacey, D. Study on thermal performance of high power LED employing aluminum filled epoxy composite as thermal interface material. Microelectron. J. 2014, 45, 1726–1733. [Google Scholar] [CrossRef]
- Wang, C.; Gong, Y.; Cunning, B.V.; Lee, S.; Ruoff, R.S. A general approach to composites containing nonmetallic fillers and liquid gallium. Sci. Adv. 2021, 7, eabe3767. [Google Scholar] [CrossRef]
- Wei, S.; Yu, Z.F.; Zhou, L.J.; Guo, J.D. Investigation on enhancing the thermal conductance of gallium-based thermal interface materials using chromium-coated diamond particles. J. Mater. Sci. Mater. Electron. 2019, 30, 7194–7202. [Google Scholar] [CrossRef]
- Tang, J.; Zhao, X.; Li, J.; Guo, R.; Zhou, Y.; Liu, J. Gallium-Based Liquid Metal Amalgams: Transitional-State Metallic Mixtures (TransM2ixes) with Enhanced and Tunable Electrical, Thermal, and Mechanical Properties. ACS Appl. Mater. Interfaces 2017, 9, 35977–35987. [Google Scholar] [CrossRef]
- Ki, S.; Shim, J.; Oh, S.; Koh, E.; Seo, D.; Ryu, S.; Kim, J.; Nam, Y. Gallium-based liquid metal alloy incorporating oxide-free copper nanoparticle clusters for high-performance thermal interface materials. Int. J. Heat Mass Transf. 2021, 170, 121012. [Google Scholar] [CrossRef]
- Ge, X.; Zhang, J.; Zhang, G.; Liang, W.; Lu, J.; Ge, J. Low Melting-Point Alloy–Boron Nitride Nanosheet Composites for Thermal Management. ACS Appl. Nano Mater. 2020, 3, 3494–3502. [Google Scholar] [CrossRef]
- Lu, Y.; Che, Z.; Sun, F.; Chen, S.; Zhou, H.; Zhang, P.; Yu, Y.; Sheng, L.; Liu, J. Mussel-Inspired Multifunctional Integrated Liquid Metal-Based Magnetic Suspensions with Rheological, Magnetic, Electrical, and Thermal Reinforcement. ACS Appl. Mater. Interfaces 2021, 13, 5256–5265. [Google Scholar] [CrossRef]
- Chen, H.; Chen, M.; Di, J.; Xu, G.; Li, H.; Li, Q. Architecting Three-Dimensional Networks in Carbon Nanotube Buckypapers for Thermal Interface Materials. J. Phys. Chem. C 2012, 116, 3903–3909. [Google Scholar] [CrossRef]
- Shahil, K.M.; Balandin, A.A. Thermal properties of graphene and multilayer graphene: Applications in thermal interface materials. Solid State Commun. 2012, 152, 1331–1340. [Google Scholar] [CrossRef]
- Qiu, L.; Wang, X.; Su, G.; Tang, D.; Zheng, X.; Zhu, J.; Wang, Z.; Norris, P.M.; Bradford, P.D.; Zhu, Y. Remarkably enhanced thermal transport based on a flexible horizontally-aligned carbon nanotube array film. Sci. Rep. 2016, 6, 21014. [Google Scholar] [CrossRef] [PubMed]
- Lv, P.; Tan, X.W.; Yu, K.H.; Zheng, R.L.; Zheng, J.J.; Wei, W. Super-elastic graphene/carbon nanotube aerogel: A novel thermal interface material with highly thermal transport properties. Carbon 2016, 99, 222–228. [Google Scholar] [CrossRef]
- Cermak, M.; Faure, X.; Saket, M.A.; Bahrami, M.; Ordonez, M. Natural Graphite Sheet Heat Sinks with Embedded Heat Pipes. IEEE Access 2020, 8, 80827–80835. [Google Scholar] [CrossRef]
- Dai, W.; Ma, T.; Yan, Q.; Gao, J.; Tan, X.; Lv, L.; Hou, H.; Wei, Q.; Yu, J.; Wu, J.; et al. Metal-Level Thermally Conductive yet Soft Graphene Thermal Interface Materials. ACS Nano 2019, 13, 11561–11571. [Google Scholar] [CrossRef]
- Rong, H.; Lin, W.Q.; Zheng, J.C.; Lu, M. Thermal characterization of a bridge-link carbon nanotubes array used as a thermal adhesive. Int. J. Adhes. Adhes. 2014, 49, 58–63. [Google Scholar] [CrossRef]
- Zhang, X.; Yeung, K.K.; Gao, Z.; Li, J.; Sun, H.; Xu, H.; Zhang, K.; Zhang, M.; Chen, Z.; Yuen, M.M.F.; et al. Exceptional thermal interface properties of a three-dimensional graphene foam. Carbon 2014, 66, 201–209. [Google Scholar] [CrossRef]
- Gao, J.; Yan, Q.; Tan, X.; Lv, L.; Ying, J.; Zhang, X.; Yang, M.; Du, S.; Wei, Q.; Xue, C.; et al. Surface Modification Using Polydopamine-Coated Liquid Metal Nanocapsules for Improving Performance of Graphene Paper-Based Thermal Interface Materials. Nanomaterials 2021, 11, 1236. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Chen, Z.; Sun, Y.; Gao, Z.; Zhang, H.; Zhang, J. Electric-Field-Assisted Growth of Vertical Graphene Arrays and the Application in Thermal Interface Materials. Adv. Funct. Mater. 2020, 30, 2003302. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Sun, B.; Wang, Y.; Zhu, Y.; Jiang, P. Vertically Aligned and Interconnected Boron Nitride Nanosheets for Advanced Flexible Nanocomposite Thermal Interface Materials. ACS Appl. Mater. Interfaces 2017, 9, 30909–30917. [Google Scholar] [CrossRef]
- An, D.; Cheng, S.; Zhang, Z.; Jiang, C.; Fang, H.; Li, J.; Liu, Y.; Wong, C.P. A polymer-based thermal management material with enhanced thermal conductivity by introducing three-dimensional networks and covalent bond connections. Carbon 2019, 155, 258–267. [Google Scholar] [CrossRef]
- Song, Q.; Zhu, W.; Deng, Y.; Hai, F.; Wang, Y.; Guo, Z. Enhanced through-plane thermal conductivity and high electrical insulation of flexible composite films with aligned boron nitride for thermal interface material. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105654. [Google Scholar] [CrossRef]
- Yi, S.Q.; Sun, H.; Jin, Y.F.; Zou, K.K.; Li, J.; Jia, L.C.; Yan, D.X.; Li, Z.M. CNT-assisted design of stable liquid metal droplets for flexible multifunctional composites. Compos. Part B Eng. 2022, 239, 109961. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, J.; Wei, N.; Yang, J.; Pei, Q.X. Recent progress in the development of thermal interface materials: A review. Phys. Chem. Chem. Phys. 2021, 23, 753–776. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Liao, Y.; Song, Y.; Wang, S.; Wan, H.; Zeng, Y.; Yin, T.; Yang, W.; He, Z. A Super-Stretchable Liquid Metal Foamed Elastomer for Tunable Control of Electromagnetic Waves and Thermal Transport. Adv. Sci. 2020, 7, 2000177. [Google Scholar] [CrossRef]
- Chen, S.; Xing, W.; Wang, H.; Cheng, W.; Lei, Z.; Zheng, F.; Tao, P.; Shang, W.; Fu, B.; Song, C.; et al. A bottom-up approach to generate isotropic liquid metal network in polymer-enabled 3D thermal management. Chem. Eng. J. 2022, 439, 135674. [Google Scholar] [CrossRef]
- Sargolzaeiaval, Y.; Ramesh, V.P.; Neumann, T.V.; Miles, R.; Dickey, M.D.; Öztürk, M.C. High Thermal Conductivity Silicone Elastomer Doped with Graphene Nanoplatelets and Eutectic GaIn Liquid Metal Alloy. ECS J. Solid State Sci. Technol. 2019, 8, 357–362. [Google Scholar] [CrossRef]
- Saborio, M.G.; Cai, S.; Tang, J.; Ghasemian, M.B.; Mayyas, M.; Han, J.; Christoe, M.J.; Peng, S.; Koshy, P.; Esrafilzadeh, D.; et al. Liquid Metal Droplet and Graphene Co-Fillers for Electrically Conductive Flexible Composites. Small 2020, 16, e1903753. [Google Scholar] [CrossRef]
- Ma, J.; Shang, T.; Ren, L.; Yao, Y.; Zhang, T.; Xie, J.; Zhang, B.; Zeng, X.; Sun, R.; Xu, J.B.; et al. Through-plane assembly of carbon fibers into 3D skeleton achieving enhanced thermal conductivity of a thermal interface material. Chem. Eng. J. 2020, 380, 122550. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Sun, B.; Jiang, P. Highly Thermally Conductive Yet Electrically Insulating Polymer/Boron Nitride Nanosheets Nanocomposite Films for Improved Thermal Management Capability. ACS Nano 2019, 13, 337–345. [Google Scholar] [CrossRef]
- Chen, J.; Wei, H.; Bao, H.; Jiang, P.; Huang, X. Millefeuille-Inspired Thermally Conductive Polymer Nanocomposites with Overlapping BN Nanosheets for Thermal Management Applications. ACS Appl. Mater. Interfaces 2019, 11, 31402–31410. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.C.; Kwan, Y.K.; Fuh, Y.K. A reduced percolation threshold of hybrid fillers of ball-milled exfoliated graphite nanoplatelets and AgNWs for enhanced thermal interface materials in high power electronics. Compos. Part B Eng. 2020, 191, 107954. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, H.; Chen, X.; Chu, S.; Liu, H.; Lin, Z.; Li, Q.; Chu, G.; Zhang, H. Liquid metal nano/micro-channels as thermal interface materials for efficient energy saving. J. Mater. Chem. C 2018, 6, 10611–10617. [Google Scholar] [CrossRef]
- Ralphs, M.I.; Kemme, N.; Vartak, P.B.; Joseph, E.; Tipnis, S.; Turnage, S.; Solanki, K.N.; Wang, R.Y.; Rykaczewski, K. In Situ Alloying of Thermally Conductive Polymer Composites by Combining Liquid and Solid Metal Microadditives. ACS Appl. Mater. Interfaces 2018, 10, 2083–2092. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Qin, Z.; Wu, H.; Li, M.; Hu, Y. Flexible thermal interface based on self-assembled boron arsenide for high-performance thermal management. Nat. Commun. 2021, 12, 1284. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Wu, W.; Zhang, Z.; Xian, Y.; Lin, Y.; Lu, Y.; Zhang, L. Advanced flexible rGO-BN natural rubber films with high thermal conductivity for improved thermal management capability. Carbon 2020, 162, 46–55. [Google Scholar] [CrossRef]
- Gao, J.; Yan, Q.; Lv, L.; Tan, X.; Ying, J.; Yang, K.; Yu, J.; Du, S.; Wei, Q.; Xiang, R.; et al. Lightweight thermal interface materials based on hierarchically structured graphene paper with superior through-plane thermal conductivity. Chem. Eng. J. 2021, 419, 129609. [Google Scholar] [CrossRef]
- Feng, C.P.; Chen, L.B.; Tian, G.L.; Bai, L.; Bao, R.Y.; Liu, Z.Y.; Ke, K.; Yang, M.B.; Yang, W. Robust polymer-based paper-like thermal interface materials with a through-plane thermal conductivity over 9 Wm−1K−1. Chem. Eng. J. 2020, 392, 123784. [Google Scholar] [CrossRef]
- Shi, L.; Plyasunov, S.; Bachtold, A.; Mceuen, P.L.; Majumdar, A. Scanning thermal microscopy of carbon nanotubes using batch-fabricated probes. Appl. Phys. Lett. 2000, 77, 4295–4297. [Google Scholar] [CrossRef]
- Jiang, P.; Qian, X.; Yang, R. Tutorial: Time-domain thermoreflectance (TDTR) for thermal property characterization of bulk and thin film materials. J. Appl. Phys. 2018, 124, 161103. [Google Scholar] [CrossRef]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Assy, A.; Gomès, S. Heat transfer at nanoscale contacts investigated with scanning thermal microscopy. Appl. Phys. Lett. 2015, 107, 109901. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Z.; Wang, Q.; Jiang, J. Measurement of temperature-dependent thermal conductivity for PVD Ti0.55Al0.45N ceramic coating by time domain thermo-reflectance method. Ceram. Int. 2019, 45, 8123–8129. [Google Scholar] [CrossRef]
- Limbu, T.B.; Hahn, K.R.; Mendoza, F.; Sahoo, S.; Razink, J.J.; Katiyar, R.S.; Weiner, B.R.; Morell, G. Grain size-dependent thermal conductivity of polycrystalline twisted bilayer graphene. Carbon 2017, 117, 367–375. [Google Scholar] [CrossRef]
- Rides, M.; Morikawa, J.; Halldahl, L.; Hay, B.; Lobo, H.; Dawson, A.; Allen, C. Intercomparison of thermal conductivity and thermal diffusivity methods for plastics. Polym. Test. 2009, 28, 480–489. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Wu, Z.K.; Bai, S.L. Thermal resistance measurement of 3D graphene foam/polymer composite by laser flash analysis. Int. J. Heat Mass Transf. 2016, 101, 470–475. [Google Scholar] [CrossRef]






| Model | Formula | Remarks | Reference |
|---|---|---|---|
| Series | Polymer is arranged in parallel to thermal flux. | [45,46] | |
| Parallel | Polymer is arranged in the direction of thermal flux. | ||
| Agari and Uno | Fillers are randomly, isotropically dispersed in a thermal conduction system based on the generalization of parallel and series conduction models. | ||
| Maxwell | Fillers as noninteracting homogeneous spheres are randomly distributed. It is only valid in low volume fractions of fillers. | [30,31] | |
| Hasselman and Johnson | Based on the Maxwell model, this model considers the influence of the size of fillers and the interfacial thermal resistance. | [32,34] | |
| Bruggeman | The model considers dilute suspensions of spheres in a homogeneous medium, and can be applied for relatively high volume fractions of fillers. | [36,37] | |
| Eshelby | The fillers do not interact with each other. It is only valid for low volume fractions of fillers. | [39,47] | |
| Mori–Tanaka | The model considers interactions between fillers. It is valid for up to 20% volume fractions of fillers. | ||
| Tavangar | The model is accurate at high volume fractions of fillers and can be applied for more than two components. | [48,49] | |
| Hamilton and Crosser | The model considers the shape effect of the particles. | [50] | |
| Lewis and Nielsen | The model considers the shape effect of the particles and the orientation of packing for a two-phase system. | [40,51] | |
| Cheng and Vachon | The model can be used to predict the thermal conductivity of heterogeneous mixtures. | [52,53] | |
| Percolation theory model (PTM) | The model considers the filler shape and size distribution. | [38,41] |
| Materials | Fabrication Method | Thermal Conductivity (W·m−1·K−1) | Thermal Measurement Method | Year [Ref.] | |
|---|---|---|---|---|---|
| Metal- based TIMs | Silver nanoparticles | Bimodal sintering | 278.5 | LFA | 2015 [65] |
| Silver paste | Pressure-less low-temperature sintering | 354 | Transient thermal measurement system (self-built) | 2016 [64] | |
| Cu-graphite-Cu | Electroplating | 526–626 | LFA | 2016 [59] | |
| EGaIn/Cu | Electrical-polarization-assisted | 50 | Hot disk TPS | 2017 [72] | |
| GaInSn/W | Oxide-layer-assisted mixing | 62 ± 2.28 | Hot disk TPS | 2019 [60] | |
| Ga/rGO | Mechanical mixing+ oscillating ball mill | 126 (parallel) 10.5 (perpendicular) | LFA | 2021 [70] | |
| Ga/graphite@ Ni | Planetary ball mill | 44.6 | LFA | 2021 [61] | |
| EGaIn/Cu@ CPTES | Molecule thermal linker | 65.9 | LFA | 2021 [62] | |
| Ga/diamond/carbon fiber | Repeated compression | 129 | LFA | 2022 [63] | |
| Carbon- based TIMs | Graphene | Optimized mixture of graphene and multilayer graphene | 14 | LFA | 2012 [23] |
| Graphene/CNT aerogel | hydrothermal method and freeze-drying | 88.5 | ASTM D5470 | 2016 [79] | |
| Graphene monolith | Mechanical machining process | 143 | LFA | 2019 [81] | |
| Graphene array | Chemical vapor deposition | 53.5 | TDTR | 2020 [85] | |
| Graphene paper | Rapid filtration | 12.6 | LFA | 2021 [103] | |
| Polymer- based TIMs | PDMS/GaInSn | Mixing and stretching | 8.3 | Thermal meter (DRL-Ⅲ) | 2018 [99] |
| PDMS/GaInSn/Cu | In situ alloying | 17 | ASTM D5470 | 2018 [100] | |
| PVDF/BNNS | Electrospinning | 16.3 | LFA | 2019 [96] | |
| PVA/BNNS | Electrostatic spraying | 21.4 | LFA | 2019 [97] | |
| Ag@Cellulose/Al2O3/graphene | Vacuum-assisted self-assembled | 9.09 | LFA | 2020 [104] | |
| Rubber/rGO/BN | Gelation and hot compression | 16.0 | LFA | 2020 [102] | |
| PDMS/graphite/AgNWs | Simple mixing | 29.2 | LW-9389 | 2020 [98] | |
| Epoxy–boron arsenide | Ice-templated self-assembled | 21 | LFA | 2021 [101] | |
| TPE/EGaIn/Cu | Hot pressing | 32.71 | LW9389 | 2022 [92] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, W.; Xu, Y.; Song, C.; Deng, T. Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics. Nanomaterials 2022, 12, 3365. https://doi.org/10.3390/nano12193365
Xing W, Xu Y, Song C, Deng T. Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics. Nanomaterials. 2022; 12(19):3365. https://doi.org/10.3390/nano12193365
Chicago/Turabian StyleXing, Wenkui, Yue Xu, Chengyi Song, and Tao Deng. 2022. "Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics" Nanomaterials 12, no. 19: 3365. https://doi.org/10.3390/nano12193365
APA StyleXing, W., Xu, Y., Song, C., & Deng, T. (2022). Recent Advances in Thermal Interface Materials for Thermal Management of High-Power Electronics. Nanomaterials, 12(19), 3365. https://doi.org/10.3390/nano12193365






