Size-Dependent Buckling and Post-Buckling Analysis of the Functionally Graded Thin Plate Al–Cu Material Based on a Modified Couple Stress Theory
Abstract
:1. Introduction
2. Formulations and Theories of FGM with MCST
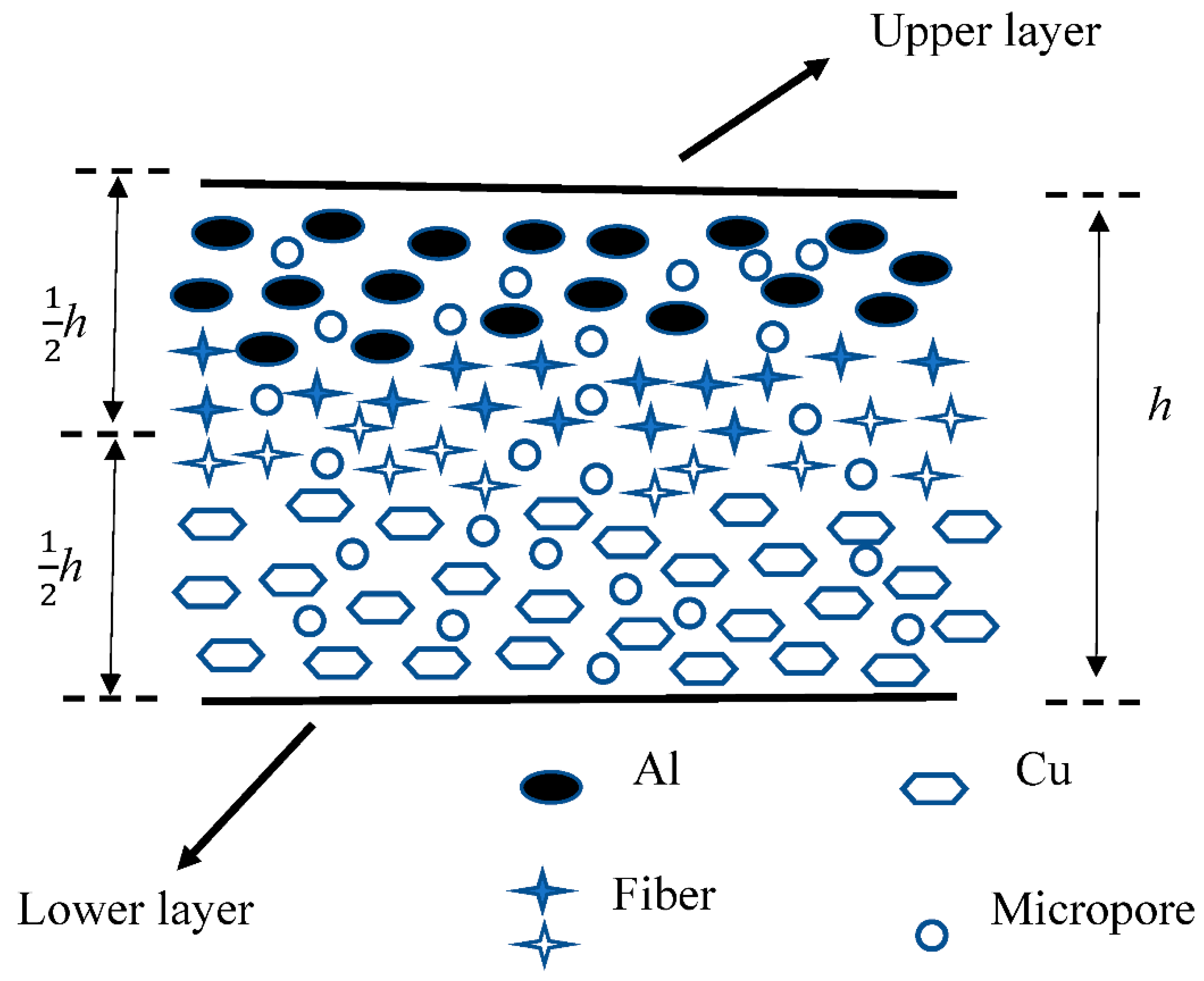
2.1. Power-Law of FGM
2.2. FGM Plate Theory Based on MCST
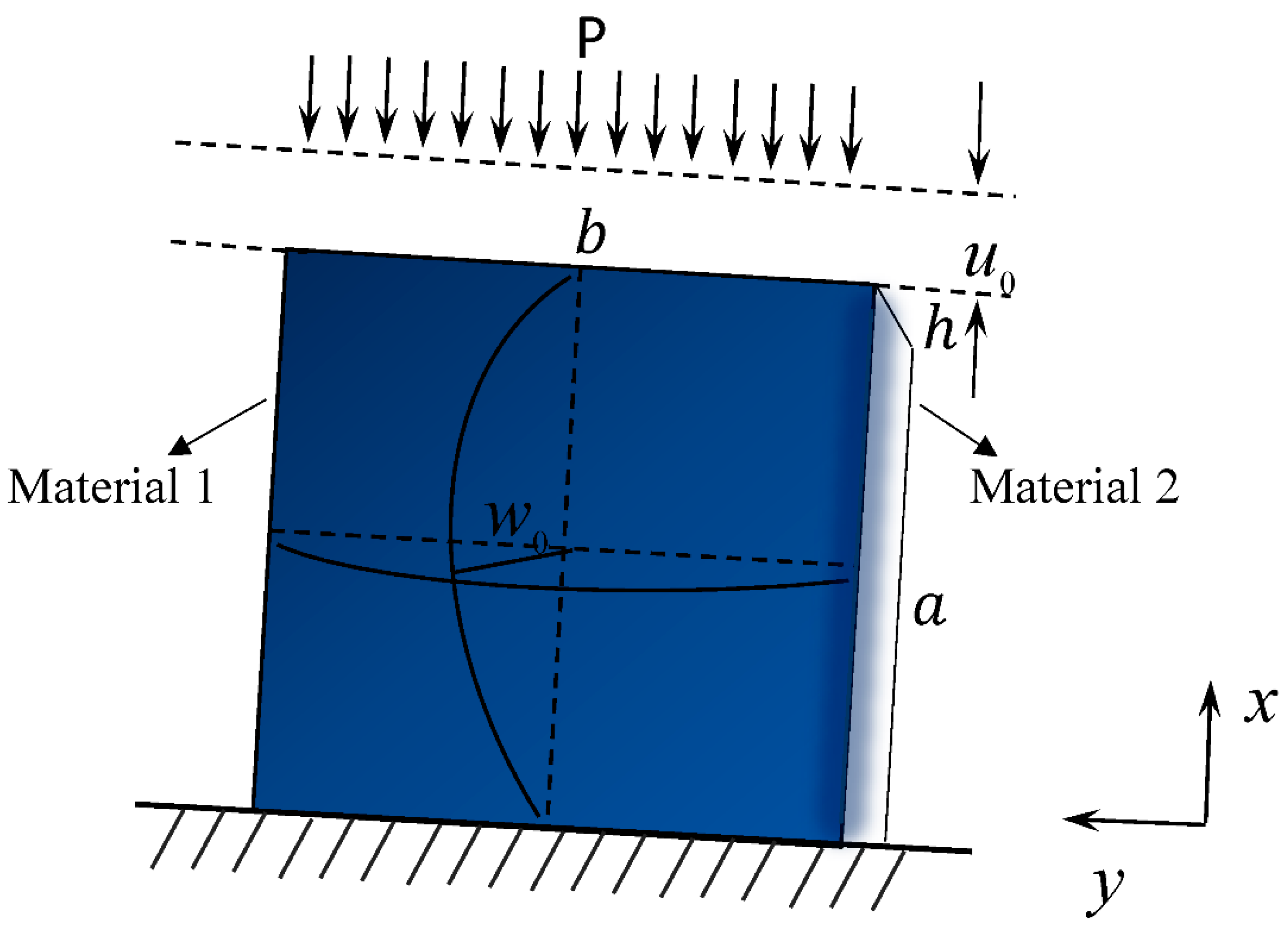
3. Post-Buckling of FGM Thin Plate
4. Numerical Results
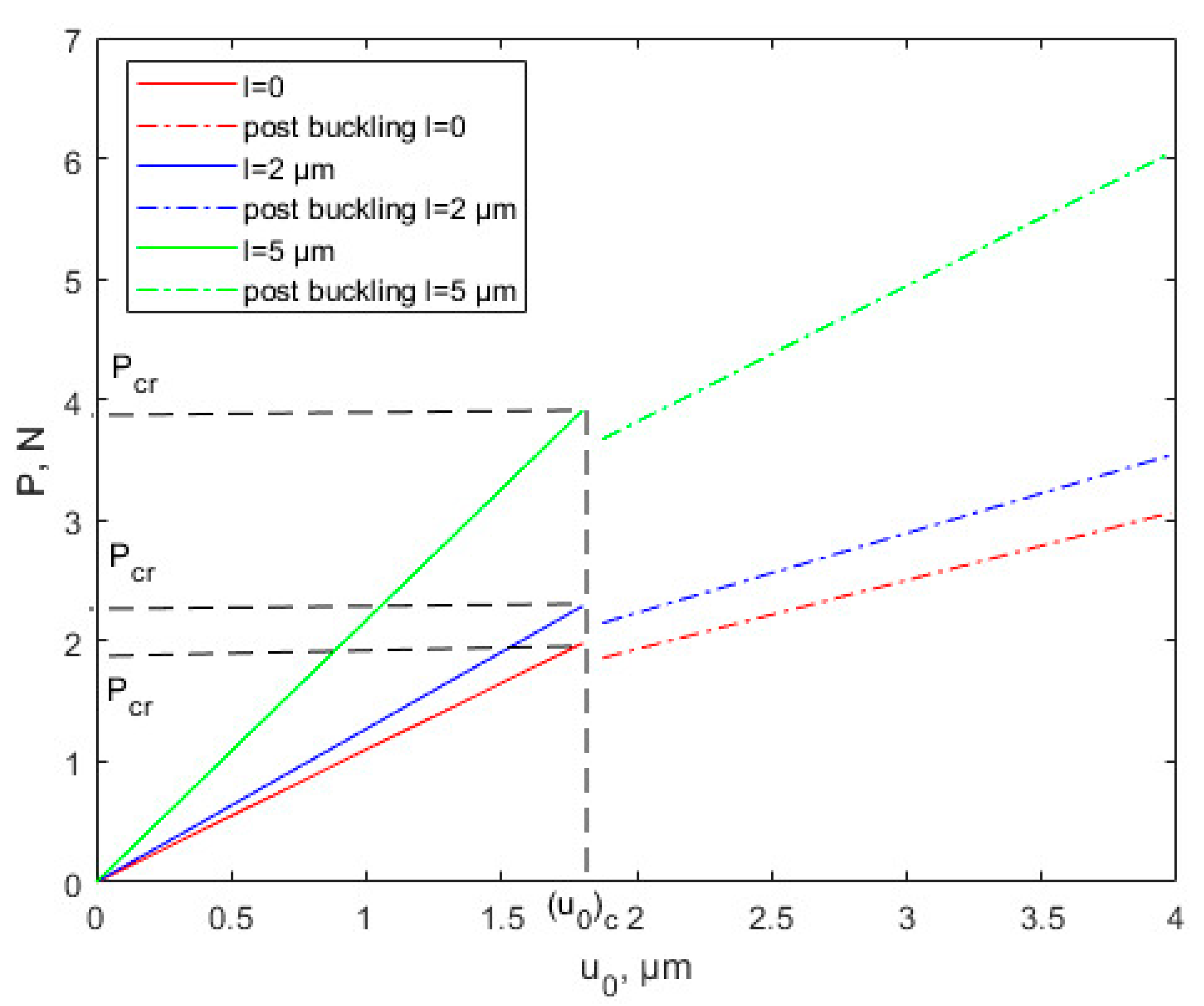
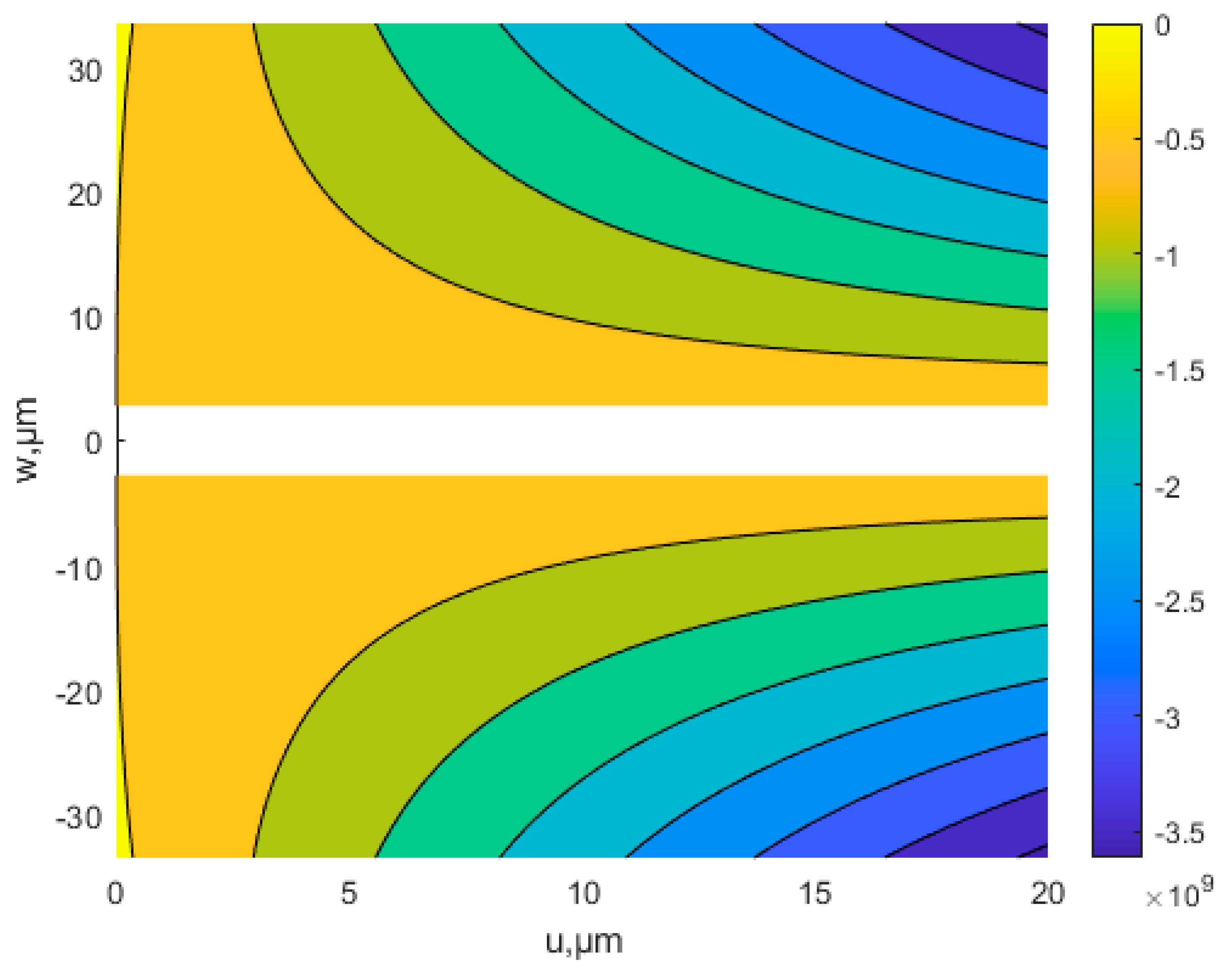
4.1. Effects of the Scale Parameter
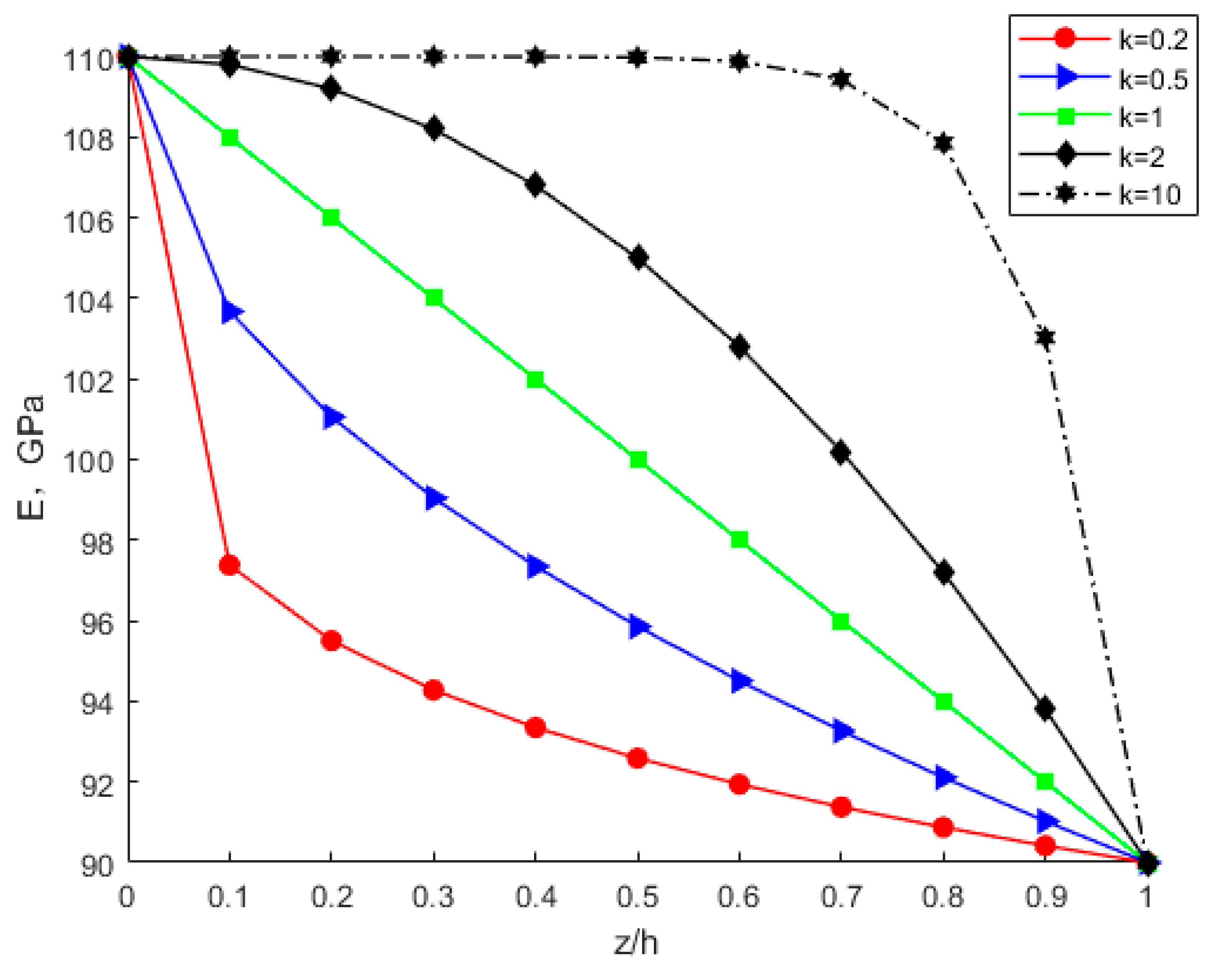
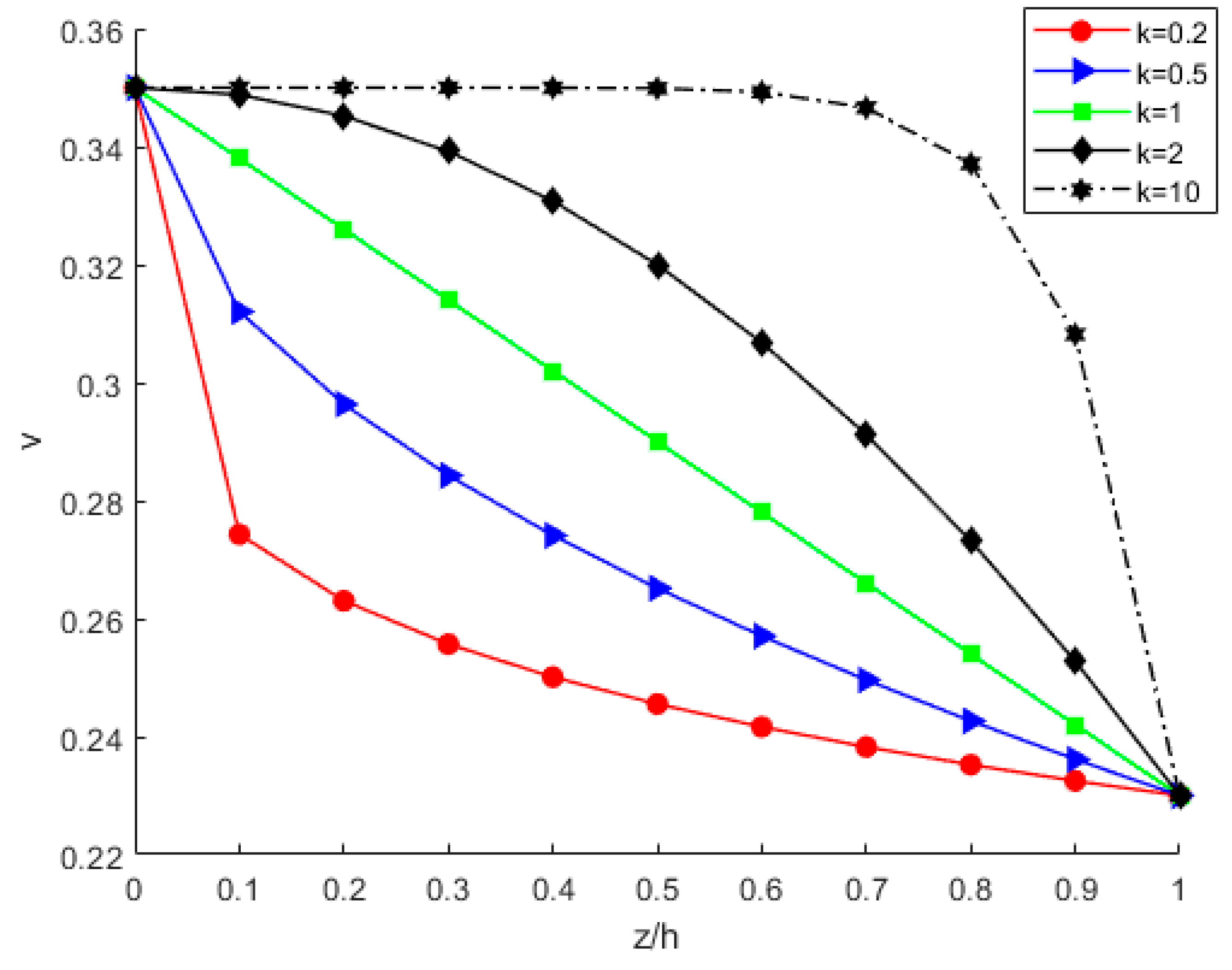
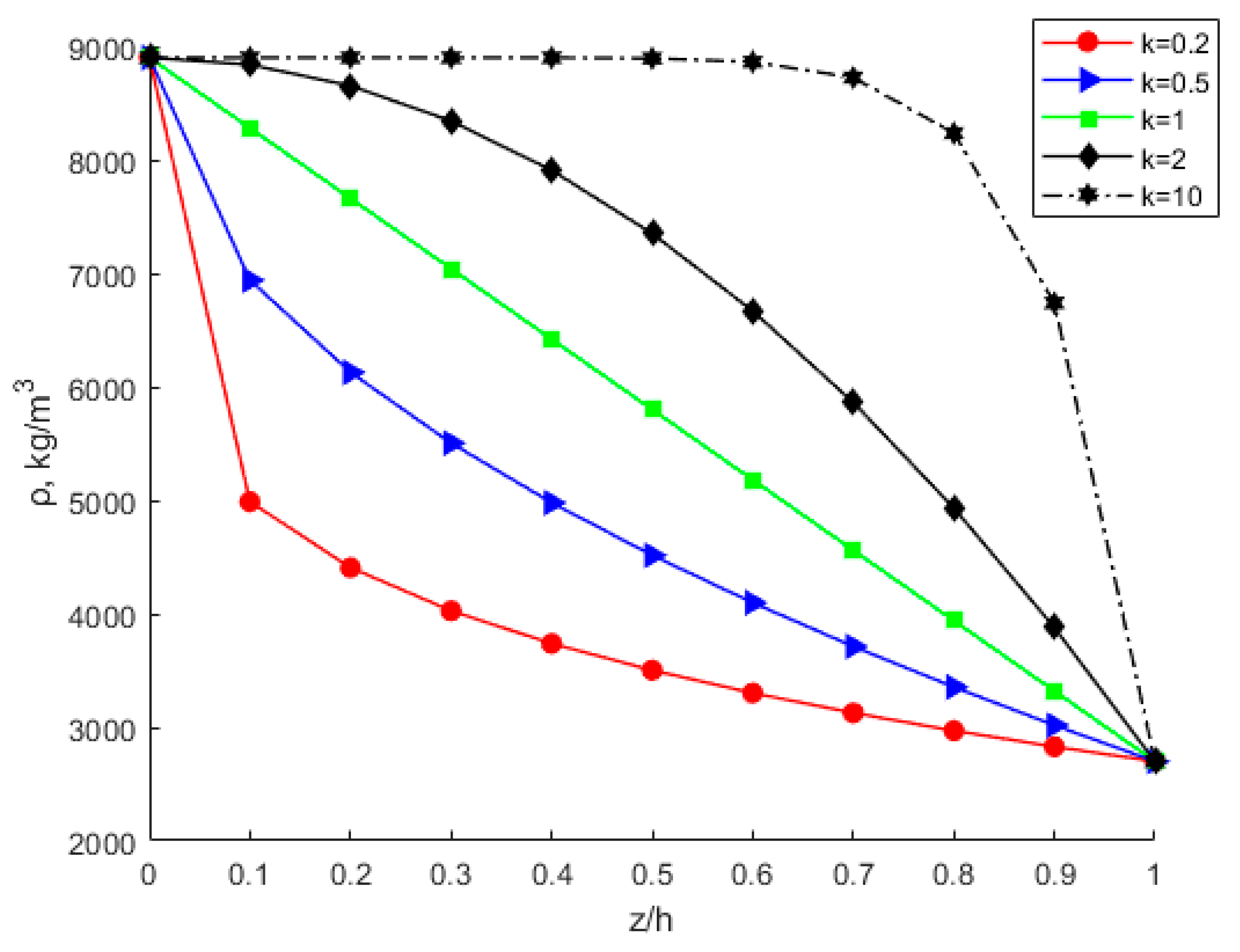
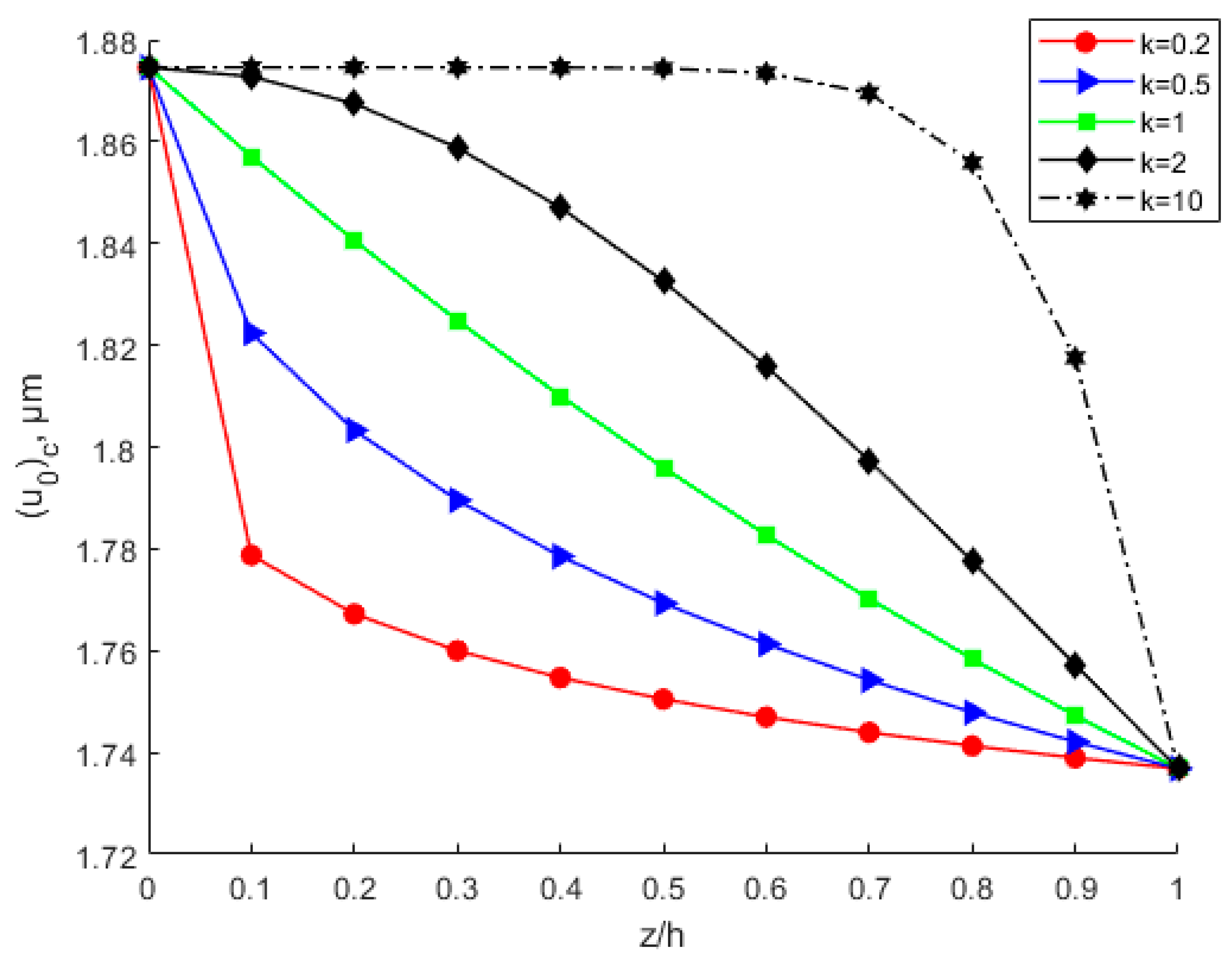
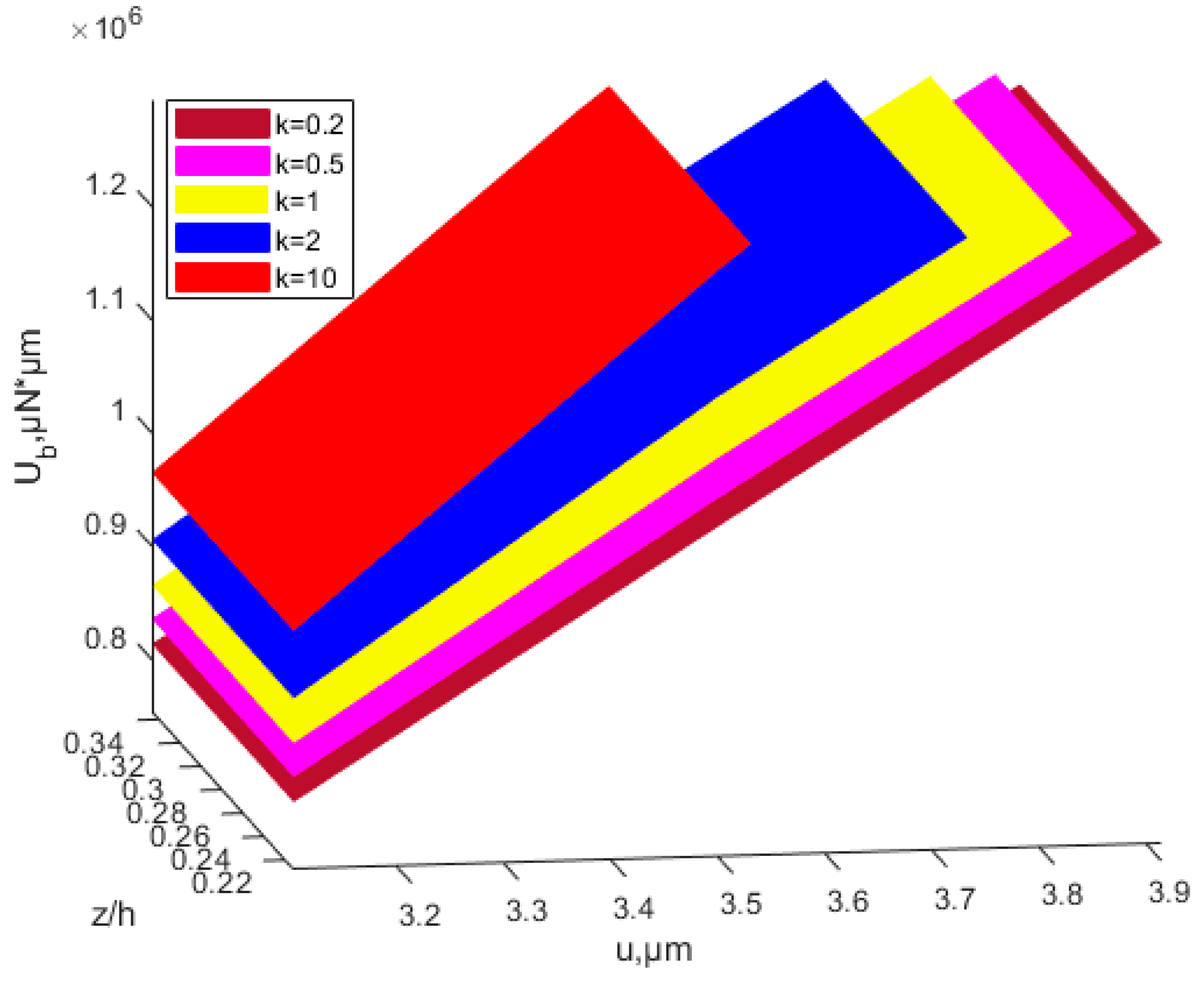
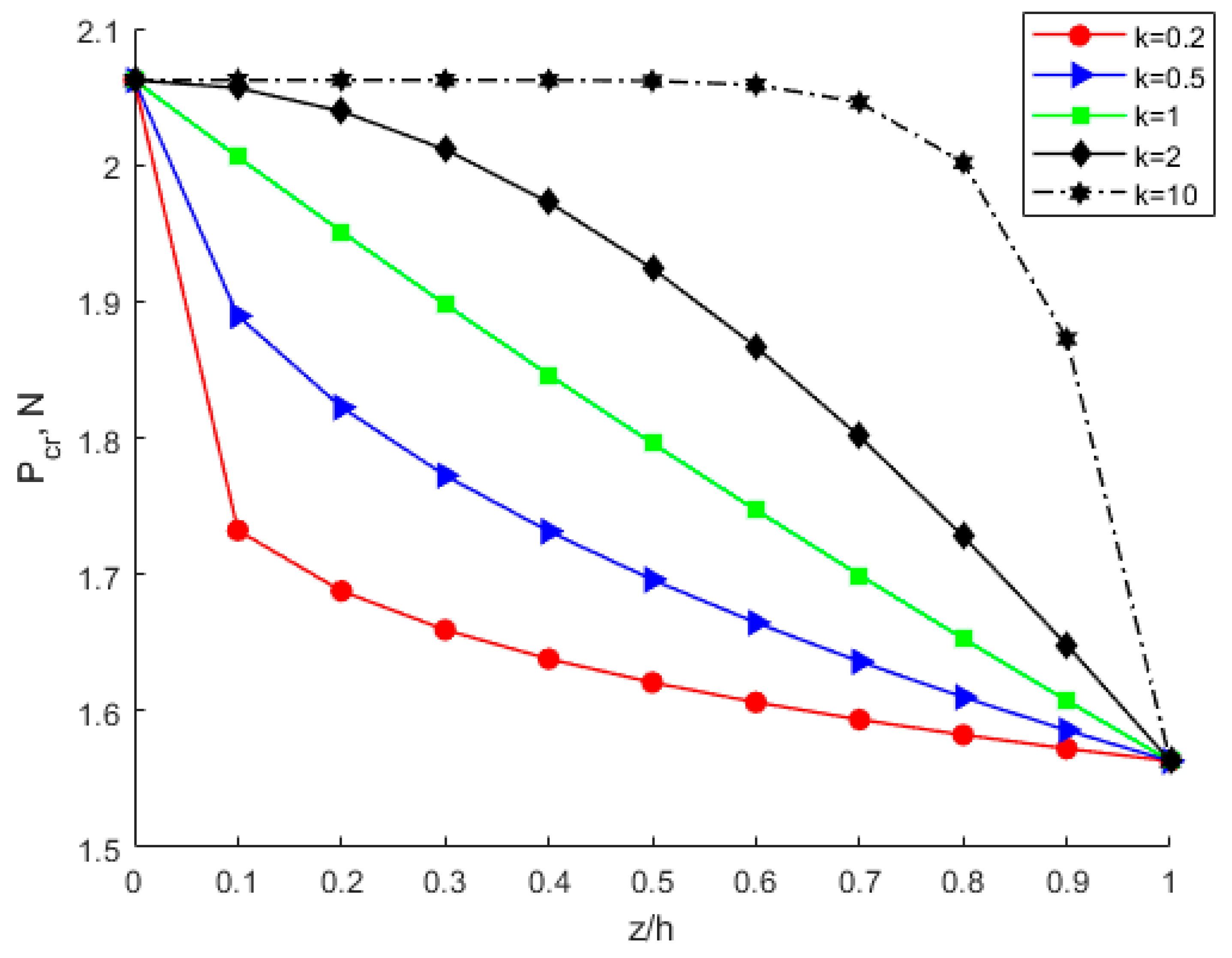
4.2. Effects of Power-Law Index Parameter k
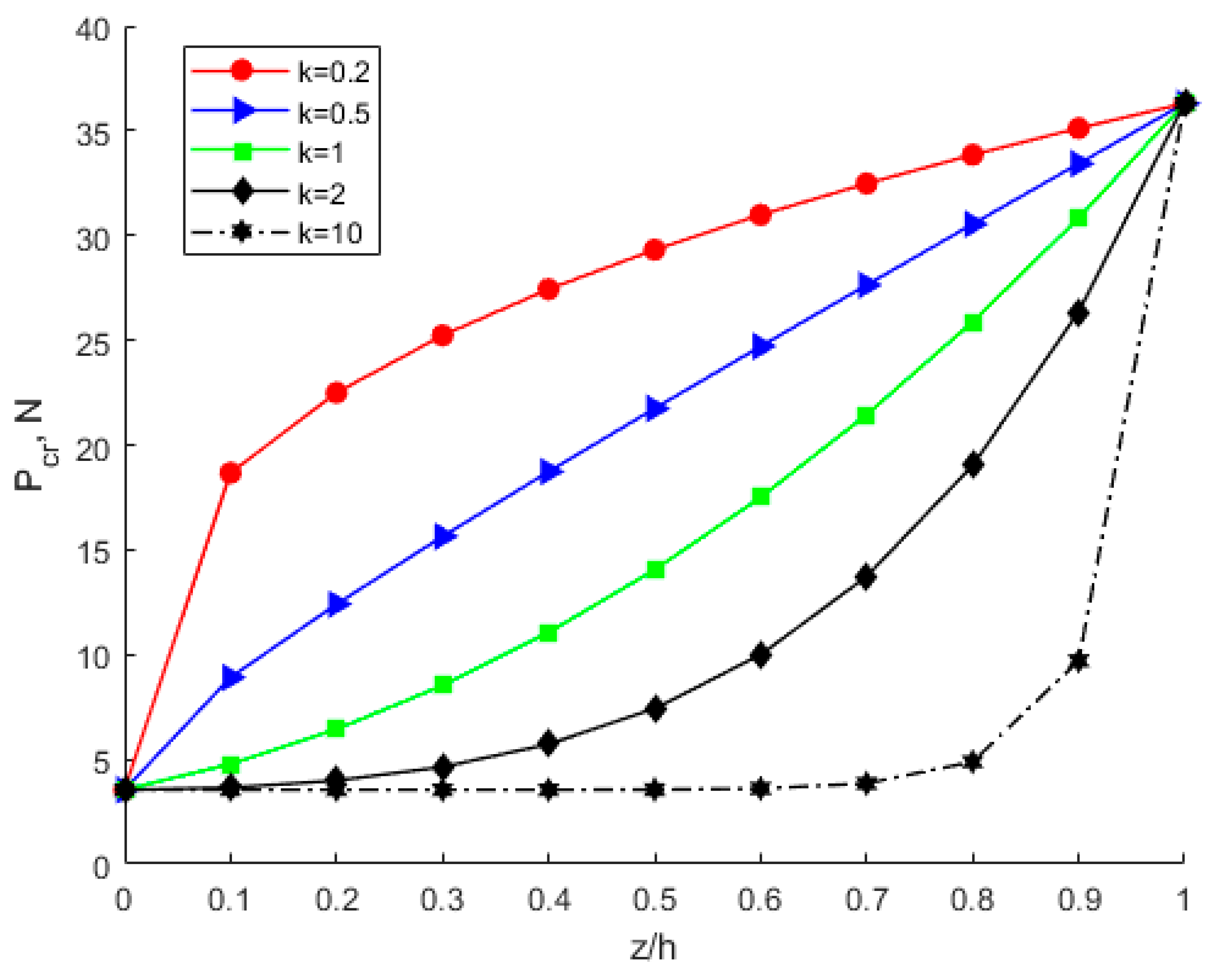
4.3. Influence of Power-Law Distribution Considering the Scale Effect
5. Concluding Remarks
- Under the same conditions, the critical buckling load, the membrane energy, and buckling strain energy increase as the scale effect parameter increases. The critical x-direction displacement is not affected by scale effects.
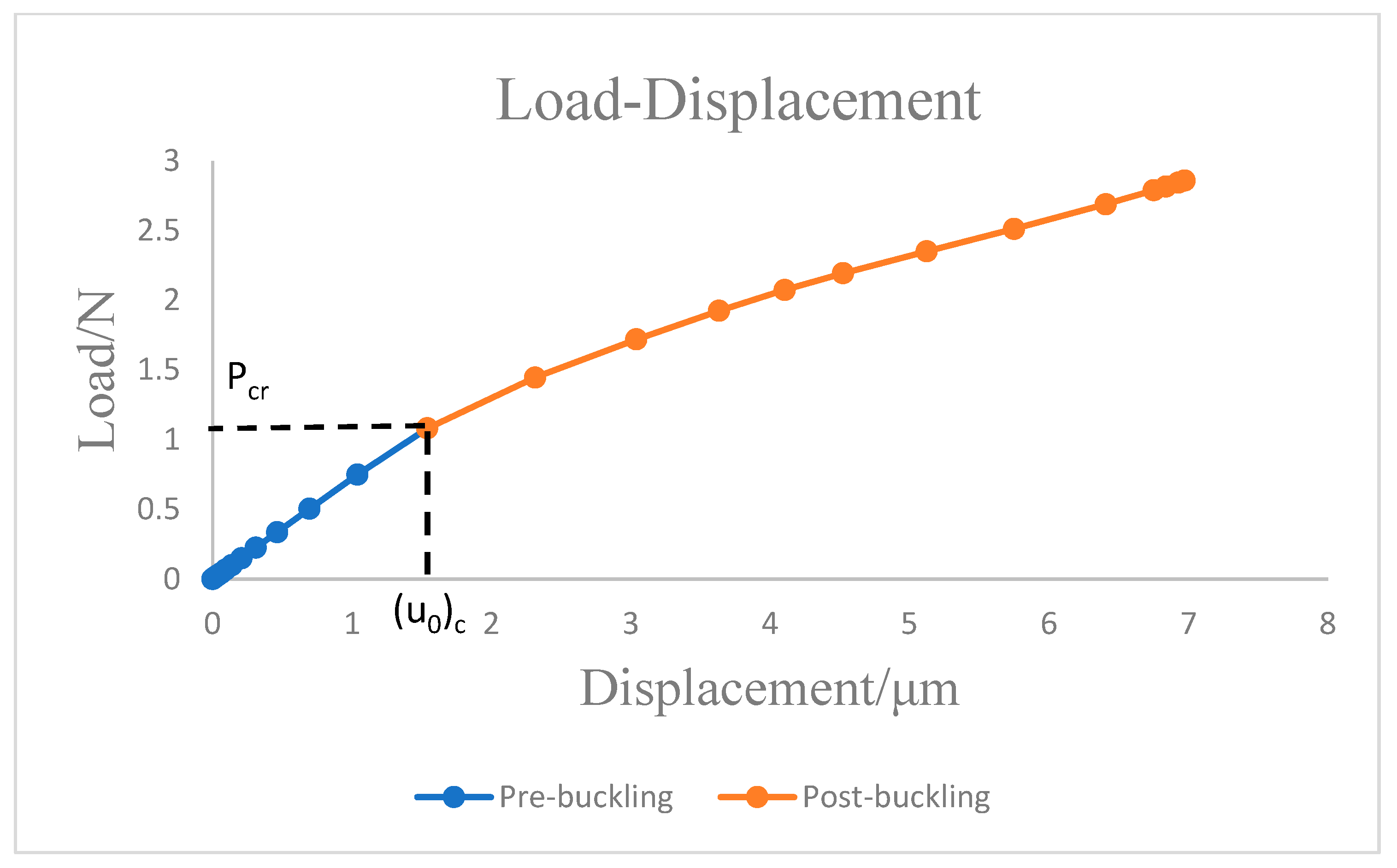
- The critical buckling displacement for nonlinear buckling is consistent with the linear buckling analysis, but the critical buckling load is smaller considering the nonlinearity of the structure
- Under the same circumstances, the modulus of elasticity, Poisson’s ratio, critical buckling load, critical buckling displacement, and buckling strain energy all increase with increasing power-law index parameter k. The membrane energy decreases as the power-law index parameter increases. As the power-law index k increases, the volume fraction of bottom copper increases. The increased modulus of elasticity of the FGM plate results in an increase in stiffness and thus an increase in the critical buckling load.
- Both the scale effect parameter l and the power-law exponent k have important effects on the FGM thin plate buckling and post-buckling problems, but in comparison, the scale effect parameter is more influential than the power-law exponent.
- The scale effect parameter can greatly increase the critical buckling load, and the correct choice of material is important for the stable design of the device. The scale effect cannot be ignored, and the research on the scale effect is of great significance for MEMS/NEMS design, and manufacture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lei, W.; Xuebao, K.; Yidi, B.; Jiangtao, W.; Liangliang, Y.; Peishuai, S.; Mingliang, Z.; Fuhua, Y.; Xiaodong, W. The recent progress of MEMS/NEMS resonators. Micromachines 2021, 12, 724. [Google Scholar]
- Ivo, S.; Eduardo, A.; Miroslav, L. Shape memory alloys and polymers for MEMS/NEMS applications: Review on recent findings and challenges in design, preparation, and characterization. Metals 2021, 11, 415. [Google Scholar]
- Javid, M.A.; Sajjad, M.; Ahmad, S.; Khan, M.A.S.; Nadeem, K.; Amin, N.; Mehmood, Z. Synthesis, electrical and magnetic properties of polymer coated magnetic nanoparticles for application in MEMS/NEMS. Mater. Sci. 2020, 38, 553–558. [Google Scholar] [CrossRef]
- Lloyd, D.J. Particle reinforced aluminum and magnesium matrix composites. Int. Mater. Rev. 1994, 39, 1–23. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Stölken, J.S.; Evans, A.G. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Victor, B.; Larry, B. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar]
- Bauer, S.; Pittrof, A.; Tsuchiya, H.; Schmuki, P. Size-effects in TiO2 nanotubes: Diameter dependent anatase/rutile stabilization. Electrochem. Commun. 2011, 13, 538–541. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gunko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Erdogan, F. Fracture mechanics of functionally graded materials. Compos. Eng. 1995, 5, 753–770. [Google Scholar] [CrossRef]
- Chaolin, T.; Youxiang, C.; Guijun, B.; Di, W.; Wenyou, M.; Yongqiang, Y.; Kesong, Z. Additive manufacturing of steel–copper functionally graded material with ultrahigh bonding strength. J. Mater. Sci. Technol. 2021, 72, 217–222. [Google Scholar]
- Kolednik, O. The yield stress gradient effect in inhomogeneous materials. Int. J. Solids Struct. 2000, 37, 781–808. [Google Scholar] [CrossRef]
- Angshuman, C.; Gopinath, M.; Sagar, S.; Vikranth, R.; Kumar, N.A. Mitigation of cracks in laser welding of titanium and stainless steel by in-situ nickel interlayer deposition. J. Mater. Process. Technol. 2022, 300. [Google Scholar]
- Baytak, T.; Bulut, O. Thermal stress in functionally graded plates with a gradation of the coefficient of thermal expansion only. Exp. Mech. 2022, 62, 655–666. [Google Scholar] [CrossRef]
- Souhir, Z.; Dhia, A.; Fakhreddine, D. Static bending analysis of beams made of functionally graded porous materials. Mech. Based Des. Struct. Mach. 2020, 50, 1–18. [Google Scholar]
- Kang, G.; Qian, H.; Sritawat, K.; Jie, Y. Nonlinear dynamic buckling of functionally graded porous beams. Mech. Adv. Mater. Struct. 2021, 28, 418–429. [Google Scholar]
- Jung, W.Y.; Park, W.T.; Han, S.C. Bending and vibration analysis of S-FGM microplates embedded in Pasternak elastic medium using the modified couple stress theory. Int. J. Mech. Sci. 2014, 87, 150–162. [Google Scholar] [CrossRef]
- Iman, E.; Serkan, D.; Nasser, S. Consideration of spatial variation of the length scale parameter in static and dynamic analyses of functionally graded annular and circular micro-plates. Compos. Part B 2015, 78, 338–348. [Google Scholar]
- Gu, S.; Song, Y.Q.; Zheng, Q. Study on the vibration of functionally graded beam immersed in fluids under photothermal excitation. Chin. J. Appl. Mech. 2021, 38, 589–596. [Google Scholar]
- Shaoyu, Z.; Zhan, Z.; Zhicheng, Y.; LiaoLiang, K.; Sritawat, K.; Jie, Y. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Song, M.T.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Yang, B.; Mei, J.; Chen, D.; Yu, F.; Yang, J. 3D thermo-mechanical solution of transversely isotropic and functionally graded graphene reinforced elliptical plates. Compos. Struct. 2018, 184, 1040–1048. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Zhang, Y.Y.; Zhang, Y.H.; Zhang, W.; Yang, J.; Kitipornchai, S. Genetic programming-assisted micromechanical models of graphene origami-enabled metal metamaterials. Acta Mater. 2022, 228. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R. The Classical Field Theories. In Principles of Classical Mechanics and Field Theory/Prizipien der Klassischen Mechanik und Feldtheorie; Springer: Berlin/Heidelberg, Germany, 1960; pp. 226–858. [Google Scholar]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stress in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, L.; Xu, M. A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation. Compos. Struct. 2011, 93, 2723–2732. [Google Scholar] [CrossRef]
- Richa, P.; Jeyaraj, P. Static stability and free vibration characteristics of a micro laminated beam under varying axial load using modified couple stress theory and Ritz method. Compos. Struct. 2022, 281. [Google Scholar]
- Jani, R.; Reddy, J.N. Experimental validation of the modified couple stress Timoshenko beam theory for web-core sandwich panels. Compos. Struct. 2014, 111, 130–137. [Google Scholar]
- Li, Z.K.; He, Y.M.; Lei, J.; Guo, S.; Liu, D.B.; Wang, L. A standard experimental method for determining the material length scale based on modified couple stress theory. Int. J. Mech. Sci. 2018, 141, 198–205. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmuller, J.; Larche, F. A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Tang, F.X.; Song, Y.Q. Wave reflection in semiconductor nanostructures. Theor. Appl. Mech. Lett. 2018, 8, 160–163. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.J.; Ling, L. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Compos. Struct. 2015, 133, 1079–1092. [Google Scholar] [CrossRef]
- Li, Y.S.; Pan, E. Bending of a sinusoidal piezoelectric nanoplate with surface effect. Compos. Struct. 2016, 136, 45–55. [Google Scholar] [CrossRef]
- Smith, T.R.G.; Sridharan, S. A finite strip method for the post-locally-buckled analysis of plate structures. Int. J. Mech. Sci. 1978, 20, 833–842. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Wang, Z.D. Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory. Compos. Struct. 2012, 94, 2038–2047. [Google Scholar] [CrossRef]
- Liu, C.; Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Buckling and post-buckling of size-dependent piezoelectric Timoshenko nanobeams subject to thermo-electro-mechanical loadings. Int. J. Struct. Stab. Dyn. 2014, 14, 1350067. [Google Scholar] [CrossRef]
- Chen, C.P.; Yuan, J.H.; Mao, Y.Q. Post-buckling of size-dependent micro-plate considering damage effects. Nonlinear Dyn. 2017, 90, 1301–1314. [Google Scholar] [CrossRef]
- Shenas, A.G.; Ziaee, S.; Malekzadeh, P. Post-buckling and vibration of post-buckled rotating pre-twisted FG microbeams in thermal environment. Thin-Walled Struct. 2019, 138, 335–360. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.J. Post-buckling analysis of functionally graded nanobeams incorporating nonlocal stress and microstructure-dependent strain gradient effects. Int. J. Mech. Sci. 2017, 120, 159–170. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Buckling analysis of nonlocal third-order shear deformable functionally graded piezoelectric nanobeams embedded in elastic medium. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 937–952. [Google Scholar] [CrossRef]
- Tlidji, Y.; Zidour, M.; Draiche, K.; Safa, A.; Bourada, M.; Tounsi, A.; Bousahla, A.A.; Mahmoud, S.R. Vibration analysis of different material distributions of functionally graded microbeam. Struct. Eng. Mech. 2019, 69, 637–649. [Google Scholar]
- Li, Y.S.; Pan, E. Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory. Int. J. Eng. Sci. 2015, 97, 40–59. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Timoshenko, S.P. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1936. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M.; Prager, W. Theory of Elastic Stability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1962; Volume 29, p. 220. [Google Scholar]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Gao, X.L.; Mahmoud, F.F. A new Bernoulli–Euler beam model incorporating microstructure and surface energy effects. Z. Angew. Math. Phys. 2014, 65, 393–404. [Google Scholar] [CrossRef]
- Xu, L.; Wang, M.C.; Zhou, Y.; Qian, Z.F.; Liu, S. An optimal structural design to improve the reliability of Al2O3–DBC substrates under thermal cycling. Microelectron. Reliab. 2016, 56, 101–108. [Google Scholar] [CrossRef]
- Gui, X.L.; Luo, X.B.; Wang, X.P.; Liu, S. Computational fluid dynamic (CFD) investigation of thermal uniformity in a thermal cycling based calibration chamber for MEMS. Heat Mass Transf. 2015, 51, 1705–1715. [Google Scholar] [CrossRef]
- Chen, M.X.; Yi, X.J.; Gan, Z.Y.; Liu, S. Reliability of anodically bonded silicon–glass packages. Sens. Actuators A Phys. 2004, 120, 291–295. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y.; Liu, S. Modeling and simulation of power electronic modules with micro-channel coolers for thermo-mechanical performance. Microelectron. Reliab. 2014, 54, 2824–2835. [Google Scholar] [CrossRef]
- Sheng, C.; Wu, G.; Sun, X.; Liu, S. Molecular Dynamics Investigation of the Thermo-Mechanical Properties of the Moisture Invaded and Cross-Linked Epoxy System. Polymers 2021, 14, 103. [Google Scholar] [CrossRef] [PubMed]
- Uymaz, B.; Aydogdu, M. Three dimensional shear buckling of FG plates with various boundary conditions. Compos. Struct. 2013, 96, 670–682. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos Struct 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Bateni, M.; Kiani, Y.; Eslami, M.R. A comprehensive study on stability of FGM plates. Int. J. Mech. Sci. 2013, 75, 134–144. [Google Scholar] [CrossRef]
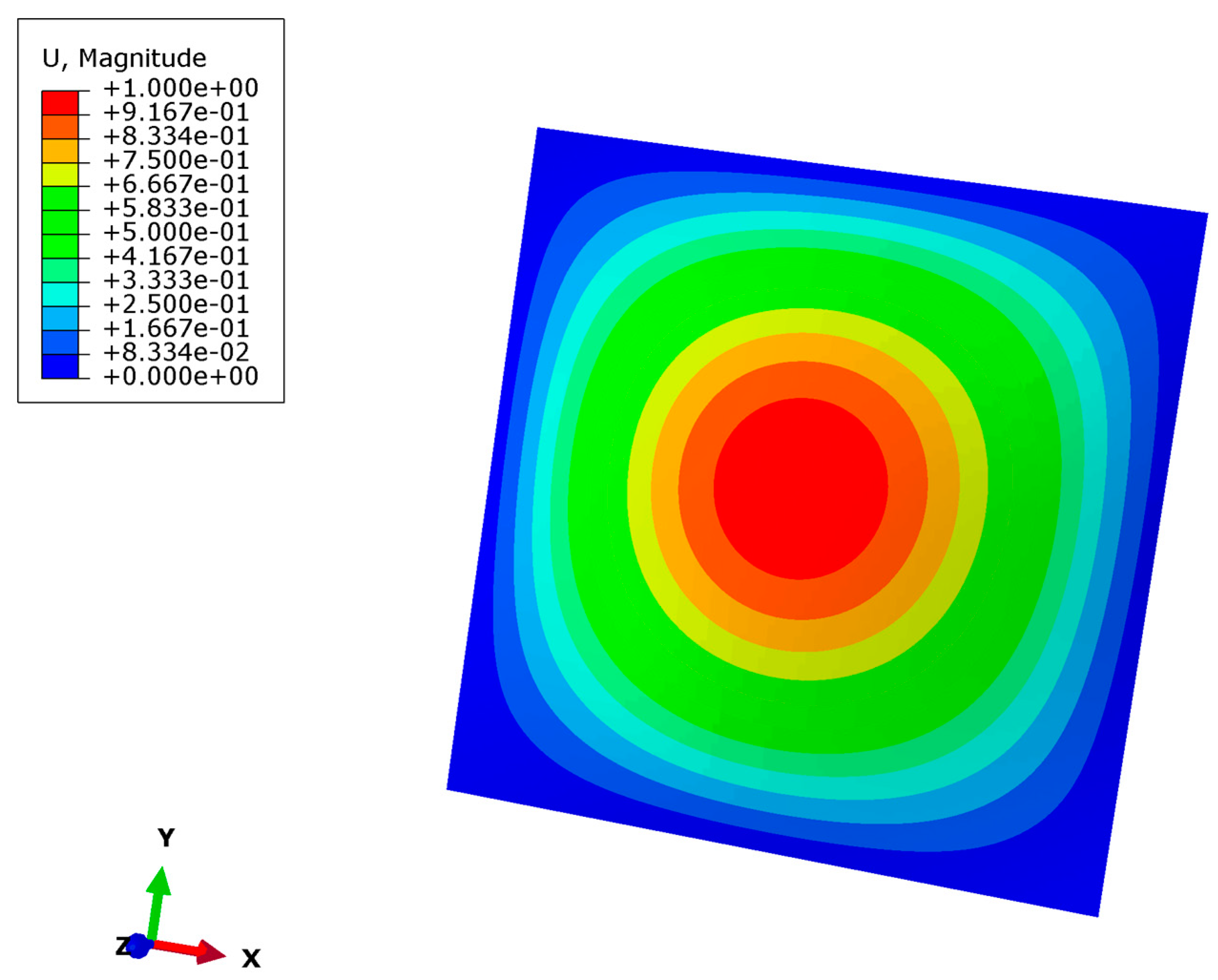
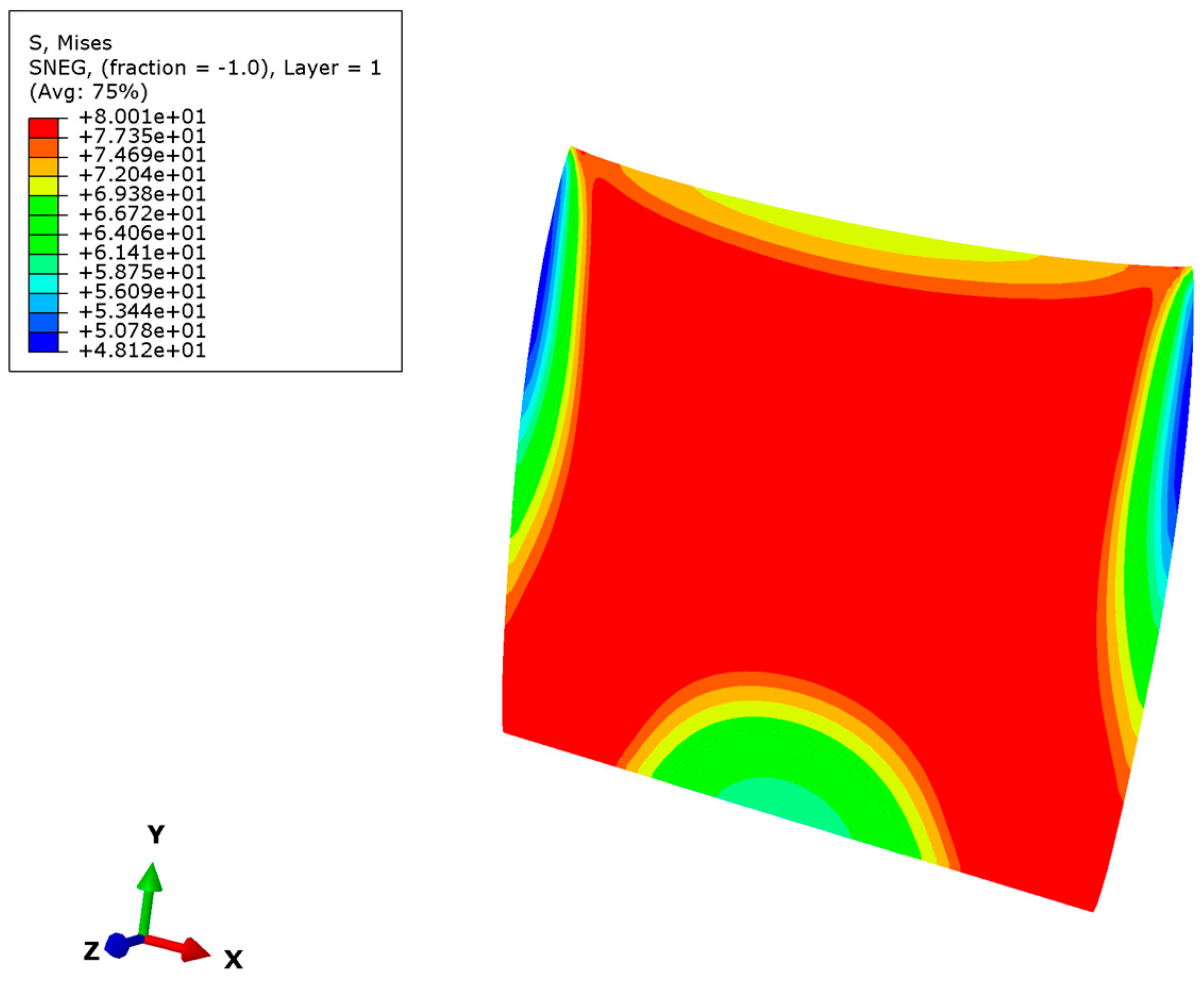
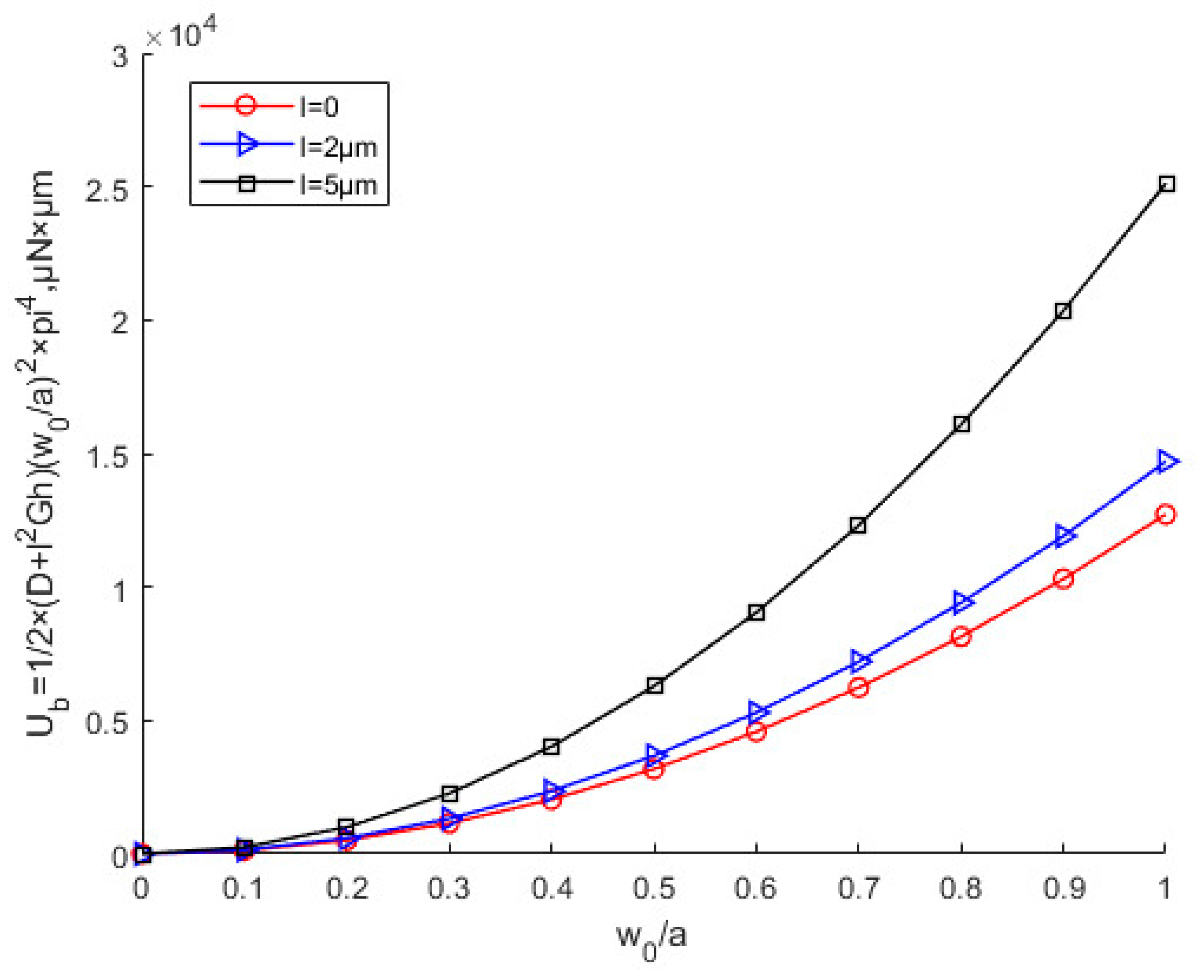
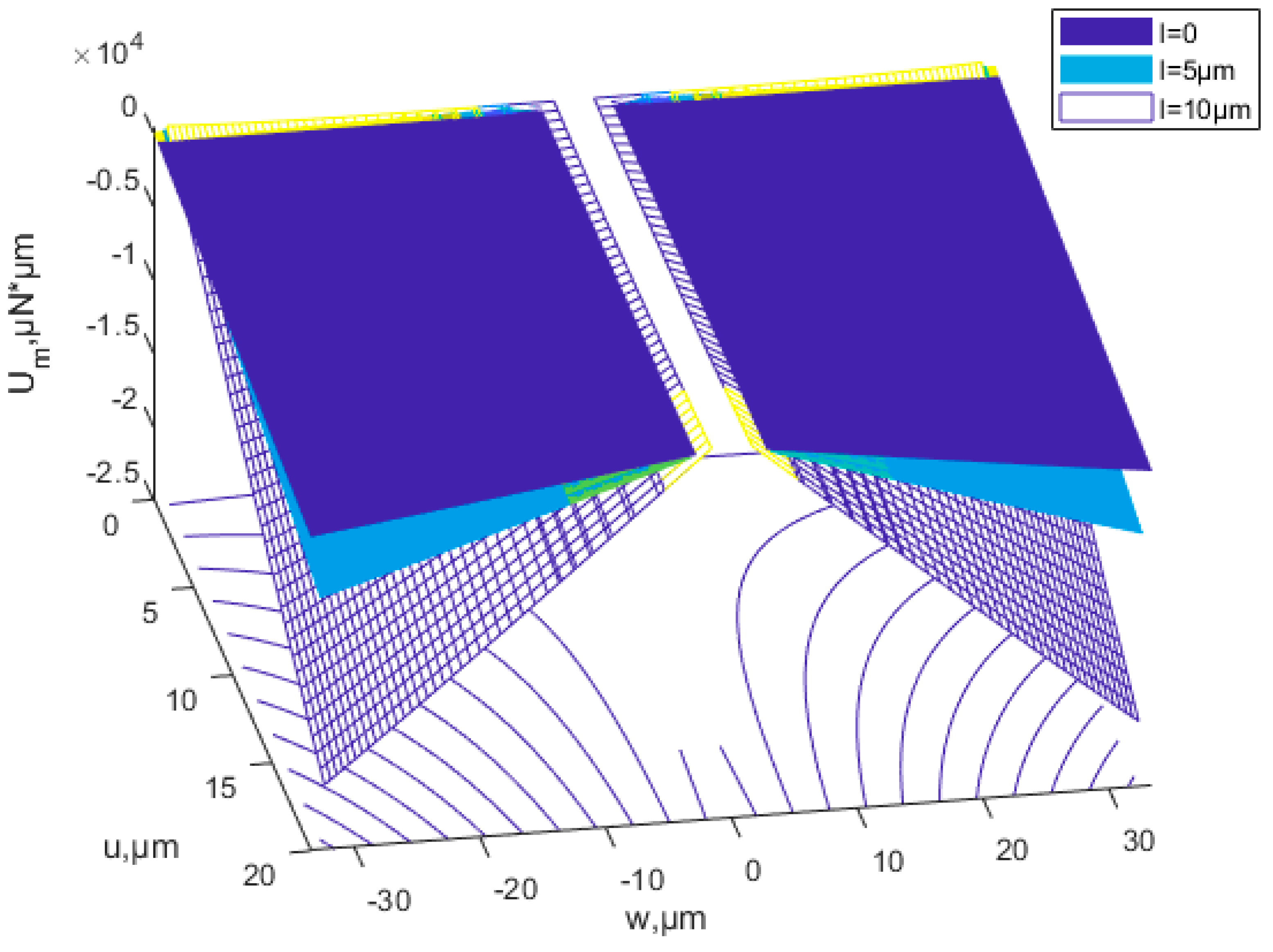


| Materials | E | υ | ρ | l [16] | h | a | b |
|---|---|---|---|---|---|---|---|
| Cu | 110 GPa | 0.35 | 8900 kg/m3 | 1.422 μm | 10 μm | 200 μm | 200 μm |
| Al [32] | 90 GPa | 0.23 | 2700 kg/m3 | 6.58 μm | 10 μm | 200 μm | 200 μm |
| Materials | Dpre of CT | Dpost of CT | Dpre of MCST (l = 2 μm) | Dpost of MCST (l = 2 μm) | Dpre of MCST (l = 5 μm) | Dpost of MCST (l = 5 μm) |
|---|---|---|---|---|---|---|
| Cu | 110 × 104 N/m | 57.2 × 104 N/m | 127.16 × 104 N/m | 66.12 × 104 N/m | 217.25 × 104 N/m | 112.86 × 104 N/m |
| Al | 90 × 104 N/m | 46.8 × 104 N/m | 104.04 × 104 N/m | 54.10 × 104 N/m | 177.75 × 104 N/m | 92.43 × 104 N/m |
| Theory | a/b | a/h | k | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 5 | 10 | |||
| ESDPT [60,61] | 1 | 20 | 8.1510 | 6.9310 | 6.4710 | 5.8410 | 5.6010 |
| 3DT [59] | 1 | 20 | 8.1099 | 6.8699 | 6.3899 | 5.7299 | 5.4899 |
| Bateni M et al. [62] | 1 | 20 | 9.6507 | 8.3142 | 7.8183 | 7.1039 | - |
| Present I | 1 | 20 | 6.0820 | 5.2508 | 4.9043 | 4.1837 | 4.0245 |
| Present II | 1 | 20 | 9.2650 | 6.6177 | 5.9370 | 5.3573 | 5.0588 |
| Present III | 1 | 20 | 6.8780 | 6.7276 | 6.6973 | 6.6842 | 6.6882 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, F.; Dong, F.; Guo, Y.; Shi, S.; Jiang, J.; Liu, S. Size-Dependent Buckling and Post-Buckling Analysis of the Functionally Graded Thin Plate Al–Cu Material Based on a Modified Couple Stress Theory. Nanomaterials 2022, 12, 3502. https://doi.org/10.3390/nano12193502
Tang F, Dong F, Guo Y, Shi S, Jiang J, Liu S. Size-Dependent Buckling and Post-Buckling Analysis of the Functionally Graded Thin Plate Al–Cu Material Based on a Modified Couple Stress Theory. Nanomaterials. 2022; 12(19):3502. https://doi.org/10.3390/nano12193502
Chicago/Turabian StyleTang, Feixiang, Fang Dong, Yuzheng Guo, Shaonan Shi, Jize Jiang, and Sheng Liu. 2022. "Size-Dependent Buckling and Post-Buckling Analysis of the Functionally Graded Thin Plate Al–Cu Material Based on a Modified Couple Stress Theory" Nanomaterials 12, no. 19: 3502. https://doi.org/10.3390/nano12193502






