Transfer Learning for Modeling Plasmonic Nanowire Waveguides
Abstract
:1. Introduction
2. Materials and Methods
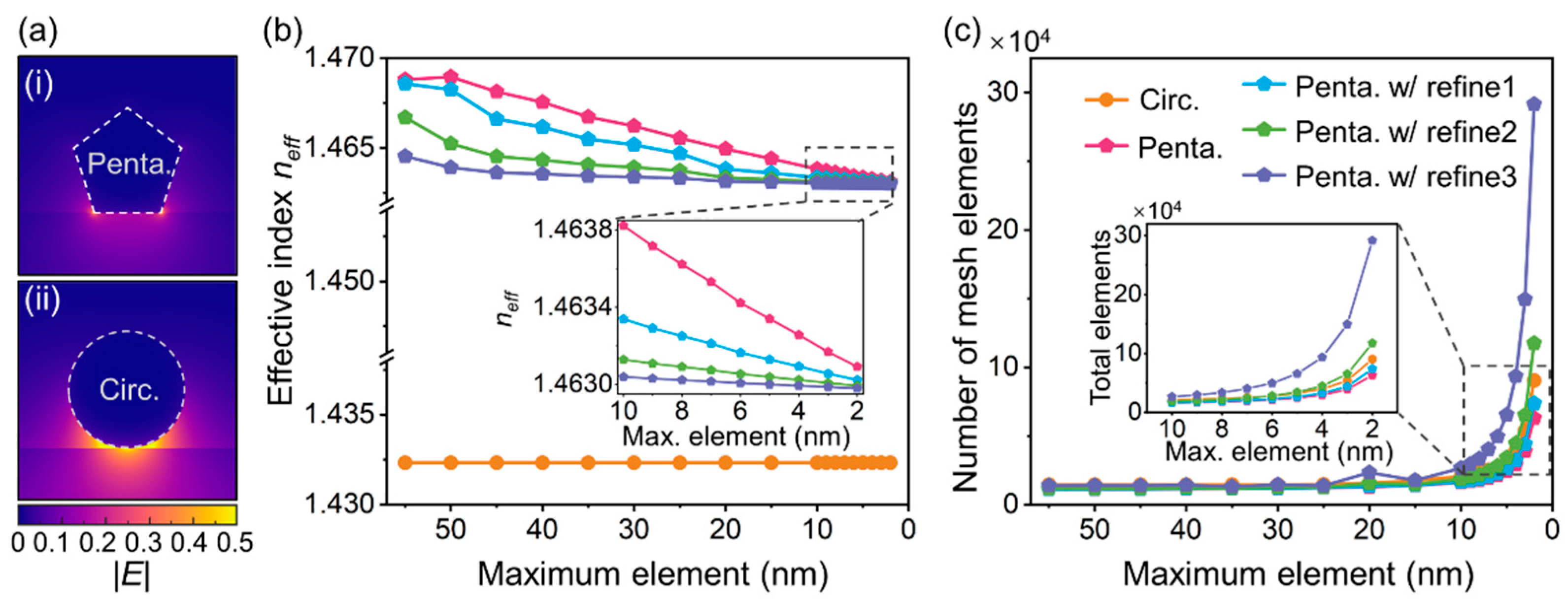
2.1. Emerging Requirement of Computational Resources for MNWs with Sharp Corners and Asymmetric Configuration
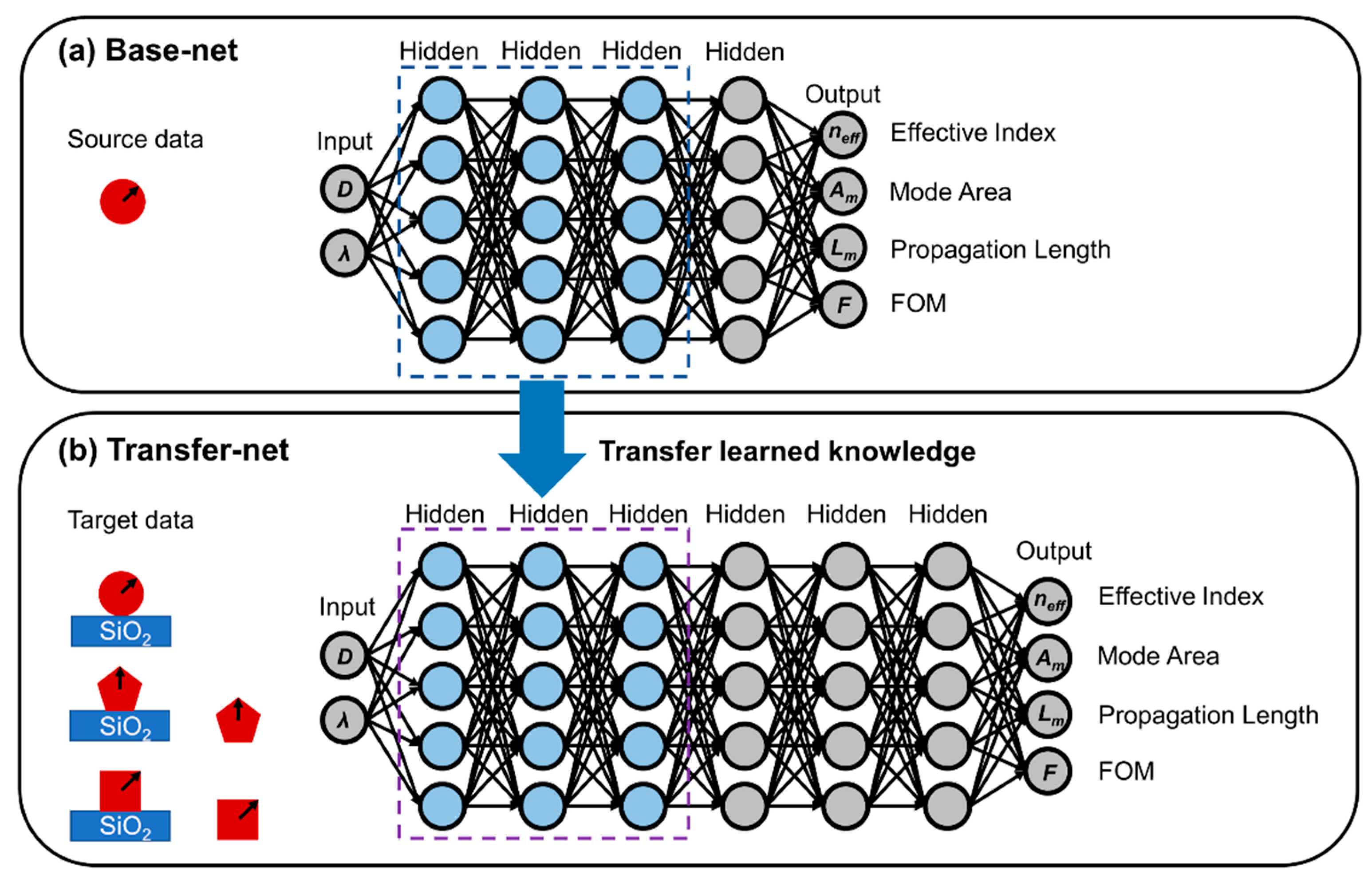
2.2. Model Architecture with Transfer Learning
3. Results and Discussion
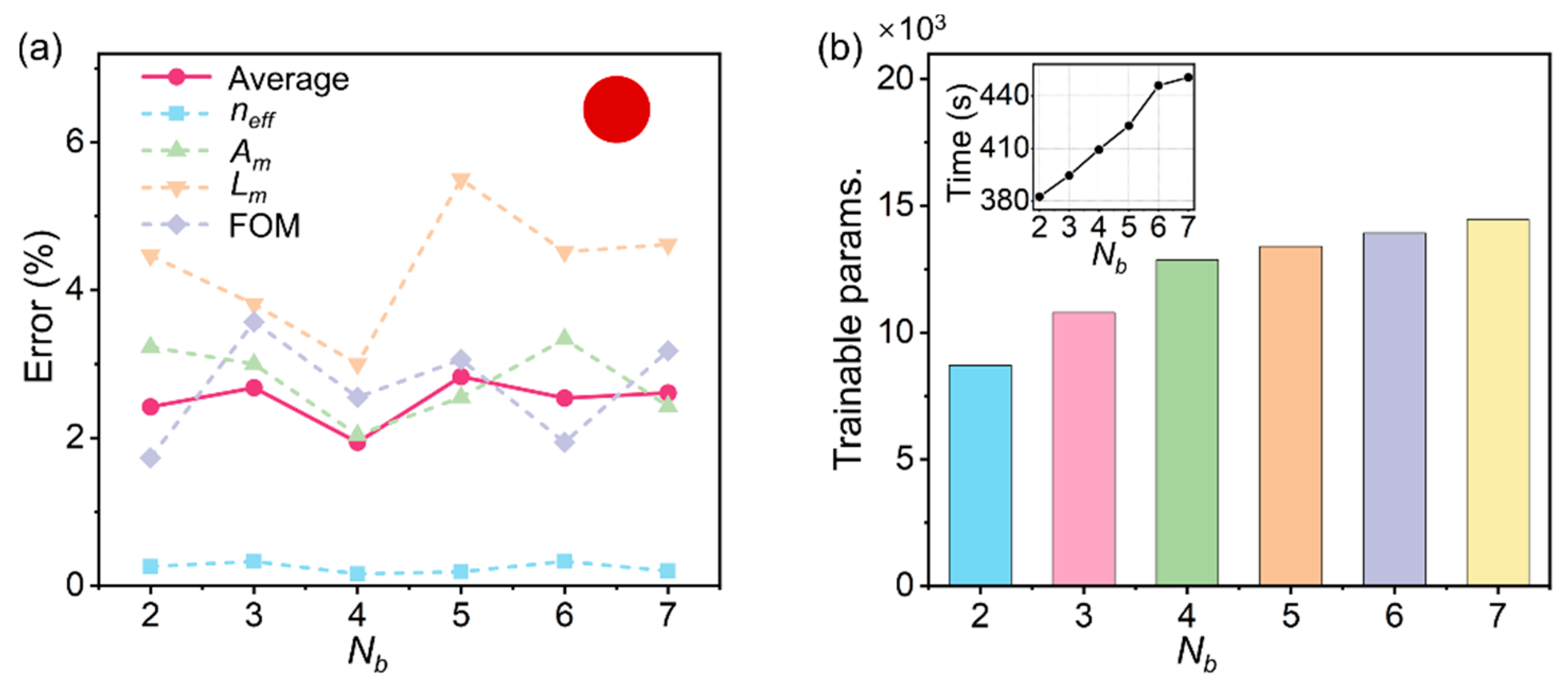
3.1. Optimized Layout for Gaining the Basic Knowledge
3.2. Performance Improvement in ft(⸳) and Reduction in Training Parameters
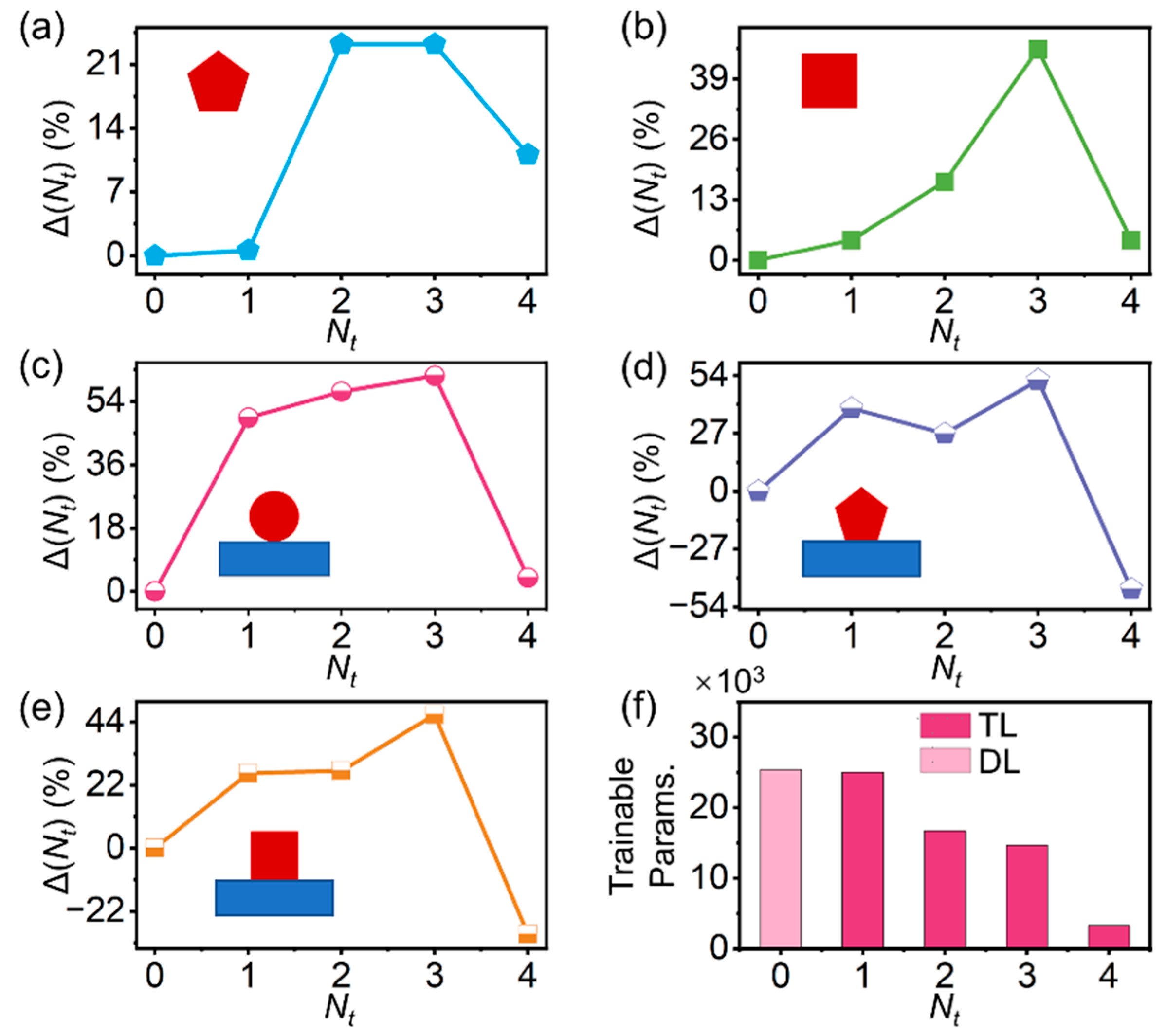
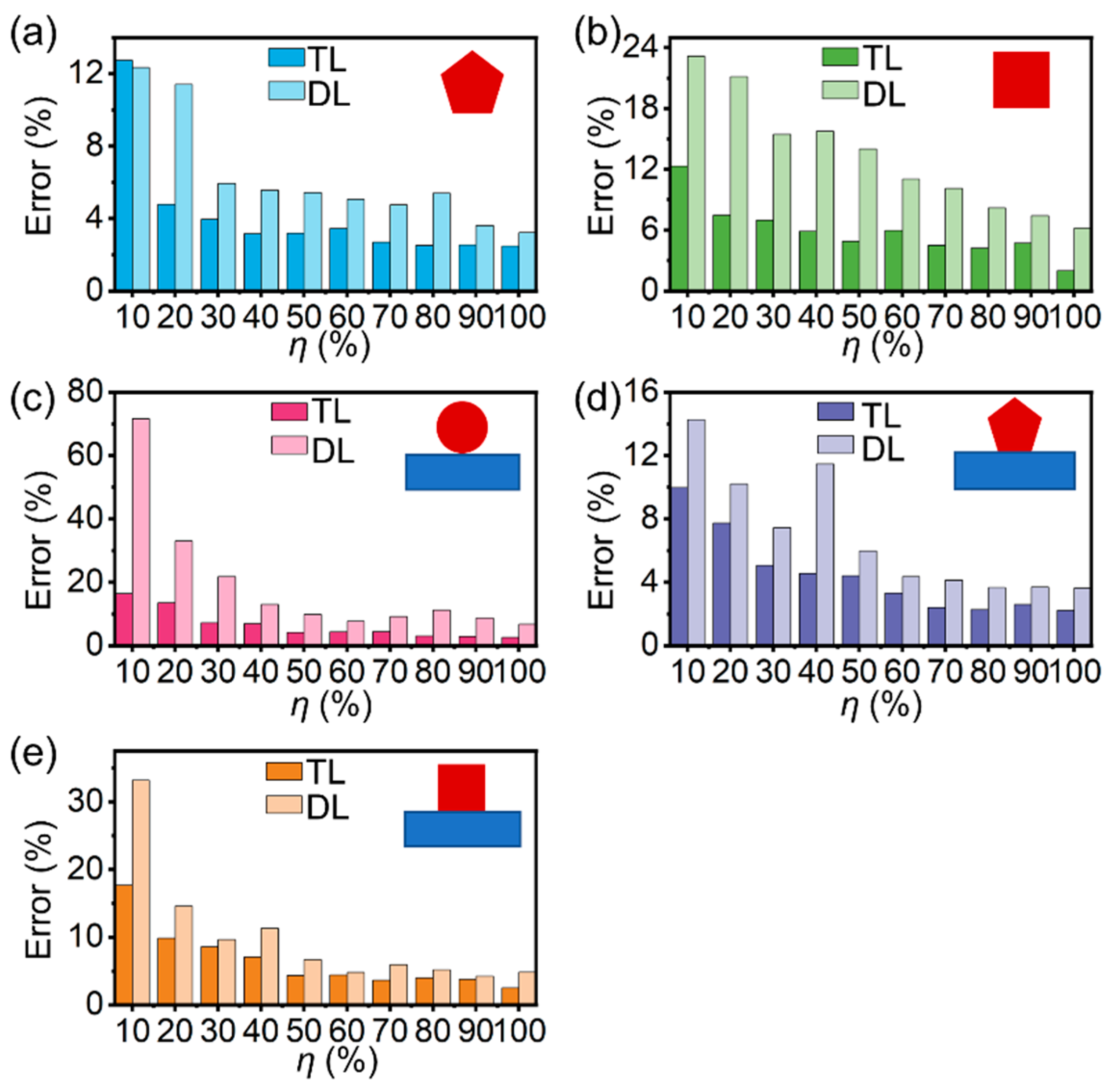
3.3. Removing the Need for a Large Set of Training Data with Reduced mt
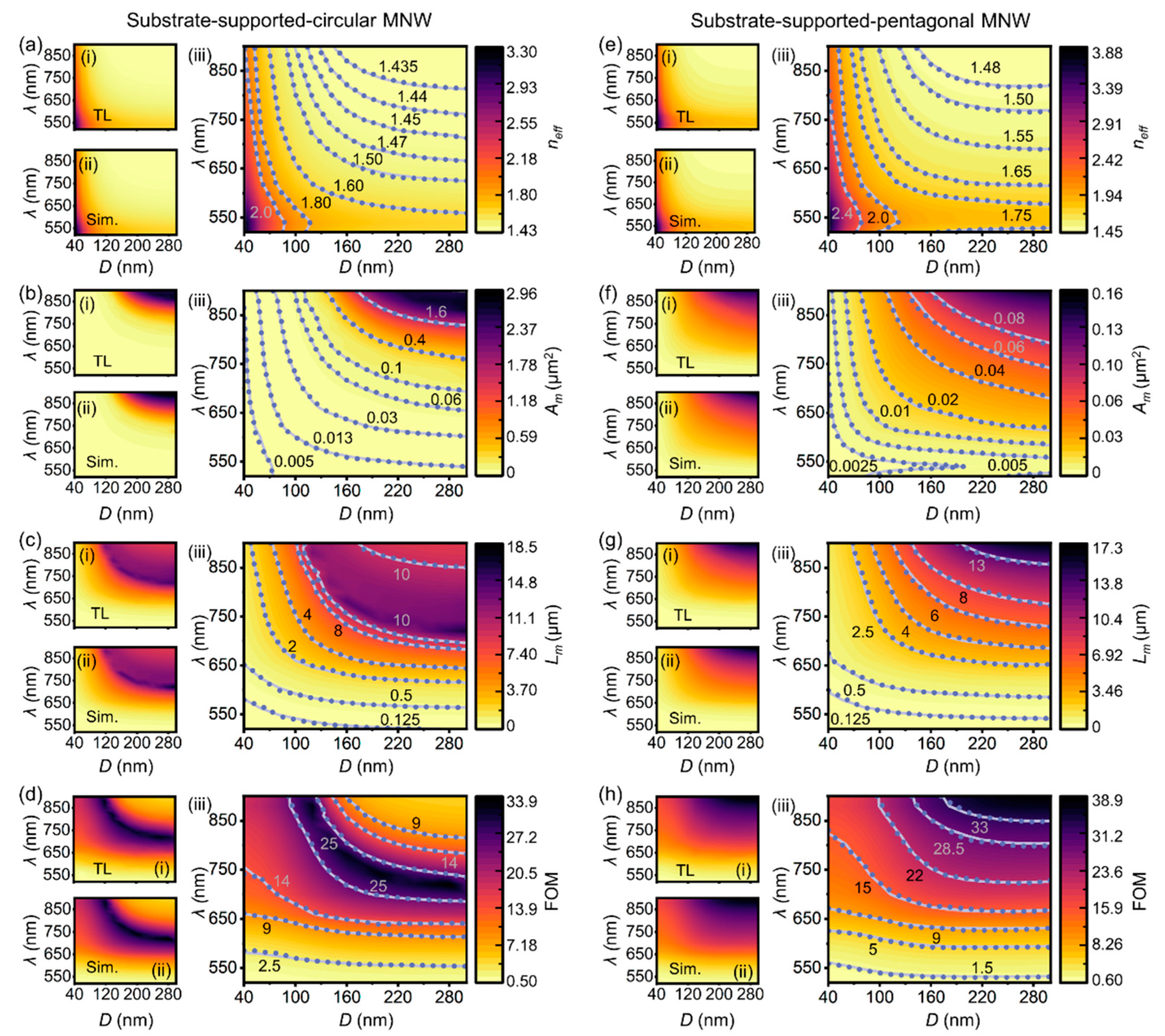
3.4. Accurate, Effective and Comprehensive Mapping of Waveguiding Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, X.; Ma, Y.; Wang, Y.; Tong, L. Nanowire Plasmonic Waveguides, Circuits and Devices. Laser Photonics Rev. 2013, 7, 855–881. [Google Scholar] [CrossRef]
- Wei, H.; Pan, D.; Zhang, S.; Li, Z.; Li, Q.; Liu, N.; Wang, W.; Xu, H. Plasmon Waveguiding in Nanowires. Chem. Rev. 2018, 118, 2882–2926. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Yan, X.; Niu, Y.; Li, Q.; Jia, Z.; Xu, H. Plasmon–Exciton Interactions: Spontaneous Emission and Strong Coupling. Adv. Funct. Mater. 2021, 31, 2100889. [Google Scholar] [CrossRef]
- Bellido, E.P.; Bicket, I.C.; Botton, G.A. The Effects of Bending on Plasmonic Modes in Nanowires and Planar Structures. Nanophotonics 2022, 11, 305–314. [Google Scholar] [CrossRef]
- Tao, A.; Kim, F.; Hess, C.; Goldberger, J.; He, R.; Sun, Y.; Xia, Y.; Yang, P. Langmuir−Blodgett Silver Nanowire Monolayers for Molecular Sensing Using Surface-Enhanced Raman Spectroscopy. Nano Lett. 2003, 3, 1229–1233. [Google Scholar] [CrossRef]
- Nauert, S.; Paul, A.; Zhen, Y.-R.; Solis, D.; Vigderman, L.; Chang, W.-S.; Zubarev, E.R.; Nordlander, P.; Link, S. Influence of Cross Sectional Geometry on Surface Plasmon Polariton Propagation in Gold Nanowires. ACS Nano 2014, 8, 572–580. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Qiu, M.; Bao, J.; Wiley, B.J.; Yang, Q.; Zhang, X.; Ma, Y.; Yu, H.; Tong, L. Direct Coupling of Plasmonic and Photonic Nanowires for Hybrid Nanophotonic Components and Circuits. Nano Lett. 2009, 9, 4515–4519. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Wang, P. Asymmetric Cavity Mode Engineering in a Single Plasmonic Nanowire. J. Light. Technol. 2021, 39, 5855–5863. [Google Scholar] [CrossRef]
- Gu, F.; Zeng, H.; Zhu, Y.B.; Yang, Q.; Ang, L.K.; Zhuang, S. Single-Crystal Pd and Its Alloy Nanowires for Plasmon Propagation and Highly Sensitive Hydrogen Detection. Adv. Opt. Mater. 2014, 2, 189–196. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.; Tong, L.; Lou, J. Modeling of Au-Nanowire Waveguide for Plasmonic Sensing in Liquids. J. Light. Technol. 2014, 32, 4233–4238. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, Y.; Meng, C.; Zhang, X.; Yu, S.; Wang, Y.; Yang, C.; Guo, X.; Ning, C.Z.; Tong, L. Hybrid Photon-Plasmon Nanowire Lasers. Nano Lett. 2013, 13, 5654–5659. [Google Scholar] [CrossRef] [PubMed]
- Sidiropoulos, T.P.H.; Röder, R.; Geburt, S.; Hess, O.; Maier, S.A.; Ronning, C.; Oulton, R.F. Ultrafast Plasmonic Nanowire Lasers near the Surface Plasmon Frequency. Nat. Phys. 2014, 10, 870–876. [Google Scholar] [CrossRef]
- Kim, S.-W.; Turng, L.-S. Three-Dimensional Numerical Simulation of Injection Molding Filling of Optical Lens and Multiscale Geometry Using Finite Element Method. Polym. Eng. Sci. 2006, 46, 1263–1274. [Google Scholar] [CrossRef]
- Lesina, A.C.; Vaccari, A.; Berini, P.; Ramunno, L. On the Convergence and Accuracy of the FDTD Method for Nanoplasmonics. Opt. Express 2015, 23, 10481–10497. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nayak, J.K.; Jha, R. Numerical Simulation on the Performance Analysis of a Graphene-Coated Optical Fiber Plasmonic Sensor at Anti-Crossing. Appl. Opt. 2017, 56, 3510–3517. [Google Scholar] [CrossRef]
- Bao, Q.; Wu, H.; Yang, L.; Wang, P.; Guo, X.; Tong, L. Circular-Area-Equivalence Approach for Determining Propagation Constants of a Single-Mode Polygonal Nanowire. J. Opt. Soc. Am. B 2022, 39, 795. [Google Scholar] [CrossRef]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse Design in Nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Plasmonic Nanostructure Design and Characterization via Deep Learning. Light Sci. Appl. 2018, 7, 60. [Google Scholar] [CrossRef] [Green Version]
- Chugh, S.; Ghosh, S.; Gulistan, A.; Rahman, B.M.A. Machine Learning Regression Approach to the Nanophotonic Waveguide Analyses. J. Light. Technol. 2019, 37, 6080–6089. [Google Scholar] [CrossRef] [Green Version]
- Chugh, S.; Gulistan, A.; Ghosh, S.; Rahman, B.M.A. Machine Learning Approach for Computing Optical Properties of a Photonic Crystal Fiber. Opt. Express 2019, 27, 36414–36425. [Google Scholar] [CrossRef]
- Yao, K.; Unni, R.; Zheng, Y. Intelligent Nanophotonics: Merging Photonics and Artificial Intelligence at the Nanoscale. Nanophotonics 2019, 8, 339–366. [Google Scholar] [CrossRef] [PubMed]
- Hegde, R.S. Deep Learning: A New Tool for Photonic Nanostructure Design. Nanoscale Adv. 2020, 2, 1007–1023. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Rahmani, M.; Ma, Y.; Smirnova, D.A.; Kamali, K.Z.; Deng, F.; Chiang, Y.K.; Huang, L.; Zhang, H.; Gould, S.; et al. Enhanced Light–Matter Interactions in Dielectric Nanostructures via Machine-Learning Approach. Adv. Photonics 2020, 2, 026003. [Google Scholar] [CrossRef]
- So, S.; Badloe, T.; Noh, J.; Rho, J.; Bravo-Abad, J. Deep Learning Enabled Inverse Design in Nanophotonics. Nanophotonics 2020, 9, 1041–1057. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep Learning for the Design of Photonic Structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Anika, N.J.; Mia, M.B. Design and Analysis of Guided Modes in Photonic Waveguides Using Optical Neural Network. Optik 2021, 228, 165785. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Arbouet, A.; Girard, C.; Muskens, O.L. Deep Learning in Nano-Photonics: Inverse Design and Beyond. Photon. Res. 2021, 9, B182. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, M.; Fan, J.A. Deep Neural Networks for the Evaluation and Design of Photonic Devices. Nat. Rev. Mater. 2021, 6, 679–700. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Y. A Physics-Based Machine Learning Approach for Modeling the Complex Reflection Coefficients of Metal Nanowires. Nanotechnology 2022, 33, 205701. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Neural Networks and Information in Materials Science. Stat. Anal. and Data Min. 2009, 1, 296–305. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar]
- Qu, Y.; Jing, L.; Shen, Y.; Qiu, M.; Soljačić, M. Migrating Knowledge between Physical Scenarios Based on Artificial Neural Networks. ACS Photonics 2019, 6, 1168–1174. [Google Scholar] [CrossRef] [Green Version]
- Sung, N.; Kim, M.; Jo, H.; Yang, Y.; Kim, J.; Lausen, L.; Kim, Y.; Lee, G.; Kwak, D.; Ha, J.-W.; et al. NSML: A Machine Learning Platform That Enables You to Focus on Your Models. arXiv, 2017; preprint. arXiv:1712.05902. [Google Scholar]
- Sudharsan, B.; Patel, P.; Breslin, J.; Ali, M.I.; Mitra, K.; Dustdar, S.; Rana, O.; Jayaraman, P.P.; Ranjan, R. Toward Distributed, Global, Deep Learning Using IoT Devices. IEEE Internet Comput. 2021, 25, 6–12. [Google Scholar] [CrossRef]
- Huang, L.; Yang, X.; Liu, T.; Ozcan, A. Few-Shot Transfer Learning for Holographic Image Reconstruction Using a Recurrent Neural Network. APL Photonics 2022, 7, 070801. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Qiu, C.; Wu, X.; Luo, Z.; Yang, H.; He, G.; Huang, B. Nanophotonic Inverse Design with Deep Neural Networks Based on Knowledge Transfer Using Imbalanced Datasets. Opt. Express 2021, 29, 28406. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic Representation and Inverse Design of Metamaterials Based on a Deep Generative Model with Semi-Supervised Learning Strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Luo, Y.; Luo, J.; Pu, M.; Zhang, Y.; Ha, Y.; Luo, X. Efficient Design of a Dielectric Metasurface with Transfer Learning and Genetic Algorithm. Opt. Mater. Express 2021, 11, 1852. [Google Scholar] [CrossRef]
- Day, O.; Khoshgoftaar, T.M. A Survey on Heterogeneous Transfer Learning. J. Big Data 2017, 4, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Li, M.; Watanabe, Y.; Kimura, T.; Matsunawa, T.; Nojima, S.; Pan, D.Z. Data Efficient Lithography Modeling With Transfer Learning and Active Data Selection. IEEE Trans. Computer-Aided Design Integr. Circuits Syst. 2019, 38, 1900–1913. [Google Scholar] [CrossRef]
- Evci, U.; Dumoulin, V.; Larochelle, H.; Mozer, M.C. Head2Toe: Utilizing Intermediate Representations for Better Transfer Learning. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 28 June 2022; pp. 6009–6033. [Google Scholar]
- Zolla, F.; Renversez, G.; Nicolet, A.; Kuhlmey, B.; Guenneau, S.; Felbacq, D. Foundations of Photonic Crystal Fibres; Imperial College Press: London, UK, 2005. [Google Scholar]
- Nicolet, A.; Geuzaine, C. Waveguide Propagation Modes and Quadratic Eigenvalue Problems. In Proceedings of the 6th International Conference on Computational Electromagnetics, Aachen, Germany, 4–6 April 2006. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How Transferable Are Features in Deep Neural Networks? In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3320–3328. [Google Scholar]
- Wang, Y.; Feng, Y.; Zeng, L.; Wu, X. Versatile and High-Quality Manipulation of Asymmetric Modes in Bent Metal Nanowires. Opt. Mater. Express 2022, 12, 2782. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Oulton, R.F.; Bartal, G.; Pile, D.F.P.; Zhang, X. Confinement and propagation characteristics of subwavelength plasmonic modes. New J. Phys. 2008, 10, 105018. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, H. Optimizing Substrate-Mediated Plasmon Coupling toward High-Performance Plasmonic Nanowire Waveguides. ACS Nano 2012, 6, 8128–8135. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, A.; Feng, Y.; Zhu, C.; Wang, Y.; Wu, X. Transfer Learning for Modeling Plasmonic Nanowire Waveguides. Nanomaterials 2022, 12, 3624. https://doi.org/10.3390/nano12203624
Luo A, Feng Y, Zhu C, Wang Y, Wu X. Transfer Learning for Modeling Plasmonic Nanowire Waveguides. Nanomaterials. 2022; 12(20):3624. https://doi.org/10.3390/nano12203624
Chicago/Turabian StyleLuo, Aoning, Yuanjia Feng, Chunyan Zhu, Yipei Wang, and Xiaoqin Wu. 2022. "Transfer Learning for Modeling Plasmonic Nanowire Waveguides" Nanomaterials 12, no. 20: 3624. https://doi.org/10.3390/nano12203624
APA StyleLuo, A., Feng, Y., Zhu, C., Wang, Y., & Wu, X. (2022). Transfer Learning for Modeling Plasmonic Nanowire Waveguides. Nanomaterials, 12(20), 3624. https://doi.org/10.3390/nano12203624






