Spin Glass State in Strained La2/3Ca1/3MnO3 Thin Films
Abstract
:1. Introduction
2. Materials and Methods
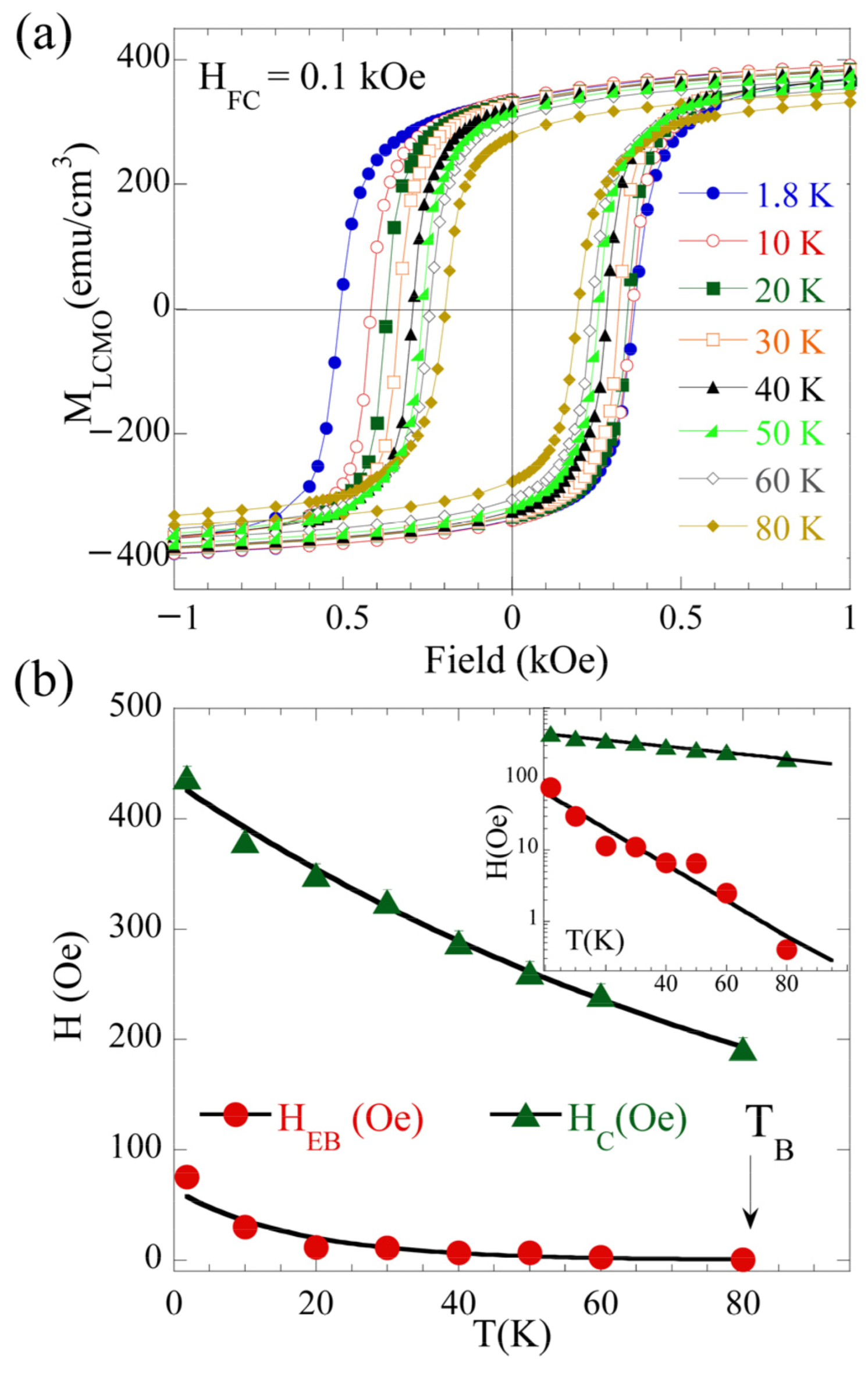
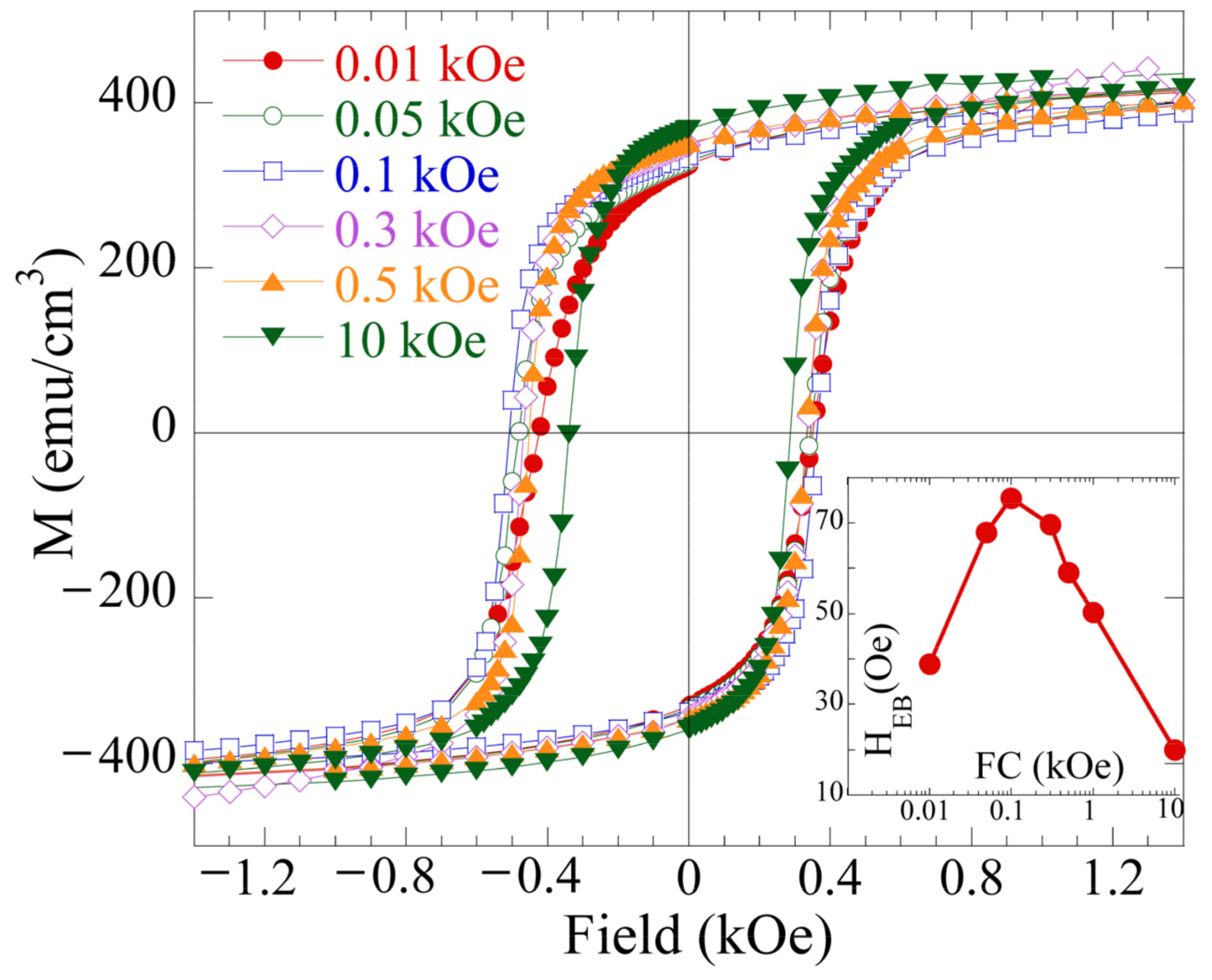
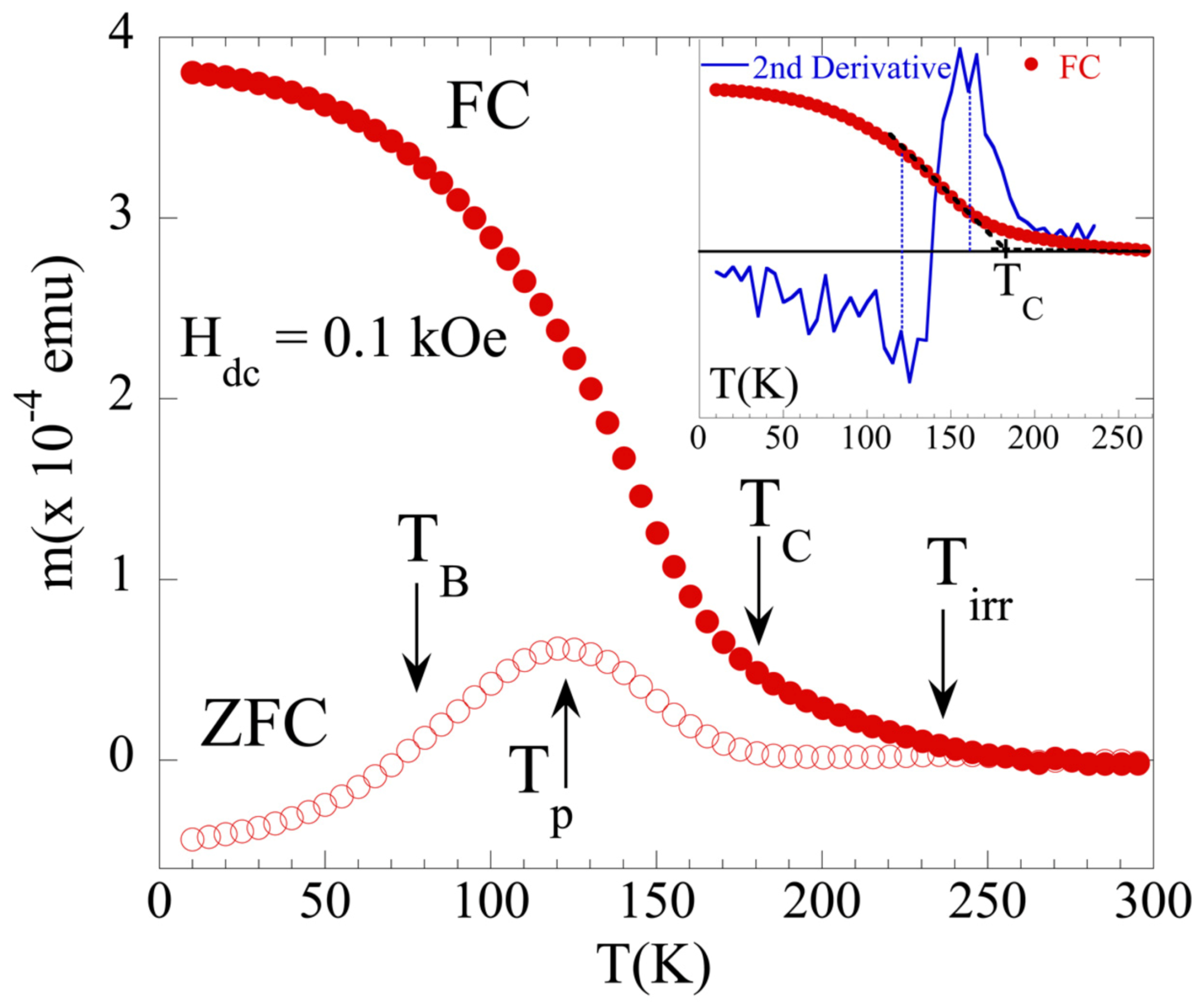
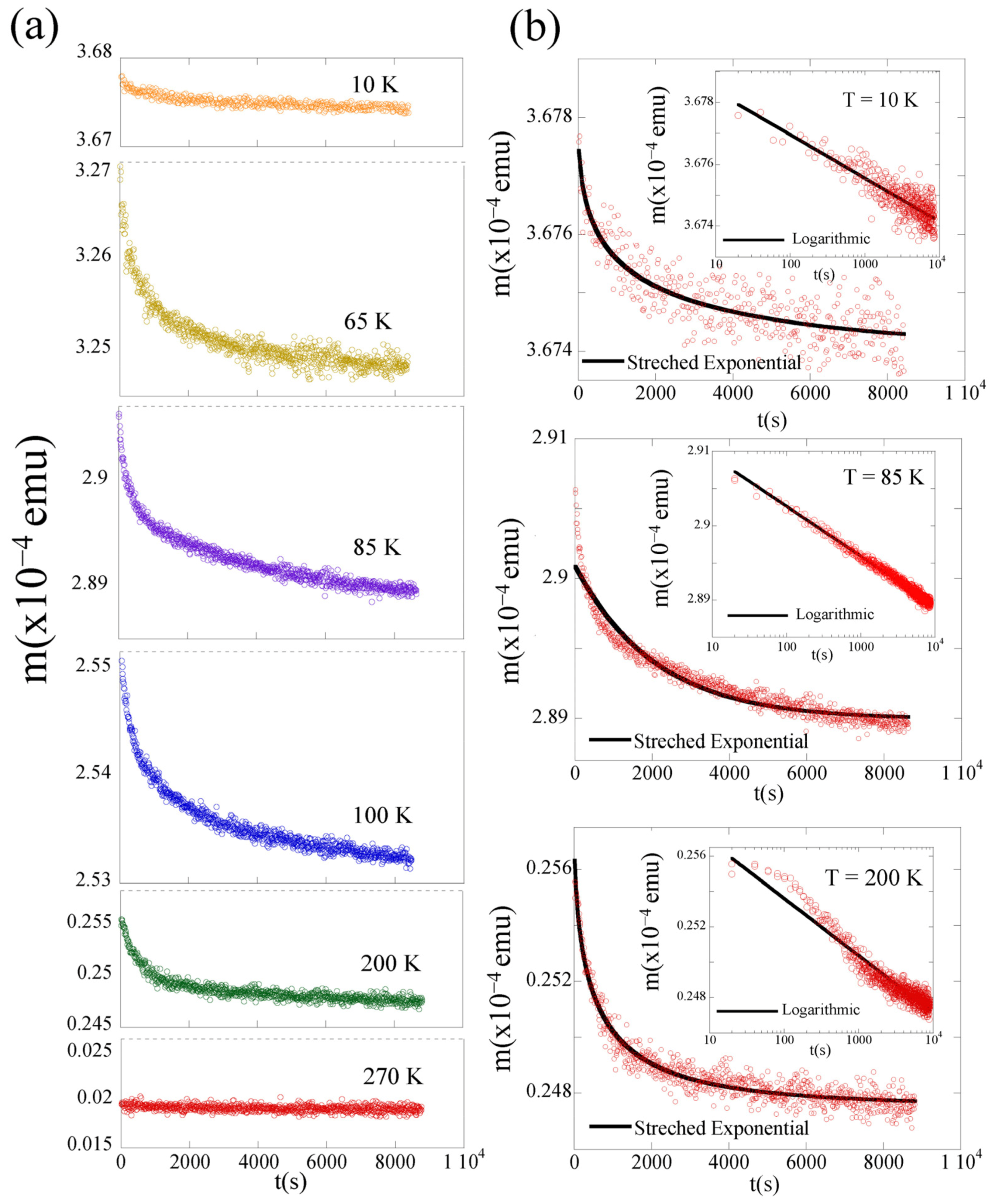
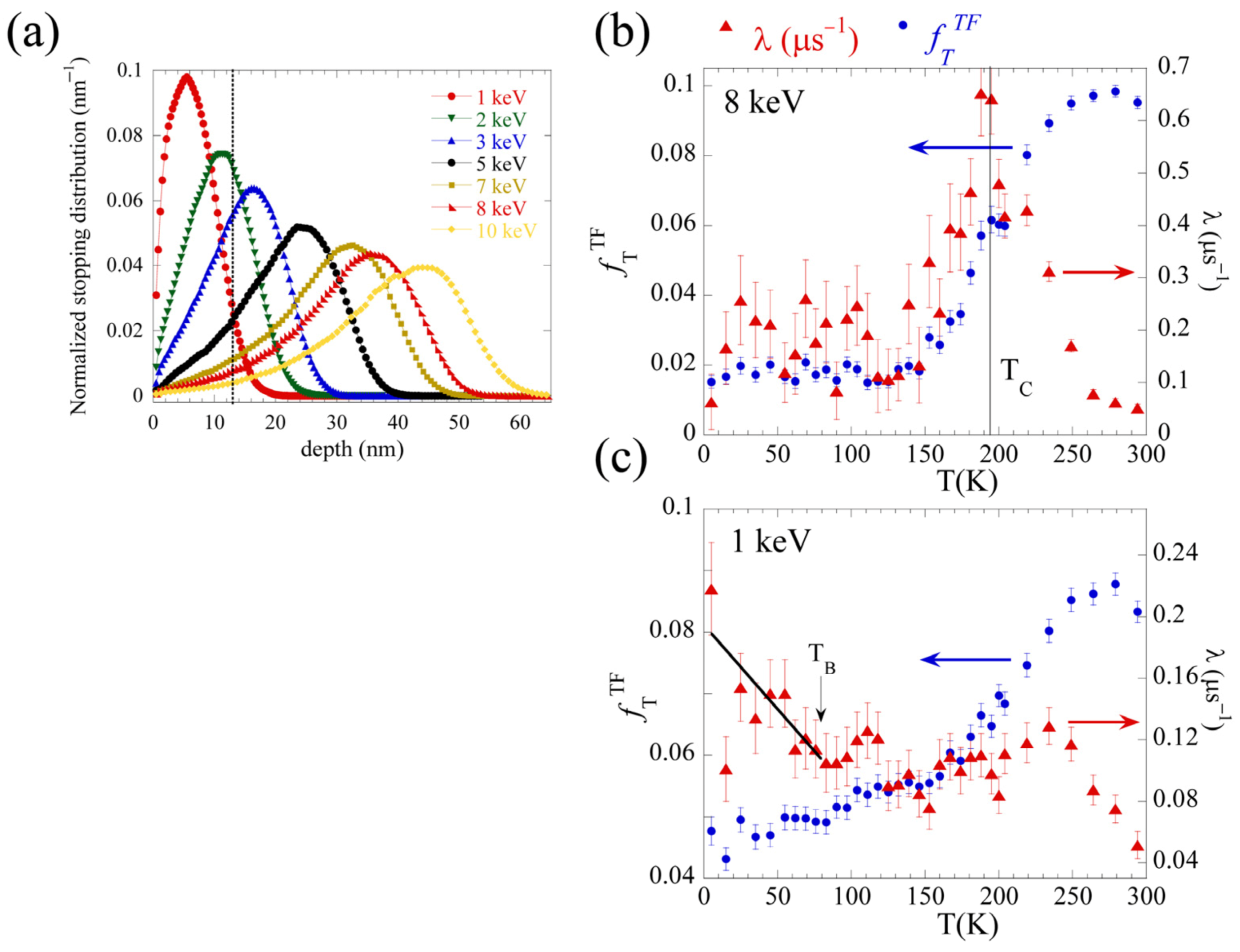
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maurel, L.; Marcano, N.; Prokscha, T.; Langenberg, E.; Blasco, J.; Suter, J.; Magén, C.; Morellón, L.; Ibarra, M.R.; Pardo, J.A.; et al. Nature of antiferromagnetic order in epitaxially strained multiferroic SrMnO3 thin films. Phys. Rev. B 2015, 92, 024419–024427. [Google Scholar] [CrossRef] [Green Version]
- Maurel, L.; Marcano, N.; Langenberg, E.; Guzmán, R.; Prokscha, T.; Magén, C.; Pardo, J.A.; Algarabel, P.A. Engineering the magnetic order in epitaxially strained Sr1−xBaxMnO3 perovskite thin films. APL Mater. 2019, 7, 041117–041123. [Google Scholar] [CrossRef] [Green Version]
- Bozovic, I.; Logvenov, G.; Belca, I.; Narimbetov, B.; Sveklo, I. Epitaxial Strain and Superconductivity in La2−xSrxCuO4 Thin Films. Phys. Rev. Lett. 2002, 89, 107001–107004. [Google Scholar] [CrossRef] [PubMed]
- Haeni, J.H.; Irvin, P.; Chang, W.; Uecker, R.; Reiche, P.; Li, Y.; Choudhury, S.; Tian, W.; Hawley, M.E.; Craigo, B.; et al. Room-temperature ferroelectricity in strained SrTiO3. Nature 2004, 430, 758–761. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abad, L.; Laukhin, V.; Valencia, S.; Gaup, A.; Gudat, W.; Balcells, L.; Martínez, B. Interfacial Strain: The Driving Force for Selective Orbital Occupancy in Manganite Thin Films. Adv. Funct. Mater. 2007, 17, 3918–3925. [Google Scholar] [CrossRef]
- Tebano, A.; Aruta, C.; Sanna, S.; Medaglia, P.G.; Balestrino, G.; Sidorenko, A.A.; De Renzi, R.; Ghiringhelli, G.; Braicovich, L.; Bisogni, V.; et al. Evidence of Orbital Reconstruction at Interfaces in Ultrathin La0.67Sr0.33MnO3 Films. Phys. Rev. Lett. 2008, 100, 137401–137404. [Google Scholar] [CrossRef] [Green Version]
- Tokura, Y.; Nagaosa, N. Orbital Physics in Transition-Metal Oxides. Science 2000, 288, 462–468. [Google Scholar] [CrossRef] [Green Version]
- Marín, L.; Rodríguez, L.A.; Magén, C.; Snoeck, E.; Arras, R.; Lucas, I.; Morellón, L.; Algarabel, P.A.; De Teresa, J.M.; Ibarra, M.R. Observation of the Strain Induced Magnetic Phase Segregation in Manganite Thin Films. Nano Lett. 2015, 15, 492–497. [Google Scholar] [CrossRef]
- Schuller, I.K.; Morales, R.; Batlle, X.; Nowak, U.; Güntherodt, G. Role of the antiferromagnetic bulk spins in exchange bias. J. Magn. Magn. Mater. 2016, 416, 2–9. [Google Scholar] [CrossRef] [Green Version]
- Huijben, M.; Martin, L.W.; Chu, Y.H.; Holcomb, M.B.; Yu, P.; Rijnders, G.; Blank, D.H.A.; Ramesh, R. Critical thickness and orbital ordering in ultrathin La0.7Sr0.3MnO3. Phys. Rev. B 2008, 78, 094413–094419. [Google Scholar] [CrossRef]
- Ali, M.; Adie, P.; Marrows, C.; Greig, D.; Hickey, B.J.; Stamps, R.L. Exchange bias using a spin glass. Nat. Mater. 2007, 6, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Cui, B.; Song, C.; Wang, G.; Mao, H.J.; Zeng, F.; Pan, F. Strain engineering induced interfacial self-assembly and intrinsic exchange bias in a manganite perovskite film. Sci. Rep. 2013, 3, 2542–2547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, G.W.; Guan, X.F.; Bai, Y.H.; Quan, Z.Y.; Jiang, F.X.; Xu, X.H. Interfacial Spin Glass State and Exchange Bias in the Epitaxial La0.7Sr0.3MnO3/LaNiO3 Bilayer. Nanoscale Res. Lett. 2017, 12, 330–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zang, J.; Zhou, G.; Bai, Y.; Quan, Z.; Xu, X. The Exchange Bias of LaMnO3/LaNiO3 Superlattices Grown along Different Orientations. Sci. Rep. 2017, 7, 10557–10563. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Liu, Q.; Chen, P.; Zhou, L.; Li, H.; Ning, X.; Qiu, C.; He, H. Interfacial spin-glass-like state and exchange bias in epitaxial iridate-manganite heterostructure. J. Alloys Compd. 2019, 789, 351–356. [Google Scholar] [CrossRef]
- Maniv, E.; Murphy, R.A.; Haley, S.C.; Doyle, S.; John, C.; Maniv, A.; Ramakrishna, S.K.; Tang, Y.L.; Ercius, P.; Ramesh, R.; et al. Exchange bias due to coupling between coexisting antiferromagnetic and spin-glass orders. Nat. Phys. 2021, 17, 525–530. [Google Scholar] [CrossRef]
- Eckstein, W. Computer Simulation of Ion-Solid Interactions, 1st ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Rojas Sánchez, J.C.; Nelson-Cheeseman, B.; Granada, M.; Arenholz, E.; Steren, L.B. Exchange-bias effect at La0.75Sr0.25MnO3/LaNiO3 interfaces. Phys. Rev. B 2012, 85, 094427–094431. [Google Scholar] [CrossRef]
- Ding, J.F.; Lebedev, O.I.; Turner, S.; Tian, Y.F.; Hu, W.J.; Seo, J.W.; Panagopoulos, C.; Prellier, W.; Van Tendeloo, G.; Wu, T. Interfacial spin glass state and exchange bias in manganite bilayers with competing magnetic orders. Phys. Rev. B 2013, 87, 054428–054434. [Google Scholar] [CrossRef]
- Jungbauer, M.; Hühn, S.; Michelmann, M.; Goering, E.; Moshnyaga, V. Exchange bias in La0.7Sr0.3MnO3/SrMnO3/La0.7Sr0.3MnO3 trilayers. J. Appl. Phys. 2013, 113, 17D709. [Google Scholar] [CrossRef]
- Moutis, N.; Christides, C.; Panagiotopoulos, I.; Niarchos, D. Exchange-coupling properties of La1−xCaxMnO3 ferromagnetic/antiferromagnetic multilayers. Phys. Rev. B 2001, 64, 094429–094438. [Google Scholar] [CrossRef]
- Aktas, B.; Öner, Y.; Durusoy, H.Z. A spin-wave resonance study on reentrant NiMn films. J. Magn. Magn. Mater. 1993, 119, 339–352. [Google Scholar] [CrossRef]
- Korenivski, V.; van Dover, R.B.; Suzuki, Y.; Gyorgy, E.M.; Phillips, J.M.; Felder, R.J. Interlayer exchange coupling in amorphous/crystalline NiFe2O4 thin film bilayers. J. Appl. Phys. 1996, 79, 5926–5928. [Google Scholar] [CrossRef]
- Nayak, S.; Manna, P.K.; Singh, B.B.; Bedanta, S. Effect of spin glass frustration on exchange bias in NiMn/CoFeB bilayers. Phys. Chem. Chem. Phys. 2021, 23, 6481–6489. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Chen, P.; Zhou, L.; Ning, X.; Deng, B.; Shi, X.; He, H. Cluster glass induced unconventional exchange bias in epitaxial LaMnO3/SrMnO3 bilayers. Mater. Lett. 2019, 242, 95–98. [Google Scholar] [CrossRef]
- Grommé, C.S.; Wright, T.L.; Peck, D.L. Magnetic properties and oxidation of iron-titanium oxide minerals in Alae and Makaopuhi lava lakes, Hawaii. J. Geophys. Res. 1969, 74, 5277–5293. [Google Scholar] [CrossRef]
- Infante, I.C.; Sánchez, F.; Fontcuberta, J.; Wojcik, M.; Jedryka, E.; Estradé, S.; Peiró, F.; Arbiol, J.; Laukhin, V.; Espinós, J.P. Elastic and orbital effects on thickness-dependent properties of manganite thin films. Phys. Rev. B 2007, 76, 224415–224427. [Google Scholar] [CrossRef] [Green Version]
- De Teresa, J.; Ibarra, M.; Algarabel, P.; Ritter, C.; Marquina, C.; Blasco, J.; García, J.; Del Moral, A.; Arnold, Z. Evidence for magnetic polarons in the magnetoresistive perovskites. Nature 1997, 386, 256–259. [Google Scholar] [CrossRef]
- De Teresa, J.; Ritter, C.; Ibarra, M.; Algarabel, P.; García-Muñoz, J.L.; Blasco, J.; García, J.; Marquina, C. Charge localization, magnetic order, structural behavior, and spin dynamics of (La-Tb)2/3Ca1/3MnO3 manganese perovskites probed by neutron diffraction and muon spin relaxation. Phys. Rev. B 1997, 56, 3317–3324. [Google Scholar] [CrossRef]
- De Teresa, J.; Ibarra, M.; Algarabel, P.; Morellón, L.; García-Landa, B.; Marquina, C.; Ritter, C.; Maignan, A.; Martin, C.; Raveau, B.; et al. Magnetic versus orbital polarons in colossal magnetoresistance manganites. Phys. Rev. B 2002, 65, 100403–100406. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin Glasses: An experimental Introduction; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Chamberlin, R.V.; Mozurkewich, G.; Orbach, R. Time Decay of the Remanent Magnetization in Spin-Glasses. Phys. Rev. Lett. 1984, 52, 867–870. [Google Scholar] [CrossRef]
- Taniyama, T.; Nakatani, I. Magnetic relaxation in Ga0.6Mo2S4 spinel. J. Appl. Phys. 1998, 83, 6323–6325. [Google Scholar] [CrossRef]
- Binder, K.; Young, A.P. Spin glasses: Experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 1986, 58, 801–976. [Google Scholar] [CrossRef]
- Cardoso, C.A.; Araujo-Moreira, F.M.; Awana, V.P.S.; Takayama-Muromachi, E.; de Lima, O.F.; Yamauchi, H.; Karppinen, M. Spin glass behavior in RuSr2Gd1.5Ce0.5Cu2O10−δ. Phys. Rev. B 2003, 67, 020407–020410. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, R.C.; Takeuchi, Y.; Ohtomo, A.; Hossain, Z. Exchange bias and spin glass states driven by antisite disorder in the double perovskite compound LaSrCoFeO6. Phys. Rev. B 2019, 21, 214436–214444. [Google Scholar] [CrossRef]
- Truong, A.; Watanabe, A.O.; Mortemousque, P.A.; Ando, K.; Sato, T.; Taniyama, T.; Itoh, K.M. Interfacial spin-glass-like state in Mn5Ge3 single crystalline films grown on germanium substrates. Phys. Rev. B 2015, 91, 214425–214433. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, S.D.; Rajeev, K.P. Signatures of spin-glass freezing in NiO nanoparticles. Phys. Rev. B 2005, 72, 104433–104441. [Google Scholar] [CrossRef] [Green Version]
- Li, D.X.; Nimori, S.; Shiokawa, Y.; Haga, Y.; Yamamoto, E.; Onuki, Y. Ac susceptibility and magnetic relaxation of R2PdSi3 (R=Nd, Tb, and Dy). Phys. Rev. B 2003, 68, 012413–012416. [Google Scholar] [CrossRef]
- Guy, C.N. Spin glasses in low DC fields. II. Magnetic viscosity. J. Phys. F Met. Phys. 1978, 8, 1309–1319. [Google Scholar] [CrossRef]
- Morenzoni, E.; Prokscha, T.; Suter, A.; Luetkens, H.; Khasanov, R. Nano-scale thin film investigations with slow polarized muons. J. Phys. Condens. Matter 2004, 16, S4583–S4601. [Google Scholar] [CrossRef]
- Prokscha, T.; Morenzoni, E.; Deiters, K.; Foroughi, F.; George, D.; Kobler, R.; Suter, A.; Vrankovic, V. The new μE4 beam at PSI: A hybrid-type large acceptance channel for the generation of a high intensity surface-muon beam. Nucl. Instrum. Methods Phys. Res. Sect. A 2008, 595, 317–331. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Yamazaki, T.; Harshman, D.R.; Senba, M.; Ansaldo, E.J. Muon-spin relaxation in AuFe and CuMn spin glasses. Phys. Rev. B 1985, 31, 546–563. [Google Scholar] [CrossRef] [PubMed]
- Morenzoni, E.; Luetkens, H.; Prokscha, T.; Suter, A.; Vongtragool, S.; Galli, F.; Hesselberth, M.B.S.; Garifianov, N.; Khasanov, R. Depth-Dependent Spin Dynamics of Canonical Spin-Glass Films: A Low-Energy Muon-Spin-Rotation Study. Phys. Rev. Lett. 2008, 100, 147205–147208. [Google Scholar] [CrossRef] [Green Version]
- Stilp, E.; Suter, A.; Prokscha, T.; Morenzoni, E.; Keller, H.; Wojek, B.M.; Luetkens, H.; Gozar, A.; Logvenov, G.; Božović, I. Magnetic phase diagram of low-doped La2−xSrxCuO4 thin films studied by low-energy muon-spin rotation. Phys. Rev. B 2013, 88, 064419–064429. [Google Scholar] [CrossRef] [Green Version]
- Suter, A.; Wojek, B.M. Musrfit: A Free Platform-Independent Framework for μSR Data Analysis. Phys. Procedia 2012, 30, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Murnick, D.E.; Fiory, A.T.; Kossler, W.J. Muon-Spin Depolarization in Spin-Glasses. Phys. Rev. Lett. 1976, 36, 100–104. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucas, I.; Marcano, N.; Prokscha, T.; Magén, C.; Corcuera, R.; Morellón, L.; De Teresa, J.M.; Ibarra, M.R.; Algarabel, P.A. Spin Glass State in Strained La2/3Ca1/3MnO3 Thin Films. Nanomaterials 2022, 12, 3646. https://doi.org/10.3390/nano12203646
Lucas I, Marcano N, Prokscha T, Magén C, Corcuera R, Morellón L, De Teresa JM, Ibarra MR, Algarabel PA. Spin Glass State in Strained La2/3Ca1/3MnO3 Thin Films. Nanomaterials. 2022; 12(20):3646. https://doi.org/10.3390/nano12203646
Chicago/Turabian StyleLucas, Irene, Noelia Marcano, Thomas Prokscha, César Magén, Rubén Corcuera, Luis Morellón, José M. De Teresa, M. Ricardo Ibarra, and Pedro A. Algarabel. 2022. "Spin Glass State in Strained La2/3Ca1/3MnO3 Thin Films" Nanomaterials 12, no. 20: 3646. https://doi.org/10.3390/nano12203646
APA StyleLucas, I., Marcano, N., Prokscha, T., Magén, C., Corcuera, R., Morellón, L., De Teresa, J. M., Ibarra, M. R., & Algarabel, P. A. (2022). Spin Glass State in Strained La2/3Ca1/3MnO3 Thin Films. Nanomaterials, 12(20), 3646. https://doi.org/10.3390/nano12203646








