Next Article in Journal
Photocatalytic and Antibacterial Activity of CoFe2O4 Nanoparticles from Hibiscus rosa-sinensis Plant Extract
Next Article in Special Issue
Actuating Bimorph Microstructures with Magnetron-Sputtered Ti-Ni-Cu Shape Memory Alloy Films
Previous Article in Journal
MXene Based Nanocomposites for Recent Solar Energy Technologies
Previous Article in Special Issue
On the Possible Cause of Sudden Storage Modulus Increase during the Heating of PM FeMnSiCrNi SMAs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 12
Issue 20
10.3390/nano12203667
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Processing Effects on the Martensitic Transformation and Related Properties in the Ni55Fe18Nd2Ga25 Ferromagnetic Shape Memory Alloy

by
Mihaela Sofronie
,
Bogdan Popescu
,
Monica Enculescu
,
Mugurel Tolea
and
Felicia Tolea
*
National Institute of Materials Physics, Atomistilor 405A, 077125 Magurele, Romania
*
Author to whom correspondence should be addressed.
Nanomaterials 2022, 12(20), 3667; https://doi.org/10.3390/nano12203667
Submission received: 20 September 2022 / Revised: 14 October 2022 / Accepted: 16 October 2022 / Published: 19 October 2022
(This article belongs to the Special Issue Nanostructural Processing Effects in Shape Memory Alloys)
Browse Figures
Versions Notes

Abstract

:
The influence of processing on the martensitic transformation and related magnetic properties of the Ni55Fe18Nd2Ga25 ferromagnetic shape memory alloy, as bulk and ribbons prepared by the melt spinning method and subjected to different thermal treatments, is investigated. Structural, calorimetric, and magnetic characterizations are performed. Thermal treatment at 1173 K induces a decrease in both the Curie and the martensitic transformation temperatures, while a treatment at 673 K produces the structural ordering of the ribbons, hence an increase in TC. A maximum value of the magnetic entropy variation of −5.41 J/kgK was recorded at 310 K for the as quenched ribbons. The evaluation of the magnetoresistive effect shows a remarkable value of −13.5% at 275 K on the bulk sample, which is much higher than in the ribbons.

1. Introduction

The Ferromagnetic Shape-Memory Alloys (FSMA) are intensively investigated due to their diversified application potential in various fields such as: biomedical [1,2]; civil structures [3]; miniature devices and robotics [4,5]; and other applications [6,7,8]. At temperatures lower than the magnetic ordering temperatures they undergo the so-called martensitic transformation (MT); this is a thermoelastic, reversible, and diffusionless transformation, which occurs between a high temperature crystalline phase of high symmetry (austenite) and a low temperature one of low symmetry (martensite) [9].
An important class of FSMA are the Heusler alloys which incorporate a huge number of magnetic members exhibiting diverse magnetic phenomena such as itinerant and localized magnetism, antiferromagnetism, helimagnetism, Pauli paramagnetism, or heavy-fermionic behavior [10,11]. Ni2MnGa is a representative and the most investigated member of this class of materials, which shows a huge magnetic-field-induced strain (MFIS) below the austenite–martensite transformation, of the order of several percent, as evidenced by Ullakko et al. [12]. However, the compound’s brittleness makes it difficult to be used in applications, and for this reason the search for new Heusler alloys that undergo an MT was extended comprising Co-Ni-Ga [13,14,15] and Ni-Mn-(Al, In, Sn) [16,17,18,19,20,21]. Ni-Fe-Ga alloys [22,23,24,25,26] have emerged as good candidates for replacing the brittle Ni-Mn-Ga in applications [27]. They show enhanced mechanical durability during the reversible austenite–martensite transformation and exceptional magnetoelastic properties promoted by their structural twinning. The improved ductility of the off-stoichiometric Ni-Fe-Ga alloys is caused by the existence of secondary phases [28], which may be controlled to some extent by suitable preparation techniques, e.g., melt spinning, where the obtained ribbons preserve a relatively good sample malleability. In addition, it is assumed that the thin melt-spun ribbons assure a more efficient heat transfer, which is desirable in magnetocaloric applications. In particular, the sample’s malleability is caused by a face-centered cubic gamma phase, which forms during the heat treatments necessary for sample structural ordering. Its presence, however, might alter the intrinsic properties of the alloy and, therefore, single phase alloys obtained by ultrafast cooling are desirable. Another approach for improving the magnetic and mechanical properties of Heusler type FSMA is by substituting with Rare Earth (RE) elements [29,30,31,32]. Thus, in Ni-Mn-Ga alloys various substitutions have been tested in order to improve their magnetic anisotropy and ductility. Research shows that the low solubility of the RE in the alloy matrix (below 0.1 at%) produce no major changes in the MT characteristics; instead new phases precipitate at the grain boundaries that positively impact the cohesion between grains. For instance, it was observed that the addition of RE (Nd, Sm, Tb) to the Ni-Mn-Ga [33] shape memory alloy significantly improves the compressive ductility of the alloy. The results obtained in the latter case also suggest the suitability of RE substitution approach in Ni-Fe-Ga based alloys, which might corroborate previous investigations on the influence of different quenching rates on the structural ordering of Ni2FeGa melt spun ribbons [34]. In addition, deviating from the exact composition (Ni50Fe25Ga25) has a tuning effect (higher/lower Curie or structural transition temperatures). In our case, one purpose was to search for concomitant magnetic and structural transitions, which has been achieved for the as-quenched ribbons, as shall be described.
The magnetocaloric effect (MCE) is defined as the heating or cooling of a magnetic material, isolated adiabatically, when a magnetic field is applied and is due to the correlation that exists between the magnetization state of a system and its entropy. In the context of global warming, materials with MCE around room temperature are an environmentally friendly alternative to conventional refrigeration. The giant magnetocaloric effect observed on Gd5Ge4 compounds [35] was explained based on the coincidence between the magnetic ordering temperature and the crystallographic transformation temperature. From this point of view, Heusler-type shape memory ferromagnetic alloys are interesting. Both the Curie temperature and the martensitic one can be modified by slight changes in the composition and using proper thermal treatments. Thus, the structural transformation can overlap with the magnetic one so that the alloy has a magnetostructural transformation. In the present paper, we evaluate the magnetic entropy changes (ΔSm) in the Ni55Fe18Nd2Ga25 alloy with concomitant or sequential structural and magnetic phase transition prepared as bulk and as ribbons in an as quenched state or subjected to thermal treatments.
Generally, the MT temperatures are correlated with a large number of parameters that might influence the transformation, such as the processing route [36], chemical and atomic order, or internal stress [37]. For this reason, various preparation routes have been tested in order to improve the magnetic or mechanical properties of FSMA alloys [22,38,39], together with complementary suitable thermal treatments to tailor the working temperature range and performance of FSMA. Thus, in this study, the properties of Ni-Fe-Ga with Nd substitutions synthesized by arc melting and melt spinning and subjected to several thermal treatments are investigated. By analyzing the bulk and, respectively, the ribbons’ properties, we expect to infer the role of preparation route, interfaces, and the microstructure, in what regards the crystalline phases present, the martensitic transformation (MT), and the magnetocaloric (MCE) and magnetoresistive (MR) effects.

2. Materials and Methods

The constituting high purity elements were weighed according to the nominal composition Ni55Nd2Fe18Ga25, and melted in an electric arc furnace under argon protective atmosphere. The samples were melted 5 times flipping the ingots in order to ensure homogeneity. The resulting ingots were cut using a low speed diamond saw and a small piece was thermally treated in high vacuum for 25 h at 1223 K, followed by quenching in iced water. The remaining ingot was subjected to melt spinning technique and inductively melted in a quartz tube under argon atmosphere, and ejected under a 40 kPa of Ar overpressure, through a nozzle of 0.5 mm in diameter, on a water-cooled copper wheel rotating at a surface velocity speed of 20 m/s. Rapidly quenched ribbons of about 15–16 µm thickness and 2–3 mm width were obtained and denoted AQ (“as quenched”). The AQ ribbons were thermally annealed in evacuated quartz ampoules followed by a direct quenching of the sample in ice water. The samples were annealed for 2 h at 673 K, and for 2 min at 1173 K and denoted T400 and T900, respectively.
The phase transitions and associated transformation temperatures of the samples were determined using a differential scanning calorimeter (DSC) model 204 F1 Phoenix (Netzsch), in the temperature range 200–400 K with a 20 K/min scanning rate. The structural investigations were carried out by room temperature (RT = 290 K) X-ray diffraction (XRD) using a Bruker D8 Advance X-ray diffractometer (Hamburg, Germany) in Bragg–Brentano geometry (Cu Kα = 1.5406 Å radiation) and lithium fluoride (LiF) monochromator. The phase composition of samples was evaluated using Bruker AXS DIFFRAC. EVA software (Bruker AXS, Karlsruhe, Germany, 2000), while the LeBail refinement method of the XRD-data was performed using the FullProf Suite software. The morphology and composition of the samples were investigated by Scanning Electron Microscopy (SEM) and Energy Dispersive X-ray Spectroscopy (EDS), respectively, employing a Zeiss Evo 50 XVP microscope. The SEM images were taken with a secondary electrons detector without chemical or ion polishing of the surfaces. The acceleration voltage of SEM is EHT = 20 kV. Magnetic measurements were performed by a Quantum Design superconducting quantum interference device (SQUID) (San Diego, CA, USA) in the Reciprocal Space Option (RSO) mode. The magnetic field was applied along the ribbon length in order to minimize the demagnetization effect. The dependences of the electrical resistivity versus temperature were performed in standard four-probe method using a Quantum Design Physical Property Measurement System (QD-PPMS), with the current applied along the longitudinal direction of the ribbons and the magnetic field perpendicular to the ribbons.

3. Results and Discussions

3.1. DSC

Reversible thermoelastic transformations are revealed by the DSC signal for all investigated samples (Figure 1). The temperatures that define the martensitic transformation are shown in Table 1: start austenite (As); final austenite (Af); start martensite (Ms); final martensite (Mf); and thermodynamic equilibrium temperature T0. The thermodynamic equilibrium temperature is the one at which the Gibbs energies of martensite and austenite are equal and can be estimated by the relation T0 = (Ms + Af)/2 [28]. In Figure 1, it is obvious that the martensitic transformation temperatures decrease as the heat treatment temperature increases. AQ ribbons exhibit not only higher MT temperatures but also the highest heat of transformation. Thus, the average value between the direct and reverse transformation heat of the AQ ribbons is approximately double (Q = 2.1 J/g) compared to the bulk alloys which have Q = 1.07 J/g [40]. This behavior is the effect of the internal stress retained in the ribbons during rapid cooling which acts as an additional driving force for MT.

3.2. XRD

Le Bail fits to the XRD-data collected at room temperature (RT) on bulk, AQ, T400 and T900 samples are shown in Figure 2. The crystalline structure of all samples is complex, and is composed of three phases that grow under the influence of the processing route and the applied thermal treatment. The phase composition of bulk samples (Figure 2) consists of two-face-centered cubic crystal phases (Fm-3m) with different lattice parameters (see Table 2) and one rhombohedral (R-3m). The same phase composition is also detected in the thermally treated ribbons having different mean crystallite sizes. Notably, the austenite cubic phase with a ~3.6 Å and the rhombohedral Nd2Fe17 type crystalline phase are detected in all samples. In the AQ ribbons, due to the fast cooling rate during synthesis, the growth of γ phase is inhibited but the tetragonal martensitic P4/mmm phase is “frozen”. Applying a thermal treatment to ribbons produces an atom reordering and the segregation of the cubic γ phase (Fm-3m, with a ~5.7 Å) corroborating the DSC results, which suggest that thermal treatments stabilize the austenite phase and lower the martensitic transformation temperatures [41,42].
The mean crystallite size of each crystalline phase (see Table 2) was calculated according to the Scherrer relation Dp = K λ/β cosθ, where K is the Scherrer constant (here 0.94), λ the wavelength, β is the half width of a reflection peak, and θ the diffraction angle. In the AQ ribbons, the ultra-fast cooling prevents the crystallite growth and consequently the samples are nanostructured with the mean crystallite size of only several tens of nm. Importantly, for the rhombohedral Nd2Fe17 phase, the crystallite size exceeds 100 nm in all samples, but as suggested by the SEM investigations, the phase abundance is reduced and might not exert an important influence on sample properties. Besides atomic reordering, the thermal treatments promote the precipitation of the γ phase on the expense of the other phases, which deprives the austenitic matrix of Fe and Ni atoms, and further reduces the valence electron concentration and the MT temperature [42]. However, the increase in the average crystallite size of the γ phase with the temperature of the TT and its concomitant diminishing for the other two phases, might also be a consequence of the austenite matrix depletion in Fe and Ni as more of these atoms will participate to the γ phase forming.

3.3. SEM

The surface and cross-section morphology at room temperature of all samples were investigated by scanning electron microscopy (SEM) with secondary electrons detector without chemical or ion polishing of the surfaces (Figure 3). The surface morphology of the AQ ribbons is typical for samples produced by melt spinning, which involves very fast cooling rates, consisting of dendritic grains with length of micron size (0.2–3.5 μm) and a visible twin microstructure (shown with black arrows), and twin thickness of several tens of nanometers. The cross-section image (Figure 3b) shows small cracks on the contact side surface (indicated by red arrows) and the existence of columnar grains, which span the entire thickness of the ribbon, a signature of temperature gradient typical for the melt-spinning technique, which induces a fast nucleation and growth process of grains along the cross-section during the rapid cooling of the melt [43]. Although the XRD suggests the existence of a Nd2Fe17 type phase, the SEM images show no clear signs of precipitates. This might be explained by the reduced amount of Nd2Fe17 phase in the ribbons and that the phase forms mostly at the grain boundaries.
As expected, on the surface of the heat-treated ribbons at high temperatures (1173 K), the γ phase precipitates inside and at the grain boundaries (indicated by the blue arrows in Figure 3c). The inset of Figure 3c shows precipitates of nanometric dimensions (~60 nm) increasing in size along the dendritic grains (~100 nm). Nevertheless, the precipitates are causing the crack’s disappearance because the gamma phase is responsible for the improved alloy ductility [28]. Similarly, the heat treatment at a lower temperature (673 K) yield nanometric precipitates of the developing γ phase at the grain boundaries (Figure 3e). The cross-section investigation shows a well-defined columnar structure with cracks at the contact side of the ribbons (Figure 3f). EDX analysis indicates that the chemical compositions are the nominal ones (within the limits of the method accuracy) for all samples.

3.4. Magnetic Properties

The hysteresis of the thermomagnetic curves recorded on cooling and heating, at low magnetic fields (0.02 T), describe the martensitic transformation of all studied samples (see Figure 4). Thermal treatments produce specific changes to the characteristic temperatures of the martensitic transformation. The 2 h treatment at 673 K induces the structural ordering, and the stress relaxation caused by the ultra-rapid cooling of the ribbons, which determines the increase in the MT temperatures, and of the Curie temperature of the T400 sample. As highlighted by the XRD patterns and SEM images, the heat treatment performed at 1173 K promotes the growth of the secondary γ phase. The γ phase has an essential role in lowering the MT temperature [42], and its presence is also indicated by the higher Curie temperature (TC > 350 K) in the T900 ribbons (red curve from the thermomagnetic measurements). The fact that TC and MT of the AQ and Bulk samples are in the same temperature range may be of great interest for applications. A first-order transition around room temperature associated with the magnetic transition (magnetostructural transformation) is of interest for the use of the associated magnetic entropy change in practical applications.

3.5. Evaluation of Magnetocaloric Effect

Here, a commonly indirect measurement technique to assess MCE is used. Magnetization was measured as a function of increasing temperature for applied magnetic field values between 0.02 T and 7 T; depending on the measurement accuracy an error of only 3–10% for the magnetic entropy change may be achieved. In Figure 5, such an example of magnetization measured on the AQ ribbons is shown. From the temperature dependence of the magnetization in the applied constant magnetic field, the magnetic entropy variation is calculated using the Maxwell equation for discrete data points:
Δ S m = ∑ i M ( T + Δ T ) − M ( T ) Δ T Δ H i
Figure 6 highlights the differences between the magnetic entropy variation in the bulk and the AQ, T400, and T900 ribbons. It follows from relation (1) that ΔSm depends on the rate of variation in magnetization with temperature and this is maximum at the Curie temperature. However, the short-range order that is preserved between the magnetic moments and above the Curie temperature makes the magnetization cancellation experimentally possible over a relatively wide temperature range. That is why the contribution of the Curie temperature to ΔSm takes place over a relatively broad temperature range. Bulk and AQ samples have TC and MT in the same temperature range. Thus, for 5 T applied field, the as-prepared ribbons show ΔSm = −5.41 J/kgK (at 310 K) and bulk alloy −4.58 J/kgK (at 282 K). The variation in the magnetic entropy has a different behavior for the T400 and T900 samples. For these, ΔSm shows a maximum (in absolute value) in the specific MT temperature range and a second peak is clear in the Curie temperature region. In addition, the martensitic transformation is highlighted on Figure 6 by the specific peak temperature of the austenite phase (TAp) obtained on the reverse martensite–austenite transformation by DSC. The Curie temperatures of the studied alloys are also marked with magenta arrows. The values obtained for the variation in the magnetic entropy change in the same trend as that reported in the literature [44,45,46,47].
The results of the DSC analysis and of the thermal variation in the magnetization in 0.2 T applied magnetic field, in the Bulk alloy (Figure 7a) and the same for AQ ribbons (Figure 7b), have been represented in order to identify the thermal overlap of the MT with that of the Curie temperature and their contributions to the ΔSm. The Curie temperature of the Bulk alloy (obtained from the first derivative of the magnetization in relation to the temperature dM/dT) is equal to the austenite finish temperature Af = 290 K. Therefore, the alloy is FSMA and shows consecutive phase transformations (the magnetic and structural transitions are successive, in close vicinity). From Figure 7b, it can be seen that the Curie temperature of martensite TCM (determined from dM/dT on the heating curve) is equal to the starting temperature of martensite Ms = 290 K, indicating the ferromagnetic ordering of martensite. At the same time, the Curie temperature of austenite (determined from dM/dT on the cooling curve) TCA = 282 K is lower than the austenite start As = 290 K, yielding a paramagnetic austenite. The AQ ribbons present concomitant magnetic transitions and phase transformation, because the MT occurred between paramagnetic austenite and ferromagnetic martensite. This behavior explains the higher value of the magnetocaloric effect obtained on the AQ bands and is in agreement with the literature [35] which emphasizes the role of magnetostructural transformation.

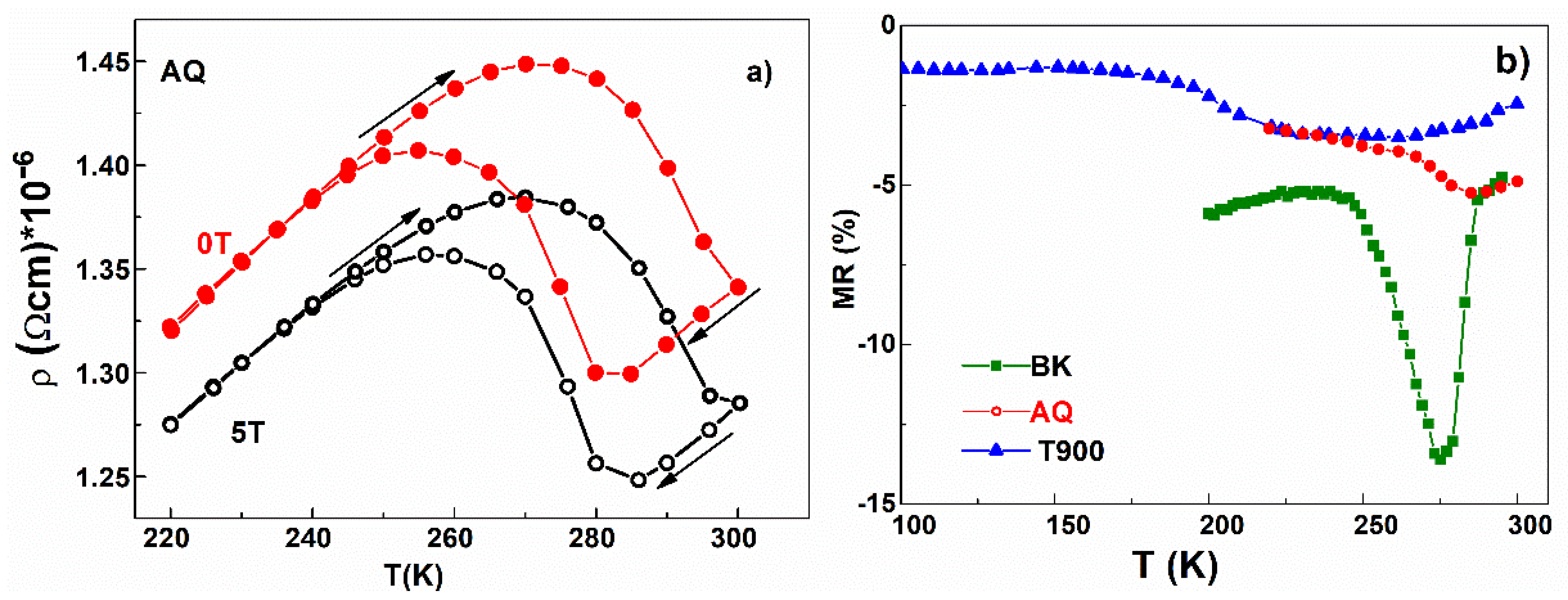
3.6. MR Evaluation from Ac Resistivity (ρ)

Another effect that gives a multifunctional character to ferromagnetic Heusler alloys with shape memory effect is the magnetoresistive effect (MR). This is due to the variation in the electrical resistivity under the effect of the magnetic field in the thermal domain of the martensitic transformation. According to Barandiaran et al. [48], the magnetoresistance anomaly in the range of martensitic transformation is the result of the combination between the change in the resistance during the phase transformation and the change in the transformation temperature under the effect of the magnetic field.
To characterize the magnetoresistive effect, the variation in electrical resistivity was measured as a function of temperature, in the temperature range specific to the martensitic transformation of each sample, without an applied magnetic field (0 T) and, respectively, in a magnetic field of 5 T. In Figure 8a, the temperature dependence of the resistivity for the AQ ribbons in both cases is shown. Temperature dependence of resistivity reveals a metallic behavior in both austenite and martensite, with a jump along the MT transformation, explained by the increase in the scattering on the boundaries of the martensite-specific of twin-variants. In addition, it is observed that the resistivity decreases when the magnetic field is applied [47,48,49], reflecting the changes made to the resistivity by the reduction in the magnetic disorder when the magnetic field is applied.
Magnetoresistance was calculated using the formula:
M R = ρ ( H ) − ρ ( 0 ) ρ ( 0 ) ,
ρ(0) and ρ(H) represent the resistivity values without applied magnetic field and, respectively, for 5 T. The continuous variation in MR% with temperature, corresponding to bulk, AQ and T900 samples, are shown in Figure 8b. The value of the MR obtained for the bulk sample of −13% at 275 K is impressive and is much higher than the values obtained in ribbons, namely −5.23% at 285 K and −3.42% at 235 K for the AQ ribbons and T900 sample, respectively.

4. Conclusions

In this study, the Heusler non-stoichiometric Ni55Nd2Fe18Ga25 alloy, prepared by the electric arc melting and melt spinning method, was investigated. The effects of the thermal treatments on the phase composition, morphology, and magneto-caloric and magneto-transport properties of the nanostructured ribbons have been examined and compared with the bulk samples. The thermal treatments produce, besides atomic ordering, the segregation of the gamma phase, which depletes the austenitic matrix in 3D elements, hence influencing the thermal positioning of the TM and of the magnetic ordering. Specifically, the Curie temperatures increase for the ordered structure, while the TM characteristic temperatures decrease with the rising TT temperature.
The bulk samples show consecutive phase transformations with the magnetic transition at a higher temperature than the structural transition. Interestingly, however, the as-quenched ribbons show a concomitant magneto–structural transition in the RT range. As a consequence, the AQ ribbons have the highest value of the magnetic entropy variation from all measured samples, of −5.41 J/kgK at 310 K. For the thermally treated ribbons, the magnetic and structural transitions are again separated, and the two maxima occur in the thermal dependence of the magnetic entropy variation in connection with the martensitic transformation and in Curie temperatures.
A remarkable magnetoresistive effect of 13.5% at 275 K was recorded in the bulk sample, which is much higher than in the ribbons (5.23% at 285 K and 3.42% at 235 K for the AQ ribbons and T900 sample, respectively).

Author Contributions

Conceptualization, M.S. and F.T.; methodology, F.T. and M.S.; software, B.P. and M.T.; validation, M.S., B.P., F.T. and M.T.; formal analysis, B.P. and M.T.; investigation, M.S., F.T., M.E. and B.P.; resources, F.T.; data curation, M.T. and F.T.; writing—original draft preparation, M.S., B.P. and F.T.; writing—review and editing, B.P. and F.T.; visualization, M.S., M.T, M.E., B.P. and F.T.; supervision, M.S. and F.T.; project administration, M.S. and F.T.; funding acquisition, F.T. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by grants from the Romanian Ministry of Research, Innovation and Digitization, CCCDI-UEFISCDI projects number PN-III-P2-2.1-PED-2019-3453 contract no. 493/2020. The fee for open access publication was supported by the project 35PFE/2021, funded by the Romanian Ministry of Research, Innovation and Digitization.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is available, upon reasonable request, by e-mail addressed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Petrini, L.; Migliavacca, F. Biomedical Applications of Shape Memory Alloys. J. Metall. 2011, 2021, 501483. [Google Scholar] [CrossRef]
  2. Morgan, N.B. Medical shape memory alloy applications—The market and its products. Mater. Sci. Eng. A 2004, 378, 16–23. [Google Scholar] [CrossRef]
  3. Song, G.; Ma, N.; Li, H.-N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
  4. Nespoli, A.; Besseghini, S.; Pittaccio, S.; Villa, E.; Viscuso, S. The high potential of shape memory alloys in developing miniature mechanicaldevices: A review on shape memory alloy mini-actuators. Sens. Actuators A 2010, 158, 149–160. [Google Scholar] [CrossRef]
  5. Furuya, Y.; Shimada, H. Shape memory actuators for robotic applications. Mater. Des. 1991, 12, 21–28. [Google Scholar] [CrossRef]
  6. Van Humbeeck, J. Non-medical applications of shape memory alloys. Mater. Sci. Eng. A 1999, 273–275, 134–148. [Google Scholar] [CrossRef]
  7. Frolova, L.; Mino, J.; Ryba, T.; Gamcova, J.; Dzubinska, A.; Reiers, M.; Diko, P.; Kavecansky, V.; Milkovic, O.; Kravcak, J. Novel compositions of Heusler-based glass-coated microwires for practical applications using shape memory effect. J Alloys Compd. 2018, 747, 21–25. [Google Scholar] [CrossRef]
  8. Caputo, M.P.; Berkowitz, A.E.; Armstrong, A.; Müllner, P.; Solomon, C.V. 4D printing of net shape parts made from Ni-Mn-Ga magnetic shape-memory alloys. Addit. Manuf. 2018, 21, 579–588. [Google Scholar] [CrossRef]
  9. Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
  10. Graf, T.; Felser, C.; Parkin Stuart, S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
  11. Wollmann, L.; Ajaya, K.N.; Stuart, S.P.P.; Felser, C. Heusler 4.0: Tunable Materials. Annu. Rev. Mater. Res. 2017, 47, 247–270. [Google Scholar] [CrossRef]
  12. Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C.; Kokorin, V.V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966. [Google Scholar] [CrossRef]
  13. Wuttig, M.; Li, J.; Craciunescu, C. A new ferromagnetic shape memory alloy system. Scr. Mater. 2001, 44, 2393–2397. [Google Scholar] [CrossRef]
  14. Liu, J.; Xie, H.; Huo, Y.; Zheng, H.; Li, J. Microstructure evolution in CoNiGa shape memory alloys. J Alloys Compd. 2006, 420, 145–157. [Google Scholar] [CrossRef]
  15. Scheibel, F.; Lauhoff, C.; Riegg, S.; Krooss, P.; Bruder, E.; Adabifiroozjaei, E.; Molina-Luna, L.; Bohm, S.; Chumlyakov, Y.I.; Niendorf, T.; et al. On the Impact of Additive Manufacturing Processes on the Microstructure and Magnetic Properties of Co-Ni-Ga Shape Memory Heusler Alloys. Adv. Eng. Mat. 2022, 2022, 2200069. [Google Scholar] [CrossRef]
  16. Mishra, A.; Dubey, P.; Chandra, R.; Srivastava, S.K. Observation of large exchange bias field in Mn rich NiMnAl Heusler alloy thin film. J. Mag. Mag. Mat. 2021, 532, 167964. [Google Scholar] [CrossRef]
  17. Lazpita, P.; Perez-Checa, A.; Barandiaran, J.M.; Ammerlaan, A.; Zeitler, U.; Chernenko, V. Suppression of martensitic transformation in Ni-Mn-In metamagnetic shape memory alloy under very strong magnetic field. J Alloys Compd. 2021, 874, 159814. [Google Scholar] [CrossRef]
  18. Zhang, Y.J.; Guo, J.P.; Zhong, M.T.; Xiang, W.W.; Wu, Z.G. Martensitic transformation behaviour and mechanical property of dual-phase Ni-Co-Mn-Sn-Fe ferromagnetic shape memory alloys. J. Mag. Mag. Mat. 2021, 521, 167540. [Google Scholar] [CrossRef]
  19. Dagdelen, F.; Ozay, C.; Ercan, E.; Emir, G.; Qader, I.N. Change of electrical resistivity during phase transitions in NiMnSn-based shape memory alloy. J. Therm. Anal. Calorim. 2022, 147, 5815–5823. [Google Scholar] [CrossRef]
  20. Czaja, P.; Przewoznik, J.; Hawelek, L.; Chrobak, A.; Zackiewicz, P.; Maziarz, W. Martensitic transformation, magnetic entropy, and adiabatic temperature changes in bulk and ribbon Ni48Mn39.5Sn12.5−xInx (x = 2, 4, 6) metamagnetic shape memory alloys. J. Mat. Res. 2021, 36, 3317–3328. [Google Scholar] [CrossRef]
  21. Bonifacich, F.G.; Lambri, O.A.; Perez-Landazabal, J.I.; Recarte, V.; Gargicevich, D.; Zelada, G.I.; Mocellini, R.R.; Sanchez-Alarcos, V.; Marenzana, A.; Plazaola, F. Study of the martensitic transition in Ni-Mn-Sn-Ti ferromagnetic shape memory alloys. Materia Rio J. 2018, 23, 12043. [Google Scholar] [CrossRef]
  22. Oikawa, K.; Ota, Y.; Ohmori, T.; Tanaka, Y.; Morito, H.; Kainuma, R.; Fukamichi, K.; Ishida, K. Magnetic and martensitic phase transitions in ferromagnetic Ni-Ga-Fe shape memory alloys. Appl. Phys. Lett. 2002, 81, 5201–5203. [Google Scholar] [CrossRef]
  23. Santamarta, R.; Font, J.; Muntasell, J.; Masdeu, F.; Pons, J.; Cesari, E.; Dutkiewicz, J. Effect of ageing on the martensitic transformation of Ni-Fe-Ga alloys. Scr. Mater. 2006, 54, 1105–1109. [Google Scholar] [CrossRef]
  24. Alvarado-Hernández, F.; Soto-Parra, D.E.; Ochoa-Gamboa, R.; Castillo-Villa, P.O.; Flores-Zúňiga, H.; Ríos-Jara, D. Thermal and structural study of Ni-Fe-Ga ferromagnetic shape memory alloys. J. Alloys Compd. 2008, 426, 442–445. [Google Scholar] [CrossRef]
  25. Biswas, A.; Singh, G.; Sarkar, S.K.; Krishnan, M.; Ramamurty, U. Hot deformation behavior of Ni-Fe-Ga-based ferromagnetic shape memory alloy—A study using processing map. Intermetallics 2014, 54, 69–78. [Google Scholar] [CrossRef]
  26. Pons, J.; Cesari, E.; Seguí, C.; Masdeu, F.; Santamartak, R. Ferromagnetic shape memory alloys: Alternatives to Ni-Mn-Ga. Mater. Sci. Eng. A 2008, 481–482, 57–65. [Google Scholar] [CrossRef]
  27. Okumura, H.; Uemura, K. Influence of quenching rate on the magnetic and martensitic properties of Ni-Fe-Ga melt-spun ribbons. J. Appl. Phys. 2010, 108, 043910. [Google Scholar] [CrossRef]
  28. Liu, J.; Scheerbaum, N.; Hinz, D.; Gutfleisch, O. Martensitic transformation and magnetic properties in Ni-Fe-Ga-Co magnetic shape memory alloys. Acta. Mater. 2008, 56, 3177–3186. [Google Scholar] [CrossRef]
  29. Gao, L.; Gao, Z.Y.; Cai, W.; Zhao, L.C. Effect of rare earth Dy addition on microstructure and martensitic transformation on polycrystalline Ni50Mn29Ga21−xDyx ferromagnetic shape memory alloys. Mater. Sci. Eng. A 2006, 438–440, 1077–1080. [Google Scholar] [CrossRef]
  30. Gao, L.; Sui, J.H.; Cai, W. Influence of rare earth Gd addition on the structural and magnetic transitions of Ni-Mn-Ga alloys. J. Mag. Mag. Mater. 2008, 320, 63–67. [Google Scholar] [CrossRef]
  31. Zhang, X.; Sui, J.; Yu, Z.; Cai, W. Structure and shape memory effect in a Ni54Mn25Ga20Gd1 alloy with a high transformation temperature. J. Alloys Compd. 2011, 509, 8032–8037. [Google Scholar] [CrossRef]
  32. Sui, J.; Zhang, X.; Gao, L.; Cai, W. Microstructure, phase transformation and mechanical properties of Ni-Mn-Ga-Y magnetic shape memory alloys. J. Alloys Compd. 2011, 509, 8692–8699. [Google Scholar] [CrossRef]
  33. Tsuchiya, K.; Tsutsumi, A.; Ohtsuka, H.; Umemoto, M. Modification of Ni-Mn-Ga ferromagnetic shape memory alloy by addition of rare earth elements. Mater. Sci. Eng. A 2004, 378, 370–376. [Google Scholar] [CrossRef]
  34. Rama Rao, N.V.; Gopalan, R.; Manivel Raja, M.; Chandrasekaran, V.; Suresh, K.G. Mössbauer studies on structural ordering and magnetic properties of melt-spun Ni-Fe-Ga ribbons. Appl. Phys. Lett. 2008, 93, 202503. [Google Scholar]
  35. Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
  36. Qian, J.F.; Liu, E.K.; Feng, L.; Zhu, W.; Li, G.J.; Wang, W.H.; Wu, G.H.; Du, Z.W.; Fu, X. Unusual magnetic anisotropy in the ferromagnetic shape-memory alloy Ni50Fe23Ga27. Appl. Phys. Lett. 2011, 99, 252504. [Google Scholar]
  37. Hamilton, R.F.; Efstathiou, C.; Sehitoglu, H.; Chumlyakov, Y. Thermal and stress-induced martensitic transformations in NiFeGa single crystals under tension and compression. Scr. Mat. 2006, 54, 465–469. [Google Scholar] [CrossRef]
  38. Chernenko, V.A.; Barandiarán, J.M.; L’Vov, V.A.; Gutiérrez, J.; Lázpita, P.; Orue, I. Temperature dependent magnetostrains in polycrystalline magnetic shape memory Heusler alloys. J Alloys Compd. 2013, 577, S305–S308. [Google Scholar] [CrossRef]
  39. Khovaylo, V.V.; Buchelnikov, V.D.; Kainuma, R.; Koledov, V.V.; Ohtsuka, M.; Shavrov, V.G. Phase transitions in Ni2+xMn1−xGa with a high Ni excess. Phys. Rev. B 2005, 72, 224408. [Google Scholar] [CrossRef] [Green Version]
  40. Tolea, F.; Crisan, A.D.; Sofronie, M.; Tolea, M.; Valeanu, M. Magnetic and Martensitic transformations in the bulk and melt spun ribbons of Ni57−xNdxFe18Ga25 Ferromagnetic Shape Memory Alloys. Mater. Today Proc. 2015, 2S, S875–S878. [Google Scholar]
  41. Picornell, C.; Pons, J.; Cesari, E.; Dutkiewicz, J. Thermal characteristics of Ni-Fe-Ga-Mn and Ni-Fe-Ga-Co ferromagnetic shape memory alloys. Intermetallics 2008, 16, 751–757. [Google Scholar] [CrossRef]
  42. Tolea, F.; Sofronie, M.; Crisan, A.D.; Enculescu, M.; Kuncser, V.; Valeanu, M. Effect of thermal treatments on the structural and magnetic transitions in melt-spun Ni-Fe-Ga-(Co) ribbons. J. Alloys Compd. 2015, 650, 664–670. [Google Scholar] [CrossRef]
  43. Albertini, F.; Besseghini, S.; Paoluzi, A.; Pareti, L.; Pasquale, M.; Passaretti, F.; Sasso, C.P.; Stantero, A.; Villa, E. Structural, magnetic and anisotropic properties of Ni2MnGa melt-spun ribbons. J. Mag. Mag. Mater. 2002, 1421, 242–245. [Google Scholar] [CrossRef]
  44. Liu, Y.; Zhang, X.; Xing, D.; Shen, H.; Chen, D.; Liu, J.; Sun, J. Magnetocaloric effect (MCE) in melt-extracted Ni-Mn-Ga-Fe Heusler microwires. J. Alloys Compd. 2014, 616, 184–188. [Google Scholar] [CrossRef]
  45. Recarte, V.; Pérez-Landazábal, J.I.; Gomez-Polo, C.; Cesari, E.; Dutkiewicz, J. Magnetocaloric effect in Ni-Fe-Ga shape memory alloys. Appl. Phys. Lett. 2006, 88, 132503. [Google Scholar]
  46. Sarkar, S.K.; Biswas, A.; Babu, P.D.; Kaushik, S.D.; Srivastava, A.; Siruguri, V.; Krishnan, M. Effect of partial substitution of Fe by Mn in Ni55Fe19Ga26 on its microstructure and magnetic properties. J. Alloys Compd. 2014, 586, 515–523. [Google Scholar] [CrossRef]
  47. Pal, D.; Mandal, K. Magnetocaloric effect and magnetoresistance of Ni-Fe-Ga alloys. J. Phys. D Appl. Phys. 2010, 43, 455002. [Google Scholar] [CrossRef]
  48. Barandiarán, J.M.; Chernenko, V.A.; Lázpita, P.; Gutiérrez, J.; Feuchtwanger, J. Effect of martensitic transformation and magnetic field on transport properties of Ni-Mn-Ga and Ni-Fe-Ga Heusler alloys. Phys. Rev. B 2009, 80, 104404. [Google Scholar] [CrossRef]
  49. Srivastava, V.K.; Chatterjee, R.; O’Handley, R.C. Effect of twin boundaries on electrical transport in Ni-Mn-Ga single crystal. Appl. Phys. Lett. 2006, 89, 222107. [Google Scholar] [CrossRef]
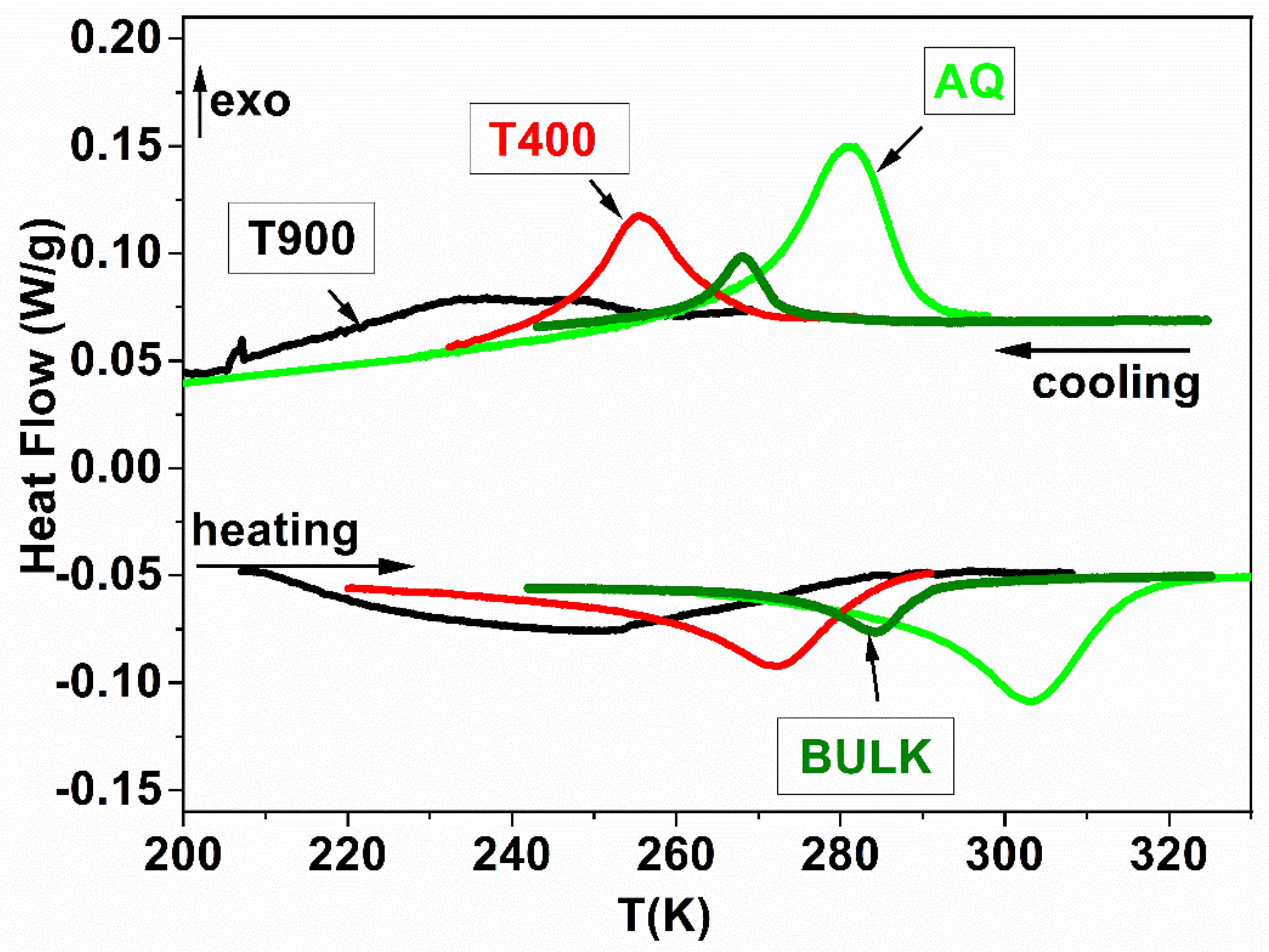
Nanomaterials 12 03667 g001 550
Figure 1. The DSC signals for Bulk and AQ, T400 and T900 ribbons.
Figure 1. The DSC signals for Bulk and AQ, T400 and T900 ribbons.
Nanomaterials 12 03667 g001
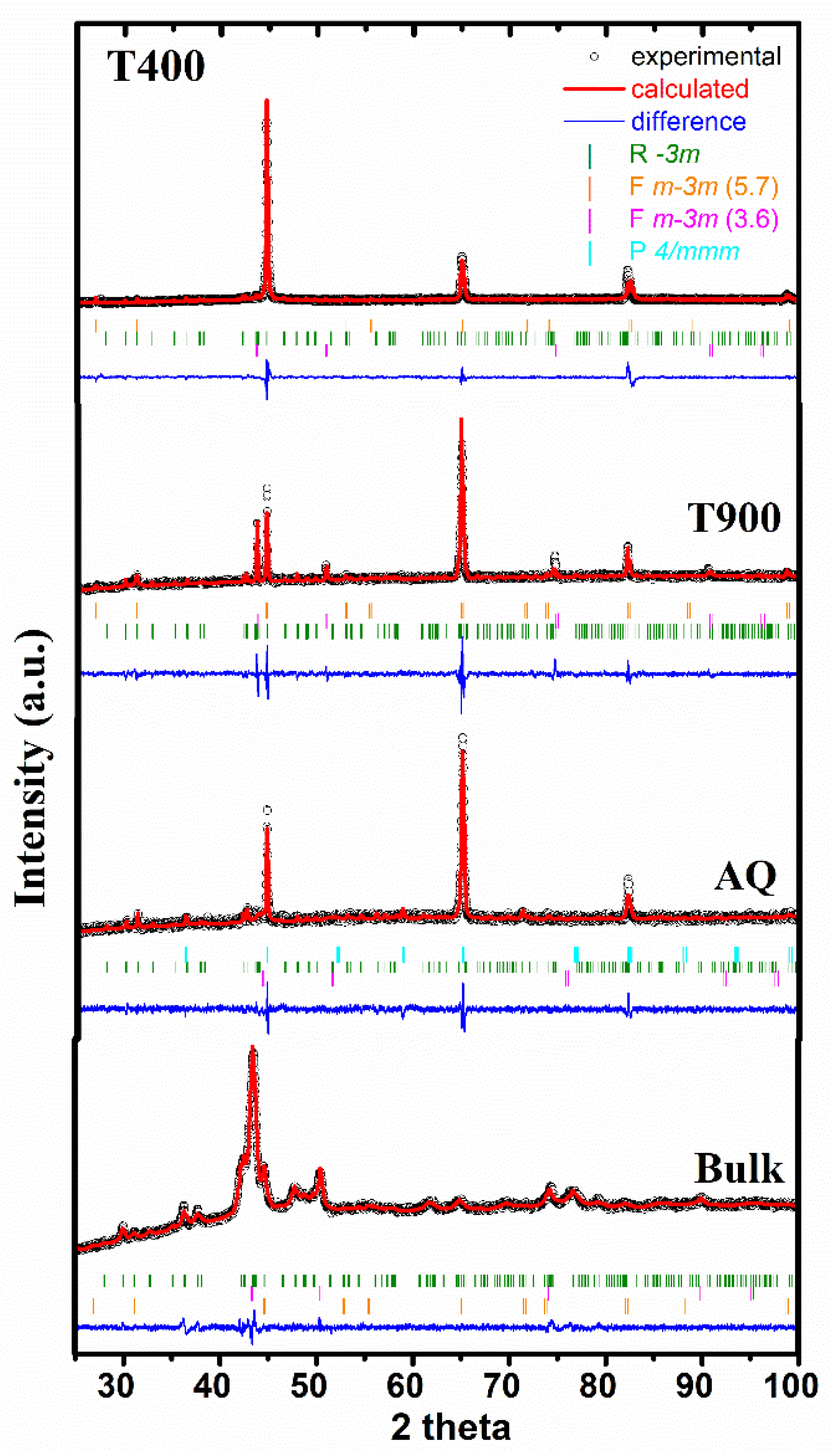
Nanomaterials 12 03667 g002 550
Figure 2. XRD spectra recorded at RT.
Figure 2. XRD spectra recorded at RT.
Nanomaterials 12 03667 g002
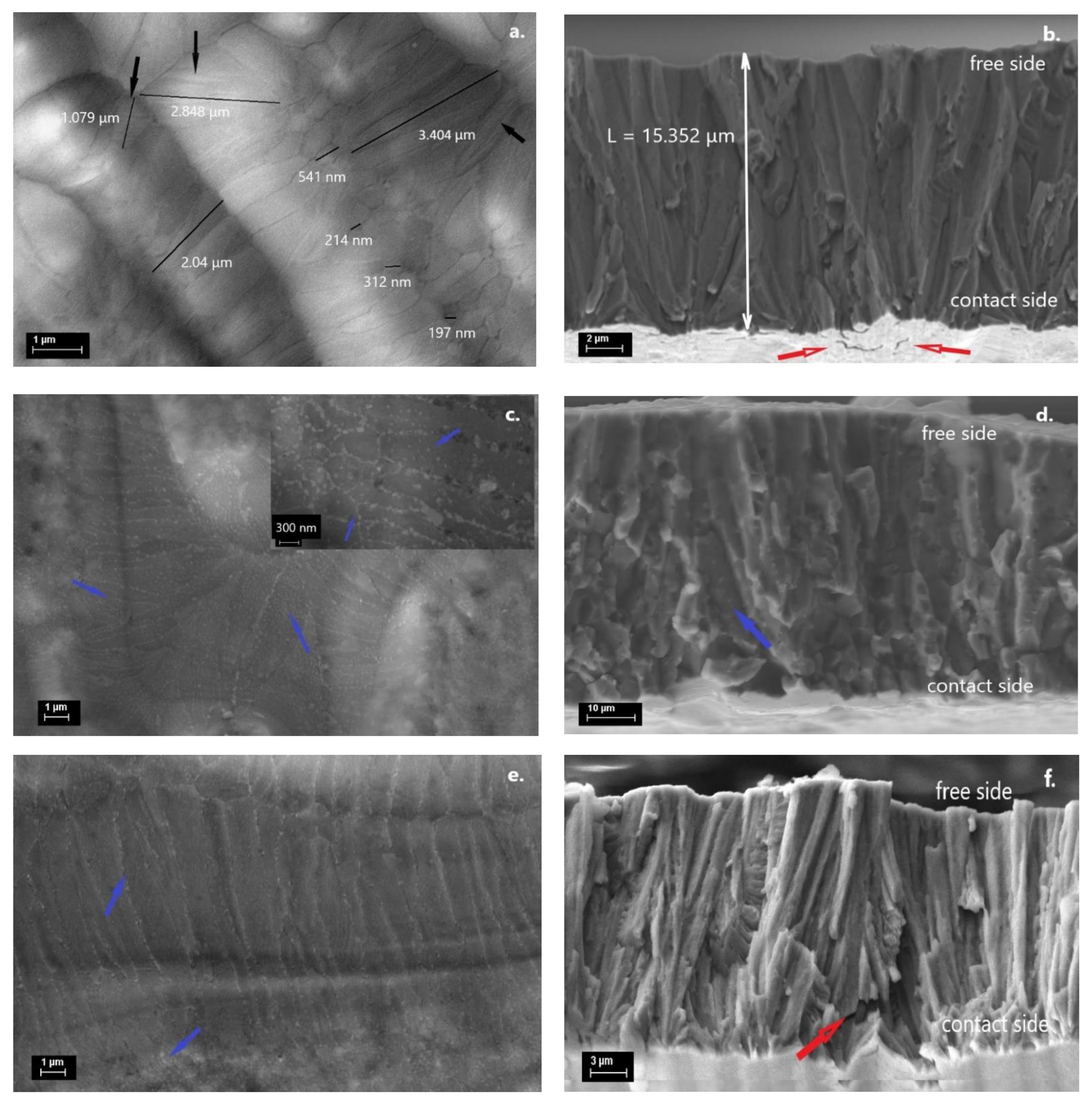
Nanomaterials 12 03667 g003 550
Figure 3. SEM images for AQ (a), T2-900 (c) (Inset with enlarged image), T1-400, (e) samples, with their cross-section images (b,d,f). The twin microstructure is indicated with black arrows (a), the small cracks are shown with red arrows (b,f) and the precipitates with blue ones (c,d,e).
Figure 3. SEM images for AQ (a), T2-900 (c) (Inset with enlarged image), T1-400, (e) samples, with their cross-section images (b,d,f). The twin microstructure is indicated with black arrows (a), the small cracks are shown with red arrows (b,f) and the precipitates with blue ones (c,d,e).
Nanomaterials 12 03667 g003
Nanomaterials 12 03667 g004 550
Figure 4. Temperature dependence of magnetization for AQ, T400 and T900 ribbons and for Bulk in inset.
Figure 4. Temperature dependence of magnetization for AQ, T400 and T900 ribbons and for Bulk in inset.
Nanomaterials 12 03667 g004
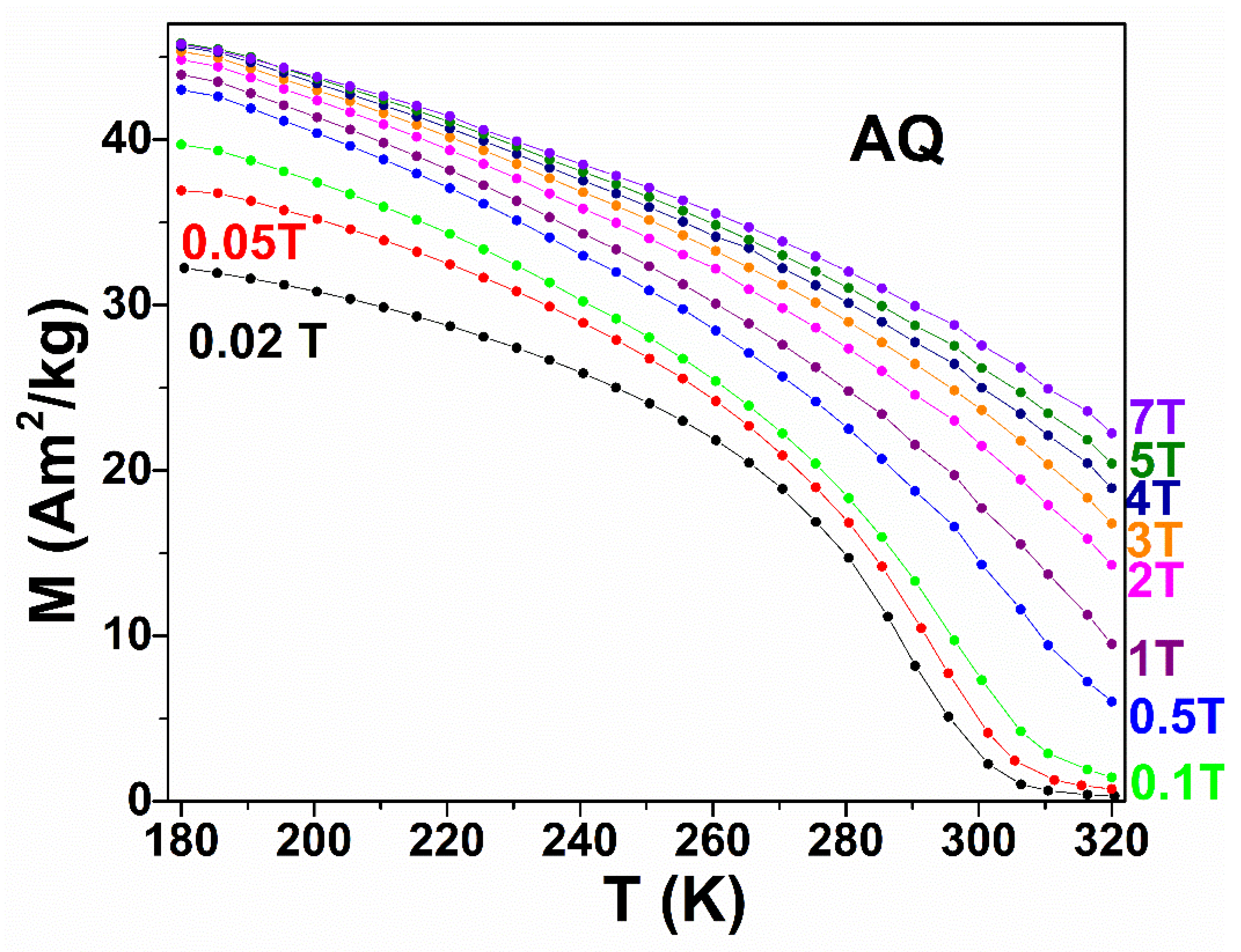
Nanomaterials 12 03667 g005 550
Figure 5. Temperature dependence of magnetization at different applied magnetic fields for AQ ribbons.
Figure 5. Temperature dependence of magnetization at different applied magnetic fields for AQ ribbons.
Nanomaterials 12 03667 g005
Nanomaterials 12 03667 g006 550
Figure 6. Magnetic entropy variation ΔSm versus raising temperature.
Figure 6. Magnetic entropy variation ΔSm versus raising temperature.
Nanomaterials 12 03667 g006
Nanomaterials 12 03667 g007 550
Figure 7. Temperature dependence of magnetization and DSC scans for (a) Bulk and (b) AQ ribbons.
Figure 7. Temperature dependence of magnetization and DSC scans for (a) Bulk and (b) AQ ribbons.
Nanomaterials 12 03667 g007
Nanomaterials 12 03667 g008 550
Figure 8. (a) Temperature dependence of resistivity in H = 0 T and H = 5 T (open symbols) for AQ ribbons; (b) Thermal variation in magnetoresistance in 5 T.
Figure 8. (a) Temperature dependence of resistivity in H = 0 T and H = 5 T (open symbols) for AQ ribbons; (b) Thermal variation in magnetoresistance in 5 T.
Nanomaterials 12 03667 g008
Table
Table 1. DSC transformation temperatures (Ms, Mf, As, Af), thermodynamic equilibrium temperature T0, the Curie temperatures (TCM, TCA) and magnetic entropy change ΔSm (at 5 T) for studied samples. TCA is determined on cooling and TCM is determined on heating.
Table 1. DSC transformation temperatures (Ms, Mf, As, Af), thermodynamic equilibrium temperature T0, the Curie temperatures (TCM, TCA) and magnetic entropy change ΔSm (at 5 T) for studied samples. TCA is determined on cooling and TCM is determined on heating.
SampleMs
(K)		Mf
(K)		As
(K)		Af
(K)		T0
(K)		TCM (K)TCA (K)ΔSm (J/kgK)
Bulk274262.6275.6290282300291−4.58
AQ291269290318304.5290282.6−5.4
T400267246261285276296291.6−3.2
T900258204210281269.5275271−3.4
Table
Table 2. Crystalline phases and lattices parameters, extracted from XRD data.
Table 2. Crystalline phases and lattices parameters, extracted from XRD data.
SamplePhasea (Å)c (Å)V (Å3)Dp (nm)
BulkFm-3m5.747 (1)-189.8-
Fm-3m3.618 (9)-47.4-
R-3m8.565 (1)12.476 (1)792.6-
AQP 4/mmm2.481 (1)3.515 (9)21.643.3
Fm-3m3.549 (9)-44.721.4
R-3m8.557 (4)12.425 (9)788125.1
T400Fm-3m5.729 (2)-188.184.6
Fm-3m3.590 (6)-46.3139.9
R-3m8.563 (1)12.449 (9)790.6147.5
T900Fm-3m5.744 (9)-189.6121.7
Fm-3m3.590 (2)-46.382.2
R-3m8.560 (1)12.459 (2)790.6131.3
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Sofronie, M.; Popescu, B.; Enculescu, M.; Tolea, M.; Tolea, F. Processing Effects on the Martensitic Transformation and Related Properties in the Ni55Fe18Nd2Ga25 Ferromagnetic Shape Memory Alloy. Nanomaterials 2022, 12, 3667. https://doi.org/10.3390/nano12203667

AMA Style

Sofronie M, Popescu B, Enculescu M, Tolea M, Tolea F. Processing Effects on the Martensitic Transformation and Related Properties in the Ni55Fe18Nd2Ga25 Ferromagnetic Shape Memory Alloy. Nanomaterials. 2022; 12(20):3667. https://doi.org/10.3390/nano12203667

Chicago/Turabian Style

Sofronie, Mihaela, Bogdan Popescu, Monica Enculescu, Mugurel Tolea, and Felicia Tolea. 2022. "Processing Effects on the Martensitic Transformation and Related Properties in the Ni55Fe18Nd2Ga25 Ferromagnetic Shape Memory Alloy" Nanomaterials 12, no. 20: 3667. https://doi.org/10.3390/nano12203667

APA Style

Sofronie, M., Popescu, B., Enculescu, M., Tolea, M., & Tolea, F. (2022). Processing Effects on the Martensitic Transformation and Related Properties in the Ni55Fe18Nd2Ga25 Ferromagnetic Shape Memory Alloy. Nanomaterials, 12(20), 3667. https://doi.org/10.3390/nano12203667

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop