pH Controlled Nanostructure and Optical Properties of ZnO and Al-Doped ZnO Nanorod Arrays Grown by Microwave-Assisted Hydrothermal Method
Abstract
:1. Introduction
2. Experimental Details
2.1. Materials
2.2. Synthesis
2.3. Characterization
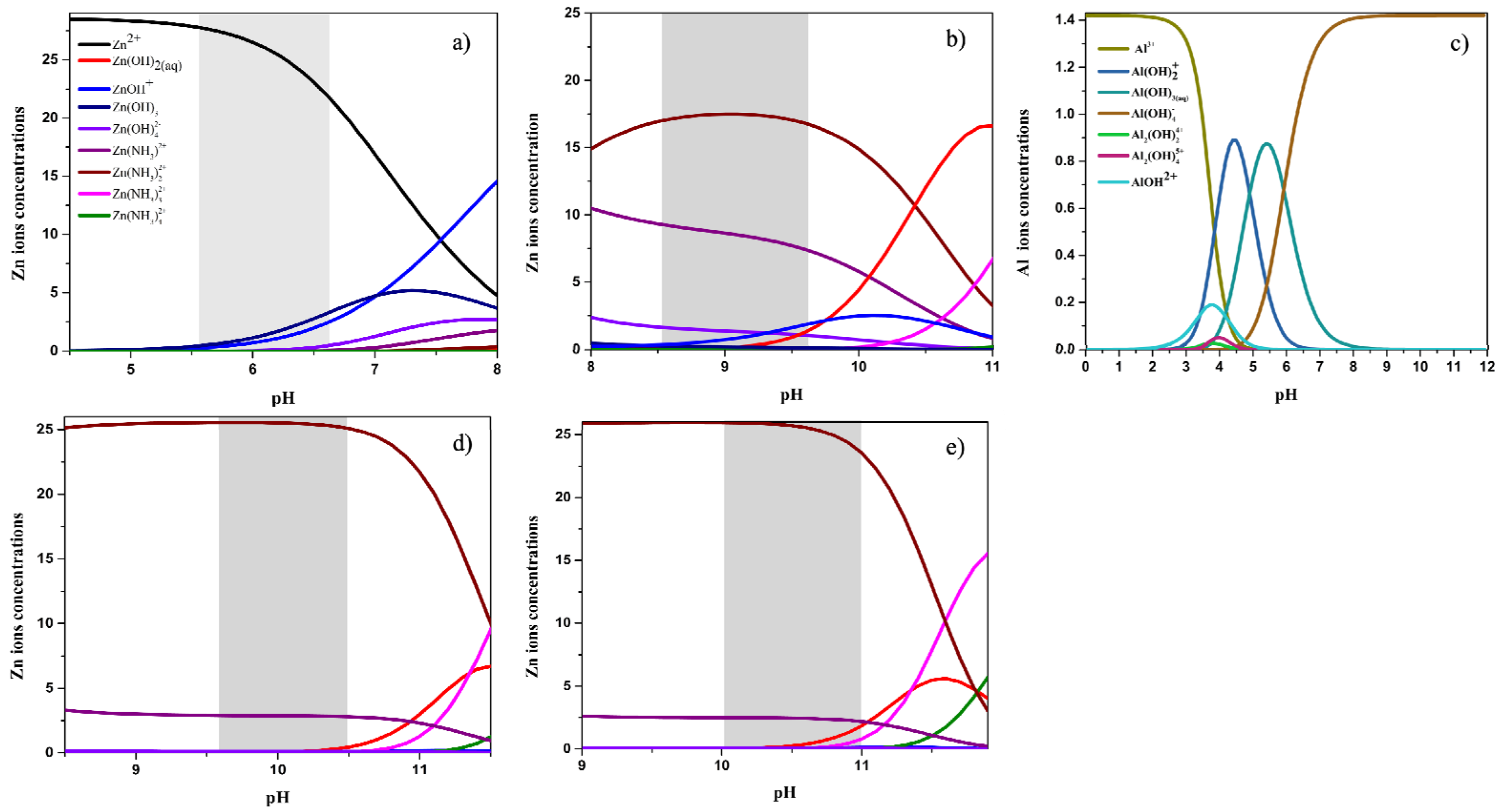
2.4. Thermodynamic Simulations
3. Results and Discussion
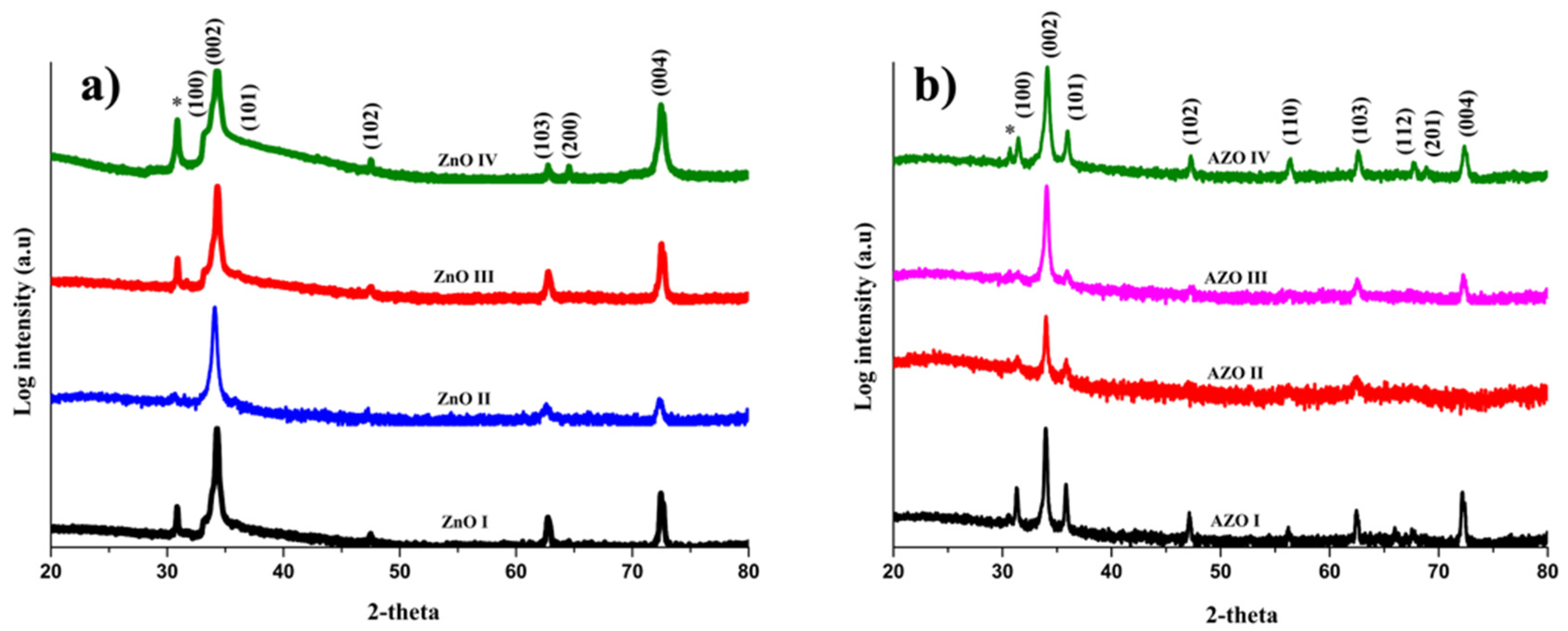
3.1. Morphological and Structural Properties
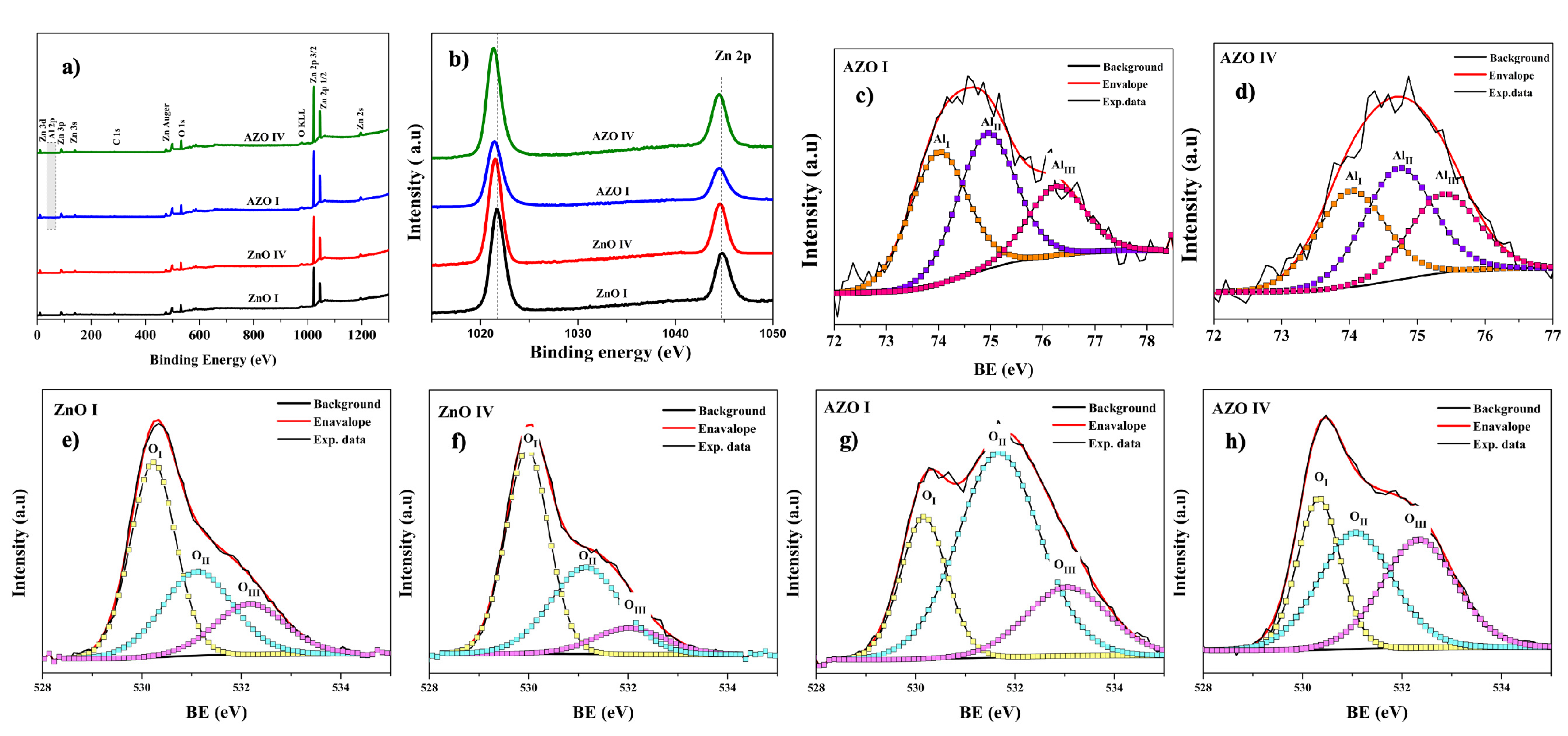
3.2. Nanorod and Surface Chemistry
3.3. Thermodynamic Simulation
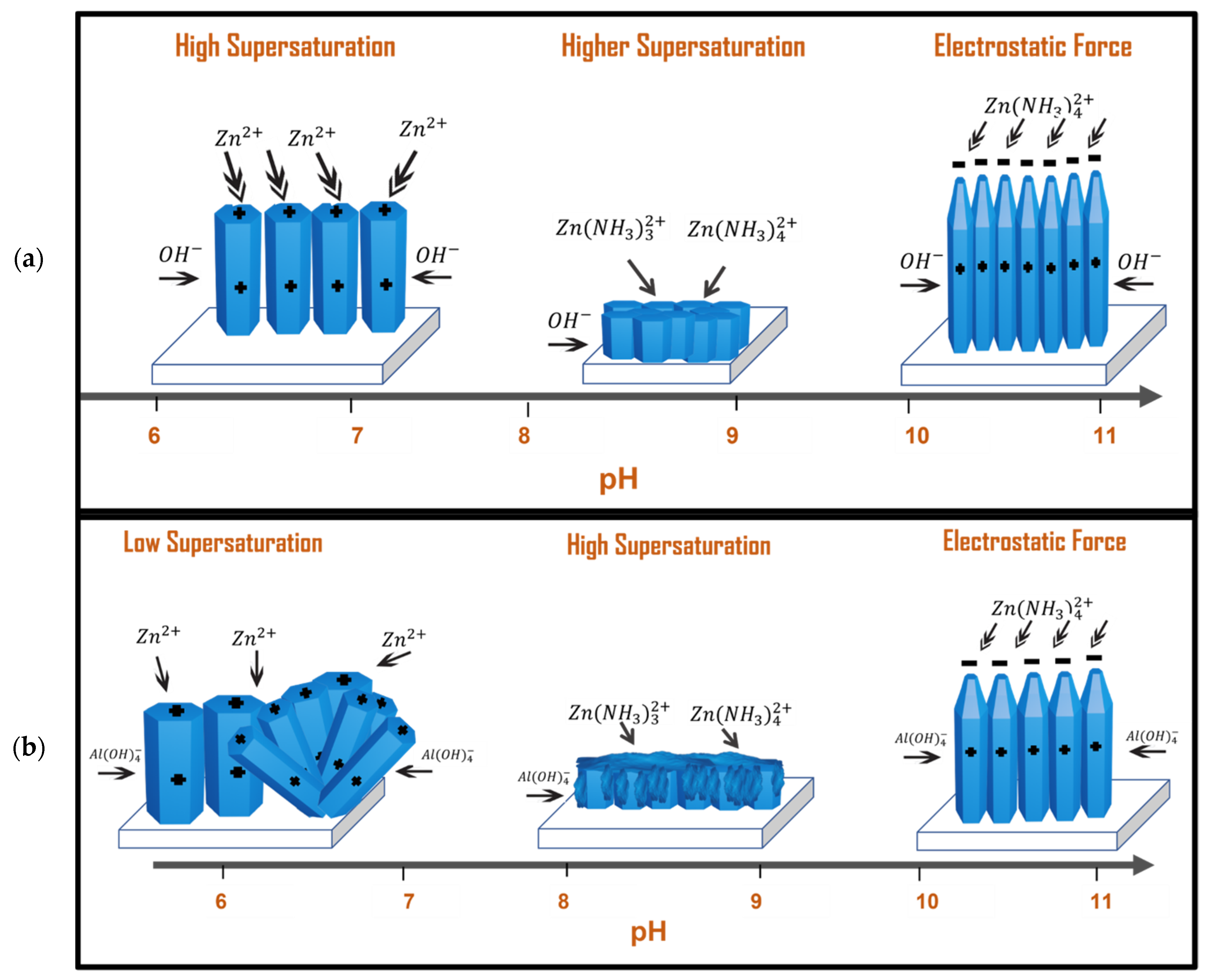
3.4. Proposed Growth Mechanism
3.4.1. Neutral/Acidic Growth Solution
3.4.2. Alkaline Growth Solutions
3.5. Nanostructure-Dependent Optical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mousavi, S.H.; Haratizadeh, H.; de Oliveira, P.W. Growth and Characterization of Wurtzite ZnO Nanocombs and Nanosaws. Mater. Lett. 2012, 70, 86–88. [Google Scholar] [CrossRef]
- Li, C.; Lin, Y.; Li, F.; Zhu, L.; Sun, D.; Shen, L.; Chen, Y.; Ruan, S. Hexagonal ZnO Nanorings: Synthesis, Formation Mechanism and Trimethylamine Sensing Properties. RSC Adv. 2015, 5, 80561–80567. [Google Scholar] [CrossRef]
- Yu, X.-L.; Ji, H.-M.; Wang, H.-L.; Sun, J.; Du, X.-W. Synthesis and Sensing Properties of ZnO/ZnS Nanocages. Nanoscale Res. Lett. 2010, 5, 644–648. [Google Scholar] [CrossRef] [Green Version]
- Luo, P.; Xie, M.; Luo, J.; Kan, H.; Wei, Q. Nitric Oxide Sensors Using Nanospiral ZnO Thin Film Deposited by GLAD for Application to Exhaled Human Breath. RSC Adv. 2020, 10, 14877–14884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bakharev, P.; Dobrokhotov, V.; McIlroy, D. A Method for Integrating ZnO Coated Nanosprings into a Low Cost Redox-Based Chemical Sensor and Catalytic Tool for Determining Gas Phase Reaction Kinetics. Chemosensors 2014, 2, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Wang, R.M.; Zhang, H.Z.; Sun, X.C.; Zhang, Z.S.; Xing, Y.J.; Yu, D.P. TEM Investigations on ZnO Nanobelts Synthesized via a Vapor Phase Growth. Micron 2004, 35, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Frade, T.; Melo Jorge, M.E.; Gomes, A. One-Dimensional ZnO Nanostructured Films: Effect of Oxide Nanoparticles. Mater. Lett. 2012, 82, 13–15. [Google Scholar] [CrossRef]
- Pimentel, A.; Nunes, D.; Duarte, P.; Rodrigues, J.; Costa, F.M.; Monteiro, T.; Martins, R.; Fortunato, E. Synthesis of Long ZnO Nanorods under Microwave Irradiation or Conventional Heating. J. Phys. Chem. C Nanomater. Interfaces 2014, 118, 14629–14639. [Google Scholar] [CrossRef]
- Urgessa, Z.N.; Oluwafemi, O.S.; Olivier, E.J.; Neethling, J.H.; Botha, J.R. Synthesis of Well-Aligned ZnO Nanorods on Silicon Substrate at Lower Temperature. J. Alloys Compd. 2013, 580, 120–124. [Google Scholar] [CrossRef]
- Hafez, H.S. Highly Active ZnO Rod-like Nanomaterials: Synthesis, Characterization and Photocatalytic Activity for Dye Removal. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 44, 1522–1527. [Google Scholar] [CrossRef]
- Lin, C.-C.; Lin, W.-H.; Hsiao, C.-Y.; Lin, K.-M.; Li, Y.-Y. Synthesis of One-Dimensional ZnO Nanostructures and Their Field Emission Properties. J. Phys. D Appl. Phys. 2008, 41, 045301. [Google Scholar] [CrossRef]
- Mohammadi, E.; Aliofkhazraei, M.; Hasanpoor, M.; Chipara, M. Hierarchical and Complex ZnO Nanostructures by Microwave-Assisted Synthesis: Morphologies, Growth Mechanism and Classification. Crit. Rev. Solid State Mater. Sci. 2018, 43, 475–541. [Google Scholar] [CrossRef]
- Wojnarowicz, J.; Chudoba, T.; Lojkowski, W. A Review of Microwave Synthesis of Zinc Oxide Nanomaterials: Reactants, Process Parameters and Morphoslogies. Nanomaterials 2020, 10, 1086. [Google Scholar] [CrossRef] [PubMed]
- Hahn, Y.-B. Zinc Oxide Nanostructures and Their Applications. Korean J. Chem. Eng. 2011, 28, 1797–1813. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, K.; Jiang, D.; Zhu, Z.; Geng, H.; Luo, L. Zinc Oxide Nanorod and Nanowire for Humidity Sensor. Appl. Surf. Sci. 2005, 242, 212–217. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, Y.; Hu, Y.; Gu, H. Ultraviolet Detectors Based on Wide Bandgap Semiconductor Nanowire: A Review. Sensors 2018, 18, 2072. [Google Scholar] [CrossRef] [Green Version]
- Mun, S.; Kim, H.C.; Ko, H.-U.; Zhai, L.; Kim, J.W.; Kim, J. Flexible Cellulose and ZnO Hybrid Nanocomposite and Its UV Sensing Characteristics. Sci. Technol. Adv. Mater. 2017, 18, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Sakurai, M.; Liao, M.; Aono, M. Giant Improvement of the Performance of ZnO Nanowire Photodetectors by Au Nanoparticles. J. Phys. Chem. C Nanomater. Interfaces 2010, 114, 19835–19839. [Google Scholar] [CrossRef]
- Kumar, S.; Sahare, P.D.; Kumar, S. Optimization of the CVD Parameters for ZnO Nanorods Growth: Its Photoluminescence and Field Emission Properties. Mater. Res. Bull. 2018, 105, 237–245. [Google Scholar] [CrossRef]
- Empizo, M.J.F.; Fukuda, K.; Arita, R.; Minami, Y.; Yamanoi, K.; Shimizu, T.; Sarukura, N.; Vargas, R.M.; Salvador, A.A.; Sarmago, R.V. Photoluminescence Properties of a Single ZnO Microstructure for Potential Scintillator Applications. Opt. Mater. 2014, 38, 256–260. [Google Scholar] [CrossRef]
- Xu, Z.; Deng, H.; Xie, J.; Li, Y.; Li, Y.; Zu, X.; Xue, S. Photoconductive UV Detectors Based on ZnO Films Prepared by Sol-Gel Method. J. Solgel Sci. Technol. 2005, 36, 223–226. [Google Scholar] [CrossRef]
- Janotti, A.; Van de Walle, C.G. Fundamentals of Zinc Oxide as a Semiconductor. Rep. Prog. Phys. 2009, 72, 126501. [Google Scholar] [CrossRef] [Green Version]
- Oba, F.; Choi, M.; Togo, A.; Tanaka, I. Point Defects in ZnO: An Approach from First Principles. Sci. Technol. Adv. Mater. 2011, 12, 034302. [Google Scholar] [CrossRef] [PubMed]
- Farid, S.; Mukherjee, S.; Sarkar, K.; Stroscio, M.A.; Dutta, M. Indium Dopant Concentration Effects on Zinc Oxide Nanowires. J. Phys. Chem. A 2019, 123, 8690–8695. [Google Scholar] [CrossRef]
- Shinde, S.S.; Rajpure, K.Y. Fast Response Ultraviolet Ga-Doped ZnO Based Photoconductive Detector. Mater. Res. Bull. 2011, 46, 1734–1737. [Google Scholar] [CrossRef]
- Young, S.-J.; Liu, Y.-H.; Shiblee, M.D.N.I.; Ahmed, K.; Lai, L.-T.; Nagahara, L.; Thundat, T.; Yoshida, T.; Arya, S.; Furukawa, H.; et al. Flexible Ultraviolet Photodetectors Based on One-Dimensional Gallium-Doped Zinc Oxide Nanostructures. ACS Appl. Electron. Mater. 2020, 2, 3522–3529. [Google Scholar] [CrossRef]
- Young, S.-J.; Chiou, C.-L.; Liu, Y.-H.; Ji, L.-W. Synthesis of Ga-Doped ZnO Nanorods by Hydrothermal Method and Their Application to Ultraviolet Photodetector. Inventions 2016, 1, 3. [Google Scholar] [CrossRef] [Green Version]
- Sreedhar, A.; Kwon, J.H.; Yi, J.; Gwag, J.S. Improved Physical Properties of Al-Doped ZnO Thin Films Deposited by Unbalanced RF Magnetron Sputtering. Ceram. Int. 2016, 42, 14456–14462. [Google Scholar] [CrossRef]
- Mohar, R.S.; Sugihartono, I.; Fauzia, V.; Umar, A.A. Dependence of Optical Properties of Mg-Doped ZnO Nanorods on Al Dopant. Surf. Interfaces 2020, 19, 100518. [Google Scholar] [CrossRef]
- Bai, S.N.; Tsai, H.H.; Tseng, T.Y. Structural and Optical Properties of Al-Doped ZnO Nanowires Synthesized by Hydrothermal Method. Thin Solid Films 2007, 516, 155–158. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Chen, D.-H. Synthesis and Conductivity Enhancement of Al-Doped ZnO Nanorod Array Thin Films. Nanotechnology 2010, 21, 285603. [Google Scholar] [CrossRef] [PubMed]
- Al Farsi, B.; Al Marzouqi, F.; Al-Maashani, M.; Souier, M.T.; Tay Zar Myint, M.; Al-Abri, M.Z. Rapid Microwave-Assisted Fabrication of Al-Doped Zinc Oxide Nanorods on a Glass Substrate for Photocatalytic Degradation of Phenol under Visible Light Irradiation. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2021, 264, 114977. [Google Scholar] [CrossRef]
- Al Farsi, B.; Souier, T.M.; Al Marzouqi, F.; Al Maashani, M.; Bououdina, M.; Widatallah, H.M.; Al Abri, M. Structural and Optical Properties of Visible Active Photocatalytic Al Doped ZnO Nanostructured Thin Films Prepared by Dip Coating. Opt. Mater. 2021, 113, 110868. [Google Scholar] [CrossRef]
- Ahn, C.H.; Han, W.S.; Kong, B.H.; Cho, H.K. Ga-Doped ZnO Nanorod Arrays Grown by Thermal Evaporation and Their Electrical Behavior. Nanotechnology 2009, 20, 015601. [Google Scholar] [CrossRef]
- Verrier, C.; Appert, E.; Chaix-Pluchery, O.; Rapenne, L.; Rafhay, Q.; Kaminski-Cachopo, A.; Consonni, V. Tunable Morphology and Doping of ZnO Nanowires by Chemical Bath Deposition Using Aluminum Nitrate. J. Phys. Chem. C Nanomater. Interfaces 2017, 121, 3573–3583. [Google Scholar] [CrossRef]
- Fuchs, P.; Hagendorfer, H.; Romanyuk, Y.E.; Tiwari, A.N. Doping Strategies for Highly Conductive Al-Doped ZnO Films Grown from Aqueous Solution: Doping Strategies for Highly Conductive Al-Doped ZnO Films. Phys. Status Solidi A 2015, 212, 51–55. [Google Scholar] [CrossRef]
- Yu, Q.; Rong, P.; Ren, S.; Jiang, L.; Li, Y. Fabrication and Electrochemical Performance of Al-Doped ZnO Nanosheets on Graphene-Based Flexible Substrates. Front. Mater. 2019, 6, 208. [Google Scholar] [CrossRef] [Green Version]
- Rakhsha, A.H.; Abdizadeh, H.; Pourshaban, E.; Golobostanfard, M.R. A Hetero-Homogeneous Investigation of Chemical Bath Deposited Ga-Doped ZnO Nanorods. AIP Conf. Proc. 2018, 1920, 020022. [Google Scholar] [CrossRef]
- Rana, A.; Kim, H.-S. NH4OH Treatment for an Optimum Morphological Trade-off to Hydrothermal Ga-Doped n-ZnO/p-Si Heterostructure Characteristics. Materials 2017, 11, 37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weber, L. Die Struktur von Zn O. Z. Fuer Krist. 1923, 58, 398–403. [Google Scholar]
- Kumar, Y.; Rana, A.K.; Bhojane, P.; Pusty, M.; Bagwe, V.; Sen, S.; Shirage, P.M. Controlling of ZnO Nanostructures by Solute Concentration and Its Effect on Growth, Structural and Optical Properties. Mater. Res. Express 2015, 2, 105017. [Google Scholar] [CrossRef]
- Mufti, N.; Damayanti, A.; Aripriharta; Arramel; Taufiq, A.; Sunaryono. The Growth of ZnO Nanorods on Stainless-Steel Foils and Its Application for Piezoelectric Nanogenerator. J. Phys. Conf. Ser. 2018, 1093, 012004. [Google Scholar] [CrossRef]
- Rasouli, F.; Rouhollahi, A.; Ghahramanifard, F. Gradient Doping of Copper in ZnO Nanorod Photoanode by Electrodeposition for Enhanced Charge Separation in Photoelectrochemical Water Splitting. Superlattices Microstruct. 2019, 125, 177–189. [Google Scholar] [CrossRef]
- Baruah, S.; Dutta, J. PH-Dependent Growth of Zinc Oxide Nanorods. J. Cryst. Growth 2009, 311, 2549–2554. [Google Scholar] [CrossRef]
- Baruah, S.; Dutta, J. Effect of Seeded Substrates on Hydrothermally Grown ZnO Nanorods. J. Solgel Sci. Technol. 2009, 50, 456–464. [Google Scholar] [CrossRef]
- Kim, K.S.; Jeong, H.; Jeong, M.S.; Jung, G.Y. Polymer-Templated Hydrothermal Growth of Vertically Aligned Single-Crystal ZnO Nanorods and Morphological Transformations Using Structural Polarity. Adv. Funct. Mater. 2010, 20, 3055–3063. [Google Scholar] [CrossRef]
- Jang, J.-M.; Kim, S.-D.; Choi, H.-M.; Kim, J.-Y.; Jung, W.-G. Morphology Change of Self-Assembled ZnO 3D Nanostructures with Different PH in the Simple Hydrothermal Process. Mater. Chem. Phys. 2009, 113, 389–394. [Google Scholar] [CrossRef]
- Amin, G.; Asif, M.H.; Zainelabdin, A.; Zaman, S.; Nur, O.; Willander, M. Influence of PH, Precursor Concentration, Growth Time, and Temperature on the Morphology of ZnO Nanostructures Grown by the Hydrothermal Method. J. Nanomater. 2011, 2011, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gao, W. Growth Process, Crystal Size and Alignment of ZnO Nanorods Synthesized under Neutral and Acid Conditions. J. Alloys Compd. 2015, 629, 84–91. [Google Scholar] [CrossRef]
- Mar, L.G.; Timbrell, P.Y.; Lamb, R.N. An XPS Study of Zinc Oxide Thin Film Growth on Copper Using Zinc Acetate as a Precursor. Thin Solid Films 1993, 223, 341–347. [Google Scholar] [CrossRef]
- Biesinger, M.C.; Lau, L.W.M.; Gerson, A.R.; Smart, R.S.C. Resolving Surface Chemical States in XPS Analysis of First Row Transition Metals, Oxides and Hydroxides: Sc, Ti, V, Cu and Zn. Appl. Surf. Sci. 2010, 257, 887–898. [Google Scholar] [CrossRef]
- Iatsunskyi, I.; Kempiński, M.; Jancelewicz, M.; Załęski, K.; Jurga, S.; Smyntyna, V. Structural and XPS Characterization of ALD Al2O3 Coated Porous Silicon. Vacuum 2015, 113, 52–58. [Google Scholar] [CrossRef]
- Rotole, J.A.; Sherwood, P.M.A. Nordstrandite (Al(OH)3) by XPS. Surf. Sci. Spectra 1998, 5, 32–38. [Google Scholar] [CrossRef]
- Yang, L.L.; Zhao, Q.X.; Willander, M.; Liu, X.J.; Fahlman, M.; Yang, J.H. Origin of the Surface Recombination Centers in ZnO Nanorods Arrays by X-Ray Photoelectron Spectroscopy. Appl. Surf. Sci. 2010, 256, 3592–3597. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.-M.; Brahma, S.; Huang, J.-H.; Wu, Z.-Z.; Lo, K.-Y. Strong Correlation between Optical Properties and Mechanism in Deficiency of Normalized Self-Assembly ZnO Nanorods. Sci. Rep. 2019, 9, 905. [Google Scholar] [CrossRef] [Green Version]
- Kashchiev, D.; van Rosmalen, G.M. Review: Nucleation in Solutions Revisited. Cryst. Res. Technol. 2003, 38, 555–574. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, G. Fundamentals of homogeneous nucleation. In Nanostructures and Nanomaterials: Synthesis, Properties, and Applications (2nd Edition): Synthesis, Properties, and Applications, 2nd ed.; World Scientific Publishing: Singapore, 2011; pp. 53–77. [Google Scholar]
- Van der Bruggen, B. Nucleation stage crystal growth. In Encyclopedia of Membranes; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–2. [Google Scholar] [CrossRef]
- Thanh, N.T.K.; Maclean, N.; Mahiddine, S. Mechanisms of nucleation and growth of nanoparticles in solution. Chem. Rev. 2014, 114, 7610–7630. [Google Scholar] [CrossRef]
- Baruah, S.; Dutta, J. Hydrothermal Growth of ZnO Nanostructures. Sci. Technol. Adv. Mater. 2009, 10, 013001. [Google Scholar] [CrossRef]
- Richardson, J.J.; Lange, F.F. Controlling Low Temperature Aqueous Synthesis of ZnO. 1. Thermodynamic Analysis. Cryst. Growth Des. 2009, 9, 2570–2575. [Google Scholar] [CrossRef]
- Joo, J.; Chow, B.Y.; Prakash, M.; Boyden, E.S.; Jacobson, J.M. Face-Selective Electrostatic Control of Hydrothermal Zinc Oxide Nanowire Synthesis. Nat. Mater. 2011, 10, 596–601. [Google Scholar] [CrossRef]
- Zhao, Z.; Lei, W.; Zhang, X.; Wang, B.; Jiang, H. ZnO-Based Amperometric Enzyme Biosensors. Sensors 2010, 10, 1216–1231. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, R.; Tripathy, N.; Ahn, M.-S.; Bhat, K.S.; Mahmoudi, T.; Wang, Y.; Yoo, J.-Y.; Kwon, D.-W.; Yang, H.-Y.; Hahn, Y.-B. Highly Efficient Non-Enzymatic Glucose Sensor Based on CuO Modified Vertically-Grown ZnO Nanorods on Electrode. Sci. Rep. 2017, 7, 5715. [Google Scholar] [CrossRef] [Green Version]
- Marsalek, R. Particle Size and Zeta Potential of ZnO. APCBEE Procedia 2014, 9, 13–17. [Google Scholar] [CrossRef] [Green Version]
- Laudise, R.A.; Ballman, A.A. Hydrothermal Synthesis of Zinc Oxide and Zinc Sulfide. J. Phys. Chem. 1960, 64, 688–691. [Google Scholar] [CrossRef]
- Li, W.-J.; Shi, E.-W.; Zhong, W.-Z.; Yin, Z.-W. Growth Mechanism and Growth Habit of Oxide Crystals. J. Cryst. Growth 1999, 203, 186–196. [Google Scholar] [CrossRef]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical properties and electronic structure of amorphous germanium. Phys. Status Solidi B Basic Res. 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Jain, A.; Sagar, P.; Mehra, R.M. Band Gap Widening and Narrowing in Moderately and Heavily Doped N-ZnO Films. Solid State Electron. 2006, 50, 1420–1424. [Google Scholar] [CrossRef]
- Galdámez-Martinez, A.; Santana, G.; Güell, F.; Martínez-Alanis, P.R.; Dutt, A. Photoluminescence of ZnO Nanowires: A Review. Nanomaterials 2020, 10, 857. [Google Scholar] [CrossRef] [PubMed]
- Kayaci, F.; Vempati, S.; Donmez, I.; Biyikli, N.; Uyar, T. Role of Zinc Interstitials and Oxygen Vacancies of ZnO in Photocatalysis: A Bottom-up Approach to Control Defect Density. Nanoscale 2014, 6, 10224–10234. [Google Scholar] [CrossRef] [Green Version]
- Singh, C.C.; Panda, E. Zinc Interstitial Threshold in Al-Doped ZnO Film: Effect on Microstructure and Optoelectronic Properties. J. Appl. Phys. 2018, 123, 165106. [Google Scholar] [CrossRef]
- Bedrouni, M.; Kharroubi, B.; Ouerdane, A.; Bouslama, M.; Guezzoul, M.; Caudano, Y.; Bensassi, K.B.; Bousmaha, M.; Bezzerrouk, M.A.; Mokadem, A.; et al. Effect of Indium Incorporation, Stimulated by UHV Treatment, on the Chemical, Optical and Electronic Properties of ZnO Thin Film. Opt. Mater. 2021, 111, 110560. [Google Scholar] [CrossRef]
- Khokhra, R.; Bharti, B.; Lee, H.-N.; Kumar, R. Visible and UV Photo-Detection in ZnO Nanostructured Thin Films via Simple Tuning of Solution Method. Sci. Rep. 2017, 7, 15032. [Google Scholar] [CrossRef] [Green Version]
- Samanta, P.K.; Chaudhuri, P.R. Substrate Effect on Morphology and Photoluminescence from ZnO Monopods and Bipods. Front. Optoelectron. China 2011, 4, 130–136. [Google Scholar] [CrossRef]
- Al-Saadi, M.J.; Al-Harthi, S.H.; Kyaw, H.H.; Myint, M.T.Z.; Bora, T.; Laxman, K.; Al-Hinai, A.; Dutta, J. Influence of Atomic Hydrogen, Band Bending, and Defects in the Top Few Nanometers of Hydrothermally Prepared Zinc Oxide Nanorods. Nanoscale Res. Lett. 2017, 12, 22. [Google Scholar] [CrossRef] [Green Version]
- Yun, S.; Lee, J.; Yang, J.; Lim, S. Hydrothermal Synthesis of Al-Doped ZnO Nanorod Arrays on Si Substrate. Phys. B Condens. Matter 2010, 405, 413–419. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Q.; Shao, H. Optical and Photoluminescent Properties of Al-Doped Zinc Oxide Thin Films by Pulsed Laser Deposition. J. Alloys Compd. 2009, 485, 529–531. [Google Scholar] [CrossRef]
- Ding, J.J.; Chen, H.X.; Ma, S.Y. Structural and Photoluminescence Properties of Al-Doped ZnO Films Deposited on Si Substrate. Phys. E Low Dimens. Syst. Nanostruct. 2010, 42, 1861–1864. [Google Scholar] [CrossRef]
- Sharma, B.K.; Khare, N.; Haranath, D. Photoluminescence Lifetime of Al-Doped ZnO Films in Visible Region. Solid State Commun. 2010, 150, 2341–2345. [Google Scholar] [CrossRef]
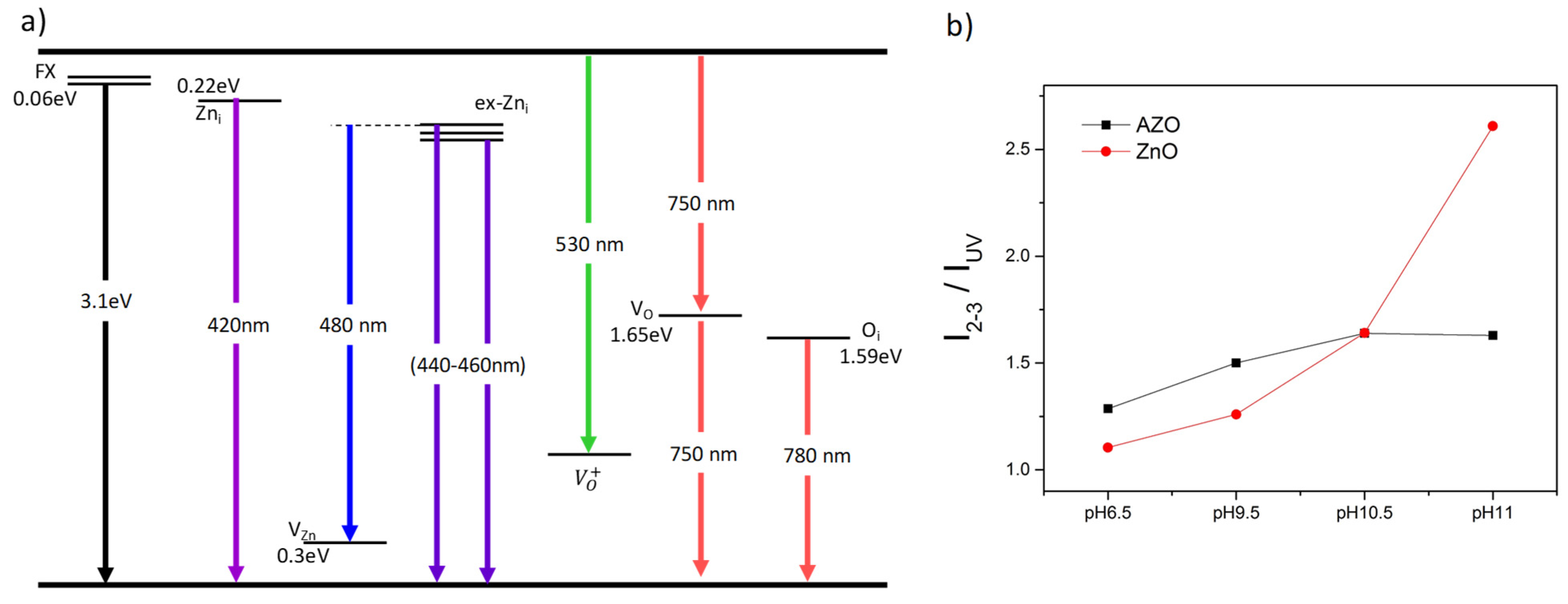
- Kumar, V.; Swart, H.C.; Ntwaeaborwa, O.M.; Kroon, R.E.; Terblans, J.J.; Shaat, S.K.K.; Yousif, A.; Duvenhage, M.M. Origin of the Red Emission in Zinc Oxide Nanophosphors. Mater. Lett. 2013, 101, 57–60. [Google Scholar] [CrossRef]
- Montenegro, D.N.; Hortelano, V.; Martínez, O.; Martínez-Tomas, M.C.; Sallet, V.; Muñoz-Sanjosé, V.; Jiménez, J. Non-Radiative Recombination Centres in Catalyst-Free ZnO Nanorods Grown by Atmospheric-Metal Organic Chemical Vapour Deposition. J. Phys. D Appl. Phys. 2013, 46, 235302. [Google Scholar] [CrossRef]



| Sample ID | pHi | pHf | NH3 vol. (mL) | NH3 conc. (mM) |
|---|---|---|---|---|
| ZnO I | 6.68 | 6.46 | 0.00 | 30.0 |
| ZnO II | 9.55 | 8.52 | 2.00 | 161.5 |
| ZnO III | 10.50 | 9.29 | 8.31 | 559.8 |
| ZnO IV | 11.00 | 9.67 | 15.05 | 959.4 |
| AZO I | 5.56 | 6.56 | 0.00 | 30.0 |
| AZO II | 9.55 | 8.77 | 2.50 | 194.0 |
| AZO III | 10.50 | 9.65 | 4.20 | 303.1 |
| AZO IV | 11.00 | 9.95 | 8.60 | 577.5 |
| Sample ID | 2θ (°) | D (nm) | c (Å) | a (Å) | c/a | FWHM (°) | Bond Length (Å) |
|---|---|---|---|---|---|---|---|
| ZnO I | 34.262 | 54 | 5.230 | 3.236 | 1.616 | 0.161 | 1.975 |
| ZnO II | 34.132 | 53 | 5.249 | 3.223 | 1.626 | 0.194 | 1.974 |
| ZnO III | 34.252 | 45 | 5.232 | 3.234 | 1.618 | 0.161 | 1.974 |
| ZnO IV | 34.194 | 66 | 5.240 | 3.219 | 1.628 | 0.132 | 1.970 |
| AZO I | 34.166 | 64 | 5.244 | 3.227 | 1.625 | 0.135 | 1.973 |
| AZO II | 34.031 | 42 | 5.265 | 3.228 | 1.631 | 0.205 | 1.976 |
| AZO III | 34.170 | 48 | 5.244 | 3.218 | 1.629 | 0.181 | 1.969 |
| AZO IV | 34.168 | 47 | 5.244 | 3.225 | 1.626 | 0.185 | 1.972 |
| Sample ID | Zn | O | C | Al | O/Zn | Al/Zn |
|---|---|---|---|---|---|---|
| ZnO I | 39.4 | 45.3 | 15.4 | - | 1.15 | - |
| ZnO IV | 42.2 | 46.2 | 11.6 | - | 1.09 | - |
| AZO I | 29.6 | 52.4 | 16.0 | 2 | 1.77 | 6.7% |
| AZO IV | 37.0 | 49.2 | 11.4 | 2.4 | 1.33 | 6.5% |
| Sample | OI | OII | OIII | |||
|---|---|---|---|---|---|---|
| BE (eV) | Area % | BE (eV) | Area % | BE (eV) | Area % | |
| ZnO I | 530.2 | 48.2 | 531.1 | 32.3 | 532.2 | 19.5 |
| ZnO IV | 530.0 | 52.5 | 531.1 | 36.5 | 532.0 | 11.0 |
| AZO I | 530.2 | 22.7 | 531.7 | 57.8 | 533.0 | 19.5 |
| AZO IV | 530.3 | 28.1 | 531.1 | 37.3 | 532.3 | 34.6 |
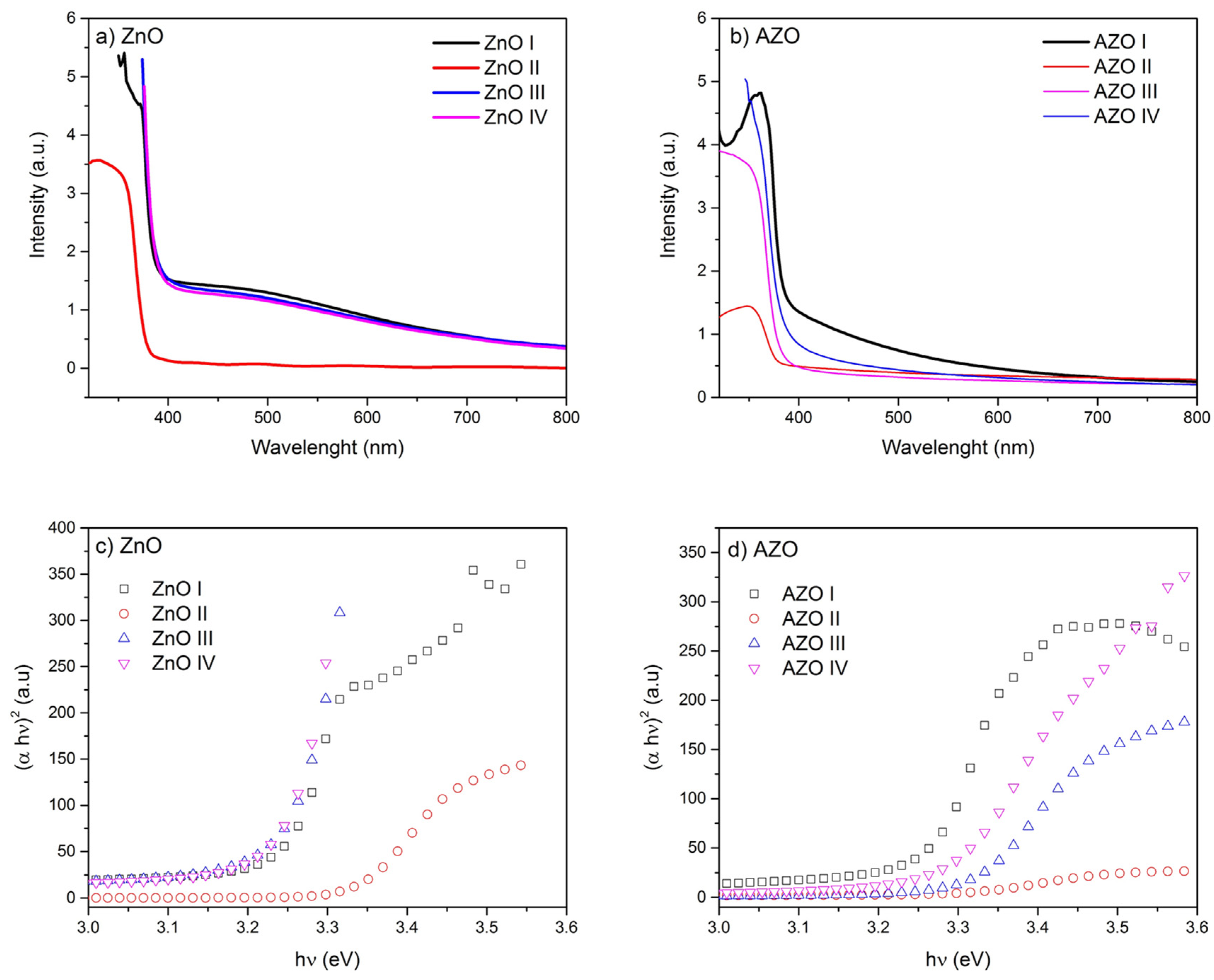
| Sample ID | Eg (eV) |
|---|---|
| ZnO I | 3.23 |
| ZnO II | 3.34 |
| ZnO III | 3.24 |
| ZnO IV | 3.28 |
| AZO I | 3.26 |
| AZO II | 3.29 |
| AZO III | 3.31 |
| AZO IV | 3.28 |
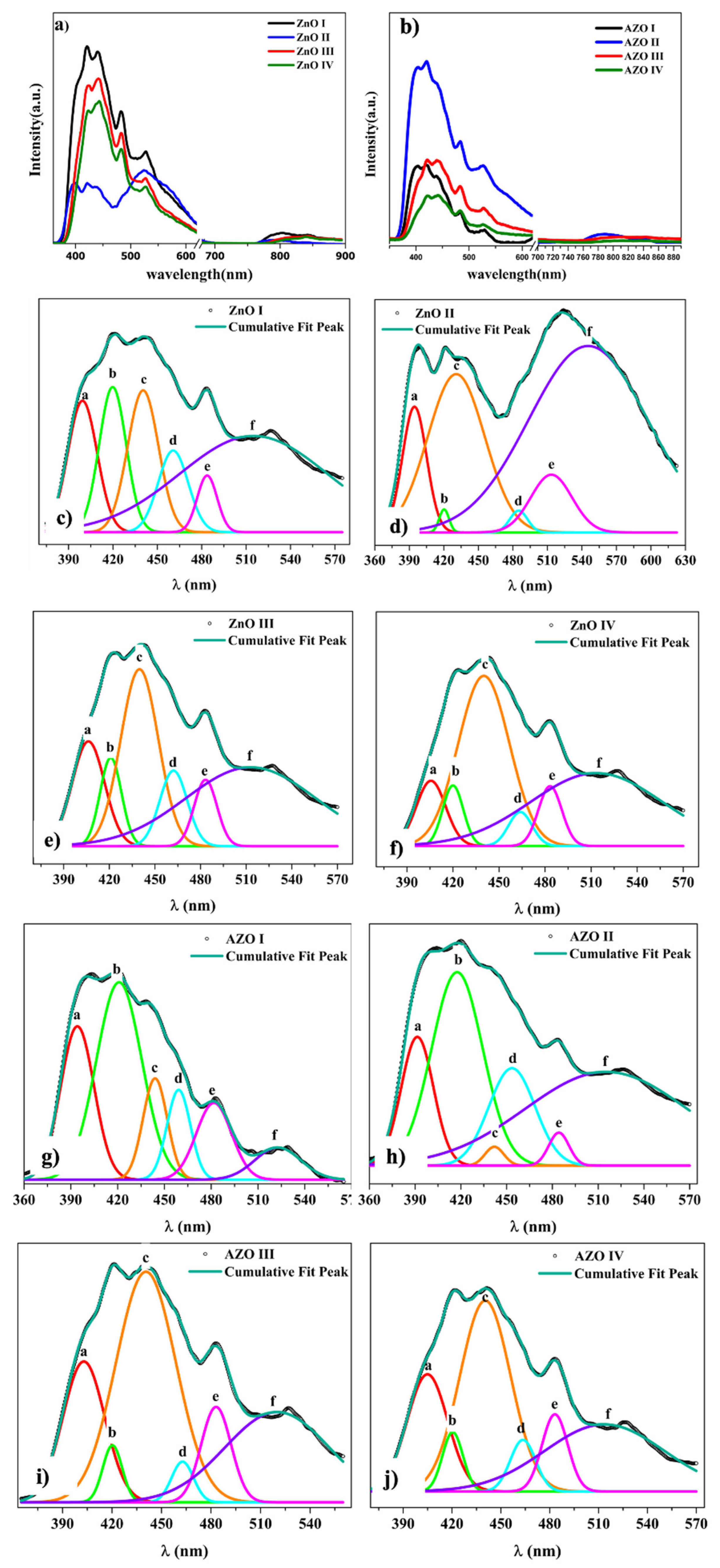
| Sample | Peak Position (nm) | FWHM (nm) | Area (a.u) | Averaged Area (%) |
|---|---|---|---|---|
| ZnO I | 399 420 440 461 484 529 | 23 21 24 24 16 117 | 397 405 452 254 117 1471 | 12.8 13.1 14.6 8.2 3.8 47.5 |
| ZnO II | 395 420 431 485 513 545 | 25 10 58 18 42 121 | 148 11 439 19 116 1080 | 8.1 0.6 24.2 1 6.4 59.6 |
| ZnO III | 406 421 440 462 483 527 | 25 17 29 21 18 101 | 299 167 587 183 134 906 | 13.1 7.3 25.8 8 5.9 39.8 |
| ZnO IV | 406 420 440 464 483 527 | 22 16 39 18 18 101 | 154 100 440 64 112 768 | 9.4 6.1 26.9 3.9 6.8 46.9 |
| AZO I | 394 421 444 459 482 529 | 25 34 18 18 26 34 | 397 694 189 163 209 114 | 22.5 39.3 10.7 9.2 11.8 6.5 |
| AZO II | 392 418 442 453 484 527 | 25 39 14 35 16 125 | 724 1718 62 784 116 2640 | 12 28.4 1 13 1.9 43.7 |
| AZO III | 403 420 441 463 483 527 | 29 14 43 16 21 75 | 390 73 914 59 189 623 | 17.3 3.2 40.7 2.6 8.4 27.7 |
| AZO IV | 405 420 440 463 483 527 | 29 15 36 18 19 86 | 207 53 422 57 87 350 | 17.6 4.5 35.9 4.9 7.4 29.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Farsi, L.; Souier, T.M.; Al-Hinai, M.; Myint, M.T.Z.; Kyaw, H.H.; Widatallah, H.M.; Al-Abri, M. pH Controlled Nanostructure and Optical Properties of ZnO and Al-Doped ZnO Nanorod Arrays Grown by Microwave-Assisted Hydrothermal Method. Nanomaterials 2022, 12, 3735. https://doi.org/10.3390/nano12213735
Al-Farsi L, Souier TM, Al-Hinai M, Myint MTZ, Kyaw HH, Widatallah HM, Al-Abri M. pH Controlled Nanostructure and Optical Properties of ZnO and Al-Doped ZnO Nanorod Arrays Grown by Microwave-Assisted Hydrothermal Method. Nanomaterials. 2022; 12(21):3735. https://doi.org/10.3390/nano12213735
Chicago/Turabian StyleAl-Farsi, Lamia, Tewfik M. Souier, Muna Al-Hinai, Myo T. Z. Myint, Htet H. Kyaw, Hisham M. Widatallah, and Mohammed Al-Abri. 2022. "pH Controlled Nanostructure and Optical Properties of ZnO and Al-Doped ZnO Nanorod Arrays Grown by Microwave-Assisted Hydrothermal Method" Nanomaterials 12, no. 21: 3735. https://doi.org/10.3390/nano12213735







