A Core-Shell Approach for Systematically Coarsening Nanoparticle–Membrane Interactions: Application to Silver Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Setup for Unconstrained Coarse Grained Molecular Dynamics
2.2. Setup for Potential of Mean Force calculation
3. Results and Discussion
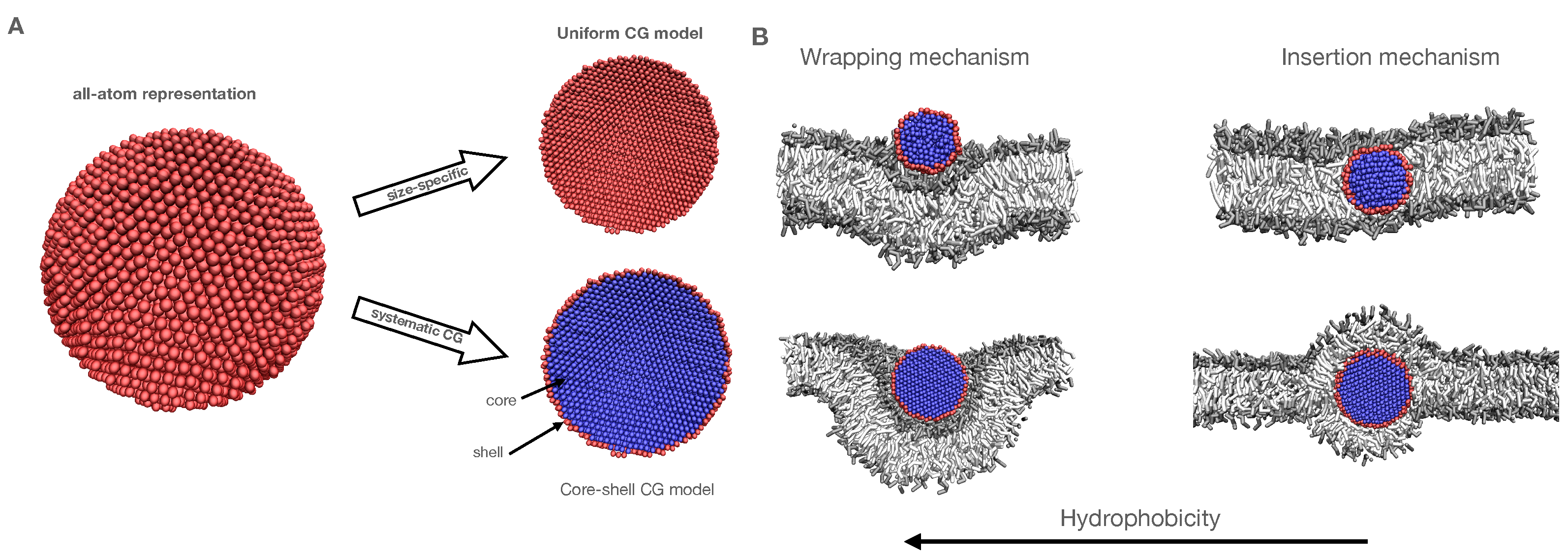
3.1. Establishing a Size-Invariant Martini CG Representation for NPs: The Ag Case
3.1.1. Analyzing the Standard Uniform NP Representation
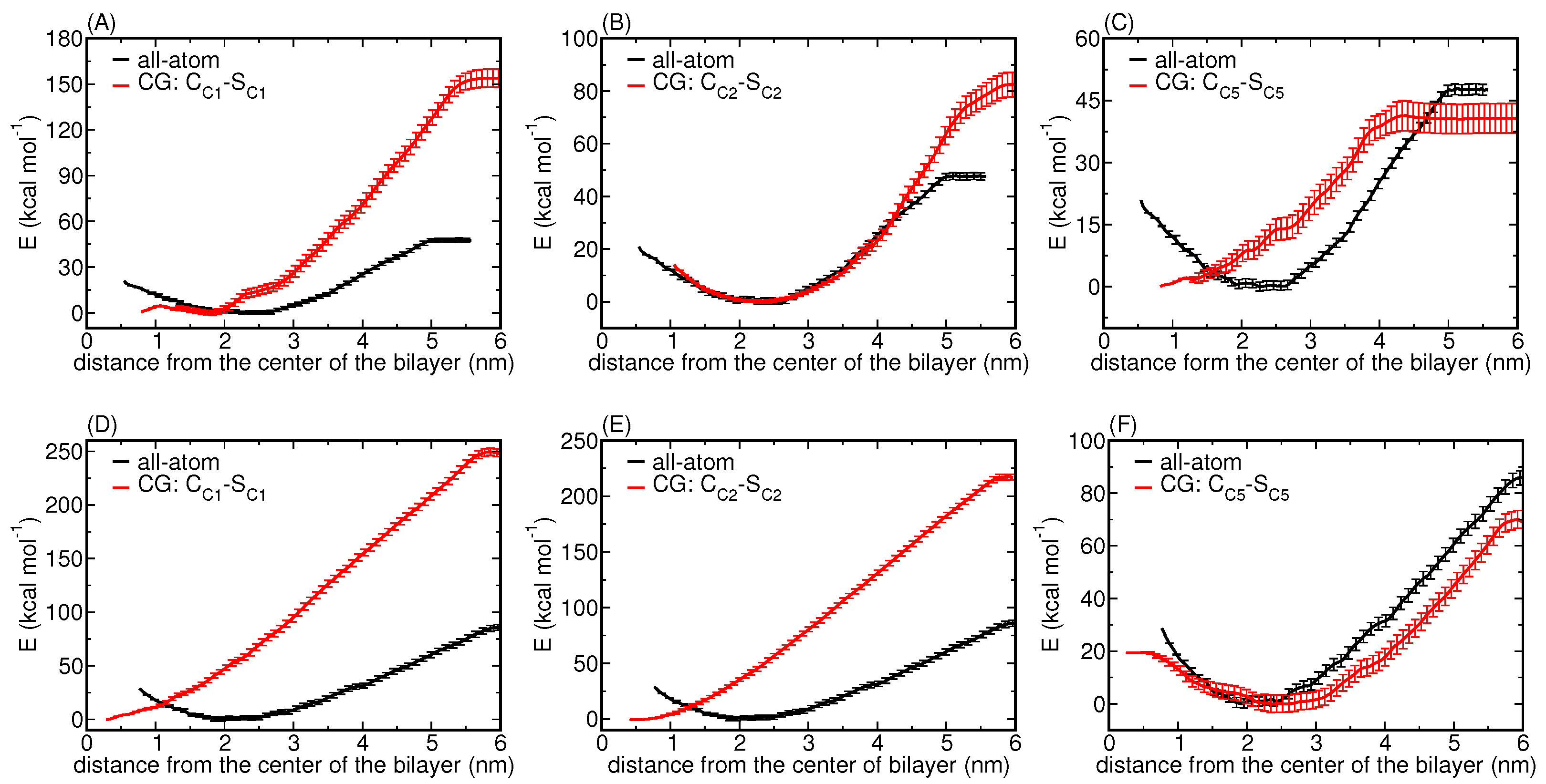
3.1.2. Potentials of Mean Force for Two NP Sizes
3.1.3. Exploring the Binding Mechanisms: Wrapping or Insertion
Stable or Metastable?
Endocytosis
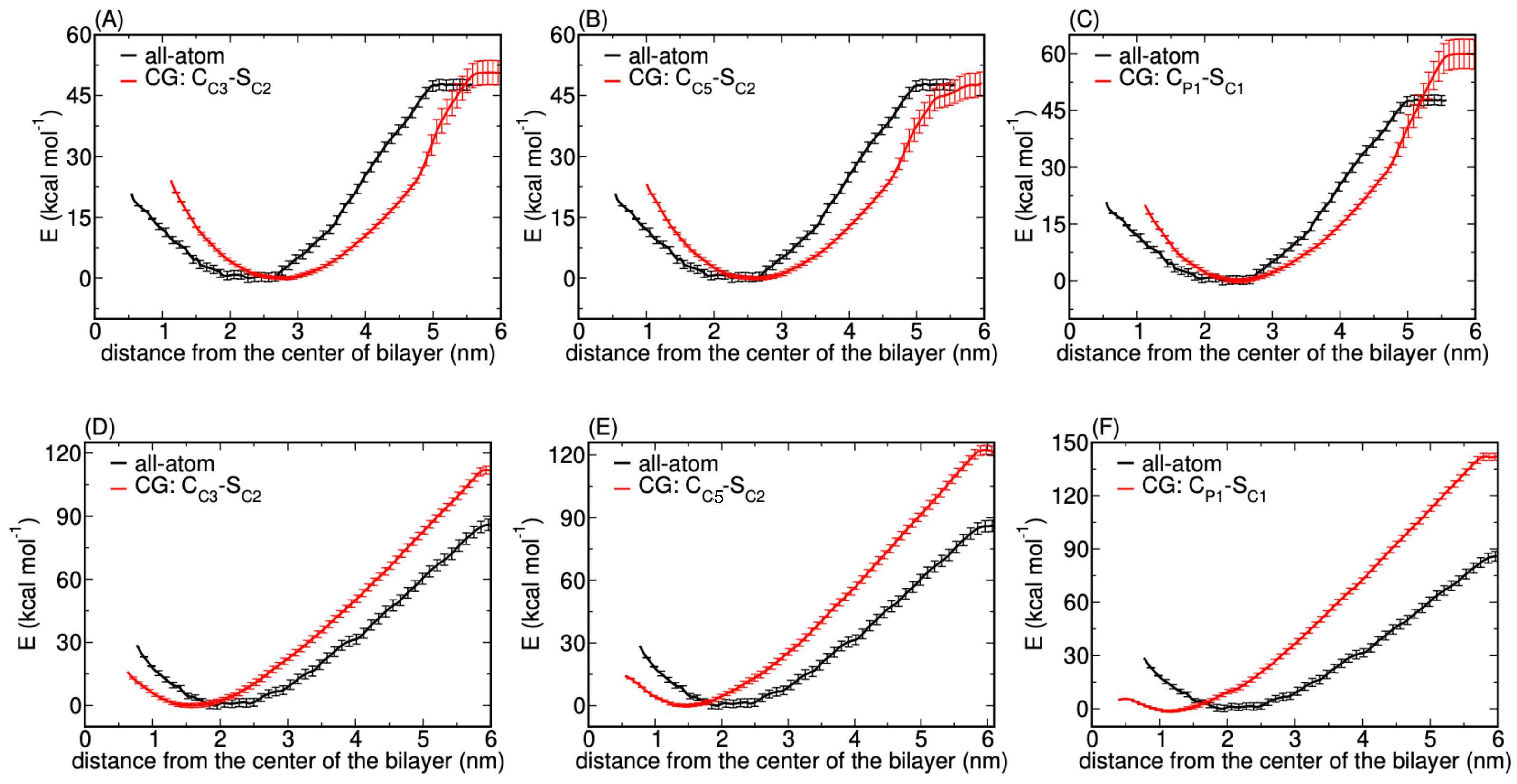
3.1.4. A Core-Shell Representation for Ag NPs
Matching AAMD and CGMD Potentials of Mean Force
Comparing Binding Mechanisms and Structural Characteristics
3.2. Increasing Scales: CGMD for a 10 nm Ag NP
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boisselier, E.; Astruc, D. Gold nanoparticles in nanomedicine: Preparations, imaging, diagnostics, therapies and toxicity. Chem. Soc. Rev. 2009, 38, 1759–1782. [Google Scholar] [CrossRef] [PubMed]
- Rana, S.; Bajaj, A.; Mout, R.; Rotello, V.M. Monolayer coated gold nanoparticles for delivery applications. Adv. Drug Deliv. Rev. 2012, 64, 200–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, P.J.; Huang, S.C.; Chen, Y.P.; Chiueh, L.C.; Shih, D.Y.C. Analysis of titanium dioxide and zinc oxide nanoparticles in cosmetics. J. Food Drug Anal. 2015, 23, 587–594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skocaj, M.; Filipic, M.; Petkovic, J.; Novak, S. Titanium dioxide in our everyday life; is it safe? Radiol. Oncol. 2011, 45, 227. [Google Scholar] [CrossRef] [Green Version]
- Deserno, M.; Gelbart, W.M. Adhesion and wrapping in colloid-vesicle complexes. J. Phys. Chem. B 2002, 106, 5543–5552. [Google Scholar] [CrossRef]
- Deserno, M.; Bickel, T. Wrapping of a spherical colloid by a fluid membrane. EPL (Europhys. Lett.) 2003, 62, 767. [Google Scholar] [CrossRef] [Green Version]
- Spangler, E.J.; Upreti, S.; Laradji, M. Partial wrapping and spontaneous endocytosis of spherical nanoparticles by tensionless lipid membranes. J. Chem. Phys. 2016, 144, 044901. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marrink, S.J.; De Vries, A.H.; Mark, A.E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef] [Green Version]
- Pak, A.J.; Dannenhoffer-Lafage, T.; Madsen, J.J.; Voth, G.A. Systematic coarse-grained lipid force fields with semiexplicit solvation via virtual sites. J. Chem. Theory Comput. 2019, 15, 2087–2100. [Google Scholar] [CrossRef]
- Srivastava, A.; Voth, G.A. Hybrid approach for highly coarse-grained lipid bilayer models. J. Chem. Theory Comput. 2013, 9, 750–765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lunnoo, T.; Assawakhajornsak, J.; Puangmali, T. In silico study of gold nanoparticle uptake into a mammalian cell: Interplay of size, shape, surface charge and aggregation. J. Phys. Chem. C 2019, 123, 3801–3810. [Google Scholar] [CrossRef]
- Michel, R.; Gradzielski, M. Experimental aspects of colloidal interactions in mixed systems of liposome and inorganic nanoparticle and their applications. Int. J. Mol. Sci. 2012, 13, 11610–11642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasch, M.R.; Rossinyol, E.; Hueso, J.L.; Goodfellow, B.W.; Arbiol, J.; Korgel, B.A. Hydrophobic gold nanoparticle self-assembly with phosphatidylcholine lipid: Membrane-loaded and janus vesicles. Nano Lett. 2010, 10, 3733–3739. [Google Scholar] [CrossRef] [PubMed]
- Contini, C.; Hindley, J.W.; Macdonald, T.J.; Barritt, J.D.; Ces, O.; Quirke, N. Size dependency of gold nanoparticles interacting with model membranes. Commun. Chem. 2020, 3, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.L.; Bothun, G.D. Nanoparticles Meet Cell Membranes: Probing Nonspecific Interactions Using Model Membranes. Environ. Sci. Technol. 2014, 48, 873–880. [Google Scholar] [CrossRef] [PubMed]
- Mendozza, M.; Caselli, L.; Salvatore, A.; Montis, C.; Berti, D. Nanoparticles and organized lipid assemblies: From interaction to design of hybrid soft devices. Soft Matter 2019, 15, 8951–8970. [Google Scholar] [CrossRef]
- Sauter, J.; Grafmüller, A. Procedure for transferable coarse-grained models of aqueous polysaccharides. J. Chem. Theory Comput. 2017, 13, 223–236. [Google Scholar] [CrossRef]
- Singhal, A.; Schneible, J.D.; Lilova, R.L.; Hall, C.K.; Menegatti, S.; Grafmüller, A. A multiscale coarse-grained model to predict the molecular architecture and drug transport properties of modified chitosan hydrogels. Soft Matter 2020, 16, 10591–10610. [Google Scholar] [CrossRef]
- Monticelli, L. On atomistic and coarse-grained models for C60 fullerene. J. Chem. Theory Comput. 2012, 8, 1370–1378. [Google Scholar] [CrossRef]
- Izvekov, S.; Violi, A.; Voth, G.A. Systematic coarse-graining of nanoparticle interactions in molecular dynamics simulation. J. Phys. Chem. B 2005, 109, 17019–17024. [Google Scholar] [CrossRef] [PubMed]
- Salassi, S.; Simonelli, F.; Bochicchio, D.; Ferrando, R.; Rossi, G. Au nanoparticles in lipid bilayers: A comparison between atomistic and coarse-grained models. J. Phys. Chem. C 2017, 121, 10927–10935. [Google Scholar] [CrossRef] [Green Version]
- Jarin, Z.; Newhouse, J.; Voth, G.A. Coarse-Grained Force Fields from the Perspective of Statistical Mechanics: Better Understanding of the Origins of a MARTINI Hangover. J. Chem. Theory Comput. 2021, 17, 1170–1180. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Yu, A.; Voth, G.A. Temperature and phase transferable bottom-up coarse-grained models. J. Chem. Theory Comput. 2020, 16, 6823–6842. [Google Scholar] [CrossRef] [PubMed]
- Centi, A.; Dutta, A.; Parekh, S.H.; Bereau, T. Inserting small molecules across membrane mixtures: Insight from the potential of mean force. Biophys. J. 2020, 118, 1321–1332. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Badhe, Y.; Mitragotri, S.; Rai, B. Permeation of nanoparticles across the intestinal lipid membrane: Dependence on shape and surface chemistry studied through molecular simulations. Nanoscale 2020, 12, 6318–6333. [Google Scholar] [CrossRef] [PubMed]
- Power, D.; Rouse, I.; Poggio, S.; Brandt, E.; Lopez, H.; Lyubartsev, A.; Lobaskin, V. A multiscale model of protein adsorption on a nanoparticle surface. Model. Simul. Mater. Sci. Eng. 2019, 27, 084003. [Google Scholar] [CrossRef]
- Nel, A.; Xia, T.; Mädler, L.; Li, N. Toxic potential of materials at the nanolevel. Science 2006, 311, 622–627. [Google Scholar] [CrossRef] [Green Version]
- Limbach, L.K.; Wick, P.; Manser, P.; Grass, R.N.; Bruinink, A.; Stark, W.J. Exposure of engineered nanoparticles to human lung epithelial cells: Influence of chemical composition and catalytic activity on oxidative stress. Environ. Sci. Technol. 2007, 41, 4158–4163. [Google Scholar] [CrossRef]
- Choi, O.; Deng, K.K.; Kim, N.J.; Ross, L., Jr.; Surampalli, R.Y.; Hu, Z. The inhibitory effects of silver nanoparticles, silver ions and silver chloride colloids on microbial growth. Water Res. 2008, 42, 3066–3074. [Google Scholar] [CrossRef]
- Choi, O.; Hu, Z. Nitrification inhibition by silver nanoparticles. Water Sci. Technol. 2009, 59, 1699–1702. [Google Scholar] [CrossRef] [PubMed]
- Lok, C.N.; Ho, C.M.; Chen, R.; He, Q.Y.; Yu, W.Y.; Sun, H.; Tam, P.K.H.; Chiu, J.F.; Che, C.M. Silver nanoparticles: Partial oxidation and antibacterial activities. JBIC J. Biol. Inorg. Chem. 2007, 12, 527–534. [Google Scholar] [CrossRef] [PubMed]
- Benn, T.M.; Westerhoff, P. Nanoparticle silver released into water from commercially available sock fabrics. Environ. Sci. Technol. 2008, 42, 4133–4139. [Google Scholar] [CrossRef] [PubMed]
- Geranio, L.; Heuberger, M.; Nowack, B. The behavior of silver nanotextiles during washing. Environ. Sci. Technol. 2009, 43, 8113–8118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singhal, A.; Sevink, G.A. The role of size and nature in nanoparticle binding to a model lung membrane: An atomistic study. Nanoscale Adv. 2021, 3, 6635–6648. [Google Scholar] [CrossRef] [PubMed]
- Singhal, A.; Sevink, G. Ag nanoparticle interaction with complex lipid bilayer: An atomistic and coarse-grained study. Biophys. J. 2022, 121, 523a. [Google Scholar] [CrossRef]
- Spangler, E.J.; Laradji, M. Discontinuous wrapping transition of spherical nanoparticles by tensionless lipid membranes. J. Chem. Phys. 2020, 152, 104902. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Veldhuizen, R.; Nag, K.; Orgeig, S.; Possmayer, F. The role of lipids in pulmonary surfactant. Biochim. Biophys. Acta (BBA)-Mol. Basis Dis. 1998, 1408, 90–108. [Google Scholar] [CrossRef]
- Baoukina, S.; Tieleman, D.P. Computer simulations of lung surfactant. Biochim. Biophys. Acta (BBA)-Biomembr. 2016, 1858, 2431–2440. [Google Scholar] [CrossRef] [PubMed]
- Wassenaar, T.A.; Ingólfsson, H.I.; Bóckmann, R.A.; Tieleman, D.P.; Marrink, S.J. Computational lipidomics with insane: A versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Fliege, J.; Svaiter, B.F. Steepest descent methods for multicriteria optimization. Math. Methods Oper. Res. 2020, 51, 479–494. [Google Scholar] [CrossRef]
- Bussi, G.; Parrinello, M. Accurate sampling using Langevin dynamics. Phys. Rev. E 2007, 75, 056707. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Roux, B. The calculation of the potential of mean force using computer simulations. Comput. Phys. Commun. 1995, 91, 275–282. [Google Scholar] [CrossRef]
- Hub, J.S.; De Groot, B.L.; Van Der Spoel, D. g_wham A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
- Sevink, G.A.; Liwo, J.A.; Asinari, P.; MacKernan, D.; Milano, G.; Pagonabarraga, I. Unfolding the prospects of computational (bio) materials modeling. J. Chem. Phys. 2020, 153, 100901. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, T.; De Nicola, A.; Montis, C.; Carlaá, F.; van der Vegt, N.F.; Berti, D.; Milano, G. Nanoparticles at biomimetic interfaces: Combined experimental and simulation study on charged gold nanoparticles/lipid bilayer interfaces. J. Phys. Chem. Lett. 2018, 10, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Bothun, G.D. Hydrophobic silver nanoparticles trapped in lipid bilayers: Size distribution, bilayer phase behavior and optical properties. J. Nanobiotechnol. 2008, 6, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prates Ramalho, J.; Gheka, P.; Sarkisov, L. Structure and phase transformations of DPPC lipid bilayers in the presence of nanoparticles: Insights from coarse-grained Molecular Dynamics simulations. Langmuir 2011, 27, 3723–3730. [Google Scholar] [CrossRef]
- Ginzburg, V.V.; Balijepalli, S. Modeling the Thermodynamics of the Interaction of Nanoparticles with Cell Membranes. Nano Lett. 2007, 7, 3716–3722. [Google Scholar] [CrossRef] [PubMed]
- Almeida, P.; Pokorny, A. Mechanisms of Antimicrobial, Cytolytic and Cell-Penetrating Peptides: From Kinetics to Thermodynamics. Biochemistry 2009, 48, 8083–8093. [Google Scholar] [CrossRef] [Green Version]
- Kabelka, I.; Vácha, R. Optimal hydrophobicity and reorientation of amphiphilic peptides translocating through membrane. Biophys. J. 2018, 115, 1045–1054. [Google Scholar] [CrossRef] [Green Version]
- Smirnova, Y.G.; Risselada, H.J.; Müller, M. Thermodynamically reversible paths of the first fusion intermediate reveal an important role for membrane anchors of fusion proteins. Proc. Nat. Acad. Sci. USA 2019, 116, 2571–2576. [Google Scholar] [CrossRef] [Green Version]
- Vácha, R.; Martinez-Veracoechea, F.J.; Frenkel, D. Receptor-mediated endocytosis of nanoparticles of various shapes. Nano Lett. 2011, 11, 5391–5395. [Google Scholar] [CrossRef]
- Cooke, I.R.; Kremer, K.; Deserno, M. Tunable generic model for fluid bilayer membranes. Phys. Rev. E 2005, 72, 011506. [Google Scholar] [CrossRef]
- Cooke, I.R.; Deserno, M. Solvent-free model for self-assembling fluid bilayer membranes: Stabilization of the fluid phase based on broad attractive tail potentials. J. Chem. Phys. 2005, 123, 224710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tämm, K.; Sikk, L.; Burk, J.; Rallo, R.; Pokhrel, S.; Mädler, L.; Scott-Fordsmand, J.; Burk, P.; Tamm, T. Parametrization of nanoparticles: Development of full-particle nanodescriptors. Nanoscale 2016, 8, 16243–16250. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knoll, A.; Horvat, A.; Lyakhova, K.; Krausch, G.; Sevink, G.; Zvelindovsky, A.; Magerle, R. Phase behavior in thin films of cylinder-forming block copolymers. Phys. Rev. Lett. 2002, 89, 035501. [Google Scholar] [CrossRef]
- Ramadurai, S.; Holt, A.; Schäfer, L.V.; Krasnikov, V.V.; Rijkers, D.T.; Marrink, S.J.; Killian, J.A.; Poolman, B. Influence of hydrophobic mismatch and amino acid composition on the lateral diffusion of transmembrane peptides. Biophys. J. 2010, 99, 1447–1454. [Google Scholar] [CrossRef] [Green Version]
- Fritz, D.; Koschke, K.; Harmandaris, V.A.; van der Vegt, N.F.; Kremer, K. Multiscale modeling of soft matter: Scaling of dynamics. Phys. Chem. Chem. Phys. 2011, 13, 10412–10420. [Google Scholar] [CrossRef]
- Koynova, R.; Caffrey, M. Phases and phase transitions of the phosphatidylcholines. Biochim. Biophys. Acta 1998, 1376, 91–145. [Google Scholar] [CrossRef]
- Jaschonek, S.; Cascella, M.; Gauss, J.; Diezemann, G.; Milano, G. Intramolecular structural parameters are key modulators of the gel-liquid transition in coarse grained simulations of DPPC and DOPC lipid bilayers. Biochem. Biophys. Res. Commun. 2018, 498, 327–333. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Chao, Y. Multifunctional quantum dots and liposome complexes in drug delivery. J. Biomed. Res. 2018, 32, 91. [Google Scholar]
- Park, S.H.; Oh, S.G.; Mun, J.Y.; Han, S.S. Loading of gold nanoparticles inside the DPPC bilayers of liposome and their effects on membrane fluidities. Colloids Surf. B Biointerfaces 2006, 48, 112–118. [Google Scholar] [CrossRef]
- Park, S.H.; Oh, S.G.; Mun, J.Y.; Han, S.S. Effects of silver nanoparticles on the fluidity of bilayer in phospholipid liposome. Colloids Surf. B Biointerfaces 2005, 44, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Rallabandi, B.; Oppenheimer, N.; Ben Zion, M.Y.; Stone, H.A. Membrane-induced hydroelastic migration of a particle surfing its own wave. Nat. Phys. 2018, 14, 1211–1215. [Google Scholar] [CrossRef]
- Saffman, P.; Delbrück, M. Brownian motion in biological membranes. Proc. Nat. Acad. Sci. USA 1975, 72, 3111–3113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haines, T.H. Water transport across biological membranes. FEBS Lett. 1994, 346, 115–122. [Google Scholar] [CrossRef] [Green Version]
- Gardner, J.M.; Deserno, M.; Abrams, C.F. Effect of intrinsic curvature and edge tension on the stability of binary mixed-membrane three-junctions. J. Chem. Phys. 2016, 145, 074901. [Google Scholar] [CrossRef]
- Noguchi, H. Line tension of branching junctions of bilayer membranes. Soft Matter 2012, 8, 3146–3153. [Google Scholar] [CrossRef] [Green Version]
- Vukovic, S.; Brennan, P.E.; Huggins, D.J. Exploring the role of water in molecular recognition: Predicting protein ligandability using a combinatorial search of surface hydration sites. J. Phys. Condens. Matter. 2016, 28, 344007. [Google Scholar] [CrossRef]
- Das, N.; Kumar, A.; Kumar Roy, S.; Kumar Satija, N.; Raja Gopal, R. Bare plasmonic metal nanoparticles: Synthesis, characterisation and in vitro toxicity assessment on a liver carcinoma cell line. IET Nanobiotechnol. 2020, 14, 851–857. [Google Scholar] [CrossRef]


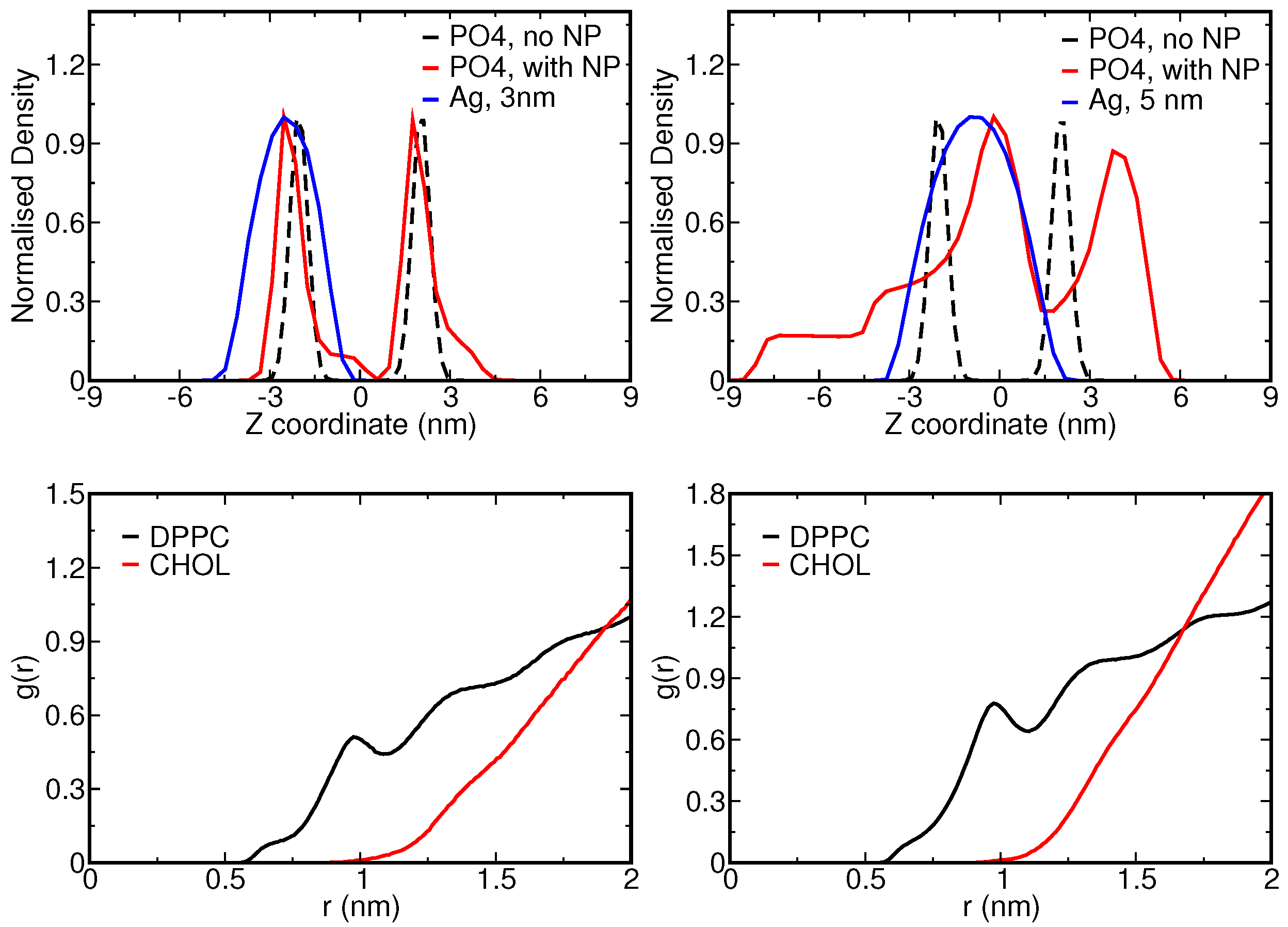

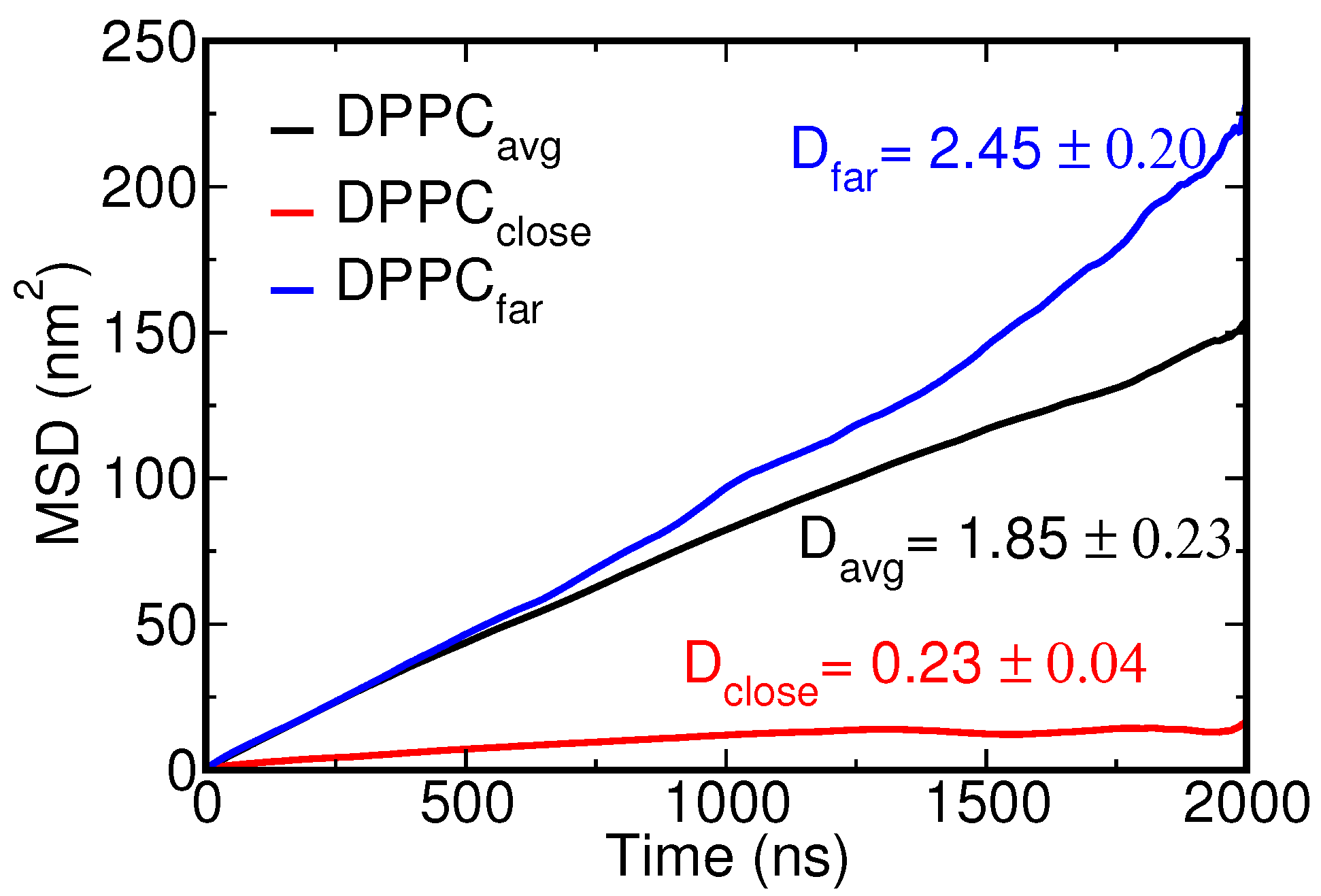


| NP Size (nm) | Bead Type (S-C) | ||||
|---|---|---|---|---|---|
| No NP | - | 3.00 ± 0.00 | 3.26 ± 0.35 | 3.44 ± 0.01 | 3.10 ± 0.03 |
| C2-C2 | 2.97 ± 0.70 | 3.24 ± 0.00 | 4.05 ± 0.24 | 3.29 ± 0.01 | |
| 3 | C5-C5 | 2.28 ± 0.12 | 2.32 ± 0.26 | 2.24 ± 0.61 | 2.49 ± 0.37 |
| C2-C5 | 5.80 ± 0.02 | 5.00 ± 0.43 | 5.65 ± 0.30 | 5.83 ± 0.90 | |
| C2-C2 | 2.23 ± 0.50 | 2.31 ± 0.90 | 2.62 ± 0.24 | 2.25 ± 0.30 | |
| 5 | C5-C5 | 3.04 ± 0.14 | 3.11 ± 0.11 | 3.00 ± 0.10 | 2.44 ± 0.22 |
| C2-C5 | 1.85 ± 0.23 | 2.03 ± 0.28 | 1.94 ± 0.23 | 1.94 ± 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singhal, A.; Sevink, G.J.A. A Core-Shell Approach for Systematically Coarsening Nanoparticle–Membrane Interactions: Application to Silver Nanoparticles. Nanomaterials 2022, 12, 3859. https://doi.org/10.3390/nano12213859
Singhal A, Sevink GJA. A Core-Shell Approach for Systematically Coarsening Nanoparticle–Membrane Interactions: Application to Silver Nanoparticles. Nanomaterials. 2022; 12(21):3859. https://doi.org/10.3390/nano12213859
Chicago/Turabian StyleSinghal, Ankush, and G. J. Agur Sevink. 2022. "A Core-Shell Approach for Systematically Coarsening Nanoparticle–Membrane Interactions: Application to Silver Nanoparticles" Nanomaterials 12, no. 21: 3859. https://doi.org/10.3390/nano12213859





