3.1. Materials and Characterization
In this work, three different materials were synthesized, starting with a polymerized silicate base that was subsequently transformed with different processes.
The first material, called GSLP, was white and semi-translucent. Two types of pellets were obtained using the conditions described in
Section 2.3. The largest pellets were 3 mm in diameter and 1 mm in thickness, with a powdery external aspect. This size was chosen for comparison with a similar material studied in a previous work, as pellets of that material had the same size. The code D3 was assigned to this pellet size. The smaller pellets were 2 mm in diameter and 1 mm in thickness and had a less powdery aspect. The code D2 was assigned to this pellet size. This size was chosen because it was smaller and, consequently, had a larger surface/volume ratio, and it could also be easily synthesized and handled. The purpose of this smaller size was to evaluate if Cr(VI) removal was increased with the reduction in the pellet size.
SEM and EDS analyses were performed for both GSLP sizes. The D3 pellets had a roughened surface and NaCl deposits could be seen on the silicate surface. NaCl is a by-product of the reaction between Na2SiO3 and HCl. The D2 pellets had a much smoother surface than the D3 pellets. NaCl was not found in deposits on the silicate surface but was spread evenly over the surface.
Chromium removal was not observed when GSLP was used in the sorption studies. This is discussed in more detail in
Section 3.3.3. Due to this fact, the GSLP was transformed by the addition of Fe(II). The new material, named GSLP-Fe, had a reddish-brown surface, and the D3 pellets no longer had a powdery aspect. SEM and EDS analyses showed that there was no NaCl on the pellet surfaces, so it was concluded that it was dissolved in the Fe(II) solution used in the synthesis. No major differences between the two pellet sizes were observed.
Figure 1 shows the SEM image of the GSLP-Fe and the EDS maps corresponding to the image as an example. In the SEM image, it can be seen that the material surface is nanostructured. The EDS maps indicate a greater presence of Fe in the areas where these formations are located. These nanostructures were not observed in the SEM images of the GSLP, which indicated that they were formed during the treatment of GSLP with the Fe(II) solution. The formations were responsible for the high BET surface of the material. These nanostructures were stable after the functionalization of the material and its subsequent use in the decontamination process since, as discussed later in this section, the area of the surface remained almost constant throughout the mentioned processes.
The surface of the GSLP-Fe was studied to determine the size of these structures present on it. The SEM images were analyzed using an image processing and analysis program called ImageJ [
21].
Figure 2 shows the histogram obtained from these analyses. Most of the particle diameters were between 100 and 200 nm. The mean particle diameter was 254 nm, with a standard deviation of 142 nm. The normal distribution curve indicated that 99% of the particle diameters were between 0 and 680 nm.
GSLP-Fe can remove Cr(VI) through adsorption, as discussed in
Section 3.3.3. However, a second transformation of the material was performed using a eucalyptus extract as a reductant agent to increase the material removal capacity. The resulting material, GSLP-Fe(0), had a black surface. The other characteristics of the pellets remained unchanged from those of GSLP-Fe. SEM and EDS analyses also showed no significant changes compared to the GSLP-Fe analyses. There were also no significant differences between the two pellet sizes. This indicated that the eucalyptus extract only changed the oxidation state of iron, black being the characteristic color of Fe(0). In
Section 2.2. it was stated that eucalyptus extract has reducing properties. During the Cr(VI) removal experiments, evidence of the change in the oxidation state of iron was also found. GSLP-Fe(0) could reduce Cr(VI) to Cr(III). This reduction was not observed when GSLP-Fe was used (see
Section 3.3.3 and
Section 3.3.4).
Thermogravimetric analyses (TGAs) were performed to check whether organic matter was adsorbed on the material during the treatment with the eucalyptus extract. GSLP-Fe(0) pellets (D3 and D2) and GSLP-Fe pellets (D3 and D2) were analyzed in the presence of air. The TGAs performed with both pellet sizes were very similar.
Figure 3 shows the TGAs of GSLP-Fe(0) and GSLP-Fe D3 as examples. All TGA graphs presented a slope indicative of multi-step decomposition. All TGAs indicated a very similar mass loss (3.5–4%) from 25 to 168 °C. This mass was associated with water loss. Between 170 °C and 400 °C, a clear difference could be seen in the slopes of the TGAs. In the GSLP-Fe(0) TGA, a mass loss of 2.5–2.8% appeared, while in the GSLP-Fe TGA, no clear mass loss was observed in this temperature range. This confirmed that, during the treatment with the eucalyptus extract, a small amount of biomass was adsorbed on the material.
The gases emitted during the TGAs were analyzed to corroborate this hypothesis. The IR spectra of the four samples at a temperature of ca. 98 °C had signals from 4000 to 3500 cm−1 corresponding to O–H stretching. Signals corresponding to O–H bending appear at 1550–1300 cm−1. These signals confirmed that the mass loss between 25 and 168 °C corresponded to water loss.
In the GSLP-Fe(0) IR spectra at approximately 260 °C, intense signals appeared at 2400–2300 cm
−1 corresponding to O=C=O stretching of CO
2. These signals proved that, at this temperature, the organic matter adsorbed during the eucalyptus extract treatment was removed from the GSLP-Fe(0) [
22,
23].
N
2 sorption tests were performed using GSLP-Fe (D3 and D2), GSLP-Fe(0) (D3 and D2), and GSLP-Fe(0) after the Cr(VI) elimination, subsequent chromium desorption, and Fe(0) regeneration. The experimental data conformed to the type-four isotherm among those described by Brunauer et al. [
24,
25]. BET surfaces between 132 and 145 m
2∙g
−1 were found. Pore size distribution (PSD) was calculated with the Barrett–Joyner–Halenda (BJH) method. The results showed a large contribution from macropores.
Figure 4 shows the BET and PSD for raw GSLP-Fe(0) D2 and the same material after chromium desorption and Fe(0) regeneration as an example. The results of all tests are summarized in
Table 1. As can be seen, the smaller pellets had larger adsorption surfaces areas. Furthermore, it was remarkable that the new and regenerated GSLP-Fe(0) had almost identical surface areas, which indicates that the material could be used and regenerated without the loss of the nanostructures present on the surface of the material.
3.1.1. GSLP Synthesis Optimization
GSLP synthesis was optimized by varying the dose of HCl used for the polymerization of the Na2SiO3–Ludox mixture for both pellet sizes. For the tests, several batches of GSLP were synthesized and subjected to the complete process of functionalization with iron, eucalyptus reduction, and Cr(VI) removal. Each test was performed in triplicate. The optimal HCl dose was chosen based on Cr(VI) removal, reproducibility, and material properties (hardness, mechanical strength, and stability in the decontamination medium). For the D3 pellets, 120 µL of 4M HCl provided very low deviation in the three trials. Higher HCl doses decreased the reproducibility, and stability problems began to appear. For the D2 pellets, a 75 µL dose of 4M HCl was used because this dose achieved the highest Cr(VI) removal with the lowest deviation.
3.1.2. Characterization of the Iron Adsorbed on GSLP-Fe
Previous studies have analyzed similar materials to the ones employed in this study using XPS. It was found that, when Fe(II) was adsorbed on the surface of an acid polymerized silicate material, rapid oxidation of Fe(II) to Fe(III) took place. After this process, the Fe present in the material was mainly Fe(III), with a small proportion of Fe(II) [
26].
An adsorption experiment involving Fe(II) on GSLP was conducted in an inert atmosphere (N2) to corroborate this hypothesis. As long as the inert atmosphere was maintained, Fe(II) adsorption occurred as usual, and the surfaces of the pellets turned from white to blue instead of the reddish-brown color characteristic of GSLP-Fe. When the inert atmosphere was removed, the surfaces of the pellets changed from blue to reddish-brown within a few hours. The color change from white to reddish-brown that took place in the normal experiments proved that very fast Fe(II) oxidation occurred on the surface of the pellets.
Despite the oxidation of Fe(II) to Fe(III), it was preferable to use an Fe(II) solution to synthetize the GSLP-Fe. When using an Fe(III) solution, the iron sorption on the material was very limited, as the natural pH of the solution was very acidic, around pH 2.5. Using Fe(II) for the synthesis allowed the material to be prepared without modifying the pH of the medium, which meant lower production costs and less preparation time.
Using an Fe(0) suspension on GSLP to directly synthesize GSLP-Fe(0) was also not viable. Fe(0) could be deposited on GSLP. However, when the material was immersed in the acidic Cr(VI) solution, the Fe(0) was released very quickly into the solution.
3.1.3. Stability of the Synthesized Materials
The stability of the materials was evaluated under the pH conditions used in the kinetic and equilibrium studies.
All materials were inert in deionized water. After one week immersed in deionized water, the pellets released less than 1% of the adsorbed iron. The materials were also mechanically resistant. Pellets withstood stirring at 200 RPM in an orbital shaker for several days without apparent degradation.
The stability of each material was significantly different at acidic pH (pH ca. 1). The stability of GSLP was similar as that in deionized water, with no apparent degradation after several days. GSLP-Fe underwent a very slow Fe(III) desorption process at pH levels between 1 and 2, taking more than a week reach completion. The stability of GSLP-Fe(0) was much better than that of GSLP-Fe in acidic media due to the organic matter adsorbed during the treatment with the eucalyptus extract, which acted as a capping agent. GSLP-Fe(0) endured 3–4 days at pH ≥ 1 without releasing Fe(III). The degradation was accelerated at pH < 1, although the material could withstand more than 72 h at pH ≈ 0.8 without degrading.
Analyses undertaken with aqueous eucalyptus extracts showed that there was a wide variety of compounds in their composition, such as 1,8-cineole, pinene, and eucalyptol, among many others [
27,
28]. The Folin–Ciocalteu method revealed a considerable number of polyphenols among these compounds. By measuring the DPPH radical scavenging capacity, the compounds present in the extract were found to demonstrate important antioxidant activity [
29,
30]. This explained the performance of the organic matter adsorbed on GSLP-Fe(0) as a capping agent.
A fast iron release was observed for both GSLP-Fe and GSLP-Fe(0) when these materials were immersed in strong acids, such as concentrated H2SO4 or HNO3. The degradation was so fast that most of the iron was stripped from both materials within 12 h (H2SO4 at pH ≈ 1) or 24 h (concentrated HNO3).
3.2. Kinetic Studies
Kinetic studies were conducted to describe the kinetic processes involved in the Fe(II) adsorption and Cr(VI) removal. For the Cr(VI) removal, experiments were performed to check if the pH and adsorbate concentration influenced the reaction rate.
The rate of adsorption of Fe(II) by GSLP was fast for both pellet sizes (D3 and D2). Eighty percent of the reaction took place in the first 2.5 h, and equilibrium was reached in about 7 h. Cr(VI) elimination was slower. With the faster kinetics (D2 pellets, pH ≈ 0.8), the equilibrium was reached in about 24 h, while with the slower kinetics, the reaction continued to progress after 72 h. With the slower kinetics, 80% of the reaction was exceeded in 24 h.
3.2.1. Kinetic Models
Two diffusion models were applied to describe the experimental data, the Webber and Morris model [
31] and the Boyd model [
32].
To determine the rate controlling step of reactions, sorption processes can be described in three stages: diffusion from the solution to the adsorbent (bulk diffusion), diffusion from the film to the adsorbent surface (film diffusion), and diffusion through the adsorbent particles (intraparticle diffusion). For a reduction process, the stages are similar, with the last stage being diffusion through the reductant particles. Bulk diffusion is minimal with efficient stirring. Therefore, this process rate is usually governed by intraparticle or film diffusion.
The Webber and Morris model is a simple model that is easy to apply using the following equation:
where q
t is the metal amount adsorbed (mg·g
−1) at time t (h), and k
i is the intraparticle constant (mg·g
−1·h
−½). This model was applied to test if the diffusion model fit the experimental data.
The Boyd model was used to study the mechanism in more detail. The Boyd model describes particle diffusion with the following equation:
where F is the fraction of metal removed at time t, defined by the following expression:
where q
t is the amount of metal removed at time t and q is the amount of metal removed at the equilibrium. The Boyd model also defines a time constant B, given by:
where D
i is the effective diffusion coefficient of the metal in the solid phase (sorbent or reductant in this case) (cm
2·h
−1) and r is the radius of the solid particle (cm).
The Boyd model can also be applied by performing a linearization of Equation (2). Reichenberg [
33] explains that, at sufficiently high values of F, only one term of the series needs to be used. When this is applied and B is substituted into Equation (2), the following expression is obtained:
This equation gives small error values for Bt when F ≈ 1, but it provides large error values at low F values, increasing to − 0.4977 when F = 0. To correct this, for the lower range of values of F (F < 0.86), Equation (5) is transformed into:
which minimize the error for F at low values [
33].
The linearized Boyd model provides useful information. If the fitting of Bt vs. t is a straight line that crosses through the origin, particle diffusion is considered the limiting step. If a straight line is obtained that does not pass through the origin, the process is governed by film diffusion.
3.2.2. Iron Sorption Kinetics
Figure 5a shows the fitting data according to the Webber and Morris model. The parameters obtained from the fitting are summarized in
Table 2 together with their associated errors. As can be seen, the model describes the data obtained in the kinetics quite well. This indicates that the adsorption of Fe(II) is a diffusion-governed process.
As mentioned in the previous section, the Boyd model was used to study the process in more detail. The nonlinear model (Equation (2) with Equations (3) and (4) substituted) was applied to the experimental data with good results. The model correctly described the experimental data, obtaining R2 values of 0.996–0.997.
The linear Boyd model was used to determine the limiting step.
Figure 5b shows the Bt vs. t fitting with the Bt data obtained from Equations (5) and (6).
Table 2 shows the values acquired for the intercept obtained from the fitting. The value of the intercept and its error for GSLP D2 included the origin of coordinates, so particle diffusion was considered the limiting step. For GSLP D3, Student’s t-test was used to determine whether the intercept was statistically 0. In this case, at 95% confidence, the ordinate was not statistically 0, although it was at 99%, so it was concluded that the process was governed by both particle and film diffusion.
3.2.3. Chromium Removal Kinetics
The Webber and Morris model was first used to study Cr(VI) removal kinetics. Using this model, two different linear trends could be observed with a nonlinear zone between them. This distribution of the experimental points was consistent with the structure in two different steps of the Cr(VI) removal process using GSLP-Fe(0). As explained in
Section 3.3.4, the Cr(VI) removal process using GSLP-Fe(0) consisted of two steps: reduction of Cr(VI) to Cr(III) and adsorption of both species onto the material. The first linear trend appeared during the first three hours for all kinetics performed. In this part of the process, reduction of Cr(VI) to Cr(III) predominated. The second linear trend began after 7 h of reaction for kinetics lasting longer than 24 h. In this part, the predominant process was the chromium adsorption. Between the two linear trends, a nonlinear zone appeared in which neither of the two processes predominated over the other. In the case of the fastest kinetics, where equilibrium was reached in about 24 h, this nonlinear zone was not observed because the reaction was faster.
The parameters of the fitting of both trends can be seen in
Table 2. For the linear trends corresponding to the reduction step, straight lines with r 0.979–0.999 were obtained. For the adsorption step, straight lines with good r (0.964–0.996) were also obtained. These results indicate that the Cr(VI) removal process was governed by diffusion.
The nonlinear Boyd model showed worse fittings for Cr(VI) removal kinetics than those obtained for Fe(II) sorption. The model fit the beginning of the kinetics well but did not correctly describe the trend of the slower kinetics where the reaction proceeded slowly and did not reach a plateau (
Figure 6a,b). R
2 values from 0.917 to 0.986 were obtained.
The linearized Boyd model was applied to each linear trend separately (
Figure 7,
Table 2). Straight lines with r 0.972–0.998 in the reduction step and 0.959–0.999 in the adsorption step were obtained. Intercepts were studied using Student’s
t-test. For the kinetics at pH 0.8, the ordinates were statistically 0 at 95% confidence, except for the kinetics of D2 at c
i 50 mg·L
−1 (
♦), which departed from 0 by a very small amount. For the two kinetics at pH 1.2, the ordinate was not statistically 0. From these data, it was concluded that, at pH 0.8, particle diffusion was the limiting step in the reduction stage. At pH 1.2, the lower proton concentration may have caused the reduction to be less dominant, so simultaneous processes affecting the intercept could have been present. In the adsorption step, the ordinates were not close to being statistically 0, except for the D2 c
i 75 mg·L
−1 kinetics (
▼). From these data, it was concluded that the adsorption step was governed by film diffusion.
After analyzing all the data, no clear influence from the initial Cr(VI) concentration on the kinetics was observed. However, pH influence was clearly observed. At pH 0.8, the reaction equilibrium was reached using GSLP-Fe(0) D2, although the Cr(VI) removal was slightly higher at pH 1.2. Since equilibrium was reached at pH 0.8 using GSLP-Fe(0) D2, to compare both pellet sizes under the same conditions, pH 0.8 and 24 h reaction time were chosen as the conditions for the elimination studies.
3.3. Equilibria Studies
3.3.1. Isotherm Models
Two isotherm models were used for the analysis of equilibrium experiments, the Langmuir–Freundlich model and a statistical thermodynamic-based model described by Sellaoui et al. [
34]. This model is very versatile, and it can be adapted to multiple types of adsorptions (monolayer, multilayer, simple, binary, etc.).
The Langmuir–Freundlich model is one of the most widely used models in adsorption studies:
where q is the amount of metal adsorbed at equilibrium, c is the metal concentration in solution at equilibrium, Q
0 is the maximum adsorption capacity, b is an affinity parameter (high b values indicate a steep beginning in the isotherm, which reflects the high affinity of the sorbent for the sorbate), and n is a parameter related to surface heterogeneity.
The Sellaoui model based on statistical thermodynamics is used under the condition of monolayer adsorption:
where q is the metal amount adsorbed at equilibrium, Q
0 is the maximum adsorption capacity, c is the metal concentration in solution at equilibrium, c
½ is the concentration at half saturation of the sorbent, and m is the number of atoms per adsorption site.
Sellaoui also describes the relationship between the concentration at half saturation and the adsorption energy with the following equation [
35]:
where c
s is the solubility of the adsorbate.
3.3.2. Iron Sorption on GSLP
The Fe(II) adsorption studies were conducted at natural pH (
ca. pH 5). Previous studies using a similar polymeric base have shown this to be the simplest and most effective condition for this process [
26]. With this condition, high adsorption is achieved, iron precipitation as hydroxide is avoided, and no time is wasted with pH modifications.
The plots of the adsorption equilibria fitted with Equations (7) and (8) were identical. Therefore, only one fit (Equation (8)) is shown in this article. A figure showing the experimental data fitted with Equation (7) can be found in the
Supplementary Materials (Figure S24).
Figure 8 shows the experimental data fitted with Equation (8). The parameters obtained from the fits are summarized with their associated errors in
Table 3. As can be seen, both models gave the same values for Q
0. Moreover, b and n are the reciprocals of c
½ and m, respectively. The adsorption energy could be calculated with Equation (9) and the parameter c
½ obtained with Equation (8). The results obtained show the high affinity that GSLP had for Fe(II). This fact was reflected by the almost vertical slope before the plateau in the isotherm, the high values of the parameter b, and the high adsorption energy. Smaller pellets (D2) adsorbed more Fe(II) when comparing the two pellet sizes due to the larger surface area exposed.
The amount of Fe adsorbed on GSLP was confirmed by desorption. A 0.25 M HCl solution was used because it caused complete stripping of the iron present in the pellets but did not alter its oxidation state. An aliquot was also taken from the stripping solution and treated with a reduction procedure to transform any Fe(III) to Fe(II) before measuring the iron in solution. Values of 13.6 ± 0.7 mg Fe·g
−1 GSLP for D3 pellets and 16.0 ± 0.1 mg Fe·g
−1 GSLP for D2 pellets were found, which were consistent with the Q
0 values obtained with Equations (7) and (8) (
Table 3).
3.3.3. Cr(VI) Sorption on GSLP and GSLP-Fe
Cr(VI) adsorption studies were performed using GSLP and GSLP-Fe, as the use of GSLP-Fe(0) adds a reduction step to the process.
No evidence of Cr(VI) adsorption was observed using GSLP as adsorbent. In the colorimetric measurements, values close to 0 were obtained, which varied randomly as the concentration was increased. In the SEM and EDS analyses of the GSLP used in this process, no chromium signals were found. The results show that GSLP only worked as a support for iron and was not involved in the Cr(VI) removal process. The iron present in GSLP-Fe and GSLP-Fe(0) was the species that acted as a Cr(VI) remover. Further information on chromium sorption on GSLP can be found in the
Supplementary Materials (Figures S25–S27).
Cr(VI) sorption was observed when GSLP-Fe was used as adsorbent.
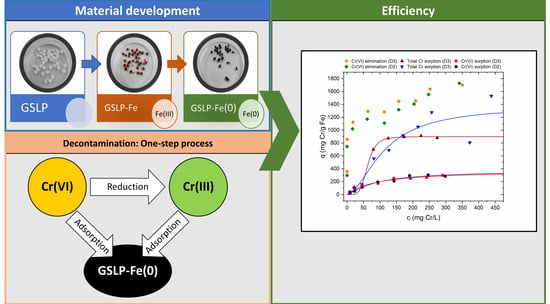
Figure 9a shows the Cr(VI) removal percentages achieved using GSLP-Fe with respect to the initial Cr(VI) concentration.
Figure 9b shows the data in isotherm form, fitted by Equation (8) (data fitted by Equation (7) can be found in the
Supplementary Materials (Figure S28)). The parameter values of the fits and their errors are listed in
Table 3, along with the R
2 values. Again, the Q
0 value was almost equal for both fittings. In this case, the errors in the parameters Q
0, b, and c
½ were higher than in the Fe(II) adsorption experiments since the saturation region of the isotherm was not reached. The errors in n and m were small because the slope of the isotherm was well-defined. The adsorption energy of Cr(VI) on GSLP-Fe was lower than the adsorption energy of iron on GSLP. This indicated that Cr(VI) did not displace the adsorbed iron, which is in concordance with the experimental data, where no iron desorption was observed.
3.3.4. Chromium Removal by GSLP-Fe(0)
When GSLP-Fe(0) was used to remove Cr(VI), it was observed that, at the end of the process, Cr(III) appeared in the reaction medium. When GSLP-Fe was used, no Cr(III) appeared at the end of the process. This confirmed that treatment with eucalyptus extract reduced Fe(III) to Fe(0), which was consistent with the properties of the extract described in
Section 2.2. Furthermore, after the first hours of reaction, GSLP-Fe(0) lost its characteristic black color and recovered the red color that is characteristic of GSLP-Fe. Therefore, the process that occurred during the treatment with eucalyptus extract was a reversible process. The following reaction is proposed:
This reaction requires a large number of protons, which explains why the largest eliminations occurred at very acidic pH.
When using GSLP-Fe(0) at higher pH, neither Cr(VI) reduction nor Cr(VI) adsorption were observed. However, when GSLP-Fe was used at the same pH, Cr(VI) adsorption was observed. This indicates that Cr(VI) adsorption occurred on Fe(III) but not on Fe(0). Therefore, in the Cr(VI) removal process with GSLP-Fe(0) at acidic pH, the adsorption did not start until Fe(0) was oxidized to Fe(III) in the reduction step.
Figure 9a shows the Cr(VI) removal percentages using GSLP-Fe(0) with respect to the initial Cr(VI) concentration.
Figure 9b shows the data in isotherm form without fitting, as this was not a pure adsorption process. One hundred percent removals of Cr(VI) were achieved up to concentrations of 25 mg·L
−1 using GSLP-Fe(0) with a low material dose (2 g·L
−1). The maximum Cr(VI) removal values were remarkably high (1.7 g Cr(VI)·g
−1 Fe).
Table 4 shows the removal efficiency of GSLP-Fe(0) compared to other materials and to typical Cr(VI) removers used in industry. Approximately 370 mg was removed by adsorption after 24 h of reaction (
Table 3). Therefore, approximately 1.33 g Cr(VI) was removed by reduction, which implies a ratio 2.86–2 between moles of Cr(VI) and moles of Fe(III), while the theoretical ratio according to Equation (10) is 2–2. There are two main reasons for this.
In the Cr(VI) adsorption experiments, the saturation zone of the isotherm was not reached. This caused a high error in the Q0 parameter, so the Cr(VI) adsorption could have been higher than 370 mg·g−1. In addition, some of the organic matter bound to the iron during the eucalyptus extract may have contributed to the reduction in Cr(VI).
3.3.5. Total Chromium Sorption on GSLP-Fe(0)
As has been shown in the previous sections, adsorption of Cr(VI) on GSLP-Fe(0) was achieved. It has also been shown that, in the Cr(VI) removal process, Cr(III) was generated by reduction. To check if Cr(III) adsorption on GSLP-Fe(0) occurred, experiments were conducted using CrCl3. Cr(III) sorption was studied using plain GSLP-Fe(0) and GSLP-Fe(0) with adsorbed Cr(VI). No adsorption of Cr(III) on plain GSLP-Fe(0) was observed, neither with Fe(0) nor after oxidizing the Fe(0) to Fe(III). Cr(III) adsorption was only observed on GSLP-Fe(0) pellets with adsorbed Cr(VI). This indicates that, during the Cr(VI) removal process, since both species were in the reaction medium, both could be adsorbed.
To study the total adsorption of chromium irrespective of its oxidation state, atomic adsorption measurements (FAAS) were conducted. As can be seen in
Figure 9b, higher adsorption values than the Cr(VI) adsorption values were obtained. The parameters obtained were similar between the two models, and the value of Q
0 was quite high. The errors in the parameters were important in the GSLP-Fe(0) D2 fitting because the saturation region of the isotherm was not well-defined.
In the SEM and EDS analyses of GSLP-Fe(0) after the removal process, chromium signals appeared. The intensity of the Cr(VI) signals was higher in the areas with high Fe(III) content. This confirmed that chromium was adsorbed mainly on the areas where Fe(III) was present and not on the silicate.
In similar removal processes, it was found that there was no influence from ionic strength or temperature on the Cr(VI) removal and total chromium adsorption processes [
26]. This is a clear advantage when using GSLP-Fe(0) as a chromium remover in industrial processes, as the removal is not affected by the salinity or temperature of the effluent.