Indefinite Graphene Nanocavities with Ultra-Compressed Mode Volumes
Abstract
:1. Introduction
2. Theoretical Model
3. Results And Disscussion
3.1. Dispersion and Resonance Conditions
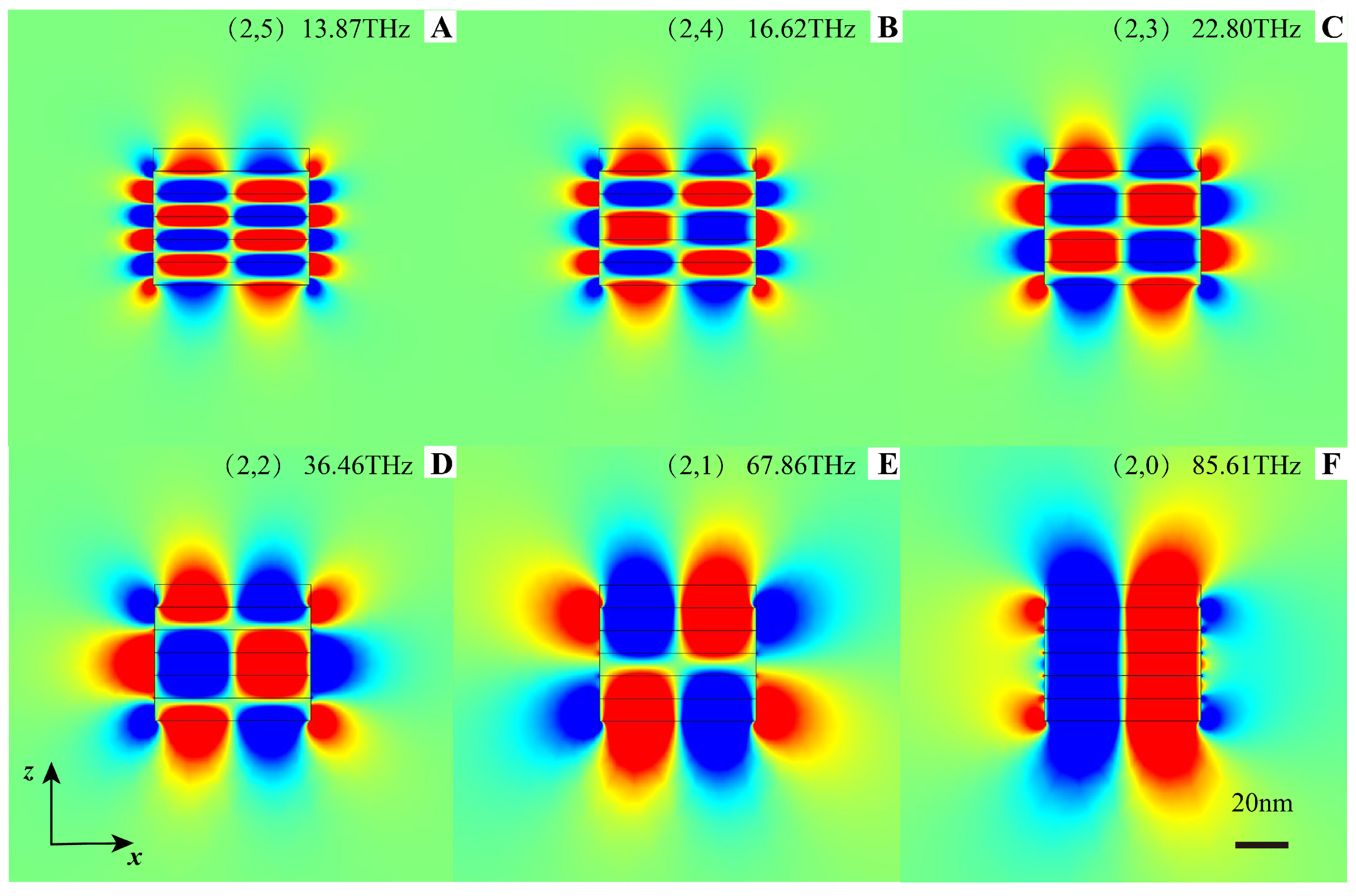
3.2. Anomalous Scaling Rules of Graphene Indefinite Nanocavities
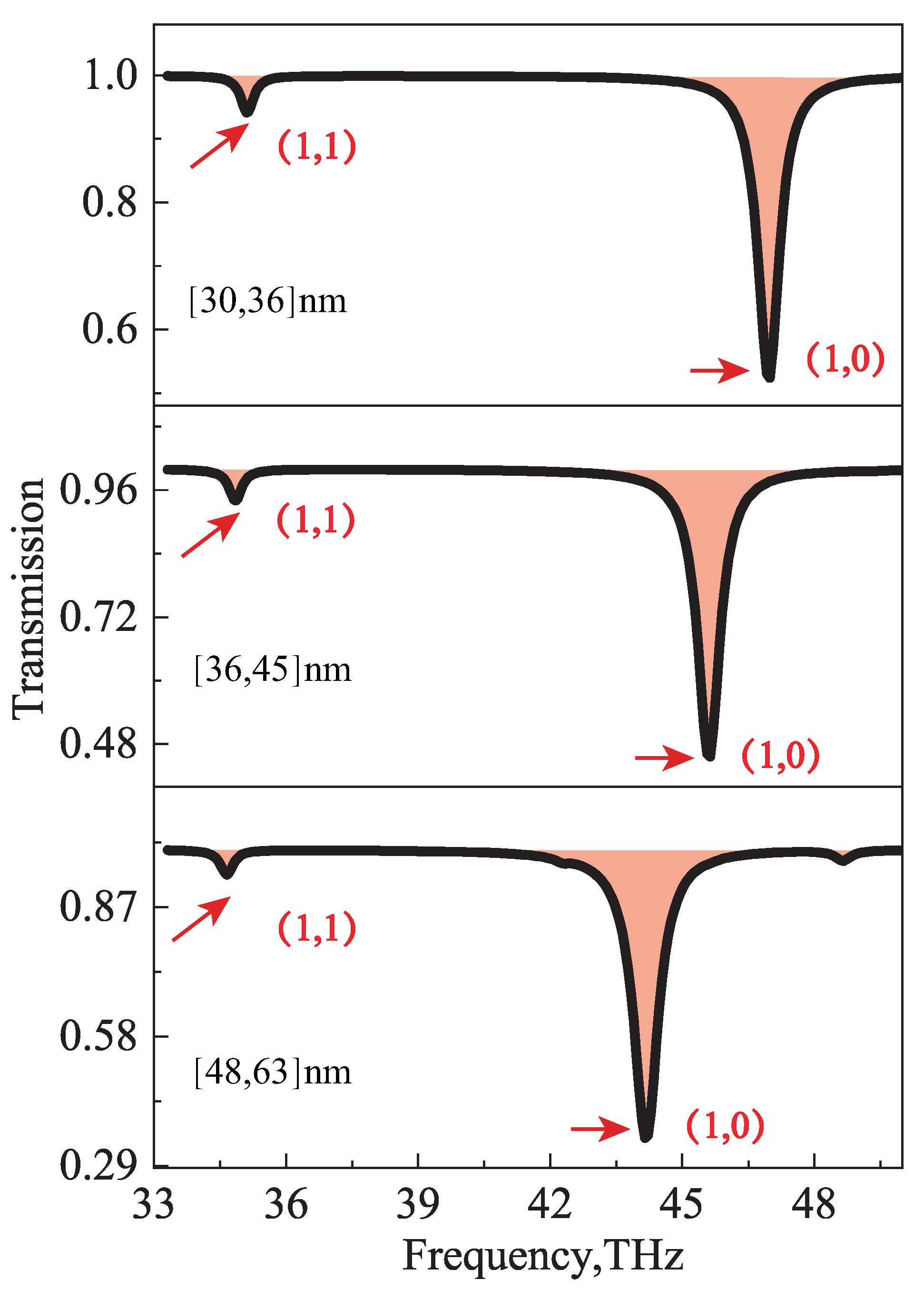
3.3. Far-Field Excitation of Indefinite Graphene Nanocavities
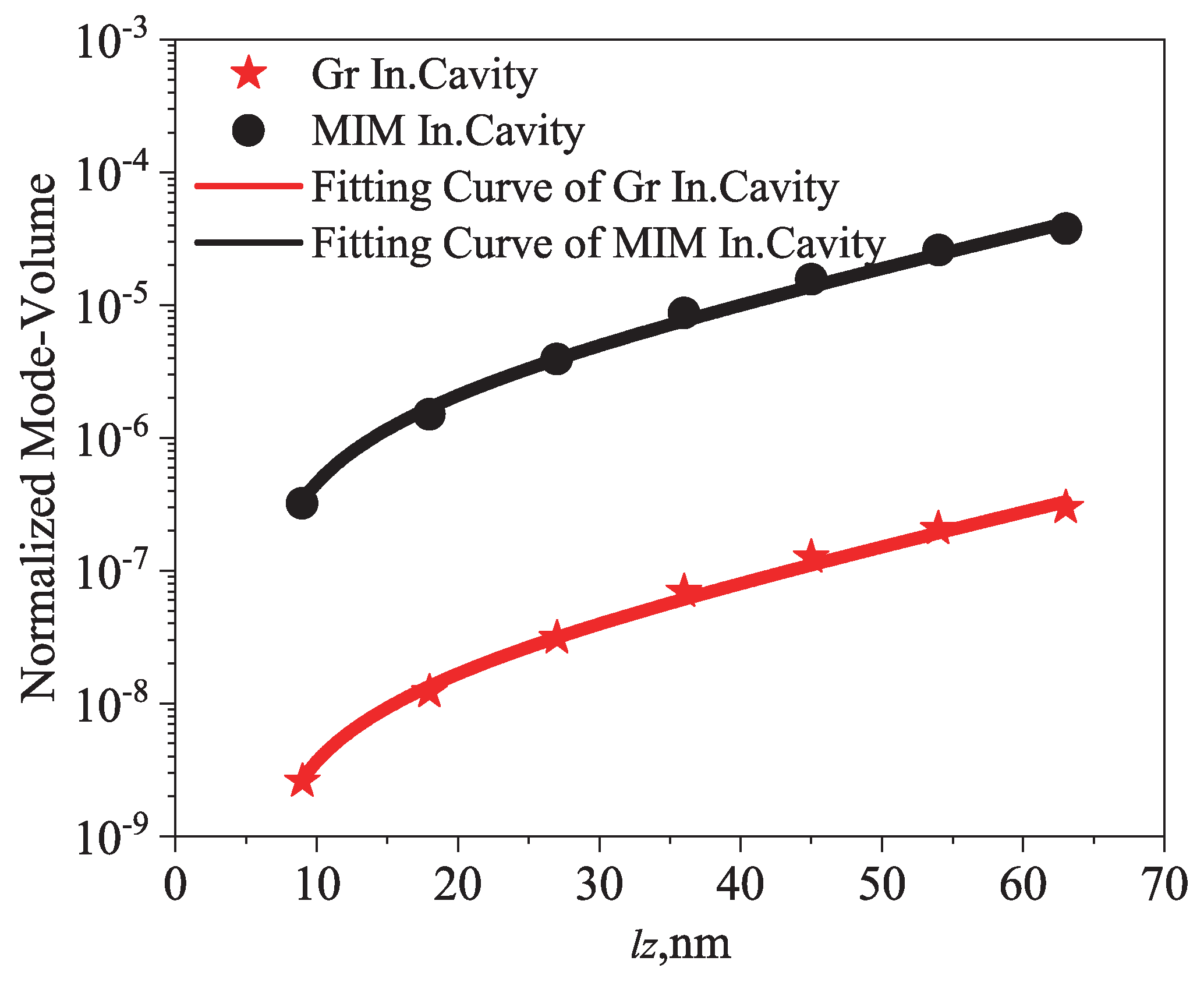
3.4. Ultra-Compressed Mode Volumes of Graphene Indefinite Nanocavities
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Adamo, G.; MacDonald, K.F.; Fu, Y.; Wang, C.; Tsai, D.; De Abajo, F.G.; Zheludev, N. Light well: A tunable free-electron light source on a chip. Phys. Rev. Lett. 2009, 103, 113901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khajavikhan, M.; Simic, A.; Katz, M.; Lee, J.; Slutsky, B.; Mizrahi, A.; Lomakin, V.; Fainman, Y. Thresholdless nanoscale coaxial lasers. Nature 2012, 482, 204–207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kotal, S.; Artioli, A.; Wang, Y.; Osterkryger, A.D.; Finazzer, M.; Fons, R.; Genuist, Y.; Bleuse, J.; Gérard, J.M.; Gregersen, N.; et al. A nanowire optical nanocavity for broadband enhancement of spontaneous emission. Appl. Phys. Lett. 2021, 118, 194002. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, F.; Hou, S.; Zhang, Z.; Chou, Y.H.; Watanabe, K.; Taniguchi, T.; Forrest, S.R.; Deng, H. Van der Waals heterostructure polaritons with moire-induced nonlinearity. Nature 2021, 591, 61. [Google Scholar] [CrossRef] [PubMed]
- Xingqiao, C.; Jianfa, Z.; Chunchao, W.; Ken, L.; Zhihong, Z.; Shiqiao, Q.; Xiaodong, Y. Optical nonlinearity and non-reciprocal transmission of graphene integrated metasurface. Carbon 2021, 173, 126–134. [Google Scholar] [CrossRef]
- Shi, J.; Guo, Q.; Shi, Z.; Zhang, S.; Xu, H. Nonlinear nanophotonics based on surface plasmon polaritons. Appl. Phys. Lett. 2021, 119, 130501. [Google Scholar] [CrossRef]
- Chen, W.; Roelli, P.; Hu, H.; Verlekar, S.; Amirtharaj, S.P.; Barreda, I.A.; Kippenberg, T.J.; Kovylina, M.; Verhagen, E.; Martinez, A.; et al. Continuous-wave frequency upconversion with a molecular optomechanical nanocavity. Science 2021, 374, 1264. [Google Scholar] [CrossRef]
- Favero, I.; Karrai, K. Optomechanics of deformable optical cavities. Nat. Photonics 2009, 3, 201–205. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, W.; He, X.; Wu, S.; Dang, J.; Peng, K.; Song, F.; Yang, L.; Ni, H.; Niu, Z.; et al. Cavity Quantum Electrodynamics with Second-Order Topological Corner State. Laser Photon. Rev. 2020, 14, 1900425. [Google Scholar] [CrossRef]
- He, Z.; Han, Z.; Yuan, J.; Sinyukov, A.M.; Eleuch, H.; Niu, C.; Zhang, Z.; Lou, J.; Hu, J.; Voronine, D.V.; et al. Quantum plasmonic control of trions in a picocavity with monolayer WS2. Sci. Adv. 2019, 5, 8763. [Google Scholar] [CrossRef]
- Li, X.; Tao, L.; Chen, Z.; Fang, H.; Li, X.; Wang, X.; Xu, J.B.; Zhu, H. Graphene and related two-dimensional materials: Structure-property relationships for electronics and optoelectronics. Appl. Phys. Rev. 2017, 4, 021306. [Google Scholar] [CrossRef]
- Gan, X.; Englund, D.; Van Thourhout, D.; Zhao, J. 2D materials-enabled optical modulators: From visible to terahertz spectral range. Appl. Phys. Rev. 2022, 9, 021302. [Google Scholar] [CrossRef]
- Alonso-Gonzalez, P.; Nikitin, A.Y.; Gao, Y.; Woessner, A.; Lundeberg, M.B.; Principi, A.; Forcellini, N.; Yan, W.; Velez, S.; Huber, A.J.; et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 2017, 12, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.H.; Yoo, D.; Avouris, P.; Low, T.; Oh, S.H. Graphene acoustic plasmon resonator for ultrasensitive infrared spectroscopy. Nat. Nanotechnol. 2019, 14, 313. [Google Scholar] [CrossRef]
- Epstein, I.; Alcaraz, D.; Huang, Z.; Pusapati, V.V.; Hugonin, J.P.; Kumar, A.; Deputy, X.M.; Khodkov, T.; Rappoport, T.G.; Hong, J.Y.; et al. Far-field excitation of single graphene plasmon cavities with ultracompressed mode volumes. Science 2020, 368, 1219. [Google Scholar] [CrossRef]
- Wen, C.; Chen, X.; Zhang, J.; Xu, W.; Luo, J.; Zhou, Y.; Zhu, Z.; Qin, S.; Yuan, X. Far-Field Excitation of Acoustic Graphene Plasmons with a Metamaterial Absorber. Adv. Photonics Res. 2021, 2, 2000066. [Google Scholar] [CrossRef]
- Wang, B.; Yu, P.; Wang, W.; Zhang, X.; Kuo, H.C.; Xu, H.; Wang, Z.M. High-Q Plasmonic Resonances: Fundamentals and Applications. Adv. Opt. Mater. 2021, 9, 2001520. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Mishra, Y.K. Toroidal Metaphotonics and Metadevices. Laser Photon. Rev. 2020, 14, 1900326. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Li, P.; Dolado, I.; Javier Alfaro-Mozaz, F.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; Nikitin, A.Y.; Velez, S.; Hillenbrand, R. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 2018, 359, 892. [Google Scholar] [CrossRef]
- Aigner, A.; Dawes, J.M.; Maier, S.A.; Ren, H. Nanophotonics shines light on hyperbolic metamaterials. Light Sci. Appl. 2022, 11, 26. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Diaz, J.S.; Alu, A. Flatland Optics with Hyperbolic Metasurfaces. ACS Photonics 2016, 3, 2211–2224. [Google Scholar] [CrossRef]
- Sun, J.; Litchinitser, N.M.; Zhou, J. Indefinite by Nature: From Ultraviolet to Terahertz. ACS Photonics 2014, 1, 293–303. [Google Scholar] [CrossRef]
- Ferrari, L.; Smalley, J.S.T.; Fainman, Y.; Liu, Z. Hyperbolic metamaterials for dispersion-assisted directional light emission. Nanoscale 2017, 9, 9034–9048. [Google Scholar] [CrossRef] [PubMed]
- Kitur, J.K.; Gu, L.; Tumkur, T.; Bonner, C.; Noginov, M.A. Stimulated Emission of Surface Plasmons on Top of Metamaterials with Hyperbolic Dispersion. ACS Photonics 2015, 2, 1019–1024. [Google Scholar] [CrossRef]
- Wu, X.; McEleney, C.A.; Gonzalez-Jimenez, M.; Macedo, R. Emergent asymmetries and enhancement in the absorption of natural hyperbolic crystals. Optica 2019, 6, 1478–1483. [Google Scholar] [CrossRef]
- Li, J.; Hu, G.; Shi, L.; He, N.; Li, D.; Shang, Q.; Zhang, Q.; Fu, H.; Zhou, L.; Xiong, W.; et al. Full-color enhanced second harmonic generation using rainbow trapping in ultrathin hyperbolic metamaterials. Nat. Commun. 2021, 12, 6425. [Google Scholar] [CrossRef]
- Jin, R.; Xu, Y.; Dong, Z.G.; Liu, Y. Optical Pulling Forces Enabled by Hyperbolic Metamaterials. Nano Lett. 2021, 21, 10431–10437. [Google Scholar] [CrossRef]
- Gelkop, Y.; Di Mei, F.; Frishman, S.; Garcia, Y.; Falsi, L.; Perepelitsa, G.; Conti, C.; DelRe, E.; Agranat, A.J. Hyperbolic optics and superlensing in room-temperature KTN from self-induced k-space topological transitions. Nat. Commun. 2021, 12, 7241. [Google Scholar] [CrossRef]
- Liu, L.; Gao, P.; Liu, K.; Kong, W.; Zhao, Z.; Pu, M.; Wang, C.; Luo, X. Nanofocusing of circularly polarized Bessel-type plasmon polaritons with hyperbolic metamaterials. Mater. Horiz. 2017, 4, 290–296. [Google Scholar] [CrossRef]
- Hu, G.; Krasnok, A.; Mazor, Y.; Qu, C.W.; Alu, A. Moire Hyperbolic Metasurfaces. Nano Lett. 2020, 20, 3217–3224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yali, Z.; Qingdong, O.; Lu, L.; Chunqi, Z.; Ziyu, W.; Youning, G.; Xiang, L.; Yupeng, Z.; Guangwei, H.; Zhilin, Y.; et al. Tailoring Topological Transitions of Anisotropic Polaritons by Interface Engineering in Biaxial Crystals. Nano Lett. 2022, 20, 4260–4268. [Google Scholar] [CrossRef]
- Chen, J.; Lin, X.; Chen, M.; Low, T.; Chen, H.; Dai, S. A perspective of twisted photonic structures. Appl. Phys. Lett. 2021, 119, 240501. [Google Scholar] [CrossRef]
- Passler, N.C.; Ni, X.H.; Hu, G.; Matson, J.R.; Garini, G.; Wolf, M.; Schubert, M.; Alu, A.; Caldwell, J.D.; Folland, T.G.; et al. Hyperbolic shear polaritons in low-symmetry crystals. Nature 2021, 602, 595–600. [Google Scholar] [CrossRef]
- Dasol, L.; Sunae, S.; Guangwei, H.; Minkyung, K.; Trevon, B.; Hanlyun, C.; Jaekyung, K.; Hongyoon, K.; ChengWei, Q.; Junsuk, R. Hyperbolic metamaterials: Fusing artificial structures to natural 2D materials. eLight 2022, 2, 01–23. [Google Scholar] [CrossRef]
- Indukuri, S.R.K.C.; Bar-David, J.; Mazurski, N.; Levy, U. Ultrasmall Mode Volume Hyperbolic Nanocavities for Enhanced Light-Matter Interaction at the Nanoscale. ACS Nano 2019, 13, 11770–11780. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Zheng, S.; Lin, Z.; Jian, S. Nanoscale dielectric-graphene-dielectric tunable infrared waveguide with ultrahigh refractive indices. Opt. Express 2013, 21, 17089–17096. [Google Scholar] [CrossRef]
- Wang, Q.; Hou, L.; Li, C.; Zhou, H.; Gan, X.; Liu, K.; Xiao, F.; Zhao, J. Toward high-performance refractive index sensor using single Au nanoplate-on-mirror nanocavity. Nanoscale 2022, 14, 10773–10779. [Google Scholar] [CrossRef]
- Yao, J.; Yang, X.; Yin, X.; Bartal, G.; Zhang, X. Three-dimensional nanometer-scale optical cavities of indefinite medium. Proc. Acad. Natl. Sci. USA 2011, 108, 11327–11331. [Google Scholar] [CrossRef] [Green Version]
- Bisht, A.; He, W.; Wang, X.; Wu, L.Y.L.; Chen, X.; Li, S. Hyperlensing at NIR frequencies using a hemispherical metallic nanowire lens in a sea-urchin geometry. Nanoscale 2016, 8, 10669–10676. [Google Scholar] [CrossRef]
- Yang, X.; Yao, J.; Rho, J.; Yin, X.; Zhang, X. Experimental realization of three-dimensional indefinite cavities at the nanoscale with anomalous scaling laws. Nat. Photonics 2012, 6, 450–454. [Google Scholar] [CrossRef]
- Yan, R.; Wang, T.; Wang, H.; Yue, X.; Wang, L.; Wang, Y.; Zhang, J. Effective excitation of bulk plasmon-polaritons in hyperbolic metamaterials for high-sensitivity refractive index sensing. J. Mater. Chem. C 2022, 10, 5200–5209. [Google Scholar] [CrossRef]
- Iorsh, I.V.; Mukhin, I.S.; Shadrivov, I.V.; Belov, P.A.; Kivshar, Y.S. Hyperbolic metamaterials based on multilayer graphene structures. Phys. Rev. B 2013, 87, 075416. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.C.; Liu, C.H.; Liu, C.H.; Zhang, S.; Marder, S.R.; Narimanov, E.E.; Zhong, Z.; Norris, T.B. Realization of mid-infrared graphene hyperbolic metamaterials. Nat. Commun. 2016, 7, 10568. [Google Scholar] [CrossRef] [Green Version]
- Dudek, M.; Kowerdziej, R.; Pianelli, A.; Parka, J. Graphene-based tunable hyperbolic microcavity. Sci. Rep. 2021, 11, 74. [Google Scholar] [CrossRef]
- Nong, J.; Tang, L.; Lan, G.; Luo, P.; Li, Z.; Huang, D.; Yi, J.; Shi, H.; Wei, W. Enhanced Graphene Plasmonic Mode Energy for Highly Sensitive Molecular Fingerprint Retrieval. Laser Photon. Rev. 2021, 15, 2000300. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, X.; Wang, Z.; Haidry, A.A.; Yao, Z.; Haque, E.; Wang, Y.; Li, G.; Daeneke, T.; McConville, C.F.; et al. Low dimensional materials for glucose sensing. Nanoscale 2021, 13, 11017–11040. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Ren, B.; Xu, K.; Jeerapan, I.; Chen, H.; Li, Z.; Ou, J.Z. Recent progress in intrinsic and stimulated room-temperature gas sensors enabled by low-dimensional materials. J. Mater. Chem. C 2021, 9, 3026–3051. [Google Scholar] [CrossRef]
- Wen, C.; Luo, J.; Xu, W.; Zhu, Z.; Qin, S.; Zhang, J. Enhanced Molecular Infrared Spectroscopy Employing Bilayer Graphene Acoustic Plasmon Resonator. Biosensors 2021, 11, 431. [Google Scholar] [CrossRef]
- Gowda, P.; Patient, D.A.; Horsley, S.A.R.; Nash, G.R. Toward efficient and tailorable mid-infrared emitters utilizing multilayer graphene. Appl. Phys. Lett. 2022, 120, 051105. [Google Scholar] [CrossRef]
- Falkovsky, L.A. Optical properties of graphene. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2008; Volume 129, p. 012004. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhang, X.; Garcia-Vidal, F.J.; Yuan, X.; Teng, J. Strong Coupling of Surface Plasmon Polaritons in Monolayer Graphene Sheet Arrays. Phys. Rev. Lett. 2012, 109, 073901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sukham, J.; Takayama, O.; Mahmoodi, M.; Sychev, S.; Bogdanov, A.; Tavassoli, S.H.; Lavrinenko, A.V.; Malureanu, R. Investigation of effective media applicability for ultrathin multilayer structures. Nanoscale 2019, 11, 12582–12588. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz Iranzo, D.; Nanot, S.; Dias, E.J.C.; Epstein, I.; Peng, C.; Efetov, D.K.; Lundeberg, M.B.; Parret, R.; Osmond, J.; Hong, J.Y.; et al. Probing the ultimate plasmon confinement limits with a van der Waals heterostructure. Science 2018, 360, 291–295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shuren, H.; Marwan, K.; Rafael, S.M.; Ernst, K.; Sebastian, E.; William, M.J.G.; Sharon, M.W. Experimental realization of deep-subwavelength confinement in dielectric optical resonators. Sci. Adv. 2018, 4, eaat2355. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, C.; Wang, Z.; Xu, J.; Xu, W.; Liu, W.; Zhu, Z.; Zhang, J.; Qin, S. Indefinite Graphene Nanocavities with Ultra-Compressed Mode Volumes. Nanomaterials 2022, 12, 4004. https://doi.org/10.3390/nano12224004
Wen C, Wang Z, Xu J, Xu W, Liu W, Zhu Z, Zhang J, Qin S. Indefinite Graphene Nanocavities with Ultra-Compressed Mode Volumes. Nanomaterials. 2022; 12(22):4004. https://doi.org/10.3390/nano12224004
Chicago/Turabian StyleWen, Chunchao, Zongyang Wang, Jipeng Xu, Wei Xu, Wei Liu, Zhihong Zhu, Jianfa Zhang, and Shiqiao Qin. 2022. "Indefinite Graphene Nanocavities with Ultra-Compressed Mode Volumes" Nanomaterials 12, no. 22: 4004. https://doi.org/10.3390/nano12224004
APA StyleWen, C., Wang, Z., Xu, J., Xu, W., Liu, W., Zhu, Z., Zhang, J., & Qin, S. (2022). Indefinite Graphene Nanocavities with Ultra-Compressed Mode Volumes. Nanomaterials, 12(22), 4004. https://doi.org/10.3390/nano12224004







