Convective Heat Transfer in Magneto-Hydrodynamic Carreau Fluid with Temperature Dependent Viscosity and Thermal Conductivity
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Statement of Problem
2.2. Transformation of Flow Governing Equations
2.3. Drag Coefficient and Nusselt Number
3. Method of Solution
- Formulate the flow governing equation in the presence of body forces with help of
- General Naiver-Stokes and boundary layer approximation. Additionally, utilizing the constitutive relations of Carreau fluid.
- Transform the achieved flow governing equations into ordinary differential equations using suitable similarity transforms.
- Introduce a set of new variables to convert the ordinary set of differential equations into an initial value problem.
- Calculate the initial guesses using Newton’s method and simulate the problem employing shooting method.
- Set the tolerance of numerical solution in MATLAB and Code the whole problem.
- Finally, achieve graphical results for different profiles. Obtain numeric outcomes for shear stress rate and Nusselt number.
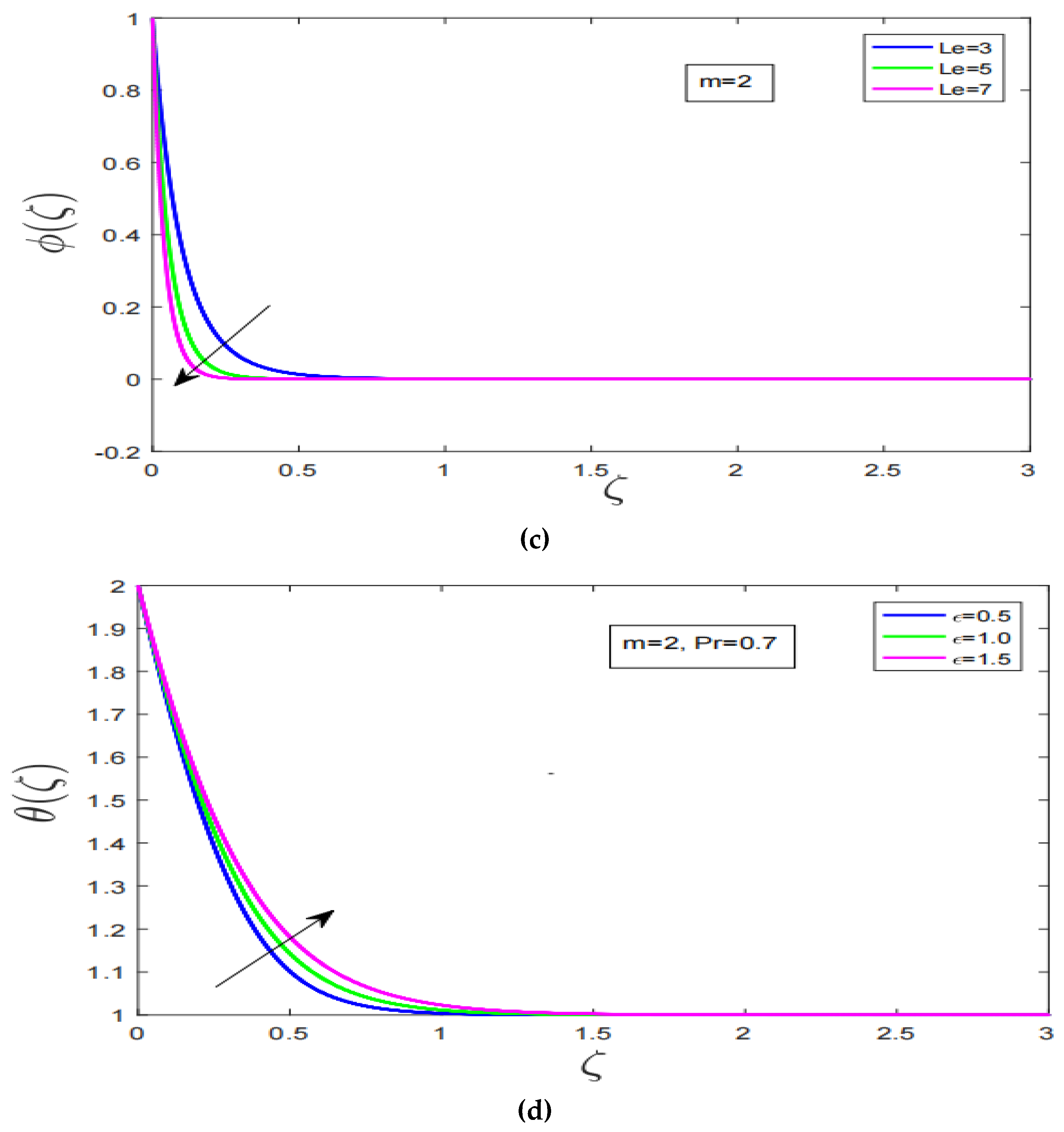
4. Results and Discussion
5. Conclusions
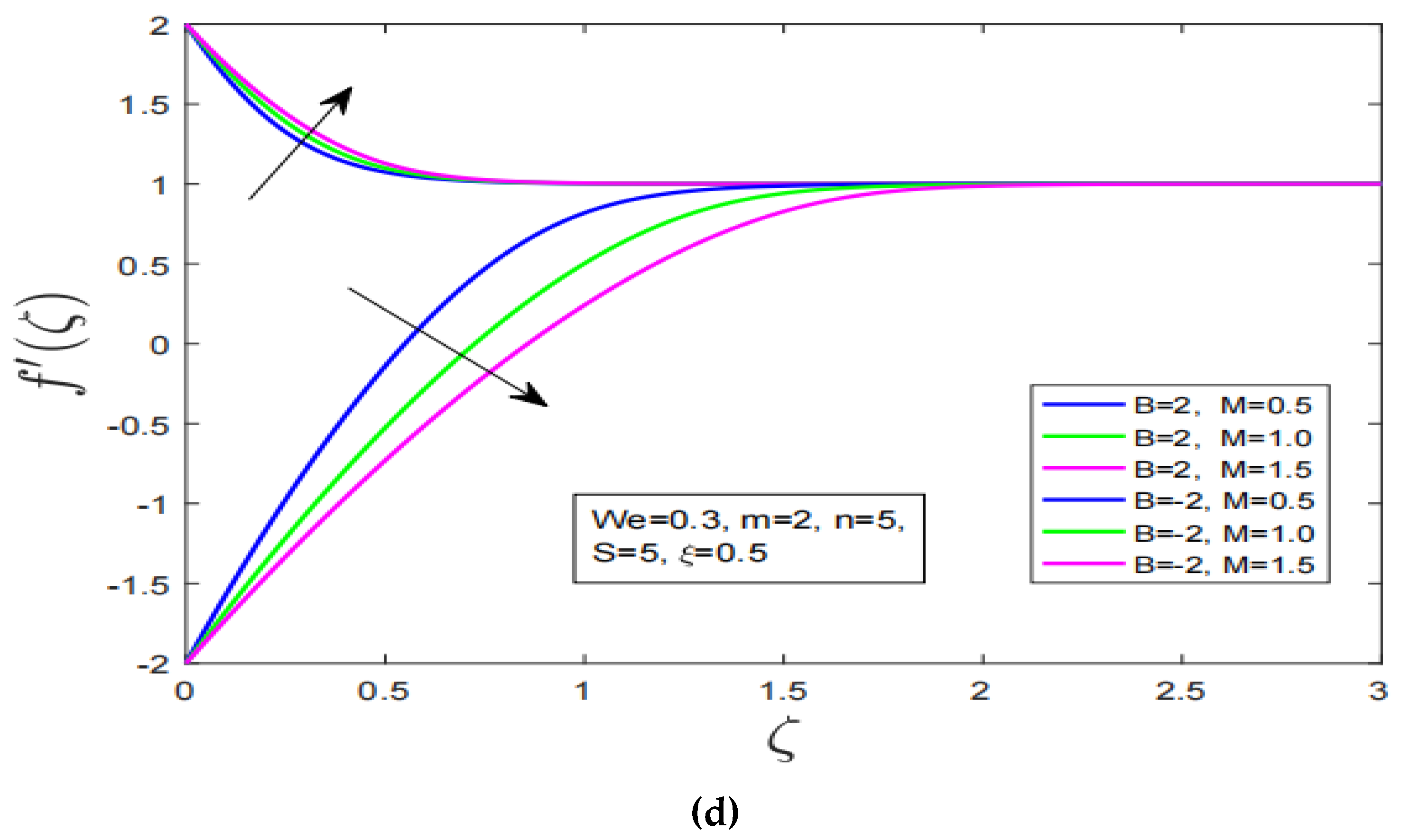
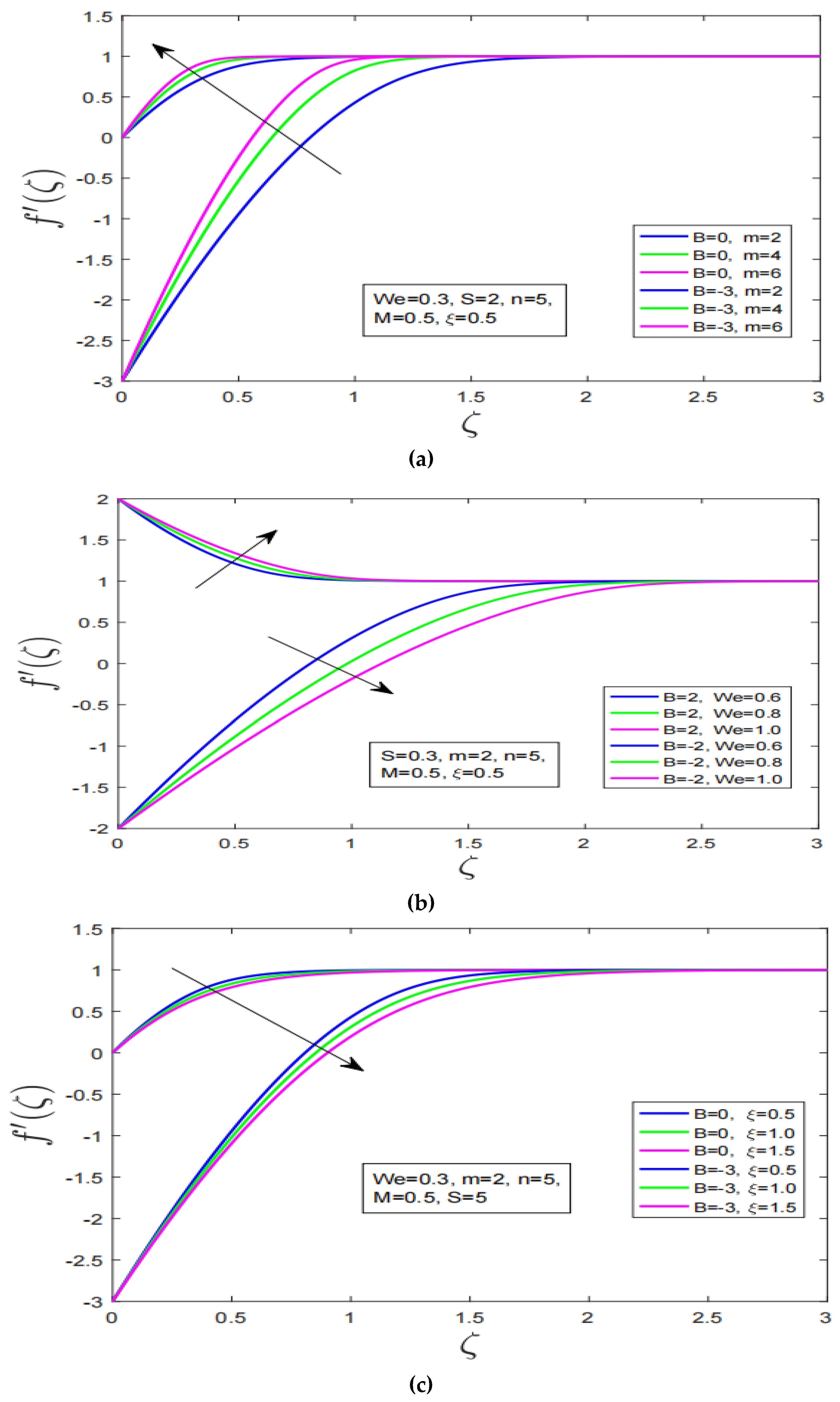
- The increment in power law index increases velocity profile for shrinking surface whereas decline has been observed in motion for stretching.
- High suction reduces the fluid motion for stretching and shrinking. Velocity profile decreased with augmentation in viscosity of fluid. Velocity profile has increased with the increase in Weissenberg number.
- Increasing the magnetization force has decreased motion of fluid for stretching surface and opposite behavior has been observed for shrinking. Additionally, the increment in highly non-linearity parameter increases the fluid motion for stretching/shrinking.
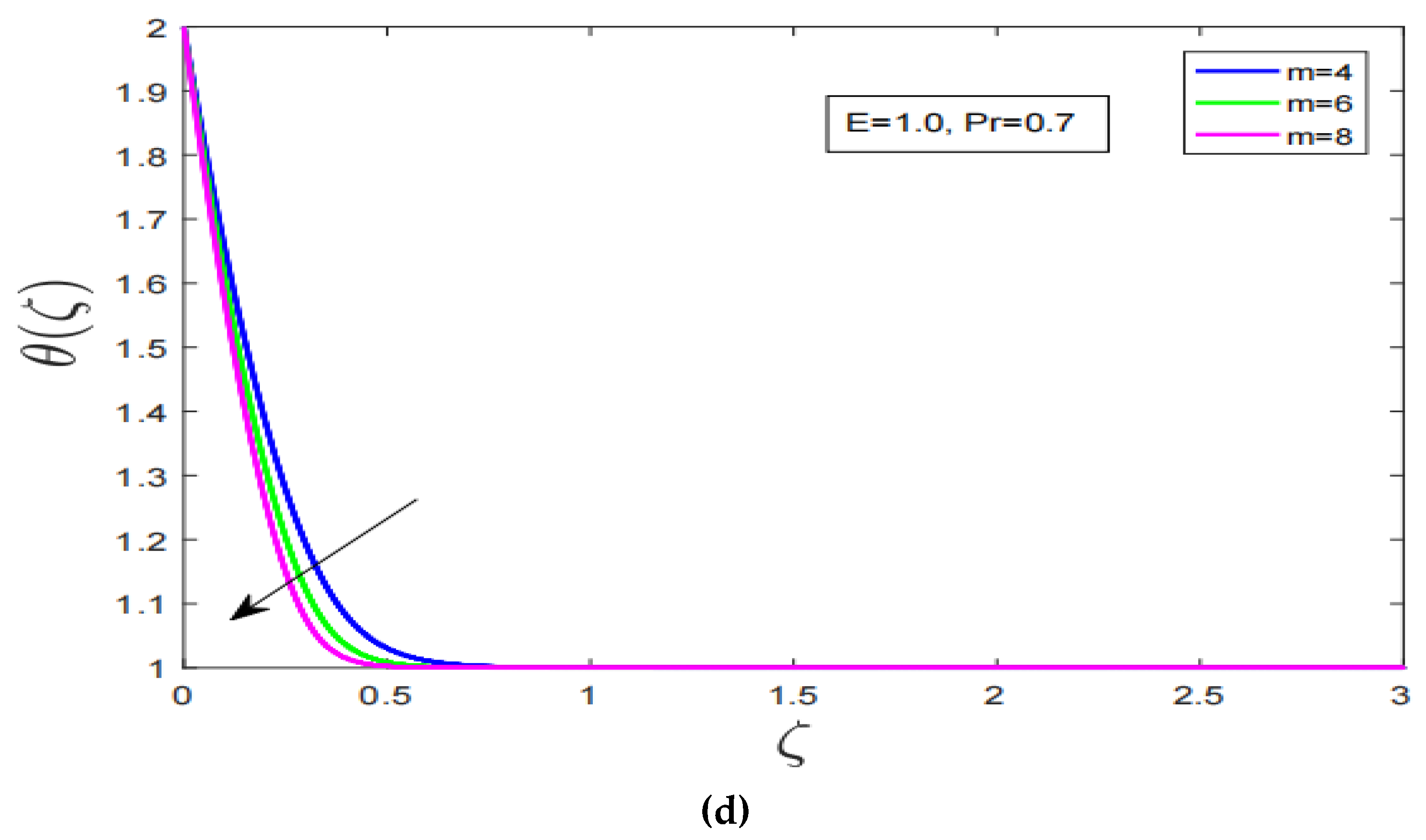
- Increment in non-linearity parameter decline the temperature profile sharply.
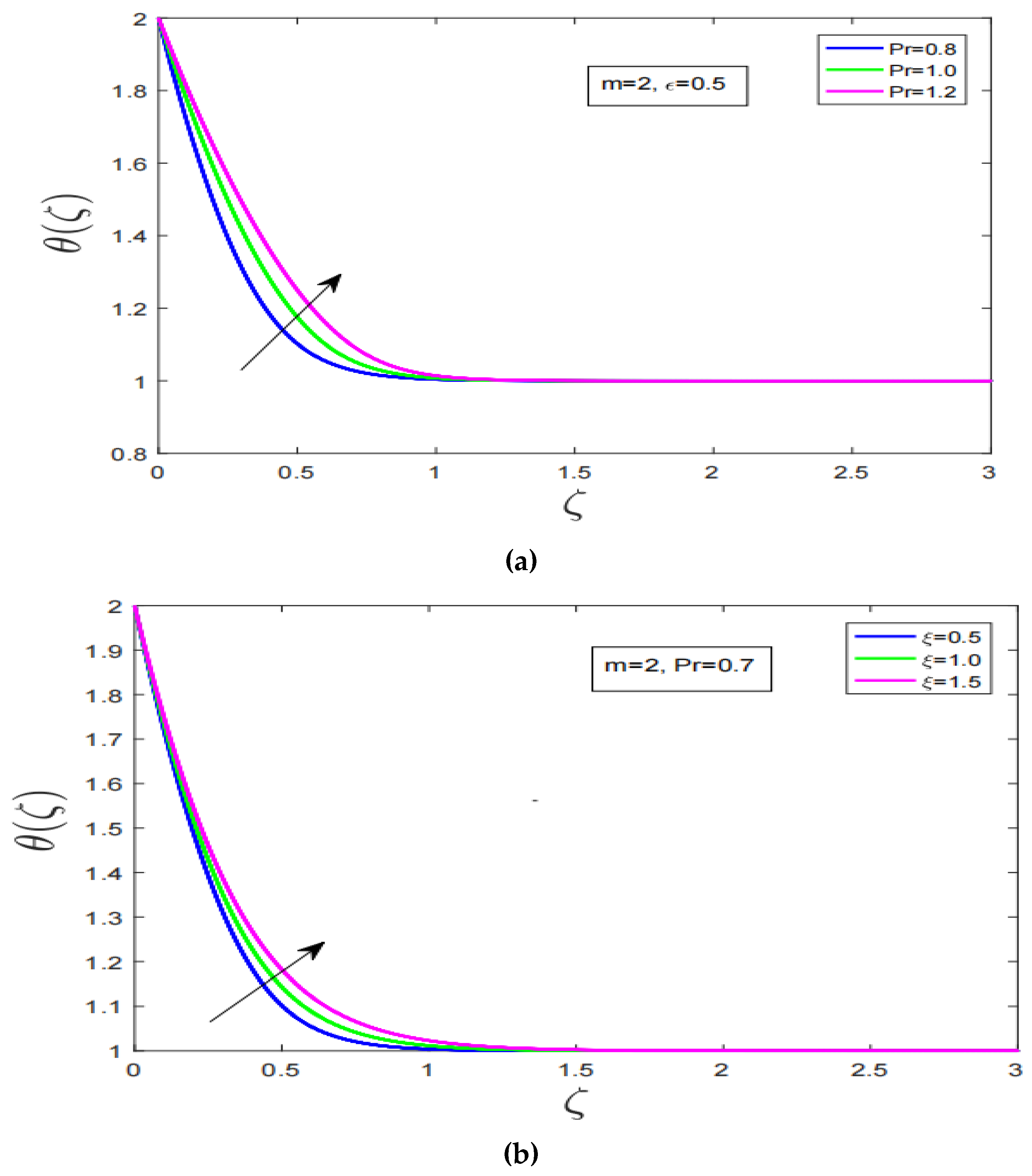
- Temperature profile increases with increase in Prandtl number consequently, thermal boundary layer thickness of the fluid expands.
- Temperature profile has increased with augmentation in viscosity and declination has been observed with increment in Lewis number.
- Temperature profile is the increasing function of variable thermal conductivity parameter.
- Nusselt number have increased with increment in non-linearity and suction influence. Minimal shear stress rate is observed under the increasing power law index.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Velocities components in respective direction | Volumetric heat capacity of Carreau fluid | ||
| Kinematic viscosity of Carreau fluid | Surface and Ambient temperature | ||
| Temperature and concentration dimensional profile | Surface and Ambient Concentration | ||
| Density of Carreau fluid | Similarity Variable | ||
| Heat capacity at constant pressure of Carreau fluid | Dynamic viscosity | ||
| f | Velocity Profile | Mass Diffusivity | |
| Temperature and concentration dimensionless profile | Suction/Injection velocity and surface heat flux, respectively | ||
| L | Dimensionless Lewis number | Effect of viscosity and thermal conductivity | |
| Some positive constant | P | Prandtl Number | |
| Some positive constant | Variable viscosity and thermal conductivity parameter, respectively | ||
| Dimensionless Suction/Injection parameter | Reynolds number | ||
| Dimensionless Weissenberg number | Dimensionless Magnetic field parameter | ||
| Boundary Layer Approximation | Stretching ratio parameter | ||
| Magneto-Hydrodynamic |
References
- Mandal, G. Convective-radiative heat transfer of micropolar nanofluid over a vertical non-linear stretching sheet. J. Nanofluids 2016, 5, 852–860. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Magnetohydrodynamic nonlinear thermal radiative heat transfer of nanofluids over a flat plate in a porous medium in existence of variable thermal conductivity and chemical reaction. Int. J. Ambient Energy 2021, 42, 1167–1177. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Erickson, L.E.; Fan, L.T.; Fox, V.G. Heat and mass transfer on moving continuous flat plate with suction or injection. Ind. Eng. Chem. Fundam. 1966, 5, 19–25. [Google Scholar] [CrossRef]
- Olajuwon, B.I. Convection heat and mass transfer in a hydromagnetic flow of a second grade fluid in the presence of thermal radiation and thermal diffusion. Int. Commun. Heat Mass Transf. 2011, 38, 377–382. [Google Scholar] [CrossRef]
- Hayat, T.; Noreen, S.; Ali, N.; Abbasbanday, S. Peristaltic motion of Phan-Thien-Tanner fluid in a planar channel. Numer. Methods Part. Differ. Equ. 2012, 28, 737–748. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Ye, S. MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: Dual solutions. Ain Shams Eng. J. 2014, 5, 1233–1239. [Google Scholar] [CrossRef]
- Suneetha, S.; Gangadhar, K.; Reddy, N.B. Thermal radiation effect on MHD stagnation point flow of a Carreau fluid with convective boundary condition. Open Sci. J. Math. Appl. 2015, 3, 121–127. [Google Scholar]
- Abou-zeid, M.Y. Numerical Treatment of Heat and Mass Transfer of MHD Flow of Carreau Fluid with Diffusion and Chemical Reaction through a Non Darcy Porous Medium. Open Math. J. 2009, 2, 22–35. [Google Scholar] [CrossRef]
- Akram, S.; Nadeem, S.; Ghafoor, A.; Lee, C. Consequences of nanofluid on peristaltic flow in an asymmetric channel. Int. J. Basic. Appl. Sci. IJBAS-IJENS 2012, 12, 75–96. [Google Scholar]
- Prilepskii, A.Y.; Fakhardo, A.F.; Drozdov, A.S.; Vinogradov, V.V.; Dudanov, I.P.; Shtil, A.A.; Bel’Tyukov, P.P.; Shibeko, A.M.; Koltsova, E.M.; Nechipurenko, D.Y.; et al. Urokinase-conjugated magnetite nanoparticles as a promising drug delivery system for targeted thrombolysis: Synthesis and preclinical evaluation. ACS Appl. Mater. Interfaces 2018, 10, 36764–36775. [Google Scholar] [CrossRef] [PubMed]
- Kurlyandskaya, G.V.; Litvinova, L.S.; Safronov, A.P.; Schupletsova, V.V.; Tyukova, I.S.; Khaziakhmatova, O.G.; Slepchenko, G.B.; Yurova, K.A.; Cherempey, E.G.; Kulesh, N.A.; et al. Water-based suspensions of iron oxide nanoparticles with electrostatic or steric stabilization by chitosan: Fabrication, characterization and biocompatibility. Sensors 2017, 17, 2605. [Google Scholar] [CrossRef] [PubMed]
- Spizzo, F.; Sgarbossa, P.; Sieni, E.; Semenzato, A.; Dughiero, F.; Forzan, M.; Bertani, R.; Del Bianco, L. Synthesis of ferrofluids made of iron oxide nanoflowers: Interplay between carrier fluid and magnetic properties. Nanomaterials 2017, 7, 373. [Google Scholar] [CrossRef] [PubMed]
- Bender, P.; Günther, A.; Tschöpe, A.; Birringer, R. Synthesis and characterization of uniaxial ferrogels with Ni nanorods as magnetic phase. J. Magn. Magn. Mater. 2011, 323, 2055–2063. [Google Scholar] [CrossRef]
- Buznikov, N.A.; Safronov, A.P.; Orue, I.; Golubeva, E.V.; Lepalovskij, V.N.; Svalov, A.V.; Chlenova, A.A.; Kurlyandskaya, G.V. Modeling of magnetoimpedance response of thin film sensitive element in the presence of ferrogel: Next step toward development of biosensor for in tissue embedded magnetic nanoparticles detection. Biosens. Bioelectron. 2018, 117, 366–372. [Google Scholar] [CrossRef]
- Jain, M.K.; Grimes, C.A. A wireless magnetoelastic micro-sensor array for simultaneous measurement of temperature and pressure. IEEE Trans. Magn. 2001, 37, 2022–2024. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G.; Vajravelu, K. Mixed Convective-Radiative Magnetohydrodynamics Heat and Mass Transfer of Nanofluids Over a Stretching/Shrinking Sheet with Viscous-Ohmic Dissipation and Heat Source/Sink. J. Nanofluids 2016, 5, 340–350. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Combined effects of heat and chemical reactions on the peristaltic flow of Carreau fluid model in a diverging tube. Int. J. Numer. Methods Fluids 2010, 67, 1818–1832. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vajravelu, K.; Subhas Abel, M.; Siddalingappa, M.N. MHD flow and heat transfer over a stretching surface with variable thermal conductivity and partial slip. Meccanica 2013, 48, 1451–1464. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Vyas, P.; Ranjan, A. Dissipative MHD boundary-layer flow in a porous medium over a sheet stretching nonlinearly in the presence of radiation. Appl. Math. Sci. 2010, 4, 3133–3142. [Google Scholar]
- Ali, M.E. On thermal boundary layer on a power-law stretched surface with suction or injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Sandeep, N.; Reddy, A.V.B.; Sugunamma, V. Effect of radiation and chemical reaction on transient MHD free convective flow over a vertical plate through porous media. Chem. Process Eng. Res. 2012, 2, 1–9. [Google Scholar]
- Shen, M.; Wang, F.; Chen, H. MHD mixed convection slip flow near a stagnation-point on a nonlinearly vertical stretching sheet. Bound. Value Probl. 2015, 2015, 78. [Google Scholar] [CrossRef]
- Akyildiz, F.T.; Siginer, D.A. Galerkin–Legendre spectral method for the velocity and thermal boundary layers over a non-linearly stretching sheet. Nonlinear Anal. Real World Appl. 2010, 11, 735–741. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Slip effects on boundary layer stagnation-point flow and heat transfer towards a shrinking sheet. Int. J. Heat Mass Transf. 2011, 54, 308–313. [Google Scholar] [CrossRef]
- Chen, C.-H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Khan, I.; Badran, M.; Mehrez, S.; Elfasakhany, A.; Abdeljawad, T.; Galal, A.M. Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study. Nanomaterials 2022, 12, 1204. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Haider, Q.; Ibrahim, A.H.; Alqurashi, M.S.; Almaliki, A.H.; Abdussattar, A. Thermophoresis and brownian effect for chemically reacting magneto-hydrodynamic nanofluid flow across an exponentially stretching sheet. Energies 2021, 15, 143. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Awrejcewicz, J.; Pawlowski, W.; Alharbi, F.M.; Karamti, H. Heat and mass transport analysis of MHD rotating hybrid nanofluids conveying silver and molybdenum di-sulfide nano-particles under effect of linear and non-linear radiation. Energies 2022, 15, 6269. [Google Scholar] [CrossRef]
- Abdou, M.M.M.; EL-Zahar, E.R. Variable viscosity effect on heat transfer over a continuous moving surface with variable internal heat generation in micropolar fluids. Appl. Math. Sci. 2012, 6, 6365–6379. [Google Scholar]
- Salem, A.M.; Odda, S.N. Influence of thermal conductivity and variable viscosity on the flow of a micropolar fluid past a continuously moving plate with suction or injection. J. Korean Soc. Ind. Appl. Math. 2005, 9, 45–53. [Google Scholar]
- Uwanta, I.J.; Usman, H. Effect of variable thermal conductivity on heat and mass transfer flow over a vertical channel with magnetic field intensity. Appl. Comput. Math. 2014, 3, 48–56. [Google Scholar]
- Abd El-hakiem, M.; Modather, M.; Abdou, M. The Effect of Variable Viscosity on MHD Natural Convection in Micropolarfluids. Int. J. Appl. Mech. Engg. 2006, 11, 301–320. [Google Scholar]
- Pal, D.; Mandal, G. Magnetohydrodynamic stagnation-point flow of Sisko nanofluid over a stretching sheet with suction. Propuls. Power Res. 2020, 9, 408–422. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Effects of aligned magnetic field on heat transfer of water-based carbon nanotubes nanofluid over a stretching sheet with homogeneous–heterogeneous reactions. Int. J. Ambient Energy 2021, 43, 5434–5446. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Shah SA, G.A.; Wróblewski, P.; Elkotb, M.A.; Abdelmohimen, M.A.; Hassan, A. Thermal energy investigation of magneto-hydrodynamic nano-material liquid flow over a stretching sheet: Comparison of single and composite particles. Alex. Eng. J. 2022, 61, 10453–10462. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M. Insight into the Significance of Viscous Dissipation and Heat Generation/Absorption in Magneto-Hydrodynamic Radiative Casson Fluid Flow with First-Order Chemical Reaction. Front. Phys. 2022, 10, 605. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Shah, S.A.G.A.; Elkotb, M.A.; Gouadria, S.; Alsehli, M.; Galal, A.M. Heat and mass transfer analysis above an unsteady infinite porous surface with chemical reaction. Case Stud. Therm. Eng. 2022, 36, 102140. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Hassan, A.; Rehman, A.; Ahmad, H.; Baili, J.; Gia, T.N. Heat transport investigation of engine oil based rotating nanomaterial liquid flow in the existence of partial slip effect. Case Stud. Therm. Eng. 2021, 28, 101500. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Alshehri, N.A. Heat transmission of engine-oil-based rotating nanofluids flow with influence of partial slip condition: A computational model. Energies 2021, 14, 3859. [Google Scholar] [CrossRef]
- Devi, S.A.; Kandasamy, R. Thermal stratification effects on laminar boundary-layer flow over a wedge with suction or injection. Mech. Res. Commun. 2001, 28, 349–354. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M. Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects. Can. J. Chem. Eng. 2013, 92, 758–767. [Google Scholar] [CrossRef]
- Mabood, F.; Shateyi, S.; Rashidi, M.M.; Momoniat, E.; Freidoonimehr, N.J.A.P.T. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 742–749. [Google Scholar] [CrossRef]
- Raptis, A.; Perdikis, C. Viscous flow over a non-linearly stretching sheet in the presence of a chemical reaction and magnetic field. Int. J. Non-Linear Mech. 2006, 41, 527–529. [Google Scholar] [CrossRef]
- Das, K.; Chakraborty, T.; Kumar Kundu, P. Slip effects on nanofluid flow over a nonlinear permeable stretching surface with chemical reaction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2473–2482. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud. Therm. Eng. 2021, 27, 101244. [Google Scholar] [CrossRef]
- Hussain, A.; Haider, Q.; Rehman, A.; Ahmad, H.; Baili, J.; Aljahdaly, N.H.; Hassan, A. A thermal conductivity model for hybrid heat and mass transfer investigation of single and multi-wall carbon nano-tubes flow induced by a spinning body. Case Stud. Therm. Eng. 2021, 28, 101449. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Arshad, M.; Rehman, A.; Matoog, R.T.; Abdeljawad, T. Numerical simulation and thermal enhancement of multi-based nanofluid over an embrittled cone. Case Stud. Therm. Eng. 2021, 28, 101614. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Alanazi, M.M.; Zahran, H.Y. Numerical and Thermal Investigation of Magneto-Hydrodynamic Hybrid Nanoparticles (SWCNT-Ag) under Rosseland Radiation: A Prescribed Wall Temperature Case. Nanomaterials 2022, 12, 891. [Google Scholar] [CrossRef]
- Salahuddin, T.; Awais, M.; Xia, W.F. Variable thermo-physical characteristics of Carreau fluid flow by means of stretchable paraboloid surface with activation energy and heat generation. Case Stud. Therm. Eng. 2021, 25, 100971. [Google Scholar] [CrossRef]
- Rehman, K.U.; Shatanawi, W.; Abodayeh, K. A group theoretic analysis on heat transfer in MHD thermally slip Carreau fluid subject to multiple flow regimes (MFRs). Case Stud. Therm. Eng. 2022, 30, 101787. [Google Scholar] [CrossRef]
- Salahuddin, T.; Awais, M. A comparative study of Cross and Carreau fluid models having variable fluid characteristics. Int. Commun. Heat Mass Transf. 2022, 139, 106431. [Google Scholar] [CrossRef]
- Hussain, S.M.; Goud, B.S.; Madheshwaran, P.; Jamshed, W.; Pasha, A.A.; Safdar, R.; Arshad, M.; Ibrahim, R.W.; Ahmad, M.K. Effectiveness of nonuniform heat generation (sink) and thermal characterization of a carreau fluid flowing across a nonlinear elongating cylinder: A numerical study. ACS Omega 2022, 7, 25309–25320. [Google Scholar] [CrossRef]
- Yang, D.; Israr Ur Rehman, M.; Hamid, A.; Ullah, S. Multiple solutions for stagnation-point flow of unsteady Carreau fluid along a permeable stretching/shrinking sheet with non-uniform heat generation. Coatings 2021, 11, 1012. [Google Scholar] [CrossRef]
- Mandal, G.; Pal, D. Entropy generation analysis of magnetohydrodynamic Darcy-Forchheimer Williamson hybrid nanofluid flow through porous medium with nonlinear thermal radiation. Spéc. Top. Rev. Porous Media Int. J. 2022, 13, 57–79. [Google Scholar] [CrossRef]
- Mandal, G.; Pal, D. Entropy generation analysis of radiated magnetohydrodynamic flow of carbon nanotubes nanofluids with variable conductivity and diffusivity subjected to chemical reaction. J. Nanofluids 2021, 10, 491–505. [Google Scholar] [CrossRef]

| Numerical Outcomes of with Fixed Parameters | |||
|---|---|---|---|
| B | S | ||
| 0 | 5 | 2.902 | 4.8292 |
| 0 | 5.5 | 3.0122 | 5.3449 |
| 0 | 6 | 3.1178 | 5.8622 |
| 0 | 6.5 | 3.2191 | 6.3808 |
| 0 | 7 | 3.3163 | 6.9004 |
| 0 | 7.5 | 3.4098 | 7.4208 |
| −3 | 5 | 4.6210 | 4.2457 |
| −3 | 5.5 | 4.8563 | 4.8175 |
| −3 | 6 | 5.0709 | 5.3808 |
| −3 | 6.5 | 5.2688 | 5.9377 |
| −3 | 7 | 5.4531 | 6.4897 |
| −3 | 7.5 | 5.6258 | 7.0380 |
| Numerical Outcomes of with Fixed Parameters | |||
|---|---|---|---|
| B | n | ||
| 2 | 5 | −3.0451 | 5.0573 |
| 2 | 6 | −2.8827 | 5.0595 |
| 2 | 7 | −2.7542 | 5.0613 |
| 2 | 8 | −2.7542 | 5.0629 |
| 2 | 9 | −2.5594 | 5.0643 |
| −2 | 5 | 4.4331 | 4.4792 |
| −2 | 6 | 4.1437 | 4.4692 |
| −2 | 7 | 3.9193 | 4.4610 |
| −2 | 8 | 3.7378 | 4.4542 |
| −2 | 9 | 3.5863 | 4.4483 |
| Numerical Outcomes of with Fixed Parameters | |||
|---|---|---|---|
| B | m | ||
| 0 | 7 | 4.4003 | 13.5537 |
| 0 | 7.5 | 4.5076 | 14.4272 |
| 0 | 8 | 4.6105 | 15.3008 |
| 0 | 8.5 | 4.7105 | 16.3008 |
| 0 | 9 | 4.8047 | 17.0482 |
| 0 | 10 | 4.9856 | 18.7959 |
| −3 | 7 | 6.8340 | 12.9560 |
| −3 | 7.5 | 6.9964 | 13.8293 |
| −3 | 8 | 7.1523 | 14.7027 |
| −3 | 9 | 7.4474 | 16.4500 |
| −3 | 10 | 7.7229 | 18.1976 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.A.G.A.; Hassan, A.; Alsubaie, N.; Alhushaybari, A.; Alharbi, F.M.; Galal, A.M.; Burduhos-Nergis, D.-P.; Bejinariu, C. Convective Heat Transfer in Magneto-Hydrodynamic Carreau Fluid with Temperature Dependent Viscosity and Thermal Conductivity. Nanomaterials 2022, 12, 4084. https://doi.org/10.3390/nano12224084
Shah SAGA, Hassan A, Alsubaie N, Alhushaybari A, Alharbi FM, Galal AM, Burduhos-Nergis D-P, Bejinariu C. Convective Heat Transfer in Magneto-Hydrodynamic Carreau Fluid with Temperature Dependent Viscosity and Thermal Conductivity. Nanomaterials. 2022; 12(22):4084. https://doi.org/10.3390/nano12224084
Chicago/Turabian StyleShah, Syed Amir Ghazi Ali, Ali Hassan, Najah Alsubaie, Abdullah Alhushaybari, Fahad M. Alharbi, Ahmed M. Galal, Diana-Petronela Burduhos-Nergis, and Costica Bejinariu. 2022. "Convective Heat Transfer in Magneto-Hydrodynamic Carreau Fluid with Temperature Dependent Viscosity and Thermal Conductivity" Nanomaterials 12, no. 22: 4084. https://doi.org/10.3390/nano12224084
APA StyleShah, S. A. G. A., Hassan, A., Alsubaie, N., Alhushaybari, A., Alharbi, F. M., Galal, A. M., Burduhos-Nergis, D.-P., & Bejinariu, C. (2022). Convective Heat Transfer in Magneto-Hydrodynamic Carreau Fluid with Temperature Dependent Viscosity and Thermal Conductivity. Nanomaterials, 12(22), 4084. https://doi.org/10.3390/nano12224084












