Multi-Directional Cloak Design by All-Dielectric Unit-Cell Optimized Structure
Abstract
:1. Introduction
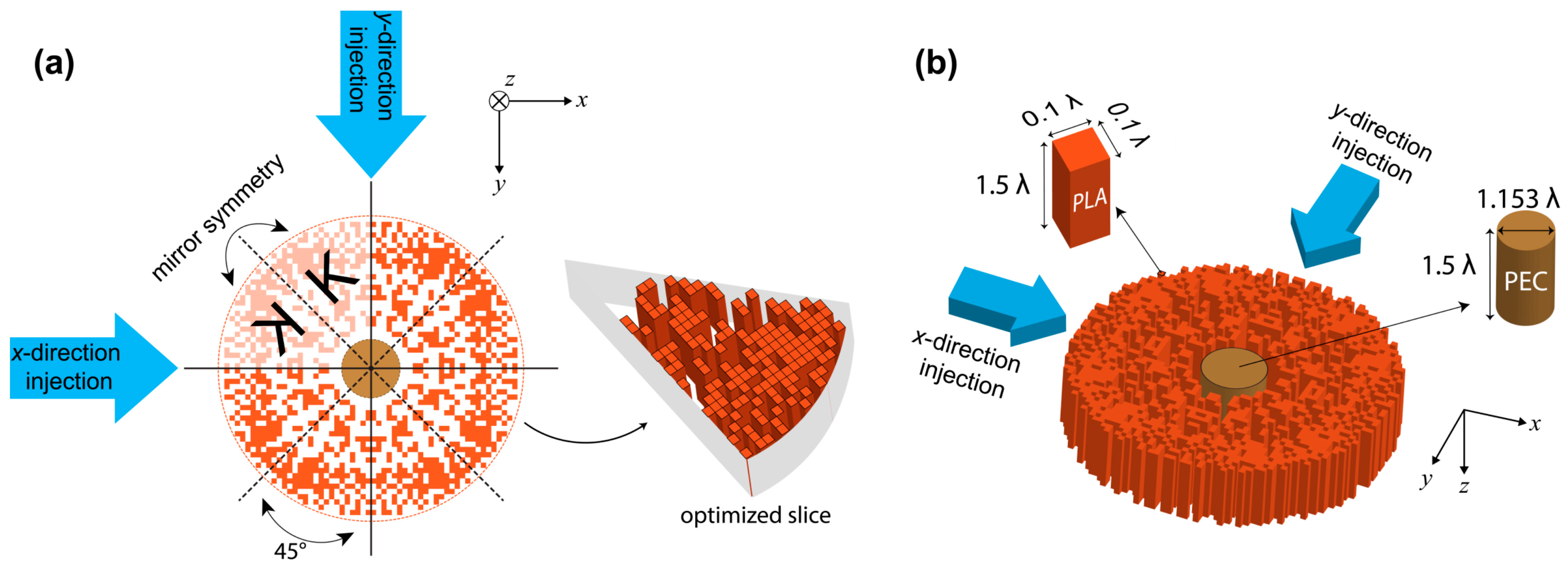
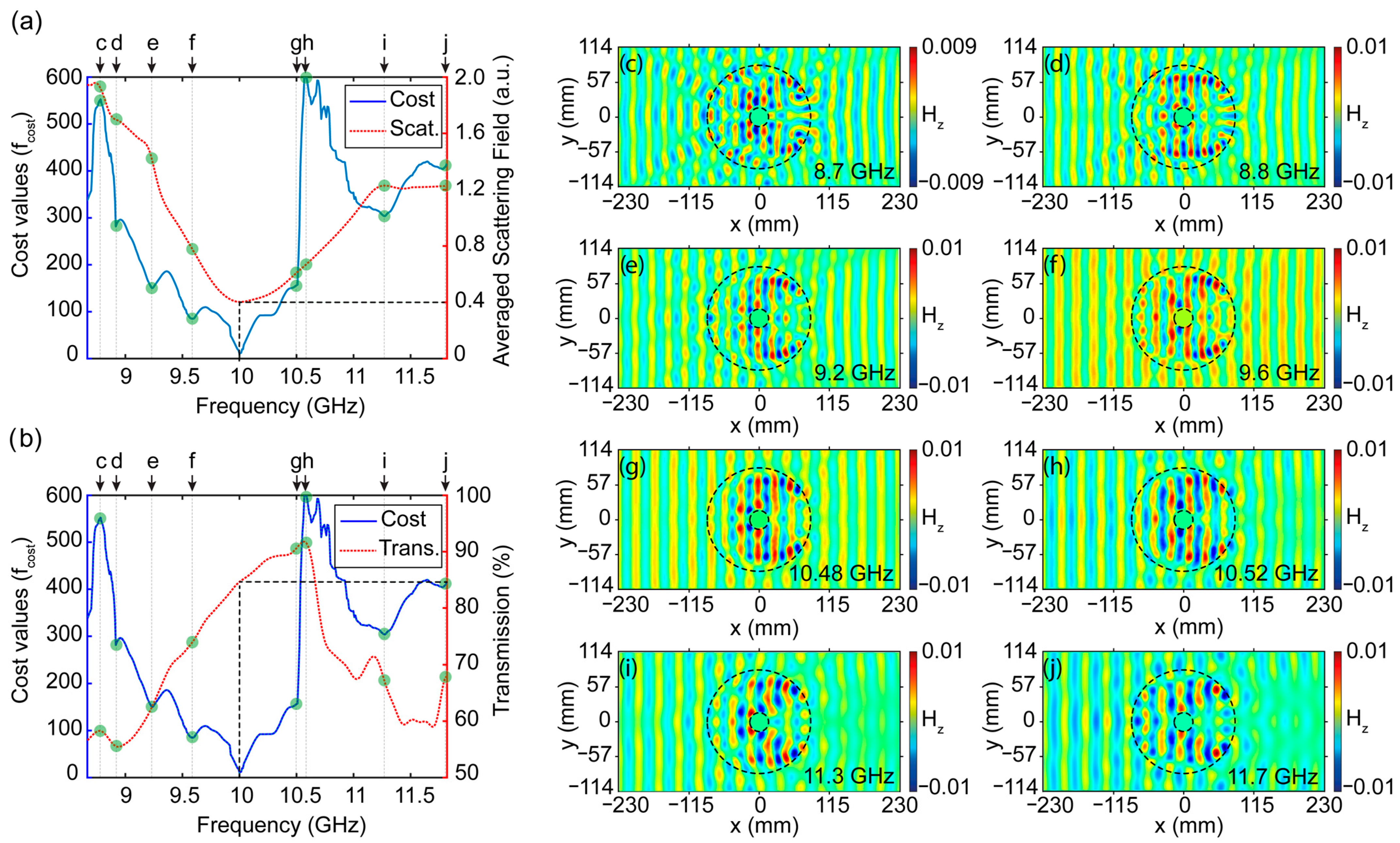
2. Design Steps and Numerical Results
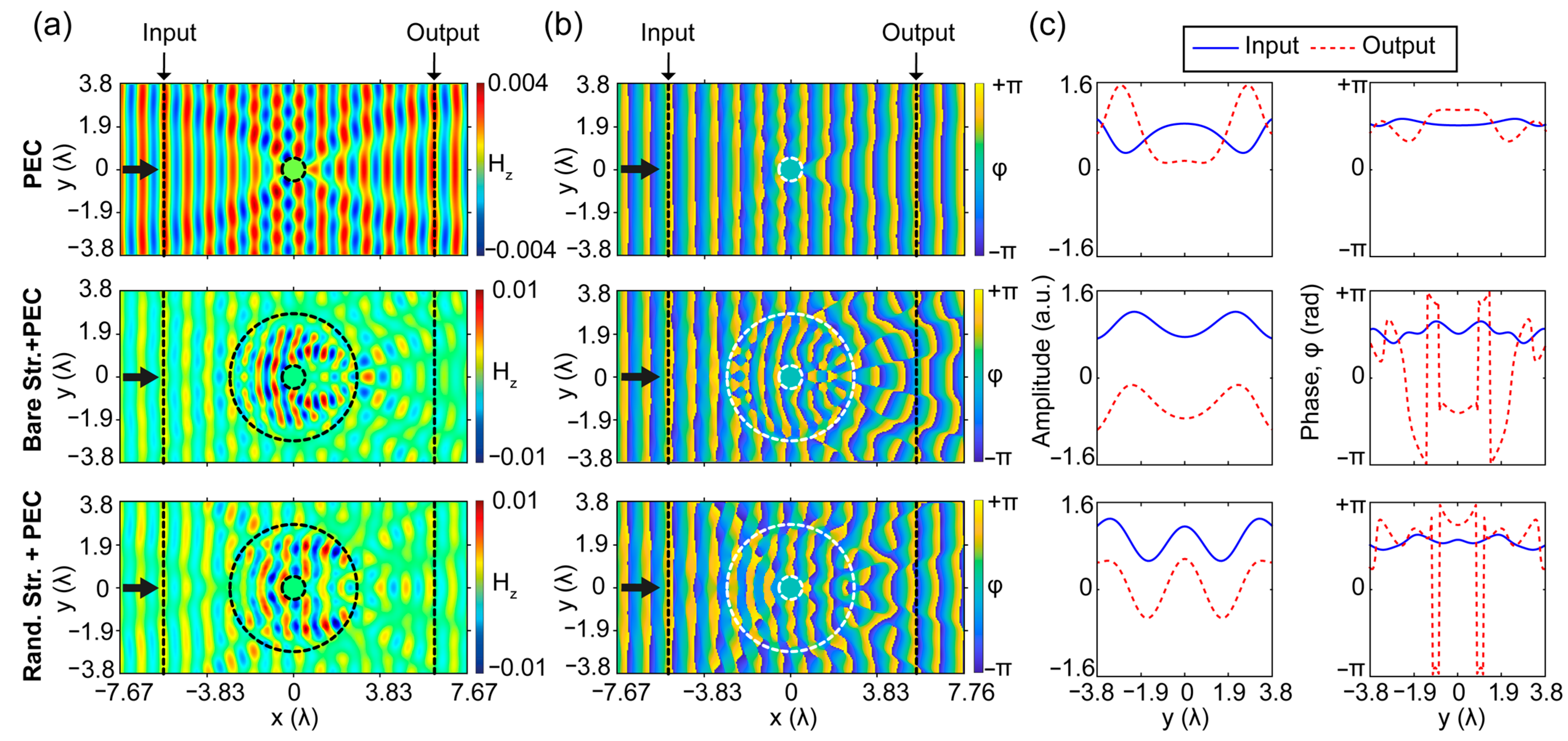
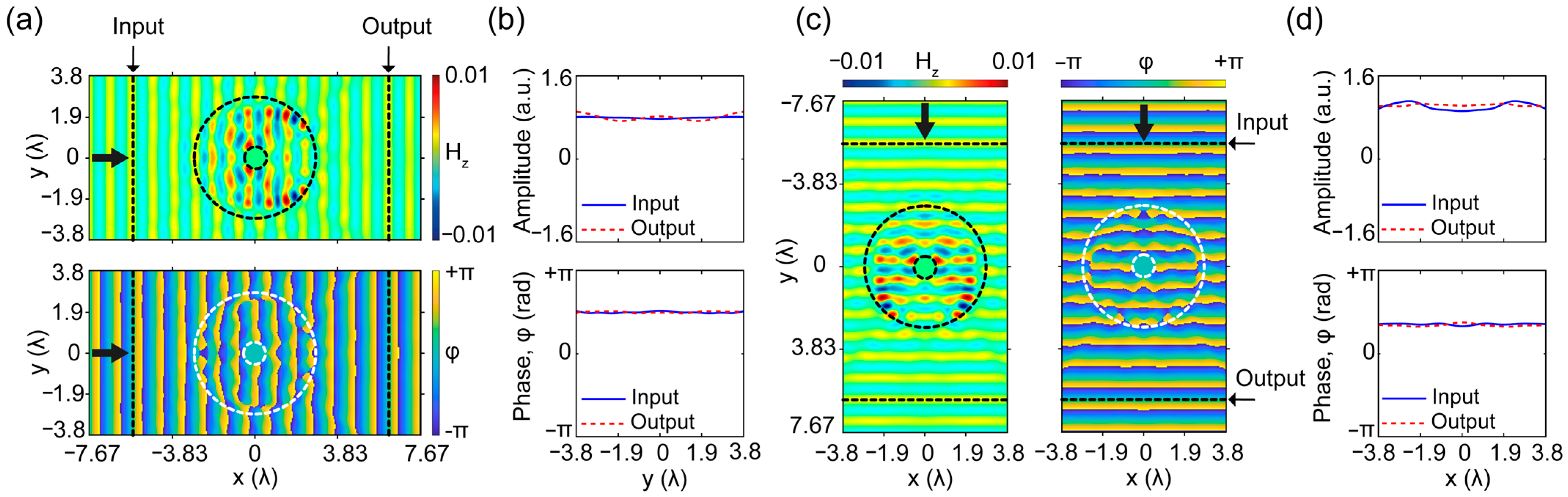
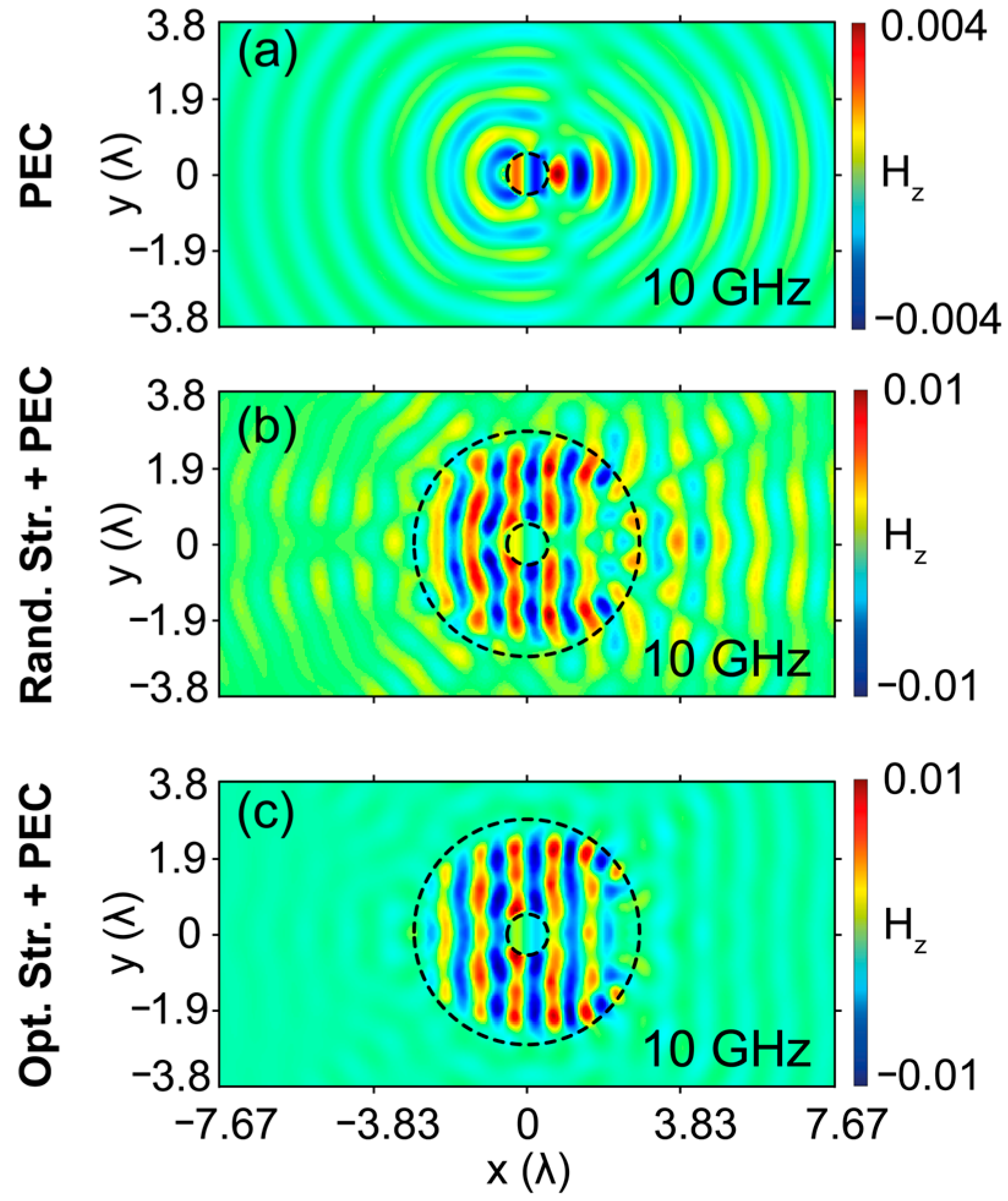
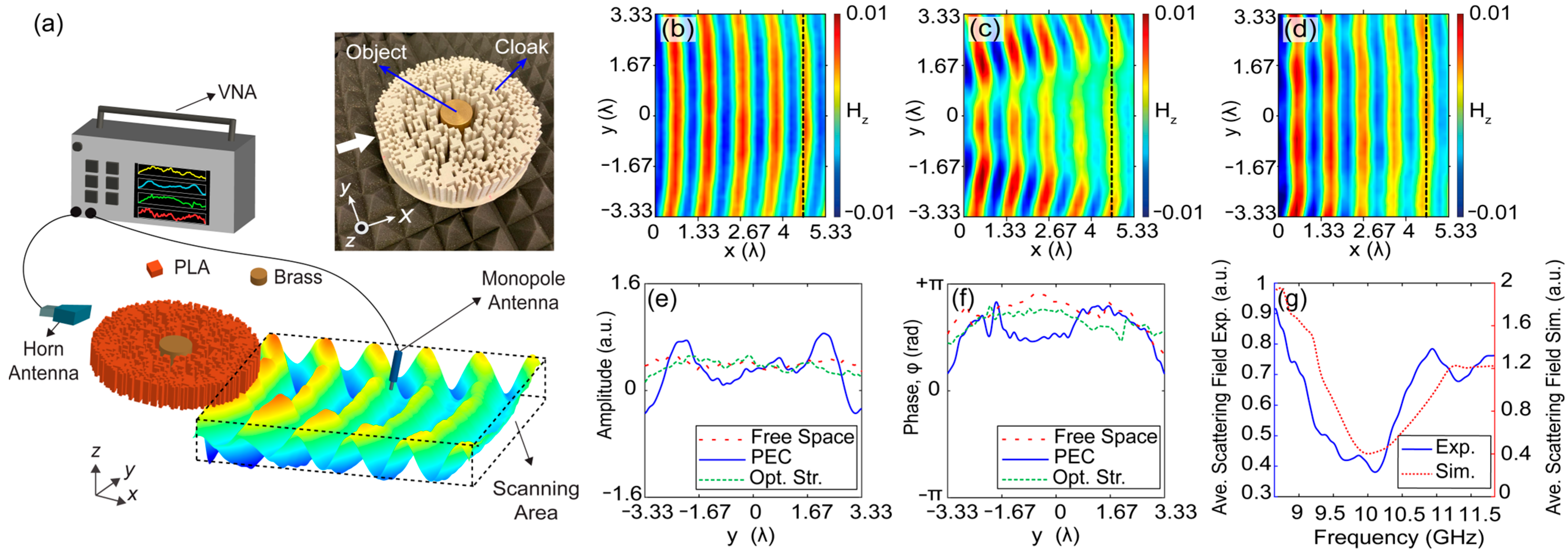
3. Experimental Verification in Microwave Regime
4. Further Discussion: The Concept of Multi-Directional Cloaking
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leonhardt, U. Optical Conformal Mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation Optics and Metamaterials. Nat. Mater. 2010, 9, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zentgraf, T.; Bartal, G.; Zhang, X. Transformational Plasmon Optics. Nano Lett. 2010, 10, 1991–1997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ozgun, O.; Kuzuoglu, M. Form Invariance of Maxwell’s Equations: The Pathway to Novel Metamaterial Specifications for Electromagnetic Reshaping. IEEE Antennas Propag. Mag. 2010, 52, 51–65. [Google Scholar] [CrossRef]
- Schurig, D.; Pendry, J.B.; Smith, D.R. Calculation of Material Properties and Ray Tracing in Transformation Media. Opt. Express 2006, 14, 9794–9804. [Google Scholar] [CrossRef]
- Valentine, J.; Li, J.; Zentgraf, T.; Bartal, G.; Zhang, X. An Optical Cloak Made of Dielectrics. Nat. Mater. 2009, 8, 568–571. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Pendry, J.B. Hiding under the Carpet: A New Strategy for Cloaking. Phys. Rev. Lett. 2008, 101, 3901–3904. [Google Scholar] [CrossRef] [Green Version]
- Leonhardt, U.; Tyc, T. Broadband Invisibility by Non-Euclidean Cloaking. Science 2009, 323, 110–112. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Ji, C.; Mock, J.J.; Chin, J.Y.; Cui, T.J.; Smith, D.R. Broadband Ground-Plane Cloak. Science 2009, 323, 366–369. [Google Scholar] [CrossRef]
- Dupont, G.; Guenneau, S.; Enoch, S. Electromagnetic Analysis of Arbitrarily Shaped Pinched Carpets. Phys. Rev. A 2010, 82, 033840. [Google Scholar] [CrossRef] [Green Version]
- Kallos, E.; Argyropoulos, C.; Hao, Y. Ground-Plane Quasicloaking for Free Space. Phys. Rev. A 2009, 79, 063825. [Google Scholar] [CrossRef] [Green Version]
- Halimeh, J.C.; Ergin, T.; Mueller, J.; Stenger, N.; Wegener, M. Photorealistic Images of Carpet Cloaks. Opt. Express 2009, 17, 19328–19336. [Google Scholar] [CrossRef]
- Danner, A.J. Visualizing Invisibility: Metamaterials-Based Optical Devices in Natural Environments. Opt. Express 2010, 18, 3332–3337. [Google Scholar] [CrossRef]
- Halimeh, J.C.; Wegener, M. Photorealistic Rendering of Unidirectional Free-Space Invisibility Cloaks. Opt. Express 2013, 21, 9457–9472. [Google Scholar] [CrossRef] [Green Version]
- Orazbayev, B.; Estakhri, N.; Beruete, M.; Alu, A. Terahertz Carpet Cloak Based on a Ring Resonator Metasurfaces. Phys. Rev. B 2015, 91, 195444. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.; Li, Q.; Liu, B.; Luo, J.; Sun, S.; Hang, Z.H.; Zhou, L.; Lai, Y. A Hybrid Invisibility Cloak Based on Integration of Transparent Metasurfaces and Zero-Index Materials. Light Sci. Appl. 2018, 7, 50. [Google Scholar] [CrossRef] [Green Version]
- Bor, E.; Gorkem Yasa, U.; Kurt, H.; Turduev, M. Demonstration of Carpet Cloaking by an Anisotropic Zero Refractive Index Medium. Opt. Lett. 2020, 45, 2423–2426. [Google Scholar] [CrossRef]
- Guild, M.D.; Haberman, M.R.; Alù, A. Plasmonic Cloaking and Scattering Cancelation for Electromagnetic and Acoustic Waves. Wave Motion 2011, 48, 468–482. [Google Scholar] [CrossRef]
- Rainwater, D.; Kerkhoff, A.; Melin, K.; Soric, J.C.; Moreno, G.; Alù, A. Experimental Verification of Three-Dimensional Plasmonic Cloaking in Free-Space. N. J. Phys. 2012, 14, 013054. [Google Scholar] [CrossRef]
- Edwards, B.; Alù, A.; Silveirinha, M.G.; Engheta, N. Experimental Verification of Plasmonic Cloaking at Microwave Frequencies with Metamaterials. Phys. Rev. Lett. 2009, 103, 153901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serebryannikov, E.A.; Alici, B.K.; Ozbay, E.; Lakhtakia, A. Thermally sensitive scattering of terahertz waves by coated cylinders for tunable invisibility and masking. Opt. Express 2018, 26, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Tretyakov, S.; Alitalo, P.; Luukkonen, O.; Simovski, C. Broadband Electromagnetic Cloaking of Long Cylindrical Objects. Phys. Rev. Lett. 2009, 103, 103905. [Google Scholar] [CrossRef] [PubMed]
- Valagiannopoulos, C.A.; Alitalo, P. Electromagnetic cloaking of cylindrical objects by multilayer or uniform dielectric claddings. Phys. Rev. B 2012, 85, 115402. [Google Scholar] [CrossRef] [Green Version]
- Ergin, T.; Stenger, N.; Brenner, P.; Pendry, J.B.; Wegener, M. Three-Dimensional Invisibility Cloak at Optical Wavelengths. Science 2010, 328, 337–339. [Google Scholar] [CrossRef] [Green Version]
- Babayiğit, C.; Evren, A.S.; Bor, E.; Kurt, H.; Turduev, M. Analytical, Numerical, and Experimental Investigation of a Luneburg Lens System for Directional Cloaking. Phys. Rev. A 2019, 99, 043831. [Google Scholar] [CrossRef] [Green Version]
- Semouchkina, E.; Duan, R.; Gandji, N.P.; Jamilan, S.; Semouchkin, G.; Pandey, R. Superluminal Media Formed by Photonic Crystals for Transformation Optics-Based Invisibility Cloaks. J. Opt. 2016, 18, 044007. [Google Scholar] [CrossRef]
- He, Q.; Xiao, S.; Li, X.; Zhou, L. Optic-Null Medium: Realization and Applications. Opt. Express 2013, 21, 28948–28959. [Google Scholar] [CrossRef]
- Sun, F.; He, S. Optical Surface Transformation: Changing the Optical Surface by Homogeneous Optic-Null Medium at Will. Sci. Rep. 2015, 5, 16032. [Google Scholar] [CrossRef]
- Wu, F.; Guo, Z.; Wu, J.; Jiang, H.; Sun, Y.; Li, Y.; Chen, H. Effective Optical Nihility Media Realized by One-Dimensional Photonic Crystals Containing Hyperbolic Metamaterials. Opt. Express 2020, 28, 33198–33207. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, Y.; Pendry, J.; Zhang, B. Transformation-invariant metamaterials. Phys. Rev. Lett. 2019, 123, 067701. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Monticone, F.; Alu, A. Suppressing the Electromagnetic Scattering with an Helical Mantle Cloak. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1598–1601. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Alù, A. Mantle Cloaking Using Thin Patterned Metasurfaces. Phys. Rev. B 2011, 84, 205110. [Google Scholar] [CrossRef]
- Alù, A. Mantle cloak: Invisibility induced by a surface. Phys. Rev. B 2009, 80, 245115. [Google Scholar] [CrossRef]
- Monti, A.; Soric, J.; Barbuto, M.; Ramaccia, D.; Vellucci, S.; Trotta, F.; Alù, A.; Toscano, A.; Bilotti, F. Mantle cloaking for co-site radio-frequency antennas. Appl. Phys. Lett. 2016, 108, 113502. [Google Scholar] [CrossRef]
- Padooru, Y.R.; Yakovlev, A.B.; Chen, P.; Alù, A. Analytical modeling of conformal mantle cloaks for cylindrical objects using sub-wavelength printed and slotted arrays. J. Appl. Phys. 2012, 112, 34907. [Google Scholar] [CrossRef] [Green Version]
- Hayran, Z.; Herrero, R.; Botey, M.; Kurt, H.; Staliunas, K. Invisibility on Demand Based on a Generalized Hilbert Transform. Phys. Rev. A 2018, 98, 013822. [Google Scholar] [CrossRef] [Green Version]
- Horsley, S.A.R.; Artoni, M.; La Rocca, G.C. Spatial Kramers–Kronig Relations and the Reflection of Waves. Nat. Photonics 2015, 9, 436–439. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.S.; Howell, J.C. Paraxial Ray Optics Cloaking. Opt. Express 2014, 22, 29465–29478. [Google Scholar] [CrossRef] [Green Version]
- Vasić, B.; Gajić, R. Self-Focusing Media Using Graded Photonic Crystals: Focusing, Fourier Transforming and Imaging, Directive Emission, and Directional Cloaking. J. Appl. Phys. 2011, 110, 053103. [Google Scholar] [CrossRef]
- Andkjær, J.; Sigmund, O. Topology Optimized Low-Contrast All-Dielectric Optical Cloak. Appl. Phys. Lett. 2011, 98, 021112. [Google Scholar] [CrossRef] [Green Version]
- Vial, B.; Hao, Y. Topology Optimized All-Dielectric Cloak: Design, Performances and Modal Picture of the Invisibility Effect. Opt. Express 2015, 23, 23551–23560. [Google Scholar] [CrossRef] [PubMed]
- Bor, E.; Babayiğit, C.; Kurt, H.; Staliunas, K.; Turduev, M. Directional Invisibility Induced by a Genetic Optimization Approach. Opt. Lett 2018, 43, 5781–5784. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Yang, Z.; Zhang, Y.; Wang, Y.; Hu, X.; Tian, X. Optimized Design for Illusion Device by Genetic Algorithm. Sci. Rep. 2021, 11, 19475. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Liu, Z.; Liu, Y.; Wu, Y. Inverse Design of Dielectric Resonator Cloaking Based on Topology Optimization. Plasmonics 2017, 12, 1717–1723. [Google Scholar] [CrossRef]
- Miguel-Torcal, A.; Abad-Arredondo, J.; García-Vidal, F.J.; Fernández-Domínguez, A.I. Inverse-Designed Dielectric Cloaks for Entanglement Generation. Nanophotonics 2022, 11, 4387–4395. [Google Scholar] [CrossRef]
- Fujii, G.; Akimoto, Y. Electromagnetic-Acoustic Biphysical Cloak Designed through Topology Optimization. Opt. Express 2022, 30, 6090–6106. [Google Scholar] [CrossRef]
- Fujii, G.; Akimoto, Y. Cloaking a Concentrator in Thermal Conduction via Topology Optimization. Int. J. Heat Mass Transf. 2020, 159, 120082. [Google Scholar] [CrossRef]
- Hua, Y.; Qian, C.; Chen, H.; Wang, H. Experimental Topology-Optimized Cloak for Water Waves. Mater. Today Phys. 2022, 27, 100754. [Google Scholar] [CrossRef]
- Lan, L.; Sun, F.; Liu, Y.; Ong, C.K.; Ma, Y. Experimentally Demonstrated a Unidirectional Electromagnetic Cloak Designed by Topology Optimization. Appl. Phys. Lett. 2013, 103, 121113. [Google Scholar] [CrossRef]
- Vial, B.; Torrico, M.M.; Hao, Y. Optimized Microwave Illusion Device. Sci. Rep. 2017, 7, 3929. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Sun, W.; Wang, Q.; Zhang, D. Nanoscale Thermal Cloaking in Silicon Film: A Molecular Dynamic Study. Materials 2022, 15, 935. [Google Scholar] [CrossRef]
- Sharon, M.; Rodriguez, S.A.L.; Sharon, C. Nanotechnology in the Defense Industry; Wiley-Scrivener Publisher: Beverly, MA, USA, 2019. [Google Scholar]
- Kumar, N.; Dixit, A. Camouflage and Stealth Technology Based on Nanomaterials. In Nanotechnology for Defence Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 155–203. [Google Scholar]
- Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. Optical Invisibility through Metasurfaces Made of Plasmonic Nanoparticles. J. Appl. Phys. 2015, 117, 123103. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, H.; Zhang, B. Design, Implementation, and Extension of Thermal Invisibility Cloaks. AIP Adv. 2015, 5, 053402. [Google Scholar] [CrossRef] [Green Version]
- Ozbay, E.; Temelkuran, B.; Bayindir, M. Microwave Applications of Photonic Crystals. Prog. Electromagn. Res. 2003, 41, 185–209. [Google Scholar] [CrossRef] [Green Version]
- Shishkin, I.; Baranov, D.; Slobozhanyuk, A.; Filonov, D.; Lukashenko, S.; Samusev, A.; Belov, P. Microwave Platform as a Valuable Tool for Characterization of Nanophotonic Devices. Sci. Rep. 2016, 6, 35516. [Google Scholar] [CrossRef] [Green Version]
- Jahani, S.; Kim, S.; Atkinson, J.; Wirth, J.C.; Kalhor, F.; Noman, A.A.; Newman, W.D.; Shekhar, P.; Han, K.; Van, V.; et al. Controlling Evanescent Waves Using Silicon Photonic All-Dielectric Metamaterials for Dense Integration. Nat. Commun. 2018, 9, 1893. [Google Scholar] [CrossRef] [Green Version]
- Minin, I.V.; Minin, O.V.; Glinskiy, I.A.; Khabibullin, R.A.; Malureanu, R.; Lavrinenko, A.V.; Yakubovsky, D.I.; Arsenin, A.V.; Volkov, V.S.; Ponomarev, D.S. Plasmonic Nanojet: An Experimental Demonstration. Opt. Lett. 2020, 45, 3244–3247. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Glinskiy, I.A.; Khabibullin, R.A.; Malureanu, R.; Lavrinenko, A.; Yakubovsky, D.I.; Volkov, V.S.; Ponomarev, D.S. Experimental Verification of a Plasmonic Hook in a Dielectric Janus Particle. Appl. Phys. Lett. 2021, 118, 131107. [Google Scholar] [CrossRef]
- Lumerical. Available online: http://www.lumerical.com/tcad-products/fdtd/ (accessed on 19 October 2022).
- Weir, W.B. Automatic Measurement of Complex Dielectric Constant and Permeability at Microwave Frequencies. Proc. IEEE Inst. Electr. Electron. Eng. 1974, 62, 33–36. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Mesotronics: Some New, Unusual Optical Effects. Photonics 2022, 9, 762. [Google Scholar] [CrossRef]
- Oskooi, F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A Flexible Free Software Package for Electromagnetic Simulations by the FDTD Method. Comput. Phys. Commun 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Berenger, J.-P. A Perfectly Matched Layer for the Absorption of Electromagnetic Waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- McGuirk, J.S.; Collins, P.J. Controlling the Transmitted Field into a Cylindrical Cloak’s Hidden Region. Opt. Express 2008, 16, 17560–17573. [Google Scholar] [CrossRef]
- Ang, P.; Eleftheriades, G.V. Active Cloaking of a Non-Uniform Scatterer. Sci. Rep. 2020, 10, 2021. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Mei, Z.L.; Tang, W.X.; Cui, T.J. Manipulating Scattering Features by Metamaterials. EPJ Appl. Metamater. 2016, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Urzhumov, Y.; Landy, N.; Driscoll, T.; Basov, D.; Smith, D.R. Thin Low-Loss Dielectric Coatings for Free-Space Cloaking. Opt. Lett. 2013, 38, 1606–1608. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayik, M.; Kurt, H.; Minin, O.V.; Minin, I.V.; Turduev, M. Multi-Directional Cloak Design by All-Dielectric Unit-Cell Optimized Structure. Nanomaterials 2022, 12, 4194. https://doi.org/10.3390/nano12234194
Ayik M, Kurt H, Minin OV, Minin IV, Turduev M. Multi-Directional Cloak Design by All-Dielectric Unit-Cell Optimized Structure. Nanomaterials. 2022; 12(23):4194. https://doi.org/10.3390/nano12234194
Chicago/Turabian StyleAyik, Muratcan, Hamza Kurt, Oleg V. Minin, Igor V. Minin, and Mirbek Turduev. 2022. "Multi-Directional Cloak Design by All-Dielectric Unit-Cell Optimized Structure" Nanomaterials 12, no. 23: 4194. https://doi.org/10.3390/nano12234194
APA StyleAyik, M., Kurt, H., Minin, O. V., Minin, I. V., & Turduev, M. (2022). Multi-Directional Cloak Design by All-Dielectric Unit-Cell Optimized Structure. Nanomaterials, 12(23), 4194. https://doi.org/10.3390/nano12234194











