Plasmonic Sensing and Switches Enriched by Tailorable Multiple Fano Resonances in Rotational Misalignment Metasurfaces
Abstract
:1. Introduction
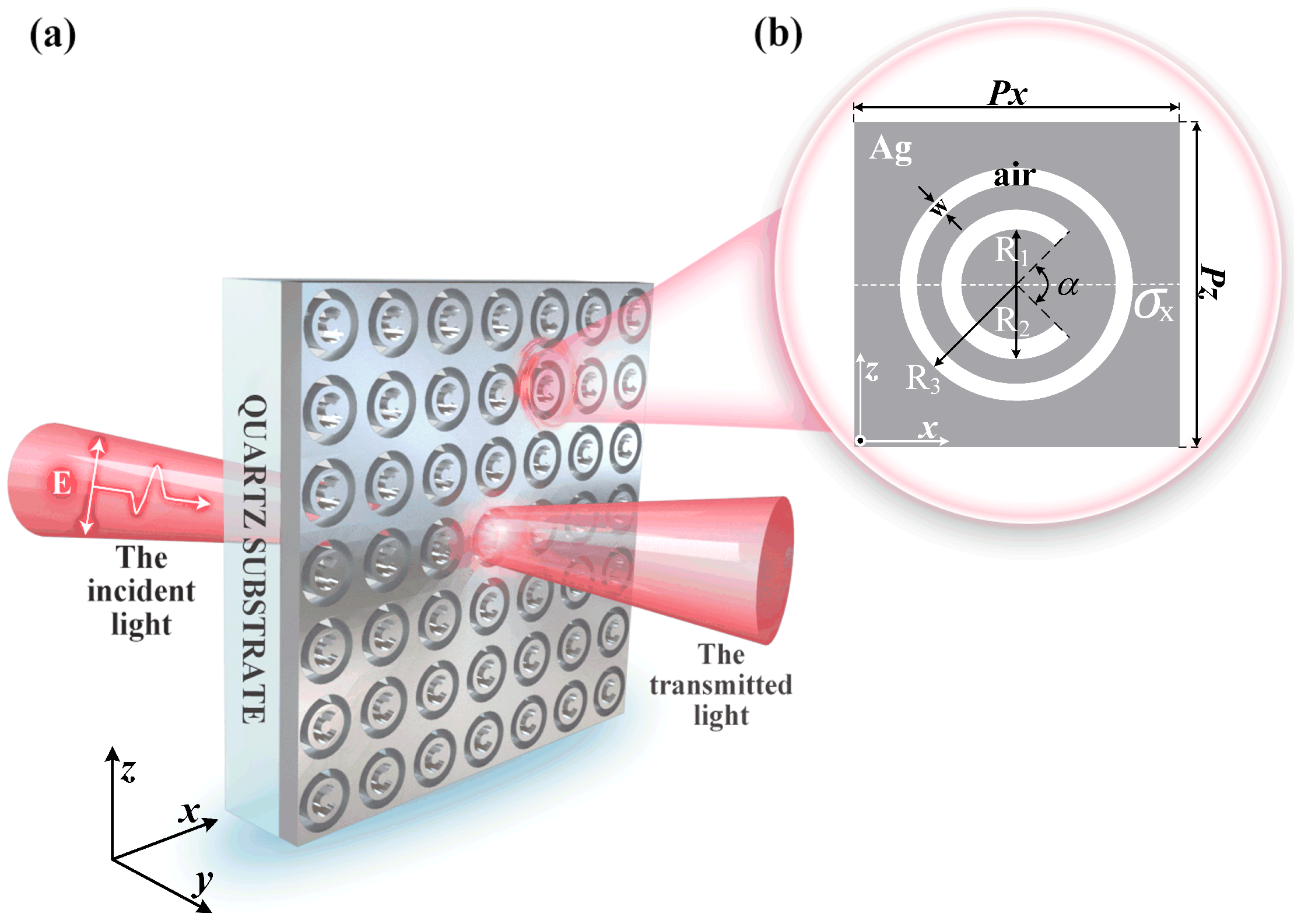
2. Structure and Model
3. Results and Discussion
3.1. Plasmonic Double Fano Resonances in a Hybrid Rotational Misalignment Metasurface
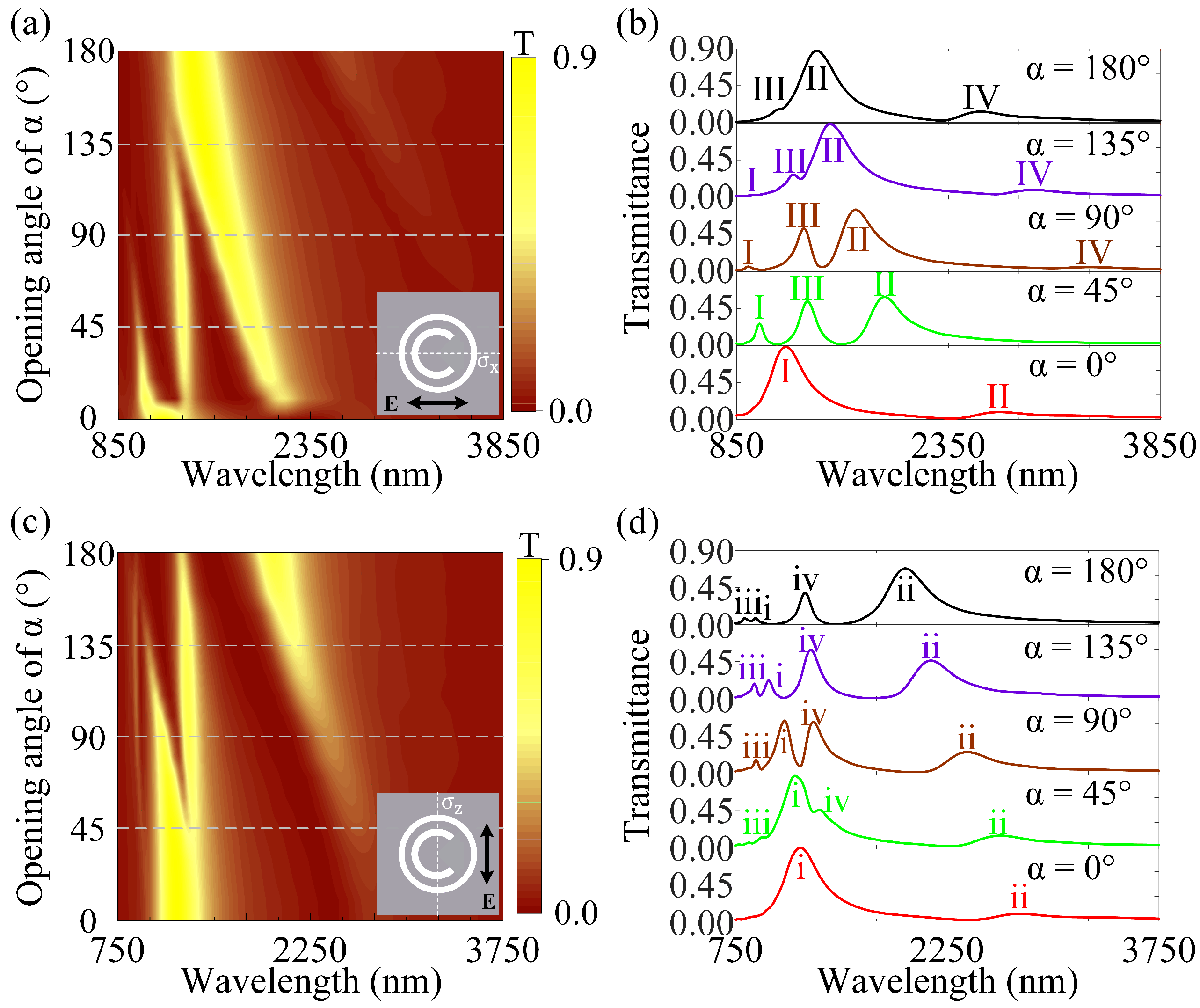
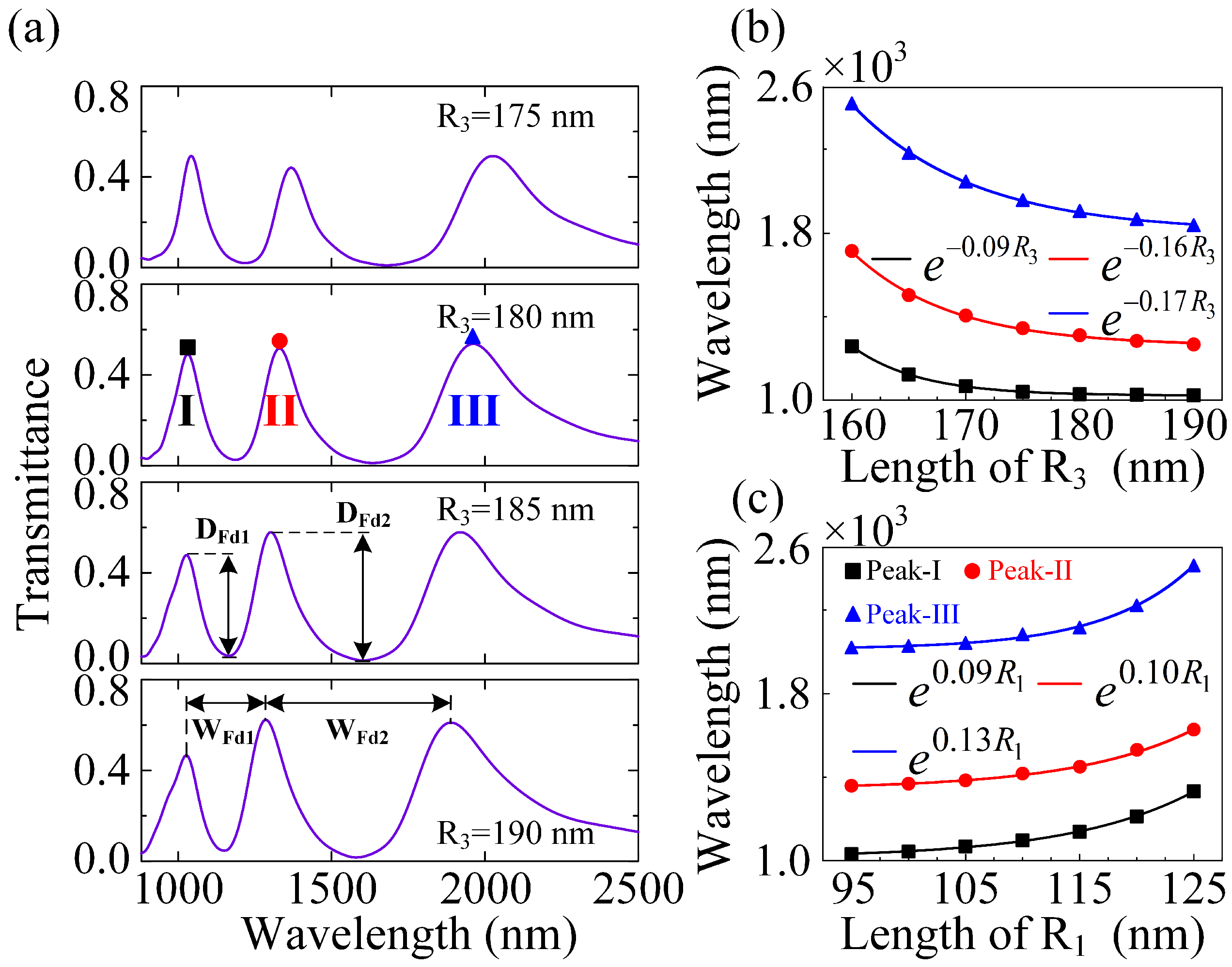
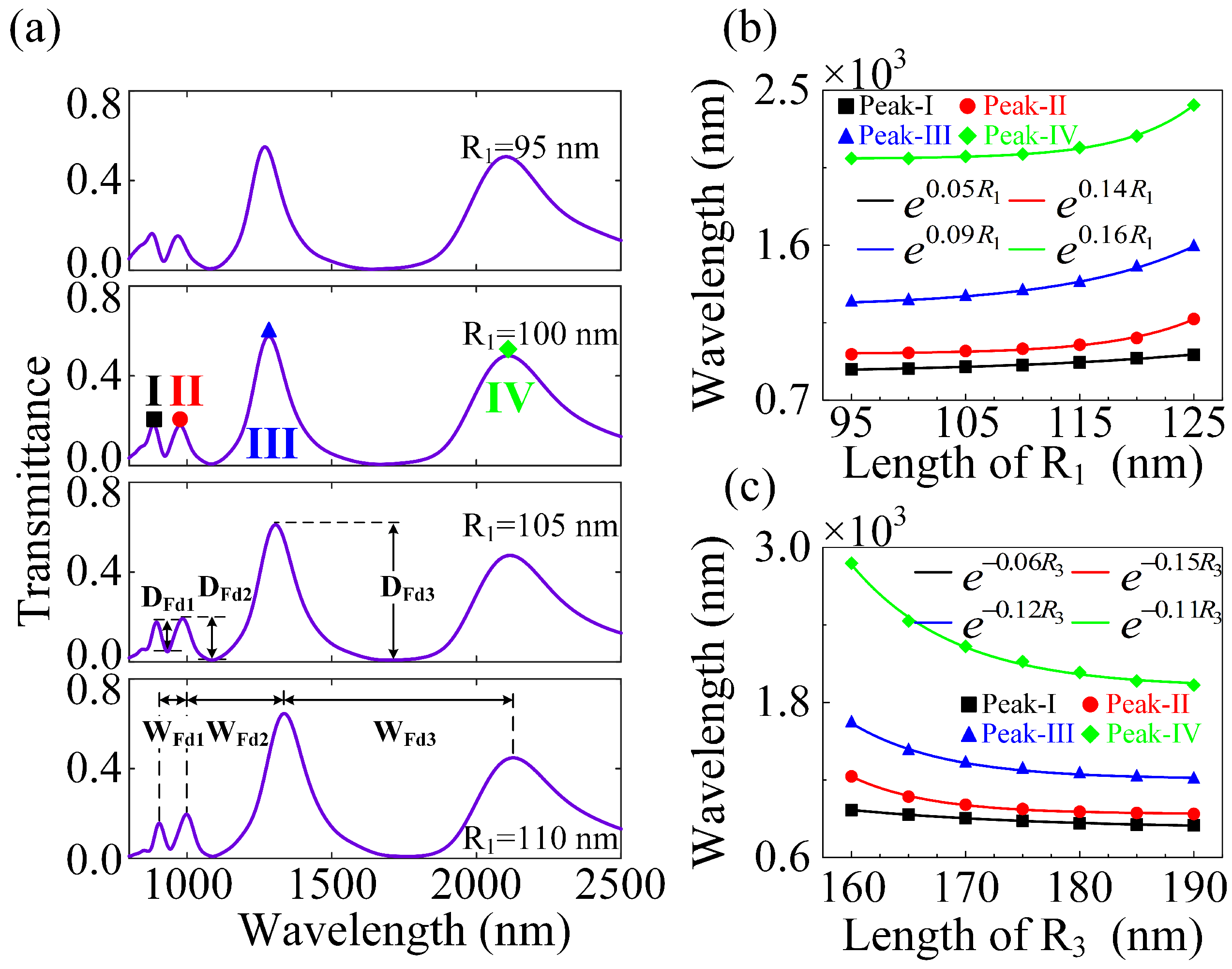
3.2. The Tailorable Plasmonic Multiple FRs with In-Plane Mirror Symmetry or Mirror Asymmetry
3.3. Plasmonic Sensing with In-Plane Mirror Symmetry and Mirror Asymmetry
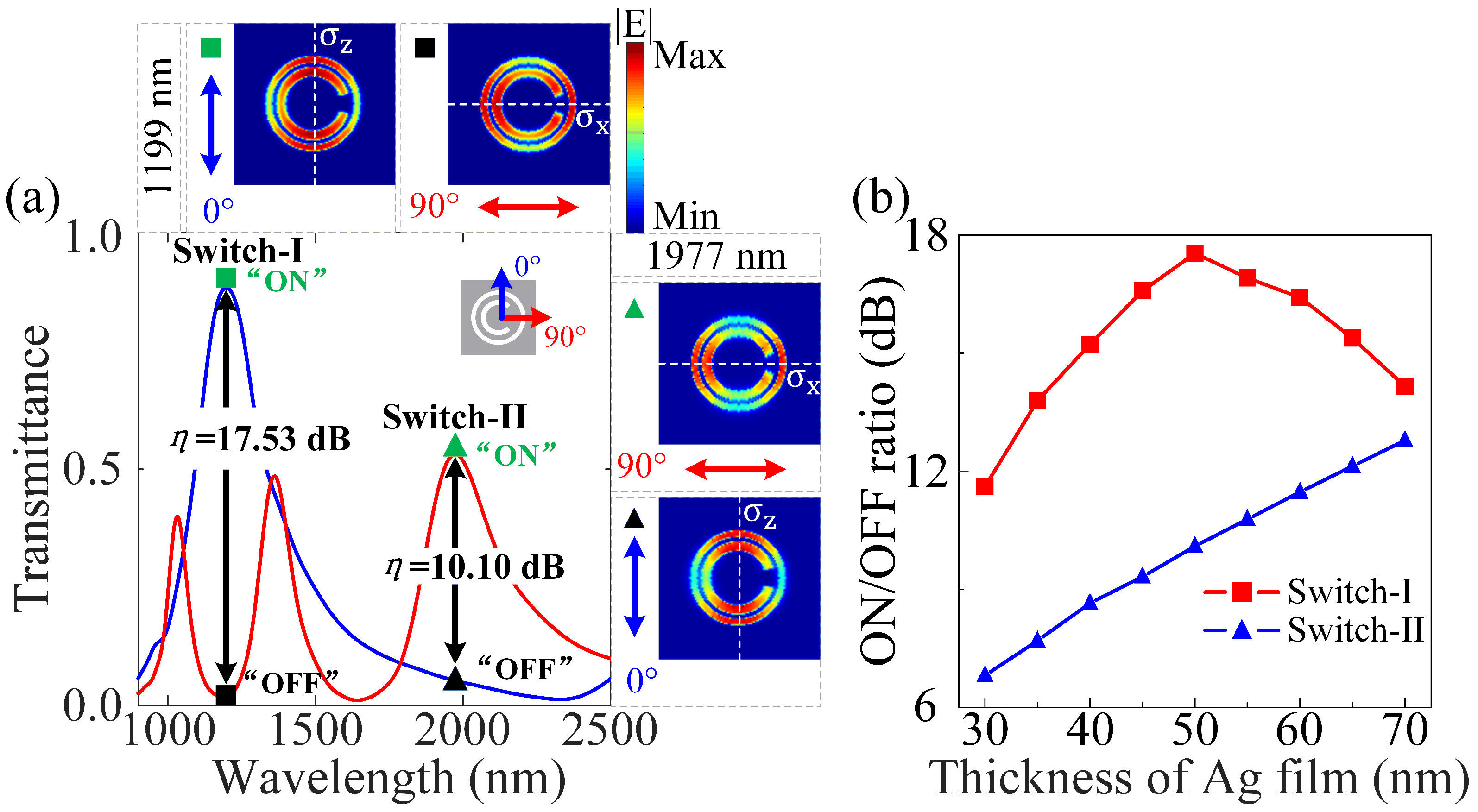
3.4. Dual-Wavelength Plasmonic Switches with In-Plane Mirror Symmetry and Mirror Asymmetry
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 255, 376–379. [Google Scholar] [CrossRef]
- Li, Y.; Kita, S.; Muñoz, P.; Reshef, O.; Vulis, D.I.; Yin, M.; Lončar, M.; Mazur, E. On-chip zero-index metamaterials. Nat. Photonics 2015, 9, 738–742. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.H.; Shao, L.Y. A review on metasurface: From principle to smart metadevices. Front. Phys. 2021, 8, 58087. [Google Scholar] [CrossRef]
- Karimi, E.; Schulz, S.A.; De Leon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light. Sci. Appl. 2014, 3, e167. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Yang, Y.; Badloe, T.; Kim, I.; Yoon, G.; Rho, J. Geometric and physical configurations of meta-atoms for advanced metasurface holography. InfoMat 2021, 3, 739–754. [Google Scholar] [CrossRef]
- Narushima, T.; Hashiyada, S.; Okamoto, H. Nanoscopic study on developing optical activity with increasing chirality for two-dimensional metal nanostructures. ACS Photonics 2014, 1, 732–738. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, J.R. High-Q chiroptical resonances by quasi-bound states in the continuum in dielectric metasurfaces with simultaneously broken in-plane inversion and mirror symmetries. Adv. Opt. Mater. 2021, 9, 2101162. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W.J.; Kong, X.H.; Wu, D.R.; Chu, J.; Qi, C.W. Can weak chirality induce strong coupling between resonant states? Phys. Rev. Lett. 2022, 128, 146102. [Google Scholar] [CrossRef] [PubMed]
- Dou, K.H.; Xie, X.; Pu, M.B.; Li, X.; Ma, X.L.; Wang, C.T.; Luo, G.X. Off-axis multi-wavelength dispersion controlling metalens for multi-color imaging. Opto-Electron. Adv. 2020, 3, 190005. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.F.; Luo, X.Q.; Zhang, J.Z.; Zhu, W.H.; Chen, Z.Y.; Li, T.F.; Liu, W.M.; Wang, X.L. Near-infrared plasmonic sensing and digital metasurface via double Fano resonances. Opt. Express 2022, 30, 5879–5895. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Liu, K.; Liu, N.; Zhu, Z.; Zhang, J. Fano-resonant metasurface with 92% reflectivity based on Lithium Niobate on insulator. Nanomaterials 2022, 12, 3849. [Google Scholar] [CrossRef]
- Cao, G.T.; Dong, S.H.; Zhou, L.M.; Zhang, Q.; Deng, Y.; Wang, C.; Zhang, H.; Chen, Y.; Qiu, C.W.; Liu, X.K. Fano resonance in artificial photonic molecules. Adv. Opt. Mater. 2020, 8, 1902153. [Google Scholar] [CrossRef]
- Luo, X.Q.; Wang, D.L.; Zhang, Z.Q.; Ding, J.W.; Liu, W.M. Nonlinear optical behavior of a four-level quantum well with coupled relaxation of optical and longitudinal phonons. Phys. Rev. A 2011, 84, 033803. [Google Scholar] [CrossRef] [Green Version]
- Cerjan, B.; Gerislioglu, B.; Link, S.; Nordlander, P.; Halas, N.J.; Griep, M.H. Towards scalable plasmonic Fano-resonant metasurfaces for colorimetric sensing. Nanotechnology 2022, 33, 405201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, J.F.; Park, Y.S.; Rho, J.; Singh, R.; Nam, S.; Azad, A.K.; Chen, H.T.; Yin, X.B.; Taylor, A.J.; et al. Photoinduced handedness switching in terahertz chiral metamolecules. Nat. Commun. 2012, 3, 942–948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, J.; Luo, X.Q.; Luo, Y.L.; Zhu, W.H.; Chen, Z.Y.; Liu, W.M.; Wang, X.L. Near-infrared dual-wavelength plasmonic switching and digital metasurface unveiled by plasmonic Fano resonance. Nanophotonics 2021, 10, 947–957. [Google Scholar] [CrossRef]
- Liu, S.D.; Yang, Z.; Liu, R.P.; Li, X.Y. Multiple Fano resonances in plasmonic heptamer clusters composed of split nanorings. ACS Nano 2012, 6, 6260–6271. [Google Scholar] [CrossRef] [PubMed]
- Lassiter, J.B.; Sobhani, H.; Fan, J.A.; Kundu, J.; Capasso, F.; Nordlander, P.; Halas, N.J. Fano resonances in plasmonic nanoclusters: Geometrical and chemical tunability. Nano Lett. 2010, 10, 3184–3189. [Google Scholar] [CrossRef] [PubMed]
- Gu, P.; Guo, Y.H.; Chen, J.; Zhang, Z.X.; Yan, Z.D.; Liu, F.X.; Tang, C.J.; Du, W.; Chen, Z. Multiple sharp Fano resonances in a deep-subwavelength spherical hyperbolic metamaterial cavity. Nanomaterials 2021, 11, 2301. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Lu, X.; Huang, J.; Chen, K.; Su, J.; Yan, Z.; Tang, C.; Cai, P. Double narrow Fano resonances via diffraction coupling of magnetic plasmon resonances in embedded 3D metamaterials for high-quality sensing. Nanomaterials 2022, 11, 3361. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.G.; Xu, Y.; Ji, C.Y.; Chen, S.S.; Li, X.P.; Zhang, X.D.; Yao, Y.G.; Li, J.F. Fano-enhanced circular dichroism in deformable stereo metasurfaces. Adv. Mater. 2020, 32, 1907077. [Google Scholar] [CrossRef]
- Wu, C.H.; Arju, N.; Kelp, G.; Fan, J.A.; Dominguez, J.; Gonzales, E.; Tutuc, E.; Brener, I.; Shvets, G. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat. Commun. 2014, 5, 3892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Besbes, M.; Hugonin, J.P.; Lalanne, P.; Van Haver, S.; Janssen, O.T.; Nugrowati, A.M.; Xu, M.; Pereira, S.F.; Urbach, H.P.; Van de Nes, A.S.; et al. Numerical analysis of a slit-groove diffraction problem. J. Eur. Opt. Soc. Rap. Public 2007, 2, 07022. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Chen, L.; Wang, X.C.; Yao, W.T.; Zhang, Q. Recent advances in noble metal based composite nanocatalysts: Colloidal synthesis, properties, and catalytic applications. Nanoscale 2015, 7, 10559–10583. [Google Scholar] [CrossRef] [PubMed]
- McMahon, J.M.; Henzie, J.; Odom, T.W.; Schatz, G.C.; Gray, S.K. Tailoring the sensing capabilities of nanohole arrays in gold films with Rayleigh anomaly-surface plasmon polaritons. Opt. Express 2007, 15, 18119–18129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhen, F.H.; Chen, Z.Z.; Zhang, J.Z. Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method. IEEE Trans. Microwave Theory Technol. 2000, 48, 1550–1558. [Google Scholar] [CrossRef] [Green Version]
- Chew, W.C.; Liu, Q.H. Perfectly matched layers for elastodynamics: A new absorbing boundary condition. J. Comput. Acous. 1996, 4, 341–359. [Google Scholar] [CrossRef]
- Muravitskaya, A.; Gokarna, A.; Movsesyan, A.; Kostcheev, S.; Rumyantseva, A.; Couteau, C.; Lerondel, G.; Baudrion, A.L.; Gaponenko, S.; Adam, P.-M. Refractive index mediated plasmon hybridization in an array of aluminium nanoparticles. Nanoscale 2020, 12, 6394–6402. [Google Scholar] [CrossRef]
- Zhang, S.P.; Bao, K.; Halas, N.J.; Xu, H.X.; Nordlander, P. Substrate-induced Fano resonances of a plasmonic nanocube: A route to increased-sensitivity localized surface plasmon resonance sensors revealed. Nano Lett. 2011, 11, 1657–1663. [Google Scholar] [CrossRef] [PubMed]
- Piao, X.; Yu, S.; Koo, S.; Lee, K.; Park, N. Fano-type spectral asymmetry and its control for plasmonic metal-insulator-metal stub structures. Opt. Express 2011, 19, 10907–10912. [Google Scholar] [CrossRef]
- Li, S.L.; Wang, Y.L.; Jiao, R.Z.; Wang, L.L.; Duan, G.Y.; Yu, L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt. Express 2017, 25, 3525–3533. [Google Scholar] [CrossRef]
- Wang, J.Y.; Yang, W.M.; Sun, G.Y.; He, Y.L.; Ren, P.W.; Yang, Z.L. Boosting anapole-exciton strong coupling in all-dielectric heterostructures. Photonics Res. 2022, 10, 1744–1753. [Google Scholar] [CrossRef]
- Shi, W.Q.; Gu, J.Q.; Zhang, X.Y.; Xu, Q.; Han, J.G.; Yang, Q.L.; Cong, L.Q.; Zhang, W.L. Terahertz bound states in the continuum with incident angle robustness induced by a dual period metagrating. Photonics Res. 2022, 10, 810–819. [Google Scholar] [CrossRef]
- Lo, C.J.; Aref, T.; Bezryadin, A. Fabrication of symmetric sub-5 nm nanopores using focused ion and electron beams. Nanotechnology 2006, 17, 3264. [Google Scholar] [CrossRef] [Green Version]
- Shi, T.; Deng, Z.L.; Geng, G.Z.; Zeng, Y.X.; Hu, G.W.; Overvig, A.; Li, J.J.; Qiu, C.W.; Alù, A.; Kivshar, Y.S.; et al. Planar chiral metasurfaces with maximal tunable chiroptical response driven by bound states in the continuum. Nat. Commun. 2022, 13, 4111. [Google Scholar] [CrossRef]
- Li, X.F.; Bian, X.Y.; Milne, W.I.; Chu, D.P. Fano resonance engineering in mirror-symmetry-broken thz metamaterials. Appl. Phys. B 2016, 112, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Špačková, B.; Wrobel, P.; Bocková, M.; Homola, J. Optical biosensors based on plasmonic nanostructures: A review. Proc. IEEE 2016, 106, 2380–2408. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Li, B.; Zang, J.; Cao, X.; Zhao, X.; Xue, C. Double Fano Resonance and Independent Regulation Characteristics in a Rectangular-like Nanotetramer Metasurface Structure. Nanomaterials 2022, 12, 3479. [Google Scholar] [CrossRef]
- Chang, W.-S.; Lassiter, J.B.; Swanglap, P.; Sobhani, H.; Khatua, S.; Nordlander, P.; Halas, N.J.; Link, S. A plasmonic Fano switch. Nano Lett. 2012, 12, 4977–4982. [Google Scholar] [CrossRef] [PubMed]
- Gerislioglu, B.; Bakan, G.; Ahuja, R.; Adam, J.; Mishra, Y.K.; Ahmadivand, A. The role of Ge2Sb2Te5 in enhancing the performance of functional plasmonic devices. Mater. Today Phys. 2020, 12, 100178. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.T.; Li, J.N.; Yan, X.; Liang, L.J.; Zhang, Z.; Huang, J.; Li, J.H.; Yang, Y.; Yao, J.Q. Amplitude modulation of anomalously reflected terahertz beams using all-optical active Pancharatnam–Berry coding metasurfaces. Nanoscale 2019, 11, 5746–5753. [Google Scholar] [CrossRef]
- Li, G.-C.; Zhang, Q.; Maier, S.A.; Lei, D.Y. Plasmonic particle-on-film nanocavities: A versatile platform for plasmon-enhanced spectroscopy and photochemistry. Nanophotonics 2018, 7, 1865–1889. [Google Scholar] [CrossRef]
- Genç, A.; Patarroyo, J.; Sancho-Parramon, J.; Bastús, N.G.; Puntes, V.; Arbiol, J. Hollow metal nanostructures for enhanced plasmonics: Synthesis, local plasmonic properties and applications. Nanophotonics 2017, 6, 193–213. [Google Scholar] [CrossRef]
- Kang, L.; Jenkins, R.P.; Werner, D.H. Recent Progress in Active Optical Metasurfaces. Adv. Opt. Mater. 2019, 7, 1801813. [Google Scholar] [CrossRef] [Green Version]
- Gorkunov, M.V.; Antonov, A.A.; Tuz, V.R.; Kupriianov, A.S.; Kivshar, Y.S. Bound States in the Continuum Underpin Near-Lossless Maximum Chirality in Dielectric Metasurfaces. Adv. Opt. Mater. 2021, 9, 2100797. [Google Scholar] [CrossRef]
- Zhang, H.L.; Cao, P.F.; Dou, J.; Cheng, L.; Niu, T.M.; Zhang, G.M. Double-exponential refractive index sensitivity of metal–semiconductor core–shell nanoparticles: The effects of dual-plasmon resonances and red-shift. RSC Adv. 2018, 8, 1700–1705. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Tang, J.; Cheng, Y.; Chen, M.; Wang, H.X.; Xiong, J.F.; Wang, T.R.; Wang, S.Z.; Zhang, Y.D.; Wen, H.; et al. Multifunctional analysis and verification of lightning-type electromagnetic metasurfaces. Opt. Express 2022, 30, 17008–17025. [Google Scholar] [CrossRef]
- Jiang, L.; Huang, Q.; Chiang, K.S. Low-power all-optical switch based on a graphene-buried polymer waveguide Mach-Zehnder interferometer. Opt. Express 2022, 30, 6786–6797. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.; Ramzan, R.; Siddiqui, O. Fano resonance based ultra high-contrast electromagnetic switch. Appl. Phys. Lett. 2017, 110, 181904. [Google Scholar] [CrossRef]
- Chen, F.; Yao, D.Z. Tunable multiple all-optical switch based on multi-nanoresonator-coupled waveguide systems containing kerr material. Opt. Commun. 2014, 312, 143–147. [Google Scholar] [CrossRef]
- Mi, Q.; Sang, T.; Pei, Y.; Yang, C.Y.; Li, S.; Wang, Y.K.; Ma, B. High-quality-factor dual-band Fano resonances induced by dual bound states in the continuum using a planar nanohole slab. Nanoscale Res. Lett. 2021, 16, 150. [Google Scholar] [CrossRef] [PubMed]
- Holsteen, A.; Lin, D.; Kauvar, I.; Wetzstein, G.; Brongersma, M.L. A light-field metasurface for high-resolution single-particle tracking. Nano Lett. 2019, 19, 2267–2271. [Google Scholar] [CrossRef]
- Yang, S.; Hong, C.C.; Jiang, Y.; Ndukaife, J.C. Nanoparticle trapping in a quasi-bic system. ACS Photonics 2021, 8, 1961–1971. [Google Scholar] [CrossRef]
- Tittl, A.; John-Herpin, A.; Leitis, A.; Arvelo, E.R.; Altug, H. Metasurface-based molecular biosensing aided by artificial intelligence. Angew. Chem. Int. Ed. 2019, 58, 14810–14822. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Luo, X.-Q.; Liu, Q.; Li, Y.; Zhu, W.; Chen, Z.; Liu, W.; Wang, X.-L. Plasmonic Sensing and Switches Enriched by Tailorable Multiple Fano Resonances in Rotational Misalignment Metasurfaces. Nanomaterials 2022, 12, 4226. https://doi.org/10.3390/nano12234226
Xu X, Luo X-Q, Liu Q, Li Y, Zhu W, Chen Z, Liu W, Wang X-L. Plasmonic Sensing and Switches Enriched by Tailorable Multiple Fano Resonances in Rotational Misalignment Metasurfaces. Nanomaterials. 2022; 12(23):4226. https://doi.org/10.3390/nano12234226
Chicago/Turabian StyleXu, Xiaofeng, Xiao-Qing Luo, Qinke Liu, Yan Li, Weihua Zhu, Zhiyong Chen, Wuming Liu, and Xin-Lin Wang. 2022. "Plasmonic Sensing and Switches Enriched by Tailorable Multiple Fano Resonances in Rotational Misalignment Metasurfaces" Nanomaterials 12, no. 23: 4226. https://doi.org/10.3390/nano12234226
APA StyleXu, X., Luo, X.-Q., Liu, Q., Li, Y., Zhu, W., Chen, Z., Liu, W., & Wang, X.-L. (2022). Plasmonic Sensing and Switches Enriched by Tailorable Multiple Fano Resonances in Rotational Misalignment Metasurfaces. Nanomaterials, 12(23), 4226. https://doi.org/10.3390/nano12234226




