1. Introduction
When building complex structures, there are a number of additive manufacturing methods available for generating three-dimensional elements on the macro- and microscale. However, with decreasing structure sizes, only a handful of possible techniques remain [
1,
2,
3], such as laser-assisted electrophoretic deposition [
4], electro-chemical printing [
5], or two-/multiphoton polymerization [
6], to name a few [
7,
8]. Another nanoscale technology, capable of depositing advanced objects with feature sizes down to 20 nm under optimized conditions [
9], is focused electron beam-induced deposition (FEBID) [
10]. This increasingly relevant method is capable of creating sophisticated three-dimensional architectures with exceedingly high resolution in a single-step procedure and is thereby a powerful tool for controlled high-precision fabrication of free-standing 3D nanostructures [
11,
12]. Other advantages of this technique include low demands on substrate morphologies and materials, object scalability, and a constantly growing number of available precursors [
13]. The working principle of FEBID is based on the interplay between a precisely controllable, focused electron beam and surface-adsorbed precursor molecules that were injected into the microscope vacuum chamber in a gaseous state. Primary, scattered and especially secondary electrons can trigger dissociation processes of precursor molecules [
14,
15], which immobilizes the non-volatile core components of the molecules, while the volatile parts are diverted by the vacuum pump system. Consequently, the former remain on the surface and form the intended deposit [
16]. The navigation of the electron beam in the XY-plane and the precise adjustment of the dwell times (deposition times in each individual position) ultimately generate the deposit morphology [
17]. Especially 3D-FEBID, where true three-dimensional architectures are built via slow lateral movements, is a very powerful tool that enables novel application concepts for plasmonics [
12], nanomagnetics [
18,
19,
20] and 3D-nanoprobe fabrication for scanning probe microscopy [
21,
22], among others. The technique that was mainly used to build mesh-like structures in the past [
23,
24], was recently expanded to closed or sheet-like objects, which strongly improved its options in terms of design flexibility [
25,
26,
27,
28]. This transition, however, entailed new challenges in terms of growth stability and spatially varying growth rates depending on the object dimensions as well as the position of the deposition point within said structure. Since the most commonly used precursor (MeCpPt
(IV)Me
3) notoriously exhibits rather high carbon contents, due to incomplete dissociation processes, the deposited structures hold low metal contents around
[
29,
30]. This has a tremendous impact on the temperature conditions during the growth process, as the energy brought into the system by the electron beam can only be dissipated towards the substrate through the carbon-dominated material, which is a poor thermal conductor [
28,
31]. This geometry-dependent electron beam heating [
32,
33] leads in turn to an increased desorption of precursor molecules, which slows down the growth rate [
34], leading to non-uniform conditions for deposition, especially for narrow but tall 3D nanostructures. The deviations of the deposited object shapes from originally intended geometries can be compensated to some extent by adjusting the individual dwell times accordingly [
27,
28]. For receiving higher electrical and thermal conductivities [
35] and/or changing the mechanical properties of the material [
36], different post-growth approaches have been introduced, that enable precise modification of the nano-granularity [
37,
38] or even the entire removal of carbon [
29,
30,
39]. This, however, can disrupt the original morphology of the deposited objects. The here relevant post-processing technique is electron beam curing (EBC) [
35,
40], which exposes the grown structures to an electron beam once again, this time, however, without precursor gas present. Effectively, this method proceeds with the dissociation process of incompletely fragmented but incorporated molecules [
13], most likely assisted by residual water molecules in the vacuum as reactants and thermal effects due to electron beam heating. This leads to slightly growing nano-grains, a modification of the carbon matrix and small volume losses due to the formation of volatile fragments upon dissociation [
36,
38]. As unintentional deformations of 3D-FEBID structures, especially pillars, were also observed after imaging and even as a co-process during fabrication in the past [
41], different theories were developed, ascribing the effect to various causes such as mechanical stress, local charging, temperature effects, or chemical modifications [
41,
42]. Following the latter path, the idea of using localized electron beam curing for the targeted deformation of sheet-like 3D architectures arose. Based on that motivation, we tested various parameters and curing pattern dimensions for controlled geometric alterations, such as the bending of vertical walls or other deposited base structures via rectangular curing strips, among others. SEM, TEM and AFM investigations were performed to uncover the underlying EBC processes, verifying the assumption that the inner structure, in terms of grain size, the density of the material and its volume are changed at cured regions. We were able to receive systematic, controlled deformations depending on the primary electron energies, the irradiation dose and the beam incidence angles during curing and substantiate our results with Monte Carlo simulations. This way we even achieved the fabrication of overhanging structures, a geometry that cannot be directly deposited with 3D-FEBID. With these first basic investigations, we open up the range of possible future applications for this post-growth processing technique, potentially even into the direction of functional imprinting or changed oscillation modes, as electron beam cured areas exhibit slightly changed properties compared to as-deposited materials, which could be utilized for various applications in research and development.
2. Results and Discussion
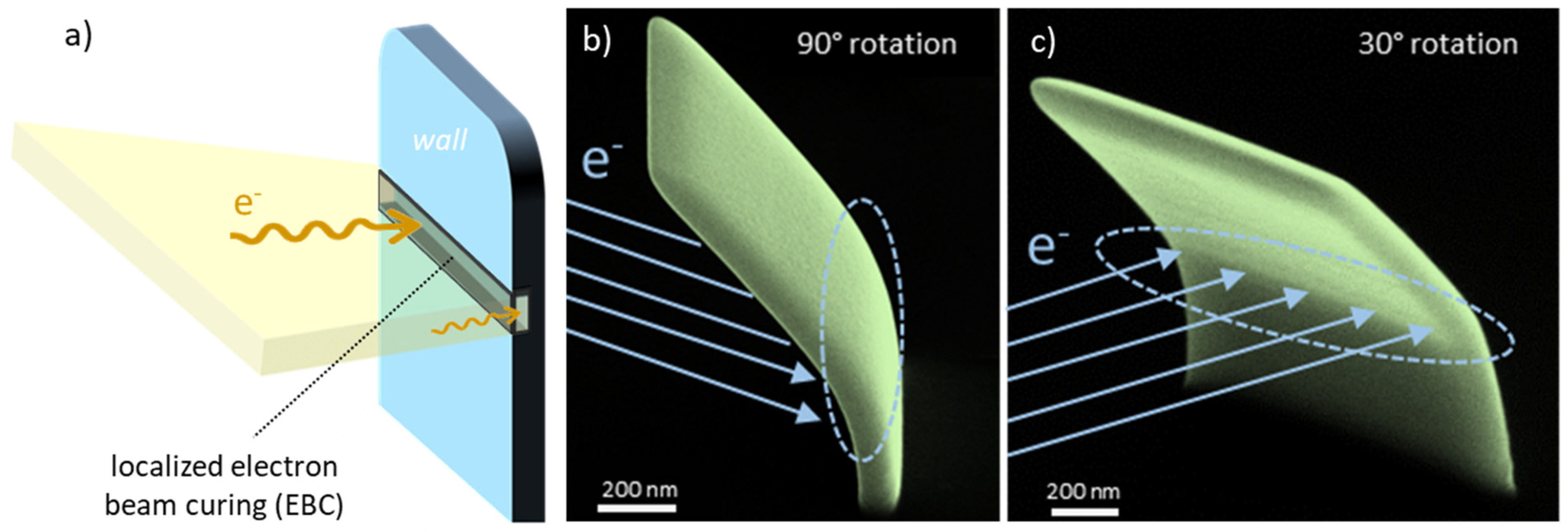
When closed or mesh-like FEBID structures are locally irradiated by electrons, targeted bending via EBC becomes possible, presumably due to structural and volumetric changes caused by reordering processes. To test this behaviour, we deposited vertical wall elements via FEBID and irradiated them again via horizontal patterning strips, as shown by the 3D scheme in
Figure 1a. A representative result is shown in
Figure 1b,c, which provides the proof-of-principle for the here-targeted post-growth deformation process via EBC.
Primary Electron Energies—To identify ideal parameters for reproducible and effective bending via EBC, we first focus on implications of varying primary electron energies
. As a test design, we chose vertical FEBID walls with widths
, heights
and thicknesses
, that were deposited at
and
by using our recently introduced compensation tool [
28]. The bending process was conducted at beam currents of
via patterning arrays of
with constant point pitches of
, dwell times of
,
passes, and an electron beam incidence angle of
, thereby maintaining the same overall doses of 7
. The resulting bending angles
are depicted in
Figure 2a, showing not only a strong
dependency for the formerly observed forward bending process, but also the possibility of backward bending for higher primary electron energies. As evident, the strongest effect for this specific wall thickness was achieved for
and
for forward (green) and backward bending (red), respectively. The reason for this behaviour lies in the spatial distribution of energy deposition according to penetration depths, which leads to structural and volumetric changes not only in the outmost layer, but inside the wall as well. In other words, EBC-affected regions are proposed to contract, which leads to a stress–strain-induced bending effect if these regions are asymmetrically distributed across the wall thickness, as it seems to be ideal for
. For decreasing energies, the affected volumes get too small to induce strong bending, above
, the bending effect also decreases, as penetration depths travel deeper inside the wall, therefore generating a more symmetric stress–strain situation. At
, bending stops entirely, which suggests that EBC is now fully spread across the wall thickness. For even higher energies, EBC travels more and more to the backside, which again induces an asymmetric situation, this time, however, leading to backward deformation. The reason why backward bending is not as efficient is attributed to (1) an increasing number of transmitted electrons, which reduces the EBC effect, and (2) the fact that the scattered electrons spread out over the entire wall thickness, with just a bias towards the backside but with reduced defined asymmetry.
Complementary Monte Carlo simulations with Casino [
43] support the aforementioned assumptions.
Figure 2b compares the electron interaction volumes for four selected primary electron energies, for wall thicknesses of
under a
tilt angle, to illustrate spatial differences. For
(yellow) the electron interaction volume only covers the foremost wall layer, causing weak forward bending, which is also depicted in the related illustration on the right with irradiated wall fractions schematically shown in dark grey. For
(green) strong forward bending occurs, due to the fact that the extent of the interaction volume covers roughly 50% of the wall thickness (as shown in the right-hand side illustration). Primary electron energies of
(blue) lead to interaction volumes that are symmetrically expanded throughout the entire wall thickness. As this is a geometrically balanced process, hardly any deformations are visible in experiments. For
(red) the electron interaction volume is altered to a cone-like shape as the majority of primary electrons pass through the structure and leave on the backside. Even though there is EBC across the entire wall due to stronger spreading of scattering, there is more energy deposition towards the backside of the structure, leading to the aforementioned backward bending effect. The less sharp asymmetry is finally responsible for the weaker bending effect in the backwards direction.
The analysis of a series of simulations for varying
reinforced the results from our experiments, as summarized in
Figure 3. The data compilation shows the varying maximum penetration depths
, with the experimentally found ideal energy of
filled green for (a) primary electrons (PE) and (b) backscattered electrons (BSE), which are also generated during EBC. A closer look into (a) suggests, that an energy of
might be even more suited to achieve a highly symmetric 50:50 cured-uncured situation. However, further effects have to be considered. First, the distribution around the penetration depth maxima has to be taken into account, as shown in (c) for PE by the full-width-half-maximum values as blue shaded part around their peak maxima. As evident,
seems to cover the front half to a far extent, although not entirely. That leads to the second aspect, which is the BSE contributions (full-width-half-maximum values as red shaded area). From
Figure 3b, it becomes evident, that for energies
electrons start to reach into the second half of the wall thickness, which is not ideal for the bending mechanism. Particularly interesting is the contribution of
PEs and BSEs, where the former are mainly found in the back part, while the latter cover the front part, leading to full EBC across the entire wall thickness, without any bending. For a clearer picture in agreement with our model,
Figure 3d depicts the percentage of primary electrons with maximum penetration depths on the anterior
of the wall. As evident, for energies up to
, practically all electrons remain within one half. For 2 keV, which was found as an ideal value during experiments (
Figure 2), a decay to about 90% is found, which will be discussed again later, once the volume loss is quantified. Furthermore, we expect this value to increase when including the impact of backscattered electrons. For higher energies, the percentage is quickly decreasing in agreement with experimental findings.
Concerning the mechanism behind this deformation process, we briefly want to mention possible temperature impacts during EBC. We acknowledge that increased temperatures might trigger additional effects; however, for the given settings, variations of only a few degrees Celsius are expected, according to previous studies [
9,
32]. We therefore assume that temperature implications are not the predominant factor, the bending mechanism suggested here is rather related to volume loss and grain growth effects, which will be investigated in more detail further down.
EBC Dose Variation—After identifying the ideal
ranges, dose variation experiments were conducted, as summarized in
Figure 4. Both, forward (
) as well as backward bending (
), showed exponential saturation trends for increasing doses, which indicates the EBC limits. Hereby, it is noteworthy that low doses are already sufficient for targeted deformation in the forward direction, whereas backward bending only works to a certain extent and needs comparatively long irradiation times and doses. We ascribe this limit to the shape of the electron interaction volumes (compare
Figure 2b), where, for forward bending, curing almost exclusively happens in the front part, whereas for backward bending there is EBC throughout the whole thickness of the walls but with a bias towards the backside, preventing a pure one-sided curing and thereby dampening the maximum possible deformation imbalance within the structures. Also noteworthy is the physical bending limit for forward bending of the structures due to the geometric positioning of the electron beam, which here comes from a tilt angle of 52°. Naturally, backward bending is not limited by geometric conditions as the deformation direction points away from the incoming beam.
Beam Incidence Angles—To explore possible bending implications by varying beam angles
, we have conducted a dedicated study. As the shape of the electron interaction volume and the maximum penetration depths change with the angle in which the electrons intrude the wall surface, significant differences can be found in both, experiments and simulations. Theoretically favourable would be an invasion that is rather flat regarding the structure surface, as in this case the most energy could be introduced in the foremost wall area. In practice, the aforementioned geometrical bending limits have to be considered.
Figure 5a shows experimentally found bending angles of single walls, that have been irradiated at
with a dose of
under different beam incidence angles (black) together with the geometrical limits (blue). As evident, the advantage of more effective bending for lower
-values could only be accessed between
and
, where for lower
-values increasing bending angles can be observed. Below
, the geometrical limits were reached, which intrinsically limits the achievable bending angles. For our further investigations, we continued using a
angle, as the advantages of slightly more effective bending are outweighed by the possibility of being able to reach higher bending angles. The same experiment was performed for adjusted curing pattern heights as well, and thereby for constant projected areas, and almost identical bending angles were received, compared to the ones depicted in
Figure 5a. We do, however, want to mention that the biggest differences between these two variants would be expected for the most gracing incidence angles, which were strongly limited in their bending angles due to inherent, geometrical reasons. Additional studies at beam incidence angles of
did, in fact, show a linear increase in the bending effectivity for larger EBC areas for the same overall doses.
Complementary Monte Carlo electron trajectory simulations in
Figure 5b illustrate the shift to higher maximum penetration depths with increasing beam incidence angles
, using primary electron energies of
. This can be nicely explained when having a look at the electron interaction volumes in
Figure 5c. In contrast to
Figure 2, here, roughly the same volumes are penetrated for different incidence angles. Compared to symmetric 90° incidence angles, the electron interaction volumes for lower
-values are transversely distorted and thereby expand to broader EBC regions and stay within smaller penetration depths. This presumably leads to larger contraction regions on the surface and thereby increases the imbalance leading to stronger controlled bending. In summary, a rather gracing incidence is theoretically favourable, but strongly limits forward bending abilities due to geometrical reasons, making
a practicable compromise.
Finally, we want to comment on the observation, that varying PoPs and DTs for the curing procedure at identical overall doses showed only minor deviations. Details on the implications of these parameters can therefore be found in the first section of the
supporting information with
Figure S1 illustrating the dependency of the bending angles on PoP and DT.
Structural Implications—
Transmission Electron Microscopy—To characterize the inner structure of EBC regions, which were irradiated at
, transmission electron microscopy (
TEM) was performed, with a focus on grain sizes and density variations.
Figure 6a shows a dark-field image of a single pillar, which was locally modified via EBC with a dose of
(see bottom right scheme). As evident, the cured region reveals brighter contrast and slightly larger platinum grains, compared to uncured regions above/below EBC areas, further confirmed by close-ups of the three indicated regions as insets. Measurements of grain size diameters
revealed minor growth of the grain size between uncured regions with
and
and cured regions with
. This is in full agreement with the current understanding of EBC, which first leads to grain growth due to the ongoing dissociation of incompletely fragmented precursor molecules [
44]. The second regime, where the carbon matrix is modified [
22,
36] is not relevant here, as the applied doses are much lower.
Figure 6b shows a freestanding wall, which was electron beam cured by using a vertical patterning strip (see bottom scheme) with a dose of
, leading to a slightly folded and tilted morphology, as shown by the SEM images in rotated side view (c) and top view (d). The central scanning-TEM-based, high angular-annual-darkfield (STEM-HAADF) image reveals a clear contrast variation between cured (red arrow) and uncured areas, which fully verifies the localized EBC effect.
Volume Losses—
Atomic Force Microscopy—After confirming the impact on the nano-granular structures via TEM, we focus on volume loss effects after EBC via atomic force microscopy (
AFM). We deposited flat,
rectangular structures, with
heights, on
substrates. The fundamental idea was for them to mimic horizontal wall structures, to prevent EBC deformations through bending and only observe possible volumetric changes. These pads were then electron beam cured by using 2 keV, identical PoPs/DTs and incidence angles of 52
in relation to the element surface, while varying the doses via the number of passes, to provide comparability for vertical wall studies. A representative 3D AFM image after high-dose EBC is shown in
Figure 7a, which immediately confirms the assumed volume loss at the curing site. Extracted height profiles showed the monotonous dependency of the volume loss on EBC doses (
Figure 7b), where height decreases of more than
between as-deposited and cured structures were observed. The figure also shows that for curing strips of
width, the rectangular base structures were altered over a width of
due to the extent of the interaction volumes for inclined electron beams, as discussed before.
Figure 7c shows the height loss more clearly, which follows an exponential trend that approaches a certain maximum. This is in full agreement with the observed limit for achievable bending angles (compare
Figure 4) and with the underlying theory of an ongoing dissociation, which, at some point, has to stop, once fragmentation in the exposed volume is completed. In the following, we studied the height loss for varying
at a constant dose of
, which revealed a clear maximum around
, as evident in
Figure 7d. The overall trend is qualitatively similar to the initial bending experiments, presented in
Figure 2a, which suggests that the volume loss itself is strongly involved as originally assumed. However, we want to mention, that the results for higher energies, presented in
Figure 7d, have to be taken with care, as volume loss effects in the lower half could lead to a delamination from the substrate, which cannot be accessed via AFM. Finally, we analysed the mean roughness of the surfaces on different areas of partially cured structures. Measurements of the mean surface roughness
revealed similar values for uncured (
) and cured areas (
), while being widely independent of EBC energies and doses. In conclusion, the here confirmed volume loss is qualitatively similar to energy- and dose-dependencies for initial bending experiments and fits well into the general model.
Advanced EBC—As an expansion to the aforementioned curing procedures, more advanced base elements were deposited via FEBID and exposed to various EBC patterns.
Figure 8a shows a screw-like structure with a constant width of
and a height of
, that was deposited as a twisted vertical base structure. Two rectangular curing strips at the marked spots created the pictured shape with two visible kinks. This way, an already deposited structure with a comparatively simple geometry could be altered to a desired, more sophisticated shape. In
Figure 8b, a sheet-like diamond structure was irradiated within a centrally located circular area, as indicated. A symmetric contraction of the geometry around the curing site was observed, while leaving the angle of the structure foundation unaltered, which can be seen particularly clear in the bottom left inset depicting a side view of the structure. Even though the architectures mentioned in (a) and (b) already constitute important achievements in how localized EBC can be applied, it would theoretically be possible to deposit these structures with direct-write 3D-FEBID alone, although challenging in its reliable calculation and with a strongly increased effort in compiling the geometry construction files.
Figure 8c, on the other hand, shows a way how EBC as a post-deposition deformation tool opens up completely new possibilities for FEBID structures. We thereby used a base structure, consisting of an inclined wall and a short vertical element on top, which was then bent against its inclination direction, via multiple rectangular curing strips from top to bottom, until a strongly overhanging geometry was achieved. The originating shape represents an entirely new kind of shape, that cannot be built by 3D-FEBID alone in a vertical, direct-write deposition process.