Superfluorescence of Sub-Band States in C-Plane In0.1Ga0.9N/GaN Multiple-QWs
Abstract
1. Introduction
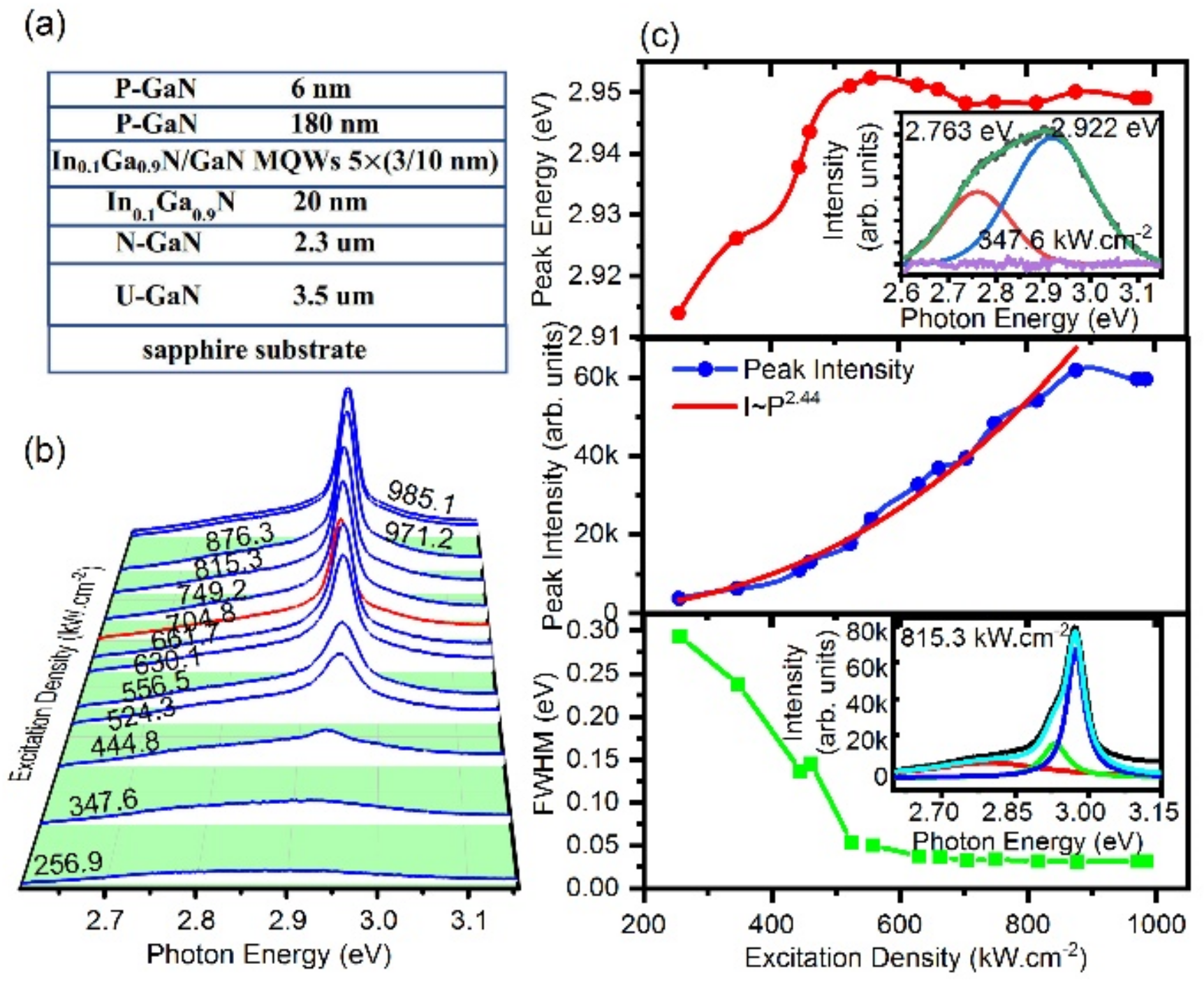
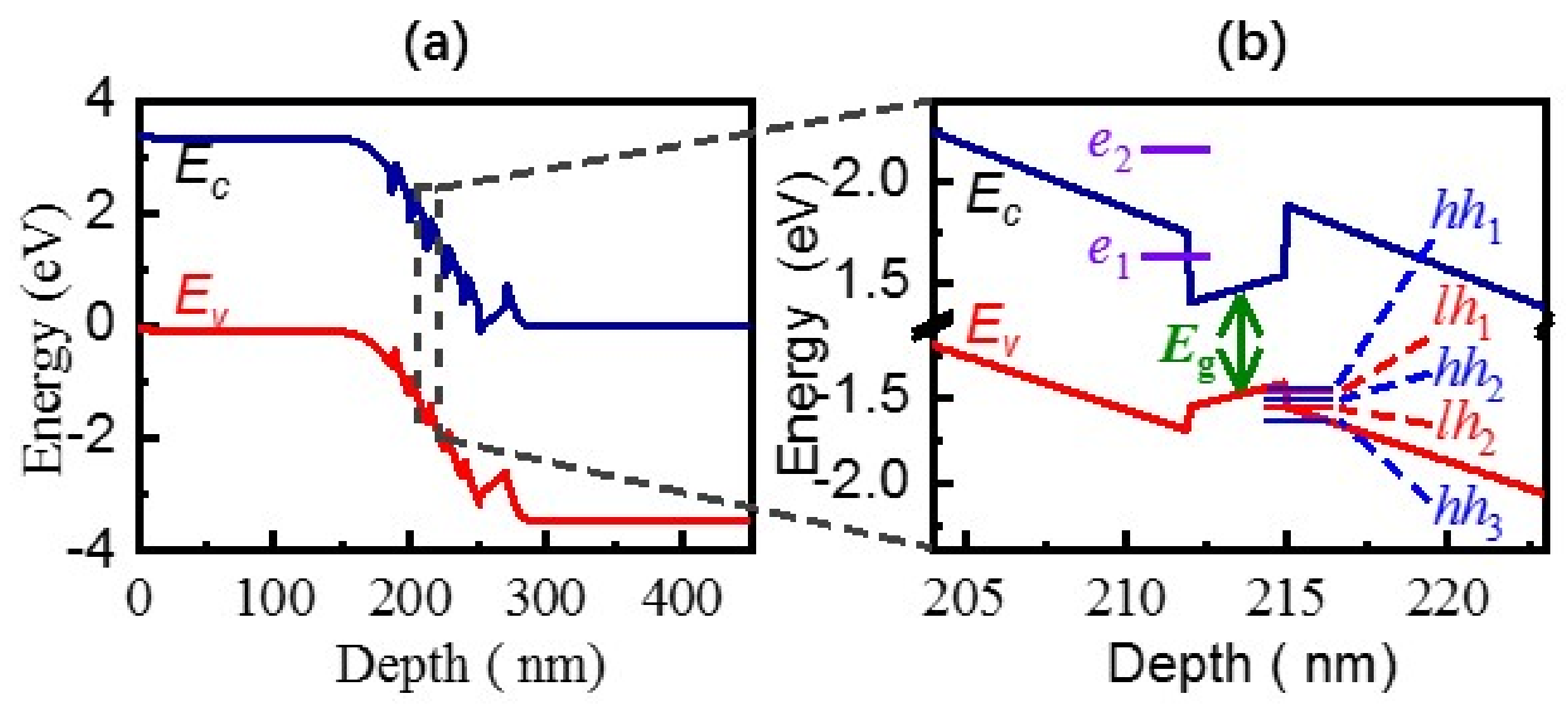
2. Materials and Methods
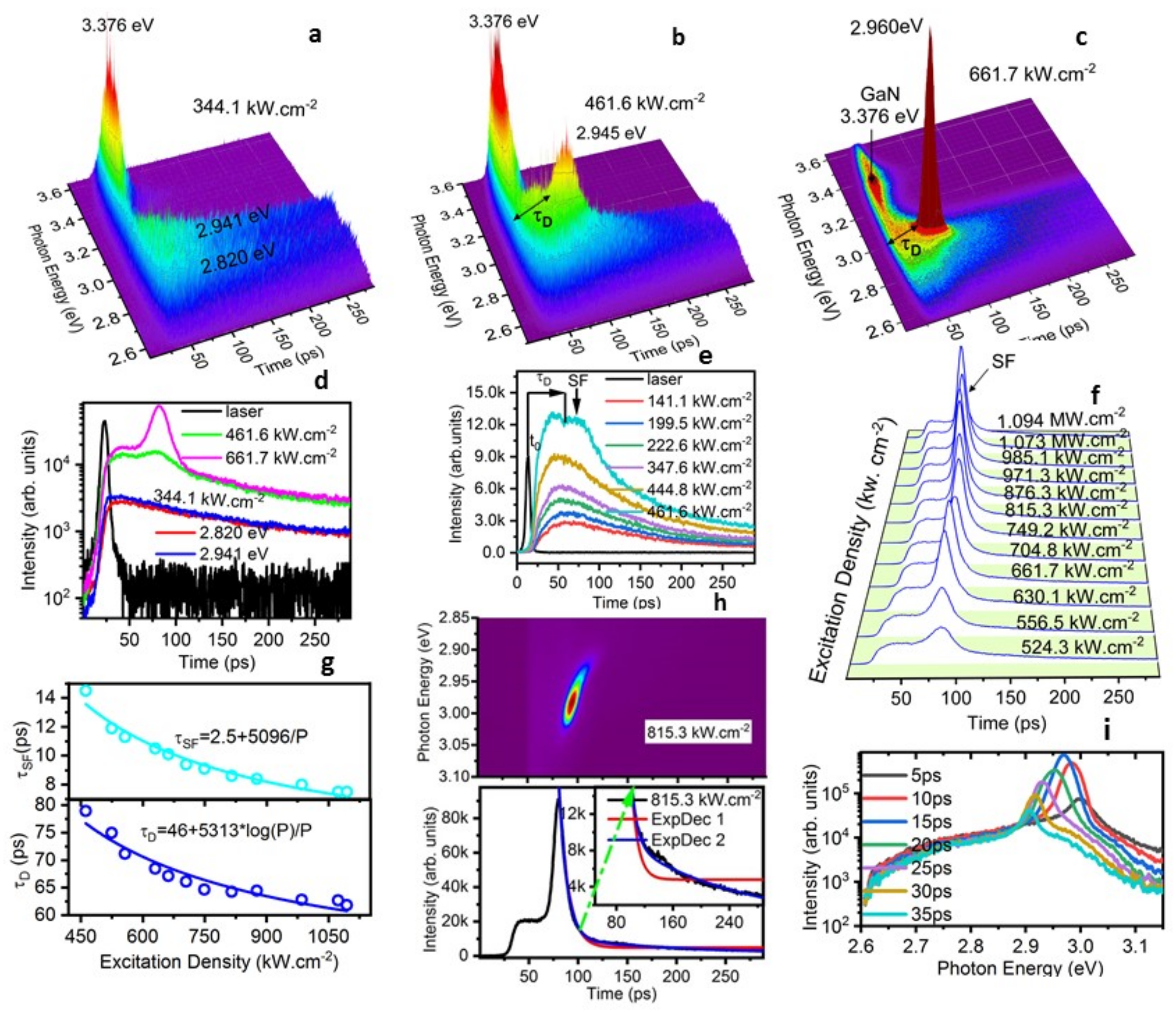
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brasser, C.; Bruckbauer, J.; Gong, Y.; Jiu, L.; Bai, J.; Warzecha, M.; Edwards, P.R.; Wang, T.; Martin, R.W. Cathodoluminescence studies of chevron features in semi-polar (1122)InGaN/GaN multiple quantum well structures. J. Appl. Phys. 2018, 123, 174502–174506. [Google Scholar] [CrossRef]
- Ryu, H.Y.; Ryu, G.H.; Onwukaeme, C.; Ma, B. Temperature dependence of the Auger recombination coefficient in InGaN/GaN multiple-quantum-well light-emitting diodes. Opt. Express 2020, 28, 27459–27472. [Google Scholar] [CrossRef] [PubMed]
- Chow, Y.C.; Lee, C.; Wong, M.S.; Wu, Y.R.; Nakamura, S.J.; Denbaars, S.P.; Bowers, J.E.; Speck, J.S. Dependence of carrier escape lifetimes on quantum barrier thickness in InGaN/GaN multiple quantum well photodetectors. Opt. Express 2020, 28, 23796–23805. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.H.; Liu, G.; Lee, C.; Alkhazragi, O.; Wagstaff, J.M.; Li, K.H.; Alhawaj, F.; Ng, T.K.; Speck, J.S.; Nakamura, S.; et al. Semipolar (2021) InGaN/GaN micro-photodetector for gigabit-per-second visible light communication. Appl. Phys. Express 2020, 13, 014001–014005. [Google Scholar] [CrossRef]
- Tanner, D.S.P.; McMahon, J.M.; Schulz, S. Interface Roughness, Carrier Localization, and Wave Function Overlap in c-Plane (In,Ga)N/GaN Quantum Wells: Interplay of Well Width, Alloy Microstructure, Structural Inhomogeneities, and Coulomb Effects. Phys. Rev. Appl. 2018, 10, 034027–034045. [Google Scholar] [CrossRef]
- Christian, G.M.; Schulz, S.; Kappers, M.J.; Humphreys, C.J.; Oliver, R.A.; Dawson, P. Recombination from polar InGaN/GaN quantum well structures at high excitation carrier densities. Phys. Rev. B 2018, 98, 155301–155309. [Google Scholar] [CrossRef]
- Poltavtsev, S.V.; Solovev, I.A.; Akimov, I.A.; Chaldyshev, V.V.; Lundin, W.V.; Sakharov, A.V.; Tsatsulnikov, A.F.; Yakovlev, D.R.; Bayer, M. Long coherent dynamics of localized excitons in (In,Ga)N/GaN quantum wells. Phys. Rev. B 2018, 98, 195315–195320. [Google Scholar] [CrossRef]
- Kazazis, S.A.; Papadomanolaki, E.; Iliopoulos, E. Tuning carrier localization in In-rich InGaN alloys: Correlations between growth kinetics and optical properties. J. Appl. Phys. 2020, 127, 225701–225711. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Kelleher, J.C.; O’Brien, M.R.; O’Reilly, E.P.; Schulz, S. Electronic structure of semiconductor nanostructures: A modified localization landscape theory. Phys. Rev. B 2020, 101, 035430–035441. [Google Scholar] [CrossRef]
- Suski, T.; Staszczak, G.; Korona, K.P.; Lefebvre, P.; Monroy, E.; Drozdz, P.A.; Muzioł, G.; Skierbiszewski, C.; Kulczykowski, M.; Matuszewski, M.; et al. Switching of exciton character in double InGaN/GaN quantum wells. Phys. Rev. B 2018, 98, 165302–165313. [Google Scholar] [CrossRef]
- Vito, A.D.; Pecchia, A.; Carlo, A.D.; Auf der Maur, M. Impact of Compositional Nonuniformity in (In,Ga)N-Based Light-Emitting Diodes. Phys. Rev. Appl. 2019, 12, 014055–014061. [Google Scholar] [CrossRef]
- Aleksiejūnas, R.; Nomeika, K.; Kravcov, O.; Nargelas, S.; Kuritzky, L.; Lynsky, C.; Nakamura, S.; Weisbuch, C.; Speck, J.S. Impact of Alloy-Disorder-Induced Localization on Hole Diffusion in Highly Excited c-Plane and m-Plane (In,Ga)N Quantum Wells. Rev. Appl. 2020, 14, 054043–054053. [Google Scholar] [CrossRef]
- Callsen, G.; Butté, R.; Grandjean, N. Probing Alloy Formation Using Different Excitonic Species: The Particular Case of InGaN. Phys. Rev. 2019, 9, 031030–031049. [Google Scholar] [CrossRef]
- Pashartis, C.; Rubel, O. Localization of Electronic States in III-V Semiconductor Alloys: A Comparative Study. Phys. Rev. Appl. 2017, 7, 064011–064022. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Eliseev, P.G.; Perlin, P.; Lee, J.; Osiński, M. Blue temperature-induced shift and band-tail emission in InGaN-based light sources. Appl. Phys.Lett. 1997, 71, 569–571. [Google Scholar] [CrossRef]
- Cho, Y.-H.; Gainer, G.H.; Fischer, A.J.; Song, J.J.; Keller, S.; Mishra, U.K.; DenBaars, S.P. “S-shaped” temperature-dependent emission shift and carrier dynamics in InGaN/GaN multiple quantum wells. Appl. Phys. Lett. 1998, 73, 1370–1372. [Google Scholar] [CrossRef]
- Dawson, P.; Schulz, S.; Oliver, R.A.; Kappers, M.J.; Humphreys, C.J. The nature of carrier localisation in polar and nonpolar InGaN/GaN quantum wells. J. Appl. Phys. 2016, 119, 181505. [Google Scholar] [CrossRef]
- Feng, S.W.; Liao, P.-H.; Leung, B.; Han, J.; Yang, F.-W.; Wang, H.-C. Efficient carrier relaxation and fast carrier recombination of N-polar InGaN/GaN light emitting diodes. J. Appl. Phys. 2015, 118, 043104–043108. [Google Scholar] [CrossRef]
- Wang, T.; Bai, J.; Sakai, S.; Ho, J.K. Investigation of the emission mechanism in InGaN/GaN-based light-emitting diodes. Appl. Phys. Lett. 2001, 78, 2617–2619. [Google Scholar] [CrossRef]
- Alam, S.; Sundaram, S.; Elouneg-Jamroz, M.; Li, X.; Gmili, Y.E.; Robin, I.C.; Voss, P.L.; Salvestrini, J.-P.; Ougazzaden, A. InGaN/InGaN multiple-quantum-well grown on InGaN/GaN semi-bulk buffer for blue to cyan emission with improved optical emission and efficiency droop. Superlattice. Microst. 2017, 104, 291–297. [Google Scholar] [CrossRef]
- Damilano, B.; Gil, B. Yellow–red emission from (Ga,In)N heterostructures. J. Phys. D Appl. Phys. 2015, 48, 403001. [Google Scholar] [CrossRef]
- Ponce, F.A.; Bour, D.P. Nitride-based semiconductors for blue and green light-emitting devices. Nature 1997, 386, 351–359. [Google Scholar] [CrossRef]
- Wu, F.; Lin, Y.D.; Chakraborty, A.; Ohta, H.; DenBaars, S.P.; Nakamura, S.; Speckv, J.S. Stacking fault formation in the long wavelength InGaN/GaN multiple quantum wells grown on -plane GaN. Appl. Phys. Lett. 2010, 96, 231912. [Google Scholar] [CrossRef]
- Takeuchi, T.; Sota, S.; Katsuragawa, M.; Komoriv, M.; Takeuchi, H.; Amano, H.; Akasaki, I. Quantum-Confined Stark Effect due to Piezoelectric Fields in GaInN Strained Quantum Wells. Jpn. J. Appl. Phys. 1997, 36, L382–L385. [Google Scholar] [CrossRef]
- Wang, T.; Parbrook, P.J.; Fan, W.H.; Fox, A.M. Optical investigation of multiple-quantum wells under high excitation. Appl. Phys. Lett. 2004, 84, 5159–5161. [Google Scholar] [CrossRef]
- Sun, G.; Xu, G.; Ding, Y.J.; Zhao, H.; Liu, G.; Zhang, J.; Tansu, N. Investigation of fast and slow decays in InGaN/GaN quantum wells. Appl. Phys. Lett. 2011, 99, 081104. [Google Scholar] [CrossRef][Green Version]
- Schulz, T.; Nirschl, A.; Drechsel, P.; Nippert, F.; Markurt, T.; Albrecht, M.; Hoffmann, A. Recombination dynamics in InxGa1−xN quantum wells—Contribution of excited subband recombination to carrier leakage. Appl. Phys. Lett. 2014, 105, 181109. [Google Scholar] [CrossRef]
- Xing, Y.; Zhao, D.; Jiang, D.; Liu, Z.; Zhu, J.; Chen, P.; Yang, J.; Liang, F.; Liu, S.; Zhang, L. Carrier Redistribution Between Two Kinds of Localized States in the InGaN/GaN Quantum Wells Studied by Photoluminescence. Nanoscale Res. Lett. 2019, 14, 88–95. [Google Scholar] [CrossRef]
- Wang, T.; Parbrook, P.J.; Whitehead, M.A.; Fanc, W.H.; Fox, A.M. Study of stimulated emission from InGaN/GaN multiple quantum well structures. J. Cryst. Growth 2004, 273, 48–53. [Google Scholar] [CrossRef]
- Ichimiya, M.; Watanabe, M.; Ohata, T.; Hayashi, T.; Ishibashi, A. Effect of uniaxial stress on photoluminescence in GaN and stimulated emission in InxGa1-xN/GaN multiple quantum wells. Phys. Rev. B 2003, 68, 035328–035334. [Google Scholar] [CrossRef]
- Minj, A.; Romero, M.F.; Wang, Y.; Tuna, Ö.; Feneberg, M.; Goldhahn, R.; Schmerber, G.; Ruterana, P.; Giesen, C.; Heuken, M. Stimulated emission via electron-hole plasma recombination in fully strained single InGaN/GaN heterostructures. Appl. Phys. Lett. 2016, 109, 221106–221110. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Xing, Y.; Yang, D.; Yu, J.; Hao, Z.; Sun, C.; Xiong, B.; Han, Y.; Wang, J.; et al. Consistency on Two Kinds of Localized Centers Examined from Temperature-Dependent and Time-Resolved Photoluminescence in InGaN/GaN Multiple Quantum Wells. ACS Photonics 2017, 4, 2078–2084. [Google Scholar] [CrossRef]
- Morel, A.; Lefebvre, P.; Kalliakos, S.; Taliercio, T.; Bretagnon, T.; Gil, B. Donor-acceptor-like behavior of electron-hole pair recombinations in low-dimensional (Ga,In)N/GaN systems. Phys. Rev. B 2003, 68, 045331–045336. [Google Scholar] [CrossRef]
- Brosseau, C.-N.; Perrin, M.; Silva, C.; Leonelli, R. Carrier recombination dynamics in InxGa1−xN/GaN multiple quantum wells. Phys. Rev. B 2010, 82, 085305–085309. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Shribanowitz, N.; Herman, I.P.; MacGillivray, J.C.; Feld, M.S. Observation of Dicke Superradiance in Optically Pumped HF Gas. Phys. Rev. Lett. 1973, 30, 309–312. [Google Scholar] [CrossRef]
- Rainò, G.; Becker, M.A.; Bodnarchuk, M.I.; Mahrt, R.F.; Kovalenko, M.V.; Stöferle, T. Superfluorescence from lead halide perovskite quantum dot superlattices. Nature 2018, 563, 671–675. [Google Scholar] [CrossRef]
- Dai, D.C.; Monkman, A.P. Observation of superfluorescence from a quantum ensemble of coherent excitons in a ZnTe crystal: Evidence for spontaneous Bose-Einstein condensation of excitons. Phys. Rev. B 2011, 84, 115206–115213. [Google Scholar] [CrossRef]
- Cong, K.; Zhang, Q.; Wang, Y.; Noe, G.T.; Belyanin, A.; Kono, J. Dicke superradiance in solids [Invited]. J. Opt. Soc. Am. B 2016, 33, C80. [Google Scholar] [CrossRef]
- Bonifacio, R.; Lugiato, L.A. Cooperative radiation processes in two-level systems: Superfluorescence. Phys. Rev. A 1975, 11, 1507–1521. [Google Scholar] [CrossRef]
- Heinzen, D.J.; Thomas, J.E.; Feld, M.S. Coherent Ringing in Superfluorescence. Phys. Rev. Lett. 1985, 54, 677–680. [Google Scholar] [CrossRef] [PubMed]
- Kuraptsev, A.S.; Sokolov, I.M. Many-body cooperative effects in an ensemble of pointlike impurity centers near a charged conductive surface. Phys. Rev. A 2019, 100, 063836. [Google Scholar] [CrossRef]
- Kuokstis, E.; Yang, J.W.; Simin, G.; Khan, M.A.; Gaska, R.; Shur, M.S. Two mechanisms of blueshift of edge emission in InGaN-based epilayers and multiple quantum wells. Appl. Phys. Lett. 2002, 80, 977–979. [Google Scholar] [CrossRef]
- Aleksiejunas, R.; Gelzinyte, K.; Nargelas, S.; Jarasiunas, K.; Vengris, M.; Armour, E.A.; Byrnes, D.P.; Arif, R.A.; Lee, S.M.; Papasouliotis, G.D. Diffusion-driven and excitation-dependent recombination rate in blue InGaN/GaN quantum well structures. Appl. Phys. Lett. 2019, 104, 022114–022117. [Google Scholar] [CrossRef]
- Holmes, M.J.; Choi, K.; Kako, S.; Arita, M.; Arakawa, Y. Room-Temperature Triggered Single Photon Emission from a III-Nitride Site-Controlled Nanowire Quantum Dot. Nano Lett. 2014, 14, 982–986. [Google Scholar] [CrossRef]
- Broeck, D.D.; Bharrat, D.; Hosalli, A.M.; El-Masry, N.A.; Bedair, S.M. Strain-balanced InGaN/GaN multiple quantum wells. Appl. Phys. Lett. 2014, 105, 031107. [Google Scholar] [CrossRef]
- Xu, G.; Sun, G.; Ding, Y.J.; Zhao, H.; Liu, G.; Zhang, J.; Tansu, N. Investigation of large Stark shifts in InGaN/GaN multiple quantum wells. J. Appl. Phys. 2013, 113, 033104–044108. [Google Scholar] [CrossRef]
- Carvalho, L.C.; Schleife, A.; Bechstedt, F. Influence of exchange and correlation on structural and electronic properties of AlN, GaN, and InN polytypes. Phys. Rev. B 2011, 84, 195105. [Google Scholar] [CrossRef]
- Kim, J.H.; Noe, G.T., II; McGill, S.A.; Wang, Y.; Wójcik, A.K.; Belyanin, A.A.; Kono, J. Fermi-edge superfluorescence from a quantum-degenerate electron-hole gas. Sci. Rep. 2013, 3, 3283–3289. [Google Scholar] [CrossRef]
- Mattar, F.P.; Gibbs, H.M.; McCall, S.L.; Feld, M.S. Transverse Effects in Superfluorescence. Phys. Rev. Lett. 1981, 46, 1123–1126. [Google Scholar] [CrossRef]
- Schuurmans, M.F.H.; Vrehen, Q.H.F.; Polder, D. Superfluorescence. Adv. Atom. Mol. Phys. 1981, 17, 167–228. [Google Scholar]
- Klingshirn, C.F. Semiconductor Optics; Springer: Berlin/Heidelberg, Germany, 1997; Chapter 22; p. 339. [Google Scholar]
- Belyani, A.; Kono, J. Superfluorescence from photoexcited semiconductor quantum wells: Magnetic field, temperature, and excitation power dependence. Phys. Rev. B 2015, 91, 235448–235457. [Google Scholar]
- Hahn, W.; Lentali, J.-M.; Polovodov, P.; Young, N.; Nakamura, S.; Speck, J.S.; Weisbuch, C.; Filoche, M.; Wu, Y.-R.; Piccardo, M.; et al. Evidence of nanoscale Anderson localization induced by intrinsic compositional disorder in InGaN/GaN quantum wells by scanning tunneling luminescence spectroscopy. Phys. Rev. B 2018, 98, 045305–045309. [Google Scholar] [CrossRef]
- Steel, D.G.; Wang, H. Dephasing of optically induced excitonic coherences in semiconductor Heterostructures. Appl. Phys. A 2000, 71, 519–524. [Google Scholar] [CrossRef][Green Version]
- Poltavtsev, S.V.; Kosarev, A.N.; Akimov, I.A.; Yakovlev, D.R.; Sadofev, S.; Puls, J.; Hoffmann, S.P.; Albert, M.; Meier, C.; Meier, T.; et al. Time-resolved photon echoes from donor-bound excitons in ZnO epitaxial layers. Phys. Rev. B 2017, 96, 035203–035207. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, C.; Lv, Z.; Zeng, X.; Zhang, B. Superfluorescence of Sub-Band States in C-Plane In0.1Ga0.9N/GaN Multiple-QWs. Nanomaterials 2022, 12, 327. https://doi.org/10.3390/nano12030327
Ding C, Lv Z, Zeng X, Zhang B. Superfluorescence of Sub-Band States in C-Plane In0.1Ga0.9N/GaN Multiple-QWs. Nanomaterials. 2022; 12(3):327. https://doi.org/10.3390/nano12030327
Chicago/Turabian StyleDing, Cairong, Zesheng Lv, Xueran Zeng, and Baijun Zhang. 2022. "Superfluorescence of Sub-Band States in C-Plane In0.1Ga0.9N/GaN Multiple-QWs" Nanomaterials 12, no. 3: 327. https://doi.org/10.3390/nano12030327
APA StyleDing, C., Lv, Z., Zeng, X., & Zhang, B. (2022). Superfluorescence of Sub-Band States in C-Plane In0.1Ga0.9N/GaN Multiple-QWs. Nanomaterials, 12(3), 327. https://doi.org/10.3390/nano12030327





